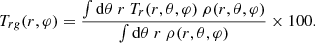EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) L3 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number L3
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202141892
Published online 08 October 2021

© ESO 2021

1. Introduction

Since their discovery in the 1970s, coronal mass ejections (CMEs) and their interplanetary counterpart (ICME) have been a main topic for the heliophysics and the space weather community, being the most prominent transient structures in the heliosphere. ICMEs drive disturbances in the interplanetary medium and they are the only structures capable of producing extreme geomagnetic storms (Kilpua et al. 2017; Luhmann et al. 2020). Although often ambiguous (Richardson & Cane 2010), the identification of ICMEs by 1 AU in situ measurements is possible thanks to certain signatures, which are generally detected in the parameters and distinguishable from the typical values of the ambient solar wind. These include stronger magnetic fields, enhanced plasma densities and speeds, lower proton temperatures, and suprathermal electron beams (Kilpua et al. 2017; Richardson & Cane 2010; Gosling et al. 1987; Zwickl et al. 1983). In addition, anomalies in the chemical composition and high charge states are often observed during ICME events. These signatures are of particular importance as they offer the possibility to directly observe material coming from the innermost layers of the solar atmosphere, inferring pre-eruption conditions (Rodriguez et al. 2016).

One of the major open problems with ICMEs is understanding how the plasma properties observed in situ that are far from the Sun are related with those of the plasma originating in the inner corona (typically observed with remote sensing data) and/or to the subsequent interplanetary evolution and possible interaction with the interplanetary medium. This is also connected to the problem of understanding the chemical composition of ICME plasma and charge state distribution, a problem that must be addressed with numerical models alone (e.g. Lynch et al. 2011) or in combination with multi-spacecraft observations (e.g. Gruesbeck et al. 2011; Reinard et al. 2012). Moreover, tracing the chemical composition of solar phenomena is a very important issue in general, as the Sun is a very dynamic system, where the plasma is continuously remixed and its chemical composition can change locally with height (from the photosphere to the corona, e.g. Feldman 1992), geographically (active versus quiet regions and solar wind, e.g. Landi & Testa 2015), and temporally (for instance during flares and eruptions, e.g. Lepri & Rivera 2021; Brooks & Yardley 2021). Spectroscopy usually provides important information about element abundances (e.g. Lee & Raymond 2012), and it has been used, for instance, to track the presence of solar energetic particles (SEP) in ICMEs (Brooks & Yardley 2021), but in situ measurements would represent the best solution for directly measuring the composition of solar mass transported by ICMEs close to Earth. Studying the chemical composition of ICME plasma allows one to trace back its origin on the different layers of the solar atmosphere, also taking advantage of the so-called first ionisation potential (FIP) effect (see recent review by Song & Yao 2020).

In order to describe the possible mixing of the CME plasma accurately with the ambient medium, it is crucial to reconstruct the ambient background condition of the heliospheric plasma since these conditions determine the interplanetary evolution of CMEs (see van der Holst et al. 2007; Maloney & Gallagher 2010; Vršnak et al. 2013; Temmer & Nitta 2015) and the propagation of solar energetic particle streams (e.g. He et al. 2011). Heliospheric magnetohydrodynamics (MHD) codes such as ENLIL (Odstrcil & Pizzo 2009), EUHFORIA (Pomoell & Poedts 2018), and SUSANOO (Shiota & Kataoka 2016) are currently able to provide real-time forecasting of the space-weather conditions from the Sun to 1 AU and beyond. Nevertheless, the ability of these models to reconstruct the ambient conditions of the interplanetary plasma is still limited (see e.g. Jian et al. 2016), and this, for instance, has consequences on the reliability of solar disturbances forecasting (Riley et al. 2018). Finer details have been shown to be reproduced by a recent approach (Biondo et al. 2021, more details in the following).

In this work we use this approach to model the propagation of a CME reliably in the heliosphere. We also show that the CME plasma does not disperse and mostly maintains its composition as it crosses Earth’s orbit, and we discuss to what extent we can expect the measured composition tracks to back the original one.

2. The model

The Reverse In-situ and MHD Approach (RIMAP) (details in Biondo et al. 2021) is aimed to bind MHD simulations of interplanetary medium to direct measurements of plasma parameters measured in situ at the distance of 1 AU. RIMAP combines, for the first time, the well known ballistic back-mapping approach (Schatten et al. 1968; Wilcox 1968) with a time-dependent MHD numerical simulation performed with the state-of-art PLUTO code (Mignone et al. 2007, 2012). It provides a method to reconstruct the real-time conditions of interplanetary plasma from the Sun to 1 AU and beyond, preserving the smaller-scale density and velocity inhomogeneities dragged by the solar wind. The computational grid used extends from 21.5 R⊙ (≈0.1 AU) up to 236.5 R⊙ (≈1.1 AU) in the radial direction and covers the entire longitudinal interval, while the latitudinal aperture is restricted to 2° centred around π/2. The time-dependent MHD equations are solved in a 3D spherical coordinate system corotating with the solar equator. The grid used has 256 cells in the radial direction (uniform with six cells up to 24.5 R⊙ and then stretched with 250 cells up to the outer boundary), eight cells in the latitudinal direction, and 768 in the longitudinal one, both angular grids uniform. We used the conservative approach to maximise the conditions of CME plasma mixing with the interplanetary medium in the ecliptic plane. Accordingly, we chose to describe an ejected cloud with no internal magnetic flux rope that is embed in the ambient magnetic field (non-MC ICME, Kilpua et al. 2017) and to assume that in the early phase the angular width and the velocity of the perturbation remain constant. The initial ICME can then be described by an ice-cream cone model (e.g., Zhao et al. 2002; Xie et al. 2004; Xue et al. 2005; Gopalswamy et al. 2009; Na et al. 2017): a homogeneous plasma cloud, isotropic in expansion and with radial bulk velocity. The small number of input parameters needed by CME cone models make them particularly convenient for routine applications in space weather forecasting (Scolini et al. 2018) despite the drawback of not including an internal magnetic field.

The kinematic parameters of a cone-modelled ICME are determined by its angular width ω and radial speed vICME (Xie et al. 2004). Assuming a nearly circular cross section, the ICME can be thought of (before entering the computational domain) as a spheroid pushed at a constant speed, and it enters at the 0.1 AU inner boundary as a time-dependant boundary condition (e.g. Odstrčil & Pizzo 1999; Pomoell & Poedts 2018). The angle subtended by the spheroid with the inner boundary surface during its passage is 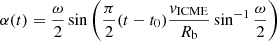, where Rb is the radius of the inner boundary and t0 is the onset time of insertion into the domain. Furthermore, α(t) is used to determine which cells on the longitudinal axis of the inner radial boundary belong to the ICME: if (φ − φ0)2 ≤ α(t)2 holds true, the background solar wind parameters are replaced with the perturbation ones. The model assumes that the ICME plasma cloud propagates homogeneously before entering the simulation domain. The velocity vICME at each point is therefore parallel to the purely radial velocity of the cells found at the longitude corresponding to the insertion φ0, and therefore it has latitudinal and longitudinal components that are non-zero and dependent on θ and φ. The number density and plasma temperature inside the ICME are also homogeneous, with values chosen close to the average event ones during solar cycle 23 and 24 (Gopalswamy et al. 2014, see Table 1).

Table 1.

ICME input parameters at 0.1 AU.

Finally, an artificial, passive scalar is added to the ICME model and used as a tracer of the CME plasma flow because it is simply advected and interacts in no way with the physical quantities of the model. Before the insertion time t0, this tracer is null throughout the computational domain. After t0, all the cells satisfying Δφ2 ≤ α(t)2, that is within the CME cone, are filled with 1. During the evolution, the tracer can flow in and out of each grid cell of the simulation domain, thus attaining a mixing with the background plasma at the grid length scale.

3. Model results

The background condition of the interplanetary Parker spiral for the ICME simulation is reconstructed by RIMAP using plasma parameters measured by Wind in 2009 between March 3 and March 29 (Biondo et al. 2021), around the minimum of solar activity cycle 23. Even if this time frame was chosen due to its relatively calm solar wind conditions, the RIMAP-reconstructed Parker spiral is highly structured in its longitudinal variability (Fig. 1), offering diverse conditions to the ICME propagation. At t0 = 0, the cloud enters the inner radial boundary at a longitude of φ0 = 112.5° at the location of a relatively high-density streamline (arrow in Fig. 1). This means that we are addressing the impact of an ICME on a dense, slow stream that may result in the interplanetary formation of geo-effective disturbances. The parameters are in Table 1.

thumbnail Fig. 1.

Contour (99%) of the ICME tracer mass (white) on colour maps of plasma number density and radial velocity at the labelled time of the MHD simulation (see text for details). The coloured diamonds (φ = 85°, 73.8°, 65°) show the position of three virtual spacecrafts, which would detect the time profiles in Fig. 2. The black arrow indicates the entry point of the ICME into the inner boundary. See online animation.

Figure 1 shows ecliptic maps of plasma density and radial speed in a frame co-rotating with the solar equator at a time in which the ICME has propagated from the insertion point at 0.1 AU almost to the outer domain boundary (1.1 AU). Even if the cloud is homogeneous in density and speed before entering the inner radial boundary, it is soon stretched and slowed down by the interaction with the interplanetary medium. The speed drops to less than 500 km s−1 at 1 AU and the CME trajectory has been deflected from being the purely radial. This deceleration to the ambient speed of solar wind is a common feature in observed ICME events (Kilpua et al. 2017; Gopalswamy et al. 2000; Lindsay et al. 1999) and simulated ones (e.g. Manchester et al. 2014). In the early stages of the propagation, a compression front forms ahead of the cloud and develops an internal structure due to the inhomogeneity of the background solar wind streams. In particular, from day 1 onward, the right edge of this front begins to detach from the rest and at t = 2.5 days it forms a separate blob. At the same time, behind the front, the cloud is expanding, its density decreases, and a void forms, where density is one-tenth of the ambient one at 1 AU.

In Fig. 1 the contours of the passive tracer Tr measure the mixing of the original perturbation plasma with the perturbed ambient plasma. Its mass percentage is calculated as

(1)

In Fig. 1 each white contour bounds the area where 99% of the tracer mass is contained and interestingly shows that, in spite of the interaction with the different arms of the Parker spiral, the original material of the ICME remains compact behind the front as a single coherent structure, and it is more co-spatial with the velocity CME field (green ‘island’ in the bottom panel). This result may have important implications regarding the chemical composition of ICME plasma measured with in situ data.

In Fig. 1 we mark three locations at 1 AU, which are along the ICME path and also in solar wind streams with different properties. In order to study how the ICME passage affects in situ measurements, we analyse the evolution of the plasma parameters and magnetic field at these locations as a function of time. This mimics the configuration in which multiple spacecrafts detect the interplanetary plasma at different locations along Earth’s orbit and/or along the CME passage. The red diamond (hereafter, position A) is taken where the tracer has its maximum on the domain, that is where there is the largest percentage of original ICME plasma at the time when the perturbation has moved to 1 AU. The blue diamond (position B) is an intermediate distance between the ICME centre and its boundaries (at 1 AU). The black diamond (position C) falls almost outside of the outer ICME contour line of the tracer and it is hit only marginally by the perturbation front.

Figure 2 shows the time profiles (from top to bottom) of the plasma density, tracer mass percentage, radial speed, total pressure, and the radial and longitudinal magnetic field, taken from the MHD simulation that would be measured at position A (red), B (blue), and C (black) lines. All quantities are averaged on the latitudinal domain.

thumbnail Fig. 2.

Time profiles of number density, percentage of tracer, radial speed, pressure, and radial and longitudinal component of the magnetic field at three different 1-AU positions, A (red), B (blue), and C (black), marked in Fig. 1. Here the ICME enter time is t0 = 0.

Approximately 2.5 days after the insertion time, a rapid increase in the density, pressure, speed, and magnetic field is detected at 1 AU in A, B, and C, marking the beginning of the ICME event. Plasma density reaches a higher peak value (∼40 cm−3) at position B, which is somewhat later than at positions A and C. This happens because, as can be seen in the animation attached to Fig. 1, the perturbation front which hits position B is more compressed against a high density stream, while at position A the front has travelled through more tenuous streams and thus accumulated less plasma. Position C is just outside of the cloud boundaries and on the trajectory of the region where the front has split into two, and there we see only a small and short-lasting bump of a few cm−3, all before t = 3 days, followed by a longer-lasting slight decrease back to the unperturbed ambient value at t = 5 days. The density bump lasts much less than 1 day at all positions. The total pressure shows similar and simultaneous bumps. After the bump, we still see a density perturbation in the form of a broad dip, which brings the density down to about 0 at position B and C, and it lasts about 1 day or more.

Interestingly, the tracer evolution shows a significantly delayed bump at positions A and even more at C, and almost no change at position B. The tracer peak at position A tells us that there, about 80% of the plasma consists of the original ICME plasma. On the other hand, this peak takes place later than the peak of total density, when the density is already steeply decreasing, that is, in the tail of the perturbation. At position C, the fraction of original ICME plasma has a much lower peak (∼30%), and this occurs even later, close to the density dip. Overall, while position A is close to the ICME core and rich in original ICME mass, and while C is intermediate, position B is still significantly perturbed, yet devoid of a tracer. Contrary to common sense, we clearly see that the original CME plasma is well detached from the compression front moving ahead of it, which is visible in the density and pressure plots, and it instead permeates the void behind it.

The radial speed shows a much longer-lasting bump, quite similar at the three positions. In both A and C, the plasma speed jumps by ∼150 − 200 km s−1 from their pre-event values up to to ∼450 − 500 km s−1, and it remains at these speeds for most of the two days of the perturbation. As Fig. 1 shows, the perturbation is quite homogeneous in velocity even at 1 AU and despite being just outside of the bulk of the ICME, C still shows a velocity jump similar to A and B. On the other hand, at position B, the perturbation hits higher density wind streams and decelerates more rapidly to the pre-event value in about 1 day.

As mentioned before, the total pressure shows sharp peaks similar to the density ones, up to about 180 pPa, lasting less than one day, while in C the bump is much smaller, up to only about 60 pPa. This is consistent with the fact that A and B are directly hit by the full perturbation front, while in C the front is attenuated by the interaction with the denser wind stream.

Despite the starting cloud having no internal magnetic flux rope, the simulated ICME perturbs the magnetic configuration at 1 AU, as shown by the Br and Bφ profiles. Both components show significant fluctuations, significantly out of phase and significantly different at the three positions, which is evidence of a strong distortion and compression of the field lines.

4. Conclusions

In this work, with the RIMAP-MHD model (Biondo et al. 2021), we simulate the propagation of an ICME inside a background solar wind reconstructed reliably from the measurements acquired in situ around the minimum of solar activity cycle 23. The original ICME plasma is tracked by using a passive tracer, and its arrival at 1 AU is sampled in situ by virtual spacecrafts located at three different longitudes. We show that, although the complex interaction with multiple fast and slow wind streams leads to ICME non-uniform deceleration and deformation, the original ICME bubble remains compact and is not eroded, thus preserving its chemical composition. On the other hand, the perturbation front is almost entirely composed of interplanetary plasma compressed during its propagation against the pre-ICME background. These results have a potential impact on the interpretation of multi-spacecraft observations of solar eruptive phenomena.

This work sheds some light on how CMEs observed near the Sun evolve, becoming ICMEs that are detected in interplanetary space. In the past, after some first attempts by using test particles (Riley et al. 1997; Odstrčil & Pizzo 1999), a real particle tracking method was applied to a MHD simulation of an ICME, for instance, by Riley et al. (2008). In that work, it was shown that in the interplanetary evolution, the counterpart of the CME front is buried within the sheath material of the ICME, which formed by upstream solar wind plasma swept up by the CME. However, using a tracer for which we describe the advection in the MHD code instead of sampling particles, we can provide a quantitative analysis of this effect. We find that only a very small fraction of the original CME plasma is present in the compression front, but also that this fraction can rise up to about 80% at other locations and times during the event. Our modelling thus confirms that strong variations of chemical composition measured at 1 AU can directly trace back, at least in part, to the original CME composition.

More recently, Brooks & Yardley (2021) have identified the source region of the energetic particles during an eruption. Again, our model corroborates and explains those findings as it shows that the ICME can maintain a distinguished chemical composition during its motion in the interplanetary space with a limited mixing of the plasma.

Movie

Movie 1 associated with Fig. 1 (n_v) Access here

Acknowledgments

This work acknowledges support from ASI/INAF Solar Orbiter contract n. 2018-30-HH.0 and from the Italian Ministero dell’Università e della Ricerca (MUR).

References

  1. Biondo, R., Bemporad, A., Mignone, A., & Reale, F. 2021, J. Space Weather Space Clim., 11, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Brooks, D. H., & Yardley, S. L. 2021, Sci. Adv., 7, eabf0068 [NASA ADS] [CrossRef] [Google Scholar]
  3. Feldman, U. 1992, Phys. Scr., 46, 202 [CrossRef] [Google Scholar]
  4. Gopalswamy, N., Lara, A., Lepping, R. P., et al. 2000, Geophys. Res. Lett., 27, 145 [NASA ADS] [CrossRef] [Google Scholar]
  5. Gopalswamy, N., Dal Lago, A., Yashiro, S., & Akiyama, S. 2009, Cent. Eur. Astrophys. Bull., 33, 115 [Google Scholar]
  6. Gopalswamy, N., Akiyama, S., Yashiro, S., et al. 2014, Geophys. Res. Lett., 41, 2673 [NASA ADS] [CrossRef] [Google Scholar]
  7. Gosling, J. T., Baker, D. N., Bame, S. J., et al. 1987, J. Geophys. Res.: Space Phys., 92, 8519 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gruesbeck, J. R., Lepri, S. T., Zurbuchen, T. H., & Antiochos, S. K. 2011, ApJ, 730, 103 [NASA ADS] [CrossRef] [Google Scholar]
  9. He, H. Q., Qin, G., & Zhang, M. 2011, ApJ, 734, 74 [NASA ADS] [CrossRef] [Google Scholar]
  10. Jian, L. K., MacNeice, P. J., Mays, M. L., et al. 2016, Space Weather, 14, 592 [CrossRef] [Google Scholar]
  11. Kilpua, E., Koskinen, H. E. J., & Pulkkinen, T. I. 2017, Liv. Rev. Sol. Phys., 14, 5 [Google Scholar]
  12. Landi, E., & Testa, P. 2015, ApJ, 800, 110 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lee, J.-Y., & Raymond, J. C. 2012, ApJ, 758, 116 [CrossRef] [Google Scholar]
  14. Lepri, S. T., & Rivera, Y. J. 2021, ApJ, 912, 51 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lindsay, G. M., Luhmann, J. G., Russell, C. T., & Gosling, J. T. 1999, J. Geophys. Res.: Space Phys., 104, 12515 [NASA ADS] [CrossRef] [Google Scholar]
  16. Luhmann, J., Gopalswamy, N., Jian, L. K., & Lugaz, N. 2020, Sol. Phys., 295, 61 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lynch, B. J., Reinard, A. A., Mulligan, T., et al. 2011, ApJ, 740, 112 [NASA ADS] [CrossRef] [Google Scholar]
  18. Maloney, S. A., & Gallagher, P. T. 2010, ApJ, 724, L127 [NASA ADS] [CrossRef] [Google Scholar]
  19. Manchester, W. B., IV, Kozyra, J. U., Lepri, S. T., & Lavraud, B. 2014, J. Geophys. Res.: Space Phys., 119, 5449 [Google Scholar]
  20. Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
  21. Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
  22. Na, H., Moon, Y., & Lee, H. 2017, ApJ, 839, 82 [CrossRef] [Google Scholar]
  23. Odstrcil, D., & Pizzo, V. J. 2009, Sol. Phys., 259, 297 [Google Scholar]
  24. Odstrčil, D., & Pizzo, V. J. 1999, J. Geophys. Res.: Space Phys., 104, 483 [NASA ADS] [CrossRef] [Google Scholar]
  25. Pomoell, J., & Poedts, S. 2018, J. Space Weather Space Clim., 8, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Reinard, A. A., Lynch, B. J., & Mulligan, T. 2012, ApJ, 761, 175 [NASA ADS] [CrossRef] [Google Scholar]
  27. Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
  28. Riley, P., Gosling, J. T., & Pizzo, V. J. 1997, J. Geophys. Res., 102, 14677 [NASA ADS] [CrossRef] [Google Scholar]
  29. Riley, P., Lionello, R., Mikić, Z., & Linker, J. 2008, ApJ, 672, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  30. Riley, P., Mays, M. L., Andries, J., et al. 2018, Space Weather, 16, 1245 [NASA ADS] [CrossRef] [Google Scholar]
  31. Rodriguez, L., Masías-Meza, J. J., Dasso, S., et al. 2016, Sol. Phys., 291, 2145 [Google Scholar]
  32. Schatten, K. H., Ness, N. F., & Wilcox, J. M. 1968, Sol. Phys., 5, 240 [NASA ADS] [CrossRef] [Google Scholar]
  33. Scolini, C., Verbeke, C., Poedts, S., et al. 2018, Space Weather, 16, 754 [NASA ADS] [CrossRef] [Google Scholar]
  34. Shiota, D., & Kataoka, R. 2016, Space Weather, 14, 56 [NASA ADS] [CrossRef] [Google Scholar]
  35. Song, H., & Yao, S. 2020, Sci. China E: Technol. Sci., 63, 2171 [Google Scholar]
  36. Temmer, M., & Nitta, N. V. 2015, Sol. Phys., 290, 919 [NASA ADS] [CrossRef] [Google Scholar]
  37. van der Holst, B., Jacobs, C., & Poedts, S. 2007, ApJ, 671, L77 [NASA ADS] [CrossRef] [Google Scholar]
  38. Vršnak, B., Žic, T., Vrbanec, D., et al. 2013, Sol. Phys., 285, 295 [Google Scholar]
  39. Wilcox, J. M. 1968, Space Sci. Rev., 8, 258 [NASA ADS] [CrossRef] [Google Scholar]
  40. Xie, H., Ofman, L., & Lawrence, G. 2004, J. Geophys. Res.: Space Phys., 109, 3109 [NASA ADS] [CrossRef] [Google Scholar]
  41. Xue, X. H., Wang, C. B., & Dou, X. K. 2005, J. Geophys. Res.: Space Phys., 110, 8103 [NASA ADS] [CrossRef] [Google Scholar]
  42. Zhao, X. P., Plunkett, S. P., & Liu, W. 2002, J. Geophys. Res.: Space Phys., 107, SSH 13 [Google Scholar]
  43. Zwickl, R. D., Asbridge, J. R., Bame, S. J., et al. 1983, NASA Conf. Publ., 228, 0.711 [NASA ADS] [Google Scholar]

All Tables

Table 1.

ICME input parameters at 0.1 AU.

In the text

All Figures

thumbnail Fig. 1.

Contour (99%) of the ICME tracer mass (white) on colour maps of plasma number density and radial velocity at the labelled time of the MHD simulation (see text for details). The coloured diamonds (φ = 85°, 73.8°, 65°) show the position of three virtual spacecrafts, which would detect the time profiles in Fig. 2. The black arrow indicates the entry point of the ICME into the inner boundary. See online animation.
In the text
thumbnail Fig. 2.

Time profiles of number density, percentage of tracer, radial speed, pressure, and radial and longitudinal component of the magnetic field at three different 1-AU positions, A (red), B (blue), and C (black), marked in Fig. 1. Here the ICME enter time is t0 = 0.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.