EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A127 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A127
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202141102
Published online 21 October 2021

© ESO 2021

1. Introduction

LS 5039 (also known as RX J1826.2-1450) is a high-mass X-ray binary system in the constellation of Scutum, whose high-energy emission was discovered within the ROSAT Galactic Plane survey (Motch et al. 1997). The binary consists of an O6.5V companion star and a compact object (Casares et al. 2005; Takata et al. 2014). The compact object, whose nature has not yet been established, is moving around the companion star in an elliptic orbit with an eccentricity e ≈ 0.35 and an orbital period Porb = 3.9060 days (Casares et al. 2005; Aragona et al. 2009; Sarty et al. 2011). The accuracy of the ephemeris first established by Casares et al. (2005), was slightly improved by a combined multiband analysis by Chang et al. (2016).

Apart from the X-rays, extended (up to 1000 AU) radio emission (Martí et al. 1998), MeV-range (Collmar & Zhang 2014), high-energy (HE) gamma-ray emission in the GeV range (Paredes et al. 2000; Abdo et al. 2009), and very high-energy (VHE) gamma-ray emission (Aharonian et al. 2005a) have also been detected from LS 5039. The extended radio emission is persistent and not orbitally modulated while the X-ray, MeV-range, and TeV-range emission from LS 5039 show clear modulation with orbital period. A modulation of GeV emission from LS 5039 has also been found (Abdo et al. 2009; Hadasch et al. 2012), however this is in anti-phase compared to the X-ray, MeV, and TeV light curves, which may indicate a different origin.

Based on notable differences in the spectral energy distribution, Aharonian et al. (2006) divided the orbit of LS 5039 into two phases: the superior conjunction phase (SUPC, ϕ ≤ 0.45 or ϕ ≥ 0.9, ϕ = 0 corresponding to the periastron) and the inferior conjunction phase (INFC, 0.45 <  ϕ <  0.9). During the INFC, the VHE spectrum is well described by an exponential cutoff power law with the index Γ ∼ 1.85 and the cutoff energy E ∼ 8.7 TeV, while during the SUPC, the spectrum is consistent with a steeper power law with Γ ∼ 2.53. The nonthermal X-ray and MeV-range gamma-ray emission from LS 5039 is likely of synchrotron origin, while the TeV-range gamma-rays are likely produced via inverse Compton (IC) scattering of the same distribution of accelerated leptons. However, the details and parameters of both radiation mechanisms likely at work in LS 5039 are still debatable (see, e.g., Goldoni et al. 2007; Takahashi et al. 2009; Takata et al. 2014, and references therein).

Yoneda et al. (2020) studied the data on the 10–30 keV emission of LS 5039 obtained with NuSTAR and Suzaku and found some signs of ∼9 s pulsations, perhaps indicating that the compact object in LS 5039 is a neutron star. However, the pulsed fraction inferred from these data vary from 0.68 down to less than 0.14 of the ∼(8–11) × 10−12 erg s−1 cm−2 flux measured in the 10–30 keV band. In the 3–10 keV band, NuSTAR data have only allowed Yoneda et al. (2020) to set a ∼3% upper limit on the pulsed fraction. Another combined analysis of NuSTAR and Suzaku data by Volkov et al. (2021) also revealed the 9 s pulsations, but the authors considered them not significant enough to conclude on the presence of a neutron star in the binary.

Hoffmann et al. (2009) analyzed about 3 Ms of INTEGRAL/ISGRI exposures of LS 5039 and were able to show that its 25–200 keV light curve follows a similar orbital profile to the emission observed in the 0.5–10 keV and TeV ranges. However, with such an exposure, the average 25–200 keV INFC flux was estimated as (35.4 ± 23.0) × 10−12 erg s−1 cm−2 and for the SUPC flux only an upper limit of 14.5 × 10−12 erg s−1 cm−2 was set. Further analysis of INTEGRAL/ISGRI data was performed by Chang et al. (2016) with a multi-band comparison of different missions light curves.

Below we analyze about 14 Ms of INTEGRAL/ISGRI exposure of LS 5039 (of which ∼9.5 Ms of the effective exposure time are employed for the phase-resolved spectral analysis) and model combined keV–MeV spectra from data taken by XMM-Newton, NuSTAR, Suzaku, and COMPTEL. We also discuss a scenario whereby the hard emission of LS 5039 originates from the zone where the powerful wind of the O6.5V companion collides with the outflow from the compact object.

It should be noted that despite the almost 14 Ms total exposure of LS 5039, the sensitivity of INTEGRAL/ISGRI is not enough to search for ∼10 s periods of 20–250 keV emission at the ∼10−11 erg s−1 cm−2 flux level. Hence, unlike the case with the Crab PWN, here it is not possible to distinguish the 20–250 keV emission coming from the LS 5039 compact object (whose nature has not yet been established) from the emission generated in its surroundings where a pulsar wind or a fast jet from a black hole collides with the wind of its O6.5V companion.

2. Observations and data reduction

The analyzed observations of LS 5039 are briefly listed in Table 1, while a more detailed description is given in the following sections.

Table 1.

Observations of LS 5039used in the present paper.

2.1. INTEGRAL

The International Gamma-Ray Astrophysics Laboratory (INTEGRAL) observations are split into pointings with a typical duration of ∼2 ks (Winkler et al. 2003). For the current analysis, we used all publicly available pointings performed in the direction of the source with position offset 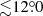from the center of the field of view, from the beginning of the INTEGRAL operations up to the time of the current analysis. These covered observations from the satellite revolution 50 (March 12, 2003) to 1939 (April 8, 2018), giving a total exposure of 13.9 Ms (not corrected for instrumental effects at the source position). We only considered data collected with the IBIS/ISGRI coded mask instrument at energies between 25 and 250 keV (Ubertini et al. 2003; Lebrun et al. 2003). All INTEGRAL data were analyzed using version 10.2 of the OSA software distributed by the ISDC (Courvoisier et al. 2003). The algorithms used for the spatial and spectral analysis are described in Goldwurm et al. (2003). We first extracted a mosaic image by combining all available pointings in the 20–100 keV energy band. In this mosaic, the source was detected at a significance of 26.5σ, which is a vast improvement on the previous reported significance of 18.3σ and 7.7σ in the (20–60 keV) as reported by Chang et al. (2016) and Hoffmann et al. (2009), respectively. We then extracted the IBIS/ISGRI light curve in the same energy band with the resolution of one pointing and converted the arrival times to the LS 5039 orbital phase using the ephemeris from Casares et al. (2005). The light-curve data were subsequently separated into the two orbital phases INFC and SUPC mentioned above (see Sect. 3). Concerning the spectral analysis, the relatively low detection significance of the source in the long-term IBIS/ISGRI mosaic allowed us to extract only one statistically meaningful spectrum for each of the INFC and SUPC orbital phases (see Sect. 4). In order to maximize the signal-to-noise ratio of the data, we adopted a response matrix created ad hoc comprising 16 energy bins logarithmically spaced between 20 and 250 keV. The total effective exposure times of the two spectra, corrected for all instrumental effects at the source position were of 5.251 Ms for the SUPC phase and 4.252 Ms for the INFC phase.

2.2. XMM-Newton

Five observations of LS 5039 have been recorded by XMM-Newton, namely the Obs. IDs 0151160201 (ϕ ∼ 0.52−0.55), 0151160301 (ϕ ∼ 0.53−0.56), and 0202950201 (ϕ ∼ 0.46−0.51) for the INFC phase, and 0202950301 (ϕ ∼ 0.99−0.02) and 0742980101 (ϕ ∼ 0.93−0.14) for the SUPC phase. The first four of them were analyzed by Bosch-Ramon et al. (2005) and Kishishita et al. (2009). For the XMM-Newton data, we analyzed all archived observations in image mode from the European Photon Imaging Camera (EPIC, Jansen et al. 2001; Turner et al. 2001; Strüder et al. 2001). Following the standard data reduction threads introduced by the XMM-Newton team, the data reduction was carried out using the Science Analysis System 18.0.0. The source spectra were extracted from a circular region with a radius of 40″ for both the pn and MOS, while the background spectra were extracted from a source-free circular region with a radius of 100″ (MOS) and 50″ (pn). For each observation, the response (RMFs) and ancillary files (ARFs) were produced by rmfgen and arfgen, respectively. All spectra can be fitted by an absorbed power-law model, with the power-law index and the unabsorbed flux (1–10 keV) in the range 1.3–1.6 and 6 × 10−12 − 1 × 10−11 erg s−1 cm−2, respectively. In the energy range 1–10 keV, the flux in Obs. ID 0202950301 is ∼6 × 10−12 erg s−1 cm−2, which is 12% lower than the averaged flux in the SUPC phase observed by Suzaku. Moreover, we find that the Obs. ID 0151160201 (0742980101) shows a similar power-law index and flux to the averaged Suzaku spectrum in the INFC (SUPC) phase. Therefore, we only use the MOS2 spectrum from Obs. ID 0151160201 for the INFC phase. For the SUPC phase, we extracted the MOS2 spectrum from Obs. ID 0742980101, which has never been published before.

2.3. SUZAKU

LS 5039 was observed with Suzaku (Serlemitsos et al. 2007) from September 9 to 15, 2007, for ∼200 ks covering one and half orbital periods. We followed the data-reduction processes from Takahashi et al. (2009), who reported the spectral results. For the XIS data analysis, the cleaned events were obtained using the ftools command aepipeline. We separately extracted the source spectra in INFC and SUPC phases from a circular region with a radius of 3′. The corresponding background spectra were extracted in a source-free region with the same radius. We combined the spectra from the XIS0 and XIS3 to increase the source photons. The RMF and ARF files were generated using xisrmfge and xissimarfgen, respectively. The standard criteria are applied to screen the Hard X-ray Detector (HXD, Takahashi et al. 2007) data using the ftools command aepipeline. The time-averaged spectra in INFC and SUPC phases of LS 5039 were extracted. The HXD-PIN background is dominated by three components, namely the time-variable instrumental background (nonX-ray background (NXB)), the cosmic X-ray background (CXB), and the Galactic ridge X-ray emission (GRXE). We used similar methods to those introduced by Takahashi et al. (2009) to obtain all the background spectra. However, we chose an updated RMF file ae_hxd_pinhxnome4_20080129.

We used an absorbed power-law model to fit the joint Suzaku/XIS-HXD spectra, and found that NH are 0.74 ± 0.03 and 0.76 ± 0.03 in units of 1022 cm−2, and the power-law index is 1.51 ± 0.02 and 1.60 ± 0.02 for the INFC and SUPC phases, respectively. The results are consistent with the values reported in Takahashi et al. (2009) at 1σ confidence level.

2.4. NuSTAR

NuSTAR observed LS 5039 on September 1, 2016 (Obs ID. 30201034002). We analyzed the data for SUPC and INFC separately. We cleaned the event file using the NuSTAR pipeline tool nupipeline for both FPMA and FPMB by activating the usrgtifile option. The spectra of SUPC and INFC were extracted from a circular region with a radius of 60″ centered on the source location of LS 5039using nuproducts, and the response files were produced simultaneously. To extract the background spectra, we chose a source-free circular background region located on the same chip with a radial aperture of 60″. Finally, we obtained the spectra during SUPC and INFC phases with the exposure time of 95.23 ks and 82.86 ks, respectively. We used the spectra from FPMA and FPMB to perform spectral analysis.

2.5. COMPTEL

LS 5039 was observed with the imaging Compton telescope (COMPTEL, Schoenfelder et al. 1993) for a total effective exposure time of around 7 Ms with the first results reported in Collmar & Zhang (2014). They extracted the flux in the standard COMPTEL energy bands 1–3, 3–10, and 10–30 MeV and subdivided into two orbital phases – INFC and SUPC. We refer to Collmar & Zhang (2014) for more details. Therefore, the data used for our spectral analysis (see Sect. 4) were taken from Collmar & Zhang (2014, see Table 5). In order to perform the XSPEC spectral fitting with the COMPTEL data, we used the ftools command flx2xsp to convert the flux to spectra and response files for the INFC and SUPC orbital phases.

3. Orbital period modulation

The INTEGRAL/ISGRI light curve, 20–100 keV band, has been extracted over all available pointing (6909) of roughly ∼2 ks each, and folded into 16 orbital phase bins using the ephemeris derived by Casares et al. (2005). The orbital light curve is shown in Fig. 1. Please note that, as our observation starts 767 days (March 12, 2003) and ends 6273 days (April 8, 2018) after the considered epoch times, T0 = 51942.59 ± 0.1 MJD1 (February 2, 2001), with the given orbital period Porb = 3.9063 ± 0.00017 days, possible phase uncertainties of ∼0.03 and ∼0.27, caused by the orbital error will be introduced. However, scanning the epoch time by some mean phase shift values between 0.03 and 0.27 did not improve the orbital period modulation amplitude, and as our orbital time bin is one-sixteenth of the orbital period, consideration of the phase correction proposed by Chang et al. (2016) did not significantly improve the shape (the maximal amplitude) of the folded light curves.

thumbnail Fig. 1.

INTEGRAL/ISGRI (20–100 keV) orbital profile of LS 5039. The light curve has been folded into 16 phase bins at the orbital period of 3.90603 days and epoch time T0 = 51942.59 MJD (at orbital phase ϕ = 0.0). The red dashed lines indicate the interval of the INFC and SUPC orbital phases. The superior conjunction and inferior conjunction are shown as blue dashed lines: ϕ = 0.058 and ϕ = 0.716, respectively. The orbital periastron and apastron are at the phases ϕ = 0.0 and ϕ = 0.5, respectively. The period is repeated once for clarity.

If we compare Fig. 1 with previously reported INTEGRAL/ISGRI folded light curves (Hoffmann et al. 2009; Chang et al. 2016), the orbital profile is modulated at the same amplitude and shows a single peaked profile with its maximum and minimum at phase ϕ ∼ 0.65 and ϕ ∼ 1.2, respectively. The profile is also comparable to the Suzaku 1–10 keV, 15–40 keV, NuSTAR 3–60 keV, COMPTEL 10–30 MeV, Fermi 30–70 MeV and 70–100 MeV, and H.E.S.S. < 1 TeV reported orbital light curves (Takahashi et al. 2009; Kishishita et al. 2009; Volkov et al. 2021; Collmar & Zhang 2014; Aharonian et al. 2006). Please note that the Fermi 0.1–3 GeV light curves show anti-correlation compared with the above-mentioned orbital profiles (see e.g., Chang et al. 2016). Starting from the superior conjunction phase, the orbital profile increases to its maximum, ϕ ∼ 0.6, then suddenly decreases slightly near the inferior conjunction phase, before increasing again to a second smaller maximum and then decreasing to its minimum at the superior conjunction orbital phase (see Fig. 1). It is clear that the orbital profile is affected at the inferior or superior conjunction phases rather than at the orbital periastron and apastron passage.

4. Spectral analysis

The spectral analysis was carried out using XSPEC version 12.6 (Arnaud et al. 1996). All uncertainties in the spectral parameters are given at 1σ confidence level for a single parameter. We divided the data into two orbital phases, namely SUPC (ϕ ≤ 0.45 or ϕ ≥ 0.9, periastron at ϕ = 0) and INFC (0.45 <  ϕ <  0.9), respectively. The spectra from XMM-Newton/Suzaku/NuSTAR/INTEGRAL were grouped to ensure each channel has 25 photons at least. The COMPTEL spectra were converted from the measured flux as introduced in Sect. 2.5.

We select the energy ranges 0.5–10 keV, 1–10 keV, 3–70 keV, 15–60 keV, 25–250 keV, 1–30 MeV for XMM-Newton, Suzaku/XIS, NuSTAR/FPMA/FPMB, Suzaku/HXD, INTEGRAL/ISGRI and COMPTEL, respectively. We first fit the joint broad-band spectra with a simple model consisting of a photoelectrically absorbed power-law model, phabs*powerlaw. A multiplication factor is included in the fit to take into account the uncertainties in the cross-calibration of the instruments, and it is fixed at unity for the NuSTAR/FPMA data because it is well calibrated and its energy range overlaps with all other spectra, except for the COMPTEL data. The multiplication factor is a free parameter for all other spectra. If the COMPTEL data are not taken into account, the power-law model fits the spectra well, and the indices are 1.59 ± 0.01 and 1.59 ± 0.01, with a red-χ2/d.o.f. of 0.94/2503 and 1.01/2941 for INFC and SUPC phases, respectively. For the INFC phase, the multiplication factor of XMM-Newton and Suzaku/XIS are 15% lower than NuSTAR. For the SUPC phase, all multiplication factors are close to one, except the multiplication factor of Suzaku/HXD, which is 1.84 ± 0.13. The results are comparable with the other works (see, e.g., Yoneda et al. 2020, 2021; Volkov et al. 2021), while the residuals of the INTEGRAL/ISGRI data show an excess around 50 keV. When the COMPTEL data are considered, the power-law indices are not changed, but the best-fit multiplication factor of the COMPTEL spectra is 3.14 ± 0.42 and 3.34 ± 0.66 for INFC and SUPC phases, respectively. However, if we assume that the available COMPTEL data are well calibrated and fix its multiplication factor at unity, then the single power-law model cannot describe the data despite the red-χ2 being close to one. This is because the whole keV-MeV data set is dominated by the data at low energies. Therefore, the high-energy data of INTEGRAL/ISGRI and COMPTEL indicate departure from a single power-law model at sufficiently high photon energies. This finding was also noticed by Yoneda et al. (2021, see Fig. 11) using the NuSTAR/COMPTEL data, suggesting an additional harder spectral component.

We then replaced the simple power law with a broken power-law model, phabs*bknpower, to make a best fit of the broad-band spectra. The main parameters of the model are the hydrogen column density, NH, the break energy, Ecut, and the photon indices, Γ1 and Γ2, below and above Ecut. In this case, a multiplication factor was also included to account for the uncertainties in the cross-calibration of the instruments, where it was fixed at unity for NuSTAR/FPMA data. First, we only consider the spectra in the energy range 0.5–250 keV. The best-fit parameters are reported in Table 2. We then extend the energy range up to 30 MeV by including the COMPTEL spectra, and show the best-fit parameters in Table 3. We note that the multiplication factors of the COMPTEL are now around one-third lower for both INFC and SUPC phases compared with NuSTAR/FPMA spectra. If we fix the multiplication factor of COMPTEL data at one, the broken power-law model can also describe the broad-band spectra up to MeV with a slightly larger and acceptable red-χ2. The unabsorbed bolometric fluxes are determined by the convolution model cflux in the 0.5–250 keV and 0.5–2 × 104 keV energy ranges. The interstellar absorption column density is consistent with previous results. Figures 2a–d show the unfolded spectra and the best-fit models.

Table 2.

Spectral fitting to the broadband spectra in INFC and SUPC phases of LS 5039 with the XMM-Newton, Suzaku, NuSTAR, and INTEGRAL observations.

Table 3.

Spectral fitting to the broadband spectra in INFC and SUPC phases of LS 5039 with the XMM-Newton, Suzaku, NuSTAR, INTEGRAL, and COMPTEL observations.

thumbnail Fig. 2.

(a) and (b) are the unfolded absorbed broad-band spectra of LS 5039 in the 0.5–250 keV energy range and separated in the INFC and SUPC phases. (c) and (d) include the COMPTEL data and thus cover the 0.5–2 × 104 keV energy range. The data points are obtained from the XMM-Newton/MOS (blue points, 0.5–9 keV), the NuSTAR/FPMA/FPMB (black/red points, 3–79 keV) Suzaku/XIS/HXD (green and magenta points, 1–10 keV and 10–70 keV, respectively), INTEGRAL/ISGRI (cyan points, 24–250 keV), and COMPTEL (orange points, 1–30 MeV). The fit represented in the top panels with a solid line was obtained with the bknpow model. The residuals from the best fits are shown in the lower panels. (e) and (f) are the contours corresponding to the spectral fit (c) and (d) of the broken power-law indices separated in the INFC and SUPC phases, respectively.

For the broad-band 0.5–250 keV spectra, we find the break energy, Ecut ∼ 50 keV, and the power-law indices, Γ1 ∼ 1.6 and Γ2 ∼ 0.9, consistent within the errors between the SUPC and INFC phases. For the broad-band 0.5–2 × 104 keV spectra, we obtain a larger index, Γ2 ∼ 1.15, while other parameters, NH, Ecut, and Γ1 are highly consistent at 1σ confidence level compared with the results from the broad-band 0.5–250 keV spectra. The contour plots between Γ1 and Γ2 are shown in Figs. 2e and f.

5. Discussion and conclusions

We analyzed a vast amount of INTEGRAL/ISGRI data for LS 5039 in order to investigate its ∼100 keV emission for the first time and discovered a spectral break at ∼50 keV, which should be accounted for within future quantitative models of high-energy emission from the binary.

Although the nature of the compact object in LS 5039 is not yet reliably established (see Paredes et al. 2000; Aharonian et al. 2005b; Marcote et al. 2015), a number of studies in the past decade have successfully reproduced the main features of its light curves and spectra assuming the presence of a neutron star (see, e.g., Zabalza et al. 2013; Takata et al. 2014; Marcote et al. 2015; Dubus et al. 2015). The interaction of a pulsar wind with the fast wind of a massive star LS 2883 is established in the case of another well-known gamma-ray binary system associated with a radio pulsar PSR B1259-63 orbiting around a Be star with a period of ∼3.4 yr (Johnston et al. 1992; Chernyakova & Illarionov 1999; Aharonian et al. 2005b; Abdo et al. 2011; Chernyakova et al. 2020). Although the systems have different periods and wind geometries, which certainly should be accounted for in their models (see e.g. Dubus 2013), they likely have some similarities in the multiwavelength spectra. Interestingly, PSR B1259-63 also shows hard X-ray indices Γ< 1.5 at different orbital phases (Chernyakova et al. 2006, 2020).

Most of the models assuming that the compact object in LS 5039 is a neutron star consider the observed X-ray emission as the synchrotron radiation of the pulsar wind leptons and the VHE emission to be in phase with the X-rays and MeV gamma-rays as the IC scattering of the stellar photons. The VHE photon index ΓTeV = 1.85 observed in the INFC phase may be produced in the Klein-Nishina regime in IC emission of leptons, producing the synchrotron X-rays with Γ ∼ ΓTeV/2 ≈ 0.9 at tens to hundreds of keV. Thus, hard X-ray indices in the INTEGRAL/ISGRI band may be consistent with the VHE index for the INFC phase. Such hard emission spectra imply hard energy distributions of leptons are produced inside the source. The X-ray spectra of LS 5039 presented in Tables 2 and 3 and shown in Fig. 2 require a specific particle distribution in the synchrotron model. While the power-law index Γ = (s+1)/2 ∼ 1.6 assumes a particle distribution f(E) ∝ E−s with s = 2.2, which is quite typical for spectra energized at the termination shocks of pulsar winds, a much harder index s ∼ 1 expected above the break energy up to some limit E = Emax would be explained by an acceleration process of some kind. Because of the severe energy losses in strong magnetic and photon fields of an O-class star, the maximal particle energy achieved in this process giving the Emax value may be defined by matching the acceleration timescale with the energy loss timescale (see, e.g., Dubus 2006). This acceleration process might be less efficient and provide lower Emax during the SUPC phase where a much softer VHE power-law index is observed. Also, the Doppler effect may boost the emission from the acceleration site in the INFC and be insignificant or may even dampen the emission in the SUPC. The acceleration site also may be simply obscured during the superior conjuction.

Modeling of particle acceleration in a complicated structure of interacting stellar wind and relativistic pulsar wind requires accurate simulation of flow dynamics. To simulate the wind interaction, both must be properly parametrized. In a recent work, Bosch-Ramon (2021) modelled gamma-ray emission as Compton upscattering of the O-star photons by the accelerated leptons of the putative cold pulsar wind in LS 5039 near the periastron of the binary. A comparison of the modelled spectra with the observed gamma-ray emission from LS 5039 led Bosch-Ramon (2021) to the conclusion that, within the considered scenario, a strongly magnetized cold wind is favored over a weakly magnetized strongly anisotropic wind. Constraints on the pulsar wind magnetization and the angular dependence of the carried momentum flux are very important for a correct modeling of the pulsar wind dynamics (see, e.g., Ponomaryov et al. 2019, 2020). Despite significant progress in the fluid-type simulations of the structure of gamma-ray binaries (see, e.g., Bosch-Ramon et al. 2015; Barkov & Bosch-Ramon 2018), modeling of the phase-resolved multi-wavelength spectra for LS 5039 is a challenging problem (see e.g., del Palacio et al. 2015). Recently, Molina & Bosch-Ramon (2020) used semi-analytical modeling to reproduce X-ray Suzaku, HE Fermi fluxes, and VHE H.E.S.S. data for SUPC. Later, Huber et al. (2021) developed a model of wind interaction in LS 5039 and computed a synthetic spectrum of the synchrotron and IC emission of the binary for various parameters, such as system inclination. However, the available models face difficulties in explaining the hard X-rays and the MeV flux, as well as the VHE flux in the INFC phase. Matching up the X-ray, MeV, and VHE data still seems to be an intricate problem (see, e.g., Dubus et al. 2015) that has not yet been solved. Modeling of the HE emission, which possibly contains a number of components (see, e.g., Takata et al. 2014), is also a complicated problem. Recently, Yoneda et al. (2021) argued for the presence of two emission components in the GeV band, including a component which does not depend on the orbital phase.

Shock acceleration is a widely used mechanism of particle energization in mildly magnetized flows produced by winds in massive star–pulsar binary systems. Diffusive acceleration by a single shock produces power-law test particle spectra of indices s ≳ 2 both at relativistic and nonrelativistic shocks (Blandford & Eichler 1987; Bykov et al. 2012). The corresponding synchrotron photon spectra show the power-law photon distribution with photon indices Γ = (s+1)/2 >  1.5. Particle spectra with a piece-wise power-law distribution, a low-energy branch of a spectral index s1 ∼ 2, and a high-energy branch of an index s2 ∼ 1 just before Emax were obtained in models of colliding shock flows (Bykov et al. 2017, 2019). These that can be expected in the wind collision systems that may model LS 5039.

Fermi I type acceleration in the colliding shock flows is likely to operate in the case of supernova shock collision with a strong stellar wind (Bykov et al. 2015), where this mechanism can accelerate protons well above PeV energies, as well as in colliding wind binaries (Grimaldo et al. 2019; Pittard et al. 2021). Pulsars moving supersonically relative to the surrounding medium can create bow-shock pulsar wind nebulae (PWNe; Reynolds et al. 2017; Bykov et al. 2017). The colliding shock flow mechanism can build up a spectrum of accelerated e± in the bow-shock PWNe with the “turn-up” shape, where the high-energy branch has an index of s2 ∼ 1 (Bykov et al. 2017). This mechanism can explain the spatially resolved hard 0.5–8 keV X-ray indices Γ <  1.5 observed by Chandra in the bow-shock-type Geminga PWN (Posselt et al. 2017) and in Vela PWN (see, e.g., Kargaltsev & Pavlov 2008). The kinetic modeling presented by Bykov et al. (2017) can be used to explain the hard X-ray indices observed in the latter case. The modeling also predicts spatial variations of X-ray photon indices across the nebula with relatively soft spectra (Γ ∼ 1.6) at the pulsar wind termination shock and in the nebular tail and those with hard index Γ ∼ 1 in the bow-shock region in coincidence with the distribution of photon indices observed in Geminga.

The eccentricity of the orbit of the compact object in LS 5039spatially rescales the colliding flow zone and provides different magnetic and seed-photon field intensities at the acceleration site during the INFC and SUPC phases, hence allowing higher Emax for the INFC phase. As such, the difference in the VHE indices may be explained by e± pairs accelerating to higher Emax in the colliding flows during the INFC phase. We note that the COMPTEL data taken in the MeV range also show harder indices for the INFC (Collmar & Zhang 2014).

Thus, Fermi I type acceleration in the colliding flows may in principle be responsible for the hard spectral component discovered by INTEGRAL/ISGRI above ∼50 keV and produce spectra consistent with the known observational results for other spectral bands. Nevertheless, the different orientation of the colliding flow zone, the Doppler boosting effects, and the spatially separated populations of accelerated particles with different spectral slopes may also play a significant role in the production of the multi-wavelength spectra discussed above.

1

The epoch is given at orbital phase ϕ = 0.

Acknowledgments

We thank an anonymous referee for the constructive comments that helped us improving the paper. A. M. B., A. M. K., and A. E. P. acknowledge support from RSF grant 21-72-20020. Some of the modeling was performed at the Joint Supercomputer Center JSCC RAS and at the “Tornado” subsystem of the St. Petersburg Polytechnic University supercomputing center. Z. L. thanks the International Space Science Institute in Bern for the hospitality. Z. L. was supported by National Natural Science Foundation of China (U1938107, U1838111).

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L56 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, L11 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aharonian, F., Akhperjanian, A. G., Aye, K. M., et al. 2005a, Science, 309, 746 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aharonian, F., Akhperjanian, A. G., Aye, K. M., et al. 2005b, A&A, 442, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 460, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [Google Scholar]
  7. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
  8. Barkov, M. V., & Bosch-Ramon, V. 2018, MNRAS, 479, 1320 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
  10. Bosch-Ramon, V. 2021, A&A, 645, A86 [EDP Sciences] [Google Scholar]
  11. Bosch-Ramon, V., Paredes, J. M., Ribó, M., et al. 2005, ApJ, 628, 388 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bosch-Ramon, V., Barkov, M. V., & Perucho, M. 2015, A&A, 577, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bykov, A., Gehrels, N., Krawczynski, H., et al. 2012, Space Sci. Rev., 173, 309 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bykov, A. M., Ellison, D. C., Gladilin, P. E., & Osipov, S. M. 2015, MNRAS, 453, 113 [Google Scholar]
  15. Bykov, A. M., Amato, E., Petrov, A. E., Krassilchtchikov, A. M., & Levenfish, K. P. 2017, Space Sci. Rev., 207, 235 [CrossRef] [Google Scholar]
  16. Bykov, A. M., Petrov, A. E., Krassilchtchikov, A. M., et al. 2019, ApJ, 876, L8 [NASA ADS] [CrossRef] [Google Scholar]
  17. Casares, J., Ribó, M., Ribas, I., et al. 2005, MNRAS, 364, 899 [Google Scholar]
  18. Chang, Z., Zhang, S., Ji, L., et al. 2016, MNRAS, 463, 495 [Google Scholar]
  19. Chernyakova, M. A., & Illarionov, A. F. 1999, MNRAS, 304, 359 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chernyakova, M., Neronov, A., Lutovinov, A., Rodriguez, J., & Johnston, S. 2006, MNRAS, 367, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  21. Chernyakova, M., Malyshev, D., Mc Keague, S., et al. 2020, MNRAS, 497, 648 [NASA ADS] [CrossRef] [Google Scholar]
  22. Collmar, W., & Zhang, S. 2014, A&A, 565, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. del Palacio, S., Bosch-Ramon, V., & Romero, G. E. 2015, A&A, 575, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Dubus, G. 2013, A&ARv, 21, 64 [Google Scholar]
  27. Dubus, G., Lamberts, A., & Fromang, S. 2015, A&A, 581, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Goldoni, P., Ribó, M., di Salvo, T., et al. 2007, Ap&SS, 309, 293 [CrossRef] [Google Scholar]
  29. Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A, 411, L223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Grimaldo, E., Reimer, A., Kissmann, R., Niederwanger, F., & Reitberger, K. 2019, ApJ, 871, 55 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hadasch, D., Torres, D. F., Tanaka, T., et al. 2012, ApJ, 749, 54 [Google Scholar]
  32. Hoffmann, A. D., Klochkov, D., Santangelo, A., et al. 2009, A&A, 494, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Huber, D., Kissmann, R., & Reimer, O. 2021, A&A, 649, A71 [EDP Sciences] [Google Scholar]
  34. Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Johnston, S., Manchester, R. N., Lyne, A. G., et al. 1992, ApJ, 387, L37 [Google Scholar]
  36. Kargaltsev, O., & Pavlov, G. G. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 171 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kishishita, T., Tanaka, T., Uchiyama, Y., & Takahashi, T. 2009, ApJ, 697, L1 [NASA ADS] [CrossRef] [Google Scholar]
  38. Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Marcote, B., Ribó, M., Paredes, J. M., & Ishwara-Chandra, C. H. 2015, MNRAS, 451, 59 [Google Scholar]
  40. Martí, J., Paredes, J. M., & Ribó, M. 1998, A&A, 338, L71 [NASA ADS] [Google Scholar]
  41. Molina, E., & Bosch-Ramon, V. 2020, A&A, 641, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Motch, C., Haberl, F., Dennerl, K., Pakull, M., & Janot-Pacheco, E. 1997, A&A, 323, 853 [NASA ADS] [Google Scholar]
  43. Paredes, J. M., Martí, J., Ribó, M., & Massi, M. 2000, Science, 288, 2340 [Google Scholar]
  44. Pittard, J. M., Romero, G. E., & Vila, G. S. 2021, MNRAS, 504, 4204 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ponomaryov, G. A., Levenfish, K. P., & Petrov, A. E. 2019, J. Phys. Conf. Ser., 1400, 022027 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ponomaryov, G. A., Levenfish, K. P., Petrov, A. E., & Kropotina, Y. A. 2020, J. Phys. Conf. Ser., 1697, 012022 [NASA ADS] [CrossRef] [Google Scholar]
  47. Posselt, B., Pavlov, G. G., Slane, P. O., et al. 2017, ApJ, 835, 66 [CrossRef] [Google Scholar]
  48. Reynolds, S. P., Pavlov, G. G., Kargaltsev, O., et al. 2017, Space Sci. Rev., 207, 175 [NASA ADS] [CrossRef] [Google Scholar]
  49. Sarty, G. E., Szalai, T., Kiss, L. L., et al. 2011, MNRAS, 411, 1293 [Google Scholar]
  50. Schoenfelder, V., Aarts, H., Bennett, K., et al. 1993, ApJS, 86, 657 [NASA ADS] [CrossRef] [Google Scholar]
  51. Serlemitsos, P. J., Soong, Y., Chan, K.-W., et al. 2007, PASJ, 59, S9 [NASA ADS] [Google Scholar]
  52. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
  53. Takahashi, T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35 [Google Scholar]
  54. Takahashi, T., Kishishita, T., Uchiyama, Y., et al. 2009, ApJ, 697, 592 [Google Scholar]
  55. Takata, J., Leung, G. C. K., Tam, P. H. T., et al. 2014, ApJ, 790, 18 [Google Scholar]
  56. Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
  57. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Volkov, I., Kargaltsev, O., Younes, G., Hare, J., & Pavlov, G. 2021, ApJ, 915, 61 [Google Scholar]
  59. Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Yoneda, H., Makishima, K., Enoto, T., et al. 2020, Phys. Rev. Lett., 125, 111103 [Google Scholar]
  61. Yoneda, H., Khangulyan, D., Enoto, T., et al. 2021, ApJ, 917, 90 [NASA ADS] [CrossRef] [Google Scholar]
  62. Zabalza, V., Bosch-Ramon, V., Aharonian, F., & Khangulyan, D. 2013, A&A, 551, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Observations of LS 5039used in the present paper.

In the text
Table 2.

Spectral fitting to the broadband spectra in INFC and SUPC phases of LS 5039 with the XMM-Newton, Suzaku, NuSTAR, and INTEGRAL observations.

In the text
Table 3.

Spectral fitting to the broadband spectra in INFC and SUPC phases of LS 5039 with the XMM-Newton, Suzaku, NuSTAR, INTEGRAL, and COMPTEL observations.

In the text

All Figures

thumbnail Fig. 1.

INTEGRAL/ISGRI (20–100 keV) orbital profile of LS 5039. The light curve has been folded into 16 phase bins at the orbital period of 3.90603 days and epoch time T0 = 51942.59 MJD (at orbital phase ϕ = 0.0). The red dashed lines indicate the interval of the INFC and SUPC orbital phases. The superior conjunction and inferior conjunction are shown as blue dashed lines: ϕ = 0.058 and ϕ = 0.716, respectively. The orbital periastron and apastron are at the phases ϕ = 0.0 and ϕ = 0.5, respectively. The period is repeated once for clarity.
In the text
thumbnail Fig. 2.

(a) and (b) are the unfolded absorbed broad-band spectra of LS 5039 in the 0.5–250 keV energy range and separated in the INFC and SUPC phases. (c) and (d) include the COMPTEL data and thus cover the 0.5–2 × 104 keV energy range. The data points are obtained from the XMM-Newton/MOS (blue points, 0.5–9 keV), the NuSTAR/FPMA/FPMB (black/red points, 3–79 keV) Suzaku/XIS/HXD (green and magenta points, 1–10 keV and 10–70 keV, respectively), INTEGRAL/ISGRI (cyan points, 24–250 keV), and COMPTEL (orange points, 1–30 MeV). The fit represented in the top panels with a solid line was obtained with the bknpow model. The residuals from the best fits are shown in the lower panels. (e) and (f) are the contours corresponding to the spectral fit (c) and (d) of the broken power-law indices separated in the INFC and SUPC phases, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.