| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A160 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202140557 | |
| Published online | 27 October 2021 | |
Spectral analysis of the low-mass X-ray pulsar 4U 1822-371: Reflection component in a high-inclination system
1
Dipartimento di Scienze Fisiche ed Astronomiche, Universitá di Palermo, via Archirafi 36, 90123 Palermo, Italy
e-mail: alessio.anitra@unipa.it
2
Dipartimento di Fisica, Universitá degli Studi di Cagliari, SP Monserrato-Sestu, KM 0.7, 09042 Monserrato, Italy
Received:
13
February
2021
Accepted:
18
August
2021
Context. The X-ray source 4U 1822-371 is an eclipsing low-mass X-ray binary and X-ray pulsar, hosting a NS that shows periodic pulsations in the X-ray band with a period of 0.59 s. The inclination angle of the system is so high (80–85°) that in principle, it should be hard to observe both the direct thermal emission of the central object and the reflection component of the spectrum because they are hidden by the outer edge of the accretion disc. Despite the number of studies carried out on this source, many aspects such as the geometry of the system, its luminosity, and its spectral features are still debated.
Aims. Assuming that the source accretes at the Eddington limit, the analysis performed in this paper aims to investigate the presence of a reflection component. No such component has been observed before in a high-inclination accretion-disc corona source such as 4U 1822-371. To do this, we use large-area instruments with sensitivity in a broad energy range.
Methods. We analysed non-simultaneous XMM-Newton and NuSTAR observations of 4U 1822-371 and studied the average broad-band spectrum. We first reproduced the results reported in the literature, then focused on the research of reflection features. We modelled the spectral emission of the source using two different reflection models, DISKLINE plus PEXRIV or, alternatively, the self-consistent reflection model RFXCONV. We also included six Gaussian components ascribable to emission lines at low energies.
Results. In our analysis, we find significant evidence of a reflection component in the spectrum, in addition to two narrow (Gaussian) lines at 6.4 and 7.1 keV associated with neutral (or mildly ionised) iron, Fe Kα, and Kβ transitions, respectively. The continuum spectrum is well fitted by a saturated Comptonisation model with an electron temperature of 4.9 keV and a thermal black-body-like component that might be emitted by the accretion disc at a lower temperature (∼0.2 keV). We identify emission lines from O VIII, Ne IX, Mg XI, and Si XIV. We also added two new eclipse times related to NuSTAR and Swift observations to the most recent ephemeris reported in literature, updating thus the ephemeris and finding a Porb = 5.57063023(34) h and a Ṗorb value of 1.51(5) × 10−10 s s−1.
Conclusions. In our proposed scenario, 4U 1822-371 is accreting at the Eddington limit with an intrinsic luminosity of ∼1038 erg s−2, while the observed luminosity is two orders of magnitude lower because of the high inclination angle of the system. Despite this high inclination, we find that a reflection component is required to fit residuals at the Fe line range and to model the hard excess observed in the NuSTAR spectrum. The inclination inferred from the reflection component is in agreement with values previously reported in literature for this source, while the best-fit value of the inner disc radius is still uncertain and model dependent. More observations are therefore needed to confirm these results, which can give important information on the central emitting region in this enigmatic and peculiar source.
Key words: X-rays: binaries / accretion, accretion disks / stars: individual: X1822-371 / stars: neutron / X-rays: general / eclipses
© ESO 2021
1. Introduction
The source 4U 1822-371 is an eclipsing low-mass X-ray binary system (LMXB) with an orbital period of 5.57h. It hosts a neutron star (NS) that shows periodic pulsations in the X-ray band (Iaria et al. 2013) with a period of 0.59 s.
As estimated by Mason & Cordova (1982) using infrared observations, the inclination angle with respect to our line of sight lies in the range 80°–85°. This high inclination angle implies that the direct emission from the innermost region should be shaded by the swelling in the external region of the accretion disc, caused by the inflowing matter transferred by the secondary star that impacts the outer disc. This source is considered the prototype of the accretion-disc corona (ADC) sources. This describes a particular system geometry in which most of the observed radiation emitted by the accretion flow is scattered by a corona that is formed by the evaporation of matter from the surface of the accretion disc, which leads to the accumulation of particles above and below the disc, forming a sandwich structure around it (Shakura & Sunyaev 1973). Another interesting feature of 4U 1822-371 is its activity as an X-ray pulsator. Analysing RXTE data, Jonker & van der Klis (2001) discovered coherent X-ray pulsations at ∼0.59 s and inferred a pulse-period derivative of (−2.85 ± 0.04) × 10−12 s s−1, indicating a spin-up of the NS. Taking the observed luminosity of 1036 erg s−1 estimated by Mason & Cordova (1982) for a distance of the source of 2.5 kpc into account, the authors also calculated the strength of the NS magnetic field. Using the relation of Ghosh & Lamb (1979) that links the luminosity and the spin-up rate, they found an extremely high value of 8 × 1016 G for the magnetic field, suggesting that the luminosity might be underestimated.
Burderi et al. (2010) studied the orbital evolution of the system and refined the orbital ephemeris of the source. They concluded that the orbital period increases at a rate of Ṗorb = 1.50(7) × 10−10 s s−1 (see also Parmar et al. 2000). This high orbital period derivative cannot be explained by a conservative mass transfer at the accretion rate inferred from the observed source luminosity. According to these authors, a highly non-conservative mass transfer is required at a rate up to seven times the Eddington limit for an NS with a mass of 1.4 M⊙ (see e.g., Burderi et al. 2010; Bayless et al. 2010; Iaria et al. 2011; Mazzola et al. 2019), indicating that a large part of the matter that is pulled off by the companion star is ejected from the system. The luminosity produced by this accretion process is about 1038 erg s−1, which differs from the luminosity reported by Mason & Cordova (1982), but the magnetic field strength inferred with this luminosity implies a more reasonable value of 8 × 1010 G (see also Jonker & van der Klis 2001).
The spectral shape of the X-ray emission is still debated. The main observed spectral component is a Comptonisation spectrum, which is the result of the inverse Compton scattering of soft thermal photons that are emitted by the compact object or by the accretion disc off the hot electrons that form the innermost part of the Corona around the NS. Hellier & Mason (1989) fitted an EXOSAT spectrum of 4U 1822-371 using a power law and a black-body component (peaked at 1.8–2.0 keV) in addition to an iron line. They measured an apparent radius for the region of the black-body emission of about 0.25 km, which is much smaller than the NS radius.
Recently, Iaria et al. (2013) performed an orbital phase-dependent spectral analysis of Chandra and XMM-Newton observations of 4U 1822-371, fitting the spectrum with a black-body at a temperature of 0.061 keV and with a Comptonised component characterised by an electron temperature of 3.01 keV and emitted by an optically thick (inner) corona having an optical depth of τ = 19.1. Both these components are partially absorbed by local neutral matter and interstellar medium (ISM). Several emission lines are observed at low energies, probably emitted by plasma in the bulge at the outermost region of the disc, in addition to two narrow fluorescence iron lines associated with Fe XXV and Fe XXVI, which are produced in the innermost regions. The authors proposed that the partial covering component observed in the source spectra may be ascribed to local neutral matter around the system that cannot accrete onto the NS because it is emitting at the Eddington limit. They also ascribed the observed low luminosity of 1036 erg s−1 to the high inclination of the source; an extended, optically thin corona (τ = 0.01) that scatters a small fraction of the inner emission along the line of sight may explain why we observe this low luminosity from the source.
In this paper we investigate the geometry of the system through a spectral analysis of X-ray data collected from non-simultaneous XMM-Newton and NuSTAR observations, taking advantage of the large effective area in a broad energy range and moderately good energy resolution at the iron-line energy. We find that the iron line may indeed be a blending of lines from iron in different ionisation states. Moreover, the large width of one of these line components and the Compton hump at high energies suggest reflection, which might represent the first evidence of a reflection component for a high-inclination system such as 4U 1822-371.
2. Observations
The source 4U 1822-371 was observed by the XMM-Newton observatory on 2017 March 3 between 01:10:54 UTC and 19:12:27 UTC (ObsId. 0784820101) for a duration of 69 ks. During this observation, the EPIC-pn and MOS2 cameras were operated in timing mode with a medium filter, while the MOS1 camera was set in small-window mode with a thick filter. The timing mode is useful to avoid photon pile-up: this effect occurs when the observed source is bright enough for different X-ray photons to arrive in a single pixel within a frame time, causing the instrument to register them as a single photon with an energy equal to the sum of the energies of the original photons. This causes a loss in photon counts as well as a hardening of the spectrum. We verified that MOS 1 was affected by pile-up because the camera was operated in imaging mode during the observation, and we found that the data collected by the Epic-pn and the MOS 2 were incompatible below 3 keV due to detector instrumental features. For these reasons, and because Epic-pn has a greater effective area than the MOS cameras in the same energy range, we preferred to use the Epic-pn data for our analysis. To obtain a better coverage of the spectrum at the lower energies, we also used data collected by the two RGS cameras, which provide a high-energy resolution in the range between 0.35 keV and 2.5 keV.
We reduced the XMM-Newton data using the Science Analysis Software (SAS) v17.0.0. We first extracted the images from the event files to select the region from which events are collected. For the EPIC-pn data, we selected the columns in the interval 26 < RAWX < 47 for the source and 3 < RAWX < 5 for the background, respectively. For the RGS background, we selected a region in CCD9 in which generally the background dominates because it is located close to the optical axis and records fewer source photons. We accumulated the EPIC-pn 0.3–10 keV light curve with a bin time of 100 seconds considering PATTERN < = 4 to extract only single and double good events, and FLAG = 0 to avoid events from the pixels at the edges of the CCD. In the light curve of the source, we found three partial eclipses separated by a period of about 20 ks; in order to exclude the time intervals during which the luminosity is reduced from the average spectrum, we created a set of good time intervals (GTI) to exclude the eclipses from the following spectral analysis. We eventually extracted source and background spectra and combined the RGS1 and RGS2 spectra, first and second order.
The NuSTAR observation was performed between 2018 April 25, 14:26:09, and April 27, 07:10:26 (ObsID 30301009002), for a total exposure time of 29 ks. We used the NUPIPELINE and NUPRODUCTS scripts within HEASOFT to obtain the average spectra: for both the source and background of FPMA and FPMB, we selected a circular region with a radius of 30 arcsec. As done for EPIC-pn data, we produced light curves and created the GTI files, after which we extracted the source and background (out-of-eclipse) average spectra, the ancillary files, and the response matrices for each of the two NuSTAR telescopes. We rebinned these spectra in order to have a minimum of 30 counts per bin. The NuSTAR spectra provide a better coverage of the spectrum at high energies: this feature makes NuSTAR a perfect complement for our work because together with the low-energy coverage provided by XMM-Newton, it allows a detailed analysis of all the main features (discrete features as well as the continuum) that characterise a reflection spectrum emitted by X-ray binaries.
3. Timing analysis
The NuSTAR ObsID 30301009002 represents the most recent observation of 4U 1822-371, and as explained in the previous section, the extracted light curve shows an eclipse that has never been used to perform an analysis aimed at studying the orbital parameters of the system. For this reason, we performed a timing analysis in order to investigate whether it is possible to extend the most recent orbital ephemeris of the system reported by Mazzola et al. (2019) and improve the accuracy of the orbital parameters.
We applied the barycentric correction to the event file, extracted as discussed in section 2, using the Ftool BARYCORR. We folded the light curve obtained from the two NuSTAR cameras, FPMA and FPMB, using as reference time Tfold = 50353.08728 MJD and a trial orbital period of Pfold = 0.232109571 days (Mazzola et al. 2019). The eclipse arrival time was evaluated by using the method described by Burderi et al. (2010), finding a value of Tecl = 58234.1536(5) MJD/TDB.
We extended the ephemeris of the source with a further eclipse arrival time extracted from a Swift observation performed between 2007 August 3, 01:20:01, and 2007 August 5, 21:07:22 (ObsID 00036691002 and 00036691003). Using the same method as adopted for the NuSTAR observation, we find an arrival time of Tecl = 54317.0587(10) MJD/TDB.
The inferred delays of the eclipse arrival times with respect to the adopted ephemeris and the corresponding number of orbital cycles are reported in Table 1. We fitted the delays as a function of the cycles using three different models. We first modelled the data with the quadratic function y = a + bN + cN2, where the parameters a and b represent the correction for the value of the eclipse time (ΔTecl) and the orbital period (ΔP/P0), respectively, while the term c describes the variation in orbital period and allows us to determine its derivative (P0/2Ṗ). We obtained a χ2 (d.o.f.) = 47.43(31) and Ṗ = 1.42(3) ×10−10 s s−1. The results are reported in Table 1.
Eclipse arrival times (top part) and best-fit values for the parameters derived with the different models described in the text (quadratic, cubic, and LQS) (bottom part).
To improve the fit, we added a cubic term (y = a + bN + cN2 + dN3) to the previous model, where the new coefficient describes the orbital period second derivative ( ). The model improves the fit and achieves a χ2 (d.o.f.) = 38.21(30). This allows us to infer Ṗ = 1.51(5) × 10−10 s/s−1 and
). The model improves the fit and achieves a χ2 (d.o.f.) = 38.21(30). This allows us to infer Ṗ = 1.51(5) × 10−10 s/s−1 and  = −0.94(35) × 10−19 s/s−2, in line with previous results (Mazzola et al. 2019). We tested the improvement of the fit with an F-TEST that compared the quadratic and cubic models, and obtained a probability of chance improvement of about 0.01. This indicates that the addition of the cubic term is significant at 99 % confidence level. Adopting the cubic ephemeris, we updated the orbital ephemeris of the source as
= −0.94(35) × 10−19 s/s−2, in line with previous results (Mazzola et al. 2019). We tested the improvement of the fit with an F-TEST that compared the quadratic and cubic models, and obtained a probability of chance improvement of about 0.01. This indicates that the addition of the cubic term is significant at 99 % confidence level. Adopting the cubic ephemeris, we updated the orbital ephemeris of the source as
Mazzola et al. (2019) inferred a possible sinusoidal modulation of the delays. To investigate this, we used a model composed of a quadratic and sinusoidal function, LQS = a + bN + cN2 + Asin[2π(N − N0)/Nmod], where A is the semi-amplitude of the modulation. The best-fit parameters are reported in the third column of Table 1, and in Fig. 1, the residuals of the cubic and LQS model are compared. We obtained a χ2 (d.o.f.) = 34.30(28) and an F-TEST probability of chance improvement of about 0.03 with respect to the quadratic model, meaning that the sinusoidal modulation improves the fit at the 97% confidence level. The origin of this modulation is still debated and may be associated with the gravitational quadrupole coupling (GQC) mechanism through tidal interaction or with a third body in the system (Mazzola et al. 2019). Future observations may allow us to further extend the ephemeris, confirming or disproving this modulation, and possibly explaining its origin.
 |
Fig. 1. Delays of the eclipse arrival times as a function of the orbital cycle for the LQS model (top panel). Residuals in units of σ, obtained with the cubic (black) and LQS (red) model, respectively (bottom panel). |
4. Spectral analysis
We initially fitted the data of the two non-simultaneous observations separately in order to understand their spectral features in detail and determine whether the two datasets were compatible with each other. We decided to adopt the energy range 4–45 keV for the NuSTAR spectrum and 0.6–10 keV for the XMM-Newton spectrum. We dropped the NuSTAR data above 45 keV and below 4 keV because at higher energies, the background spectrum overcomes the source, and at lower energies, the spectrum diverges due to a flux excess in the FPMA camera (Madsen et al. 2020). For XMM-Newton, we considered the RGS data only between 0.6–2 keV because above this threshold, the instrument is not well calibrated, and below it, some systematic features are expected, for instance, at the oxygen edge. In addition, we ignored EPIC-pn data lower than 2 keV because of some systematic features at 1.8 keV (caused by an instrumental Si edge).
4.1. Comparison with a previous spectral decomposition
We initially used the model proposed by Iaria et al. (2013), which presents the most recent spectral analysis of 4U 1822-371 in the literature to date, with the aim to test whether a model without a reflection component can adequately describe our spectra. The model comprises a Comptonised component (COMPTT in XSPEC) that is partly absorbed by neutral local matter and partly by the ISM. In this case, we assumed the same abundance (Asplund et al. 2009) and the same cross-section (Verner et al. 1996) as were chosen Iaria et al. (2013), with the aim to compare our results to those available in the literature. For both datasets, we took possible inter-calibration issues into account by including a constant multiplicative component, fixed to 1 for Epic-pn and for the NuSTAR FPMA camera. The component was kept free to vary for the other instruments (note that the RGS parameters are linked to those of pn, while the FPMB parameters are linked to those of FPMA ). The contribution of the interstellar photoelectric absorption was modelled by the PHABS component, while to take the partial photoelectric absorption due to local matter into account, we used the model phabs*[c*cabs*phabs*(CompTT)+(1-c)*CompTT]. The first term in the brackets represents the partially absorbed Comptonisation spectrum, where C is a constant limited between 0 and 1 that expresses the partial covering fraction. The second PHABS component is the photo-absorption due to local matter, while CABS, which takes into account the effect of Thomson scattering, is linked to the second PHABS, under the assumption that local matter mainly causes this effect.
To obtain a constraint on photoelectric absorption, we firstly fit EPIC-pn and RGS data together, taking advantage of the good spectral coverage of the RGS at low energies, where the effect of photoelectric absorption is more relevant. We used the same strategy to constrain the partial photo-absorption by the local matter in the system. Because 4U 1822-371 has always shown a steady behaviour with little spectral variations, we do not expect a great difference between the parameters of the model of the two observations, although they were taken one year apart. After a first attempt, we realised that several emission features were present in the XMM-Newton and NuSTAR spectra, so that we added three Gaussian lines at energies of 6.49 keV, 6.67 keV, and 7.1 keV to improve the fit that are attributable to Fe I Kα, Fe XXV, and Fe I Kβ emission, respectively. In the NuSTAR spectrum, the Kα emission lines are less distinguishable, and the energy of the line at 7.1 keV was fixed during the fit because it showed a tendency to overlap with the other Gaussian profiles. We also improved the model by adding four emission lines at lower energies to fit localised features in the XMM-Newton band at 0.65 keV, 0.916 keV, 1.346 keV, and 2.002 keV, respectively. The centroids of the Gaussian components are in line with those reported by Iaria et al. (2013), and we associate them with transitions of O VII, Ne IX, Mg XI, and Si XIV ions, respectively.
The best-fit values obtained for the model parameters are shown and compared to the parameter reported by Iaria et al. (2013) in Table 2. Only part of the values found for the XMM-Newton spectra are consistent within the errors wit those reported previously. In particular, the equivalent hydrogen column density of the interstellar photoelectric absorption and the seed-photon temperature deviate from previous results. From the fit of the NuSTAR data, most of the parameters slightly deviate from those found in Iaria et al. (2013). In addition to the parameters related to the components PHABS and CABS (linked to the previous fit), the temperature of the electron cloud and seed photons reaches significantly higher values than what was found by Iaria et al. (2013) and for the XMM-Newton spectrum. The best-fit normalisation value of the Gaussian at 7.1 keV, which is 18% of the value found for the Fe I emission line, as well as its centroid energy, are in agreement with the association of this line with the Fe I Kβ transition. Figure 2 shows that the NuSTAR spectrum shows peculiar residuals in the iron emission region and from 10 to 40 keV. It is possible that the mismatch between the model and the data indicates that the spectrum needs a reflection continuum component because the latter residuals can be attributable to the Compton reflection hump, which is a typical signature of a reflection component.
 |
Fig. 2. Spectra and residuals in units of sigma with respect to the model: constant ⋅ phabs[c ⋅ cabs ⋅ phabs ⋅ (CompTT)+(1 − c)CompTT + 7 gaussian lines] for the XMM-Newton spectrum (top panel) and NuSTAR spectrum (bottom panel). Data were rebinned for visual purposes. |
Comparison of best-fit values for the parameters of the model described in the text, with those found by Iaria et al. (2013).
4.2. Testing a reflection component
To test the possible presence of a reflection component, we tried two different models: in MODEL 1, we used the self-consistent model RFXCONV, while in MODEL 2, the reflection is described by the combination of DISKLINE and PEXRIV models.
We initially modified the previous model by replacing COMPTT with another Comptonisation model (NTHCOMP), substituting the PHABS model with TBABS, that is, the Tuebingen-Boulder as for NS, ISM absorption model, setting the most recent ISM abundance and cross-section (see Wilms et al. 2000; Verner et al. 1996). We decided to analyse the XMM-Newton and NuSTAR spectra simulatenously because the Epic-pn and NuSTAR data overlap in the iron emission-line region, which guarantees a better statistics. Moreover, by merging the low-energy range of XMM-Newton and the higher-energy range of NuSTAR, we can analyse all the reflection spectral features (because the Compton hump is visible only in the NuSTAR spectrum because the Epic-pn one is limited to 10 keV). Nevertheless, we left the continuum parameters free to vary among the two spectra and constrained only the inner disc radius, the ionisation parameter, and the inclination angle to be the same. This is because when the ionisation parameter is left free, the best fit gives compatible values for the two spectra. Moreover, we do not expect changes in the inner disc radius because the accretion rate in this source is quite stable over the years. We improved the fit by removing the partially covering component and by introducing a soft black-body (BBODY in Xspec) with a temperature kTbb = 0.2 keV. We also added the reflection model, which is used to replace the broad Gaussian line at 6.7 keV, and kept the two Gaussian emission lines related to Fe I Kα and Kβ, respectively. As done before, the inter-calibration constant was set to 1 for the Epic-pn and FPMA data sets, as the normalisation relative to the NuSTAR spectra (as many other spectral parameters) are free and not fixed to those of XMM-Newton. The RGS spectral parameters were linked to the pn parameters, except for the inter-calibration constant, which was left free to vary, and similarly for the FPMB spectrum with respect to the FPMA spectrum.
The first reflection model that we used includes the convolution model RFXCONV (developed by Kolehmainen et al. 2011), which we used to reproduce only the reflection component. We applied to the continuum Comptonisation model NTHCOMP, whose parameters are linked to those of the continuum NTHCOMP that is already included in the model. The reflection component is smeared by the convolution model RELCONV (Dauser et al. 2010) to take Doppler and relativistic effects into account. The RELCONV model assumes a broken power law for the disc emissivity law, with two different indexes below and above a given radius Rbr. We forced the two indexes to assume the same value because our spectra are not sensitive enough to reveal a difference in the emissivity index.
The second model includes the DISKLINE model, which only describes the smeared iron emission line profile. This was combined with the PEXRIV model, which is used to represent only the reflection component, which is an exponentially cutoff power-law spectrum reflected from ionised material (Zdziarski et al. 1996). The parameters of PEXRIV that characterise the continuum spectrum were appropriately linked to those of the NTHCOMP component: we set the electron temperature to 2.7 times that of the NTHCOMP (as is appropriate for a saturated Comptonisation, see also Egron et al. 2013), and we linked the photon index of the power law in PEXRIV with the index of the Comptonisation component. In order to smear the spectrum for relativistic effects, we multiplied the reflection component by the convolution model RDBLUR (developed by Fabian et al. 1989). To fit the residuals evident in the spectra at low energies (see Fig. 2), we added several Gaussian components in addition to the two that are related to the iron K-shell emission, which are interpreted as the emission lines associated with the atomic transitions shown in Table 3. We also added an absorption edge at 9.44 keV, which can be traced back to the Fe XXVI K-edge that is necessary to fit the NuSTAR residuals. Because this feature is not required to fit the XMM-Newton spectrum, it may be a systematic feature, and therefore we froze its absorption depth to zero for the RGS and Epic-pn spectra.
Emission lines at soft X-ray energies.
We also tried to model the spectrum with other reflection models: with the self-consistent model RELXILLCP (Dauser et al. 2016), and with a variant of Model 2, where the component PEXRIV is replaced by PEXRAV. Model RELXILLCP should predict a soft excess in the data that might also account for the BBODY component; moreover, the PEXRIV component may not adequately describe the ionised reflection physics, and for this reason, we tried to replace it with PEXRAV, which assumes neutral matter in the disc. However, the RELXILLCP component proved unable to model the spectrum of this source adequately (the χ2/d.o.f. is 2193.0/1558 and 1636.3/1376 for the XMM-Netwon and NuSTAR data, respectively). The inadequacy of RELXILLCP in describing our data might be related to the temperature of the seed photons, which is fixed at 0.06 keV in the model. This is significantly different from the temperature of 0.6–0.8 keV that we find for this system. We added a low-energy exponential roll-off to the model using the EXPABS component to solve this problem, but without the EXPABS or BBODY component the XMM-Newton spectrum shows significant residuals at low energies (Fig. A.1). The associated χ2 over d.o.f. is 3830.3/2935 and 3472.6/2932 for the model without and with the BBODY component, respectively, and the best-fit parameters are reported in Table A.1. The model including PEXRAV achieved a good fit to the data, with a lower χ2 than what we obtain with PEXRIV (χ2/d.o.f. = 3291.1/2929), with consistent best-fit values of the parameters when the inner disc radius is fixed to 75 Rg. When this parameter was left free to vary, however, the fit is unstable and the best-fit values are physically inconsistent. We therefore conclude that these models do not provide a better fit to the data in our case. The results obtained by these fits are shown and discussed in Appendix A.
The shape of the relativistic iron line profile is mainly affected by different parameters that characterise the reflection models: the inner disc radius Rin, the system inclination with respect to our line of sight, the ionisation parameter ξ, and the reflection fraction defined as the fraction of the radiation reflected by the disc in terms of the solid angle Ω/2π that the disc subtends, as seen from the corona (Kolehmainen et al. 2011). In our first fit session, we realised that the model that includes the RFXCONV component was unable to constrain the value of the disc inner radius and the system inclination. Considering that the value of the system inclination has been discussed several times in the literature, we therefore decided to keep it frozen at the value found by Jonker et al. (2003), 82 degrees, while we kept the disc inner radius fixed at the magnetospheric radius expected for this source, that is, 75 Rg. We estimated this value as a fraction ϕ of the Alfvén radius RA, defined by the relation given by Frank et al. (2002),
where M1 is the mass of the NS in units of 1.4 M⊙, R6 is its radius in units of 106 cm, L37 is the luminosity in units of 1037 erg s−1, and μ30 is the magnetic dipole moment in units of 1030 G cm3. The parameter ϕ, set to ∼0.4, takes the case of accretion of matter through a geometrically thin disc into account, which reduces the size of the magnetosphere in the equatorial plane. Considering that Jonker & van der Klis (2001) have estimated a magnetic field of 8 × 1010 G assuming a luminosity at the Eddington limit of 1.8 × 1038 erg s−1, we obtained an inner radius of 149 km, that is, about 75 Rg (see also Iaria et al. 2015).
The best-fit values related to the models are reported in Table 4: the obtained parameters are consistent with the expected parameters, and the residuals (shown in Fig. 4) suggest a good fit of the data. We tested the improvement of the fit using the statistical test F-TEST by comparing our model, which includes the self-consistent reflection component, with a model containing the same components except for the reflection, which was instead fitted with another broad Gaussian at 6.7 keV that was used to model the Fe XXV fluorescence line. We obtain a probability of chance improvement of ∼9 × 10−34, meaning that the inclusion of the RFXCONV significantly improves the quality of the fit with respect to a simple Gaussian component.
Best-fit values for the parameters of the two models described in the text.
We also fitted the data to a model that uses a combination of PEXRIV and DISKLINE to fit the reflection component instead of RFXCONV. Although this model is not self-consistent in the sense that the iron line is not self-consistently calculated from the reflection spectrum, we find that this provides a better fit with respect to RFXCONV, as shown by the results reported in Table 4. It clearly improves the χ2 value and allows obtaining a constraint both for the system inclination and for the inner disc radius, perfectly in line with what we expect for the system. We tested the improvement of the fit using the statistical test F-TEST that compared the two relativistic models, and we obtained a probability of chance improvement of ∼5.4 × 10−22, meaning that MODEL 2 ensures a significantly better fit to the data.
Keeping the inclination parameter fixed, we tried to let the inner radius free to vary between 6 and 200 Rg in the RFXCONV model, and we note that the χ2 value improves significantly, ranging from 3430 with 2921 d.o.f. (degrees of freedom) to 3378 with 2920 (d.o.f.), reaching a best-fit value of 15 ± 3 Rg (see Table 4).
To test the χ2 improvement, we used the Xspec command steppar to perform a fit while stepping the value of the parameter through the range between 6 and 200 Rg, with 39 steps, using MODEL 3 and MODEL 2. The results related to the RFXCONV model show that the χ2 reaches a minimum at the best-fit value and increases rapidly as the radius increases, achieving higher but flat values between 50 and 125 Rg, and then increasing again for higher values of the radius (Fig. 3). This result suggests a geometry of the system in which the inner region of the accretion disc is close to the NS surface, although the presence of coherent pulsating emission and the estimated value of the magnetospheric radius make this low value for the inner radius of the accretion disc unlikely. However, this high improvement in the fit quality cannot be neglected; for this reason, we discuss this result in the following section. It is also noteworthy that this result is in contrast with what we find using the PEXRIV+DISKLINE to model the reflection spectrum because in this case, an absolute minimum of the χ2 is found for an inner disc radius in the range of  Rg (bottom panel of Fig. 3).
Rg (bottom panel of Fig. 3).
 |
Fig. 3. Variation in χ2 as a function of different values of the inner radius of the disc from 6 to 200 Rg using MODEL 3 (top panel) and MODEL 2 (bottom panel). The highlighted boxes in the figures show the best-fit value of the inner disc radius for the two models (Rin = 15 ± 3 Rg and |
 |
Fig. 4. Spectra and residuals in units of sigma with respect to the models described in the text. Top panel: fit to the model constant ⋅ edge ⋅ TBabs ⋅ (6gaussian + bbody + relconv ⋅ rfxconv ⋅ nthComp + nthComp) together with the residuals in units of sigma obtained by fixing the parameter Rin to 75 Rg, and those obtained when Rin assumes its best-fit value of 15 Rg. Bottom panel: fit to MODEL 2: constant ⋅ edge ⋅ TBabs ⋅ (6gaussian + bbody + diskline + rdblur ⋅ pexriv + nthComp) together with the residuals in units of sigma with respect to the model. |
5. Discussion
We analysed non-simultaneous XMM-Newton and NuSTAR observations of 4U 1822-371 by studying the average broad-band spectra and focusing on the possible presence of reflection features. As seen in the previous section, the addition of the reflection models improved the fit by reducing the residuals related to the iron fluorescence line and Compton reflection hump. The quality of our analysis was then ascertained using an F-test statistics, which returned a very low probability of chance improvement and confirmed the need of a reflection component, despite the high inclination of the system (note that the emission of the accretion disc decreases as the cosine of the inclination angle).
In the following, we first summarize the best-fit results, discussing the case in which the accretion disc extends close to the NS, and then we propose a possible scenario that can explain the observed features.
The continuum emission is well fitted by the BBODY and NTHCOMP components. The first marks the presence of a black-body emission at 0.196 keV that may be produced by the disc or the NS surface. The saturated Comptonisation spectrum is produced in an optically thick corona with τ ∼ 19 − 20 with an electron temperature for Model 1 and Model 2 of 3.31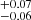 keV and 3.26 ± 0.03 keV, respectively, for the EPIC/pn plus RGS spectrum and 5.02 ± 0.03 keV and 4.87 ± 0.02 keV for the NuSTAR spectra. The mismatch between the temperatures of the Comptonisation component may depend on the different epoch in which the two observations were performed. Although the two spectra show small but significant differences, we do not expect a significant variation in the reflection continuum spectrum because the latter contributes to a small fraction of the total spectrum.
keV and 3.26 ± 0.03 keV, respectively, for the EPIC/pn plus RGS spectrum and 5.02 ± 0.03 keV and 4.87 ± 0.02 keV for the NuSTAR spectra. The mismatch between the temperatures of the Comptonisation component may depend on the different epoch in which the two observations were performed. Although the two spectra show small but significant differences, we do not expect a significant variation in the reflection continuum spectrum because the latter contributes to a small fraction of the total spectrum.
To understand the geometry of the system, we first determine which region produces the continuum emission. We calculated the black-body radius for both models, that is, the radius of the (spherical) region from which the black-body radiation is emitted. Then we inferred the size of the (spherical) region producing the seed photons experiencing inverse Compton scattering off the hot electrons of the corona. Matching the expression that defines the normalisation parameter in the BBODY component with the Stefan-Boltzmann law, which links the radiation flux to the fourth power of the temperature, we have that
where σ is the Stefan-Boltzmann constant that takes the value σ = 5.6704 × 10−5 erg/(cm2s K4), K is the black-body normalisation, which depends on the black-body observed flux, and D is the distance to the source, which was assumed to be 2.5 kpc (Mason & Cordova 1982). We did not take the error on the distance during the calculations of the parameters into account because Mason & Cordova (1982) reported the average value without an associated error. Taking these parameters into account, we find a black-body radius of 10.7 ± 0.3 km and 10.1 ± 0.4 km for Model 1 and Model 2, respectively. Both radii have to be corrected by a hardening factor of ∼1.4 because of distortions of the black-body spectrum mostly due to Thomson scattering (see e.g., Foster et al. 1986). This results in a black-body radius of 15.0 ± 0.4 km and 14.2 ± 0.6 km, respectively.
To determine the seed-photon emission radius, we analysed the best-fit values obtained for the Comptonisation spectrum and de-Comptonised it to trace the continuum emission before it interacted with the corona. From the two models, we extrapolated the value of the flux, Fx = (1.65–0.92) × 10−9 erg s−1 cm−2, and calculated the bolometric luminosity. We can derive the optical depth of the corona using the relation of Zdziarski et al. (1996),
Using the best-fit values of the parameters, we obtained values of the optical depth of τ = 19 ± 1 and 20.4 ± 0.2 for the two models. Hence we can state that the Comptonisation spectrum is emitted by an optically thick corona surrounding the region of the system in which the seed photons are emitted, as we expect from the fact that we found a saturated Comptonisation spectrum, with a shape quite similar to that of a black-body, with low values of the photon index and electron temperature.
In order to obtain the flux associated with the de-Comptonised spectrum fseed, we divided the bolometric flux of the Comptonisation component by the factor (1 + y), where y is the Compton y-parameter calculated under the assumption of the optically thick case (y = 9(1) − 10.6(2)), and we finally derived the seed-photon radius Rsp from the following equation:
obtaining a value of 0.9 ± 0.1 km and 1.16 ± 0.02 km for Models 1 and 2, respectively.
Because we found a black-body radius of 15.0 ± 0.4 km and 14.2 ± 0.6 km, which is compatible with the NS radius, it would be natural to associate the black-body emission region with the NS surface, while the value found for the seed-photon radius suggests an emission from a smaller region, such as the magnetic polar caps of the NS. The latter hypothesis may be justified by the coherent pulsations at 0.59 s detected by Jonker & van der Klis (2001). However, it is difficult to think that these two thermal emissions might originate in the compact object because the temperatures of the two components are very different (the seed-photon temperature is about 0.9 keV, and the black-body temperature is 0.2 keV) and because we would expect some (thermal black-body-like) contribution from the accretion disc (see below).
The value we found for the emissivity-law index for the reflection component agreeswith what we expect: we obtained a value of  and 2.3 ± 0.3 for Model 1 and Model 2, respectively. We expect an emissivity index of about 2-3 depending on whether the reflection spectrum is dominated by the illuminating flux coming from the central source (in this case, the flux illuminating the disc decreases with distance as r−2) or by the intrinsic disc emission (whose intensity decreases with distance approximately as r−3). We found a value of the ionisation parameter ξ (defined as ξ = 4πFx/neFabian et al. (2000), where Fx is the X-ray flux and ne is the electron number density,) of 9 ± 2 and a log ξ of 2.00
and 2.3 ± 0.3 for Model 1 and Model 2, respectively. We expect an emissivity index of about 2-3 depending on whether the reflection spectrum is dominated by the illuminating flux coming from the central source (in this case, the flux illuminating the disc decreases with distance as r−2) or by the intrinsic disc emission (whose intensity decreases with distance approximately as r−3). We found a value of the ionisation parameter ξ (defined as ξ = 4πFx/neFabian et al. (2000), where Fx is the X-ray flux and ne is the electron number density,) of 9 ± 2 and a log ξ of 2.00 for the two models, respectively, which is in line with the energies of the emission lines observed in the spectrum. This ionisation parameter implies a relatively low ionisation state of matter in the disc; the iron line is dominated by the Fe I-XX Kα transition (Fabian et al. 2000).
for the two models, respectively, which is in line with the energies of the emission lines observed in the spectrum. This ionisation parameter implies a relatively low ionisation state of matter in the disc; the iron line is dominated by the Fe I-XX Kα transition (Fabian et al. 2000).
As mentioned in the previous section, we found two different minima of the χ2 for Model 1, which differ for the values of the inner accretion disc radius. In the first case, the radius is truncated at the magnetospheric radius predicted for this pulsar, that is, 75 Rg, while for the second case, we obtained a configuration in which the disc extends closer to the NS (with an inner radius of 15 Rg), corresponding to a significantly lower χ2 value. When we used Model 2 to fit the spectrum, we find a clear minimum of the χ2 for a value for the inner disc radius of about ∼75 Rg, compatible with the estimated position of the magnetospheric radius of the source. In correspondence, we find different values of the reflection fraction: when the radius is kept frozen at 75 Rg, this parameter assumes the stable value of 0.61 , while when we let the inner radius free, the reflection fraction tends to the value of 0.9, suggesting that when the accretion disc approaches the central object, the portion of the radiation reflected by the disc has to increase. The reflection fraction of Model 2 is instead fixed at –1: we cannot simultaneously determine the reflection fraction and the normalisation of the PEXRIV component because its normalisation cannot be fixed to that of the Comptonisation spectrum. These parameters are defined in different ways and cannot be easily compared. Thus we decided to let the PEXRIV normalisation free and fixed the reflection fraction at its maximum expected value. However, in order to give an estimation of the reflection fraction in this case, we evaluated the flux of the reflection component (RDBLUR*PEXRIV+DISKLINE) and the flux of the Comptonisation continuum both in the energy range 0.1 − 100 keV in order to calculate their ratio. The reflection component corresponds to ∼7% of the Comptonisation component.
, while when we let the inner radius free, the reflection fraction tends to the value of 0.9, suggesting that when the accretion disc approaches the central object, the portion of the radiation reflected by the disc has to increase. The reflection fraction of Model 2 is instead fixed at –1: we cannot simultaneously determine the reflection fraction and the normalisation of the PEXRIV component because its normalisation cannot be fixed to that of the Comptonisation spectrum. These parameters are defined in different ways and cannot be easily compared. Thus we decided to let the PEXRIV normalisation free and fixed the reflection fraction at its maximum expected value. However, in order to give an estimation of the reflection fraction in this case, we evaluated the flux of the reflection component (RDBLUR*PEXRIV+DISKLINE) and the flux of the Comptonisation continuum both in the energy range 0.1 − 100 keV in order to calculate their ratio. The reflection component corresponds to ∼7% of the Comptonisation component.
In the following, we discuss the results described above considering a scenario in which the intrinsic luminosity of the central source is at the Eddington limit and most of this emission is blocked by the outer rim of the accretion disc. In this case, what we see is just the fraction of the intrinsic emission of the central source that is scattered along our line of sight by an extended optically thin corona.
5.1. Two coronae
The results discussed above are obtained considering the observed source luminosity of ∼1036 erg s−1. However, this luminosity may not be the intrinsic source luminosity. Three independent arguments are present in the literature, suggesting that the observed luminosity does not reflect the intrinsic luminosity emitted by the source: (i) Burderi et al. (2010) studied the orbital period evolution of the system and found a constraint on the orbital period derivative of Ṗ = 1.50(7) × 10−10 s s−1, which is three orders of magnitude larger than that calculated for a system assuming a conservative mass transfer. This constraint led the authors (see also Bayless et al. 2010; Iaria et al. 2011; Mazzola et al. 2019) to suggest a scenario in which the mass transfer rate from the companion is more than three times the Eddington limit (i.e. 1.8 × 10−8 M⊙ yr−1 for a NS of 1.4 M⊙), thus proposing a non-conservative mass-transfer scenario, where the mass in excess is expelled from the system. (ii) Hellier & Mason (1989) fitted an EXOSAT spectrum of 4U 1822-371 and found a ratio of the X-ray luminosity to the optical one of Lx/Lo ∼ 20, a factor 50 lower than the typical value usually found for LMXBs, which might indicate that the observed luminosity is reduced by at least a factor 50 compared to the intrinsic one. (iii) Jonker & van der Klis (2001) found a pulse period derivative for 4U 1822-371 of (−2.85 ± 0.04) × 10−12 s s−1, concluding that the source is spinning up (see also Mazzola et al. 2019; Iaria et al. 2015; Jain et al. 2010). Using the relation between observed luminosity and spin-up rate given by Ghosh & Lamb (1979), the authors find that for a luminosity of 1036 erg s−1, the NS magnetic field should be about 8 × 1016 G, which is extremely odd for an NS in a LMXB, while for a luminosity of 1038 erg s−1, around the Eddington limit, the expected value for the magnetic field is a more conceivable value of 8 × 1010 G.
Notwithstanding the high inclination angle of the system, we observe not only X-ray pulsations coming from the NS, but also a weak black-body spectrum that seems to be emitted from the NS surface, as well as signatures of a reflection component such as a Compton hump at high energy (10–30 keV) in the NuSTAR spectrum and a broad Fe emission line with a profile compatible with a smearing produced by Doppler effects in the inner accretion disc. A possible way to justify these pieces of evidence is to introduce an extended optically thin corona above the whole system that scatters only 1% of the intrinsic luminosity emitted by the central source into the line of sight (as proposed by Iaria et al. 2013). The consequence of this hypothesis is that all the flux that we observe is the part of the total emission that is produced by the source that is scattered along the line of sight. If the extended Corona is optically thin, so that τc ≪ 1, the scattered flux would be (Iaria et al. 2013)
Assuming a distance to the source of D = 2.5 kpc, to obtain an intrinsic luminosity of 1038 erg s−1 (Eddington limit) with an observed one of 1036 erg s−1, τc must be ∼0.01. The presence of a tenuous corona around the system can also explain the values found for the black-body radius and seed-photon radius. In deriving the value of the two radii, we considered the observed luminosity of 1036 erg s−1, while we should have used the intrinsic luminosity that is probably two orders of magnitude higher. Because the luminosity is proportional to R2, we must multiply the previous values by a factor 10 to determine the correct radii. With this, we obtain more reasonable values of Rbb = 140 km and Rsp = 11 km, respectively. In this case, we can identify the black-body emission as due to the inner rim of the accretion disc, which is truncated by the magnetosphere at ∼140 km from the NS centre, and the seed-photon emission region as the NS surface. This interpretation agrees with the fact that the black-body temperature is lower than the seed-photon temperature because the temperature in the system is expected to decrease at larger distances from the compact object. In this case, the best-fit value of the inner radius that is found using the reflection component RFXCONV of 15 ± 3 Rg is hard to reconcile with a black-body emission produced at 140 km (i.e. 70 Rg) from the NS.
5.2. Inner accretion disc radius
In the following, we show that a value for the inner disc radius as low as ∼15 Rg may be obtained for this source provided that the magnetic field is not stronger than 4 × 1010 G. To understand this, it is necessary to study the variation of the inner accretion disc radius of the system with respect to its mass accretion rate and magnetic field. For this purpose, we assumed a NS mass of 1.69 M⊙, as estimated by Iaria et al. (2011) for the 4U 1822-371 system, and a NS radius of R = 106 cm. We calculated the inner disc radius by varying the mass accretion rate in a range 1–10 times the Eddington limit (which is assumed to be 1.53 × 10−8 M⊙ yr−1 for a NS with a mass of 1.69 M⊙) and the magnetic field in a range of 1-8 × 1010 G, using the expression reported by Sanna et al. (2017),
where G is the gravitational constant, M is the NS mass assumed to be 1.69 M⊙, μ the star’s magnetic dipole moment, and Ṁ is the mass accretion rate. The factor ϕ depends on the structure of the accretion disc, but we can estimate it with the following expression Sanna et al. (2017):
where μ26, R6, Ṁ−9 and m are the NS magnetic moment in units of 1026 G cm3, the NS radius in units of 106 cm, the mass accretion rate in unit of 10−9 M⊙ yr−1, and the NS mass in units of solar mass. The mean molecular weight κ can be assumed equal to 0.615 for fully ionised matter, while the parameter α that expresses the disc viscosity in the standard Shakura-Sunyaev model is usually set equal to 0.1 (Shakura & Sunyaev 1973). The results are plotted in the top panel of Fig. 5: the region between the dotted lines at 12 and 18 Rg represents the range of our best-fit value. It is easy to understand that this value can be found with a different combination of Ṁ and B, for example assuming an accretion rate of few times Eddington and a magnetic field with a strength of few 1010 G.
 |
Fig. 5. Inner radius of the accretion disc plotted vs. the intrinsic source luminosity for different values of the magnetic field (solid lines), obtained with Eq. (6) (top panel). Derivative of the spin period as a function of luminosity for different values of the magnetic field on a logarithmic scale as indicated in the labels (bottom panel). The dotted lines shown in the plot are the logarithmic of −2.595(11)×10−12 s s−1, i.e. the spin period derivative reported in the literature (Mazzola et al. 2019). |
In order to verify whether these values may be plausible for 4U 1822-371, we used the Ghosh & Lamb (1979) equation, which links the spin-period derivative of the NS, its magnetic field and its luminosity, in order to understand which pairs of values return the spin period derivative reported in the literature for this source,
In this relation, M1 is the NS mass in units of 1 M⊙, I45 is the NS moment of inertia in units of 1045 g cm2, and P is the spin period of the source, that is, 0.5915669 s (Mazzola et al. 2019). The parameter n(ωs) is the dimensionless accretion torque that is a function of the fastness parameter ωs. When ωs < 0.95, we can use the following approximate expressions (Ghosh & Lamb 1979):
The values of luminosity and magnetic field used in the equations above vary in a range from 0.5 to 10 times the Eddington value and from 1010 to 8 × 1010 G, respectively. The results are shown in the bottom panel of Fig. 5, where the dotted line represents the derivative of the spin period measured for the source, (−2.59 ± 0.03) × 10−12 s s−1 (e.g., Mazzola et al. 2019). Figure 5 shows that a luminosity and a magnetic field of the order of those found with the Eq. (6) are compatible with Ṗ relative to the source. In other words, we may obtain a magnetospheric radius as small as ∼15 Rg assuming an intrinsic luminosity of a few times the Eddington limit and a magnetic field strength below 4 × 1010 G.
However, our discussion cannot fully justify this small inner accretion disc radius, which would be incompatible with the inner disc radius we infer from the black-body component (see above). Furthermore, although the assumed intrinsic luminosity may be plausible, the magnetic field value reported by several authors in the literature is ∼8 × 1010G. This value has been reported, for instance, by Iaria et al. (2015), who detected a possible cyclotron absorption feature at ∼0.7 keV in the low-energy spectrum of the source. On the other hand, the best-fit value constrained with MODEL 2 (Rin =  Rg), which ensures the best fit to our data with the lowest χ2, is perfectly in line with the value of luminosity and magnetic field expected for this system.
Rg), which ensures the best fit to our data with the lowest χ2, is perfectly in line with the value of luminosity and magnetic field expected for this system.
Alternatively, the low value indicated by the best-fit parameters of the reflection component RFXCONV, if confirmed, might be explained by an excess of smearing of the iron line. It is possible that although the line is actually emitted at 45 − 75 Rg, it appears more distorted than it should be, resulting in a lower inner disc value. The reason for this distortion is unclear (stronger Compton broadening than expected in the reflection models, blending of lines produced by different ions of iron, disc winds with high turbulent velocities), and may be connected to the accretion rate at the Eddington limit and how it changes the geometry of the disc that is viewed at this high inclination angle. Otherwise, considering that the best fit is obtained by separately fitting the iron line and the remaining reflection component, this result may be caused by a poor consistency between the line and the other reflection features, which may be due to the edge-on view and the fact that we do not directly observe the inner region, but just observe its emission scattered into the line of sight by the optically thin corona. The model with RFXCONV returns a warning related to the slope of the power law, that exceeds the tabulated range, suggesting again that more suitable models are required to describe the reflection component of sources such as 4U 1822-371.
5.3. Emission lines at low energies
As reported in Table 3, we detected four emission lines at soft X-rays that can be associated with emission from O VII, Ne IX, Mg XI, and Si XIV ions. We identified the Ne and Mg lines with the inter-combination lines, while the O and Si lines can easily be associated with the Lyman-alpha transition. To prove the improvement of the χ2 to the introduction of the four Gaussian lines, we used the F-test statistic. This method generally works when nested models are compared, and in principle, it should not be used to verify the addition of a Gaussian component in the model because the boundary of the possible values of the normalisation parameter is the null value (Protassov et al. 2002). However, when we extend the range of possible normalisation values to negative values, the F-test can be adopted to prove the improvement of the fit. We compared the best fit obtained with MODEL 2 with a fit in which we individually removed each of the Gaussian lines. We find that the addition of all the Gaussian lines has a significance higher than 6σ. Because of the expected emission lines at these energies, we can therefore state that these features are most probably real and not related to systematic features. In addition to the F-test, another method to ascertain the significance of the lines is considering their normalisation and comparing the latter with the error, at 1 sigma, associated with the parameter. In this case, the significance of the lines is also higher than 6 sigmas for the emission lines associated with O VII, Ne IX, and Mg XI, and higher than 3 sigmas for the line associated with Si XIV. Because the lines do not show evidence of Doppler effects, we propose that they are emitted from an outer region of the disc (in accordance with Iaria et al. 2011). However, further investigations are needed to accurately determine the emission region.
6. Conclusions
We have analysed XMM-Newton and NuSTAR observations of 4U 1822-371 with the aim of highlighting the presence of a reflection component in the spectrum, despite the high inclination angle of the system. We first tried to reproduce the result obtained by Iaria et al. (2013), who fitted the source spectrum without any reflection component, but with respect to this model, we obtained residuals at the iron line region and an excess of emission above ∼10 keV, reminiscent of a Compton hump caused by a reflection component. We tried to fit the complex residuals at the iron line region with three Gaussian lines, but achieved unsatisfactory results. Therefore we tested two reflection models, RFXCONV and DISKLINE + PEXRIV, to fit the spectrum. We obtained a significant improvement in the fit, suggesting a detection of this component at the 7 sigma confidence level. To our knowledge, no reflection component in a source with this high inclination has been observed before because reflection should be very faint and difficult to detect in a source with an inclination angle higher than 80 degrees. The main continuum emission is well fitted by a thermal black-body emission, with a temperature of 0.2 keV, and a satured Comptonised component with an electron temperature of 3.26 − 4.87 keV, generated by the inverse Compton scattering of seed photons with a temperature of 0.8 keV in an optically thick corona (τ = 19 − 20), located in the innermost region of the system, possibly around the NS. We observe several emission lines that can be associated with O VIII, Ne IX, Mg XI, and Si XIV in the RGS spectrum. These lines may be produced in the bulge in the outer region of the accretion disc, as previously proposed (e.g., Iaria et al. 2011), although a detailed orbital phase-resolved spectral analysis is required to corroborate this hypothesis (Somero et al. 2012).
We updated the orbital ephemeris of the source by adding two eclipse arrival times derived from NuSTAR (2018) and Swift (2007) observations to those reported by Mazzola et al. (2019). We fitted the delays of the eclipse arrival times with a quadratic, a cubic, and a sinusoidal model. We proved that by adopting the latter two instead of the quadratic model, the fit significantly improves. In this way, we found an orbital period Porb = 5.57063023(34) h and a Ṗorb value of 1.51(5) × 10−10 s s−1. In line with other results present in the literature, we assumed that the source is emitting at an intrinsic Eddington luminosity of 2 × 1038 erg s−1, even though the observed luminosity is just 1036 erg s−1. To explain the discrepancy between the intrinsic and the observed luminosity, as well as the presence of a reflection component in the spectrum, an extended optically thin corona (τ ∼ 0.01) around the whole system has been suggested, which would scatter about 1% of the intrinsic luminosity produced by the central source along the line of sight. Because the whole emission is scattered, this mechanism enables us to observe a reflection component, which otherwise would be very difficult to detect at such a high inclination angle.
In our analysis, we found a singular feature related to the inner accretion disc radius: the best-fit value of the inner radius achieved with the relativistic component RFXCONV is 15 ± 3 Rg, with a clear improvement of the χ2 over the fit in which the inner radius was fixed to 75 Rg, which is the theoretically predicted value of the magnetospheric radius in this source. We discussed the possibility that the iron line is really emitted in a disc region so close to the compact object and concluded that this hypothesis at the Eddington luminosity requires a magnetic field of 1010 G, which deviates from the value reported in the literature for this source (of 8.8 × 1010Iaria et al. 2015). This result would also be at odds with the inferred radius of the black-body emission region of ∼140 km that we identify with the inner rim of the accretion disc. Alternatively, the iron line might be emitted at the predicted magnetospheric radius, but the line profile appears to be more smeared than it should be, resulting in a lower value of the inner radius. The mechanism(s) originating this line distortion are unclear and might be related to the accretion rate at the Eddington limit and to the scattering the line photons undergo in their travel along the line of sight. However, using a combination of DISKLINE and PEXRIV to fit the reflection component, we obtained an inner disc radius of ∼75 Rg and a (slightly) better quality of the fit, showing that this value is still model dependent. Future high-statistics broad-band observations may help to solve this ambiguity.
Acknowledgments
The authors acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.0 from INAF mainstream (PI: A. De Rosa), and from the HERMES project financed by the Italian Space Agency (ASI) Agreement n. 2016/13 U.O and from the ASI-INAF Accordo Attuativo HERMES Technologic Pathfinder n. 2018-10-H.1-2020. We also acknowledge support from the European Union Horizon 2020 Research and Innovation Framework Programme under grant agreement HERMES-Scientific Pathfinder n. 821896. R. I. and T. D. S. acknowledge the research grant iPeska (PI: Andrea Possenti) funded under the INAF national call Prin-SKA/CTA approved with the Presidential Decree 70/2016. R. I. acknowledges financial contribution from the agreement ASI-INAF n.2017-14-H.0, from INAF mainstream (PI: T. Belloni).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bayless, A. J., Robinson, E. L., Hynes, R. I., Ashcraft, T. A., & Cornell, M. E. 2010, ApJ, 709, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Riggio, A., et al. 2010, A&A, 515, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [Google Scholar]
- Dauser, T., García, J., Walton, D. J., et al. 2016, A&A, 590, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Egron, E., Di Salvo, T., Motta, S., et al. 2013, A&A, 550, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [Google Scholar]
- Fabian, A., Iwasawa, K., Reynolds, C., & Young, A. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. J., Ross, R. R., & Fabian, A. C. 1986, MNRAS, 221, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., Raine, D., & King, B. 2002, Accretion Power in Astrophysics, Accretion Power in Astrophysics (Cambridge University Press) [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [Google Scholar]
- Hellier, C., & Mason, K. O. 1989, MNRAS, 239, 715 [CrossRef] [Google Scholar]
- Iaria, R., di Salvo, T., Burderi, L., et al. 2011, A&A, 534, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iaria, R., Di Salvo, T., D’Aì, A., et al. 2013, A&A, 549, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iaria, R., Di Salvo, T., Matranga, M., et al. 2015, A&A, 577, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jain, C., Paul, B., & Dutta, A. 2010, MNRAS, 409, 755 [CrossRef] [Google Scholar]
- Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., van der Klis, M., & Groot, P. J. 2003, MNRAS, 339, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Kolehmainen, M., Done, C., & Díaz Trigo, M. 2011, MNRAS, 416, 311 [NASA ADS] [Google Scholar]
- Madsen, K. K., Grefenstette, B. W., Pike, S., et al. 2020, ArXiv e-prints [arXiv:2005.00569] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [Google Scholar]
- Mason, K. O., & Cordova, F. A. 1982, ApJ, 262, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzola, S. M., Iaria, R., Di Salvo, T., et al. 2019, A&A, 625, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmar, A. N., Oosterbroek, T., Del Sordo, S., et al. 2000, A&A, 356, 175 [NASA ADS] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., Fabian, A. C., & Young, A. J. 1999, MNRAS, 306, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Riggio, A., Burderi, L., et al. 2017, MNRAS, 469, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Somero, A., Hakala, P., Muhli, P., Charles, P., & Vilhu, O. 2012, A&A, 539, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Another reflection component
As discussed in Section 4.2, we tried to fit the data using two other reflection models, RELXILLCP and a variant of Model 2, where the PEXRIV component is replaced by PEXRAV. We initially fitted the XMM-Newton and NuSTAR data separately using the model RELXILLCP, which is expected to predict the soft excess in the data that we previously described with the BBODY component. However, it proved unable to model the spectrum of this source adequately, and as shown in Fig. A.1, XMM-Newton data show peculiar residuals in the Epic-pn band (the χ2/dof is 2193.0/1558 and 1636.3/1376 for the XMM-Netwon and NuSTAR data, respectively). We have to take into account that RELLXILCP includes a Comptonisation spectrum, with a temperature of the soft seed-photons fixed at 0.06 keV, which differs from the seed-photon temperature that we find for this source (0.6-0.8 keV). To solve this problem, we added a low-energy exponential roll-off to the model using the EXPABS component in order to mimic a cut-off at the seed-photon temperature. We also tried to model our data using RELXILLCP to describe the reflection component alone. We set the reflection fraction to -1, but allowed the normalisation to vary and linked the continuum parameters to those of the continuum fitted by the NTHCOMP component. Differently from our best-fit model, RELXILLCP fails to reach stable values of Rin and inclination angle. We hence fixed these values at the expected values, while the other parameters such as the ionisation parameter assume different values depending on the dataset (see Tab A.1). We cannot use the F-test statistics to compare this fit with the fit that includes RFXCONV because in this case, the lower chi square has the higher number of degrees of freedom. Therefore it is preferable to choose the model with RFXCONV because the associated fit presents a lower chi square despite the higher number of degrees of freedom. It is clear that using the RELXILLCP component does not ensure a better fit of the model to the data in this case. Furthermore, using RELXILLCP alone does not fit the soft excess in the data that is modelled with the black-body spectrum, and the data still require a low-energy component to fit soft residuals in the Epic-pn band (Fig. A.1).
 |
Fig. A.1. Spectra and residuals in units of sigma with respect to MODEL 4, defined as constant ⋅ edge ⋅ tbabs ⋅ (6gaussian + relxillCp), for the XMM-Newton spectrum (top panel) and NuSTAR spectrum (bottom panel), respectively. Data were rebinned for visual purposes. |
Comparison of best-fit values for the parameters of the models that includes different reflection component.
Although MODEL 2 ensures the best fit to data with the lowest χ2, the component PEXRIV may be not appropriate to model the continuum because it may not be suitable for describing a highly ionised reflection spectrum (Ross et al. 1999). Therefore we tried to replace it with PEXRAV, an exponentially cut-off power-law spectrum reflected from neutral material (Magdziarz & Zdziarski 1995). We performed the fit and kept the inner disc radius fixed at 75 Rg because if this parameter is left free to vary, the fit is unstable and the best-fit values obtained are physically inconsistent. As shown in Tab. A.1, we obtain reasonable values of the parameters even if the inclination angle is too small with respect to the expected value. Although the model that includes PEXRAV shows a slight improvement of the fit, by using PEXRIV, we can constrain the ionisation parameter, and the whole set of best-fit values obtained with this model is coherent with what we expect from the source. This shows that PEXRIV does not affect the results too much, also considering that the ionisation parameter obtained using the other models is quite low and PEXRIV should be able to adequately describe the effects of a mild ionisation.
All Tables
Eclipse arrival times (top part) and best-fit values for the parameters derived with the different models described in the text (quadratic, cubic, and LQS) (bottom part).
Comparison of best-fit values for the parameters of the model described in the text, with those found by Iaria et al. (2013).
Comparison of best-fit values for the parameters of the models that includes different reflection component.
All Figures
 |
Fig. 1. Delays of the eclipse arrival times as a function of the orbital cycle for the LQS model (top panel). Residuals in units of σ, obtained with the cubic (black) and LQS (red) model, respectively (bottom panel). |
| In the text | |
 |
Fig. 2. Spectra and residuals in units of sigma with respect to the model: constant ⋅ phabs[c ⋅ cabs ⋅ phabs ⋅ (CompTT)+(1 − c)CompTT + 7 gaussian lines] for the XMM-Newton spectrum (top panel) and NuSTAR spectrum (bottom panel). Data were rebinned for visual purposes. |
| In the text | |
 |
Fig. 3. Variation in χ2 as a function of different values of the inner radius of the disc from 6 to 200 Rg using MODEL 3 (top panel) and MODEL 2 (bottom panel). The highlighted boxes in the figures show the best-fit value of the inner disc radius for the two models (Rin = 15 ± 3 Rg and |
| In the text | |
 |
Fig. 4. Spectra and residuals in units of sigma with respect to the models described in the text. Top panel: fit to the model constant ⋅ edge ⋅ TBabs ⋅ (6gaussian + bbody + relconv ⋅ rfxconv ⋅ nthComp + nthComp) together with the residuals in units of sigma obtained by fixing the parameter Rin to 75 Rg, and those obtained when Rin assumes its best-fit value of 15 Rg. Bottom panel: fit to MODEL 2: constant ⋅ edge ⋅ TBabs ⋅ (6gaussian + bbody + diskline + rdblur ⋅ pexriv + nthComp) together with the residuals in units of sigma with respect to the model. |
| In the text | |
 |
Fig. 5. Inner radius of the accretion disc plotted vs. the intrinsic source luminosity for different values of the magnetic field (solid lines), obtained with Eq. (6) (top panel). Derivative of the spin period as a function of luminosity for different values of the magnetic field on a logarithmic scale as indicated in the labels (bottom panel). The dotted lines shown in the plot are the logarithmic of −2.595(11)×10−12 s s−1, i.e. the spin period derivative reported in the literature (Mazzola et al. 2019). |
| In the text | |
 |
Fig. A.1. Spectra and residuals in units of sigma with respect to MODEL 4, defined as constant ⋅ edge ⋅ tbabs ⋅ (6gaussian + relxillCp), for the XMM-Newton spectrum (top panel) and NuSTAR spectrum (bottom panel), respectively. Data were rebinned for visual purposes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






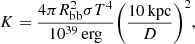
![$$ \begin{aligned} \Gamma +\frac{1}{2}=\left[\frac{9}{4}+\frac{1}{\left(k T / m_{\rm e} c^{2}\right) \tau (1+\tau / 3)}\right]^{1 / 2}. \end{aligned} $$](/articles/aa/full_html/2021/10/aa40557-21/aa40557-21-eq69.gif)





![$$ \begin{aligned}&n\approx 1.39\left\{ 1-\omega _{s}\left[4.03\left(1-\omega _{s}\right)^{0.173}-0.878\right]\right\} \left(1-\omega _{s}\right)^{-1} , \nonumber \\&\omega _{s} \approx 1.35\; \mu _{30}^{6 / 7} M_{1}^{-2/7} \left(P L_{37}^{3 / 7}\right)^{-1} . \end{aligned} $$](/articles/aa/full_html/2021/10/aa40557-21/aa40557-21-eq78.gif)