| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202140729 | |
| Published online | 09 August 2021 | |
Stark broadening for Br VI and Kr V-VII lines in hot star atmospheres
1
Observatoire de Paris, PSL University, Sorbonne Université, CNRS, LERMA,
92190
Meudon,
France
e-mail: sylvie.sahal-brechot@obspm.fr
2
GRePAA, Laboratoire de Spectroscopie et Dynamique Moléculaire, Faculty of Sciences of Bizerte, Carthage University,
Tunisia
e-mail: haykel.elabidi@fsb.rnu.tn
3
Department of Physics, Common First Year Deanship, Umm Al-Qura University,
Makkah Almukarramah,
Saudi Arabia
e-mail: haelabidi@uqu.edu.sa
Received:
4
March
2021
Accepted:
27
June
2021
Context. This paper provides missing Stark broadening of the Br VI and Kr V-VII lines recently discovered in the ultraviolet spectrum of the hot white dwarf RE 0503–289 and investigates the importance of the Stark broadening mechanism versus the Doppler mechanism in that star. As far as we know, this is the first time that Stark widths of Br VI and Kr V-VII lines have been calculated.
Aims. The recent discovery of new lines of Br VI and Kr V-VII encourages us to provide their Stark broadening to enrich the STARK-B database and for use in interpretations of the observed spectra.
Methods. We used our quantum mechanical method for calculating electron impact broadening to provide Stark widths. The method starts with an evaluation of the structure and collision parameters using the University College London codes SUPERSTRUCTURE/DISTORTED WAVE/JAJOM, which are adapted to the line broadening calculations. We then used the collision parameters to calculate the line widths using our programs.
Results. We provide the missing widths of 35 lines of Br VI and Kr V-VII at different electron temperatures and at density Ne = 1017 cm−3. We find that the Stark broadening mechanism is preponderant compared to the Doppler one for almost all the plasma conditions of the considered DO white dwarf atmospheres.
Key words: line: profiles / atomic processes / scattering / atomic data / white dwarfs / stars: individual: RE 0503-289
© ESO 2021
1 Introduction
Stellar-atmosphere modelling demands reliable measurements and calculations of atomic and line broadening data. Rauch et al. (2016a) showed that the lack of atomic data of many elements, especially for high ionisation stages (IV-VII), is an obstacle to their abundance analysis. The analyses and interpretation of the spectra recorded by the spectrographs are performed using mainly atomic and line broadening parameters of the emitters. Stark broadening is the principal broadening mechanism of the line wings of the atmospheres of hot stars of the principal sequence, and of white dwarfs. Consequently, neglecting the Stark broadening can significantly affect the accuracy of element abundance determination. Here we are interested in white dwarfs, which were known in the past as hydrogen-rich (DA) and helium-rich (DB) types. The density of charged particles in white dwarf atmospheres is very high so that collisions have a high impact on the broadening of their spectral lines. Contrary to Doppler broadening, Stark broadening depends on the electron density, and then there is a significant difference between Stark and Doppler broadening in white dwarf atmospheres (Aloui et al. 2019a). Many recent works (Werner et al. 2012, 2018a,b) have shown the existence of spectral lines emitted by heavy elements in the ultraviolet (UV) spectra of hot DO white dwarfs. Up to now, 18 trans-iron elements (Z ≥ 30) have been identified in the RE 0503–289 star (Rauch et al. 2020), which is a hot DO-type white dwarf. A further eight trans-iron elements (Zn, Ga, Ge, Se, Sr, Sn, Te, I) were found in PG 0109+111 (Hoyer et al. 2018). The white dwarf RE 0503–289 was described as unique in Hoyer et al. (2018) because of the discovery of a large number of trans-iron elements in its photosphere, since 484 lines of trans-iron elements (including Br and Kr) were recently identified in the DAO-type white dwarf, especially BD–22°3467 (Löbling et al. 2019).
We focus in the present work on two ions: firstly Br VI, lines of which have been detected in the spectrum of the DO white dwarfs RE 05030-289 and HD 149499 B (Werner et al. 2018a), and secondly Kr V-VII ions, lines of which have been detected for the first time in the far ultraviolet (FUV) spectrum of the DO white dwarf RE 05030–289 (Werner et al. 2012; Rauch et al. 2016b). Spectra have been taken with the Far Ultraviolet Spectroscopic Explorer (FUSE) and the Hubble Space Telescope (HST). The evaluation of Stark broadening of these lines is primordial for stellar-atmosphere modelling of hot stars (A, B, O) and white dwarfs. As far as we know, there are no other line broadening calculations for these ions. The lines considered here are those listed in two papers (Werner et al. 2018a; Rauch et al. 2016b). In addition, we investigate the influence of Stark broadening versus Doppler broadening in the atmospheres of hot white dwarfs.
To perform our calculations, we have used our quantum mechanical method (Elabidi et al. 2004, 2008), which has been applied many times (Elabidi & Sahal-Bréchot 2018, 2019; Aloui et al. 2018, 2019a,b) and has given good results compared to fother approaches. We have also used it to study several physical problems such as fine structure effects (Elabidi et al. 2009), strong collisions and quadrupolar potential contributions to Stark broadening (Elabidi et al. 2014), and scaling of line widths with temperature and ionic charge (Elabidi & Sahal-Bréchot 2018, 2019). Recently, Elabidi (2021) investigated the systematic trend of Stark broadening with the spectroscopic charge Z, where new Stark broadening of about 160 lines has been calculated for eight neon-like ions, and a linear relation between log (W) and log (Z) has been established. This relation allows us to predict the considered line widths for all the Ne-like ions between Mg III and Br XXVI.
In Sect. 2, we introduce our theoretical background and the numerical procedure used in our calculations, and we discuss the validity conditions of the approximations used in Sect. 3. We present our Stark broadening results in Sect. 4. We present a study of the importance of Stark and Doppler broadening mechanisms in the spectrum of hot DO white dwarfs in Sect. 5 and we conclude in Sect. 6.
2 Theory and numerical procedure
Our quantum method for electron impact broadening is described in Elabidi et al. (2004, 2008) and Aloui et al. (2018). Here we present onlya brief description. The calculations are made within the frame of the impact approximation. The starting point is the general expression of the electron impact broadening of a spectral line arising from a transition from an upper level i to a lower one, f (Baranger 1958a):
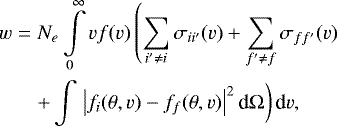 (1)
(1)
where Ne is the electron density, v the velocity of the scattered electron, f(v) the Maxwellian electron velocity distribution and 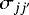 (j = i∕f) are inelastic cross sections connecting the initial or final levels (j) to their perturbing (j′) ones. The fj(θ, v) (j = i∕f) are elastic scattering amplitudes for the emitter in the initial and final levels, and the integral is performed over the scattering angle θ, where dΩ is the element of solid angle. In Elabidi et al. (2004, 2008), fine structure effects and relativistic corrections resulting from the non-validity of the LS coupling approximation for the target have been taken into account by using the intermediate coupling schema. We have deduced the following formula of the full width at half maximum (FWHM) W expressed in angular frequency units:
(j = i∕f) are inelastic cross sections connecting the initial or final levels (j) to their perturbing (j′) ones. The fj(θ, v) (j = i∕f) are elastic scattering amplitudes for the emitter in the initial and final levels, and the integral is performed over the scattering angle θ, where dΩ is the element of solid angle. In Elabidi et al. (2004, 2008), fine structure effects and relativistic corrections resulting from the non-validity of the LS coupling approximation for the target have been taken into account by using the intermediate coupling schema. We have deduced the following formula of the full width at half maximum (FWHM) W expressed in angular frequency units:
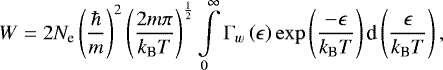 (2)
(2)
where m is the electron mass, kB the Boltzmann constant, Ne the electron density, T the electron temperature, ϵ the incident electron energy, and
![\begin{eqnarray*}\Gamma _{w}(\epsilon) &=&\sum_{\substack{J_{i}^{T}J_{f}^{T} \\lK_{i}{K_{f}}}} \frac{(2K_{i}+1) (2K_{f}+1) (2J_{i}^{T}+1) (2J_{f}^{T}+1)}{2} \nonumber \\&&\times \left\{\begin{array}{c}J_{i}K_{i}l \\K_{f}J_{f}1\end{array}\right\} ^{2}\left\{\begin{array}{c}K_{i}J_{i}^{T}s \\J_{f}^{T}K_{f}1\end{array}\right\} ^{2} \nonumber \\&&\times \left[1-\left(\Re(\mathbb{S}_{i})\Re(\mathbb{S}_{f})+\Im(\mathbb{S}_{i})\Im(\mathbb{S}_{f})\right) \right],\end{eqnarray*}](/articles/aa/full_html/2021/08/aa40729-21/aa40729-21-eq4.png) (3)
(3)
where Lj+Sj = Jj, Jj+l = Kj and Kj+s = 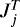 (j = i∕f). The orbital and spin momenta of the emitter are L and S, l and s are those of the perturber (electron), and all the parameters denoted by T refer to the system of electron+ion. The scattering matrix elements are denoted by
(j = i∕f). The orbital and spin momenta of the emitter are L and S, l and s are those of the perturber (electron), and all the parameters denoted by T refer to the system of electron+ion. The scattering matrix elements are denoted by 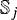 while
while 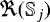 and
and 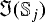 are their real and imaginary parts for the level j (j = i∕f). These matrices are written in the base of the intermediate coupling schema and evaluated at the same perturber energy
are their real and imaginary parts for the level j (j = i∕f). These matrices are written in the base of the intermediate coupling schema and evaluated at the same perturber energy 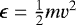 . The terms
. The terms  are the 6–j symbols.
are the 6–j symbols.
To achieve the calculations of Eq. (3), we need to evaluate 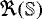 and
and 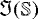 in the initial i and final f levels. This task is performed using the UCL codes SUPERSTRUCTURE (SST), DISTORTED WAVE (DW), and JAJOM, which we have adapted to line broadening calculations (Elabidi et al. 2008).
in the initial i and final f levels. This task is performed using the UCL codes SUPERSTRUCTURE (SST), DISTORTED WAVE (DW), and JAJOM, which we have adapted to line broadening calculations (Elabidi et al. 2008).
2.1 Atomic structure
Energy levels and atomic radiative data are computed using the SST code (Eissner et al. 1974), where configuration interactions are taken into account. The radial functions are calculated assuming a scaled Thomas-Fermi-Dirac-Amaldi (TFDA) potential depending on the scaling parameters λl. Relativistic corrections are taken into account through the Breit-Pauli approach (Bethe & Salpeter 1957) as a perturbation to the non-relativistic Hamiltonian. The SST program also produces the term coupling coefficients (TCCs) that will be used later in the scattering part (Elabidi et al. 2004).
2.2 Electron-ion scattering
The scattering problem is treated in two parts: firstly, we use the DW code of Eissner (1998) to calculate the reactance matrices in LS coupling approximations. The distorted waves approach is adopted in the code DW. Secondly, the code JAJOM (Saraph 1978) uses these reactance matrices and the TCCs to calculate collision strengths in intermediate coupling. In the present work, we have transformed JAJOM into JAJPOLARI (Elabidi & Dubau, unpublished results) to produce the reactance matrices R in intermediate coupling. Then, the program RtoS (Dubau, unpublished results) evaluates the real and the imaginary parts of the scattering matrix using the expressions (conserving the unitarity of the S matrices)
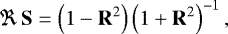 (4)
(4)
The matrices in Eqs. (4) and (5) enter our code when evaluating expression (3) and then expression (2) of the Stark broadening. In our calculations, the sum over the perturber (electron) orbital momentum l in expression (3) is carried out in the codes DW and JAJPOLARI from l = 0 to lmax= 19.
3 Approximations and validity conditions
We performed line broadening calculations for several temperatures and one electron density, 1017 cm−3. The choice of this density value is based firstly on the common density of the considered white dwarf atmospheres (1017 −1020 cm−3, and secondly it is chosen to respect the ideality of the plasma and the impact approximation. In the following sections, we examine theapproximations used in our calculations and their validity conditions.
3.1 Impact approximation
The impact approximation states that the interactions are separated in time. This means that the atom interacts with only one perturber at a given time, so the duration τ of an interaction must be much smaller than the mean interval time Δt between two successive collisions (Baranger 1958b): τ ≪ Δt, where Δt is of order of the inverse of collisional line width W. The condition of impact approximation can be written
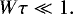 (6)
(6)
The duration of an interaction τ can be expressed as 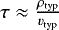 , where ρtyp is a typical impact parameter, and vtyp represents amean typical velocity of the incident electron. The collisional line width W can be roughly expressed as
, where ρtyp is a typical impact parameter, and vtyp represents amean typical velocity of the incident electron. The collisional line width W can be roughly expressed as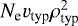 . Thus, the validity condition of the impact approximation can be written as
. Thus, the validity condition of the impact approximation can be written as
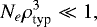 (7)
(7)
where 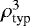 is called the ’collision volume’ and must be smaller than the volume per perturber
is called the ’collision volume’ and must be smaller than the volume per perturber 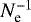 . In other words,the perturbers are independent and their effects are additive. We express the impact parameter in terms of the temperatureand the orbital momentum of the perturber: we use the fact that the classical angular momentum l = ρmv can be related to the eigenvalues of the corresponding quantum-mechanical operator L2 by
. In other words,the perturbers are independent and their effects are additive. We express the impact parameter in terms of the temperatureand the orbital momentum of the perturber: we use the fact that the classical angular momentum l = ρmv can be related to the eigenvalues of the corresponding quantum-mechanical operator L2 by 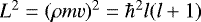 and the velocity
and the velocity 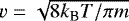 , and we find that a typical ‘collision volume’ can be written as (with Ttyp = 105 K and ltyp = 19):
, and we find that a typical ‘collision volume’ can be written as (with Ttyp = 105 K and ltyp = 19):
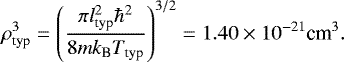 (8)
(8)
If Ne = 1017 cm−3, we find that 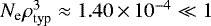 . Consequently, the impact approximation is valid with the electron density Ne = 1017 cm−3. We check that this condition is valid for all the considered temperature values and for electron densities lower than 1021 cm−3.
. Consequently, the impact approximation is valid with the electron density Ne = 1017 cm−3. We check that this condition is valid for all the considered temperature values and for electron densities lower than 1021 cm−3.
3.2 Complete collision approximation
The complete collision approximation states that a radiating atom has no time to emit (or absorb) a photon during the collision process. In other words, the atom – radiation and atom – perturber interactions are decoupled, which implies that the collision must be considered as instantaneous in comparison with the time 1∕Δω, characteristic of the evolution of the excited state under the effect of the interaction with radiation, where Δω is the detuning. So we can write this approximation as
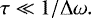 (9)
(9)
In line wings, the atom may emit photons before the perturber has any time to move and the complete collision approximation breaks down but it always remains valid in the line centre. If the impact approximation and the complete collision approximation are both valid, the line broadening theory becomes an application of the theory of collisions between theradiating atom and the surrounding perturbers, where we evaluate the real and imaginary parts of the S−matrix from Eqs. (4) and (5) to enter expression (3) and then the Stark broadening expression (2).
3.3 Approximation of isolated lines
A line is considered as isolated if non-degenerate energy levels broadened by collisions do not overlap. If 2Wi and 2Wi are the corresponding level widths, then the condition of isolated lines can be written as
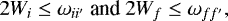 (10)
(10)
where 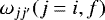 is the frequency difference between level j and its nearest perturbing one. The line is isolated if
is the frequency difference between level j and its nearest perturbing one. The line is isolated if 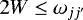 where W is the total width at half maximum of the line and
where W is the total width at half maximum of the line and 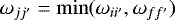 . From Eq. (10), we can deduce the higher limit Nmax of electron density for which the line can be considered as isolated as
. From Eq. (10), we can deduce the higher limit Nmax of electron density for which the line can be considered as isolated as
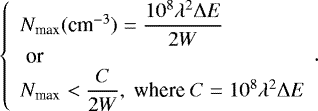 (11)
(11)
In Eq. (11), λ is the wavelength of the transition expressed in Å, ΔE is the energy difference (in cm−1) between the two levels, and W is the total width of the line calculated at the considered electron density; here 1017 cm−3. Thus C∕W provides an estimation of the higher density at which the line may be treated as isolated and then the presented values may be used. In the tables of Stark broadening results, we calculate factor C for each line.
3.4 Plasma ideality
Plasma shielding effects due to electron and ion interaction can be important in the physical conditions of white dwarf atmospheres because of their high density. With the increase of density or decrease of temperature, the plasma becomes non-ideal. We establish the criterion of plasma ideality using the Debye length (or Debye radius) RD, which is defined in plasma physics as the distance over which electric charges screen out the electric fields:
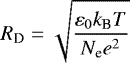 (12)
(12)
where ε0 is the permittivity of free space and e is the elementary charge in S.I. units. To keep a plasma ideal the number of particles (perturbers) ND inside the Debye sphere of radius RD must be greater than 1. This can be written as (Dimitrijevic et al. 1991)
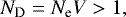 (13)
(13)
where 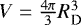 is the volume of the Debye sphere. We can write inequality Eq. (13) as
is the volume of the Debye sphere. We can write inequality Eq. (13) as
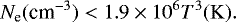 (14)
(14)
As an example, if we take the lowest temperature T = 5 × 104 K, we find that Ne < 2.38 × 1020 cm−3. So our plasma is ideal for the considered density Ne = 1017 cm−3 and temperatures. Stark broadening can therefore be deduced for other densities using a linear relationship between W and Ne (for a given temperature) provided that these densities are lower than 1023 cm−3. In Fig. 1, we present couples (T, Ne) at which the plasma can be considered as ideal.
 |
Fig. 1 Temperatures and densities at which a plasma is treated as ideal. |
3.5 Distorted wave (DW) approximation for electron collision
The emitter–electron system is described by an anti-symmetric total wave-function Ψ consisting in a wave-function ψ for the N−electrons of the emitter and a scattered free electron wave-function ϕ:
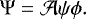 (15)
(15)
Equation (15) does not couple emitter states. This means that the distortion caused by the emitter potential on the wave functions of the projectile before and after the collision is included but in an approximate manner. Eissner & Seaton (1972) show that the condition of neglecting the coupling between atomic states is always satisfied for contributions from sufficiently large total orbital angular momentum. For highly ionised systems (in practice more than about two or three times ionised), the method can be used for the calculation of all angular momentum contributions. It has been also shown that the agreement between distorted wave results and more sophisticated close-coupling results is known to be good for such highly ionised atoms. In fact, Burgess et al. (1991) computed partial collision strengths for optically allowed transitions between the 2s2 2p2 and 2s2p3 configurations of Mg VII using the codes RMATRX (Berrington et al. 1978) and DSTWAV (Eissner & Seaton 1972) based on the close coupling and distorted wave approximations, respectively. They found that the difference between the two calculations is about 3% for the studied cases.
4 Results and discussions
In our method, we start the calculations by evaluating the structure and the collision parameters used later in the line broadening evaluations. The Br VI ion is a Zn-like ion (N = 30). The configurations taken into account are: [Ar]3d10(4s2, 4s4p, 4p2, 4s4d) yielding 14 fine structure levels. For the krypton (Kr), we consider the three ions Kr V-VII. We use six configurations for Kr V (Ge-like, N = 32): [Ar]3d10(4s24p2, 4s4p3, 4s2 4p4d, 4s2 4p5s, 4s2 4p5p, 4s2 4p5d) yielding 53 fine structure levels. We use six configurations for Kr VI (Ga-like, N = 31): [Ar]3d10(4s24p, 4s4p2, 4s2 4d, 4s2 5s, 4p3, 4s2 5p) yielding 20 fine structure levels, and for Kr VII (Zn-like, N = 30), we use seven configurations: [Ar]3d10(4s2, 4s4p, 4p2, 4s4d, 4s5s, 4s5p, 4s5d).
Stark widths of the three Br VI lines identified in Werner et al. (2018a) at different electron temperatures and at electron density 1017 cm−3.
4.1 Stark broadening for Br VI
The three Br VI lines recently identified in RE 0503–289 and in HD 149499 B by Werner et al. (2018a) are the resonance line 4s2 1S0−4s4p 3P (94.596 nm), and the two strongest ones, 4s4p 1P
(94.596 nm), and the two strongest ones, 4s4p 1P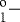 4p2 3P2 (98.142 nm) and 4s4p 1P
4p2 3P2 (98.142 nm) and 4s4p 1P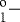 4p2 3P1 (105.055 nm). The lines are weaker in HD 149499 B than those in RE 0503–289. We provide here the widths of the three cited lines in addition to nine others. The results W are presented at five electron temperatures from 5 × 104 K to 5 × 105 K, and at an electron density of 1017 cm−3. The results of the three lines cited in Werner et al. (2018a) are displayed in Table 1. The nine others are displayed in Table 2. The wavelengths displayed in Table 1 are taken from Werner et al. (2018a). Those presented in Table 2 are taken from our structure code SST. There is no line identification in the National Institute of Standards and Technology (NIST) database (Kramida et al. 2020) for Br VI.
4p2 3P1 (105.055 nm). The lines are weaker in HD 149499 B than those in RE 0503–289. We provide here the widths of the three cited lines in addition to nine others. The results W are presented at five electron temperatures from 5 × 104 K to 5 × 105 K, and at an electron density of 1017 cm−3. The results of the three lines cited in Werner et al. (2018a) are displayed in Table 1. The nine others are displayed in Table 2. The wavelengths displayed in Table 1 are taken from Werner et al. (2018a). Those presented in Table 2 are taken from our structure code SST. There is no line identification in the National Institute of Standards and Technology (NIST) database (Kramida et al. 2020) for Br VI.
We also calculate Stark widths for some Br VI lines using the Cowley approximate formula (Cowley 1971) in order to compare them with our quantum results. The approximate formula is proposed for one electron temperature T =104 K, and Cowley (1971) mentioned that the formula is not recommended when detailed calculations or experimental results are available. We use it here to show that it overestimates the Stark broadening, as mentioned in Dimitrijević et al. (2005). The Stark broadening WCow, expressed inÅ, is calculated by the formula (Cowley 1971)
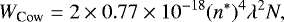 (16)
(16)
where N is the electron density in cm−3, λ is the wavelength of the considered transition incentimetres, and n* is the effective principal quantum number of the upper level defined by
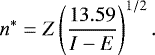 (17)
(17)
In Eq. (17), Z is the charge seen by the active electron (Z = 1 for neutral atoms,...), E is the energy of the level, and I is the appropriate series limit. Table 3 displays our quantum Stark broadening data for some Br VI lines compared to those calculated using the Cowley approximate formula (Cowley 1971) at two electron temperature values. The electron density is N = 1017 cm−3. We recall that Formula (16) is proposed for one electron temperature T = 104 K, so the Stark broadening values WCow in Table 3 are the same for different temperatures.
Firstly, it is clear that in almost all the cases the approximate formula gives line widths that are greater than ours. Secondly, even at an electron temperature of T = 104 K, for which the formula is proposed, the two results disagree for almost all the lines: the ratio WCow∕W varies between 0.68 and 5. Finally, we note that for the electron temperature T = 5 × 104 K, the ratio between the two results can reach 11, and we can predict that for other temperatures further away from T = 5 × 104 K, the agreement will be worse. Consequently, while the approximate formula (16) is very easy to use, it is not recommended when more rigourous calculations can be performed.
4.2 Stark broadening for Kr V-VII
Several lines of the three ions Kr V-VII have been identified for the first time in the FUV spectrum of the DO white dwarf RE 05030–289 (Werner et al. 2012; Rauch et al. 2016b). There are ten lines for Kr V, 14 for Kr VI and one line for Kr VII (see Table 3 of Rauch et al. 2016b). In Table 4, we present the widths of the three ions Kr V-Kr VII lines together with their wavelengths taken from the database NIST (Kramida et al. 2020). Two lines have not been presented in Table 4. One is the Kr V line (λ = 158.3456 nm), which does not exist in NIST (Kramida et al. 2020) or in the most recent work dealing with the KrV radiative data calculations (Raineri et al. 2012). The other is the Kr VI line (λ = 101.1133 nm), for which one of the involved levels is given by the configuration 4s4p4d, which is not considered in our structure calculations,so the line is not given by SST. Consequently, in total we have presented nine lines for Kr V, 13 lines for Kr VI, and one line for Kr VII.
In total, we have calculated the Stark broadening of 35 lines of Br VI, Kr V–VII ions. The presented results will enrich the Stark broadening database STARK-B (Sahal-Bréchot et al. 2021). We hope that the new Stark broadening results for Bromine and Krypton ions, together with the existing atomic data such as wavelengths, oscillator strengths, and radiative decay rates could be of interest in stellar-atmosphere modelling.
5 Influence of Stark broadening in the spectra of hot white dwarfs
It is essential to explore the importance of the Stark broadening mechanism in the atmosphere of the considered stars in order to prove the necessity of our Stark broadening calculations. To perform this task, we compared the influence of Stark and Doppler broadening in different atmospheric layers and for several stellar atmospheres. We used the model atmospheres of Wesemael (1981), which are Local Thermodynamic Equilibrium models assuming plane-parallel geometry and pure helium composition. Doppler broadening is given by
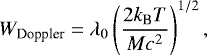 (18)
(18)
where M is the atomic mass of the radiating atom (Br or Kr) and c is the speed of light in a vacuum expressed in the S.I. system.
During the calculations, we noticed that the behaviours of Stark and Doppler broadening are the same for all the considered lines of the three studied ions, and lead to the same conclusions. Consequently, we chose one Br VI line, 4s2 1S0−4s4p 3P (λ = 95.825 nm) displayed in Fig. 2, and one Kr V line, 4s24p5s 1P
(λ = 95.825 nm) displayed in Fig. 2, and one Kr V line, 4s24p5s 1P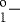 4s24p5p 1S0 (λ = 176.4478 nm) displayed in Fig. 3.
4s24p5p 1S0 (λ = 176.4478 nm) displayed in Fig. 3.
We present Stark and Doppler widths for the Br VI line (λ = 95.825 nm) as a function of atmospheric layer temperatures (Fig. 2a), and as a function of the Rosseland optical depth (Fig. 2b) for the atmospheric models with effective temperatures of Teff = 7 × 104 − × 105 K and a surface gravity logg = 8 (Wesemael 1981). For T > 7.5 × 104 K, Stark broadening becomes more dominant than Doppler broadening for all the considered atmospheric layer temperatures. That dominance is clearly higher at deeper atmospheric layers. Stark broadening is also more important than Doppler for all the Rosseland optical depths of the DO white dwarf atmospheres, even at the surface (Fig. 2b): WStark ≃ 1.3 × WDoppler. We also investigated the behaviours of Stark and Doppler broadening as a function of atmospheric layer temperatures (Fig. 2c), and as a function of the Rosseland optical depth (Fig. 2d) but for the atmospheric models (Wesemael 1981) with log g = 6 to log g = 9 and Teff = 8 × 104 K. We see that for a gravity surface logg = 7−9, Stark broadening becomes significant for temperatures about 105 K (Fig. 2c). For logg = 6, Doppler broadening is more important than Stark broadening for lower temperatures (5 × 104−1.8 × 105 K), but at T = 2 × 105 K, Stark broadening starts to dominate Doppler broadening. For logg = 9, we see that WStark ≈ 1.9 × WDoppler for the deepest atmospheric layer T = 2.5 × 105 K. Regarding the variation of Stark and Doppler broadening with the Rosseland optical depth, Stark broadening is dominant for all the optical depths for the four atmospheric models log g = 6−9 and is more than twice the Doppler one for logg = 9.
Almost the same conclusions can be drawn when examining the Stark and Doppler broadening of the Kr V 4s2 4p5s 1P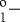 4s24p5p 1S0 line. The dominance of the Stark broadening compared to the Doppler one is clear for all the considered atmospheric models, especially where WStark is approximately approaching2.5 × WDoppler for logg = 9 (Fig. 3d). We can end this section by concluding that Stark effect is the significant mechanism of line broadening compared to the Doppler broadening for all the atmospheric models of the considered DO white dwarf atmospheres.
4s24p5p 1S0 line. The dominance of the Stark broadening compared to the Doppler one is clear for all the considered atmospheric models, especially where WStark is approximately approaching2.5 × WDoppler for logg = 9 (Fig. 3d). We can end this section by concluding that Stark effect is the significant mechanism of line broadening compared to the Doppler broadening for all the atmospheric models of the considered DO white dwarf atmospheres.
Our quantum Stark widths W for Br VI lines compared to the results of the Cowley formula WCow (Cowley 1971) at two electrons temperatures and at electron density N = 1017 cm−3.
6 Conclusion
In the present paper, we have calculated the Stark widths of 12 Br VI lines, 9 Kr V lines, 13 Kr VI lines, and 1 Kr VII line that have been recently detected for the first time in the atmosphere of hot white dwarfs. The results are new and will be implemented in the database STARK-B (Sahal-Bréchot et al. 2021). We chose to consider these lines because they are the only ones cited in the papers of Werner et al. (2012, 2018a), and Rauch et al. (2016b). Werner et al. (2018a) observed the Br VI lines in the spectrum of the DO white dwarfs RE 05030-289 and HD 149499 B. Werner et al. (2012) and Rauch et al. (2016b) observed the Kr V-VII lines in the FUV spectrum of the DO white dwarf RE 05030–289. We used our quantum mechanical method to perform the line broadening calculations. The method starts by studying the structure of the emitter, and then treats the collisionemitter-electron in the distorted wave approximation. Using the obtained structure and collision data, we evaluated the Stark broadening using our codes. The results are presented for electron temperatures 5− 10 × 104 K suitable for many astrophysical investigations, and at electron density 1017 cm−3. We also show that, for densities less than 2.38 × 1023, Stark broadening can be deduced by assuming a linear relationship between W and Ne. Finally, we investigated the importance of the role of Stark and the Doppler broadening in the atmospheres of the considered white dwarfs. The principal conclusion drawn here is that Stark broadening is more significant than Doppler for almost all the atmosphericmodels (Wesemael 1981) studied here. This conclusion shows the importance of Stark broadening data in the investigation and modelling of stellar-atmospheres.
Stark widths of the Kr V-VII lines identified in Rauch et al. (2016b) at different temperatures and at electron density 1017 cm−3.
 |
Fig. 2 Stark WStark and Doppler WDoppler widths for the Br VI line 4s2 1S0−4s4p 3P |
Acknowledgements
This work has been supported by the French Research Unit UMR 8112 and the Tunisian Laboratory of Molecular Spectroscopy and Dynamics LR18ES02. It has also been supported by the Paris Observatory and the CNRS. We also acknowledgefinancial support from the ‘Programme National de Physique Stellaire’ (PNPS) of CNRS/INSU, CEA and CNES, France.
References
- Aloui, R., Elabidi, H., Sahal-Bréchot, S., & Dimitrijević, M. 2018, Atoms, 6, 20 [CrossRef] [Google Scholar]
- Aloui, R., Elabidi, H., Hamdi, R., & Sahal-Bréchot, S. 2019a, MNRAS, 484, 4801 [CrossRef] [Google Scholar]
- Aloui, R., Elabidi, H., & Sahal-Bréchot, S. 2019b, J. Quant. Spectr. Rad. Transf., 239, 106675 [CrossRef] [Google Scholar]
- Baranger, M. 1958a, Phys. Rev., 112, 855 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baranger, M. 1958b, Phys. Rev., 111, 481 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Berrington, K. A., Burke, P. G., Le Dourneuf, M., et al. 1978, Comput. Phys. Commun., 14, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. A., & Salpeter, E. E. 1957, Quantum Mechanics of One–and Two–Electron Atoms (Berlin, Göttingen: Springer) [CrossRef] [Google Scholar]
- Burgess, A., Mason, H. E., & Tully, J. A. 1991, ApJ, 376, 803 [CrossRef] [Google Scholar]
- Cowley, C. R. 1971, The Observatory, 91, 139 [NASA ADS] [Google Scholar]
- Dimitrijevic, M. S., Sahal-Brechot, S., & Bommier, V. 1991, A&AS, 89, 581 [Google Scholar]
- Dimitrijević, M. S., Ryabchikova, T., Popović, L. Č., Shulyak, D., & Khan, S. 2005, A&A, 435, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eissner, W. 1998, Comput. Phys. Commun., 114, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Eissner, W., & Seaton, M. J. 1972, J. Phys. B Atm. Mol. Phys., 5, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Elabidi, H. 2021, J. Quant. Spectr. Rad. Transf., 259, 107407 [CrossRef] [Google Scholar]
- Elabidi, H., & Sahal-Bréchot, S. 2018, MNRAS, 480, 697 [CrossRef] [Google Scholar]
- Elabidi, H., & Sahal-Bréchot, S. 2019, MNRAS, 484, 1072 [CrossRef] [Google Scholar]
- Elabidi, H., Ben Nessib, N., & Sahal-Bréchot, S. 2004, J. Phys. B Atm. Mol. Opt. Phys., 37, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Elabidi, H., Ben nessib, N., Cornille, M., Dubau, J., & Sahal-Brechot, S. 2008, J. Phys. B Atm. Mol. Opt. Phys., 41, 025702 [Google Scholar]
- Elabidi, H., Ben Nessib, N., & Sahal-Bréchot, S. 2009, Eur. Phys. J. D, 54, 51 [EDP Sciences] [Google Scholar]
- Elabidi, H., Sahal-Bréchot, S., & Dimitrijević, M. S. 2014, Adv. Space Res., 54, 1184 [Google Scholar]
- Hoyer, D., Rauch, T., Werner, K., & Kruk, J. W. 2018, A&A, 612, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., et al. 2020, NIST Atomic Spectra Database (ver. 5.8)., https://physics.nist.gov/asd, [Online; accessed 29-September-2020]. National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Löbling, L., Maney, M. A., Rauch, T., et al. 2019, MNRAS, 492, 528 [Google Scholar]
- Raineri, M., Gallardo, M., Pagan, C., Trigueiros, A., & Reyna Almandos, J. 2012, J. Quant. Spectr. Rad. Transf., 113, 1612 [Google Scholar]
- Rauch, T., Quinet, P., Hoyer, D., et al. 2016a, A&A, 587, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Quinet, P., Hoyer, D., et al. 2016b, A&A, 590, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Gamrath, S., Quinet, P., et al. 2020, A&A, 637, A4 [EDP Sciences] [Google Scholar]
- Sahal-Bréchot, S., Dimitrijević, M. S., & Moreau, N. 2021, STARK-B database, http://stark-b.obspm.fr, [Online; accessed 30-Jan-2021]. Observatory of Paris, LERMA and Astronomical Observatory of Belgrade [Google Scholar]
- Saraph, H. E. 1978, Comput. Phys. Commun., 15, 247 [Google Scholar]
- Werner, K., Rauch, T., Ringat, E., & Kruk, J. W. 2012, ApJ, 753, L7 [Google Scholar]
- Werner, K., Rauch, T., Knörzer, M., & Kruk, J. W. 2018a, A&A, 614, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., Rauch, T., & Kruk, J. W. 2018b, A&A, 609, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesemael, F. 1981, ApJS, 45, 177 [Google Scholar]
All Tables
Stark widths of the three Br VI lines identified in Werner et al. (2018a) at different electron temperatures and at electron density 1017 cm−3.
Our quantum Stark widths W for Br VI lines compared to the results of the Cowley formula WCow (Cowley 1971) at two electrons temperatures and at electron density N = 1017 cm−3.
Stark widths of the Kr V-VII lines identified in Rauch et al. (2016b) at different temperatures and at electron density 1017 cm−3.
All Figures
 |
Fig. 1 Temperatures and densities at which a plasma is treated as ideal. |
| In the text | |
 |
Fig. 2 Stark WStark and Doppler WDoppler widths for the Br VI line 4s2 1S0−4s4p 3P |
| In the text | |
 |
Fig. 3 Same as in Fig. 2 but for the Kr V line 4s24p5s1 P |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.