| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140784 | |
| Published online | 15 June 2021 | |
LoTSS jellyfish galaxies
I. Radio tails in low redshift clusters
1
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: iroberts@strw.leidenuniv.nl
2
University of Birmingham School of Physics and Astronomy, Edgbaston, Birmingham, UK
3
Thüringer Landessternwarte, Sternwarte 5, 07778 Tautenburg, Germany
4
INAF-Osservatorio Astronomico di Padova, Vicolo Osservatorio 5, 35122 Padova, Italy
5
ASTRON, the Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA Dwingeloo, The Netherlands
6
GEPI & USN, Observatoire de Paris, CNRS, Université Paris Diderot, 5 Place Jules Janssen, 92190 Meudon, France
7
Centre for Radio Astronomy Techniques and Technologies, Department of Physics and Electronics, Rhodes University, Grahamstown 6140, South Africa
Received:
11
March
2021
Accepted:
8
April
2021
Context. The cluster environment has a strong impact on galaxy star formation, as seen by the fact that clusters host proportionally more red, passive galaxies relative to the field. Ram pressure stripping may drive this environmental quenching by directly stripping cold gas from galactic disks. In some cases, ram pressure stripping gives rise to ‘jellyfish galaxies’, observed with clear ‘tentacles’ of stripped gas extending beyond the optical extent of the galaxy.
Aims. In this paper we present a large sample of jellyfish galaxies in low redshift clusters (z < 0.05), identified through 120−168 MHz radio continuum from the LOFAR Two-metre Sky Survey (LoTSS).
Methods. From a parent sample of 29 X-ray-detected SDSS galaxy clusters and their spectroscopic members, we visually identify 95 star-forming, LoTSS jellyfish galaxies with 144 MHz radio tails. Star formation rates (SFRs) and stellar masses are obtained for all galaxies from SED fits. For each jellyfish galaxy we determine the tail orientation with respect to the cluster centre and quantify the prominence of the radio tails with the 144 MHz shape asymmetry.
Results. After carefully accounting for redshift-dependent selection effects, we find that the frequency of jellyfish galaxies is relatively constant from cluster to cluster. LoTSS jellyfish galaxies are preferentially found at small clustercentric radius and large velocity offsets within their host clusters and have radio tails that are oriented away from the cluster centre. These galaxies also show enhanced star formation, relative to both ‘normal’ cluster galaxies and isolated field galaxies, but generally fall within the scatter of the L144 MHz − SFR relation.
Conclusions. The properties of the LoTSS jellyfish galaxies identified in this work are fully consistent with expectations from ram pressure stripping. This large sample of jellyfish galaxies will be valuable for further constraining ram pressure stripping and star formation quenching in nearby galaxy clusters. We show that LOFAR is a powerful instrument for identifying ram pressure stripped galaxies across extremely wide fields. Moving forward, we will push the search for jellyfish galaxies beyond this initial cluster sample, including a comprehensive survey of the galaxy group regime.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: irregular / radio continuum: galaxies
© I. D. Roberts et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Satellite galaxies in clusters are significantly more likely to be red and passive relative to similar mass galaxies in the field. This fact is known as the environmental quenching of galaxy star formation, which has been firmly established in the nearby Universe (e.g. Dressler 1980; Blanton & Moustakas 2009; Peng et al. 2010; Wetzel et al. 2012; Haines et al. 2015; Roberts et al. 2019) and also observed out to z ∼ 1 and beyond (e.g. Muzzin et al. 2014; Foltz et al. 2018; Ji et al. 2018; Old et al. 2020). Increasingly, ram pressure stripping (RPS) is invoked as a physical driver of this environmental quenching. As galaxies orbit through the cluster potential, the interaction with the dense intracluster medium (ICM), the strength of which scales as ρICM × v2 (e.g. Gunn & Gott 1972) where ρICM is the density of the ICM and v is the galaxy velocity relative to the ICM, can directly strip gas out of the disk leaving behind a wake of material trailing the galaxy. If enough cold, star-forming gas is removed via this process, RPS will lead to rapid galaxy quenching in dense environments. Even if it is just the diffuse atomic gas that is efficiently stripped, this can still lead to star formation quenching, albeit over longer timescales, as the galaxy is exhausting its remaining molecular gas reserves. Despite RPS being a mechanism to quench galaxies (e.g. Gunn & Gott 1972; Quilis et al. 2000; Roediger & Hensler 2005; Bekki 2009; Steinhauser et al. 2016; Roberts et al. 2019), star formation may be briefly enhanced during the early stages of the ram pressure interaction, as predicted by simulations (e.g. Bekki & Couch 2003; Steinhauser et al. 2012; Troncoso Iribarren et al. 2016, 2020; Ramos-Martínez et al. 2018) and seen in observations (e.g. Gavazzi & Jaffe 1985; Poggianti et al. 2016; Vulcani et al. 2018; Roberts & Parker 2020). This star formation enhancement should occur prior to substantial stripping of disk gas and is likely a result of compression in the interstellar medium (ISM). Ram pressure stripping strongly impacts galaxy star formation in clusters; therefore constraining the properties of galaxies experiencing RPS is a key ingredient to understanding the evolution of galaxies in dense environments.
The high ICM densities and large velocity dispersions in massive galaxy clusters are conducive to strong RPS, and therefore clusters are excellent laboratories to study this process in detail. To do so, one must first identify which cluster galaxies are currently undergoing RPS or which cluster galaxies have experienced strong RPS in the past. While signatures of RPS have been observed in molecular gas (e.g. Sivanandam et al. 2010, 2014; Vollmer et al. 2012; Jáchym et al. 2014, 2019; Moretti et al. 2020), dust (e.g. Crowl et al. 2005), far-ultraviolet (e.g. Smith et al. 2010; Boissier et al. 2012; George et al. 2018), and X-rays (e.g. Sun et al. 2006, 2010; Poggianti et al. 2019a), most commonly HI or Hα observations are used to identify jellyfish galaxies (e.g. Gavazzi et al. 2001; Yoshida et al. 2002; Kenney et al. 2004; Oosterloo & van Gorkom 2005; Chung et al. 2007, 2009; Sun et al. 2007; Yagi et al. 2007, 2010; Kenney et al. 2015; Poggianti et al. 2017; Boselli et al. 2018). Similarly, cluster galaxies that have highly truncated HI or Hα profiles (relative to the stellar disk) are interpreted as galaxies that have recently been stripped (e.g. Vollmer & Huchtmeier 2007; Jaffé et al. 2018). HI and Hα observations both trace components that are relatively diffuse and can be strongly influenced by RPS. As a result, these observations reveal clear RPS tails, leading to highly reliable identification of RPS galaxies. Furthermore, spectroscopic observations provide detailed kinematic information, giving important insight into the stellar and gas dynamics in these highly disturbed galaxies (e.g. Fumagalli et al. 2014; Bellhouse et al. 2017; Kalita & Ebeling 2019). Beyond just the Hα line, optical integral field unit spectroscopy probes stellar kinematics as well as ionization mechanisms via optical line ratios. Spectroscopic observations provide a wealth of information; however, the downside is that this approach requires expensive observations, typically over relatively small fields of view (FOVs). This makes it difficult to survey entire galaxy clusters, or better yet many galaxy clusters, and instead leads to observations focused on a relatively small number of bright, prominent galaxies. Narrow-band imaging of Hα (e.g. Yagi et al. 2010; Boselli et al. 2018) sacrifices kinematic information but provides much larger FOVs and shorter integration times. Narrow-band Hα filters are tied to a specific redshift (outside of tunable filters), which does then limit the scope for observations over multiple galaxy clusters.
An alternative approach is to identify galaxies likely undergoing RPS according to their rest-frame optical morphologies (e.g. McPartland et al. 2016; Poggianti et al. 2016; Roberts & Parker 2020). The biggest advantage to this approach is the wide-field imaging capabilities of many telescopes, allowing for entire clusters to be efficiently imaged, sometimes in a single pointing. Furthermore, broadband imaging is far less observationally expensive than spectroscopy. Therefore, imaging permits a more efficient search for RPS in clusters, which can be applied over a range of redshifts. The tradeoff is in the reliability of the RPS galaxies identified in this way. Rest-frame optical imaging primarily traces the stellar component of the galaxy, which is less perturbed by RPS than H I or Hα. This means that the RPS features observed in optical imaging are more subtle, making it difficult to conclusively say if a galaxy is undergoing RPS based solely on its optical morphology – especially since there are other cluster-specific processes that also lead to disturbed optical morphologies, for example tidal effects and/or harassment (e.g. Moore et al. 1996; Mayer et al. 2006; Chung et al. 2007).
The optimal search for galaxies experiencing RPS will include the best of both by: (a) observing a galaxy component that is readily stripped so that ram pressure tails can be conclusively identified, and (b) surveying a wide-field covering entire clusters so that an unbiased search across all cluster members can be performed. The LOFAR Two-metre Sky Survey (LoTSS, Shimwell et al. 2017, 2019) is an excellent survey to accomplish this. The LoTSS wide area survey will eventually image the entire northern sky at 120 − 168 MHz, 6″ resolution, and 100 μJy beam−1 noise. The wide-field nature of LoTSS allows for a uniform survey across many galaxy clusters. In star-forming galaxies, LoTSS is sensitive to synchrotron emission from cosmic rays accelerated by supernovae. For star-forming galaxies experiencing RPS, tails of synchrotron emission may be observed as these cosmic rays are stripped from the galaxy disk. In fact LOFAR has already detected extended emission at 144 MHz around a known jellyfish galaxy in Abell 2626 (Poggianti et al. 2019b; Ignesti et al. 2020). Additionally, previous works have observed RPS features in radio continuum within nearby clusters (primarily around 1.4 GHz, Gavazzi & Jaffe 1987; Miller et al. 2009; Murphy et al. 2009; Vollmer et al. 2009; Chen et al. 2020; Müller et al. 2021). There is some evidence that RPS tails have steep spectral indices (Chen et al. 2020; Müller et al. 2021), which only furthers the strengths of LoTSS as the low frequencies probed by LOFAR are ideal for detecting steep spectrum sources.
In this work we use LoTSS 144 MHz radio continuum observations to perform a systematic search for galaxies undergoing RPS (‘jellyfish galaxies’) across 29 X-ray-detected, low redshift (z < 0.05) galaxy clusters. For the purpose of this work, our definition of jellyfish galaxies are galaxies with stripped tails extending asymmetrically in one direction beyond the optical galaxy disk. We consider all star-forming member galaxies in these clusters and identify ∼100 jellyfish galaxies with extended, one-sided radio tails. Here we introduce the sample and present the general properties of these LoTSS jellyfish galaxies, both relative to other cluster galaxies as well as isolated galaxies in the field. The paper is outlined as follows. In Sect. 2 we describe the datasets that we use in this work along with the method we take to identify jellyfish galaxies. In Sect. 3 we describe the general demographics of the jellyfish galaxy sample, including stellar mass and redshift distributions as well as active galactic nuclei (AGN) fractions. In Sect. 4 we carefully control for redshift-dependent selection effects in order to explore how the frequency of jellyfish galaxies differ from cluster to cluster. In Sect. 5 we present the positions of LoTSS jellyfish galaxies in projected phase space relative to normal cluster galaxies. In Sect. 6 we present the orientations of observed 144 MHz tails with respect to the centre of the host cluster for all jellyfish galaxies. In Sect. 7 we present the star-forming properties of LoTSS jellyfish galaxies, both relative to the star-forming main sequence and in the context of the radio luminosity – star formation rate relation. Finally, in Sect. 8 we present a discussion of our results and highlight the main conclusions from this work.
Throughout this paper we have assumed a Λ cold dark matter cosmology with ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
2. Data and methods
2.1. The LOFAR Two-metre Sky Survey (LoTSS)
The LOFAR (van Haarlem et al. 2013) Two-metre Sky Survey is an ongoing programme to eventually image the entire northern sky with the LOFAR high-band antenna (HBA) at 120−168 MHz, achieving a typical noise level of ∼100 μJy beam−1 and a resolution of 6″ for most declinations. We will give a brief description of LoTSS here; however, a full outline of the survey and observing strategy can be found in Shimwell et al. (2017), and the first LoTSS data release (DR1) is described in Shimwell et al. (2019).
LoTSS pointings tile the northern sky with typical separations of ∼2.58°, with each pointing observed for 8 h to reach the desired depth of ∼100 μJy beam−1 with direction-dependent calibration (Tasse et al. 2021). With a primary beam FWHM of ∼4° at 144 MHz, LoTSS observes the entirety of virtually all low-z clusters in a single pointing. Our sample includes 29 clusters at z < 0.05 (see subsequent section) that are observed in LoTSS. 13/29 of these clusters fall within the LoTSS data release 2 (DR2) footprint (Tasse et al. 2021; Shimwell et al., in prep.), and the other 16/29 have been observed and processed by LoTSS but fall outside of DR2. For the clusters in our sample, the typical 144 MHz noise levels range from ∼50 − 250 μJy beam−1. LoTSS noise levels are declination-dependent, with the highest noise levels in our sample corresponding to more equatorial clusters.
2.2. Cluster sample
The galaxy clusters in this work were selected from the Sloan Digital Sky Survey (SDSS, York et al. 2000; Abazajian et al. 2009), which has substantial overlap with the LoTSS footprint. We selected galaxy clusters from the SDSS-ROSAT All Sky Survey (RASS, Voges et al. 1999) cluster catalogue from Wang et al. (2014), hereafter W14. W14 measure RASS X-ray luminosities around optical SDSS clusters from the Yang et al. (2007), hereafter Y07, catalogue. From the W14 catalogue, we selected all low redshift (z < 0.05) clusters with X-ray detections that had also been observed by LOFAR at 144 MHz at the time of writing. Specifically, we select clusters from the W14 catalogue with redshifts < 0.05, RASS X-ray detections with S/N > 3, halo masses ≥1014 h−1 M⊙, and require that the cluster has been observed by LOFAR at 144 MHz. For the clusters in W14, we take the corresponding halo masses, Mhalo, from the Y07 catalogue. These halo masses are computed via abundance matching and we use the masses that are matched according to the characteristic stellar mass for each cluster. A full description of the abundance matching method is given in Sect. 3.5 in Y07, and comparison to mocks shows that this method is able to reproduce halo masses without bias and with a scatter of ∼0.2 dex.
The criteria above yield a final sample of 29 X-ray-detected SDSS clusters with LoTSS observations. These clusters and their basic properties are listed in Table 1. For each cluster we determined the 1D velocity dispersion assuming the following scaling from Y07
Cluster sample.
Following Y07 we also calculated the virial radius for each cluster as
where R180 is the radius that encloses an average density equal to 180 times the critical mass density of the Universe.
2.3. Galaxy samples
2.3.1. Cluster galaxies
For this sample of clusters we assign member galaxies, and corresponding star formation rates (SFRs) and stellar masses (Mstar), with SDSS spectroscopy. For each cluster we select galaxies with projected separations from the cluster X-ray centre < R180 and 1D velocity offsets from the cluster redshift < 3σ. This is a relatively loose membership criterion that may include a small number of galaxies that are not formally bound to the cluster, especially galaxies that have both large separations from the cluster centre and large velocity offsets from the cluster redshift. We opt for this approach to ensure that we do not miss galaxies that have recently started their infall onto the cluster. For member galaxies we take stellar masses and SFRs from the GALEX-SDSS-WISE catalogue (GSWLC-2, Salim et al. 2016, 2018). These stellar masses and SFRs are determined by fitting galaxy spectral energy distributions (SEDs) with the CIGALE code (Boquien et al. 2019). The SED fits include GALEX UV photometry, SDSS optical photometry, and the total IR luminosity estimated from templates using WISE mid-IR fluxes. In this paper we focus on star-forming cluster galaxies, that we define to be galaxies with a specific star formation rate (sSFR = SFR/Mstar) > 10−11 yr−1 (Wetzel et al. 2013). These selections give a total sample of 1968 star-forming galaxies within our sample of clusters. For the remainder of the paper we will refer to this sample (excluding galaxies identified as jellyfish, see Sect. 2.4) as ‘SDSS cluster galaxies’.
For comparison purposes, we also identify a subset of the SDSS cluster galaxies that are detected by LOFAR at 144 MHz, but are not classified as jellyfish galaxies (see Sect. 2.4). To do so we cross match the SDSS cluster galaxy sample with the forthcoming LoTSS DR2 source catalogs (see Williams et al. 2019 for a description of previous LoTSS source catalogs), requiring separations between matching galaxies to be no larger than 3″. 3″ is equal to half of the LoTSS FWHM and corresponds to 1.2 − 2.9 kpc over the redshift range of our sample. We note that the majority of matches have separations of 1″ or less. This gives a sample of 330 galaxies, that we will refer to as ‘LoTSS cluster galaxies’.
2.3.2. Matched field galaxies
For further comparison we also compiled a sample of SDSS isolated field galaxies from Roberts & Parker (2017). This sample was derived from N = 1 ‘groups’ in the Y07 group catalogue, in other words, galaxies that were not assigned to a group of multiple galaxies. The sample of isolated field galaxies consists of all N = 1 Y07 galaxies that are separated from their nearest ‘bright neighbour’ by at least 1 Mpc and 1000 km s−1. Bright neighbours are defined as any galaxy brighter than the SDSS r-band absolute magnitude limit at z = 0.05 (the upper redshift limit of our cluster sample). We then selected all galaxies from the Roberts & Parker (2017) field sample with redshifts < 0.05 and with stellar masses and SFRs from the GSWLC-2 catalog. Finally, we match the stellar mass and redshift distributions of the field sample to the sample of cluster galaxies. To do so, for each cluster galaxy we randomly selected five field galaxies within 0.1 dex in stellar mass and 1000 km s−1 in redshift to the cluster galaxy. This gives a final field sample of 10315 unique galaxies that is well matched to the cluster sample in mass and redshift.
2.3.3. Stellar mass completeness
The SDSS is a flux limited spectroscopic survey; therefore, the stellar mass completeness of our galaxy sample will be a clear function of redshift. To evaluate this stellar mass completeness we use all star-forming galaxies (sSFR > 10−11 M⊙) in the GSWLC-2 catalogue (Salim et al. 2016, 2018) with z < 0.05, and follow Pozzetti et al. (2010), Weigel et al. (2016) by determining the mass, Mlim, that a given galaxy would have if its magnitude was equal and the limiting magnitude of the SDSS spectroscopic survey, mr, lim = 17.77 (e.g. Abazajian et al. 2009). At fixed redshift, this limiting mass can be calculated for each galaxy as
where Mstar is the galaxy stellar mass and mr is the observed r-band magnitude. This relation assumes a constant mass-to-light ratio for each galaxy, which is a reasonable assumption given that we are only including star-forming galaxies.
The Mlim is computed for each galaxy in the sample. In narrow bands of redshift (Δz = 0.005) we selected the faintest 20% of galaxies (in terms of mr) and determined the value of Mlim below which 90% of this faint subsample lies. This value of Mlim corresponds to our stellar mass completeness limit for each redshift bin (Pozzetti et al. 2010; Weigel et al. 2016). In Fig. 1 we show the stellar mass as a function of redshift for each galaxy (grey points), as well as Mlim for galaxies in the faintest 20% (blue points) and our stellar mass completeness limits as a function of redshift (large grey circles).
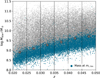 |
Fig. 1. Stellar mass versus redshift for star-forming galaxies in GSWLC-2 (Salim et al. 2016, 2018) with z < 0.05. Blue points show the limiting stellar mass value for the faintest 20% of galaxies in each redshift bin and large circles show the stellar mass completeness limits as a function of redshift. |
We opted to apply a stellar mass completeness cut for each individual cluster, corresponding to the cluster redshift. This means that lower redshift clusters in our sample will have a completeness cut at smaller stellar mass than higher redshift clusters. This ranges from Mstar > 108.9 M⊙ at z = 0.02 − 0.025 to Mstar > 109.7 M⊙ at z = 0.045 − 0.05. As an exception to this, any direct cluster to cluster comparisons were always done using the stellar mass completeness cut corresponding to our highest redshift cluster, Mstar > 109.7 M⊙. This is a conservative choice to ensure that any cluster to cluster comparisons are made across a range in stellar mass that is complete for every cluster in the sample.
2.4. Identifying jellyfish galaxies
We identify jellyfish galaxies with by-eye classifications. For each star-forming cluster galaxy we make 100 × 100 kpc cutouts from PanSTARRS g-band and LoTSS 144 MHz images. To classify galaxies we use the g-band cutout images with LoTSS 144 MHz contours overlaid. In these overlays we only show 144 MHz contours that are at, or above, the 2σ level (similar to Chen et al. 2020). The overlay images for all jellyfish galaxies identified in this work are shown in Appendix A.
We visually identify LoTSS jellyfish galaxies as those star-forming cluster galaxies that show: 144 MHz emission that is resolved and clearly asymmetric with respect to the stellar disk of the galaxy (as traced by the g-band flux). Specifically, we look for ‘one-sided’ asymmetries such that the classifier is able to confidently assign a tail direction visually. This excludes objects that have complex, asymmetric radio emission that is not one-sided. We note that many galaxies in our sample are not detected by LoTSS, and therefore we certainly miss some jellyfish galaxies, particularly at low galaxy masses and/or low star formation rates. The mass distribution of LoTSS detections compared to our total sample of SDSS cluster galaxies is discussed more thoroughly in Sect. 3.1.
Through this procedure we identified 95 jellyfish galaxies with LoTSS radio tails. These galaxies are distributed through 21/29 clusters, whereas eight clusters in our sample have no identified jellyfish galaxies. The majority of these radio continuum tails are new detections. Gavazzi & Jaffe (1985, 1987) originally identified radio continuum tails at 1.4 GHz for two of the galaxies in this sample (in Abell 1367, SDSS J114313.08+200017.4 and KUG 1140+202A). Miller et al. (2009) also identified radio continuum tails at 1.4 GHz for two of the Coma Cluster galaxies in our sample (GMP 4555 and IC 4040). Finally, Chen et al. (2020) presented newly detected radio continuum tails (again at 1.4 GHz) for six of the Coma Cluster galaxies in this sample (NGC 4848, NGC 4858, D100, GMP 2599, Mrk 0058, GMP 3271). Otherwise, to the best of our knowledge, the rest of the radio continuum tails presented in this work are new detections. In Fig. 2 we show optical+radio images of three example jellyfish galaxies in our sample. The optical imaging in Fig. 2 is from the MegaCam instrument on the Canada-France-Hawaii Telescope1 (CFHT).
 |
Fig. 2. Composite optical (CFHT, RGB) plus radio (LOFAR, 144 MHz) images of three LoTSS jellyfish galaxies in our sample. The scale bar in each panel corresponds to a physical size of 10 kpc. The radio continuum tail for SDSS J114313.08+200017.4 was first detected at 1.4 GHz by Gavazzi & Jaffe (1985, 1987), the radio continuum tail for SDSS J162857.99+391908.7 is a new detection, and the radio continuum tail for NGC 4858 was first detected at 1.4 GHz by Chen et al. (2020). |
2.5. LoTSS asymmetries
We measure the ‘shape asymmetry’ (Pawlik et al. 2016) of the 144 MHz emission for the identified jellyfish galaxies. The shape asymmetry is similar to the commonly used CAS rotational asymmetry (Abraham et al. 1996; Conselice 2003), but instead of being calculated from the flux image it is calculated from a binary detection map for a given source. In this sense, it is a measure of asymmetry that is not flux-weighted, therefore making it very sensitive to low surface brightness features such as stripped tails. This asymmetry, AS, is given by
where X0 is the LoTSS segmentation map and X180 is the LoTSS segmentation map rotated by 180°. We measure AS with respect to the optical centre of each galaxy. Segmentation maps are generated using the photutils.detect_sources function in PYTHON and require sources to have at least 5 connected pixels above a 2σ threshold. All segmentation maps are checked manually to ensure that they accurately capture all radio emission from the jellyfish galaxies. In a small number of cases (∼5%) the segmentation maps blend two sources together, and for these cases photutils.deblend_sources deblends the segmentation map at saddle points in the image using watershed segmentation.
3. Jellyfish galaxy demographics
3.1. Mass and redshift distributions
The sample of cluster or field galaxies with SDSS spectroscopy are subject to different selection functions, in terms of galaxy stellar mass and redshift, than the sample of galaxies detected by LoTSS at 144 MHz. Since our cluster sample comprises a range of redshifts (zcluster ∼ 0.02 − 0.05) and galaxy stellar masses, it is important to understand these different selection effects in order to ensure fair comparisons throughout our galaxy samples and between jellyfish galaxy populations from cluster to cluster.
In Fig. 3a we plot empirical distribution functions (EDFs) of galaxy redshift for SDSS cluster galaxies (blue, solid), SDSS field galaxies (black, dashed), LoTSS jellyfish galaxies (red, solid), and LoTSS cluster galaxies (gold, dashed). As discussed in Sect. 2.3.2, the SDSS field sample is explicitly matched to the SDSS cluster sample in terms of redshift (and stellar mass), so the identical distributions between the two in Fig. 3a is by construction. The redshift distribution of LoTSS cluster galaxies is also essentially identical to the SDSS cluster and field samples; however, this is not by construction. On one hand this is unsurprising as the LoTSS cluster sample is a subset of the SDSS cluster sample, but it does show that galaxies detected by LOFAR are not preferentially found at the low redshift end of our sample. On the other hand, LoTSS jellyfish galaxies have a distribution that is clearly shifted to low redshifts. While the galaxies in the LoTSS jellyfish sample would be detected in LoTSS across the entire redshift range of our sample (similar to the LoTSS cluster galaxies), it does become more difficult to identify a galaxy as a jellyfish at the higher redshift end. This is the result of a combination of factors: (a) while the galaxy as a whole may be detected in LoTSS across the entire redshift range, low surface brightness tails from RPS can fall below the detection limit in higher redshift clusters, and (b) the size of the beam in physical units increases with redshift, making it more difficult to identify asymmetric tails as they become more blurred at higher redshifts.
 |
Fig. 3. Empirical distribution functions (EDFs) for galaxy redshift (top) and galaxy stellar mass (bottom). EDFs are shown for SDSS cluster galaxies (blue, solid), SDSS field galaxies (black, dashed), LoTSS jellyfish galaxies (red, solid), and normal star-forming galaxies from the LoTSS DR2 source catalogue (red, dashed). |
In Fig. 3b we plot EDFs of stellar mass for the same four samples. Again, by construction the SDSS cluster sample and the matched SDSS field sample have identical distributions. In terms of stellar mass, both LoTSS cluster galaxies and LoTSS jellyfish galaxies have systematically high masses relative to the pure SDSS samples. This difference is introduced by the sensitivity limit of LoTSS which does not reach the necessary depths to detect the lowest-mass galaxies in the SDSS samples. As a result of this selection effect, with this sample we are only able to probe jellyfish galaxies with log Mstar/M⊙ ≳ 9.5 − 10 or so. This does not mean that there are no jellyfish galaxies below these masses, previous studies actually suggest that the frequency of jellyfish galaxies likely increases towards lower masses (Yun et al. 2019; Roberts et al. 2021), but deeper observations are needed to probe the regime around 109 M⊙.
The distributions in both panels of Fig. 3 show that any comparisons between the number of jellyfish galaxies from cluster to cluster need to be done with care to account for different selection effects for clusters at different redshifts. In Sect. 4 we treat these selection biases in more detail as we explore whether the frequency of jellyfish galaxies differs from cluster to cluster.
3.2. AGN contamination
Tailed radio galaxies in clusters typically originate from bent AGN jets (e.g. Miley 1980; Garon et al. 2019). Given that the search in this work focuses on star-forming galaxies, the source of the 144 MHz tails that we observe is likely not due to AGN. That said, we can further test for any evidence of AGN emission in these galaxies with optical emission line and mid-IR AGN diagnostics.
In Fig. 4a we plot the fractions of jellyfish galaxies, as a function of galaxy mass, belonging to each of the four classes from the BPT diagram (star-forming, composite, LINER, and Seyfert; Baldwin et al. 1981). BPT classifications are from SDSS spectroscopy and are taken from Thomas et al. (2013). Star-forming, composite, and AGN type emission are differentiated using the Kewley et al. (2001) and Kauffmann et al. (2003) dividing lines. The AGN class is further subdivided into Seyfer and LINER using the dividing line from Schawinski et al. (2007). For all stellar masses, the fraction of galaxies with LINER- or Seyfert-type emission is very small, at most 5 − 10%. Low-mass galaxies are dominated (75−100%) by star-forming emission line ratios. Only for the highest-mass galaxies is there a substantial contribution from composite-type emission, suggesting for high-mass galaxies that there may be a blend of star formation and AGN emission contributing to the observed line ratios. On the whole, 72% of jellyfish galaxies are classified as star-forming by the BPT diagram and 93% are classified as either star-forming or composite. We see no evidence for a prominant population of BPT AGN amongst the jellyfish galaxies as only 2% of jellyfish are classified as Seyfert-type. Including both Seyfert- and LINER-type emission only raises this fraction to 7%.
 |
Fig. 4. Top: fraction of jellyfish galaxies in the sample according to their BPT classification: star-forming (solid line), composite (dashed line), LINER (dot-dashed line), and Seyfert (dotted line). Bottom: WISE colour-colour diagram. Dashed line shows the dividing line of W1 − W2 > 0.8 for AGN classifications from Stern et al. (2012) and the solid line shows the AGN region from Jarrett et al. (2011). |
Mid-IR photometry is also a useful test for AGN activity (e.g. Stern et al. 2005). In Fig. 4b we plot W1 − W2 colour versus W2 − W3 colour along with the standard WISE AGN selection regions from Jarrett et al. (2011; solid line) and Stern et al. (2012; W1 − W2 > 0.8, dashed line). The red stars mark the positions of LoTSS jellyfish galaxies in this plane. WISE Vega magnitudes and errors are taken from the unWISE-SDSS catalogue (Lang et al. 2016), and all jellyfish galaxies have S/N > 5 in all three WISE bands. The mid-IR colours do not identify any AGN in the sample of jellyfish galaxies, further suggesting that the 144 MHz emission in these galaxies is likely driven by star formation. Even if we use a less strict AGN selection of W1 − W2 > 0.5 (e.g. Blecha et al. 2018), that would only identify one AGN galaxy out of the entire jellyfish sample.
4. Frequency of jellyfish galaxies per cluster
With the large sample of clusters in this work, we can test whether the frequency of jellyfish galaxies is relatively constant from cluster to cluster, or whether there are certain clusters that are particularly rich in jellyfish. In order to do this properly, it is crucial to take care of the selection biases in terms of redshift and stellar mass discussed in Sects. 2.3.3 and 3.1.
We first exclude any galaxies with Mstar < 109.7 M⊙. This corresponds to the stellar mass completeness limit for our highest redshift clusters (z = 0.045 − 0.050) and ensures that we are only considering stellar masses that are complete for every cluster in the sample. Still, there are further selection effects that need to be accounted for before cluster to cluster comparisons are possible:
First, the variation in sensitivity for 144 MHz images of different clusters. LOFAR is most sensitive at large declinations (δ ≳ 20 − 30°); therefore, the sensitivity level for equatorial clusters in our sample at δ ≲ 20° will be negatively impacted. Additionally, poor ionosphere conditions or bright sources in the field can introduce high levels of noise, even for observations at high declinations.
Second, we identify jellyfish galaxies according to 144 MHz contours beginning at 2× the rms noise for each 100 × 100 kpc cutout image. Therefore, for lower redshift clusters we are tracing inherently fainter 144 MHz luminosities. Since tails from RPS are faint, it will be easier to identify these features for galaxies in low redshift clusters, for a fixed rms noise.
Third, the angular size of the LoTSS beam is fixed, that means that the physical scale that the beam traces will change with redshift. In terms of physical scales, the size of the 6″ LoTSS beam ranges from 2.7 kpc to 5.4 kpc over the redshift range of our cluster sample. Since galaxies in higher redshift clusters will be more strongly blurred by the LoTSS beam, it becomes more difficult to identify asymmetric features with increasing redshift.
All of these effects need to be addressed before a fair comparison can be made between clusters at different redshifts. The approach that we take is to degrade the quality of the LoTSS jellyfish images, so that the image quality is relatively constant across our entire cluster sample. We take the following steps to do so:
(a) For all jellyfish galaxies, 144 MHz images are convolved to a physical resolution of 5.4 kpc. This corresponds to 6″ at our highest cluster redshift.
(b) We overlay 144 MHz contours (from the images convolved to 5.4 kpc) on PanSTARRS g-band images for each jellyfish galaxy. The lowest contour is set to 2 × 0.25 mJy beam−1 × (0.046/z)2. 0.25 mJy beam−1 corresponds to the maximum rms noise from the sample of jellyfish galaxies, and the factor of (0.046/z)2 ensures that the contour levels are set at ∼constant luminosity instead of constant flux.
(c) These ‘degraded’ images are reclassified by-eye in order to check whether the asymmetric radio tails are still visible.
Galaxies where tails are still apparent after this image degradation form a new sample of ‘degraded’ jellyfish galaxies. 39/95 jellyfish galaxies still show radio tails in the degraded images. The remainder of the radio tails were either not detected above the stricter contour levels, were blurred by the larger beam such that they no longer appeared asymmetric, or the jellyfish galaxy fell below the stricter stellar mass completeness cut of M⋆ ≥ 109.7 M⊙ for all clusters. We note that restricting the sample to M⋆ ≥ 109.7 M⊙ reduces the number of SDSS cluster galaxies from 1968 to 1056. In Appendix A we show the original LoTSS images as well as the degraded LoTSS images for all jellyfish galaxies. This smaller ‘degraded’ jellyfish galaxy sample can now be readily used to compare the frequency of jellyfish galaxies between clusters. The reduced sample size is a necessity in order to ensure a fair comparison, but unfortunately then limits our ability to make strong statements about the frequency of jellyfish galaxies from cluster to cluster.
In Fig. 5 we plot the fraction of jellyfish galaxies in each cluster. The fractions for each cluster are measured relative to all star-forming member galaxies, only include galaxies with Mstar ≥ 109.7 M⊙ (for stellar mass completeness), and only include jellyfish galaxies from the ‘degraded’ jellyfish galaxy sample. We stress that these absolute fractions for each cluster are not particularly meaningful since many legitimate jellyfish galaxies are not included due to the image degradation process. What are meaningful are the difference between fractions for various clusters and this allows us to explore whether certain clusters are more or less jellyfish-rich than average. Many clusters in Fig. 5 host no jellyfish galaxies from the ‘degraded’ jellyfish sample, including the eight clusters that had no jellyfish from the full sample and also six additional clusters that have jellyfish galaxies identified from the original LoTSS images but either do not have jellyfish galaxies identified from the degraded LoTSS imaging or only have jellyfish galaxies with Mstar < 109.7 M⊙.
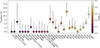 |
Fig. 5. Fraction of star-forming galaxies identified as LoTSS jellyfish for each cluster. Error bars are 1σ binomial confidence intervals (Cameron 2011). In order to ensure a fair comparison from cluster to cluster, jellyfish fractions in this plot are measured using only galaxies with Mstar > 109.7 M⊙ and only include jellyfish galaxies identified from the degraded LoTSS imaging. |
On the whole, the clusters in Fig. 5 are essentially consistent with one another, suggesting that the clusters in this sample all host a relatively constant proportion of jellyfish galaxies. Though again, it is important to note that by homogenizing the selection of jellyfish galaxies through the image degradation, the sample size becomes significantly smaller. We stress that the fact that we find no strong variation from cluster to cluster does not mean that there is no variation, just that we cannot strongly constrain this with the sample at hand. The only clusters that show any evidence for a departure from the mean value are A2199 and Coma (A1656), but even then those departures are only at the ∼2.5σ level.
5. Projected phase space
Projected phase space (PPS) diagrams for galaxy clusters are a commonly used tool to constrain cluster accretion and infall history. Galaxies infall at large velocity offsets (from the cluster systemic velocity) during their first approach to pericentre and after multiple orbits approach the core of phase space at small cluster-centric radius and small velocity offsets (see Fig. 1 in Rhee et al. 2017 for a schematic diagram). This infall structure in phase space is very clear in simulations where full phase space information is available (e.g. Mahajan et al. 2011; Oman et al. 2013; Haines et al. 2015). Projection effects remove some of this clear structure; however, even in projection, galaxies with short times-since infall are generally found at large cluster-centric radius and/or large velocity offsets (e.g. Mahajan et al. 2011; Rhee et al. 2017; Pasquali et al. 2019). Given that the strength of ram pressure scales as ρICMv2, it is expected that jellyfish galaxies should preferentially inhabit regions of PPS at small radius and large velocity offsets. Indeed, previous observational works have reported high numbers of RPS galaxies in such PPS regions (e.g. Yoon et al. 2017; Jaffé et al. 2018; Roberts & Parker 2020).
In Fig. 6a we plot the PPS diagram for the cluster galaxies in our sample. The background 2D histogram shows the PPS distribution of SDSS cluster galaxies and the red stars correspond to jellyfish galaxies. The above-axis histograms show the 1D distributions for clustercentric radius and velocity offset, showing that relative to the SDSS cluster galaxies, jellyfish are more commonly found at small clustercentric radius and slightly larger velocity offsets.
 |
Fig. 6. Distribution of SDSS cluster galaxies and LoTSS jellyfish galaxies in projected phase space. Left: velocity offset versus projected clustercentric radius. 2D histogram shows distribution for star-forming cluster galaxies and red stars correspond to jellyfish galaxies. We also show the 1D distributions of projected radius and velocity offset over the corresponding axes. Right, top: excess of jellyfish galaxies with respect to star-forming cluster galaxies (see text), for the four different regions in projected phase space. Right, bottom: median 144 MHz asymmetry for each of the four phase space regions. Error bars show the statistical error on the median and shaded regions show the interquartile range. |
We also split PPS into quadrants divided at Rproj/R180 = 0.5 and Δvlos/σ = 1.5, that we label one through four in Fig. 6a. For each quadrant we measure the ‘excess’ of jellyfish galaxies relative to SDSS cluster galaxies. We define this excess as the ratio between the fraction of jellyfish galaxies in a given quadrant (relative to all jellyfish galaxies) and the fraction of SDSS cluster galaxies in a quadrant (relative to all SDSS cluster galaxies), namely:
where 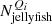 is the number of LoTSS jellyfish galaxies in each quadrant, Qi, and Njellyfish is the total number of LoTSS jellyfish galaxies, and similarly
is the number of LoTSS jellyfish galaxies in each quadrant, Qi, and Njellyfish is the total number of LoTSS jellyfish galaxies, and similarly 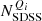 is the number of SDSS cluster galaxies in each quadrant, Qi, and NSDSS is the total number of SDSS cluster galaxies. In Table 2 we list the number of LoTSS jellyfish galaxies and SDSS cluster galaxies in each of the four phase space quadrants.
is the number of SDSS cluster galaxies in each quadrant, Qi, and NSDSS is the total number of SDSS cluster galaxies. In Table 2 we list the number of LoTSS jellyfish galaxies and SDSS cluster galaxies in each of the four phase space quadrants.
Galaxy distribution in phase space regions.
In Fig. 6b we plot this jellyfish galaxy excess as a function of phase space region. There is a clear excess of jellyfish relative to SDSS cluster galaxies in region 2, that corresponds to small clustercentric radius and large velocity offsets. This excess is fully consistent with expectations from RPS, as ρICMv2 will be highest in region 2. There is also a small deficit of jellyfish galaxies in region 4, corresponding to large clustercentric radius and small velocity offsets. This region of phase space is difficult to interpret in terms of galaxy infall histories, as it contains a mixture of galaxies just starting their infall onto the cluster as well as ‘backsplash’ galaxies that have already made a pericentric passage and are now approaching their orbital apocentre. For either case, a small number of jellyfish galaxies may be expected. For the former, galaxies may have not yet reached the dense part of the ICM required to drive highly asymmetric tails, and for the latter, after a passage through the core of the cluster galaxies may already be mostly stripped.
In Fig. 6c we compare the median 144 MHz shape asymmetries in each of the PPS quadrants. The error bars correspond to statistical errors on the median and the shaded regions cover the interquartile range. There are no strong trends between 144 MHz asymmetry and PPS region, but the regions corresponding to small clustercentric radii (regions 2 and 3) do have shape asymmetries that scatter to larger values than the regions covering the cluster outskirts. This is again consistent with prominent, asymmetric tails being primarily driven as galaxies interact with the dense ICM near the centre of the cluster. While here we have used the non-flux-weighted shape asymmetry parameter, due to its sensitivity to low surface brightness, we note that the same qualitative conclusions arise from using the more standard flux-weighted CAS asymmetry (Abraham et al. 1996; Conselice 2003).
6. Tail orientations
Ram pressure stripping makes clear predictions for the orientations of stripped galaxy tails, namely, tails should be observed extending opposite to the direction of motion, which for infalling galaxies on radial orbits will point away from the cluster centre. This simple interpretation is complicated by variation in galaxy orbital parameters as well as projection effects; however, previous works have reported stripped features extending away from the cluster centre for ram pressure galaxies (e.g. Chung et al. 2007; Smith et al. 2010; Roberts & Parker 2020).
We visually estimate the orientation of the observed 144 MHz tails following the same method as Roberts & Parker (2020). In short, tail directions are estimated from the 144 MHz cutouts as an angle between 0° and 360°, where 0° = west and 90° = north. The dot product between the vector along the tail direction and the vector between the galaxy and the cluster X-ray centre gives an orientation angle between the tail direction and the cluster centre. This orientation angle ranges between 0° and 180°, where an angle of 0° points directly towards the cluster centre and an angle of 180° points directly away from the cluster centre. These tail direction estimates are shown on the LoTSS jellyfish cutout images in Appendix A.
In Fig. 7 we show a histogram of the LoTSS tail orientations for the jellyfish galaxies in this work. If observed tails were randomly distributed then the distribution of orientations would be flat, that clearly is not the case in Fig. 7. Instead, Fig. 7 shows a distribution that peaks broadly at angles > 110°, as expected for tails oriented away from the cluster centre. These tail orientations are consistent with jellyfish galaxies being primarily stripped on first infall towards the cluster centre, and on relatively radial orbits. An orientation of 180° is only expected for galaxies on purely radial orbits, since cluster galaxy orbits have non-zero tangential components (e.g. Biviano et al. 2013), a broader distribution of angles should be expected.
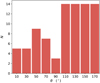 |
Fig. 7. Orientation of LoTSS tails with respect to the X-ray centre of the host cluster. An angle of 0° corresponds to a tail directed towards the cluster centre and an angle of 180° corresponds to a tail directed away from the cluster centre. The method for determining tail orientations is outlined in the main text. |
7. Jellyfish galaxy star formation
The process of RPS should have a strong impact on galaxy star formation. Not only can RPS quench star formation by removing galaxy gas reserves, but simulations also predict a brief enhancement in star formation, prior to gas removal, due to compression in the ISM through the galaxy-ICM interaction (e.g. Steinhauser et al. 2012; Ramos-Martínez et al. 2018; Troncoso Iribarren et al. 2020). This picture is supported by recent observations that have shown enhanced levels of star formation in galaxies thought to be undergoing RPS (Ebeling et al. 2014; Poggianti et al. 2016; Vulcani et al. 2018; Roberts & Parker 2020). With the sample in this work we are able to both, test whether LoTSS jellyfish galaxies show enhanced SFRs and explore whether or not jellyfish galaxies fall along the standard 144 MHz luminosity versus SFR relation.
7.1. The star-forming main sequence
We begin by exploring the position of LoTSS jellyfish galaxies with respect to the star-forming main sequence (SFMS). In Fig. 8a we plot SFR versus stellar mass. Galaxies from the isolated field sample are shown by the 2D histogram, SDSS cluster galaxies are shown by the blue contours, LoTSS cluster galaxies are shown by the gold contours, and jellyfish galaxies are shown as the red stars. We overplot the best-fit SFMS relationship for our data, which we obtain by fitting a power-law to the relationship between SFR and stellar mass for galaxies in our isolated field sample. The fits were performed with the BCES (‘bivariate correlated errors and intrinsic scatter’, Akritas & Bershady 1996; Nemmen et al. 2012) method with stellar mass as the independent variable, and gives a best-fit SFMS of
 |
Fig. 8. Star-forming properties of SDSS cluster galaxies, LoTSS cluster galaxies, and LoTSS jellyfish galaxies. Left: star formation rate versus stellar mass for galaxies from the isolated field sample (greyscale), SDSS cluster galaxies (blue contours), LoTSS cluster galaxies (gold contours), and jellyfish galaxies (red stars). The best-fit star-forming main sequence relation (assuming a power-law relationship) is shown as the solid black line. Right: median offset from the SFMS as a function of galaxy mass, for SDSS cluster galaxies (blue circle), LoTSS cluster galaxies (gold cross), and LoTSS jellyfish galaxies (red star). Error bars correspond to the 1σ standard error on the median for each stellar mass bin and dashed lines span the interquartile range. |
In Fig. 8a we see clear differences between the various galaxy samples. In terms of stellar mass, both LoTSS cluster galaxies and LoTSS jellyfish galaxies are skewed towards high masses. This is almost certainly a product of LoTSS not being sensitive to the very low-mass galaxies, as was discussed in Sect. 3.1. In terms of star formation rate, SDSS cluster galaxies skew slightly below the SFMS, LoTSS cluster galaxies mostly straddle the SFMS (though are slightly skewed to high SFRs), and LoTSS jellyfish galaxies lie systematically above the SFMS. Eighty per cent of jellyfish galaxies are above the SFMS.
The qualitative observations are confirmed quantitatively in Fig. 8b, where we plot the offset from the SFMS as a function of stellar mass. SDSS cluster galaxies (blue) fall below the SFMS by roughly 0.2 dex, with no strong trend with stellar mass. LoTSS cluster galaxies fall near the SFMS, but do show a small positive offset especially at intermediate and low masses. The difference between LoTSS cluster galaxies and SDSS cluster galaxies is being driven by selection effects. The luminosity at 144 MHz is a strong function of star formation activity (Gürkan et al. 2018; Smith et al. 2021); therefore, the galaxies in our sample that are detected by LOFAR will be biased towards high SFRs. While the same selection effects will also apply to the LoTSS jellyfish galaxies, Fig. 8b shows that jellyfish galaxies have enhanced star formation rates even when compared to the LoTSS cluster galaxy sample. Therefore SFRs for LoTSS jellyfish galaxies are enhanced at a level above and beyond simple selection effects. This suggests a physical enhancement of star formation in galaxies undergoing RPS in clusters.
7.2. The radio continuum – SFR relation
Previous work has established a tight relationship between 144 MHz luminosity and SFR (Gürkan et al. 2018; Smith et al. 2021). We now consider whether the LoTSS jellyfish galaxies identified in this work fall along this normal L144 MHz − SFR relation. This potentially gives insight into the source of cosmic rays in the observed tails. For example, if the cosmic ray emission in jellyfish galaxies is not solely due to star formation then offsets from the L144 MHz − SFR relation could be expected. Conversely, if the cosmic rays in the tails are from star formation within the disk of the galaxy, and then were subsequently stripped, we expect jellyfish galaxies to follow the standard L144 MHz − SFR relation as long as the flux from the entire tail is accounted for.
In Fig. 9 we plot the L144 − SFR relationship for the sample from this work. LoTSS cluster galaxies are shown with the gold points and LoTSS jellyfish galaxies are shown with the red stars. We also show the best-fit L144 − SFR relation (solid line) published in Gürkan et al. (2018), given by:
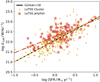 |
Fig. 9. 144 MHz luminosity versus star formation rate. Gold points show the relationship for LoTSS cluster galaxies and red stars correspond to LoTSS jellyfish galaxies. We also show the best-fit L144 MHz − SFR relationship for LoTSS cluster (gold, dash) and LoTSS jellyfish galaxies (red, dot-dash), with shaded regions corresponding to 1σ bootstrap confidence intervals. The solid black line shows the L144 MHz − SFR relationship from Gürkan et al. (2018). |
Star formation rates in Gürkan et al. (2018) are measured via SED fits to optical (SDSS ugriz) and IR photometry (WISE 3.4, 4.6, 12, and 22 μm and Herschel 100, 160, 250, 350, 500 μm) with the MAGPHYS code. For LoTSS cluster galaxies, 144 MHz luminosities are taken from the LoTSS DR2 source catalogue, where total flux densities are computed using PYBDSF (Mohan & Rafferty 2015). 144 MHz luminosities for jellyfish galaxies are computed by summing emission over the same segmentation maps used to calculate 144 MHz asymmetries. These segmentation maps have been individually inspected to ensure that they cover all extended emission from the jellyfish galaxies; therefore, calculating luminosities in this way ensures that we are including the diffuse emission from the extended tails. We note for the jellyfish galaxies the luminosities calculated from the segmentation maps agree well with those from the LoTSS source catalogue, with a median ratio (and 1σ scatter) between the two luminosities of 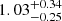 .
.
Figure 9 shows that the data in this work largely follow the relation found by Gürkan et al. (2018). There is a slight offset to large radio luminosities for LoTSS jellyfish galaxies, though they generally fall within the scatter of other cluster galaxies. In Fig. 9 we also show the best-fit power-law relations for the samples in this work, the LoTSS cluster galaxies and the LoTSS jellyfish galaxies. For LoTSS cluster galaxies we find a relation of:
and for LoTSS jellyfish galaxies we find a relation of:
The fits are performed with the BCES method with stellar mass as the independent variable. The best-fit relationship for LoTSS cluster galaxies is completely consistent with the Gürkan et al. (2018) relation, in fact it returns the same slope and normalization. For LoTSS jellyfish galaxies, the best-fit relation shows some deviation from the Gürkan et al. (2018) relationship, particularly at low SFRs, with the slopes differing at the ∼3σ level and the normalizations differing at the ∼5σ level. This could suggest that for some jellyfish galaxies there is a secondary source of cosmic rays, outside of star formation within the galaxy disk, contributing to the 144 MHz luminosity. Potentially, this could be low level star formation within the stripped tail (Vulcani et al. 2018), or also weak AGN emission (for example, from the ‘Composite’ objects in Fig. 4a). The difference between the best-fit LoTSS jellyfish relation and the Gürkan et al. (2018) relation is largest at low SFRs. For high-SFR galaxies, star formation within the galaxy disk should dominate the 144 MHz luminosity and as such these galaxies should agree with the Gürkan et al. (2018) relation. At the low SFR end there may be more room for these secondary sources to contribute to a more substantial portion of L144 MHz.
8. Discussion and conclusions
Here we have presented a sample of ∼100 jellyfish galaxies in clusters identified on the basis of radio continuum tails at 144 MHz. These objects are consistent with being primarily stripped on their first infall towards the cluster centre and show enhanced levels of star formation. As discussed throughout this paper, both of these facts can be explained by strong ram pressure influencing cluster satellite galaxies shortly after infall. LoTSS 144 MHz observations have proven a very effective tool for identifying jellyfish galaxies over extremely wide areas. In the remainder of this discussion we will highlight some of the unique ways in which radio continuum observations can constrain the process of RPS moving forward, as well as the prospects for detecting more jellyfish galaxies with LoTSS over a range of environments.
8.1. Tracing ram pressure with the radio continuum
Moving forward, radio continuum observations should prove a valuable tool to identify, and constrain the properties of galaxies experiencing RPS. LoTSS has already observed a substantial portion of the northern sky; however, the survey is not yet complete. As the rest of the northern sky is observed with LOFAR, more and more jellyfish galaxies will be identified in newly observed clusters. Furthermore, the number of galaxy groups (Mhalo < 1014 M⊙) vastly surpasses the number of massive clusters in the sky. In a future study we plan to similarly survey galaxy groups in LoTSS to search for jellyfish galaxies in these lower mass systems. Because of the very large areas covered by LoTSS, this will be the most extensive search for RPS in galaxy groups to date.
Previous works (e.g. Murphy et al. 2009; Vollmer et al. 2009; Chen et al. 2020; Müller et al. 2021) have used radio continuum observations to probe the effects of RPS in clusters. In particular, the VLA observations of the Coma Cluster from Chen et al. (2020) can be directly compared to the LoTSS jellyfish galaxies that we identify in Coma in this work. Chen et al. (2020) identify 10 galaxies with 1.4 GHz radio continuum tails out of a total sample of 20 Coma galaxies. We also detect radio continuum tails at 144 MHz for the 8 tailed galaxies from Chen et al. (2020) that pass our stellar mass completeness cut (GMP 4570 and GMP 4629 fall below the SDSS stellar mass completeness limit at the redshift of Coma). Furthermore, we also detect radio tails at 144 MHz for IC 3949 and NGC 4853 that are not detected at 1.4 GHz in Chen et al. (2020). Chen et al. (2020) present marginal evidence for steeper spectral indices in the tail regions relative to the galaxy disks. This could explain why we are able to detect tails at 144 MHz that are not seen at 1.4 GHz. For the 8 galaxies with tails detected at both frequencies, the VLA and LOFAR images could be used in conjunction to more accurately constrain the spectral indices in these ram pressure stripped tails. We leave this for a future work since this only comprises a narrow subset of the total jellyfish sample.
Beyond Coma, as more of the LoTSS footprint is also observed with the LOFAR low-band antenna (LBA) via the LOFAR LBA Sky Survey (LoLSS, de Gasperin et al. 2021), as well as APERTIF and RACS (McConnell et al. 2020), multi-frequency observations will become available for a number of the jellyfish galaxies identified in this work. The results of this work are consistent with the cosmic rays observed in these tails mostly originating from star formation within the disk, that are subsequently stripped out of the galaxy. If this is indeed the case, steeper spectral indices should be observed in the tail regions due to spectral ageing of the stripped electrons. As the multi-frequency observations become available, spectral index maps can be produced for the jellyfish galaxies presented here and this prediction can be directly tested. We do note that compared to the HBA, the LBA has a higher noise level (in terms of flux density) and lower resolution (∼15″); therefore, such spectral index maps may only be possible for the brightest, most prominent jellyfish galaxies in our sample. Müller et al. (2021) show that the stripped tail in the jellyfish galaxy J0206 has a clear spectral index gradient, with the spectral index, α, steepening to 2 in the tail compared to 0.7 in the galaxy disk (for Sν ∝ ν−α). If steep spectra are a generic feature of RPS tails, then LOFAR is truly an ideal instrument to identify these objects due to its low-frequency coverage.
A related question is how much time needs to elapse after stripping before the stripped plasma has aged sufficiently for a spectral index gradient to be observable (assuming no re-acceleration after stripping)? From Bruno et al. (2019), the radiative age of such a plasma, with spectral index at t = 0 of Γ and an observed spectral index α, measured between frequencies ν1 and ν2 (in GHz) is given by
where B is the magnetic field strength in μG, z is the redshift, and BCMB = 3.25 (1 + z)2 [μG] is the equivalent CMB magnetic field strength. Taking a ∼ μG magnetic field, ν1 = 144 MHz, ν2 = 54 MHz for the HBA and LBA, and z = 0.035 (roughly the median for our sample), we can ask what is the radiative age that corresponds to the minimum spectral index difference measurable with HBA and LBA? If we are sensitive to spectral index differences of α − Γ ≳ 0.5 (for example, Γ ∼ 0.5, α ≳ 1), this corresponds to a radiative age of ∼200 Myr. Therefore, if the plasma that we observe in these tails was stripped more than 200 Myr ago, we should be able to measure a spectral index gradient along the tail with the HBA and LBA, if a simple picture of synchrotron ageing is correct.
One way to roughly estimate the time since stripping for the observed tails, is to assume a stripping speed in conjunction with observed tails lengths. For an average stripping speed, the travel time between the centre of the galaxy and the far edge of the stripped tail is given by
where ℓtail is the length of the observed tail and 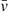 the average speed at which the plasma is stripped from the galaxy. We note that the tail lengths that we observe are likely shorter than the intrinsic tails lengths, both due to sensitivity limitations of the observations and projection effects. Therefore, Eq. (8) is really a lower limit on the travel time. If we assume
the average speed at which the plasma is stripped from the galaxy. We note that the tail lengths that we observe are likely shorter than the intrinsic tails lengths, both due to sensitivity limitations of the observations and projection effects. Therefore, Eq. (8) is really a lower limit on the travel time. If we assume 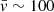 km s−1 (e.g. Tonnesen & Stone 2014), for the shortest tails in our sample, ℓtail ∼ 10 kpc, the travel time is ∼100 Myr and therefore spectral index steepening along the tail may be difficult to observe in those objects. For the longest tails in our sample, ℓtail ∼ 50 kpc, the travel time becomes ∼500 Myr. Thus, the more extreme examples are most promising for measuring any spectral index gradients. We stress that this argument is highly dependent on the stripping speed,
km s−1 (e.g. Tonnesen & Stone 2014), for the shortest tails in our sample, ℓtail ∼ 10 kpc, the travel time is ∼100 Myr and therefore spectral index steepening along the tail may be difficult to observe in those objects. For the longest tails in our sample, ℓtail ∼ 50 kpc, the travel time becomes ∼500 Myr. Thus, the more extreme examples are most promising for measuring any spectral index gradients. We stress that this argument is highly dependent on the stripping speed, 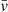 , which is not well constrained. If
, which is not well constrained. If 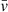 is closer to 1000 km s−1, then the travel times become very short. Recently, Bellhouse et al. (2019) estimate a stripping timescale of ∼0.6 − 1.2 Gyr for the GASP jellyfish galaxy JO201. If such a timescale also holds for the jellyfish galaxies in our sample, then this would imply that measuring spectral index steepening along the tails should be feasible with the HBA and LBA.
is closer to 1000 km s−1, then the travel times become very short. Recently, Bellhouse et al. (2019) estimate a stripping timescale of ∼0.6 − 1.2 Gyr for the GASP jellyfish galaxy JO201. If such a timescale also holds for the jellyfish galaxies in our sample, then this would imply that measuring spectral index steepening along the tails should be feasible with the HBA and LBA.
8.2. Simulations of magnetized ram pressure stripping
Recent work has explored the impact of ∼ μG magnetic fields on the rate of gas removal via RPS and the structure of RPS tails by comparing purely hydrodynamic (HD) and magneto-hydrodynamic (MHD) simulations. While the amount of gas removed by RPS is similar in both the HD and MHD case (Tonnesen & Stone 2014), the structure of the tails differ. In the MHD case, tails are smoother and narrower, and in some cases filametary, whereas for pure HD simulations stripped tails appear far clumpier (Ruszkowski et al. 2014; Vijayaraghavan & Ricker 2017). In the plane of the sky these filamentary tails can appear bifurcated, which is consistent with some observed RPS tails in nearby cluster galaxies (e.g. Sun et al. 2006, 2010).
The simple fact that we observe jellyfish tails through synchrotron emission is clear evidence that many (perhaps all) RPS tails are magnetized. With a 6″ beam we are not able to resolve structure within the observed tails; therefore, we cannot comment on whether the predicted filamentary, bifurcated structure is present, or even whether the tails are smooth or clumpy. That said, by incorporating the international LOFAR baselines it is possible for LOFAR to reach subarcsecond resolution at 144 MHz (Varenius et al. 2015; Ramírez-Olivencia et al. 2018; Sweijen et al. 2021). If the sensitivity at subarcsecond resolutions remains high enough to detect these stripped tails, such features will be highly resolved and it will be possible to comment on the tail morphologies. We do stress that this will only be possible for tails that are very bright at 144 MHz, due to the large amount of extended flux that is resolved out by the long baselines. Therefore this would likely be limited to some of the most extreme examples.
Ramos-Martínez et al. (2018) also perform wind tunnel simulations of RPS, both for a pure HD case and an MHD case. Ramos-Martínez et al. (2018) reach similar conclusions regarding the smoother tail morphology when including MHD compared to a clumpier tail in the pure HD case. They also show that the inclusion of magnetic fields leads to a strongly flared disk, which results in oblique shocks at the interaction interface driving increased gas densities and gas inflows towards the centre of the galaxy. These gas inflows are clear in the MHD case, but far weaker in the purely HD run. Ramos-Martínez et al. (2018) speculate that this should lead to episodes of enhanced star formation for galaxies undergoing RPS, which is fully consistent with the enhanced SFRs that we report in this work (Fig. 8).
8.3. Prospects for automated selection of LoTSS jellyfish galaxies
As mentioned in Sect. 8.1, the large fraction of the SDSS spectroscopic footprint that has been imaged by LoTSS makes this an ideal survey to search for jellyfish galaxies in lower mass SDSS groups. Groups are an important regime for studies of environmental quenching since the majority of galaxies in the local Universe reside in galaxy groups, and previous works have shown that star formation quenching in groups prior to accretion onto galaxy clusters (known as ‘pre-processing’) may account for a substantial portion of the cluster red sequence (e.g. Fujita 2004; McGee et al. 2009; von der Linden et al. 2010; Haines et al. 2015; Roberts & Parker 2017; Pallero et al. 2020). There are ∼10 times more galaxies in groups than clusters at low-z (e.g. Eke et al. 2005); therefore, for such a search the volume of galaxies requiring visual identification of RPS tails will quickly become overwhelming. It would be ideal if instead jellyfish galaxies in LoTSS could be selected by an automated algorithm, or at the very least, that an automated process could flag a subset of jellyfish candidates that could then be reasonably checked by-eye for confirmation. A full exploration of this subject is beyond the scope of this paper; however, below we will discuss one simple scheme that can automatically select LoTSS jellyfish galaxies reasonably well.
The sample of by-eye identified jellyfish galaxies from this work is a valuable set for testing any potential automated classification schemes (i.e. how well do automated selections reproduce the by-eye identifications from this work?). We suggest the ‘shape asymmetry’ (AS, Pawlik et al. 2016) of the 144 MHz segmentation maps, as described in Sect. 2.5, as a potentially useful selection tool for LoTSS jellyfish galaxies. In Fig. 10 we plot EDFs of the 144 MHz shape asymmetry for both LoTSS cluster galaxies (gold) and LoTSS jellyfish galaxies (red). There is clear separation between the LoTSS cluster galaxies and LoTSS jellyfish, with the jellyfish galaxies shifted to large shape asymmetries. For example, selecting sources with AS > 0.3 only excludes ∼15% of LoTSS jellyfish galaxies but excludes 70% of LoTSS cluster galaxies. We stress that we only include star-forming galaxies, which removes much of the potential contamination from bent AGN jets (e.g. head-tail radio galaxies). Such a simple selection does not produce a pure sample of jellyfish galaxies, but it is effective at pruning the large sample to a much smaller subset of ‘jellyfish candidates’ for visual inspection.
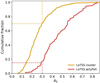 |
Fig. 10. Empirical distribution functions of 144 MHz shape asymmetry for LoTSS cluster galaxies (gold) and LoTSS jellyfish galaxies (red). High asymmetries correspond to larger AS. |
We show this simple example for illustrative purposes, but a more sophisticated selection based on multiple parameters could likely do even better. Furthermore, this problem may lend itself well to machine learning techniques. The sample of LoTSS jellyfish in this work is still fairly small as a training set; however, as the search for LoTSS jellyfish galaxies extends to more groups and clusters and the sample size increases, this may become feasible.
8.4. Summary
In this paper we use the high sensitivity, wide-field, and high-resolution observations from the LOFAR Two-metre Sky Survey to identify 95 jellyfish galaxies, across 21 low-z clusters, with stripped radio tails at 144 MHz. The primary results of this work are the following:
-
The cosmic rays observed in the tails of LoTSS jellyfish are consistent with primarily originating from star formation in the disk. There is no evidence for widespread AGN activity in this sample of jellyfish galaxies.
-
After carefully controlling for redshift-dependent selection effects, with find no evidence for strong variations in the frequency of jellyfish galaxies from cluster to cluster.
-
In projected phase space, jellyfish galaxies are found preferentially at small cluster-centric radius and large velocity offsets. Relative to normal star-forming cluster galaxies, jellyfish galaxies are 2−3 times more likely to occupy this phase space region.
-
The asymmetries of 144 MHz tails, relative to the optical centre of the galaxy, are largest for jellyfish galaxies at small cluster-centric radii.
-
Observed 144 MHz tails are systematically oriented away from the cluster centre, suggesting that most jellyfish galaxies are being stripped on their first infall.
-
LoTSS jellyfish galaxies show enhanced star formation rates. This is true relative to the field star-forming main sequence, relative to normal star-forming cluster galaxies, and relative to LoTSS-detected cluster galaxies without radio tails.
-
LoTSS cluster galaxies fall along the normal L144 MHz − SFR relation for low-z galaxies published by Gürkan et al. (2018). The L144 MHz − SFR relation for LoTSS jellyfish galaxies has a shallower slope and larger normalization compared to the Gürkan et al. (2018) relation.
This study is the first search for jellyfish galaxies in a wide-area radio survey. In this initial work we have focused on low redshift clusters; however, moving forward we will extend this approach to lower mass groups as well as higher redshifts. These methods have proven effective at identifying a large number of jellyfish galaxies, and such a sample will be valuable for constraining the properties of these extreme objects moving forward.
Acknowledgments
The authors thank the anonymous referee for their helpful suggestions and Bianca Poggianti for providing comments on an earlier draft. IDR and RJvW acknowledge support from the ERC Starting Grant Cluster Web 804208. SLM acknowledges support from STFC through grant number ST/N021702/1. AB acknowledges support from the VIDI research programme with project number 639.042.729, which is financed by the Netherlands Organisation for Scientific Research (NWO). AD acknowledges support by the BMBF Verbundforschung under the grant 05A20STA. This paper is based on data obtained with the International LOFAR Telescope (ILT). LOFAR (van Haarlem et al. 2013) is the LOw Frequency ARray designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources) and are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland; The Istituto Nazionale di Astrofisica (INAF), Italy. This research made use of the Dutch national e-infrastructure with support of the SURF Cooperative (e-infra 180169) and the LOFAR e-infra group. The Jülich LOFAR Long Term Archive and the GermanLOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputinge.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). This research made use of the University of Hertfordshire high-performance computing facility (http://uhhpc.herts.ac.uk) and the LOFAR-UK computing facility located at the University of Hertfordshire and supported by STFC [ST/P000096/1], and of the Italian LOFAR IT computing infrastructure supported and operated by INAF, and by the Physics Department of Turin University (under an agreement with Consorzio Interuniversitario per la Fisica Spaziale) at the C3S Supercomputing Centre, Italy. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [Google Scholar]
- Abraham, R. G., Tanvir, N. R., Santiago, B. X., et al. 1996, MNRAS, 279, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bekki, K. 2009, MNRAS, 399, 2221 [Google Scholar]
- Bekki, K., & Couch, W. J. 2003, ApJ, 596, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bellhouse, C., Jaffé, Y. L., Hau, G. K. T., et al. 2017, ApJ, 844, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Bellhouse, C., Jaffé, Y. L., McGee, S. L., et al. 2019, MNRAS, 485, 1157 [CrossRef] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., & Moustakas, J. 2009, ARA&A, 47, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, L., Snyder, G. F., Satyapal, S., & Ellison, S. L. 2018, MNRAS, 478, 3056 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., Boselli, A., Duc, P. A., et al. 2012, A&A, 545, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Fossati, M., Ferrarese, L., et al. 2018, A&A, 614, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruno, L., Gitti, M., Zanichelli, A., & Gregorini, L. 2019, A&A, 631, A173 [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H., Sun, M., Yagi, M., et al. 2020, MNRAS, 496, 4654 [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., & Vollmer, B. 2007, ApJ, 659, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., Crowl, H., & Vollmer, B. 2009, AJ, 138, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Crowl, H. H., Kenney, J. D. P., van Gorkom, J. H., & Vollmer, B. 2005, AJ, 130, 65 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Williams, W. L., Best, P., et al. 2021, A&A, 648, A104 [CrossRef] [EDP Sciences] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Stephenson, L. N., & Edge, A. C. 2014, ApJ, 781, L40 [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2005, MNRAS, 362, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Foltz, R., Wilson, G., Muzzin, A., et al. 2018, ApJ, 866, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y. 2004, PASJ, 56, 29 [NASA ADS] [Google Scholar]
- Fumagalli, M., Fossati, M., Hau, G. K. T., et al. 2014, MNRAS, 445, 4335 [Google Scholar]
- Garon, A. F., Rudnick, L., Wong, O. I., et al. 2019, AJ, 157, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., & Jaffe, W. 1985, ApJ, 294, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., & Jaffe, W. 1987, A&A, 186, L1 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Mayer, L., et al. 2001, ApJ, 563, L23 [NASA ADS] [CrossRef] [Google Scholar]
- George, K., Poggianti, B. M., Gullieuszik, M., et al. 2018, MNRAS, 479, 4126 [Google Scholar]
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [Google Scholar]
- Gürkan, G., Hardcastle, M. J., Smith, D. J. B., et al. 2018, MNRAS, 475, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Pereira, M. J., Smith, G. P., et al. 2015, ApJ, 806, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Ignesti, A., Shimwell, T., Brunetti, G., et al. 2020, A&A, 643, A172 [CrossRef] [EDP Sciences] [Google Scholar]
- Jáchym, P., Combes, F., Cortese, L., Sun, M., & Kenney, J. D. P. 2014, ApJ, 792, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Jáchym, P., Kenney, J. D. P., Sun, M., et al. 2019, ApJ, 883, 145 [Google Scholar]
- Jaffé, Y. L., Poggianti, B. M., Moretti, A., et al. 2018, MNRAS, 476, 4753 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [Google Scholar]
- Ji, Z., Giavalisco, M., Williams, C. C., et al. 2018, ApJ, 862, 135 [CrossRef] [Google Scholar]
- Kalita, B. S., & Ebeling, H. 2019, ApJ, 887, 158 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kenney, J. D. P., van Gorkom, J. H., & Vollmer, B. 2004, AJ, 127, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Kenney, J. D. P., Abramson, A., & Bravo-Alfaro, H. 2015, AJ, 150, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, D., Hogg, D. W., & Schlegel, D. J. 2016, AJ, 151, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S., Mamon, G. A., & Raychaudhury, S. 2011, MNRAS, 416, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Mastropietro, C., Wadsley, J., Stadel, J., & Moore, B. 2006, MNRAS, 369, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, D., Hale, C. L., Lenc, E., et al. 2020, PASA, 37 [CrossRef] [Google Scholar]
- McGee, S. L., Balogh, M. L., Bower, R. G., Font, A. S., & McCarthy, I. G. 2009, MNRAS, 400, 937 [Google Scholar]
- McPartland, C., Ebeling, H., Roediger, E., & Blumenthal, K. 2016, MNRAS, 455, 2994 [Google Scholar]
- Miley, G. 1980, ARA&A, 18, 165 [Google Scholar]
- Miller, N. A., Hornschemeier, A. E., & Mobasher, B. 2009, AJ, 137, 4436 [CrossRef] [Google Scholar]
- Mohan, N., & Rafferty, D. 2015, Astrophysics Source Code Library [record ascl:1502.007] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Paladino, R., Poggianti, B. M., et al. 2020, ApJ, 889, 9 [CrossRef] [Google Scholar]
- Müller, A., Poggianti, B. M., Pfrommer, C., et al. 2021, Nat. Astron., 5, 159 [Google Scholar]
- Murphy, E. J., Kenney, J. D. P., Helou, G., Chung, A., & Howell, J. H. 2009, ApJ, 694, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., van der Burg, R. F. J., McGee, S. L., et al. 2014, ApJ, 796, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Nemmen, R. S., Georganopoulos, M., Guiriec, S., et al. 2012, Science, 338, 1445 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Old, L. J., Balogh, M. L., van der Burg, R. F. J., et al. 2020, MNRAS, 493, 5987 [CrossRef] [Google Scholar]
- Oman, K. A., Hudson, M. J., & Behroozi, P. S. 2013, MNRAS, 431, 2307 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterloo, T., & van Gorkom, J. 2005, A&A, 437, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallero, D., Gómez, F. A., Padilla, N. D., et al. 2020, MNRAS, submitted [arXiv:2012.08593] [Google Scholar]
- Pasquali, A., Smith, R., Gallazzi, A., et al. 2019, MNRAS, 484, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlik, M. M., Wild, V., Walcher, C. J., et al. 2016, MNRAS, 456, 3032 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Fasano, G., Omizzolo, A., et al. 2016, AJ, 151, 78 [Google Scholar]
- Poggianti, B. M., Moretti, A., Gullieuszik, M., et al. 2017, ApJ, 844, 48 [Google Scholar]
- Poggianti, B. M., Ignesti, A., Gitti, M., et al. 2019a, ApJ, 887, 155 [Google Scholar]
- Poggianti, B. M., Gullieuszik, M., Tonnesen, S., et al. 2019b, MNRAS, 482, 4466 [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 1617 [Google Scholar]
- Ramírez-Olivencia, N., Varenius, E., Pérez-Torres, M., et al. 2018, A&A, 610, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramos-Martínez, M., Gómez, G. C., & Pérez-Villegas, Á. 2018, MNRAS, 476, 3781 [NASA ADS] [CrossRef] [Google Scholar]
- Rhee, J., Smith, R., Choi, H., et al. 2017, ApJ, 843, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, I. D., & Parker, L. C. 2017, MNRAS, 467, 3268 [Google Scholar]
- Roberts, I. D., & Parker, L. C. 2020, MNRAS, 495, 554 [CrossRef] [Google Scholar]
- Roberts, I. D., Parker, L. C., Brown, T., et al. 2019, ApJ, 873, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, I. D., Parker, L. C., Gwyn, S., et al. 2021, MNRAS, submitted [Google Scholar]
- Roediger, E., & Hensler, G. 2005, A&A, 433, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruszkowski, M., Brüggen, M., Lee, D., & Shin, M. S. 2014, ApJ, 784, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sivanandam, S., Rieke, M. J., & Rieke, G. H. 2010, ApJ, 717, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Sivanandam, S., Rieke, M. J., & Rieke, G. H. 2014, ApJ, 796, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., Hammer, D., et al. 2010, MNRAS, 408, 1417 [Google Scholar]
- Smith, D. J. B., Haskell, P., Gürkan, G., et al. 2021, A&A, 648, A6 [EDP Sciences] [Google Scholar]
- Steinhauser, D., Haider, M., Kapferer, W., & Schindler, S. 2012, A&A, 544, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinhauser, D., Schindler, S., & Springel, V. 2016, A&A, 591, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stern, D., Eisenhardt, P., Gorjian, V., et al. 2005, ApJ, 631, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Jones, C., Forman, W., et al. 2006, ApJ, 637, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Donahue, M., & Voit, G. M. 2007, ApJ, 671, 190 [Google Scholar]
- Sun, M., Donahue, M., Roediger, E., et al. 2010, ApJ, 708, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Sweijen, F., Morabito, L. K., Harwood, J., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202039871 [Google Scholar]
- Tasse, C., Shimwell, T., Hardcastle, M. J., et al. 2021, A&A, 648, A1 [EDP Sciences] [Google Scholar]
- Thomas, D., Steele, O., Maraston, C., et al. 2013, MNRAS, 431, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Tonnesen, S., & Stone, J. 2014, ApJ, 795, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Troncoso Iribarren, P., Padilla, N., Contreras, S., et al. 2016, Galaxies, 4, 77 [CrossRef] [Google Scholar]
- Troncoso Iribarren, P., Padilla, N., Santander, C., et al. 2020, MNRAS, 497, 4145 [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varenius, E., Conway, J. E., Martí-Vidal, I., et al. 2015, A&A, 574, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vijayaraghavan, R., & Ricker, P. M. 2017, ApJ, 841, 38 [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Vollmer, B., & Huchtmeier, W. 2007, A&A, 462, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2009, A&A, 496, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Braine, J., et al. 2012, A&A, 537, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von der Linden, A., Wild, V., Kauffmann, G., White, S. D. M., & Weinmann, S. 2010, MNRAS, 404, 1231 [Google Scholar]
- Vulcani, B., Poggianti, B. M., Gullieuszik, M., et al. 2018, ApJ, 866, L25 [Google Scholar]
- Wang, J., Fu, J., Aumer, M., et al. 2014, MNRAS, 441, 2159 [NASA ADS] [CrossRef] [Google Scholar]
- Weigel, A. K., Schawinski, K., & Bruderer, C. 2016, MNRAS, 459, 2150 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., & Conroy, C. 2012, MNRAS, 424, 232 [Google Scholar]
- Wetzel, A. R., Tinker, J. L., Conroy, C., & van den Bosch, F. C. 2013, MNRAS, 432, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, W. L., Hardcastle, M. J., Best, P. N., et al. 2019, A&A, 622, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yagi, M., Komiyama, Y., Yoshida, M., et al. 2007, ApJ, 660, 1209 [Google Scholar]
- Yagi, M., Yoshida, M., Komiyama, Y., et al. 2010, AJ, 140, 1814 [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, H., Chung, A., Smith, R., & Jaffé, Y. L. 2017, ApJ, 838, 81 [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Yoshida, M., Yagi, M., Okamura, S., et al. 2002, ApJ, 567, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, K., Pillepich, A., Zinger, E., et al. 2019, MNRAS, 483, 1042 [Google Scholar]
Appendix A: Jellyfish galaxies
In this appendix we list all LoTSS jellyfish galaxies in Table A.1, we also show 100 × 100 kpc Pan-STARRs g-band images with LOFAR 144 MHz contours overlaid for each jellyfish galaxy in Fig. A.1. We show both the original LoTSS contours as well as the ‘degraded’ LoTSS contours described in Sect. 4. Panels that are highlighted in blue correspond to galaxies that are identified as jellyfish galaxies with both the original LoTSS imaging and the degraded LoTSS imaging. Panels highlighted in red correspond to galaxies identified as jellyfish galaxies with both the original LoTSS imaging and the degraded LoTSS imaging but with stellar masses < 109.7 M⊙. For three galaxies, IC 4040, D100, and SDSS J114313.08+200017.4, the lowest contour corresponds to 3× the rms instead of 2× the rms. This is for visibility reasons as those galaxies are spatially coincident with diffuse radio sources in their host clusters that can obscure the tail.
 |
Fig. A.1. 100 × 100 kpc Pan-STARRs g-band, LOFAR 144 MHz overlay images for LoTSS jellyfish galaxies. 144 MHz contours are logarithmically spaced starting at 2× the rms. The estimated direction of the stripped tail is also marked for each galaxy. For each galaxy the original LoTSS contours (left) and the degraded LoTSS contours (right, see text) are shown. Galaxies classified as jellyfish according to both the original and the degraded LoTSS images are highlighted in blue. Galaxies classified as jellyfish according to both the original and the degraded LoTSS images, but with Mstar < 109.7 M⊙, are highlighted in red. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
LoTSS jellyfish galaxies.
All Tables
All Figures
 |
Fig. 1. Stellar mass versus redshift for star-forming galaxies in GSWLC-2 (Salim et al. 2016, 2018) with z < 0.05. Blue points show the limiting stellar mass value for the faintest 20% of galaxies in each redshift bin and large circles show the stellar mass completeness limits as a function of redshift. |
| In the text | |
 |
Fig. 2. Composite optical (CFHT, RGB) plus radio (LOFAR, 144 MHz) images of three LoTSS jellyfish galaxies in our sample. The scale bar in each panel corresponds to a physical size of 10 kpc. The radio continuum tail for SDSS J114313.08+200017.4 was first detected at 1.4 GHz by Gavazzi & Jaffe (1985, 1987), the radio continuum tail for SDSS J162857.99+391908.7 is a new detection, and the radio continuum tail for NGC 4858 was first detected at 1.4 GHz by Chen et al. (2020). |
| In the text | |
 |
Fig. 3. Empirical distribution functions (EDFs) for galaxy redshift (top) and galaxy stellar mass (bottom). EDFs are shown for SDSS cluster galaxies (blue, solid), SDSS field galaxies (black, dashed), LoTSS jellyfish galaxies (red, solid), and normal star-forming galaxies from the LoTSS DR2 source catalogue (red, dashed). |
| In the text | |
 |
Fig. 4. Top: fraction of jellyfish galaxies in the sample according to their BPT classification: star-forming (solid line), composite (dashed line), LINER (dot-dashed line), and Seyfert (dotted line). Bottom: WISE colour-colour diagram. Dashed line shows the dividing line of W1 − W2 > 0.8 for AGN classifications from Stern et al. (2012) and the solid line shows the AGN region from Jarrett et al. (2011). |
| In the text | |
 |
Fig. 5. Fraction of star-forming galaxies identified as LoTSS jellyfish for each cluster. Error bars are 1σ binomial confidence intervals (Cameron 2011). In order to ensure a fair comparison from cluster to cluster, jellyfish fractions in this plot are measured using only galaxies with Mstar > 109.7 M⊙ and only include jellyfish galaxies identified from the degraded LoTSS imaging. |
| In the text | |
 |
Fig. 6. Distribution of SDSS cluster galaxies and LoTSS jellyfish galaxies in projected phase space. Left: velocity offset versus projected clustercentric radius. 2D histogram shows distribution for star-forming cluster galaxies and red stars correspond to jellyfish galaxies. We also show the 1D distributions of projected radius and velocity offset over the corresponding axes. Right, top: excess of jellyfish galaxies with respect to star-forming cluster galaxies (see text), for the four different regions in projected phase space. Right, bottom: median 144 MHz asymmetry for each of the four phase space regions. Error bars show the statistical error on the median and shaded regions show the interquartile range. |
| In the text | |
 |
Fig. 7. Orientation of LoTSS tails with respect to the X-ray centre of the host cluster. An angle of 0° corresponds to a tail directed towards the cluster centre and an angle of 180° corresponds to a tail directed away from the cluster centre. The method for determining tail orientations is outlined in the main text. |
| In the text | |
 |
Fig. 8. Star-forming properties of SDSS cluster galaxies, LoTSS cluster galaxies, and LoTSS jellyfish galaxies. Left: star formation rate versus stellar mass for galaxies from the isolated field sample (greyscale), SDSS cluster galaxies (blue contours), LoTSS cluster galaxies (gold contours), and jellyfish galaxies (red stars). The best-fit star-forming main sequence relation (assuming a power-law relationship) is shown as the solid black line. Right: median offset from the SFMS as a function of galaxy mass, for SDSS cluster galaxies (blue circle), LoTSS cluster galaxies (gold cross), and LoTSS jellyfish galaxies (red star). Error bars correspond to the 1σ standard error on the median for each stellar mass bin and dashed lines span the interquartile range. |
| In the text | |
 |
Fig. 9. 144 MHz luminosity versus star formation rate. Gold points show the relationship for LoTSS cluster galaxies and red stars correspond to LoTSS jellyfish galaxies. We also show the best-fit L144 MHz − SFR relationship for LoTSS cluster (gold, dash) and LoTSS jellyfish galaxies (red, dot-dash), with shaded regions corresponding to 1σ bootstrap confidence intervals. The solid black line shows the L144 MHz − SFR relationship from Gürkan et al. (2018). |
| In the text | |
 |
Fig. 10. Empirical distribution functions of 144 MHz shape asymmetry for LoTSS cluster galaxies (gold) and LoTSS jellyfish galaxies (red). High asymmetries correspond to larger AS. |
| In the text | |
 |
Fig. A.1. 100 × 100 kpc Pan-STARRs g-band, LOFAR 144 MHz overlay images for LoTSS jellyfish galaxies. 144 MHz contours are logarithmically spaced starting at 2× the rms. The estimated direction of the stripped tail is also marked for each galaxy. For each galaxy the original LoTSS contours (left) and the degraded LoTSS contours (right, see text) are shown. Galaxies classified as jellyfish according to both the original and the degraded LoTSS images are highlighted in blue. Galaxies classified as jellyfish according to both the original and the degraded LoTSS images, but with Mstar < 109.7 M⊙, are highlighted in red. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



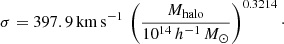
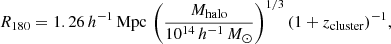
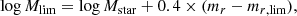
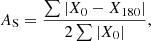
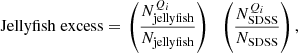
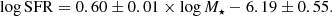
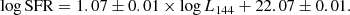
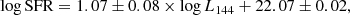
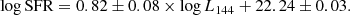
![$$ \begin{aligned} t_{\rm rad} = 1590\,\frac{\sqrt{B}}{(B^2+B_{\rm CMB}^2)\sqrt{1+z}}\,\sqrt{\frac{(\alpha -\Gamma )\ln (\nu _1/\nu _2)}{\nu _1-\nu _2}}\,\mathrm{[Myr]}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa40784-21/aa40784-21-eq16.gif)
![$$ \begin{aligned} t_{\rm tail} \simeq 100\,\left(\frac{\ell _{\rm tail}}{10\,\mathrm{kpc}}\right)\,\left(\frac{100\,\mathrm{km\,s^{-1}}}{\bar{{ v}}}\right)\,\mathrm{[Myr]}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa40784-21/aa40784-21-eq17.gif)