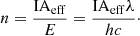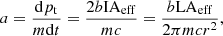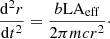EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 649 (May 2021) A&A, 649 (2021) L17 Full HTML
Free Access
Issue
A&A
Volume 649, May 2021
Article Number L17
Number of page(s) 4
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202141283
Published online 02 June 2021

© ESO 2021

1. Introduction

‘Oumuamua (1I/2017 U1) was discovered on 19 October 2017 (Meech et al. 2017) by the Panoramic Survey Telescope and Rapid Response System 1 (Pan-STARRS1) survey (Denneau et al. 2013; Wainscoat et al. 2016). The highly hyperbolic trajectory, with a speed of 26 km s−1, indicated that the object originated from outside of the Solar System in the direction of Lyra (Meech et al. 2017). As the first detection of a visitor unbound by the Sun’s gravity, ‘Oumuamua has generated much interest and much controversy, specifically over the origin of its 5  ×  10−6 m s−2 non-gravitational acceleration (Micheli et al. 2018). While this has been disputed (e.g. Katz 2019), in ruling out the usual suspects, such as thrust from a cometary tail, it has been suggested that radiation pressure drives the acceleration (Bialy & Loeb 2018). That is to say, ‘Oumuamua is a light sail.

Over the past century, radiation pressure has been proposed as a means to propel a payload through space (Zander 1925; Forward 1984; Fu et al. 2016). Indeed, the principle was put into practice when using the solar panels to correct the trajectory of Mariner 10 during its flyby of Mercury in 1974. The advantage of a light sail is that it is powered by an external source, such as a star, releasing it from the burden of an onboard fuel supply, which is the main disadvantage of a rocket. This necessity is further compounded by the rocket needing fuel not just to accelerate the payload, but the mass of the fuel itself. Thus, light sails possibly offer a more practical means of exploring deep space, with accelerations to relativistic velocities often suggested, allowing us to reach the nearest extrasolar star, Proxima Centauri (at 4.22 light years distance), in a matter of decades (e.g. Lubin 2016; Popkin 2017; Worden et al. 2018; Lingam & Loeb 2020).

Here we show that, even if we neglect slowing (and damage) by interplanetary material, there exists an effective terminal velocity beyond which the sail barely accelerates. This velocity is much lower than the relativistic speeds proposed for conceptual light sails (e.g. Kipping 2017), meaning that the travel times are vastly underestimated. Using the properties of ‘Oumuamua, we find the terminal velocity to be ≲1 km s−1, thus requiring, at the very least, millions of years for interstellar travel.

2. Analysis

2.1. Acceleration by light

The intensity of radiation on an object at distance r from a source of luminosity L is I = L/(4πr2), with the power intercepted over a projected facing surface area, Aeff, being P = IAeff. The energy carried by each photon is E = hc/λ and so the number of photons intercepted each second is

The momentum carried by each photon is p = h/λ, of which 2bp cos θ is imparted to the sail, where the factor of two conserves the momentum for a perfectly reflected photon, b is the albedo and θ is the angle the photon strikes with respect to the normal to the sail. For θ = 0, over the whole sail, the total momentum imparted each second is therefore

Since the force F ≡ dpt/dt, in the non-relativistic regime the acceleration is given by

(1)

where m is the total mass (sail plus payload).

2.2. Interstellar travel by conceptual light sails

2.2.1. Terminal velocity

From the sail properties (Eq. (1)), the acceleration is maximised by maximising the albedo and area and minimising the mass. For example, a theoretical sail of size 1 km on a side, constructed from lithium (the lightest metal with a density of ρ = 530 kg m−3, Wright 1992) and of mass 1 kg would have a thickness of 1.8 nm. This constitutes a sail thickness only a few atoms wide, which must remain flat and stiff over its million square metre area, while surviving the rigours of space travel. Neglecting the considerable challenge in materials science and engineering required, if launched from the Earth’s orbit, this would have an initial acceleration of 8.17 m s−2 (0.83 g) and, if sustained, would give a travel time of just 2.2 years to Proxima Centauri.

However, many conceptual light powered journeys do not consider that a large acceleration removes you from the illuminating power source quicker, causing a large decrease in further acceleration. This is described by the second order ordinary differential equation

(2)

Solving this numerically, using the equations of motion over small time ranges (from Δt = 10−9 s, depending upon the regime), we find that, while the acceleration asymptotically approaches zero, never quite reaching it, it rapidly gets so small as to take cosmological timescales to increase the speed by an additional metre per second. This introduces an effective terminal velocity, which in the case of the conceptual sail above is 1563 km s−1 (0.0052c)1, thus taking the sail 810 years to reach Proxima Centauri (Fig. 1)2. While a terminal velocity has been discussed previously (Kipping 2017), this occurs in the relativistic regime.

thumbnail Fig. 1.

Acceleration (top), velocity (middle), and distance (bottom panel) travelled by a conceptual light sail (Aeff = 106 m2, b = 0.9) for different masses starting at 1 AU (149 597 871 km) from the Sun.

2.2.2. Maximising the acceleration

From Eq. (1), the acceleration can be increased by increasing the sail area and albedo or by decreasing the distance to the power source or the total mass. Increasing the area and albedo is clearly challenging, although the distance can be decreased by a swing-by around the Sun (Cai et al. 2015).

For example, a million square metre sail of total mass 1 kg launched 0.1 AU from the Sun3 would have an initial acceleration of 817 m s−2 and a terminal velocity of 4943 km s−1 (0.016c), reducing the journey to Proxima Centauri to 260 years (Fig. 2). In addition to the loads on this conceptual sail, the thermal properties must be considered, given that, even for the reflectivities discussed for concept sails (b = 0.9), for a thin sail4 in thermal equilibrium temperatures would be in excess of 200 °C at 0.1 AU (Fig. 3).

thumbnail Fig. 2.

Acceleration (top), velocity (middle), and distance (bottom panel) travelled by a conceptual light sail (Aeff = 106 m2, b = 0.9) with a total mass of 1 kg at different launch distances from the Sun.

thumbnail Fig. 3.

Temperature of a black body as a function of distance from the Sun for different albedos.

Other materials, such as polyethylene terephthalate (mylar) and carbon fibre, have been proposed in order to lighten conceptual sails (Landis 1999, 2003). Both are, however, denser than lithium (ρ = 1400 and 1800 kg m−3, respectively), although the latter, if porous, can be as low as ρ = 270 kg m−3 (Spradling & Guth 2003). However, this is only about half the density of lithium, resulting in similar sail widths while not being as strong, with a tensile strength of 1.7 MPa, compared to 15 MPa for lithium. Furthermore, carbon fibre would require a reflective coating, further increasing the mass, to have a similar albedo as a metal.

We can conceptualise the fastest ‘possible’ theoretical solar driven sail by assuming the ability to construct and deploy a sail of an arbitrarily large size with a thickness of one atom and perfect reflectivity (b = 1). The only constraint is the minimum mass dictated by the volume of the sail, for which we neglect the mass of the payload and other ancillary requirements (such as strengthening, stiffening, and unfurling mechanisms). We choose the material to be lithium (diameter 3 Å) since this is only slightly denser than a carbon fibre foam, which, by definition, cannot form a structure only one atom thick. Since the area and mass are degenerate, bAeff/m < 6.086 × 106 m2 kg−1 no matter the area. Therefore, the ideal sail gives, at best, vterm = 4066 km s−1 (0.014c), which results in a > 310 year journey to Proxima Centauri. As discussed above, the acceleration can be increased by launching closer to the Sun. For a launch at 0.1 AU, the initial acceleration is 5.53 × 103 m s−2 (564 g), and the terminal velocity vterm = 1.29 × 104 km s−1 (0.043c, Fig. 4), thus taking 98 years to reach Proxima Centauri.

thumbnail Fig. 4.

Velocity of the best possible theoretical sail at different launch distances from the Sun.

The conceptual project Breakthrough Starshot proposes taking advantage of the high initial acceleration by using 100 GW of Earth-based laser power for several minutes only, accelerating a 4 m wide sail of 2.4 g mass to 0.2c over this time, reaching Proxima Centauri in 20 years (Lubin 2016). However, not only is such laser power a million times more powerful than current continuous lasers, for the lowest densities discussed above (ρ = 270 kg m−3 for porous carbon fibre), the width of the sail remains incredibly thin at 0.5 μm, without additional payload, which must survive an initial acceleration of 7 × 105 m s−2 (80 000 g). Other fundamental technical challenges include widening of the laser beam (dictated by diffraction), reducing the incident power, and vaporisation of the sail by the laser (Kipping 2017; Katz 2021).

2.3. ‘Oumuamua as a light sail

If the acceleration of ‘Oumuamua is driven by radiation pressure, it qualifies as a light sail. Furthermore, if this is the sole source of its acceleration, from its measured area the object must be relatively thin, thus the motivation for proposing an artificial origin (Bialy & Loeb 2018; Loeb 2018a,b, 2021; Williams 2018). Here we examine the feasibility of this suggestion by comparing the implications of it being a light sail with the conceptual examples discussed above.

The dimensions of ‘Oumuamua are degenerate with its albedo (Table 1). Given that the acceleration was 4.9 ± 0.2 × 10−6 m s−2 when it was at 0.2556 AU from the Sun (Micheli et al. 2018) results in a mass of 42 × 103 kg. If of a rock and iron composition, similar to the Earth (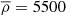 kg m−3), the thickness is somewhere between 50 μm and 1 mm, depending upon the actual area (Table 1). The former is of the order of the width of a human hair, although this range can be increased from 1 mm to 2 cm if constructed of a more exotic material such as porous carbon fibre.

Table 1.

Effective diameter and albedo of ‘Oumuamua (Trilling et al. 2018; Bannister et al. 2019).

From the observed parameters of ‘Oumuamua (Trilling et al. 2018; Bannister et al. 2019), we determine a terminal velocity of 610 m s−1 (Fig. 5), at which it would take 2 × 106 years to reach Proxima Centauri. The acceleration can be increased by launching from closer to the parent star and at 0.1 AU from a star of solar luminosity; the acceleration increases by an order of magnitude to 3.2 × 10−5 m s−2, giving a terminal velocity of close to 1 km s−1, although, from the range of possible albedos (b = 0.01 − 0.2, Table 1), the temperature is high at 540−750°C. If sent by an alien civilisation, we can envisage exotic materials, where close to 100% reflectivity (b ≈ 1) is possible, allowing launches arbitrarily close to the star, giving a much larger kick in acceleration. However, not only is such a large albedo not observed for ‘Oumuamua, but, as seen from Fig. 2, the benefits from a large initial acceleration are tempered by a more rapid distancing from the power source, thus not yielding a proportionate return for the effort. In addition to the incident flux, the acceleration is limited by the area of the sail and the mass (Eq. (1)). For ‘Oumuamua, the former is constrained by observation (Table 1) and the latter is constrained by the presumption that the acceleration is due to radiation pressure. If working under this presumption, from the travel times (of the order of a million years to the nearest star), it is clear that this is much inferior to the light sails being conceived by ourselves.

thumbnail Fig. 5.

Velocity of ‘Oumuamua based upon its observed acceleration.

3. Discussion and conclusion

We have shown that, based on its observed parameters, ‘Oumuamua would take two million years to cover the distance to the nearest extrasolar star (at just 4.22 light years distance). This is a vast timescale, even in comparison to conceptual man-made light sails, for which we show the estimated travel times to be vastly optimistic. Based upon its trajectory, a more distant (≈200 light years) point of origin is proposed (Gaidos et al. 2017), suggesting a travel time of the order of half a billion years.

From its measured velocity of 26 km s−1 (Meech et al. 2017), it would take ‘Oumuamua 50 000 years to travel from Proxima Centauri and 400 000 years to travel 10 pc (Zuckerman 2021), encompassing the nearest 357 main sequence stars (Henry et al. 2018). However, we have shown that such a velocity cannot be achieved by ‘Oumuamua as a solar sail, with the measured speed being due to the Sun’s gravitational attraction. Even at a travel time of 400 000 years, it has been argued that an advanced civilisation would use its resources to explore interstellar space via electromagnetic waves, rather than the “construction and launch of an ‘Oumuamua-like probe” (Zuckerman 2021).

There is of course the possibility of using lasers to accelerate a sail to relativistic speeds in the space of a few minutes, as proposed for Breakthrough Starshot. However, even for a mass of just 2.4 g and a theoretical albedo of b > 0.9999, which no metal has, even in the microwave band, this is fraught with many, perhaps insurmountable, challenges (Katz 2021). ‘Oumuamua has a much lower, and realistic, albedo and even if we assume the possibility that the surface has been tarnished from b ≈ 1 by its journey, its mass implies a power requirement of ∼1018 W, which is ∼1013 times today’s most powerful lasers. Other fantastic power sources include massive stars, microquasars, supernovae, pulsars, and active galactic nuclei (Lingam & Loeb 2020). However, life cannot evolve in proximity to any of these objects and there is no discussion of how the sail would be transported close enough in order to take advantage of their immense power output. Thus, the Sun (or any parent star) remains the best option since it provides vast amounts of continuous power for free, the full utilisation of which would be an indicator of an advanced civilisation (Dyson 1960).

It has been suggested that ‘Oumuamua is in fact accelerated by outgassing (Micheli et al. 2018). However, even if this is ruled out (Lingam & Loeb 2020; Siraj & Loeb 2021) so that ‘Oumuamua is indeed a light sail (Bialy & Loeb 2018), given the likely cosmological timescales required to traverse between stars, we conclude that it is unlikely that ‘Oumuamua has been sent by an extraterrestrial civilisation and more likely that it is just an unusually shaped rock, which has happened to wander into the Solar System.

1

Modelled from a = 8.17 to 9.9 × 10−19 m s−2.

2

Either by passing at this speed or using Proxima Centauri to decelerate around the halfway mark, assuming a solar luminosity.

3

Within Mercury’s orbit of 0.44 AU.

4

Asurface ≈ 2Aeff.

Acknowledgments

I would like to thank the anonymous referee for their helpful comments. This research has made use of NASA’s Astrophysics Data System Bibliographic Service.

References

  1. Bannister, M. T., Bhandare, A., Dybczyński, P. A., et al. 2019, Nat. Astron., 3, 594 [Google Scholar]
  2. Bialy, S., & Loeb, A. 2018, ApJ, 868, L1 [Google Scholar]
  3. Cai, X., Li, J., & Gong, S. 2015, Sci. China Phys. Mech. Astron., 58, 1 [Google Scholar]
  4. Denneau, L., Jedicke, R., Grav, T., et al. 2013, PASP, 125, 357 [Google Scholar]
  5. Dyson, F. J. 1960, Science, 131, 1667 [Google Scholar]
  6. Forward, R. L. 1984, J. Spacecr. Rockets, 21, 187 [Google Scholar]
  7. Fu, B., Sperber, E., & Eke, F. 2016, Prog. Aerosp. Sci., 86, 1 [Google Scholar]
  8. Gaidos, E., Williams, J., & Kraus, A. 2017, Res. Notes Am. Astron. Soc., 1, 13 [Google Scholar]
  9. Henry, T. J., Jao, W.-C., Winters, J. G., et al. 2018, AJ, 155, 265 [Google Scholar]
  10. Katz, J. I. 2019, Astrophys. Space Sci., 364, 51 [Google Scholar]
  11. Katz, J. I. 2021, ArXiv e-prints [arXiv:2102.07871] [Google Scholar]
  12. Kipping, D. 2017, AJ, 153, 277 [Google Scholar]
  13. Landis, G. A. 1999, Advanced Solar and Laser-pushed Lightsail Concepts (Ohio Aerospace Institute) [Google Scholar]
  14. Landis, G. A. 2003, in Interstellar Travel and Multi-Generation Space Ships, eds. Y. Kondo, F. Bruhweiler, J. H. Moore, & C. Sheffield (Burlington, Canada: Apogee Books), 52 [Google Scholar]
  15. Lingam, M., & Loeb, A. 2020, ApJ, 894, 36 [Google Scholar]
  16. Loeb, A. 2018a, 6 Strange Facts about the Interstellar Visitor ’Oumuamua, Scientific American, https://blogs.scientificamerican.com/observations/6-strange-facts-about-the-interstellar-visitor-oumuamua/ [Google Scholar]
  17. Loeb, A. 2018b, How to Search for Dead Cosmic Civilizations, Scientific American, https://blogs.scientificamerican.com/observations/how-to-search-for-dead-cosmic-civilizations/ [Google Scholar]
  18. Loeb, A. 2021, Extraterrestrial: The First Sign of Intelligent Life Beyond Earth (Boston: Houghton Mifflin Harcourt) [Google Scholar]
  19. Lubin, P. 2016, Interplanet. Soc., 67, 40 [Google Scholar]
  20. Meech, K. J., Weryk, R., Micheli, M., et al. 2017, Nature, 552, 378 [Google Scholar]
  21. Micheli, M., Farnocchia, D., Meech, K. J., et al. 2018, Nature, 559, 223 [Google Scholar]
  22. Popkin, G. 2017, Nature, 542, 20 [Google Scholar]
  23. Siraj, A., & Loeb, A. 2021, ArXiv e-prints [arXiv:2103.14032] [Google Scholar]
  24. Spradling, D. M., & Guth, R. A. 2003, Adv. Mater. Proc., 161, 29 [Google Scholar]
  25. Trilling, D. E., Mommert, M., Hora, J. L., et al. 2018, AJ, 156, 261 [Google Scholar]
  26. Wainscoat, R., Chambers, K., Lilly, E., et al. 2016, in Asteroids: New Observations, New Models, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, 318, 293 [Google Scholar]
  27. Williams, M. 2018, Could ’Oumuamua be an Extraterrestrial Solar Sail?, Universe Today, https://phys.org/news/2018-11-oumuamua-extraterrestrial-solar.html [Google Scholar]
  28. Worden, S. P., Drew, J., & Klupar, P. 2018, New Space, 6, 262 [Google Scholar]
  29. Wright, J. L. 1992, Space Sailing (London: Gordon and Breach Science Publishers) [Google Scholar]
  30. Zander, F. A. 1925, Technika i Zhizn, 13, 15 [Google Scholar]
  31. Zuckerman, B. 2021, AAS J., submitted [arXiv:2103.05559] [Google Scholar]

All Tables

Table 1.

Effective diameter and albedo of ‘Oumuamua (Trilling et al. 2018; Bannister et al. 2019).

In the text

All Figures

thumbnail Fig. 1.

Acceleration (top), velocity (middle), and distance (bottom panel) travelled by a conceptual light sail (Aeff = 106 m2, b = 0.9) for different masses starting at 1 AU (149 597 871 km) from the Sun.
In the text
thumbnail Fig. 2.

Acceleration (top), velocity (middle), and distance (bottom panel) travelled by a conceptual light sail (Aeff = 106 m2, b = 0.9) with a total mass of 1 kg at different launch distances from the Sun.
In the text
thumbnail Fig. 3.

Temperature of a black body as a function of distance from the Sun for different albedos.
In the text
thumbnail Fig. 4.

Velocity of the best possible theoretical sail at different launch distances from the Sun.
In the text
thumbnail Fig. 5.

Velocity of ‘Oumuamua based upon its observed acceleration.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.