| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 20 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202040027 | |
| Published online | 13 April 2021 | |
Multi-instrumental view of magnetic fields and activity of ϵ Eridani with SPIRou, NARVAL, and TESS
1
Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, CNRS, CNES,
14 avenue Edouard Belin,
31400
Toulouse,
France
e-mail: ppetit@irap.omp.eu
2
Department of Physics & Space Science, Royal Military College of Canada,
PO Box 17000 Station Forces,
Kingston,
ON,
K7K 0C6,
Canada
3
Departamento de Física Teórica e Experimental, Universidade Federal do Rio Grande do Norte,
Natal,
RN 59072-970,
Brazil
4
Harvard-Smithsonian Center for Astrophysics,
60 Garden St.,
Cambridge,
MA
02138,
USA
5
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
6
University of Southern Queensland, Centre for Astrophysics,
Toowoomba,
QLD 4350,
Australia
7
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, CNRS,
34095,
France
8
School of Physics, Trinity College Dublin, University of Dublin,
Dublin-2,
Ireland
Received:
30
November
2020
Accepted:
5
January
2021
Aims. We report on observations of the active K2 dwarf ϵ Eridani based on contemporaneous SPIRou, NARVAL and TESS data obtained over two months in late 2018, when the activity of the star was reported to be in a non-cyclic phase.
Methods. Near-infrared (NIR) spectropolarimetry was obtained using SPIRou over four nights in late September, while visible spectropolarimetry was collected with NARVAL over 20 nights, spread between 18 September and 07 November. We first recovered the fundamental parameters of the target from both visible and NIR spectral fitting. The large-scale magnetic field was investigated from polarimetric data. From unpolarized spectra, we estimated the total magnetic flux through Zeeman broadening of magnetically sensitive NIR lines and the chromospheric emission using the CaII H&K lines. The photometric monitoring, secured with TESS between 19 October and 15 November, is modelled with pseudo-periodic Gaussian process regression.
Results. Fundamental parameters of ϵ Eridani derived from visible and NIR wavelengths provide us with consistent results, which also agree with published values. We report a progressive increase of macroturbulence towards larger NIR wavelengths. Zeeman broadening of individual lines highlights an unsigned surface magnetic field Bmono = 1.90 ± 0.13 kG, with a filling factor f = 12.5 ± 1.7% (unsigned magnetic flux Bf = 237 ± 36 G). The large-scale magnetic field geometry, chromospheric emission and broadband photometry display clear signs of non-rotational evolution over the course of data collection. Characteristic decay times deduced from the light curve and longitudinal field fall in the range 30–40 days, while the characteristic timescale of surface differential rotation, as derived through the evolution of the magnetic geometry, is equal to 57 ± 5 days. The large-scale magnetic field exhibits a combination of properties not observed previously for ϵ Eridani, with a surface field among the weakest previously reported, but this field is also mostly axisymmetric, and is dominated by a toroidal component.
Key words: stars: activity / stars: solar-type / stars: magnetic field / stars: rotation
© P. Petit et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Most Sun-like stars experience a strong magnetic activity during the first billion years of their evolution as a consequence of an efficient global dynamo triggered by their high spin rate. The variable phenomena induced at the stellar surface and in upper atmospheric layers span a wide range of spatial scales, temporal scales, and spread their signatures over most of the electromagnetic spectrum, shaping the extended environment of the star around which young planets may orbit (do Nascimento et al. 2016). Widely studied manifestations of stellar activity include core emission in chromospheric lines (Noyes et al. 1984; Boro Saikia et al. 2018), spectroscopic and broad-band photometric signatures of dark spots and plages (see Berdyugina 2005, for a review), polarized Zeeeman signatures (e.g. Donati et al. 1990; Marsden et al. 2014), and Zeeman broadening of magnetically sensitive spectral lines (Saar 1988; Lavail et al. 2019). Owing to the diverse instrumentation and modelling tools needed to study these fragmented diagnoses, most studies concentrate on a specific tracer of activity, getting in return a very incomplete view of a complex phenomenon. In this work, we propose to grasp a more diverse view of stellar activity for the specific case of ϵ Eridani, taking advantage of contemporaneous observations gathered with three different instruments.
With a distance of 3.2028 ± 0.0047 pc (Gaia Collaboration 2018), ϵ Eridani is one of the closest solar-type stars. Given its location in the solar neighborhood, interferometric radius measurements were performed for this object (R = 0.74 ± 0.01R⊙, di Folco et al. 2007; Baines & Armstrong 2012), thereby confirming its status as a main-sequence dwarf. The combined knowledge of the distance and radius allows us to infer its surface black-body temperature (Teff = 5076 ± 30 K; Heiter et al. 2015). This estimate is consistent with its K2V spectral type (Keenan & McNeil 1989) and mostly agrees with its spectroscopic seffective temperature (Teff = 5146 ± 30 K; Valenti & Fischer 2005). Spectroscopic and interferometric studies also agree with each other on a mass estimate, with 0.856± 0.08 M⊙ given by Valenti & Fischer (2005) or 0.80 ± 0.06 M⊙ from Heiter et al. (2015).
Radio observations have unveiled a debris disc (Gillett 1986) taking the form of a narrow ring with arc-like azimuthal structures (Booth et al. 2017). This circumstellar residual from the stellar formation is indicative of a young age; 439 ± 52 Myr was proposed by Barnes (2007). The geometrical ring properties may reveal a resonant interaction with massive planetary companions. A first planet was detected at 3.4 AU by Hatzes et al. (2000) with a mass M. sin i = 0.86 MJ, and the detection was later confirmed by Anglada-Escudé & Butler (2012). This eccentric planetary companion (e = 0.6) may share the neighbourhood of ϵ Eridani with a second, unconfirmedplanet of ≈0.1 MJ at 40 AU from the star, according to numerical simulations of the debris disc (Quillen & Thorndike 2002).
Owing to its young age, ϵ Eridani is rotating relatively fast and has a sustained CaII H&K emission exhibiting a 11.68 days period (Donahue et al. 1996). The long-term variability of the chromospheric emission was first reported to be chaotic in nature (Baliunas et al. 1995), before new observations revealed that the magnetic activity has become more regular during the last two decades, following a 2.95 yr chromospheric cycle (Metcalfe et al. 2013). This cyclic pattern lasted until about 2017, and less regular variations have been reported after this date (Coffaro et al. 2020). The surface magnetic field of ϵ Eridani was first detected through Zeeman broadening at infrared wavelengths (Valenti et al. 1995) and then in the visible domain (Rueedi et al. 1997). Zeeman–Doppler Imaging (ZDI) was applied to spectropolarimetric observations of ϵ Eridani; monitoring of the evolution of the large-scale magnetic geometry was carried out over timescales as long as several years (Jeffers et al. 2014)and as short as a few months (Jeffers et al. 2017).
We present quasi-simultaneous observations of this prototypical young, active solar-type star using spectropolarimetric data collected from the ground with SPIRou and NARVAL, and space-borne photometric data delivered by the TESS spacecraft. We first describe the data sets (Sect. 2) and then present our determination of fundamental stellar parameters (Sect. 3), as well as the measurements and modelling of the longitudinal magnetic field (Sect. 4), Zeeman broadening (Sect. 5), chromospheric emission (Sect. 6), radial velocities (Sect. 7), brightness fluctuations (Sect. 8), large-scale magnetic geometry (Sect. 9), and surface differential rotation (Sect. 10). We finally summarize, compare, and discuss these different measurements (Sect. 11).
2 Observations
We report on three time series of observations of ϵ Eridani taken with three different instruments in 2018, over a period of about two months spread from late September to late November. Spectropolarimetric data were obtained in the visible and NIR domain, using NARVAL and SPIRou, respectively. Photometric monitoring was performed on board the TESS spacecraft.
2.1 SPIRou NIR spectra
The SPIRou instrument is a cryogenic, NIR, high-resolution échelle spectropolarimeter and velocimeter recently installed at CFHT (Donati et al. 2020). Each spectrum covers the Y, J, H, and K bands (nominal spectral range from 0.98 to 2.35 μm) at a spectral resolution of 70 000 with a radial velocity (RV) precision of between 1 and 2 m s−1 RMS. Similar to its optical predecessors ESPaDOnS and NARVAL, Stokes V sequences produced by SPIRou consist of four sub-exposures collected with multiple rotation angles of the half-wave Fresnel rhombs in the Cassegrain mounted polarimeter. This procedure ensures that the two polarimetric states exchange their position on the H4RG detector, so that spurious polarimetric signatures can be removed at first order (Semel et al. 1993; Donati et al. 1997).
The data reduction was performed with an adapted version of the LIBREESPRIT pipeline (Donati et al. 1997). Because the spectral domain of SPIRou is affected by a large number of telluric lines, their subtraction was performed with a principal component analysis approach inspired by Artigau et al. (2014). This method uses a large number of observations of hot stars (with very few photospheric lines in the near infrared) as a learning data set featuring a variety of configurations of the telluric spectrum.
Observations of ϵ Eridani were obtained as part of the science verification of the instrument. One to five Stokes V spectra were obtained daily between 21 September and 25 September, with one missing night over this period (23 September). The integration time, first set to 11.1 s per sub-exposure on September 21, was then increased to 33.4 s per sub-exposure. The peak signal-to-noise ratio (S/N) in Stokes I spectra ranges from about 800 on 21 September to 1300 during the following nights; this peak value is reached at a wavelength of around 2.1 μm. The polarimetric sequence was obtained only once on 25 Sept., and was repeated four times on 22 September and five times on 21 September and 24 September (for a total of 15 spectra over the four nights).
2.2 NARVAL visible spectra
The NARVAL instrument is a high-resolution échelle spectropolarimeter installed at Télescope Bernard Lyot (Pic du Midi Observatory, France; Aurière 2003). Its spectral resolution in polarimetric mode is close to 65 000, and it is able to cover, in a single exposure, a spectral domain ranging from 370 to 1000 nm (except for small wavelength gaps between the redmost spectral orders). We only collected circularly polarized sequences (Stokes parameters I and V), because the amplitude of Zeeman signatures ismaximal in this polarization state. All spectra were reduced by the automated LIBREESPRIT pipeline (Donati et al. 1997).
The NARVAL data set is constituted of 20 visits to the target, obtained as part of the Bcool Large Programme (Marsden et al. 2014). This observing sequence of observations started on September 18, and we accumulated new data until November 16. Four NARVAL spectra were obtained during the SPIRou observing window, and six spectra are collected during the TESS monitoring (see Sect. 2.3).
The choice to adopt integration times of 4 × 200 s in polarimetric sequences resulted in peak S/N (reached in order #31, at about 730 nm) mostly comprised between 1200 and 2000. Only two spectra, taken on October 08 and 12, have their peak S/N slightly below 1000. The collected temporal sequence suffers from a few gaps; the most extended one spans 13 nights between October 25 and November 07 (immediately followed by a new five night gap).
All NARVAL data used here are publicly available on the PolarBase archive (Petit et al. 2014).
2.3 TESS photometry
The Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015) performed observations of ϵ Eridani as part of the Sector 4 sequence, lasting from October 20 to November 19 (HJD 2 458410.9–2 458436.8). The public, reduced light curve was retrieved from the MAST archive.
Each data point in the light curve is delivered with a 12-bit quality flag, and each bit indicates an abnormal data condition if positive. All the flagged data points were discarded from our study. We also rejected data obtained between Julian dates 2 458 420 and 2 458 424 because (a) this fraction of the light curve exhibited a periodicity and amplitude inconsistent with the rest of the time series, and (b) other light curves of stars on the same detector (e.g. δ Eri, 7 Eri, HD 19349) also show a similarly abnormal behaviour at the same dates, which lead us to conclude that TESS was undergoing sub-nominal conditions while taking these measurements. The resulting time series is a constituted of 13 989 points (Fig. 1).
 |
Fig. 1 Normalized TESS light curve of ϵ Eridani, as a function of the barycentric Julian date. The red points show the observations affected by a non-zero quality flag. The grey points were impacted by measurement instabilities that were also recorded on other targets observed by the same detector. The blue points indicate those retained for our study. |
3 Fundamental parameters
The physical parameters of ϵ Eri are generally well known. There have been numerous spectroscopic studies, some of which reach very good precision (e.g. Valenti & Fischer 2005). Furthermore, two interferometric diameter estimates (di Folco et al. 2007; Baines & Armstrong 2012), provide independent cooroboration of these estimates. The star was included in the meta-analysis of Heiter et al. (2015) of Gaia FGK benchmark stars. In this context, an additional spectroscopic analysis is not urgent, however with both visible and IR spectra we can perform a detailed comparison between parameters derived in widely separated spectral regions using contemporaneous observations.
Our analysis proceeded by directly fitting synthetic spectra to the observations by χ2 minimization. The stellar parameters fit were effective temperature (Teff), surface gravity (log g), macroturbulence (ξmac), microturbulence (ξmic), metallicity, and RV. Line broadening from macroturbulence and v sin i is ambiguous for such a slow rotator, thus we used the interferometric radius of di Folco et al. (2007, 0.74 ± 0.01 R⊙) and the equatorial rotation period and inclination of Jeffers et al. (2014, Peq = 10.33 d, i = 46°) to infer a v sin i of 2.59 km s−1. We calculated synthetic spectra using the ZEEMAN spectrum synthesis code (Landstreet 1988; Wade et al. 2001). This calculates atomic line spectra in LTE, using plane–parallel model atmospheres. Input model atmospheres from the MARCS grid of Gustafsson et al. (2008) were used. Input atomic data from VALD (Piskunov et al. 1995; Ryabchikova et al. 1997, 2015; Kupka et al. 1999, 2000) were used. The analysis proceeded by fitting several spectroscopic windows independently, then taking the average as the best value and the standard deviation as the uncertainty on that value. This may overestimate the uncertainty, since the standard deviation may be driven by the worst spectroscopic window. However, we prefer this approach to simply using the covariance matrix, since this more completely accounts for possible systematic errors in the model and atomic data.
To achieve a high degree of precision in spectrum modelling across many lines, empirical corrections to atomic line oscillator strengths are commonly needed. We find this is particularly true in the IR, possibly because this less commonly used data is less accurate, or the lower density of lines per nanometer causes errors to average out less effectively. We derive empirical oscillator strength corrections by modelling the solar spectrum. We used observations of sunlight reflected from the moon with NARVAL and SPIRou. A synthetic spectrum was calculated for solar parameters, then discrepant lines were identified by hand, and oscillator strengths for those lines were iteratively fit, further discussed in Sect. 3.2.
3.1 NARVAL visible analysis
For the analysis in the visible we used the NARVAL spectrum from the night of 25 September 2018. The Stokes I spectrum did not vary noticeably and the S/N was high enough that co-adding spectra was unnecessary. The fitting procedure closely followed Folsom et al. (2016, 2018a). We used six spectral windows that were roughly 100 Å long: 6025–6100, 6100–6200, 6200–6275, 6314–6402, 6402–6500, and 6590–6700 Å (upper panel of Fig. 2). Regions contaminated with telluric lines, as well as a few other features not present in our line list, were avoided. The Li line at 6707.8 Å was not unambiguously detectable in the observation, so a reliable Li abundance could not be derived. We used a fixed v sin i of 2.59 km s−1 and fit macroturbulence. However, if we were to assume no macroturbulence and fit for v sin i we would get 2.87 ± 0.26 km s−1, which is consistent with the value based on the rotation period and radius plus a small amount of turbulent broadening. The resulting best-fit stellar parameters averaged over the windows are presented in Table 1. Our results generally agree with the results of Valenti & Fischer (2005), and Heiter et al. (2015).
 |
Fig. 2 ZEEMAN adjustment (red) of spectral lines in the SPIRou wavelength domain after removal of telluric lines (black line). The dashed line shows the SPIRou spectrum prior to the subtraction of tellurics. The vertical blue ticks show the wavelength position of spectral lines included in the ZEEMAN analysis. |
Physical parameters for ϵ Eri derived from visible and IR spectra.
3.2 SPIRou infrared analysis
For the analysis in the IR we used the SPIRou spectra from 21 September and co-added them to produce one high S/N spectrum for the night, using the telluric correction provided by our upgraded LIBREESPRIT pipeline. We found no clear variability between nights in the absorption lines, and the results of this analysis from different nights were consistent within the noise. Typically, there are fewer spectral lines per Å in the IR than in the visible for a K star, so we used larger spectral windows. Since regions of the spectrum that are dominated by telluric lines are very difficult to fully correct, such regions wereavoided entirely. This lead to using large windows of 10 500–10 920, 11 760–12 600, 15 110–15 697, 15 815–16 390, 16 439–17 140, and 21 017–22 850 Å. This spans most of the usable spectral range of SPIRou, in six independentwindows. Within these windows there were several gaps, avoiding stronger telluric features (most notably from 15 985 to 16 145 Å), a few broad features not present in our model spectra, and stronger molecular lines. Comparing the telluric corrected and uncorrected spectra was very helpful for identifying regions for which the telluric correction may not have been sufficiently accurate (lower panel of Fig. 2), and such regions were avoided.
A major limitation of ZEEMAN is that it does not currently compute molecular lines in stellar spectra. In the visible, molecular lines can easily be identified and avoided for K stars, particularly since VALD version 3 contains extensive molecular line lists. However in some regions of the SPIRou domain this becomes more difficult, even for a star of ~ 5000 K. We took care to identify and avoid molecular features, however a few very weak lines of CN and OH could not be avoided in the 11 760–12 600, 15 815–16 390, and 16 439–17 140 Å regions, and a larger number of very weak CN lines were unavoidable in the 15 110–15 697 Å region. A number of CN lines are also present in the 21 017–22 850 Å region but they can be more practically avoided owing to thelarge spacing between lines. Since these very weak lines are at or near the noise level, we do not expect them to have a large impact on the results, but they may contribute to our uncertainties by increasing the standard deviation of results from different windows. The 15 110–15 697 Å region may be viewed as the least reliable as a consequence of the larger number of contaminating molecular lines.
The atomic line data in the SPIRou domain appears to be less reliable than in the visible, or at least obtaining accurate results is more reliant on corrections to the input atomic data. There is a good agreement on the presence of lines in VALD and in the observation, with a few exceptions, and the wavelengths generally appear to be correct. However line strengths are in many cases wrong, and the width of the Lorentzian component of the line also appears to be incorrect in some stronger lines. To correct for this, we used a spectrum of sunlight reflected off the Moon obtained with SPIRou. We computed synthetic spectra with solar parameters as follows: Teff = 5777 K, log g = 4.4 (with g in cm s−1), v sin i = 2 km s−1, ξmic = 0.9 km s−1, and macroturbulence of 3 km s−1; we visually identified discrepant lines. We then fit the oscillator strength (log gf) of the lines by χ2 minimization. For some lines it was also necessary to fit the van der Waals broadening coefficient, which is typically the dominant Lorentzian broadening source in K stars; the van der Waals broadening was included in a simultaneous fit with log gf. These empirical corrections were essential for deriving accurate stellar parameters and achieving reasonable fits to the infrared observations. Corrections for 480 lines were used in our final results, as detailed in Appendix C. To verify the reliability of these empirical corrections, we fit the solar spectrum using the corrections to derive Teff, log g, ξmic, macroturbulence, and metallicity. This ensured that we obtained results consistent with the solar values.
The best-fit parameters for individual windows in the SPIRou spectrum are presented in Table B.1 and the final average and standard deviation are in Table 1. We found a good agreement in Teff, log g, and metallicity across all six spectral windows in the infrared and a very good agreement between the average results for the visible and infrared spectra. For comparison we included well-established literature values in Table 1 and found good agreement within our uncertainty. For microturbulence, there are two windows for which we found anomalously low values, which may be due to the influence of weak unidentified blends or incompletely removed telluric lines. Rejecting the most extreme microturbulence value as likely wrong, we obtained an average that is in good agreement with the optical and literature values, albeit with a larger uncertainty. The larger macroturbulence value found in the infrared is discussed in Appendix B.
4 Longitudinal field measurements
The least-square deconvolution method (LSD; Donati et al. 1997; Kochukhov et al. 2010), was applied to every NARVAL and SPIRou reduced spectrum to get the S/N boost necessary to the detection of polarized Zeeman signatures and to precise RV measurements. We used a visible and infrared list of photospheric spectral lines computed for effective temperature and surface gravity closely matching the stellar parameters derived in Sect. 3 (and ignoring portions of the spectra blended with chromospheric lines or heavily affected by telluric absorption). The adopted lists feature close to 8000 lines in the SPIRou domain and 11 000 lines in the visible domain. The outcome of this procedure is a single, pseudo line profile with a typical S/N in Stokes V as large as 18 000 for SPIRou observations, versus about 50 000 for NARVAL data.
The projection on the line of sight of the disc-integrated magnetic field (Beff) can be estimated through the first moment of Stokes V LSD profiles (Rees & Semel 1979; Donati et al. 1997), as follows:
 (1)
(1)
where v is the RV, λ0 is the central wavelength of LSD pseudo-profiles, and geff its effective Landé factor.
The series of Beff measurements is plotted in Fig. 3, as a function of the rotational phase. The phases were computed using a rotation period equal to 11.68 days (Donahue et al. 1996), and the null phase is set at HJD = 2458399.36, which corresponds to the mean date of the NARVAL observations. We note that the four SPIRou measurements are consistent with NARVAL estimates obtained at close-by phases, although the shorter exposure times, smaller number of lines used to compute the SPIRou LSD pseudo-profiles, and lower line depth in the NIR lead to larger error bars.
The rotational modulation of Beff is obvious, with a smooth transition from values close to −5 G around phase 0.6 to +3 G at phase 0.2. Some scatter is also observed, showing that the temporal variability is not entirely controlled by stellar rotation. We note that a fair part of the scatter is due to the most recent NARVAL observations. We observe differences as large as 2 G between the oldest and most recent observations and there is a global trend to get larger field estimates (negative fields becoming weaker and positive fields becoming stronger) in more recent data.
To model both the rotational modulation and its temporal evolution, we fit the series of Beff measurements by means of Gaussian process regression (GPR; Haywood et al. 2014; Yu et al. 2017). We used a pseudo-periodic co-variance function, defined for times t and t′ and for the four hyperparameters θ1 to θ4 by the following equation:
![\begin{equation*} K(t,t') = \theta_1^2\exp\left[-\frac{(t - t')^2}{\theta_3^2} - \frac{\sin^2\left(\frac{\pi(t - t')}{\theta_2}\right)}{\theta^2_4}\right] \end{equation*}](/articles/aa/full_html/2021/04/aa40027-20/aa40027-20-eq2.png) (2)
(2)
where θ1 is the amplitude (in gauss) of the GP, θ2 the cycle length (i.e. the rotation period, in days), θ3 the decay timescale (in days, describing the lifetime of magnetic spots contributing to the large-scale magnetic geometry), and θ4 a smoothing parameter in the [0,1] interval.
The hyperparameter domain is explored through the Markov Chain Monte Carlo method (MCMC, Table 2). The result of the MCMC simulation is illustrated in Fig. 4. The resulting cycle length is equal to 11.4± 0.3 days, with an amplitude of 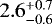 G, a decay time equal to
G, a decay time equal to  days, and a smoothing parameter of 0.7 ± 0.2.
days, and a smoothing parameter of 0.7 ± 0.2.
 |
Fig. 3 Longitudinal magnetic field measurements, as a function of the rotational phase. The red symbols show SPIRou estimates. The blue and green symbols correspond to NARVAL measurements, with bluer (resp. greener) symbols showing older (resp. more recent) observations. |
Priors used for the MCMC exploration of the hyperparameter space.
 |
Fig. 4 Outcome of the MCMC run for the four GP hyperparameters of the Beff model. The decay time and cycle length are expressed in days, the GP amplitude in gauss, and the smoothing parameter is dimensionless. The dashed lines show the best parameters, while the dotted lines indicate the error bars. |
5 Zeeman broadening
The strength of the stellar magnetic field can be estimated from the impact of Zeeman splitting in Stokes I. Stokes V observations are sensitive to the sign of the line-of-sight component of the magnetic field, thus they are relatively sensitive to the geometry of the magnetic field, but nearby regions of opposite sign can cancel out, effectively becoming undetectable. Stokes I is relatively insensitive to geometry, because it is sensitive to the strength but not the orientation of the magnetic field1. Thus for a magnetic field distribution similar to that of the Sun, Stokes I provides a measure of small intense magnetic field regions that cover a small fraction of the stellar surface and largely cancel out in Stokes V. Since the Zeeman effect scales as λ2 while most other broadening processes scale with λ, lines furtherinto the infrared provide a more sensitive diagnostic. Our approach is to directly fit a small number of carefully selected lines with synthetic spectra computed by ZEEMAN.
This method relies on a selection of good lines with a range of Landé factors, and the wide spectral domain of SPIRou offers many possibilities. We looked for lines with particularly large or small effective Landé factors (geff), minimal blending, preferred wavelengths longer than 15 000 Å, and avoided anything blended with strong telluric lines in case of imperfections in the telluric correction. We focussed on lines that are strong enough to limit the impact of noise, but not so strong that they have large Lorentzian wings. The S/N of the observation begins to decrease beyond 2 μm, so lines in the K band are less optimal.
We adopted four Fe I lines for this analysis, at 15 343.79 (geff = 2.63), 15 381.96 (geff = 0.01), 15 611.14 (geff = 1.83), and 15 648.51 (geff = 2.98) Å. The Fe I 15 381.96 Å line has an effective Landé factor near zero, and provides a magnetically insensitive diagnostic for turbulent and rotational broadening. The Fe I 15 648.51 and 15343.79 Å lines have exceptionally large effective Landé factors, while the 15 611.14 line is also very sensitive. The Fe I 15 648.51 Å line has been used by several other authors (e.g. Valenti et al. 1995; Lavail et al. 2017).
Some alternate lines that were considered but not used include the Fe I 15 534.3 Å line (Valenti et al. 1995). This line has a large effective Landé (1.95) factor but may have weak CN blends in the red wing, so we excluded it. Similarly, the very low Landé factor Fe I 15 560.8 Å line (Valenti et al. 1995) is weak and appears to have a weak OH or CN blend in the blue wing making it unsuitable. The Fe I 15 621.65 and 15 662.0 Å lines (Lavail et al. 2017) are strong with large Lorentzian wings in ϵ Eridani, which makes distinguishing pressure and Zeeman broadening more difficult, thus they were not used. The Ti I 22 211.2, 22 232.9, 22 274.0, and 22 310.6 Å lines (Johns-Krull et al. 2004) have large effective Landé factors (up to 2.5 for 22 310.6 Å), but are relatively weak and in a lower S/N portion of the ϵ Eridani spectrum. In some observations, these can be blended with strong telluric lines. Thus they would be good choices for cooler stars, but are not optimal for ϵ Eridani.
The oscillator strengths of the four lines we focussed on for Zeeman broadening, as well as a weak blending Fe I line at 15 647.41 Å, were corrected by fitting synthetic spectra to a solar spectrum, as was done in Sect. 3.2. For the Fe I 15 648.51 line, we adopted the oscillator strength of Valenti et al. (1995), since it provided an adequate fit for ϵ Eridani and was consistent with our best fit solar value. The adopted oscillator strengths, the effective Landé factors, and van der Waals damping coefficients are provided in Table 3.
The model spectra assume a radial magnetic field uniformly distributed over some fraction of the stellar surface, thus the spectra are effectively a combination of a uniform radial magnetic model and a non-magnetic model. The fraction of the surface containing magnetic field is parameterized as a filling factor. This is clearly much simpler than the real magnetic field of a star, but Zeeman broadening in Stokes I is relatively insensitive to magnetic geometry, so a more realistic geometry would add more free parameters but would not improve the fit to the observations. We used the Teff, log g, v sin i, and microturbulence derived from the visible range in Sect. 3, however, we allowed metallicity and macroturbulence to be free parameters. This allows the model to fit line strength through metallicity and line width through macroturbulence, so that assumptions in these parameters do not unduly influence the derived magnetic field strength.
We considered two approaches to fitting Zeeman broadening parameters. First we considered a model with free parameters for a characteristic magnetic field strength (Bmono) covering a filling factor (f), and the remaining surface is non-magnetic (the “two-component” model). This is consistent with the approach of, for example Marcy (1984), Gray (1984), and Valenti et al. (1995), and is reasonable for ϵ Eridani since Zeeman broadening does not dominate over other broadening processes. Later, we considered a second approach using a model with a grid of fixed magnetic field strengths, and filling factors for those strengths as free parameters (the “multi-component" model; e.g. Johns-Krull et al. 1999; Shulyak et al. 2019). Since the magnetic field of ϵ Eridani is not extremely strong, we cannot derive an extended distribution of filling factors, but we can place limits on the presence of multi-kilogauss magnetic fields.
For the co-added spectrum from 21 September, the best-fit two-component model we find has magnetic field Bmono = 1898 ± 129 G with a filling factor of 0.125 ± 0.017. The full set of parameters are presented in Table 4, and the fits are presented in Fig. 5, contrasted with a non-magnetic model that fits the Landé factor 0.01 line. The uncertainties are based on the diagonal of the covariance matrix, scaled by the square root of the reduced χ2, thus they account for noise butnot systematic uncertainties in input parameters. We repeated this analysis for the nightly co-added spectra for all four nights and found an average Bmono of 1835 G and a standard deviation of 43 G; the average filling factor is 0.138 with a standard deviation of 0.014. The small standard deviation in Bmono suggests we may have overestimated the random uncertainties, although this may simply be due to small number statistics. We find no statistically significant variation in Bmono or f over the four co-added spectra.
To estimate the impact of uncertainties in other parameters, we tried to vary the input parameters by a reasonable uncertainty, reran the fit, and checked the impact on the magnetic field and filling factor. Varying Teff by ± 80 K changes Bmono by ± 30 G and the filling factor by ±0.005, and log g has a smaller impact. Varying v sin i by ± 0.3 km s−1 changes Bmono by ± 8 G and the filling factor by ±0.001, since the free macroturbulence parameter offsets this change. Changing the microturbulence by ± 0.15 km s−1 changes Bmono by ± 10 G and the filling factor by ±0.007, but has a stronger impact on the inferred metallicity. If we assume an error in the line oscillator strengths of ± 0.1 dex in log gf, the impact is between 50 and 150 G in Bmono, and 0.02–0.03 in filling factor. The formal uncertainties from fitting the oscillator strengths are less than 0.1 (except for the very weak 15 647.413 Å line), but this may still be the dominant source of systematic error.
We then considered a multi-component model, largely to constrain the possibility of very strong magnetic fields covering small areas. For the multi-component model, we chose a grid of magnetic field strengths of 0, 2, 4 and 6 kG2. Experiments using a grid spaced only 1 kG apart suggests such small bins are not fully resolved, leading to strong covariances between filling factors and potentially a poorly constrained model. Fitting the co-added 21 September spectrum (see Table 4) produces a significant filling factor in the 2 kG bin (f2 kG = 0.118 ± 0.017), while the filling factors for the 4 kG bin (f4 kG = 0.001 ± 0.022) and 6 kG bin (f6 kG = 0.050 ± 0.033) are consistent with zero, and most of the surface is in the 0 kG bin (f0 kG = 0.831 ± 0.043). The co-added 22 September spectrum produces results consistent within 1σ with f0 kG = 0.840 ± 0.057, f2 kG = 0.131 ± 0.023, f4 kG = 0.028 ± 0.028, and f6 kG = 0.000 ± 0.044, and there is no statistically significant variability on the September 24 or September 25. From this, we find no evidence for a magnetic field that is stronger than 2 kG on the star.
The magnetic field we derive in this work broadly agrees with previous measurements of the magnetic field through Zeeman broadening. Valenti et al. (1995) determine a magnetic field and filling factor from infrared lines, finding B = 1445 ± 58 G and a filling factor f = 0.088 ± 0.008. This is similar to, but not formally consistent with our values, however they adopted a somewhat larger log g (4.70) and Teff (5133 K) than we did. In exploring the systematic impact of log g and Teff they tested the model with log g = 4.55 and Teff = 4960 K, finding B = 1553 G and f =0.096, which agrees with our results within 3σ in B and 2σ in f; these differences are possibly linked to intrinsic magnetic variability. A number of earlier magnetic estimates based on Zeeman broadening in the visible exist (Marcy 1984; Gray 1984; Saar 1988; Mathys & Solanki 1989; Marcy & Basri 1989, e.g.), but produce significantly larger values of B or f and Valenti et al. (1995) questioned their reliability. Rueedi et al. (1997) provide a more consistent analysis of Zeeman broadening in the visible, although they preferred to report the product Bf since they considered it less vulnerable to systematic errors. This is supported by the analysis of Valenti et al. (1995) and we also find a possible negative covariance between the parameters. Rueedi et al. (1997) find Bf = 165 ± 30 G, which is consistent with Valenti et al. (1995) Bf = 127 ± 13 G, and somewhat smaller than the product of the values from our two-component model Bf = 237 ± 36 G, but within 2σ of our joint uncertainties. From our multi-component model we calculate ∑iBifi = 542 ± 219, although this quantity is dominated by the larger field bins with small, uncertain filling factors, thus we consider it effectively an upper limit. More recently, Lehmann et al. (2015) investigated Zeeman broadening in ϵ Eridani spectra spanning 5 yr, using an approach based on principal component analysis. These authors report 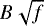 values varying between 124 ± 25 and 230 ± 21 G, possibly varying with a 3-yr cycle (e.g. Metcalfe et al. 2013). They interpret this as a surface average magnetic field strength for a filling factor of 1, although for Zeeman broadening studies the filling factor is likely smaller, thus a direct comparison with our results is less obvious. This quantity is consistent with our Bf, as well as Valenti et al. (1995) and Rueedi et al. (1997), but is much smaller than our
values varying between 124 ± 25 and 230 ± 21 G, possibly varying with a 3-yr cycle (e.g. Metcalfe et al. 2013). They interpret this as a surface average magnetic field strength for a filling factor of 1, although for Zeeman broadening studies the filling factor is likely smaller, thus a direct comparison with our results is less obvious. This quantity is consistent with our Bf, as well as Valenti et al. (1995) and Rueedi et al. (1997), but is much smaller than our  and that of Valenti et al. (1995). While some discrepancies between studies are likely due to systematic errors or underestimated uncertainties, the results of Lehmann et al. (2015) suggest that there is also important temporal variability to the Zeeman broadening of ϵ Eridani.
and that of Valenti et al. (1995). While some discrepancies between studies are likely due to systematic errors or underestimated uncertainties, the results of Lehmann et al. (2015) suggest that there is also important temporal variability to the Zeeman broadening of ϵ Eridani.
 |
Fig. 5 Infrared spectral lines of ϵ Eridani observed with SPIRou (black points) and modelled with ZEEMAN. The wavelength of lines is shown as green vertical ticks, and the effective Landé g factors are indicated to the right of each modelled line name. The best two-component magnetic model (blue) provides an acceptable fit to all lines, while a model with no magnetic field but otherwise the same parameters (red) only fits the magnetically insensitive line (top right panel). A multi-component model (orange) provides a comparable fit to the two-component model. The observation before telluric correction (dashed line) is shown for reference. |
Atomic line data for the Fe I lines used in the Zeeman broadening analysis, including the effective Landé g factor and van der Waals damping parameter.
Best-fit Zeeman broadening results for ϵ Eridani.
6 CaII H and K emission
The NARVAL spectra cover the CaII H & K lines at 396.847 and 393.366 nm. Their core is seen in emission in all our set of ϵ Eridani spectra, as an effect of the sustained chromospheric activity. As a standard way to estimate the chromospheric emission and compare its value with archival measurements, we extracted S-index values from our data following the guidelines of Noyes et al. (1984). This chromospheric indicator integrates the light flux in the cores of CaII H & K using triangular bandpasses, and normalizes the core flux over two broader continuum bands (using a rectangular bandpass) taken on both sides of the doublet. Our measurements are calibrated according to Marsden et al. (2014) to produce NARVAL S-index estimates that can be directly compared to Mount Wilson values. The resulting S-index time series is reported in Table 5. The average value is close to 0.45, which is in the lower half of typical chromospheric emission measures for ϵ Eridani for which S-index values over the last five decades generally range from 0.4 to 0.6 (Metcalfe et al. 2013). Our values are in overall agreement with the contemporaneous monitoring of Coffaro et al. (2020), who report an unexpected drop in chromospheric activity with respect to the previously regular S-index fluctuations. Thus our set of observations, which was expected to be close to an S-index maximum, is typical of a lower activity state.
Statistical error bars can be computed for every individual estimate. But these formal uncertainties are, in practice, dominated by residual inaccuracies in continuum normalisation around the calcium doublet even if, by definition, the S-index corrects a fair part of normalization issues. To obtain an empirical estimate of typical error bars, we considered the dispersion of S-index measurements for Pollux, a quiet red giant with chromospheric emission close to the basal level, and a K0 spectral type relatively close to the spectral type of ϵ Eridani. From a series of 266 observations performed with NARVAL and ESPaDOnS over several years, at an S/N close to that achieved in this work, we measured a standard deviation of the S-index of ~ 0.002 (Aurière et al. 2021). This value is taken as a proxy of the S-index uncertainty for ϵ Eridani.
The S-index variations are plotted, against rotational phases, in Fig. 6. The phase dependence is not as prominent as that recorded for the longitudinal field, to the point that the rotation period cannot be unambiguously identified using a GPR model similar to that described in Sect. 4, or using a simple Lomb-Scargle approach. Fast evolution of chromospheric structures may be responsible for the relatively large scatter. Non-rotational evolution is especially obvious between phases 0.2 and 0.4, where S-index levels have sharply dropped during the time span of observations. In the phase range [0.16, 0.18], we record a decrease from S ≈ 0.48 at HJD = 2458389.6 to S ≈ 0.44 at HJD = 2458436.5, which is well above uncertainties. During a comparable time interval, a more limited drop is observed at phases 0.67–0.68, where S-index values decrease from 0.45 to 0.44. We therefore observe a sudden transition from a marked rotational modulation of chromospheric emission to a flatter one. Most of the recorded evolution is taking place during the last three days of the monitoring. Prior to this specific event, the rotational modulation is more visible. The strongest emission is around phase 0.4, and the weakest chromospheric flux around phase 0.7. Even during this first part of the time series, a significant scatter is present and may be a hint that frequent transitory events contribute to the S-index.
We also estimated an Hα index, following the methodology of Gizis et al. (2002), and obtain a similar trend, although the contrast between high and low emission is not as large using this specific chromospheric tracer (see Fig. A.1). We finally checked the chromospheric emission in the CaII IRT triplet, using the index defined by Petit et al. (2013). In this last case (not shown), neither the early rotational modulation or the late drop are visible in the time series.
Journal of SPIRou and NARVAL observations.
 |
Fig. 6 NARVAL S-index measurements, as a function of the rotational phase. The bluer (resp. greener) symbols show older (resp. more recent) observations. |
7 Radial velocities
Radial velocities have been estimated for both sets of SPIRou and NARVAL LSD profiles, with values reported in Table 5. The accuracy of NARVAL RV estimates is mainly limited by the wavelength calibration using telluric lines, as part of the standard reduction process. From observations of τ Boo, Moutou et al. (2007) reported a precision of the order of 30 m s−1. Uncertainties for SPIRou are taken equal to the standard deviation of the values obtained for a given night and range between 1 and 2 m s−1. The SPIRou RVs tend to be smaller than NARVAL ones. Although the difference stays mostly within uncertainties, a different absolute calibration between the two instrument is likely causing this offset.
All available values are plotted against the rotation phase in Fig. A.1. The rotational signal is not detected in the NARVAL time series, which agrees with a peak-to-peak activity jitter of about 30 m s−1 reported by Giguere et al. (2016), which is below our detection threshold. The SPIRou measurements are too sparse to reveal any rotational dependence. Variations observed over the four nights reach 24 m s−1 peak-to-peak, which remains at a level that we should not expect to detect with NARVAL.
8 Brightness fluctuations
The temporal variability of the optical light curve across the TESS observing window is dominated by quasi-periodic, smooth variations that, to the naked eye, look roughly consistent with the known rotation period of 11.68 days. The ~ 2 mmag amplitude is smaller than the ~6 mmag reported by Giguere et al. (2016), suggesting that our observing epoch was characterized either by a smaller number of spots and plages or by a more axisymmetric distribution of surface brightness inhomogeneities. We modelled the photometric variations through a GPR model, based on a pseudo-periodic type of GP and a MCMC exploration of the hyperparameter space similar to that described in Sect. 4.
With this aim, we first reduce the number of data points by rebinning the light curve because the temporal sampling offered by TESS far exceeds the number of observations required to sample the rotation period of ϵ Eridani. In each bin, the average is weighted with the inverse square of the error bars, for both time and flux, and the error is the weighted standard deviation, as described by the following equations.
 (3)
(3)
 (4)
(4)
 (5)
(5)
where BJD is the barycentric Julian date, F is the flux, and σi is the error bar on each photometric measurement. We chose to represent the local error σ⟨F⟩,bin by the standard deviation because the observed dispersion is around five times higher than the photon noise level. We generated one light curve with 0.2 days bins (114 points in total), and a second light curve with 0.05 days bins (456 points).
Using 0.2 days bins, the most likely values of the GP hyperparameters include a rotation period of 11.62 ± 0.15 days (best: 11.63 days) and a decay time of 43 days (best: 42 days). Using 0.05 days bins, the same procedure leads to a rotation period of 11.56 ± 0.19 days (best: 11.42 days) and a decay time equal to 33
days (best: 42 days). Using 0.05 days bins, the same procedure leads to a rotation period of 11.56 ± 0.19 days (best: 11.42 days) and a decay time equal to 33 days (best: 35 days), in agreement (within uncertainties) with the values obtained using 0.2 days bins.
days (best: 35 days), in agreement (within uncertainties) with the values obtained using 0.2 days bins.
While intrinsic evolution of the spot pattern is likely to dominate the observed non-rotational variability of the light curve, a few transitory events visible in Fig. 1 (e.g. at Julian date ~ 2 458 417) may also contribute to reduce the decay time. This may be reflected in the slightly smaller decay time derived with 0.05 days bins, since short-term fluctuations are better filtered out using 0.2 days bins.
9 Tomographic mapping of the large-scale surface magnetic field
The series ofNARVAL Stokes V pseudo-profiles was used to model the large-scale magnetic field geometry by means of ZDI. This tomographic approach was first proposed by Semel (1989) and is based on a maximum entropy regularisation of the ill-posed problem of inverting a set of circularly polarised Zeeman signatures. More specifically, we used a magnetic model in which the surface magnetic field is decomposed over a spherical harmonics frame (Donati et al. 2006), through the Python implementation of Folsom et al. (2018a). We also assume that the local Stokes I line profiles (associated to each surface pixel of our model) take the shape of a Voigt profile, following Morin et al. (2008) and Folsom et al. (2018b).
The input projected rotational velocity and the inclination angle are taken equal to the values selected by Jeffers et al. (2014, 2017), with v sin i = 2.59 km s−1 (see Sect. 3.2) and i = 46°. The differential rotation parameters were refined compared to the earlier estimate of Jeffers et al. (2014), but this specific point will be discussed in Sect. 10. The set of observed Stokes V LSD profiles, as well as the set of synthetic profiles produced by the ZDI model, are plotted in Fig. 7.
The magnetic map of Fig. 8 (including differential rotation) highlights a complex distribution of magnetic regions, although the small v sin i value limits the spatial resolution of the ZDI inversion. The average field strength is equal to 9.2 G, while the peak field modulus reaches 20 G. The toroidal magnetic component hosts most of the surface magnetic energy (68%). The field geometry is also predominantly axi-symmetric, with as much as 73% of the magnetic energy in spherical harmonics modes with m = 0. A majority of the magnetic energy is obtained in the lowest-order components of the spherical harmonics expansion; 92% are in modes with 1 ≤ ℓ ≤ 3. If we consider the poloidal field component alone, we find 34% of its magnetic energy in the dipole, 28% in the quadrupole, and 17% in the octupole.
Comparing these general field properties to values previously published by Jeffers et al. (2014, 2017) is hampered by the differentlocal profile shape used in our study (Voigt versus Gaussian), as well as a slightly different v sin i value (2.2 km s−1 in these previous studies). To allow for a more direct comparison, we reconstructed a magnetic model based on these alternate ZDI settings. The fit to Stokes I profiles is significantly better with a Voigt profile that allows for a good adjustment of both the core and wings of LSD pseudo-profiles, while a Gaussian profile provides only a good fit to the line core. The consequence on the Stokes V adjustment is, in practice, less dramatic with general reconstructed field characteristics reasonably close to those found using a Voigt profile. The alternate model leads to a mean field strength of 8 G, 64% of the magnetic energy in the toroidal component, or 68% of the energy in axisymmetric modes. The average field value obtained in this work is on the lower end of previously published values (obtained close to activity minimum). On the other hand, the fraction of energy in the toroidal component is the highest reported to date. As described in See et al. (2015), higher toroidal fields generally correspond to higher field axisymmetry, which is also observed in this paper with a magnetic geometry among the most axisymmetric recorded so far for ϵ Eridani. This atypical combination of magnetic properties may suggest that the dynamo activity of ϵ Eridani which was already reported in the past to change from chaotic to cyclic (Metcalfe et al. 2013), may have entered a new phase, as suggested by the absence of the expected activity maximum in early 2019 (Coffaro et al. 2020) and low flaring activity in radio observations obtained in 2019 by Suresh et al. (2020).
 |
Fig. 7 Time series of NARVAL Stokes V LSD profiles (black dots), and synthetic profiles produced by the ZDI model (red lines). Successive profiles are translated vertically for display purposes, with vertical shifts proportional to phase gaps. The rotation cycle is indicated on the right side of the plot. the dashed blue horizontal lines depict the zero level of each profiles. |
 |
Fig. 8 Reconstruction by ZDI of the large-scale surface magnetic geometry of ϵ Eridani using NARVAL data. Every chart displays a different component of the field in spherical coordinates and is colour coded according tothe field strength (expressed in gauss). The vertical ticks on top of the radial field map show the rotational phases of observations. |
10 Surface differential rotation
Reconstructing the magnetic field geometry of ϵ Eridani under the simple assumption of solid-body rotation leads to a disappointing reduced χ2 ( hereafter) equal to 3.2. In this section, we try to improve the model by assuming that the surface experiences a latitudinal shear.
hereafter) equal to 3.2. In this section, we try to improve the model by assuming that the surface experiences a latitudinal shear.
The ZDI model includes the possibility for the surface field geometry to change with time, under the progressive shear imposed by a solar-like differential rotation law described by the following equation:
 (6)
(6)
In this equation, Ω(l) is the rotation rate at stellar latitude l, Ωeq the rotation rate at equatorial latitude, and dΩ stands for the difference in rotation rate between the equator and pole. Following Donati et al. (2000) and Petit et al. (2002), the two free parameters of this simple law are estimated by running a large number of ZDI models over a grid of values of the two parameters (Ωeq;dΩ), searching for values that optimize the ZDI model (i.e. that minimize the  of the model, at fixed entropy value).
of the model, at fixed entropy value).
A clear minimum is found in the χ2 landscape (Fig. 9) for an equatorial rotation period Peq= 2π∕Ωeq = 10.77 ± 0.06 days and d Ω = 0.11 ± 0.01 rad d−1. The resulting  value is close to 1.5, unveiling a much better fit to the data when the surface is assumed to be sheared by differential rotation. The fact that our best
value is close to 1.5, unveiling a much better fit to the data when the surface is assumed to be sheared by differential rotation. The fact that our best  is still larger than one is indicative that other phenomena (e.g. continuous emergence and decay of magnetic spots) contribute to the magnetic evolution as well.
is still larger than one is indicative that other phenomena (e.g. continuous emergence and decay of magnetic spots) contribute to the magnetic evolution as well.
The periods derived from longitudinal field measurements and photometry (Sects. 4 and 8) are longer than the equatorial period obtained through the ZDI model. They are also shorter than the rotation period we can extrapolate at polar latitude from Eq. (6) (about 13.3 days). This is expected if the main surface features contributing to the longitudinal magnetic field or to photometric variability are located at intermediate latitudes. The shear level obtained here is about twice the solar value, and leads to a laptime (the time it takes for the equator to be one rotation cycle ahead of the pole) of 2π∕dΩ = 57 ± 5 days, providing uswith a third typical timescale of surface intrinsic evolution.
 |
Fig. 9 Reduced χ2 landscape obtained for a grid of ZDI models implementing Eq. (6). The three concentric, white contours depict the 1σ, 2σ, and 3σ limits around the |
11 Discussion
11.1 Phase dependence of activity tracers
The different tracers of the magnetic activity at photospheric and chromospheric levels investigated in this work produce a diversity of temporal signatures, which are primarily highlighted by their different rotational dependence. In absolute value, the longitudinal magnetic field is maximal around phase 0.6, which on the magnetic map is translated as a peak in the radial field strength (with negative polarity). In the light curve, this specific rotation phase is off any extrema, with a brightness maximum at phase 0.75, while the minimum in the light flux is recorded around phase 0.45.
The longitudinal field switches from positive to negative at phase 0.4, close to the minimum light flux recorded by TESS. On the magnetic map, this phase is mostly characterized by a minimum in the azimuthal field, as well as a transition from a positive to a negative radial field polarity at intermediate and low latitudes, which may suggest that the magnetic equator preferentially hosts cooler spots than the magnetic pole. Another zero-crossing of the longitudinal field is recorded around phases 0.95–1, where the radial field at intermediate latitudes on the ZDI map goes from a negative to a positive polarity. This second field minimum has no remarkable counterpart on the light curve, which stays close to its average value in the same phase interval.
Prior to its weakening during the last days of the NARVAL time series, the S-index of ϵ Eridani was maximal around phase 0.4, where in November the light curve was near its minimum, and where the radial component of the large-scale magnetic field was switching polarity. During the last rotation period covered in the time series, the phase dependence of the S-index seems to become flatter, although we are missing late observations of phases above 0.7 to track this fast evolution throughout the whole rotation cycle. We note that this sharp evolution, taking place within a few days, is not reflected in the longitudinal field values, for which the phase modulation is mostly stable over the whole time series. The TESS data, which are representative of the second half of the time-span covered by NARVAL, display a same peak-to-peak amplitude (about 5 mmag) in the first and second observed rotation period (top panel of Fig. A.1). The incomplete phase coverage of the first period (with no available data for phases above 0.65, missing the phase of maximal flux) leads to this apparent stability, while the photometric amplitude seems to have mostly decreased between the two periods, at least for the brightest phases (phases 0.0–0.35, and phases above 0.6), while the dimmest phases seem to be unaffected by this evolution.
Among the possible explanations of the apparently discrepant phase dependence of the different magnetic tracers, one obviously at play is their different spatial resolution. Magnetic fields on ϵ Eridani are likely distributed in a complex pattern featuring both field polarities, and nearly identical RVs (owing to the relatively small v sin i). The visible magnetic spots have most of their Stokes V signatures mutually cancelled, and the remaining signal is limited to the largest spatial scales of the surface field. Zeeman broadening, in contrast, does not depend on field polarity, explaining the much weaker field strength reconstructed in the ZDI map compared to the Zeeman broadening of NIR lines (a detailed discussion of this aspect can be found in See et al. 2019). The absence of any detectable phase dependence of the Zeeman broadening tends to support the picture of complex distribution of magnetic regions. The broad-band stellar photometry is a degenerate observation, with a disc-integrated brightness that reflects the surface balance between dark and bright surface features. Finally, the chromospheric emission is a cumulative effect that is unaffected by the local orientation of the chromospheric magnetic field.
Another effect contributing to a different phase dependence between the different quantities investigated in this paper is their different limb visibility. While polarized Zeeman signatures produced by spots with radial magnetic fields are best seen close to disc centre, azimuthal magnetic fields have larger Stokes V amplitudes at intermediate limb angles (Donati & Brown 1997). Similar considerations impact the interpretation of the TESS light curve; the contribution of dark spots is maximal close to disc centre while, by analogy with the Sun, faculae may be brighter close to the limb (Hirayama & Moriyama 1979), which may also affect the phase dependence of the S-index.
11.2 Characteristic timescales for short-term surface evolution
Longitudinal field measurements, photometric variations and the differential rotation model provide us with three independent estimates of evolution timescales. Two decay times are obtained from GPR applied to Beff and TESS data, while 2π∕dΩ gives a characteristic timescale of the surface shear. All three estimates are consistent within uncertainties. The longest one is the differential rotation laptime (57 ± 5 days). The decay time deduced from photometry comes second and is equal to 43 days, while the same quantity estimated from Beff measurements is the shortest and is equal to
days, while the same quantity estimated from Beff measurements is the shortest and is equal to  days. The laptimeis linked to the specific component of the surface evolution driven globally by differential rotation, while the two other estimates also include the contribution of the limited lifetime of surface structures. The laptime estimated for differential rotation can also be biased whenever the shear tracers come and go (see Petit et al. 2002). We interpret this difference as the cause of the shorter timescales obtained out of the light curve and longitudinal field data.
days. The laptimeis linked to the specific component of the surface evolution driven globally by differential rotation, while the two other estimates also include the contribution of the limited lifetime of surface structures. The laptime estimated for differential rotation can also be biased whenever the shear tracers come and go (see Petit et al. 2002). We interpret this difference as the cause of the shorter timescales obtained out of the light curve and longitudinal field data.
12 Conclusions and prospects
This multi-instrumental view of ϵ Eridani reveals how different tracers of magnetism and activity carry different and complementary information about the surface activity linked to the vivid dynamo action of young solar-like stars. Each available measurement brings its own set of clues about the underlying emergence and decay of active regions, each specific tracer being limited by its own degeneracy, spatial resolution, temporal resolution, or limb dependence. The conclusions that we can draw from the diverse data presented in this work are also limited by the non-simultaneity of the observations. This would advocate the future development of high-resolution spectropolarimeters covering both the optical and NIR domain, as would be offered by a combination of SPIRou and ESPaDOnS. In addition to help reach a better understanding of photospheric and chromospheric stellar activity, such instruments would help progress in the filtering of stellar activity, as part of RV exoplanet search and characterization around cool active stars.
Acknowledgements
JFD acknowledges funding from the European Research Council (ERC) under the H2020 research and innovation programme (grant agreement # 740651 NewWorlds). AAV acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 817540, ASTROFLOW). This research made use of the SIMBAD database operated at CDS, Strasbourg, France, and the NASA’s Astrophysics Data System Abstract Service.
Appendix A Synthetic view of all activity tracers
 |
Fig. A.1 Synthetic view of all activity tracers, as a function of the rotational phase. From top to bottom: normalized TESS light curve, with the first period in blue and the second in orange, the longitudinal magnetic field, S index, Hα index, and RVs. |
Appendix B Extra source of line broadening in the infrared domain
We find an unexpected trend in macroturbulence towards larger values for longer wavelengths. Alternatively modelling the line broadening as v sin i produces the same trend. The other best-fit parameters do not vary with wavelength, thus this appears to be a feature of the observations, not an error in our methodology. To investigate if this is real, we fit the solar spectrum obtained with SPIRou for the same spectral windows, assuming v sin i = 2 km s−1 and using macroturbulence as a free parameter. We find a trend that is similar but weaker and less consistent, from 2.5 km s−1 in the blue to 3.8 km s−1 in the red. This is unlikely to be an artefact of the instrument or data reduction process, since calibration images show a consistent line width acrossthe spectrum. To further check for instrumental effects we fit Gaussian profiles to 77 telluric lines in the observation of ϵ Eridani, distributed across the SPIRou domain. While there is some scatter in Gaussian widths, we find consistent widths as a function of wavelength, and widths of the narrower lines are consistent with an R of 70 000. Thus this does not appear to be an instrumental or data reduction effect.
Rotational broadening (v sin i) should be consistent across a spectrum, apart from a wavelength dependence in limb darkening, which our models account for. Turbulent broadening may be depth dependent, and widely separated wavelengths have different opacities, thus the physical depth of formation ofspectra lines varies with wavelength. However, it is not clear if changes in turbulence with depth could explain a 3.5 km s−1 difference between 6000 and 22 000 Å. The contribution of cool spots to the spectrum increases with wavelength, however it is not clear that cool spots would have much large turbulent broadening than the rest of the photosphere since convection is generally considered to be suppressed in these regions. Thus this does not offer an obvious explanation.
The relative impact of Zeeman broadening increases with wavelength, that is Zeeman effect scales as λ2 while most other broadening processes scale as λ, thereby offering a possible explanation. In Sect. 5 using Zeeman broadening we find a 1800 G magnetic field covering 14% of the stellar surface. We repeated the above spectroscopic analysis assuming this magnetic model, rather than no magnetic field. This produced a lower reduced χ2 (by 1 or 2) than for the model with no magnetic field in all windows, except one where reduced χ2 was largely unchanged. We find Teff, log g, and metallicity that are virtually unchanged, as well as a microturbuence that is reduced to 0.78 ± 0.15 km s−1; however there still is a systematic trend in macroturbulence with wavelength from 1.90 km s−1 in the blue-most window up to 4.01 km s−1 in the red-most. Thus including this magnetic field only slightly reduced the wavelength dependence of macroturbulence and is not sufficient to explain it.
Parameters derived from individual windows in the IR spectrum.
To further investigate whether this wavelength-dependent broadening could be Zeeman broadening, we fit the 10 500–10 920 and 21 017–22 850 Å windows simultaneously, adding a magnetic field strength and filling factor to the free parameters of Teff, log g, microturbulence, and metallicity. Macrotrublence was fixed to the value of the bluer window from above (1.90 km s−1), since if left free it tends to a larger intermediate value that is too broad for the bluer window. This produced a best-fit magnetic field of 1587 G and filling factor of 0.291, while Teff, log g, and metallicity were consistent with above (microturbulence was smaller at 0.36 km s−1). As a second attempt the 11 760–12 600 and 16 439–17 140 Å windows were fit simultaneously using the same approach. This produced a magnetic field of 2107 G and a filling factor of 0.284, and otherwise consistent stellar parameters. These two models did a good job fitting the line widths in the redder and bluer windows, but both produced filling factors that are inconsistently large for the Zeeman broadening analysis in Sect. 5. Specifically, the Fe I 15 343.79, 15 611.14, and 15 648.51 Å lines analysed below all show wings that are too deep with these two models. Thus including Zeeman broadening is important for accurately determining line broadening in the infrared, but apparently not sufficient to explain the wavelength dependence in line broadening we find in this work.
We tried allowing the temperature of the magnetic region to differ from the non-magnetic area. This involves effectively calculating spectra for the two regions using different model atmospheres, interpolated from the same grid and assuming the same log g, but using different Teff. The flux ratio between cool and warm regions increases further to the infrared. If the magnetic regions were cooler, perhaps this could help produce extra Zeeman broadening further into the infrared without increasing the filling actor. Fitting the 10 500–10 920 and 21 017–22 850 Å windows with this model we found a magnetic field of 1652 G, a filling factor of 0.262, a temperatureof 4731K° in the magnetic region, and a temperature of 5182 K in the non-magnetic region. Fitting the 11 760–12 600 and 16 439–17 140 Å windows we found a magnetic field of 2066 G, filling factor of 0.307, temperature in the magnetic region of 4615 K, and temperature in the non-magnetic region of 5321 K. However, on closer inspection, the temperature in the cooler region appears to be driven largely by the strength of a few lines with very low excitation potentials. This suggests a possible spot temperature of 4600–4700 K, but does a poor job of providing a model that could explain the wavelength-dependent line broadening.
From these tests, it appears that the wavelength-dependent line broadening is real and cannot be fully explained by Zeeman broadening. This suggests that a depth-dependent turbulent velocity should be investigated. However, that goes beyond the simple micro- and macro-turbulence approximation and may require 3D hydrodynamic model atmospheres to properly investigate.
Appendix C Corrections to atomic line data
The corrections to atomic line data that we adopted in the SPIRou wavelength range are presented in this appendix. The data were initially extracted from VALD version 3, on 14 February 2019, using an “extract stellar” request for the parameters of ϵ Eridani, and the default “line list configuration” (i.e. selection of input line lists). An extensive list of empirical corrections to the oscillator strengths were derived by fitting a solar spectrum, as discussed in Sect. 3.2. The modified line data are presented inTable C.1. Lines that did not require modification are omitted for brevity. A number of theoretical transitions were predicted to be detectable but were not present in our observations. These are indicated in Table C.1 with an ‘*’. A few lines in VALD were apparent duplicates from different sources, specifically components of Mg I blends. These are also listed with an ‘*’. For some SI lines we adopted log gf from the NIST Atomic Spectra Database, with the original data from Zatsarinny & Bartschat (2006). Since these provided adequate fits to the observation, these adopted values are included in the table. Also included are empirical log gf corrections for a few Fe I lines from Valenti et al. (1995), and Ti I lines from Johns-Krull et al. (2004), since these provided an adequate match to the observations.
Additionally, for lines with visible disagreement between the model and observation in the widths of the wings, empirical corrections to the van der Waals damping parameter (γ6) were derived. In some cases, γ6 values were unavailable and calculations in the Unsöld approximation appeared to be insufficient, so empirical values were derived. The empirical corrections to the transition data likely depend on the parameters of star being investigated and the limitations of the model being employed, thus they should be treated with caution.
While there are a significant number of apparent errors in the oscillator strengths currently available from VALD in the infrared, the list of atomic lines is largely complete. Very few atomic lines in our observations were missing a theoretical counterpart in VALD. While we did not investigate them in detail, the molecular line list also appears to be largely complete. However, outside of G and K spectral types, especially towards cooler M dwarfs, the completeness of the line list may become an issue.
Empirical modifications to the line data adopted.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Artigau, É., Astudillo-Defru, N., Delfosse, X., et al. 2014, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 9149, Telluric-line subtraction in high-accuracy velocimetry: a PCA-based approach, 914905 [Google Scholar]
- Aurière, M. 2003, in EAS Publications Series, 9, eds. J. Arnaud, & N. Meunier, 105 [CrossRef] [EDP Sciences] [Google Scholar]
- Aurière, M., Petit, P., Mathias, P., et al. 2021, A&A, 646, A130 [EDP Sciences] [Google Scholar]
- Baines, E. K., & Armstrong, J. T. 2012, ApJ, 744, 138 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Living Rev. Solar Phys., 2, 8 [Google Scholar]
- Booth, M., Dent, W. R. F., Jordán, A., et al. 2017, MNRAS, 469, 3200 [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coffaro, M., Stelzer, B., Orlando, S., et al. 2020, A&A, 636, A49 [EDP Sciences] [Google Scholar]
- di Folco, E., Absil, O., Augereau, J. C., et al. 2007, A&A, 475, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- do Nascimento, J. D., J., Vidotto, A. A., Petit, P., et al. 2016, ApJ, 820, L15 [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., & Brown, S. F. 1997, A&A, 326, 1135 [Google Scholar]
- Donati, J. F., Semel, M., Rees, D. E., Taylor, K., & Robinson, R. D. 1990, A&A, 232, L1 [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron A. 1997, MNRAS, 291, 658 [Google Scholar]
- Donati, J. F., Mengel, M., Carter, B. D., et al. 2000, MNRAS, 316, 699 [Google Scholar]
- Donati, J.-F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [Google Scholar]
- Donati, J. F., Kouach, D., Moutou, C., et al. 2020, MNRAS, 498, 5684 [Google Scholar]
- Folsom, C. P., Petit, P., Bouvier, J., et al. 2016, MNRAS, 457, 580 [Google Scholar]
- Folsom, C. P., Bouvier, J., Petit, P., et al. 2018a, MNRAS, 474, 4956 [Google Scholar]
- Folsom, C. P., Fossati, L., Wood, B. E., et al. 2018b, MNRAS, 481, 5286 [Google Scholar]
- Gaia Collaboration, (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giguere, M. J., Fischer, D. A., Zhang, C. X. Y., et al. 2016, ApJ, 824, 150 [Google Scholar]
- Gillett, F. C. 1986, Astrophysics and Space Science Library, 124, IRAS observations of cool excess around main sequence stars, ed. F. P. Israel, 61–69 [Google Scholar]
- Gizis, J. E., Reid, I. N., & Hawley, S. L. 2002, AJ, 123, 3356 [Google Scholar]
- Gray, D. F. 1984, ApJ, 277, 640 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., Cochran, W. D., McArthur, B., et al. 2000, ApJ, 544, L145 [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Hirayama, T., & Moriyama, F. 1979, Sol. Phys., 63, 251 [Google Scholar]
- Jeffers, S. V., Petit, P., Marsden, S. C., et al. 2014, A&A, 569, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Boro Saikia, S., Barnes, J. R., et al. 2017, MNRAS, 471, L96 [NASA ADS] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., & Koresko, C. 1999, ApJ, 516, 900 [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., & Saar, S. H. 2004, ApJ, 617, 1204 [Google Scholar]
- Keenan, P. C., & McNeil, R. C. 1989, ApJS, 71, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Landstreet, J. D. 1988, ApJ, 326, 967 [Google Scholar]
- Lavail, A., Kochukhov, O., Hussain, G. A. J., et al. 2017, A&A, 608, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lavail, A., Kochukhov, O., & Hussain, G. A. J. 2019, A&A, 630, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmann, L. T., Künstler, A., Carroll, T. A., & Strassmeier, K. G. 2015, Astron. Nachr., 336, 258 [Google Scholar]
- Luck, R. E., & Heiter, U. 2005, AJ, 129, 1063 [Google Scholar]
- Marcy, G. W. 1984, ApJ, 276, 286 [Google Scholar]
- Marcy, G. W., & Basri, G. 1989, ApJ, 345, 480 [Google Scholar]
- Marsden, S. C., Petit, P., Jeffers, S. V., et al. 2014, MNRAS, 444, 3517 [Google Scholar]
- Mathys, G., & Solanki, S. K. 1989, A&A, 208, 189 [NASA ADS] [Google Scholar]
- Metcalfe, T. S., Buccino, A. P., Brown, B. P., et al. 2013, ApJ, 763, L26 [Google Scholar]
- Morin, J., Donati, J. F., Petit, P., et al. 2008, MNRAS, 390, 567 [Google Scholar]
- Moutou, C., Donati, J. F., Savalle, R., et al. 2007, A&A, 473, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Donati, J.-F., & Collier Cameron, A. 2002, MNRAS, 334, 374 [Google Scholar]
- Petit, P., Aurière, M., Konstantinova-Antova, R., et al. 2013, Magnetic Fields and Convection in the Cool Supergiant Betelgeuse, eds. J.-P. Rozelot, & C. E. Neiner, 857, 231 [Google Scholar]
- Petit, P., Louge, T., Théado, S., et al. 2014, PASP, 126, 469 [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
- Quillen, A. C., & Thorndike, S. 2002, ApJ, 578, L149 [Google Scholar]
- Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1 [NASA ADS] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes, Instrum. Syst., 1, 014003 [Google Scholar]
- Rueedi, I., Solanki, S. K., Mathys, G., & Saar, S. H. 1997, A&A, 318, 429 [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astron., 6, 244 [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [Google Scholar]
- Saar, S. H. 1988, ApJ, 324, 441 [Google Scholar]
- See, V., Jardine, M., Vidotto, A. A., et al. 2015, MNRAS, 453, 4301 [Google Scholar]
- See, V., Matt, S. P., Folsom, C. P., et al. 2019, ApJ, 876, 118 [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Semel, M., Donati, J. F., & Rees, D. E. 1993, A&A, 278, 231 [Google Scholar]
- Shulyak, D., Reiners, A., Nagel, E., et al. 2019, A&A, 626, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suresh, A., Chatterjee, S., Cordes, J. M., Bastian, T. S., & Hallinan, G. 2020, ApJ, 904, 138 [Google Scholar]
- Valenti, J. A.,& Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
- Valenti, J. A., Marcy, G. W., & Basri, G. 1995, ApJ, 439, 939 [Google Scholar]
- Wade, G. A., Bagnulo, S., Kochukhov, O., et al. 2001, A&A, 374, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yu, L., Donati, J. F., Hébrard, E. M., et al. 2017, MNRAS, 467, 1342 [Google Scholar]
- Zatsarinny, O., & Bartschat, K. 2006, J. Phys. B: At. Mol. Phys., 39, 2861 [Google Scholar]
Zeeman broadening in Stokes I also typically lacks Doppler resolution across the surface of the star, since it is only reliably detectable when it is comparable to, or larger than, the rotational broadening. This is another important difference with respect to Stokes V measurements, which can still reliably detect Zeeman splitting when it is much less than rotational or other line broadening processes.
All Tables
Atomic line data for the Fe I lines used in the Zeeman broadening analysis, including the effective Landé g factor and van der Waals damping parameter.
All Figures
 |
Fig. 1 Normalized TESS light curve of ϵ Eridani, as a function of the barycentric Julian date. The red points show the observations affected by a non-zero quality flag. The grey points were impacted by measurement instabilities that were also recorded on other targets observed by the same detector. The blue points indicate those retained for our study. |
| In the text | |
 |
Fig. 2 ZEEMAN adjustment (red) of spectral lines in the SPIRou wavelength domain after removal of telluric lines (black line). The dashed line shows the SPIRou spectrum prior to the subtraction of tellurics. The vertical blue ticks show the wavelength position of spectral lines included in the ZEEMAN analysis. |
| In the text | |
 |
Fig. 3 Longitudinal magnetic field measurements, as a function of the rotational phase. The red symbols show SPIRou estimates. The blue and green symbols correspond to NARVAL measurements, with bluer (resp. greener) symbols showing older (resp. more recent) observations. |
| In the text | |
 |
Fig. 4 Outcome of the MCMC run for the four GP hyperparameters of the Beff model. The decay time and cycle length are expressed in days, the GP amplitude in gauss, and the smoothing parameter is dimensionless. The dashed lines show the best parameters, while the dotted lines indicate the error bars. |
| In the text | |
 |
Fig. 5 Infrared spectral lines of ϵ Eridani observed with SPIRou (black points) and modelled with ZEEMAN. The wavelength of lines is shown as green vertical ticks, and the effective Landé g factors are indicated to the right of each modelled line name. The best two-component magnetic model (blue) provides an acceptable fit to all lines, while a model with no magnetic field but otherwise the same parameters (red) only fits the magnetically insensitive line (top right panel). A multi-component model (orange) provides a comparable fit to the two-component model. The observation before telluric correction (dashed line) is shown for reference. |
| In the text | |
 |
Fig. 6 NARVAL S-index measurements, as a function of the rotational phase. The bluer (resp. greener) symbols show older (resp. more recent) observations. |
| In the text | |
 |
Fig. 7 Time series of NARVAL Stokes V LSD profiles (black dots), and synthetic profiles produced by the ZDI model (red lines). Successive profiles are translated vertically for display purposes, with vertical shifts proportional to phase gaps. The rotation cycle is indicated on the right side of the plot. the dashed blue horizontal lines depict the zero level of each profiles. |
| In the text | |
 |
Fig. 8 Reconstruction by ZDI of the large-scale surface magnetic geometry of ϵ Eridani using NARVAL data. Every chart displays a different component of the field in spherical coordinates and is colour coded according tothe field strength (expressed in gauss). The vertical ticks on top of the radial field map show the rotational phases of observations. |
| In the text | |
 |
Fig. 9 Reduced χ2 landscape obtained for a grid of ZDI models implementing Eq. (6). The three concentric, white contours depict the 1σ, 2σ, and 3σ limits around the |
| In the text | |
 |
Fig. A.1 Synthetic view of all activity tracers, as a function of the rotational phase. From top to bottom: normalized TESS light curve, with the first period in blue and the second in orange, the longitudinal magnetic field, S index, Hα index, and RVs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



