| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202039885 | |
| Published online | 09 March 2021 | |
Characterisation of the hydrospheres of TRAPPIST-1 planets
1
Aix-Marseille Univ., CNRS, CNES, LAM,
Marseille,
France
e-mail: lorena.acuna@lam.fr
2
LATMOS/IPSL, UVSQ Université Paris-Saclay, Sorbonne Université, CNRS,
Guyancourt,
France
Received:
10
November
2020
Accepted:
19
January
2021
Context. Planetary mass and radius data suggest that low-mass exoplanets show a wide variety of densities. This includes sub-Neptunes, whose low densities can be explained with the presence of a volatile-rich layer. Water is one of the most abundant volatiles, which can be in the form of different phases depending on the planetary surface conditions. To constrain their composition and interior structure, models must be developed that accurately calculate the properties of water at its different phases.
Aims. We present an interior structure model that includes a multiphase water layer with steam, supercritical, and condensed phases. We derive the constraints for planetary compositional parameters and their uncertainties, focusing on the multi-planetary system TRAPPIST-1, which presents both warm and temperate planets.
Methods. We use a 1D steam atmosphere in radiative-convective equilibrium with an interior whose water layer is in supercritical phase self-consistently. For temperate surface conditions, we implement liquid and ice Ih to ice VII phases in the hydrosphere. We adopt a Markov chain Monte Carlo inversion scheme to derive the probability distributions of core and water compositional parameters.
Results. We refine the composition of all planets and derive atmospheric parameters for planets ‘b’ and ‘c’. The latter would be in a post-runaway greenhouse state and could be extended enough to be probed by space missions such as JWST. Planets ‘d’ to ‘h’ present condensed ice phases, with maximum water mass fractions below 20%.
Conclusions. The derived amounts of water for TRAPPIST-1 planets show a general increase with semi-major axis, with the exception of planet d. This deviation from the trend could be due to formation mechanisms, such as migration and an enrichment of water in the region where planet d formed, or an extended CO2-rich atmosphere.
Key words: planets and satellites: interiors / planets and satellites: composition / planets and satellites: atmospheres / planets and satellites: individual: TRAPPIST-1 / methods: statistical / methods: numerical
© L. Acuña et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Ongoing space missions such as CHEOPS (Benz 2017) and TESS (Ricker et al. 2015), and their follow-up with ground-based radial velocity telescopes, are confirming the existence of low-mass exoplanets with a wide range of densities. These densities range from the values typically inferred for the Earth or Mercury to those measured in Uranus and Neptune. The exoplanets in the former class are mainly composed of a Fe-rich core and a silicate mantle, while the latter class has a layer that is rich in volatiles. Water is the most abundant and least dense volatile after H and He (Forget & Leconte 2014), which makes it a likely species to constitute the volatile reservoir in these planets. Several studies have investigated the interior structure and composition of water-rich planets (Sotin et al. 2007; Seager et al. 2007; Dorn et al. 2015; Zeng et al. 2019), but focused mainly on its condensed phases. Nonetheless, many sub-Neptunes are close to their host star and receive enough irradiation to trigger a runaway greenhouse state in which water is present as steam. In some cases, the high pressure and temperature conditions can render the hydrosphere supercritical and plasma, or even lead to superionic phases (Mazevet et al. 2019; French et al. 2016). Therefore, it is crucial to include the modelling of all possible phases of water in order to provide an accurate description of its presence on the planetary surface. Moreover, the surface conditions are determined by the greenhouse effect caused by atmospheric gases, making the modelling of radiative-convective equilibrium in atmospheres a key parameter to determine the phase in which water could be present on the surface. Most interior structure models represent the planetary atmosphere as a gas layer with a simplified isothermal temperature profile (Dorn et al. 2018, 2017b), which is very different from the temperature profile in the convective deep layers of thick atmospheres (Marcq 2012).
Multi-planetary systems are unique environments that present both planets that can hold condensed phases and highly irradiated planets with steam atmospheres. In this study, we develop a planet interior model suitable for the different conditions at which water can be found in low-mass planets. Our implementation includes a supercritical water layer, introduced in Mousis et al. (2020), coupled with a 1D radiative-convective atmosphere model (Marcq 2012; Marcq et al. 2017; Pluriel et al. 2019) to calculate the total radius of the highly irradiated planets with water self-consistently. Furthermore, for temperate planets, we have updated the interior model presented in Brugger et al. (2016, 2017) to include ice phases Ih, II, III, V, and VI. We introduce these models in a Markov chain Monte Carlo (MCMC) Bayesian analysis scheme adapted from Dorn et al. (2015). This allows us to derive the water mass fraction (WMF) and core mass fraction (CMF) that reproduce the observed radius, mass, and stellar composition measurements.
We use this model to explore the possible water content of the TRAPPIST-1 system, an ultra-cool M dwarf that hosts seven low-mass planets in close-in orbits. Three of these planets are located in the habitable zone (Grimm et al. 2018), meaning that they can hold liquid water or ice Ih on their surfaces. Although all planets in TRAPPIST-1 system have masses and radii that are characteristic of rocky planets, their differences in density indicate that each planet has a different volatile content. This makes this planetary system ideal for testing planet interior, atmospheric structure, and formation scenarios.
In Sect. 2 we describe the complete interior structure model, including the new updates for the supercritical and ice phases, the coupling between the interior and the atmosphere for steam and supercritical planets, and the MCMC Bayesian algorithm. The parameters for the TRAPPIST-1 planets used in this study are summarised in Sect. 3, including mass, radius, and Fe/Si molar ratio. The results of our analysis of the hydrospheres of TRAPPIST-1 planets are described in Sect. 4. We compare our results with those of previous works and discuss the implications of our water estimates for planet formation in Sect. 5. We finally provide conclusions in Sect. 6.
2 Planetary structure model
For consistency, we recall the main principles of the interior structure model. The basis of our model is explained in Brugger et al. (2016, 2017). The 1D interior structure model takes as input the mass and the compositionof the planet, which are parameterised by the CMF and WMF. The structure of the planet is stratified in three layers: a core, a mantle, and a hydrosphere. The pressure, temperature, gravity acceleration, and density are computed at each point of the 1D spatial grid along the radius of the planet. The pressure, P(r), is obtained by integrating the hydrostatic equilibrium (Eq. (1)); the gravitational acceleration, g(r), by solving Gauss’s theorem (Eq. (2)); the temperature, T(r), with the adiabatic gradient (Eq. (3)); and the density, ρ(r), with the equation of state (EOS). In Eq. (2), m is the mass at radius r, G is the gravitational constant, and γ and ϕ are the Gruneisen and the seismic parameters, respectively. Their formal macroscopic definitions are shown in Eq. (4), where E is the internal energy and V is the volume. The Gruneisen parameter is a thermodynamic parameter that describes the dependence of the vibrational properties of a crystal with the size of its lattice. It relates the temperature in a crystalline structure to the density, which is calculated by the EOS. The seismic parameter defines how seismic waves propagate inside a material. It is related to the slope of the EOS at constant temperature (Brugger et al. 2017; Sotin et al. 2007).
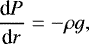 (1)
(1)
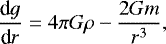 (2)
(2)
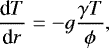 (3)
(3)
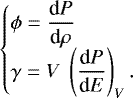 (4)
(4)
The boundary conditions are the temperature and pressure at the surface, and the gravitational acceleration at the centre of the planet. The value of the latter is zero. The total mass of the planet is calculated with Eq. (5), which is derived from the conservation of mass (Brugger et al. 2017; Sotin et al. 2007). Once the total input mass of the planet is reached and the boundary conditions are fulfilled, the model has converged.
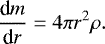 (5)
(5)
Depending on the surface conditions, the hydrosphere can be present in supercritical, liquid, or ice states. For each of these phases of water, we use a different EOS and Gruneisen parameter to compute their P-T profiles and density accurately. In Sect. 2.1 we describe the updates to the supercritical water layer with respect to the model depicted in Mousis et al. (2020), while in Sect. 2.2 we present the implementation of the hydrosphere in ice phases. Finally, the coupling between the atmosphere and the interior model with planets whose hydrosphere is in steam or supercritical phases is explained in Sect. 2.3, followed by the description of the MCMC algorithm in Sect. 2.4.
2.1 Supercritical water
If the planetis close enough to its host star, the upper layer of the hydrosphere corresponds to a hot steam atmosphere, whose temperatureat the base is determined by the radiative–convective balance calculated by the atmosphere model (Marcq 2012; Marcq et al. 2017). When the pressure and temperature at the surface, which is defined as the base of the hydrospherelayer, are above the critical point of water, we include a supercritical water layer extending from the base of the hydrosphereto a height corresponding to the phase change to steam (Mousis et al. 2020). We updated the EOS for this layer tothe EOS introduced by Mazevet et al. (2019), which is a fit to the experimental data provided by the International Association for the Properties of Water and Steam (IAPWS; Wagner & Pruß 2002) for the supercriticalregime, and quantum molecular dynamics (QMD) simulations data for plasma and superionic water (French et al. 2009). The IAPWS experimental data span a temperature range of 251.2 to 1273 K and of 611.7 to 109 Pa in pressure, while their EOS can be extrapolated up to 5000 K in temperature and 1011 Pa in pressure (Wagner & Pruß 2002). The validity range of the EOS presented in Mazevet et al. (2019) includes that of the IAPWS plus the region in which the QMD simulations are applicable, which corresponds to a temperature from 1000 K to 105 K and densities in the 1–102 g cm−3 range. These densities are reached at high pressures, that is, in the 109 –1012 Pa range. Following Eq. (3), the adiabatic gradient of the temperature is specified by the Gruneisen and the seismic parameters. These are dependent on the derivatives of the pressure with respect to the density and the internal energy (Eq. (4)). We make use of the specific internal energy and density provided by Mazevet et al. (2019) to calculate them.
2.2 Ice phases
We extended the hydrosphere in Brugger et al. (2016, 2017) with liquid and high-pressure ice VII by adding five more condensed phases: ice Ih, II, III, V, and VI. An EOS for ice Ih was developed by Feistel & Wagner (2006) with minimisation of the Gibbs potential function from the fit of experimental data. It covers the whole pressure and temperature range in which water forms ice Ih.
Fei et al. (1993) proposed a formalism to derive the EOSs of ices II, III, and V. These EOSs take the form V = V (P, T), which can be found by integrating the following differential equation (Tchijov et al. 2004):
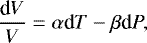 (6)
(6)
where α is the thermal expansion coefficient and β the isothermal compressibility coefficient. If the relationship between the specific volume, V, and the pressure, P, at a constant temperature T = T0 is determined, Eq. (6) can be integrated as:
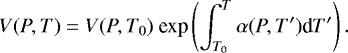 (7)
(7)
Fei et al. (1993) proposed the following expression for the thermal expansion coefficient α:
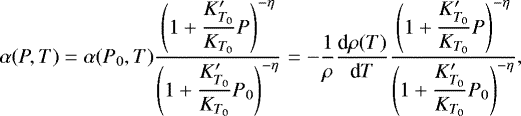 (8)
(8)
where η is an adjustable parameter estimated from the fitting of experimental data. Its value is 1.0 for ice II and ice III (Leon et al. 2002) and 7.86 for ice V (Shaw 1986). ρ is the density, α(P0, T) is the coefficient of thermal expansion ata reference pressure P0, 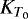 is the isothermal bulk modulus at the reference temperature T0, and
is the isothermal bulk modulus at the reference temperature T0, and 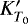 is the first derivative of the isothermal bulk modulus at the reference temperature. Hence, by substituting Eq. (8) in Eq. (7) and integrating, we obtain the following EOS for high-pressure ice:
is the first derivative of the isothermal bulk modulus at the reference temperature. Hence, by substituting Eq. (8) in Eq. (7) and integrating, we obtain the following EOS for high-pressure ice:
![\begin{equation*}V(P,T) = V(P,T_{0}) \ \textrm{exp} \left[ \textrm{ln} \left( \dfrac{ \rho(T_{0}) }{ \rho(T) } \right) \dfrac{\left( 1 +\dfrac{K'_{T_{0}}}{K_{T_{0}}} P \right)^{-\eta} }{\left(1 +\dfrac{K'_{T_{0}}}{K_{T_{0}}} P_{0} \right)^{-\eta} } \right] .\end{equation*}](/articles/aa/full_html/2021/03/aa39885-20/aa39885-20-eq11.png) (9)
(9)
The final expression (Eq. (9)) requires knowledge of the variation of the specific volume, V (P, T0), with pressure at the reference temperatureT0. Moreover, the variation of the density with temperature, ρ(T), and the bulk modulus with its derivative at the reference temperature, 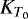 and
and 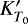 , must also be provided. In Table 1 we specify the data and references to obtain these parameters for each ice phase.
, must also be provided. In Table 1 we specify the data and references to obtain these parameters for each ice phase.
In the case of ice VI, we adopt the second-order Birch-Murnaghan (BM2) formulation, which is
![\begin{equation*}P = \dfrac{3}{2} K_{T_{0}} \left[ \left(\dfrac{\rho}{\rho_{0}} \right)^{\dfrac{7}{3}} - \left(\dfrac{\rho}{\rho_{0}} \right)^{\dfrac{5}{3}} \right], \end{equation*}](/articles/aa/full_html/2021/03/aa39885-20/aa39885-20-eq14.png) (10)
(10)
where ρ0 is the reference density for ice VI. We also introduce a thermal correction to the density because the pressure also depends on the temperature:
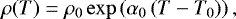 (11)
(11)
where α0 is the reference coefficient of thermal expansion. Interfaces between liquid and ice layers are established by phase transition functions from Dunaeva et al. (2010).
EOS and reference thermal parameters for ices Ih, II, III, V, and VI.
2.3 Interior-atmosphere coupling
We use a 1D atmosphere model designed to compute radiative transfer and pressure–temperature (P, T) profiles for water and CO2 atmospheres(Marcq 2012; Marcq et al. 2017). The formation of water clouds is considered in the computation of the albedo. The atmosphere is in radiative equilibrium, and presents a composition of 99% water and 1% CO2. The density of steam is obtained using a non-ideal EOS (Haar et al. 1984).
If the surface pressure is below 300 bar, the atmosphere and the interior are coupled at the atmosphere–mantle boundary and water does not reach the supercritical regime. However, if the surface pressure is greater than 300 bar, the atmosphere and the interior are coupled at this pressure level and a layer of water in supercritical phase forms between the atmosphere and the mantle. The pressure level at 300 bar is close enough to the critical point of water at 220 bar to avoidthe atmosphere model to take over pressures and temperatures where the temperature profile is adiabatic.
The pressure at the top of the atmosphere is set to 20 mbar, which corresponds to the observable transiting radius (Mousis et al. 2020; Grimm et al. 2018). We denote the radius and mass from the centre of the planet to this pressure level the total radius and mass, Rtotal and Mtotal, respectively.We also define the radius and the mass that comprise the core, mantle, and supercritical layers as the bulk radius and mass, Rbulk and Mbulk, respectively.The atmosphere model provides the outgoing longwave radiation (OLR), albedo, thickness, and mass of the atmosphere as a function of the bulk mass and radius, and the surface temperature. If the atmosphere of the planet is in radiative equilibrium, the OLR is equal to the radiation the planet absorbs from its host star, Fabs. The OLR depends on the effective temperature because OLR 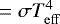 , where σ corresponds to the Stefan-Boltzmann constant. To calculate the absorbed radiation Fabs, we first compute the equilibrium temperature, which is
, where σ corresponds to the Stefan-Boltzmann constant. To calculate the absorbed radiation Fabs, we first compute the equilibrium temperature, which is
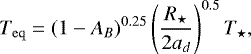 (12)
(12)
where AB is the planetary albedo, R⋆ and T⋆ are the radius and effective temperature of the host star, respectively, and ad is the semi-major axis of the planet. The absorbed radiation is then calculated as
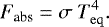 (13)
(13)
Figure 1 shows the algorithm we implemented to couple the planetary interior and the atmosphere. The interior structure model calculates the radius from the centre of the planet to the base of the steam atmosphere. For a fixed set of bulk mass and radius, the OLR depends on the surface temperature. Consequently, the surface temperature at which the OLR is equal to theabsorbed radiation corresponds to the surface temperature that yields radiative equilibrium in the atmosphere.This is estimated with a root-finding method. As the bulk radius is an output of the interior model (Rinterior) and an input of the atmosphere model, we first need to calculate the surface temperature for a certain mass and composition with an initial guess bulk radius. This surface temperature is then the input for the interior model, which provides the bulk radius. With this bulk radius, we can generate a new value of the surface temperature. This scheme is repeated until the bulk radius converges to a constant value, to which we add the thickness of the atmosphere, z, to get the total radius of the planet Rtotal. The total mass Mtotal is obtained as the sum of the bulk mass Mbulk plus the atmospheric mass Matm. The tolerance used to determine if the bulk radius has achieved convergence is 2% of the bulk radius in the previous iteration. This is approximately 0.02 R⊕ for an Earth-sized planet.
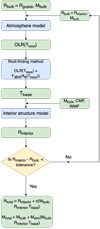 |
Fig. 1 Structural diagram of the coupling between the interior structure model and the atmosphere model. Tbase is the temperature at the bottom of the steam atmosphere in radiative-convective equilibrium. z and Matm denote the atmospheric thickness and mass, respectively. Rbulk and Mbulk correspond to the planet bulk radius and mass, respectively. Rguess refers to the initial guess of the bulk radius, while Rinterior is the output bulk radius of the interior structure model in each iteration. |
2.4 MCMC Bayesian analysis
We adaptedthe MCMC Bayesian analysis algorithm described in Dorn et al. (2015) to our coupled interior and atmosphere model. The input model parameters are the bulk planetary mass Mbulk, the CMF, and the WMF. Therefore, 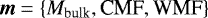 following the notation in Dorn et al. (2015). Depending on the planetary system and their available data, we can have observational measurements of the total planetary mass and radius and the stellar composition, or only the total planetary mass and radius. The available data in the former case are denoted as
following the notation in Dorn et al. (2015). Depending on the planetary system and their available data, we can have observational measurements of the total planetary mass and radius and the stellar composition, or only the total planetary mass and radius. The available data in the former case are denoted as 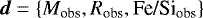 , while the data in the latter case are represented as
, while the data in the latter case are represented as 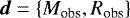 . The uncertainties on the measurements are σ(Mobs), σ(Robs), and σ(Fe/Siobs).
. The uncertainties on the measurements are σ(Mobs), σ(Robs), and σ(Fe/Siobs).
The CMF and WMF prior distributions are uniform distributions between 0 and a maximum limit. This maximum limit is 75% for the CMF, which is derived from the maximum estimated Fe/Si ratio of the proto-Sun (Lodders et al. 2009). With this limit on the CMF, we are assuming that the exoplanets have not been exposed to events during or after their formation that could have stripped away all of their mantle, such as mantle evaporation or giant impacts. In addition, the maximum WMF is set to 80%, which is the average water proportion found in comets in the Solar System (McKay et al. 2019). The prior distribution for the mass is a Gaussian distribution whose mean and standard deviations correspond to the central value and uncertainties of the observations.
The MCMC scheme first starts by randomly drawing a value for each of the model parameters from its respective prior distributions. This set of values is denoted 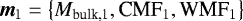 . The index i = 1 corresponds to the first proposed set of input values within the first chain, n = 1. The model calculates the total mass and radius and the theoretical Fe/Si mole ratio, which are the set of output parameters
. The index i = 1 corresponds to the first proposed set of input values within the first chain, n = 1. The model calculates the total mass and radius and the theoretical Fe/Si mole ratio, which are the set of output parameters 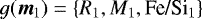 . The likelihood of a set of model parameters is then calculated via the following relationship (Dorn et al. 2015):
. The likelihood of a set of model parameters is then calculated via the following relationship (Dorn et al. 2015):
![\begin{align*}L({\bm m}_{i} \mid {\bm d}) = \;& C \ \textrm{exp} \ \Biggl(-\frac{1}{2} \Biggl[ \left(\frac{(R_{i}-R_{\textrm{obs}})}{\sigma(R_{\textrm{obs}})}\right)^{2} + \left(\frac{(M_{i}-M_{\textrm{obs}})}{\sigma(M_{\textrm{obs}})} \right)^{2}\nonumber\\ &+ \left(\frac{(\textrm{Fe/Si}_{i}-{\textrm{Fe/Si}_{\textrm{obs}}})}{\sigma({\textrm{Fe/Si}_{\textrm{obs}}})} \right)^{2} \Biggr] \Biggr), \end{align*}](/articles/aa/full_html/2021/03/aa39885-20/aa39885-20-eq24.png) (14)
(14)
where the normalisation constant of the likelihood function C is defined as:
![\begin{equation*}C = \dfrac{1}{(2 \pi)^{3/2} \left[ \sigma^{2}(M_{\textrm{obs}}) \cdot \sigma^{2}(R_{\textrm{obs}}) \cdot \sigma^{2}({\textrm{Fe/Si}_{\textrm{obs}}}) \right]^{1/2} }. \end{equation*}](/articles/aa/full_html/2021/03/aa39885-20/aa39885-20-eq25.png) (15)
(15)
When the Fe/Si mole ratio is not available as data, the square residual term of the Fe/Si mole ratio is removed from Eq. (14), as is its squared uncertainty in Eq. (15).
Subsequently we draw a new set of input parameters, 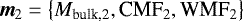 , from the prior distributions within the same chain, n. We assure that the absolute difference between the values for i = 1 and i = 2 is lower than a fixed step, which is the maximum size of the perturbation. This guarantees that the new state m2 is uniformly bounded and centred around the old state, m1. The maximum perturbation size is selected so that the acceptance rate of the MCMC, which is defined as the ratio between the number of models that are accepted and the number of proposed models, is above 20%. After m2 is chosen, the forward model calculates its corresponding output parameters and obtains their likelihood L(m2∣d), as shown in Eq. (14). The acceptance probability is estimated with the log-likelihoods l(m ∣d) = log(L(m∣d)) as:
, from the prior distributions within the same chain, n. We assure that the absolute difference between the values for i = 1 and i = 2 is lower than a fixed step, which is the maximum size of the perturbation. This guarantees that the new state m2 is uniformly bounded and centred around the old state, m1. The maximum perturbation size is selected so that the acceptance rate of the MCMC, which is defined as the ratio between the number of models that are accepted and the number of proposed models, is above 20%. After m2 is chosen, the forward model calculates its corresponding output parameters and obtains their likelihood L(m2∣d), as shown in Eq. (14). The acceptance probability is estimated with the log-likelihoods l(m ∣d) = log(L(m∣d)) as:
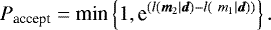 (16)
(16)
If Paccept is greater than a number drawn from a uniform distribution between 0 and 1, m2 is accepted and the chain moves to the state characterised by m2, starting the next chain n + 1. Otherwise, the chain remains in the state of m1 and a different set of model parameters is proposed as m3. To ensure that the posterior distributions converge and that the whole parameter space is explored, we run 104 chains. In other words, with acceptance rates between 0.2 and 0.6, the MCMC proposes between 1.6 and 5 × 104 sets of model inputs.
3 System parameters of TRAPPIST-1
Agol et al. (2021) performed an analysis of transit timing variations (TTVs) that includes all transit data from Spitzer since the discovery of the system. We adopt these data for the mass, radius, and semi-major axis in our interior structure analysis (Table 2).
Data are not available regarding the chemical composition of TRAPPIST-1. However, the Fe/Si abundance ratio can be estimated assuming that TRAPPIST-1 presents a similar chemical composition to that of other stars of the same metallicity, age, and stellar population. As proposed by Unterborn et al. (2018), we select a sample of stars from the Hypatia Catalogue (Hinkel et al. 2014, 2016, 2017). We choose the set of stars by constraining the C/O mole ratio to be less than 0.8, and the stellar metallicity between −0.04 and 0.12, as this is the metallicity range calculated for TRAPPIST-1 by Gillon et al. (2017). We discard thick disc stars because TRAPPIST-1 is likely a thin disc star. Our best-fit Gaussian to the distribution of the Fe/Si mole ratio shows a mean of 0.76 and a standard deviation of 0.12. As this Fe/Si value is an estimate based on the chemical composition of a sample of stars that belong to the same stellar population as TRAPPIST-1, we present two scenarios for each planet. In scenario 1, the only available data are the planetary mass and radius, while scenario 2 includes the estimated stellar Fe/Si mole ratio to constrain the bulk composition.
For temperate planets that cannot have a steam atmosphere, we set the surface temperature in our interior model to their equilibrium temperatures assuming an albedo zero (Table 2). Although surface temperatures for thin atmospheres are lower than that obtained with this assumption, the dependence of the bulk radius on surface temperature for planets with condensed water is low. For example, if we assume a pure-water planet of 1 M⊕ with a surface pressure of 1 bar, the increase in radius due to a change of surface temperature from 100 to 360 K is 0.002 R⊕, which is lessthan 0.2% of the total radius, which is ten times less than our convergence criterion. Additionally, the atmospheres of TRAPPIST-1 planets in the habitable zone and farther are significantly thinner than those of the highly irradiated planets. Lincowski et al. (2018) estimated thicknesses of approximately 80 km for temperate planets in TRAPPIST-1, which is negligible compared to their total radius. Therefore, we only calculate the atmospheric parameters (OLR, surface temperature, albedo, and thickness of the atmosphere) for planets that present their hydrospheres in steam phase.
Masses, radii, and semi-major axis for all planets in TRAPPIST-1 (Agol et al. 2021).
4 Characterisation of hydrospheres
4.1 CMFand WMF posterior distributions
Tables 3 and 4 show the retrieved parameters, including the total planetary mass and radius, and the Fe/Si mole ratio. In both scenarios, we retrieve the mass and radius within the 1σ–confidence interval of the measurements for all planets. In scenario 1, where only the mass and radius data are considered, we retrieve Fe/Si mole ratios without any assumptions on the chemical composition of the host star. Although the uncertainties on these estimates are more than 50% in some cases, we can estimate a common Fe/Si mole ratio for the planetary system. This common Fe/Si range is determined by the overlap of the 1σ confidence intervals of all planets, which corresponds to Fe/Si = 0.45–0.97. This interval is compatible with the Fe/Si mole ratio of 0.76 ± 0.12 proposed byUnterborn et al. (2018). This overlap can also be seen in Fig. 2, which presents the 1σ–confidence regions derived from the 2D marginalised posterior distributions of the CMF and WMF. The minimum value of the common CMF is determined by the lower limit of the confidence region of planet g, which is approximately 0.23, whereas the common maximum CMF value corresponds to the upper limit of planets b and c, which is 0.4. This is partially in agreement with the CMF obtained in scenario 2, where we assume the Fe/Si mole ratio proposed by Unterborn et al. (2018), which is found to be between 0.2 and 0.3 (Table 4). Thus, the CMF of the TRAPPIST-1 planets could be compatible with an Earth-like CMF (CMF⊕ = 0.32).
In scenario 1, the retrieved WMFs for all planets in the system are below 20% within their uncertainties. This maximum WMF limit reduces to 10% for scenario 2. This indicates that the TRAPPIST-1 system is poor in water and other volatiles, especially the inner planets b and c. Both planets are compatible with a dry composition in both scenarios, although the presence of an atmosphere cannot be ruled out given the possible CMF range estimated in scenario 1.
Output parameters retrieved by the MCMC method for all TRAPPIST-1 planets.
Output parameters retrieved by the MCMC method for all TRAPPIST-1 planets.
4.2 Water phases
Figure 3 shows the OLR calculated by the atmosphere model and the absorbed radiation (Eqs. (12) and (13)) for planets b, c, and d. For temperatures lower than ~ Tsurf = 2000 K, the OLR has little dependency on the surface temperature. This is caused by the nearly constant temperature (between 250 and 300 K) of the radiating layers in the thermal IR range (Goldblatt et al. 2013) and it is related to the runaway greenhouse effect (Ingersoll 1969). We obtain a constant OLR or an OLR limit (Nakajima et al. 1992) of 274.3, 273.7, and 254.0 W m−2 for planets b, c, and d, respectively. These are close to the OLR limit obtained by Katyal et al. (2019) of 279.6 W m−2 for an Earth-like planet. The small difference is due to their different surface gravities. As explained in Sect. 2.3, if the atmosphere model can find a surface temperature at which the OLR and the absorbed radiation are equal, their atmospheres are in global radiative balance. This is the case for planets b and c, whose surface temperatures are approximately 2450 and 2250 K, respectively. These are above the temperatures where the blanketing effect is effective, named Tε in Marcq et al. (2017), implying that the atmospheres of planets b and c are in a post-runaway state. However, planet d is not in global radiative balance as its absorbed radiation never exceeds its OLR. This means that planet d would be cooling down, and an internal flux of approximately 33 W m−2 would be required to supply the extra heat to balance its radiative budget. TRAPPIST-1 inner planets are likely to present an internal heat source due to tidal heating (Barr et al. 2018; Dobos et al. 2019; Turbet et al. 2018). The tidal heat flux estimated for planet d is Ftidal = 0.16 W m−2 (Barr et al. 2018), which is one order of magnitude lower than needed for radiative–convective balance of a steam atmosphere. Due to the blanketing effect of radiation over the surface of planet d, the OLR limit is larger than the absorbed radiation and hence the planet can cool enough to present its hydrosphere in condensed phases.
Figure 4 shows the (P,T) profiles and the different phases of water we can find in the hydrospheres of the TRAPPIST-1 planets. The maximum WMF of planets b and c are 8.1 × 10−5 and 4.4 × 10−6, which correspond to a surface pressure of 128.9 and 4.85 bar, respectively.
The thermal structure of their steam atmospheres are dominated by a lower, unsaturated troposphere where water condensation does not occur. Then the atmosphere consists of a middle, saturated troposphere where cloud formation would be possible, extending up to 10 mbar, and finally an isothermal mesosphere above. As we consider a clear transit radius of 20 mbar (Grimm et al. 2018; Mousis et al. 2020), the presence of clouds above this pressure level would flatten the water features in the planetary spectrum (Turbet et al. 2019; Katyal et al. 2020). On the other hand, planets d and e could present water in liquid phase, which could be partially or completely covered in ice Ih. While the hydrosphere of planet h is not massive enough to attain the high pressures required for ice VII at its base, planets d to g can reach pressures up to a 100 GPa.
 |
Fig. 2 Top panel: 1σ-confidence regions derived from the 2D posterior distributions for the first scenario, where only the masses and radii are available as data. Bottom panel: 1σ-confidence regions derived from the 2D posterior distributions for the second scenario, where the Fe/Si abundance ratio from Unterborn et al. (2018) is considered together with the mass and radius for each planet. The axis of the ternary diagram indicates the CMF, the WMF, and the mantle mass fraction MMF = 1 – CMF – WMF. |
 |
Fig. 3 Outgoing longwave radiation (OLR) and absorbed radiation as a function of surface temperature for the steam atmospheres of TRAPPIST-1 b, c, and d. Vertical dotted lines indicate the surface temperature at which the absorbed flux is equalto the OLR for planets b and c. |
 |
Fig. 4 (P,T) profiles of the hydrospheres of TRAPPIST-1 planets. The dashed-dotted grey horizontal line indicates the 20 mbar pressure level (see text). Thicker lines indicate the profile for the minimum WMF estimated for each planet in scenario 1, while thinner lines mark the profile for the maximum WMF under the same scenario. The minimum WMF of planets b, c, and h is zero. |
4.3 Retrieval of atmospheric parameters
Figure 5 shows the output atmospheric parameters (surface temperature, atmospheric thickness, albedo, and atmospheric mass) of TRAPPIST-1 b and c for a water-dominated atmosphere in scenario 1. The total thickness of an atmosphere is related to its scale height, which is defined as H = RT∕μg, where R = 8.31 J K−1 mol is the gas constant, T is the mean atmospheric temperature, μ the mean molecular mass, and g the surface gravity acceleration. For planets b and c, the mean atmospheric temperatures are 940.4 and 499.4 K, and their surface gravities are 10.8 and 10.7 m s−2, respectively. The mean molecular mass for a 99% water and 1% CO2 atmosphere is 18.3 g mol−1. The mean temperature increases with surface temperature, while the mean molecular mass is determined by the composition of the atmosphere.
For the same composition and surface gravity, the scale height and therefore the thickness of the atmosphere are directly correlated to the surface temperature. As shown in Fig. 5, the atmospheric thickness, zatm, increases with the surface temperature Tsurf. This is known as the runaway greenhouse radius inflation effect (Goldblatt 2015; Turbet et al. 2019), where a highly irradiated atmosphere is more extended than a colder one despite having similar composition. For planet b, its atmosphere can extend up to 450 km, while planet c presents a maximum extension of 300 km. The minimum limit for the thicknesses is zero, which corresponds to the case of a dry composition. Ortenzi et al. (2020) estimated that for a planet of 1–1.5 M⊕ the maximum atmospheric thickness due to the outgassing of an oxidised mantle is 200 km, which is compatible with the ranges we obtain for the atmospheric thicknesses. Scenario 2 shows the same trends for the atmospheric parameters but with lower atmospheric mass and surface pressure. With their WMF posterior distributions centred in zero and low standard deviation, the surface pressure is below 1 bar and atmospheric thicknesses are below 100 km in most of the accepted models, which means that in scenario 2 planets b and c are most likely dry rocky planets.
 |
Fig. 5 One- and two-dimensional marginal posterior distributions for the atmospheric parameters (surface temperature Tsurf, atmospheric thickness zatm, albedo, and atmospheric mass Matm), and bulk mass and radius, Mbulk and Rbulk, of TRAPPIST-1 b (left panel) and c (right panel). These were derived under scenario 1, where we do not consider Fe/Si data. |
 |
Fig. 6 Water mass fraction as a function of the distance to the star for the TRAPPIST-1 system. Upper panel: our estimates for scenario 1 and those of Barr et al. (2018), where only mass and radius data were taken into account. Lower panel: corresponds to scenario 2, whose CMF is constrained in a narrow range between 0.2 and 0.3, while for Agol et al. (2021) we show the WMF for a CMF of 0.25. |
5 Discussion
5.1 WMF comparison with previous works
Agol et al. (2021) use the interior and atmosphere models presented in Dorn et al. (2018) and Turbet et al. (2020b) to obtain the WMF estimated for the TRAPPIST-1 planets with updated and more precise radii and masses data from Spitzer TTVs (Agol et al. 2021). We therefore limited the comparison to the sole results of Agol et al. (2021) with the same input values. By doing so, we can be certain that the variations in WMF estimates are due to our different modelling approach. Figure 6 shows that planets b and c are most likely dry in scenario 2, where the resulting CMFs are between 0.2 and 0.3 for the whole system. We obtain maximum estimates of 3.4 × 10−6 and 2.7 × 10−6 for b and c, respectively. For the same density, the estimated value of the WMF depends on the CMF that is considered. Therefore, we compare WMF estimates for similar CMFs in this work and Agol et al. (2021). We show our WMF in scenario 2, because the CMF of all planets spans a narrow range between 0.2 and 0.3, which are the most similar values to one of the CMFs assumed by Agol et al. (2021), CMF = 0.25. Our WMF for the steam planets of the TRAPPIST-1 system are in agreement with those of Agol et al. (2021), who calculated a maximum WMF of 10−5 for a constant CMF of 0.25. We are able to reduce the maximum limit of the water content of the highly irradiated planets compared to previous studies and establish the most likely WMF with our coupled atmosphere–interior model. The calculation of the total radius requires precise determination of the atmospheric thickness. This depends strongly on the surface temperature and the surface gravity, which are obtained with radiative transfer in the atmosphere, and the calculation of the gravity profile for a bulk mass and composition in the interior self-consistently.
In the case of planet d, we estimate a WMF of 0.036 ± 0.028, while Agol et al. (2021) obtain an upper limit of 10−5. The latter estimate considers that water is in vapour form, which is less dense than condensed phases, while our model shows that the surface conditions allow liquid or ice phases, resulting in a higher WMF. This discrepancy in the possible water phases on the surface of planet d is due to different atmospheric compositions. We consider a water-dominated atmosphere with 1% CO2, while Agol et al. (2021) and Turbet et al. (2020b) assume a N2 and H2O mixture. This difference in composition changes the radiative balance because CO2 is a strong absorber in the IR compared to N2, which is a neutral gas. Nonetheless, N2 is subject to stellar-wind-driven escape and is unlikely to be stable for the inner planets of TRAPPIST-1, while CO2 is more likely to survive thermal and ion escape processes (Turbet et al. 2020a).
Our WMF for planets e to h are in agreement within uncertainties with those of Agol et al. (2021), although their central values are significantly lower. The EOS employed to compute the density of the water layers in Agol et al. (2021) is also used in Dorn et al. (2018) and Vazan et al. (2013), which agrees well with the widely used SESAME and ANEOS EOSs (Baraffe et al. 2008). These EOS are not consistent with experimental and theoretical data because they overestimate the density at pressures higher than 70 GPa (Mazevet et al. 2019). This yields an underestimation of the WMF for the same total planetary density and CMF.
For the specific case of scenario 1, with no assumptions on the stellar composition and the Fe/Si mole ratio, we compared our CMF and WMF with those obtained in Barr et al. (2018) (Fig. 6 and Table 5). These latter authors use masses and radii data given by Wang et al. (2017); they obtain lower masses compared to Agol et al. (2021) while their radii are approximately the same, which would explain why Barr et al. (2018) tend to overestimate the water content of the TRAPPIST-1 planets. Moreover, most of the mass uncertainties in Wang et al. (2017) are 30–50%, while the mass uncertainties obtained by Agol et al. (2021) are 3–5%. This causes Barr et al. (2018) to calculate wider CMF and WMF 1σ confidence intervals. In addition, there are differences between our interior modelling approach and that of Barr et al. (2018). For example, according to the results of these latter authors, planet b can have up to 50% of its mass as water. This high WMF value is due to the assumption that the hydrosphere is in liquid and ice I phases, and high-pressure ice polymorphs (HPPs), which are more dense than the steam atmosphere we consider. In contrast, the CMF seems to be closer to our estimates, especially for planets b, d, and e, where their maximum CMF is approximately 0.40, in agreement with our CMF 1σ intervals.
We can also discuss the possible habitability of the hydrospheres of the TRAPPIST-1 planets by comparing our WMF estimates with the layer structure as a function of planetary mass and water content obtained by Noack et al. (2016). According to Noack et al. (2016), a habitable hydrosphere must be structured in a single liquid water oceanor in several ice layers that enable the formation of a lower ocean layer. This lower ocean would be formed by the heat supplied by the mantle that melts the high-pressure ice in the ice-mantle boundary (Noack et al. 2016). For planet d, a surface liquid ocean would form for all its possible WMF if the atmosphere allows for the presence of condensed phases. For planets e, f, and g, the hydrosphere could be stratified in a surface layer of ice Ih and a liquid or ice II-VI layer. In the case of low-pressure ices II-VI, their base could be melted by the heat provided by the mantle, and form a lower ocean layer as suggested by Noack et al. (2016). At WMF ≥ 0.10, less than 50% of the possible configurations enable a habitable sub-surface ocean layer, and at a WMF ≥ 0.14, the hydrosphere is uninhabitable. In scenario 1, planets e to g reach these values within uncertainties, although their minimum values extend down to 0–0.03 in WMF, which would be the habitable regime.
Comparison between our 1D 1σ confidence regions for the CMF and those of Barr et al. (2018).
5.2 System formation and architecture
In the case of scenario 1, where no Fe/Si data are assumed, the WMF increases with the distance to the star with the exception of planet h, whose WMF is similar to that of planet d. In the case of scenario 2, where a common Fe/Si of 0.76 ± 0.12 is assumed for the whole system, the WMF increases with the distance to the star (Fig. 6) with the exception of planet d whose WMF is similar to that of planet f, which is more water-rich than planet e. This slight deviation from the observed trend could be explained by migration, where planet d could have formed beyond the snow line before migrating inwards (Raymond et al. 2018). In addition, pebble ablation and water recycling back into the disc could have been less efficient for planet d than for planet e (Coleman et al. 2019). On the other hand, the gas at the distance at which planet d formed could have been more enriched in volatiles than the outer planets, accreting more water ice than planet e in a ‘cold finger’ (Stevenson & Lunine 1988; Cyr et al. 1998). Pebble formation in the vicinity of the water ice line can induce important enhancements of the water ice fraction in those pebbles due to the backward diffusion of vapour through the snowline and the inward drift of ice particles. Therefore, if a planet forms from this material, it should be more water-rich than those formed further out (Mousis et al. 2019). These formation scenarios could explain the high WMF of planet d when we assume that its water layer is in condensed phases. Post-formation processes could also have shaped the trend of the WMF with axis, such as atmospheric escape due to XUV and X-ray emission from their host star. Bolmont et al. (2017) estimated a maximum water loss of 15 Earth Oceans (EO) for TRAPPIST-1 b and c and 1 EO for planet d. If we were to assume that the current WMFs are the central values of the posterior distributions we derived in scenario 1, planets b, c, and d would have had an initial WMF of 2.37 × 10−3, 2.50 × 10−3 and 0.085, respectively. Therefore, atmospheric escape would have decreased the individual WMF of each planet, but the increase of WMF with distance from the star would have been preserved.
In addition to the WMF–axis trend, we can differentiate the very water-poor, close-in planets, b and c, from the outer, water-rich planets, d to h. This has been reported as a consequence of pebble accretion in the formation of other systems, such as the Galilean moons. While Io is dry, Callisto and Ganymede are water-rich, with Europa showing an intermediate WMF of 8% (Ronnet et al. 2017). Pebble-driven formation can produce planets with WMF ≥ 15% if these are formed at the water ice line (Coleman et al. 2019; Schoonenberg et al. 2019). In contrast, planets formed within the ice line would present WMFs of less than 5% (Liu et al. 2020; Coleman et al. 2019), which is close to the mean value we calculate for planet h, 5.5%. The maximum WMF limit in the first scenario is approximately 20%. This maximum limit is significantly lower than the typical WMF generated by the planetesimal accretion scenario, which is 50–40% (Miguel et al. 2020). Therefore, our results are consistent with the pebble-driven formation scenario.
 |
Fig. 7 Mass–radius relationships for planets with CO2-dominated atmospheres assuming different CMFs. The surface pressure is 300 bar. The black dot and its error bars indicate the location anduncertainties of planet d in the mass–radius diagram. |
5.3 Alternative atmospheric compositions
However, the atmosphere of planet d could be dominated by other atmospheric gases different from H2 O-based mixtures, which could produce an extended atmosphere and increase the total planetary radius. Hydrogen-dominated atmospheres have been deemed unlikely as one of the possible atmospheric compositions for all planets in the TRAPPIST-1 system, both cloud-free (de Wit et al. 2016, 2018) and with high-altitude clouds and hazes (Grimm et al. 2018; Ducrot et al. 2020). Similarly, CH4-dominated atmospheres are not probable according to the photometry data of the Spitzer Space Telescope (Ducrot et al. 2020). Therefore, our best candidate to explain the low density of planet d in a water-poor scenario is CO2. We find that a CO2-dominated atmosphere with 1% water vapour in planet d would be in radiative-convective equilibrium by computing the OLR and absorbed radiation, as we have for water-dominated atmospheres. The resulting surface temperature is approximately 950 K, which is slightly higher than the surface temperature of Venus (700 K) with a higher water vapour mixing ratio. Figure 7 introduces the mass–radius relationships for different CMFs, assuming a CO2-dominated atmosphere with a surface pressure of 300 bar. Planet d appears to be compatible with a planet with a CO2-dominated atmosphere and CMF between 0.2 and 0.3, which is a very likely CMF range for TRAPPIST-1 planets based on our analysis. Surface pressures lower than 300 bar would yield lower atmospheric thicknesses, and so it would be necessary to consider a lower CMF to explain the observed density of planet d. CO2 in the case of planet d can be provided by volcanic outgassing (Ortenzi et al. 2020), as its internal heat flux produced by tidal heating is in the range 0.04–2 W m−2, which favours plate tectonics (Papaloizou et al. 2018). Secondary CO2-dominated atmospheres could have traces of O2, N2, and water vapour.
6 Conclusions
We present an interior structure model for low-mass planets at different irradiations that is valid for a wide range of water phases and was derived from the approaches of Brugger et al. (2017) and Mousis et al. (2020). For highly irradiated planets, we couple a 1D water steam atmosphere in radiative–convective equilibrium with a high-pressure convective layer in supercritical phase. The density in this layer is computed using an accurate EOS for high-pressure and high-temperature water phases. For temperate planets whose surface conditions allow the formation of condensed phases, we implemented a hydrosphere with liquid water and ice phases Ih, II, III, V, VI and VII. In addition, we adapted the MCMC Bayesian algorithm described in Dorn et al. (2015) to our interior model to derive the posterior distributions of the compositional parameters, WMF and CMF, given mass, radius, and stellar composition data. We then applied our interior model to the particular case of TRAPPIST-1 planets using the latest mass and radius data from Spitzer (Agol et al. 2021).
We characterised the hydrospheres of TRAPPIST-1 planets by calculating their P-T profiles and thermodynamic phases. Planets b and c are warm enough to present steam atmospheres. They could hold post-runaway greenhouse atmospheres with thicknesses of up to 450 km and surface temperatures of up to 2500 K, which means that they are extended enough to be suitable targets for atmospheric characterisation by future space-based facilities such as James Webb Space Telescope (JWST). Moreover, planets d to g present hydrospheres in condensed phases. These hydrospheres can contain high-pressure ices that start to form at 109 −1010 Pa.
We obtained CMF and WMF probability distributions for all planets in the system. We find that the Fe/Si mole ratio of the system is in the 0.45–0.97 range without considering any assumption on the chemical composition of the stellar host. This Fe/Si range corresponds to a CMF value in the 0.23–0.40 range, making the CMF of TRAPPIST-1 planets compatible with an Earth-like value (0.32). In addition, our WMF estimates agree within uncertainties with those derived by Agol et al. (2021), although their most likely values are considerably lower for planets with condensed phases. In the case of planets with steam hydrospheres, their densities are compatible with dry rocky planets with no atmospheres. Nevertheless, we cannot rule out the presence of an atmosphere with the Fe/Si range we derive without any assumption on the chemical composition of the host star. When considering a possible estimate of the Fe/Si ratio of the host star (scenario 2), we obtain lower maximum limits of the WMF for planets b and c compared to previously calculated limits by Agol et al. (2021) for a similar CMF of 0.25. Our estimated WMFs in steam and condensed phases are consistent with an increase in the WMF with progressing distance from the host star. This trend, as well as the maximum WMF we calculate, favour pebble-driven accretion as a plausible formation mechanism for the TRAPPIST-1 system. However, planet d presents a slightly higher WMF than planet e. This could be due to processes that took place during planet formation, such as migration, a low-efficient ablation of pebbles, and gas recycling, or an enhancement of the water ice fraction in pebbles at the distance of the disc where planet d formed. An extended atmosphere dominated by greenhouse gases different from a water-dominated atmosphere, such as CO2, could also explain the low-density of planet d compared to planet e.
Future work should include more atmospheric processes and species that determine the mass–radius relations of planets with secondary atmospheres in the super-Earth and sub-Neptune regime. These can vary the atmospheric thickness and increase the total planetary radius with varying atmospheric mass while other compositional parameters change the bulk radius. These should be integrated into one single interior-atmosphere model combined in a MCMC Bayesian framework such as the one we used in this study. This statistical approach has been employed with interior models for planets with H/He-dominated atmospheres (Dorn et al. 2017b,a, 2018), or dry planets (Plotnykov & Valencia 2020), but not for planets with secondary, CO2 and steam-dominated atmospheres. The integrated model should also include a description of escape processes, such as hydrodynamic or Jeans escapes, which is particularly interesting for exploration of the lifetime of secondary atmospheres. Close-in, low-mass planets are likely to outgas atmospheric species such as CO2, and form O2 via photodissociation of outgassedH2O during theirmagma ocean stage or due to plate tectonics (Chao et al. 2020). A mixture of these gases should therefore beconsidered to study the thermal structure of planets with secondary atmospheres. Planets b and c in the TRAPPIST-1 system could present magma oceans due to their high surface temperatures (T ≥ 1300 K) (Barr et al. 2018; Chao et al. 2020), and the maximum surface pressure we have obtained here can be used to assess the current outgassing rate in magma ocean studies (Noack et al. 2017; Baumeister et al., in prep.) and better constrain the WMF for the interior magma ocean models (e.g. Katyal et al. 2020) in the future.
Acknowledgements
M.D. and O.M. acknowledge support from CNES. We acknowledge the anonymous referee whose comments helped improve and clarify this manuscript.
References
- Agol, E., Dorn, C., Grimm, S. L., et al. 2021, Planet. Sci. J., 2, 1 [Google Scholar]
- Báez, L. A., & Clancy, P. 1995, J. Chem. Phys., 103, 9744 [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barr, A. C., Dobos, V., & Kiss, L. L. 2018, A&A, 613, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, W. 2017, CHEOPS Fifth Science Workshop, 1 [Google Scholar]
- Bezacier, L., Journaux, B., Perrillat, J.-P., et al. 2014, J. Chem. Phys., 141, 104505 [Google Scholar]
- Bolmont, E., Selsis, F., Owen, J. E., et al. 2017, MNRAS, 464, 3728 [Google Scholar]
- Brugger, B., Mousis, O., Deleuil, M., & Lunine, J. I. 2016, ApJ, 831, L16 [Google Scholar]
- Brugger, B., Mousis, O., Deleuil, M., & Deschamps, F. 2017, ApJ, 850, 93 [Google Scholar]
- Chao, K.-H., deGraffenried, R., Lach, M., et al. 2020, arXiv e-prints, [arXiv:2012.07337] [Google Scholar]
- Choukroun, M., & Grasset, O. 2010, J. Chem. Phys., 133, 144502 [Google Scholar]
- Coleman, G. A. L., Leleu, A., Alibert, Y., & Benz, W. 2019, A&A, 631, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cyr, K. E., Sears, W. D., & Lunine, J. I. 1998, Icarus, 135, 537 [Google Scholar]
- de Wit, J., Wakeford, H. R., Gillon, M., et al. 2016, Nature, 537, 69 [Google Scholar]
- de Wit, J., Wakeford, H. R., Lewis, N. K., et al. 2018, Nat. Astron., 2, 214 [Google Scholar]
- Dobos, V., Barr, A. C., & Kiss, L. L. 2019, A&A, 624, A2 [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 577, A83 [EDP Sciences] [Google Scholar]
- Dorn, C., Hinkel, N. R., & Venturini, J. 2017a, A&A, 597, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Venturini, J., Khan, A., et al. 2017b, A&A, 597, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Mosegaard, K., Grimm, S. L., & Alibert, Y. 2018, ApJ, 865, 20 [Google Scholar]
- Ducrot, E., Gillon, M., Delrez, L., et al. 2020, A&A 640, A112 [Google Scholar]
- Dunaeva, A. N., Antsyshkin, D. V., & Kuskov, O. L. 2010, Sol. Syst. Res., 44, 202 [Google Scholar]
- Fei, Y., Mao, H.-K., & Hemley, R. J. 1993, J. Chem. Phys., 99, 5369 [Google Scholar]
- Feistel, R., & Wagner, W. 2006, J. Phys. Chem. Ref. Data, 35, 1021 [Google Scholar]
- Forget, F., & Leconte, J. 2014, Phil. Trans. R. Soc. London Ser. A, 372, 20130084 [Google Scholar]
- French, M., Mattsson, T. R., Nettelmann, N., & Redmer, R. 2009, Phys. Rev. B, 79, 054107 [Google Scholar]
- French, M., Desjarlais, M. P., & Redmer, R. 2016, Phys. Rev. E, 93, 022140 [Google Scholar]
- Gagnon, R. E., Kiefte, H., Clouter, M. J., & Whalley, E. 1990, J. Chem. Phys., 92, 1909 [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [Google Scholar]
- Goldblatt, C. 2015, Astrobiology, 15, 362 [Google Scholar]
- Goldblatt, C., Robinson, T. D., Zahnle, K. J., & Crisp, D. 2013, Nat. Geosci., 6, 661 [Google Scholar]
- Grimm, S. L., Demory, B.-O., Gillon, M., et al. 2018, A&A, 613, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haar, L., Gallagher, J. S., & Kell, G. S. 1984, NBS/NRC steam tables thermodynamic and transport properties and computer programs for vapor and liquid states of water in SI units (Taylors & Francis Inc.) https://www.osti.gov/biblio/5614915 [Google Scholar]
- Hinkel, N. R., Timmes, F. X., Young, P. A., Pagano, M. D., & Turnbull, M. C. 2014, AJ, 148, 54 [Google Scholar]
- Hinkel, N. R., Young, P. A., Pagano, M. D., et al. 2016, ApJS, 226, 4 [Google Scholar]
- Hinkel, N. R., Mamajek, E. E., Turnbull, M. C., et al. 2017, ApJ, 848, 34 [Google Scholar]
- Ingersoll, A. P. 1969, J. Atm. Sci., 26, 1191 [Google Scholar]
- Katyal, N., Nikolaou, A., Godolt, M., et al. 2019, ApJ, 875, 31 [Google Scholar]
- Katyal, N., Ortenzi, G., Lee Grenfell, J., et al. 2020, A&A, 643, A81 [Google Scholar]
- Leon, G. C., Rodrguez Romo, S., & Tchijov, V. 2002, J. Phys. Chem. Solids, 63, 843 [Google Scholar]
- Lincowski, A. P., Meadows, V. S., Crisp, D., et al. 2018, ApJ, 867, 76 [Google Scholar]
- Liu, B., Lambrechts, M., Johansen, A., Pascucci, I., & Henning, T. 2020, A&A, 638, A88 [EDP Sciences] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, Landolt Börnstein, 4B, 712 [Google Scholar]
- Marcq, E. 2012, J. Geophys. Res. Planets, 117, E01001 [Google Scholar]
- Marcq, E., Salvador, A., Massol, H., & Davaille, A. 2017, J. Geophys. Res. Planets, 122, 1539 [Google Scholar]
- Mazevet, S., Licari, A., Chabrier, G., & Potekhin, A. Y. 2019, A&A, 621, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKay, A. J., DiSanti, M. A., Kelley, M. S. P., et al. 2019, AJ, 158, 128 [Google Scholar]
- Miguel, Y., Cridland, A., Ormel, C. W., Fortney, J. J., & Ida, S. 2020, MNRAS, 491, 1998 [NASA ADS] [Google Scholar]
- Mousis, O., Ronnet, T., & Lunine, J. I. 2019, ApJ, 875, 9 [Google Scholar]
- Mousis, O., Deleuil, M., Aguichine, A., et al. 2020, ApJ, 896, L22 [Google Scholar]
- Nakajima, S., Hayashi, Y.-Y., & Abe, Y. 1992, J. Atm. Sci., 49, 2256 [Google Scholar]
- Noack, L., Höning, D., Rivoldini, A., et al. 2016, Icarus, 277, 215 [Google Scholar]
- Noack, L., Rivoldini, A., & Van Hoolst, T. 2017, Phys. Earth Planet. Inter., 269, 40 [Google Scholar]
- Ortenzi, G., Noack, L., Sohl, F., et al. 2020, Sci. Rep., 10, 10907 [Google Scholar]
- Papaloizou, J. C. B., Szuszkiewicz, E., & Terquem, C. 2018, MNRAS, 476, 5032 [Google Scholar]
- Plotnykov, M., & Valencia, D. 2020, MNRAS, 499, 932 [Google Scholar]
- Pluriel, W., Marcq, E., & Turbet, M. 2019, Icarus, 317, 583 [Google Scholar]
- Raymond, S. N., Boulet, T., Izidoro, A., Esteves, L., & Bitsch, B. 2018, MNRAS, 479, L81 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Ronnet, T., Mousis, O., & Vernazza, P. 2017, ApJ, 845, 92 [Google Scholar]
- Schoonenberg, D., Liu, B., Ormel, C. W., & Dorn, C. 2019, A&A, 627, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumder, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [Google Scholar]
- Shaw, G. H. 1986, J. Chem. Phys., 84, 5862 [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [Google Scholar]
- Stevenson, D. J., & Lunine, J. I. 1988, Icarus, 75, 146 [Google Scholar]
- Tchijov, V., Ayala, R. B., Leon, G. C., & Nagornov, O. 2004, J. Phys. Chem. Solids, 65, 1277 [Google Scholar]
- Tulk, C. A., Gagnon, R. E., Kiefte, H., & Clouter, M. J. 1997, J. Chem. Phys., 107, 10684 [Google Scholar]
- Turbet, M., Bolmont, E., Leconte, J., et al. 2018, A&A, 612, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- Turbet, M., Ehrenreich, D., Lovis, C., Bolmont, E., & Fauchez, T. 2019, A&A, 628, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turbet, M., Bolmont, E., Bourrier, V., et al. 2020a, Space Sci. Rev., 216, 100 [Google Scholar]
- Turbet, M., Bolmont, E., Ehrenreich, D., et al. 2020b, A&A, 638, A41 [Google Scholar]
- Unterborn, C. T., Desch, S. J., Hinkel, N. R., & Lorenzo, A. 2018, Nat. Astron., 2, 297 [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 434, 3283 [Google Scholar]
- Wagner, W., & Pruß, A. 2002, J. Phys. Chem. Ref. Data, 31, 387 [Google Scholar]
- Wang, S., Wu,D.-H., Barclay, T., & Laughlin, G. P. 2017, arXiv e-prints, [arXiv:1704.04290] [Google Scholar]
- Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, Proc. Natl. Acad. Sci., 116, 9723 [Google Scholar]
All Tables
Masses, radii, and semi-major axis for all planets in TRAPPIST-1 (Agol et al. 2021).
Comparison between our 1D 1σ confidence regions for the CMF and those of Barr et al. (2018).
All Figures
 |
Fig. 1 Structural diagram of the coupling between the interior structure model and the atmosphere model. Tbase is the temperature at the bottom of the steam atmosphere in radiative-convective equilibrium. z and Matm denote the atmospheric thickness and mass, respectively. Rbulk and Mbulk correspond to the planet bulk radius and mass, respectively. Rguess refers to the initial guess of the bulk radius, while Rinterior is the output bulk radius of the interior structure model in each iteration. |
| In the text | |
 |
Fig. 2 Top panel: 1σ-confidence regions derived from the 2D posterior distributions for the first scenario, where only the masses and radii are available as data. Bottom panel: 1σ-confidence regions derived from the 2D posterior distributions for the second scenario, where the Fe/Si abundance ratio from Unterborn et al. (2018) is considered together with the mass and radius for each planet. The axis of the ternary diagram indicates the CMF, the WMF, and the mantle mass fraction MMF = 1 – CMF – WMF. |
| In the text | |
 |
Fig. 3 Outgoing longwave radiation (OLR) and absorbed radiation as a function of surface temperature for the steam atmospheres of TRAPPIST-1 b, c, and d. Vertical dotted lines indicate the surface temperature at which the absorbed flux is equalto the OLR for planets b and c. |
| In the text | |
 |
Fig. 4 (P,T) profiles of the hydrospheres of TRAPPIST-1 planets. The dashed-dotted grey horizontal line indicates the 20 mbar pressure level (see text). Thicker lines indicate the profile for the minimum WMF estimated for each planet in scenario 1, while thinner lines mark the profile for the maximum WMF under the same scenario. The minimum WMF of planets b, c, and h is zero. |
| In the text | |
 |
Fig. 5 One- and two-dimensional marginal posterior distributions for the atmospheric parameters (surface temperature Tsurf, atmospheric thickness zatm, albedo, and atmospheric mass Matm), and bulk mass and radius, Mbulk and Rbulk, of TRAPPIST-1 b (left panel) and c (right panel). These were derived under scenario 1, where we do not consider Fe/Si data. |
| In the text | |
 |
Fig. 6 Water mass fraction as a function of the distance to the star for the TRAPPIST-1 system. Upper panel: our estimates for scenario 1 and those of Barr et al. (2018), where only mass and radius data were taken into account. Lower panel: corresponds to scenario 2, whose CMF is constrained in a narrow range between 0.2 and 0.3, while for Agol et al. (2021) we show the WMF for a CMF of 0.25. |
| In the text | |
 |
Fig. 7 Mass–radius relationships for planets with CO2-dominated atmospheres assuming different CMFs. The surface pressure is 300 bar. The black dot and its error bars indicate the location anduncertainties of planet d in the mass–radius diagram. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


