EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 646 (February 2021) A&A, 646 (2021) L4 Full HTML
Free Access
Issue
A&A
Volume 646, February 2021
Article Number L4
Number of page(s) 9
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202040178
Published online 05 February 2021

© ESO 2021

1. Introduction

Increasingly more early-type main-sequence (MS) stars in the Galactic halo have been reported to move at very high space velocities (see, e.g., Irrgang et al. 2019; Koposov et al. 2020; Raddi et al. 2021, and references therein), and some may even exceed their local Galactic escape velocity (Brown 2015; Boubert et al. 2018, and references therein). These stars are believed to have been born in the star-forming regions of the Milky Way, that is, inside the Galactic disk, and then been ejected from their birth environment. They are therefore generally referred to as runaway stars. Two classical ejection mechanisms are typically considered, the binary supernova scenario (BSS, Blaauw 1961) and the dynamical ejection scenario (DES, Poveda et al. 1967). In the BSS, the runaway star is the former companion of a massive star that underwent a core-collapse supernova. The corresponding explosion disrupted the binary and released the secondary with almost its orbital velocity. In the DES, the runaway star is ejected from young clusters and associations through close stellar encounters. These dynamical interactions mostly occur during the initial relaxation phase of the star cluster and are most efficient between two close binaries.

These two classical scenarios can hardly explain the acceleration of stars to velocities beyond ∼400 km s−1 (see Irrgang et al. 2018a; Evans et al. 2020, and references therein). Consequently, in order to produce what is commonly called a hypervelocity star (HVS), that is, a star moving faster than its local Galactic escape velocity, the so-called Hills mechanism (Hills 1988) was invoked when the first HVSs were discovered (Brown et al. 2005; Hirsch et al. 2005; Edelmann et al. 2005). Hills (1988) showed that the tidal forces of a supermassive black hole could disrupt nearby binaries, with one component being captured in a tight orbit while the other is ejected at a velocity (thousands of km s−1) that is well sufficient to overcome the gravitational attraction of the Galaxy. A systematic radial-velocity survey led to the discovery of 21 late B-type stars that qualified as candidate HVSs (Brown et al. 2014). However, because astrometric data of sufficient precision and accuracy were lacking, it was not possible at that time to verify whether these 21 objects were indeed Hills stars, that is, objects ejected by the supermassive black hole at the Galactic center (GC). Nevertheless, the Hills mechanism was assumed to be the most likely explanation of the very high space motions of the HVS candidates.

While not useful for the HVS candidates, the quality of astrometric measurements in the pre-Gaia era at least allowed more nearby runaway stars to be studied. Based on proper motions from the HIPPARCOS mission, Heber et al. (2008) concluded that the massive B-type star HD 271791 is gravitationally unbound to the Milky Way, although its does not stem from the GC but from the outer rim of the Galactic disk. In order to distinguish these stars from HVSs, Przybilla et al. (2008) coined the term hyper-runaway star. In addition to the spatial origin, the ejection velocity is another crucial quantity for characterizing the nature of runaway stars. In a comprehensive study, Silva & Napiwotzki (2011) derived ejection velocities for a compilation of 96 B-type MS runaway stars. A high-velocity population of 11 stars with ejection velocities between 400 and 500 km s−1 was identified. Unfortunately, the respective uncertainties were large because of the currently poor quality of the underlying ground-based and HIPPARCOS proper motions.

The unprecedented precision of the Gaia second data release (DR2, Gaia Collaboration 2016, 2018) became a game changer. Boubert et al. (2018) revisited the more than 500 mostly late-type HVS candidates proposed before and found most of them to be bound. Only for fewer than 100 of them did the probability to be unbound exceed 1%, and only for 41 does it exceed 50%. Irrgang et al. (2018a) and Kreuzer et al. (2020) reanalyzed 40 of the 42 most extreme stars from the MMT-HVS survey (Brown et al. 2014), including most of the 21 HVS candidates mentioned above, and ruled out the Hills mechanism in the GC for almost all of the 18 targets that did have a relatively well-constrained spatial origin. Hattori et al. (2019) and Koposov et al. (2020) came to the same conclusion for the four HVS candidates from the LAMOST survey (Zheng et al. 2014; Huang et al. 2017; Li et al. 2018), and Irrgang et al. (2019) showed that the relatively bright B-type MS star PG 1610+062 was ejected with a velocity of no less than 550 ± 40 km s−1. However, overwhelming observational evidence for the operation of the Hills mechanism has also been found by Koposov et al. (2020). They discovered that the A-type star S5-HVS 1 travels at a Galactic rest-frame velocity of 1755 ± 50 km s−1 and most likely originates in the GC.

Nevertheless, there is a clear trend that most of the original HVS candidates are found to be runaway stars from the Galactic disk instead of Hills stars when the precision of the underlying astrometry is sufficient to distinguish between these two options. This is an interesting result because the ejection velocities of these discarded Hills stars still exceed the predicted limits of the classical ejection mechanisms (Bromley et al. 2009; Perets & Šubr 2012; Kenyon et al. 2014; Tauris 2015; Evans et al. 2020), which depend on stellar mass. For instance, Tauris (2015) reported that the maximum ejection velocity in the BSS is 540 km s−1 for a 3.5 M⊙ star, while it is only 320 km s−1 for a 10 M⊙ star. Consequently, the high observed ejection velocities of disk runaways call for an as yet mostly neglected mechanism possibly involving very massive stars (Gvaramadze 2009; Gvaramadze et al. 2009) or intermediate-mass black holes (Fragione & Gualandris 2019), see Irrgang et al. (2018a) for a more detailed discussion. With proper motions of significantly improved accuracy and precision from the Gaia early data release 3 (EDR3, Gaia Collaboration 2021; Lindegren et al. 2021), it is now possible to determine whether this trend continues.

2. Target selection

Our initial sample comprised all 40 stars of the MMT-HVS survey that were revised by Kreuzer et al. (2020), together with 30 runaway stars from the collection of Silva & Napiwotzki (2011) for which we were able to obtain spectra. This covers the majority of objects with high ejection velocities in that compilation. This group was complemented by the prototype hyper-runaway star HD 271791 (Heber et al. 2008), the potential hyper-runaway stars SDSS J013655.91+242546.0 (J0136+2425 for short, Tillich et al. 2009) and HIP 60350 (Irrgang et al. 2010), the extreme disk-runaway star PG 1610+062 (Irrgang et al. 2019), the four candidate HVSs from the LAMOST survey (Zheng et al. 2014; Huang et al. 2017; Li et al. 2018), and the probable Hills star S5-HVS 1 (Koposov et al. 2020). Based on proper motions from Gaia EDR3, we then carried out spectroscopic and kinematic analyses (see Sects. 3 and 4 for details) of all members of this initial sample to filter out those with both a high ejection velocity and a relatively well-constrained origin within the Galactic disk. In order to account for the fact that massive stars are typically ejected at lower velocity, we chose a mass-dependent threshold for the deduced 1σ upper limit of the ejection velocity, that is, 400 km s−1 or 320 km s−1 for stars with masses below or above 5 M⊙, respectively. The first cut applies to almost all stars from the MMT-HVS survey, while most of the others fall into the second category. The chosen thresholds roughly represent the limits for the classical ejection scenarios (see, e.g., Tauris 2015; Irrgang et al. 2018a, and references therein). A disk origin was granted when the 1σ lower limit of the inferred galactocentric plane-crossing radius was below 25 kpc (motivated by Xu et al. 2015), while visual inspection was used to judge whether the origin was sufficiently well constrained. These criteria left us with 14 stars from the MMT-HVS survey, 7 stars from the Silva & Napiwotzki (2011) sample, all 4 stars from the LAMOST survey, and the 5 individual targets mentioned above, yielding a final sample of 30 program stars, the names of which are listed in Table 1.

Table 1.

Ejection velocity, galactocentric radius at plane intersection, and stellar mass of the program stars.

3. Quantitative spectrophotometric analysis

Although Gaia EDR3 provides astrometric data of unprecedented precision and accuracy, distances estimated from the measured parallaxes are still considerably less precise than those obtained from spectrophotometry, which have typical uncertainties smaller than 10%, mainly because our targets are found at distances beyond the current capabilities of Gaia. Consequently, we used spectrophotometric distance estimates as input for our kinematic investigation. For half of the sample, that is, for the 14 stars from the MMT-HVS survey and for PG 1610+062, we used our previously published results (see Irrgang et al. 2019; Kreuzer et al. 2020). Seeking homogeneity, we also carried out quantitative spectral analyses of the remaining targets using the same techniques as applied for the others. This was possible for all stars except S5-HVS 1 and LAMOST HVS 2, for which we were not able to obtain spectra and thus had to rely on literature values. We also used the latter for J0136+2425 because the atmospheric parameters inferred by us do not deviate from the published ones by Tillich et al. (2009).

Our analysis strategy and the adopted model atmospheres are extensively outlined in previous papers (Irrgang et al. 2014, 2018b, 2019; Heber et al. 2018; Kreuzer et al. 2020). We therefore briefly summarize the key details here. Atmospheric parameters such as effective temperature Teff, surface gravity log(g), projected rotational velocity vsin(i), and radial velocity vrad were determined by fitting the most recent model spectra of appropriate chemical composition to observed spectra. The resulting parameters were then used to compute a synthetic spectral energy distribution that was fit to measured magnitudes, which usually cover the ultraviolet, optical, and infrared regime, in order to derive the angular diameter Θ of the star and the interstellar extinction. The latter is typically very small for our program stars owing to their position above or below the Galactic disk. Stellar masses M and ages τevol were inferred by comparing the position of a star in the Kiel diagram to evolutionary tracks by the Geneva group (Ekström et al. 2012; Georgy et al. 2013). The spectrophotometric distance d finally followed from solving the definition of the surface gravity, g = GMR−2, with G being the gravitational constant, for the stellar radius R and inserting the latter in the definition of the angular diameter, Θ = 2R/d. The resulting atmospheric and stellar parameters as well as information about the available optical spectra are summarized in Table A.1.

4. Gaia EDR3 update on kinematics

The spectrophotometric distances and radial velocities were combined with proper motions from Gaia EDR3 to trace back the trajectories of the program stars to the Galactic plane in order to derive their ejection velocities with respect to the rotating Galactic disk and to identify their spatial origins within the disk.

To this end, we used the Milky Way mass model I of Irrgang et al. (2013), which is a three-component Galactic potential with standard analytical forms for the central spherical bulge, an axisymmetric disk, and a spherical dark matter halo. The model reproduces a variety of observational constraints such as the Galactic rotation curve, and according to Irrgang et al. (2018a), is still valid with Milky Way mass measurements based on the motions of globular clusters, satellite galaxies, and extreme velocity halo stars as derived from Gaia DR2 astrometry. The corresponding equations of motions are numerically solved with a fourth-order Runge-Kutta-Fehlberg method with adaptive stepsize control that ensures an absolute numerical accuracy in each integration step of less than 10−10 for positions in kpc and velocities in km s−1. Error propagation for the four input parameters (spectrophotometric distance, radial velocity, and proper motion in right ascension and declination) is handled with a Monte Carlo simulation with one million runs, using Gaussian distributions that allow for asymmetric error bars and the correlation between the two proper motion components. Uncertainties in the distance of the Sun to the GC and in its relative motion to the local standard of rest (Schönrich et al. 2010) are treated analogously. To account for the nonzero height of the Galactic disk, the backward integration of the Monte Carlo orbits is not stopped exactly at the Galactic mid-plane, but at vertical offsets randomly drawn from a Gaussian probability distribution with a mean value of zero and a standard deviation of 0.1 kpc (motivated, e.g., by Buckner & Froebrich 2014; Li et al. 2019). Because stars in the outer disk have been observed at much larger vertical distances of up to several kpc (see, e.g., Feast et al. 2014; Price-Whelan et al. 2015; Bergemann et al. 2018), we used a standard deviation of 5 kpc for targets originating from galactocentric radii larger than 16 kpc. Owing to the high space velocities of our targets, the derived properties at plane intersection are only marginally affected by considering a nonzero height for the disk, however.

To demonstrate the immense gain in precision from DR2 to EDR3, we show the inferred plane-crossing areas for five selected targets for both cases in Fig. 1. While all resulting kinematic parameters are summarized in Table A.2, we focus in the following on the ejection velocities vej and galactocentric radii at plane intersection rp, which are also given in Table 1 or are visualized in Fig. 2. Three subgroups may be identified in our sample: stars originating in the GC, bona fide disk runaways, and stars that were presumably ejected from the outer rim of the Galactic disk.

thumbnail Fig. 1.

Inferred spatial origin within the Galactic plane for five selected objects (upper row; see Fig. A.1 for all program stars). The most likely plane-crossing point is marked by a black cross, while the shaded areas visualize the corresponding 1σ (light red) and 2σ (light blue) contours. Circles centered at the GC (black plus sign) with radii of 1 kpc (dotted black line), 8.3 kpc (solar circle; dashed red line), and 25 kpc (solid blue line) are shown for reference. The galactocentric coordinate system is Cartesian and right-handed, with the Sun (red square) on the negative x-axis and the z-axis pointing to the Galactic north pole. The panels in the lower row show the same, except that proper motions from Gaia DR2 are used as input, demonstrating the improved precision of EDR3.

thumbnail Fig. 2.

Ejection velocity (relative to the rotating Galactic disk) vs. galactocentric radius at plane intersection for all program stars except S5-HVS 1, which is beyond the ordinate scale. Error bars are 1σ confidence intervals. The identification numbers above the data points correspond to those in Table 1. The colors mark objects that could stem from the GC (red) or from the outer disk (blue), see Fig. A.1.

4.1. Possible origin in the Galactic center

Only three program stars have galactocentric radii at plane intersection that are smaller than 1 kpc and may thus stem from the GC: S5-HVS 1, B576, and B598. These three are also among the top four with the highest ejection velocities, with S5-HVS 1 clearly standing out with vej = 1810 ± 60 km s−1. It is also the only object that is gravitationally unbound to the Milky Way. Within the error bars, our result for this object agrees with that of Koposov et al. (2020), which is expected because we used the same input for the kinematic investigation, except for updated proper motions, and the latter have not changed significantly between DR2 and EDR3. The conclusions of Koposov et al. (2020) are therefore still valid and S5-HVS 1 can be considered as evidence for the Hills mechanism. Changes in proper motions for the other two objects in this subgroup, B576 and B598, are also negligible, which is why the results reported by Kreuzer et al. (2020) are basically confirmed here. However, we note that the nature of these two stars is not yet clear1.

Interestingly, the ejection velocities of all program stars are lower than half of the ejection velocity of S5-HVS 1. Kreuzer et al. (2020) argued that HVS 22 (Gaia EDR33897063727354575488), which is not part of the current sample because its origin is still not constrained at all, could be similarly extreme, but our reanalysis based on EDR3 proper motions led to a substantially lower ejection velocity of 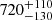720 − 130 + 110 $ 720^{+110}_{-130} $ km s−1 instead of 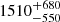1510 − 550 + 680 $ 1510^{+680}_{-550} $ km s−1, demonstrating that S5-HVS 1 is a truly exceptional case.

4.2. Origin in the Galactic disk

This group, which represents the vast majority of the program stars, contains objects that have past trajectories that unambiguously indicate an origin in the Galactic disk. A possible but unlikely exception is B537, which is also included in this group although its 2σ plane-crossing contour covers the GC. For this particular target, the change in proper motions from DR2 to EDR3 significantly affects the inferred place of origin, see Fig. 1, as well as the deduced ejection velocity, 750 ± 60 km s−1 instead of 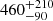460 − 90 + 210 $ 460^{+210}_{-90} $ km s−1, making it the target with the second highest ejection velocity in the entire sample. Although slightly less extreme in terms of ejection velocity ( 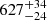627 − 24 + 34 $ 627^{+34}_{-24} $ km s−1), HVS 5 is certainly one of the most interesting targets because it is, on the one hand, clearly gravitationally unbound to the Milky Way, and on the other hand, its place of origin is now so precisely constrained to lie in the current solar neighborhood that a possible origin in the GC, as statistically favored by Brown et al. (2018), can be definitely ruled out. LAMOST HVS 1 and LAMOST HVS 4 are two further examples for such so-called hyper-runaway stars. For the former, we note that our revised analysis solves the difference between stellar age and flight time as reported by Hattori et al. (2019). Interestingly, the object for which the hyper-runaway class was originally coined, HD 271791, no longer qualifies as member because it is clearly bound to the Milky Way. The same applies to HIP 60350. Whether LAMOST HVS 2, J0136+2425, and HVS 8 are hyper-runaway stars depends on the choice of the applied Galactic mass model. The higher precision of Gaia EDR3 also allows us to strengthen our previous argument that the well-studied MS disk-runaway star PG 1610+062 is a serious challenge for classical ejection scenarios (Irrgang et al. 2019).

4.3. Possible origin in the outer rim of the Galactic disk

It is intriguing that a group of five stars (HVS 6, B481, B434, HVS 7, and B711) appears to separate itself from the others with respect to the galactocentric radius at plane intersection rp, see Fig. 2. The distribution of the most likely value for rp is more or less continuous up to ∼15 kpc, a number that fairly well coincides with the observed dimension of the spiral arms (Hou & Han 2014), then there is a gap of about 6 kpc before another group of runaway stars appears. Moreover, it is interesting to note that the ejection velocities of four of the five outer-rim stars are higher than those of most of the objects that are classified as disk-runaway stars in Table 1. Although based on low-number statistics and data points with relatively large error bars, this observation might indicate a distinct population of runaway stars with regard to spatial origin and ejection mechanism. Overdensities in MS star counts in form of concentric rings around the GC with radii of at least 25 kpc have been observed (see Xu et al. 2015, and references therein), which could be the origin of the five targets discussed in this paragraph. The same scenario, that is, the accretion of small satellite galaxies, has been suggested as possible explanation for the presence of the rings (Xu et al. 2015) and high-velocity runaway stars (Abadi et al. 2009). Our results may not only indicate that this mechanism is in fact operating, but is also able to produce HVSs because HVS 6 is unbound to the Milky Way while B481 and HVS 7 might be.

5. Summary and conclusion

Based on partly new spectrophotometric distances and the unprecedented precision of proper motions from Gaia EDR3, we have revisited the kinematics of 30 of the most extreme blue runaway candidates known to date in order to derive their ejection velocity from and their spatial origin within the Galactic disk. In addition to S5-HVS 1, which can still be considered as evidence for the ejection of stars from the GC through the Hills mechanism, there are only two other targets, B576 and B598, for which an origin in the GC is likely, provided that their stellar nature is confirmed by future analyses of currently unavailable high-quality spectra. For a fourth object, B537, the place of origin is still poorly constrained, therefore we cannot rule out a GC origin.

Despite these four stars, Gaia EDR3 corroborates the trend that most of the former Hills candidates turn out to be extreme runaway stars from the Galactic disk when their kinematic properties are sufficiently known. This particularly applies to the gravitationally unbound stars HVS 5 and HVS 6 here, for which the GC no longer is a valid birth place. Moreover, all program stars have such high ejection velocities that they considerably differ from the classical scenarios for an ejection from the Galactic disk, that is, the BSS and the DES. This strengthens the idea that mechanisms that involve dynamical encounters with very massive stars or intermediate-mass black holes are responsible for the majority of the most extreme runaway stars. The latter option is particularly interesting because no intermediate-mass black hole is currently known in the Galactic disk (Greene et al. 2020). The inferred spatial origins of extreme disk-runaway stars may give useful indications of where to search for them.

Five stars in the sample have galactocentric radii at disk intersection that are larger than 21 kpc, which implies that their birth places are probably not related to the spiral arms but to the outer Galactic rings. The ejection velocities of these five stars are also mostly higher than those of the inner disk runaways. Because high-velocity runaway stars and Galactic rings were suggested to result from the accretion of small satellite galaxies, this finding may be taken as another indication for the variety of mechanisms that produce runaway stars.

1

Kreuzer et al. (2020) argued that B576 is probably a blue horizontal branch star, but an MS nature could not be ruled out. B598 was speculated to be the progenitor of an extremely low mass white dwarf, but an MS nature was again a viable option. Although still not very precise, the parallaxes from EDR3 keep favoring the blue-horizontal-branch scenario for B576, but now at least tend to prefer an MS scenario for B598. If the latter were indeed an MS star, it had to be rejuvenated in the course of its evolution to reconcile its inferred stellar age (5 ± 1 Myr) with its flight time (50 ± 5 Myr), and it may therefore be a blue straggler.

Acknowledgments

We thank Adrian M. Price-Whelan for a very constructive referee report. A.I. and U.H. acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) through grants IR190/1-1, HE1356/70-1, and HE1356/71-1. R.R. has received funding from the postdoctoral fellowship program Beatriu de Pinós, funded by the Secretary of Universities and Research (Government of Catalonia) and by the Horizon 2020 program of research and innovation of the European Union under the Maria Skłodowska-Curie grant agreement No 801370. We thank John E. Davis for the development of the SLXFIG module used to prepare the figures in this Letter. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 067.D-0010(A), 088.A-9003(A), 088.D-0064(A), 091.D-0061(A), 093.D-0302(A), 282.D-5065(A), and 383.D-0909(A). Based on observations made with the Nordic Optical Telescope, operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences.

References

  1. Abadi, M. G., Navarro, J. F., & Steinmetz, M. 2009, ApJ, 691, L63 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bergemann, M., Sesar, B., Cohen, J. G., et al. 2018, Nature, 555, 334 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blaauw, A. 1961, Bull. Astron. Inst. Neth., 15, 265 [NASA ADS] [Google Scholar]
  4. Boubert, D., Guillochon, J., Hawkins, K., et al. 2018, MNRAS, 479, 2789 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bromley, B. C., Kenyon, S. J., Brown, W. R., & Geller, M. J. 2009, ApJ, 706, 925 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brown, W. R. 2015, ARA&A, 53, 15 [Google Scholar]
  7. Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2005, ApJ, 622, L33 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brown, W. R., Geller, M. J., & Kenyon, S. J. 2014, ApJ, 787, 89 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brown, W. R., Lattanzi, M. G., Kenyon, S. J., & Geller, M. J. 2018, ApJ, 866, 39 [NASA ADS] [CrossRef] [Google Scholar]
  10. Buckner, A. S. M., & Froebrich, D. 2014, MNRAS, 444, 290 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 534 [CrossRef] [Google Scholar]
  13. Edelmann, H., Napiwotzki, R., Heber, U., Christlieb, N., & Reimers, D. 2005, ApJ, 634, L181 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Evans, F. A., Renzo, M., & Rossi, E. M. 2020, MNRAS, 497, 5344 [Google Scholar]
  16. Feast, M. W., Menzies, J. W., Matsunaga, N., & Whitelock, P. A. 2014, Nature, 509, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Fragione, G., & Gualandris, A. 2019, MNRAS, 489, 4543 [Google Scholar]
  18. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202039657 [Google Scholar]
  21. Georgy, C., Ekström, S., Granada, A., et al. 2013, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Greene, J. E., Strader, J., & Ho, L. C. 2020, ARA&A, 58, 257 [CrossRef] [Google Scholar]
  23. Gvaramadze, V. V. 2009, MNRAS, 395, L85 [NASA ADS] [Google Scholar]
  24. Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2009, MNRAS, 396, 570 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hattori, K., Valluri, M., Castro, N., et al. 2019, ApJ, 873, 116 [NASA ADS] [CrossRef] [Google Scholar]
  26. Heber, U., Edelmann, H., Napiwotzki, R., Altmann, M., & Scholz, R.-D. 2008, A&A, 483, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Heber, U., Irrgang, A., & Schaffenroth, J. 2018, Open Astron., 27, 35 [Google Scholar]
  28. Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
  29. Hirsch, H. A., Heber, U., O’Toole, S. J., & Bresolin, F. 2005, A&A, 444, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Hou, L. G., & Han, J. L. 2014, A&A, 569, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Huang, Y., Liu, X. W., Zhang, H. W., et al. 2017, ApJ, 847, L9 [NASA ADS] [CrossRef] [Google Scholar]
  32. Irrgang, A., Przybilla, N., Heber, U., Nieva, M. F., & Schuh, S. 2010, ApJ, 711, 138 [NASA ADS] [CrossRef] [Google Scholar]
  33. Irrgang, A., Wilcox, B., Tucker, E., & Schiefelbein, L. 2013, A&A, 549, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Irrgang, A., Przybilla, N., Heber, U., et al. 2014, A&A, 565, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Irrgang, A., Kreuzer, S., & Heber, U. 2018a, A&A, 620, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Irrgang, A., Kreuzer, S., Heber, U., & Brown, W. 2018b, A&A, 615, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Irrgang, A., Geier, S., Heber, U., Kupfer, T., & Fürst, F. 2019, A&A, 628, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
  39. Kenyon, S. J., Bromley, B. C., Brown, W. R., & Geller, M. J. 2014, ApJ, 793, 122 [NASA ADS] [CrossRef] [Google Scholar]
  40. Koposov, S. E., Boubert, D., Li, T. S., et al. 2020, MNRAS, 491, 2465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Kreuzer, S., Irrgang, A., & Heber, U. 2020, A&A, 637, A53 [CrossRef] [EDP Sciences] [Google Scholar]
  42. Li, Y.-B., Luo, A.-L., Zhao, G., et al. 2018, AJ, 156, 87 [NASA ADS] [CrossRef] [Google Scholar]
  43. Li, C., Zhao, G., Jia, Y., et al. 2019, ApJ, 871, 208 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202039709 [Google Scholar]
  45. Perets, H. B., & Šubr, L. 2012, ApJ, 751, 133 [NASA ADS] [CrossRef] [Google Scholar]
  46. Poveda, A., Ruiz, J., & Allen, C. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 86 [Google Scholar]
  47. Price-Whelan, A. M., Johnston, K. V., Sheffield, A. A., Laporte, C. F. P., & Sesar, B. 2015, MNRAS, 452, 676 [NASA ADS] [CrossRef] [Google Scholar]
  48. Przybilla, N., Fernanda Nieva, M., Heber, U., & Butler, K. 2008, ApJ, 684, L103 [Google Scholar]
  49. Raddi, R., Irrgang, A., Heber, U., Schneider, D., & Kreuzer, S. 2021, A&A, 645, A108 [EDP Sciences] [Google Scholar]
  50. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
  51. Sharp, R., Saunders, W., Smith, G., et al. 2006, in SPIE Conf. Ser., eds. I. S. McLean, & M. Iye, 6269, 62690G [Google Scholar]
  52. Sheinis, A. I., Bolte, M., Epps, H. W., et al. 2002, PASP, 114, 851 [NASA ADS] [CrossRef] [Google Scholar]
  53. Silva, M. D. V., & Napiwotzki, R. 2011, MNRAS, 411, 2596 [NASA ADS] [CrossRef] [Google Scholar]
  54. Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
  55. Tauris, T. M. 2015, MNRAS, 448, L6 [Google Scholar]
  56. Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [NASA ADS] [CrossRef] [Google Scholar]
  57. Tillich, A., Przybilla, N., Scholz, R. D., & Heber, U. 2009, A&A, 507, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Xu, Y., Newberg, H. J., Carlin, J. L., et al. 2015, ApJ, 801, 105 [NASA ADS] [CrossRef] [Google Scholar]
  59. Zheng, Z., Carlin, J. L., Beers, T. C., et al. 2014, ApJ, 785, L23 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional tables and figure

thumbnail Fig. A.1.

Inferred spatial origin within the Galactic plane for all program stars. The stars are arranged in the same order as in Table 1, that is, with decreasing ejection velocity starting from the top left panel. As in Fig. 1, the most likely plane-crossing point is marked by a black cross, and the shaded areas visualize the corresponding 1σ (light red) and 2σ (light blue) contours. Note the different scales: Circles centered at the GC (black plus sign) with radii of 1 kpc (dotted black line), 8.3 kpc (solar circle; dashed red line), and 25 kpc (solid blue line) are shown for reference, when appropriate. The current position of the Sun (red square) is also marked.

Table A.1.

Atmospheric and stellar parameters of the program stars.

Table A.2.

Kinematic parameters of the program stars for Galactic mass model I of Irrgang et al. (2013).

All Tables

Table 1.

Ejection velocity, galactocentric radius at plane intersection, and stellar mass of the program stars.

In the text
Table A.1.

Atmospheric and stellar parameters of the program stars.

In the text
Table A.2.

Kinematic parameters of the program stars for Galactic mass model I of Irrgang et al. (2013).

In the text

All Figures

thumbnail Fig. 1.

Inferred spatial origin within the Galactic plane for five selected objects (upper row; see Fig. A.1 for all program stars). The most likely plane-crossing point is marked by a black cross, while the shaded areas visualize the corresponding 1σ (light red) and 2σ (light blue) contours. Circles centered at the GC (black plus sign) with radii of 1 kpc (dotted black line), 8.3 kpc (solar circle; dashed red line), and 25 kpc (solid blue line) are shown for reference. The galactocentric coordinate system is Cartesian and right-handed, with the Sun (red square) on the negative x-axis and the z-axis pointing to the Galactic north pole. The panels in the lower row show the same, except that proper motions from Gaia DR2 are used as input, demonstrating the improved precision of EDR3.
In the text
thumbnail Fig. 2.

Ejection velocity (relative to the rotating Galactic disk) vs. galactocentric radius at plane intersection for all program stars except S5-HVS 1, which is beyond the ordinate scale. Error bars are 1σ confidence intervals. The identification numbers above the data points correspond to those in Table 1. The colors mark objects that could stem from the GC (red) or from the outer disk (blue), see Fig. A.1.
In the text
thumbnail Fig. A.1.

Inferred spatial origin within the Galactic plane for all program stars. The stars are arranged in the same order as in Table 1, that is, with decreasing ejection velocity starting from the top left panel. As in Fig. 1, the most likely plane-crossing point is marked by a black cross, and the shaded areas visualize the corresponding 1σ (light red) and 2σ (light blue) contours. Note the different scales: Circles centered at the GC (black plus sign) with radii of 1 kpc (dotted black line), 8.3 kpc (solar circle; dashed red line), and 25 kpc (solid blue line) are shown for reference, when appropriate. The current position of the Sun (red square) is also marked.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.