| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202039319 | |
| Published online | 13 January 2021 | |
Parking planets in circumbinary discs
1
Institut für Astronomie und Astrophysik, Universität Tübingen,
Auf der Morgenstelle 10
72076, Germany
e-mail: anna.penzlin@uni-tuebingen.de
2
Astronomy Unit, School of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK
Received:
1
September
2020
Accepted:
5
December
2020
The Kepler space mission has discovered about a dozen planets orbiting around binary stars systems. Most of these circumbinary planets lie near their instability boundaries, at about three to five binary separations. Past attempts to match these final locations through an inward migration process were only shown to be successful for the Kepler-16 system. Here, we study ten circumbinary systems and attempt to match the final parking locations and orbital parameters of the planets with a disc-driven migration scenario. We performed 2D locally isothermal hydrodynamical simulations of circumbinary discs with embedded planets and followed their migration evolution using different values for the disc viscosity and aspect ratio. We found that for the six systems with intermediate binary eccentricities (0.1 ≤ ebin ≤ 0.21), the final planetary orbits matched the observations closely for a single set of disc parameters, specifically, a disc viscosity of α = 10−4 and an aspect ratio of H∕r ~ 0.04. For these systems the planet masses are large enough to open at least a partial gap in their discs as they approach the binary, forcing the discs to become circularised and allowing for further migration towards the binary – ultimately leading to a good agreement with the observed planetary orbital parameters. For systems with very small or large binary eccentricities, the match was not as good as the very eccentric discs and the large inner cavities in these cases prevented close-in planet migration. In test simulations with higher than observed planet masses, a better agreement was found for those systems. The good agreement for six out of the ten modelled systems, where the relative difference between observed and simulated final planet orbit is ≤10% strongly supports the idea that planet migration in the disc brought the planets to their present locations.
Key words: planets and satellites: dynamical evolution and stability / binaries: general / planet-disk interactions
© ESO 2021
1 Introduction
The first circumbinary planet (CBP) discovered by the Kepler space mission was Kepler-16b (Doyle et al. 2011). Since then, about a dozen more circumbinary p-type planets have been discovered (see overview in Martin 2019 and Table 1). In 2012, multiple CBPs around Kepler-47 were detected (Orosz et al. 2012b, 2019). Some time later, the Planet Hunters project discovered a planet in the quadruple star system PH1b, also named Kepler-64b (Schwamb et al. 2013). The most recent discovery is TOI-1338b by the TESS mission (Kostov et al. 2020).
All of the above systems, and most of the discovered innermost CBPs, share a set of comparable properties in their orbits. Firstly, they are in good alignment with the binary’s orbital plane, hinting at their formation in a protoplanetary disc that was aligned with the binary. Secondly, the planetary orbits (the semi-major axes) are all near 3.5 binary separations, which is close to the instability limit (Dvorak 1986). Additionally, the eccentricities of the planetary orbits are small. All of this points to a common formation mechanism for most observed CBPs in aligned, coplanar discs.
Concerning the general stability of circumbinary discs it has been suggested that in addition to the coplanar situation, the perpendicular case is also a stable binary-disc configuration (Martin & Lubow 2017; Lubow & Martin 2018; Cuello & Giuppone 2019). However, no planets have been observed in perpendicular orbits yet due to observational constraints.
The in situ formation of planets at such close orbits around binaries is an unlikely scenario. Tidal forces close to the binary cause perturbations in the inner disc that inhibit planetesimal and dust accretion (Paardekooper et al. 2012; Silsbee & Rafikov 2015; Meschiari 2012), while the turbulence induced by hydrodynamical parametric instabilities can dramatically reduce pebble accretion efficiencies (Pierens et al. 2020). A more likely formation scenario is based on planet formation in the outer disc and subsequent disc-driven migration to the observed close orbits (Pierens & Nelson 2008; Bromley & Kenyon 2015). However, this scenario does not in itself explain the particular stopping positions of most CBPs.
Several studies have already been dedicated to the investigation of planetary migration in circumbinary discs (Pierens & Nelson 2008, 2013; Kley & Haghighipour 2014, 2015; Kley et al. 2019). Due to gravitational torques, the binary clears out an inner cavity and, hence, planet migration is halted at the inner edge of the disc at a location close to the binary, but the findings does not yet match the observations in most cases studied. Numerical simulations have shown that the shape of the inner disc and, hence, the final orbital parameters of the given planet depend on disc parameters such as viscosity and scale height, and the mass ratio and eccentricity of the binary (Mutter et al. 2017; Thun & Kley 2018).
Two recent studies by Mutter et al. (2017) and Kley et al. (2019) were able to reproduce the observed CBP orbits for Kepler-16b and Kepler-38b. In the current work, we plan to find a common formation scenario for most observed CBPs using a sample of ten planets, as described in Table 1.
To limitthe parameter space, we consider discs characterised by properties that are in agreement with the low α-viscosity that was observed in the D-sharp survey (Dullemond et al. 2018) and scale heights comparable to the results of Kley et al. (2019). There, we also showed that the geometry of the disc, specifically the eccentricity of the inner cavity, can be influenced by an embedded planet. Gap-opening planets typically circularise the disc, while lighter planets or discs with higher viscosity exhibit eccentric holes. We will explore the effect of a wider disc parameter range on the disc architecture in a future study.
To study the parking of planets, we performed numerical hydrodynamical simulations of circumbinary discs using three different parameter sets for the disc physics in order to find a likely combination of viscosity and scale height that results in disc shapes that allow for suitable stopping locations of the planets. Hence, this study extends the work of Pierens & Nelson (2013), where the authors looked at a subset of three systems. The binary and planet parameters used in our simulations are those given by the observations, as presented in Table 1.
In Sect. 2, the adopted model assumptions and initial conditions are defined. Section 3 shows the results of the simulations, where we discuss the influence of viscosity on the planet migration in general and show the effects of different sets of disc parameters on the final orbits of the observed Kepler planets. We discuss the difficulties related to reaching thefinal orbit and the limitations of our model and we summarise our findings in Sect. 4.
Observed circumbinary parameters.
2 Simulations
We used the Pluto Code (Mignone et al. 2007) in the GPU version by Daniel Thun (Thun et al. 2017) to simulate 2D hydrodynamic disc models. We chose a cylindrical grid stretching from 1 to 40 abin with 684 logarithmically spaced radial grid cells and 584 azimuthal cells. The general design of the simulation follows the setup of Thun & Kley (2018). We modelled nine of the known Kepler binary planet systems, in addition to TOI-1338, for which we used the observed binary and planet properties, as displayed in Table 1.
For the surface density profile, we use Σ ∝ R−3∕2 with a disc mass of Md = 0.01 Mbin. To speed up the equilibration process for the disc, we initialised the surface density with an inner cavity reaching to about 2.5 abin. Inside of this region, the disc is expected to be cleared due to the action of the binary.
All discs are evolved initially for >25 000 binary orbits, Tbin, without a planet being present, depending on the specific system setup. A typical time scale for a locally isothermal protoplanetary disc around a binary to reach a convergent quasi-equilibrium state is a few 10 000 Tbin. Hence, in this work, we use locally isothermal models as they converge faster than a viscously heated radiative disc, which can require up to 200 000 Tbin, but they eventually reach comparable final states with a pressure profile that is consistent with an unflared inner disc with a constant aspect ratio between 0.05 and 0.03, depending on the system; see Kley et al. (2019) for details. During this initialisation phase the binary is not influenced by the disc. As the final planetary orbits depend on disc properties, we simulated discs for the observed systems in Table 1 for different values of h and α. The viscously heated, radiative models in Kley et al. (2019) result in an unflared inner disc. Therefore, we chose a constant aspect ratio of h = H∕R. Based on our previous experience (Thun & Kley 2018; Kley et al. 2019), we chose the following three combinations: h = 0.04, α = 10−3;h = 0.04, α = 10−4; and h = 0.03, α = 10−4. It was only for Kepler-38 that we additionally used h = 0.05.
After the disc reached a convergent behaviour, we added a planet with an observed mass (see Table 1) in the outer disc that is a fewabin beyond the maximum of the surface density in the disc. In cases where only a upper planet-mass limit was observed, aswith Kepler-38, we used the observed upper limit. This might overestimate the actual mass of a planet, but it is still in agreement with the observations. Across the whole sample, the planet masses range from 0.05 Mjup to 0.38 Mjup. The disc exerts gravitational forces on the planet, which will then start migrating through the disc. The disc forces acting on the central binary star are also switched on at this point, but during the time span of the simulations, the binary elements do not change substantially.
3 Results
In this section, we present the results of our numerical studies of the systems quoted in Table 1. We first present the results for different viscosities on the specific system Kepler-35 and then we go on to concentrate on the complete set of systems. An overview of the disc shapes that resulted in planetary evolutions that matched best with the observations is given below in Sect. 3.2.
3.1 Influence of viscosity
To analyse in greater detail the impact of viscosity on the inner cavity, we present the results on the Kepler-35 system in more detail, starting with the disc structure without a planet and then the impact of the planet. The binary system Kepler-35 has a mass ratio that is close to unity, qbin = 0.91, and a relatively small eccentricity of ebin = 0.14, which puts the system on the lower branch of the bifurcation diagram in the precession period versus cavity size graph (Thun & Kley 2018). In Fig. 1, equilibrium discs with different α-values are displayed for a given scale height h = 0.04 to show howmuch the viscosity influences the disc and cavity structure. The cavity parameters are calculated as described in Thun et al. (2017), meaning that they correspond to the parameters of an ellipse fitted to the location where the azimuthally averaged density is 10% of the maximum density. The cavity and planet orbital parameters are calculated using Jacobi coordinates for the planet-binary system. The disc eccentricity decreases with decreasing viscosity, while the sharpness of the density maximum increases. As all observed planets reside in orbits with relatively low eccentricity, low eccentric cavities will be favourable for their formation, however the presence of the planet will also change the geometry of the disc, as discussed in Mutter et al. (2017) and Kley et al. (2019). Planets with orbits near the inner edge of the disc can circularise the cavity and disc. But high disc eccentricities, as they occur for binaries on circular andhigh eccentric orbits (Thun & Kley 2018), can hinder a planet from reaching this orbit. Therefore, lower viscosities leading to less eccentric discs are favourable in explaining planet migration into the observed orbits.
A planet with the observed mass of Kepler-35 (0.12 mjup) is embedded in the disc at an initial distance of 6 abin on a circular orbit and allowed to migrate in the disc. Initially, the embedded planet follows the eccentric gas flow in the disc which makes its orbit eccentric. Planets that do not open a gap in the disc remain embedded and are pushed back by the overdensity at the cavity (see Fig. 1) to a parking position on an eccentric orbit within the disc. This case is shown in the left panel of Fig. 2, where the high disc viscosity does not allow for a planetary gap to be cleared.
However, if planet and disc parameters are such that the planet can open a gap (high planet mass and low disc viscosity and temperature as discussed in Crida et al. 2006), the disc goes on to be circularised and it can pass through the cavity overdensity to a more circular orbit inside of the cavity, as shown in Mutter et al. (2017) and Kley et al. (2019). Kepler-35b and all other observed planets have masses much lower than a Jupiter mass which puts constraints on the disc parameters that are linked to gap opening, such as the viscosity and aspect ratio.
In Fig. 2, the final position and orbit of the planet in these discs is displayed. The gradual deepening of the planetary gap is evident between α = 10−2 to α = 10−3. Even though the gap in the middle panel is only partially open, it has already begun leading to a reduction in the orbital eccentricity of the cavity and planet. However, in both cases the planet is still too firmly embedded in the disc and influenced by its dynamics, such that the orbit of the planet and the cavity are fully aligned and precess at the same rate, as was also observed in Kley et al. (2019) and Penzlin et al. (2019). For an even lower viscosity of α = 10−4 (right panel), the planet opens a deeper gap that directly erases the disc-driven planet dynamics and allows the planet to reach a stable orbit inside the cavity. Therefore, a low disc viscosity tends to have a positive effect on disc structure and planet migration because this favours final planet orbits with low eccentricity, as observed in many systems. Colder and less viscous discs have, on average, a less eccentric cavity. This aids the passage of the planet through the inner cavity.
 |
Fig. 1 Surface density for discs around a Kepler-35 like binary for different α-values and an aspect ratio of 0.04. The dashed white line denotes a fitted ellipse (Thun & Kley 2018) which marks the edge of the inner cavity with the parameters displayed in the top left corner. |
 |
Fig. 2 Discs for a Kepler-35 like system with different α-values with a planet embedded for 29 900 binary orbits. The dashed white line marks the edge of the inner cavity with the parameters displayed in the top right corner. The light blue line marks the orbits of the planet with the parameter displayed in the top left corner. |
 |
Fig. 3 Surface density of eight modelled Kepler circumbinary systems, listed in Table 1, before the planet was embedded. The chosen h and α correspond to those models that eventually could reproduce the observed final planetary orbits best. The white dashed ellipse marks the inner cavity edge with the parameters shown in the top left. |
3.2 Kepler systems
After having demonstrated the main impact of the viscosity on the disc structure and outcome of the planet orbit for Kepler-35, we now present the results for the other systems. Instead of presenting results on the general impact of disc and binary parameters on the cavity dynamics, here we focus solely on that parameter set for which the simulations most successfully reproduced the observed planetary orbits and which is reasonable for a protoplanetary disc. We defer our analysis of a broader parameter range to a future work.
In Fig. 3, we display the disc structure for models that could most successfully reproduce the planetary orbits. The discs are shown at a time before the planet was embedded. As suggested by the results for Kepler-35, discs with low viscosity and also small aspect ratios are favourable in producing the observed orbits, as this combination of disc parameters ensures that the planet opens a gap in its orbit, which results in a more circular disc cavity that allows the planet to migrate closer to the binary. In the top row, we give examples where the final planet orbits matched the observed locations well, while in the lower panel, we show where the agreement was not as good. Indeed, the main difference between the ‘successful’ top row and the ‘unsuccessful’ bottom row is the cavity’s eccentricity. While the discs in the top row are typically more circular even without any planet, the bottom row discs are noticeably eccentric even for low α-values, due to the low (Kepler-47, Kepler-413, and Kepler-453) or high (Kepler-34) binary eccentricities.
After the discs reached a quasi-equilibrium structure, the planets with the observed masses were embedded in the disc at a distance ≥6abin. Their subsequent migration histories are illustrated in Fig. 4 for those six cases where the match between simulated and observed location was closest. The systems with an intermediate value of ebin show good convergence to the observed orbits for an α-value of 10−4 and an aspect ratio of 0.04 to 0.03. We find here that a low viscosity of α = 10−4 is needed for the discs to allow the migration into the observed orbits. For Kepler-38b, we performed an additional run with a higher aspect ratio, h = 0.05, because Kepler-38b is the most massive planet of the sample and, as shown in Fig. 4, it reaches just the success-limit with α = 10−3, h = 0.05 and is expected to cross the dashed line after 120 000Tbin. With this slightly higher pressure the density maximum of the disc is reduced leading to a reduce positive torque of the disc onto the planet, allowing it to park closer to the binary than with lower temperatures. Another important factor for this single planet is its high mass. As shown in Table 2, all other planet orbits stay further out for α = 10−3, h = 0.04 than Kepler-38b. Thereby, Kepler-16, -35, -38, -64, TOI-1338, and also the recently discovered Kepler-1661b (Socia et al. 2020), can be simulated with a single parameter set of α ~10−4, h = 0.04 to produce a final orbit with an accuracy of 0.1 ap,obs, as shown in Fig. 4. As can also be seen in Fig. 4, the initial migration in the outer disc is typically very fast because the planets are fully embedded in the disc and have not yet opened any gap. The systems Kepler-1661, -64, and TOI-1338b have a comparable migration rate as their planet-to-binary-mass ratios are very similar. When they reach the high density ring at around 5 abin or 1.5 aobs, the migration is slowed down. They are influenced by the high density inner disc region and the binary and subsequently experience some variations in their semi-major axis and eccentricity evolutions. The first migration reversal occurs when they are getting close to a semi-major axis of about 4 abin.
The two systems Kepler-16 and -38 show initially a very fast inward migration. As they have a higher planet-binary mass ratio than the other planets, they would – in the embedded type-I migration phase – exhibit faster inward migration (Kley & Nelson 2012). Additionally, being in the Saturn mass range they are subject to rapid type-III migration (Masset & Papaloizou 2003). In the later evolutionary phase, they begin to circularise the disc and can migrate inwards smoothly. This is especially evident in the unique model of Kepler-38 with high viscosity where the disc eccentricity drops from ecav ≈ 0.37 without a planet to ecav ≈ 0.09 with an embedded planet.
Eventually all of them reach an orbit close to the inner cavity edge and stop their inward migration there because the migration torques vanish due to the changing disc structure. The cavity acts in the same way as a classic planet trap where a positive density gradient can stop a planet (Masset et al. 2006). This can be seen in the top row of Fig. 5, where we display the final surface density distribution for the previously shown discs, now with embedded planets, after their migration has stopped. Displayed are the orbital elements of the disc cavity and the planet, in the top left and right corners, respectively. As discussed above, the ‘successful’ evolutions have a final disc structure with small eccentricity, reduced by the presence of the planet. The planets typically reach a final destination with nearly circular orbits at a distance of approximately 3.4 to 3.6 abin, as shown in top row of Fig. 5
As already shown in Thun & Kley (2018), binaries with very low and high eccentricities form highly eccentric inner cavities, as shown in Fig. 3 (bottom row). The planet has to overcome the density bulk at the cavity. This is more difficult for more eccentric cavities that have a higher peak density and, therefore, for the high and low ebin systems Kepler-34, -413, -435, and -47. Figure 5 shows the best models of these system with ‘non-successful’ evolutions in the bottom row. In the top row, the planets reach a final position close to the observed one, whereas in the bottom row, the planets stall further out. In comparing the top systems the lower systems, the discs clearly show a different structure, namely, one in which the planets around the high and low eccentric binaries are more embedded in the disc and remain at larger distances from the binary, also exhibiting a more eccentric orbit. In Fig. 5, the blue and white ellipses in the bottom row show the same orientation, which indicates that the disc-driven planet orbit has become fully aligned with the eccentric cavity. This is shown for Kepler-413 in Fig. 6, the final pericentres of planet and disc orbits are aligned and the ellipses precess at the same rate, as also seen in Kley & Haghighipour (2015), Kley et al. (2019) and Penzlin et al. (2019). There are no clear signs of dynamical interaction (e.g. an oscillation of Δω) visible. However, the determination of the elements of the disc is quite noisy. All the final orbits are aligned with the disc either embedded within the disc or located at the inner cavity edge.
The orbital evolution of the embedded planets in these “unsuccessful” systems (shown in Fig. 7) starts with the same fast initial migration as in the previous cases, but then the inward migration is stalled by the disc too far out. Kepler-34, being the most eccentric binary with an eccentricity of 0.52, produces an eccentric disc with a large cavity and subsequently a planet on a large orbit.
Kepler-453b has the furthest observed orbit of all CBPs (normalised to the binary separation) around low eccentric binaries and it almost reaches the required orbit. In this case, the planet-to-binary-mass ratio is very small, such that the planet is not able to alter the disc structure considerably with the given disc parameters. Kepler-453bhas a four times smaller planet-to-binary-mass ratio than Kepler-413b, which is observed to be 0.75 abin further in. This hints, in a qualitative sense, at the importance of the planet mass for reaching orbits closer to the binary since the dimensions of these systems are comparable. We explore the effect of mass in detail in the next section using models that only shift the planet masses. However, in these simulations, both are stopped by the disc rather than reach an orbit inside the inner cavity. The planets’ distant final location for systems with nearly circular binaries and low disc viscosity is not necessarily caused by low planet masses because Kepler-413b has a relatively high mass, with 0.21 mjup.
In order to test the hypothesis that the ability of the planet to open a gap is crucial for its detachment from the disc and to reach the observed low eccentric orbits, we ran additional simulations for the low and high ebin systems with planets of two and ten times the observed best-fit mass. Due to the transit observation method, the uncertainty of the observed masses is high and the confidence interval reaches masses of around a factor of two of the best-fit model. For the ten-times heavier model, we chose to vastly overestimate the mass of the planet for the sake of the theoretical exploration and no longer work within the constraints of the observation. We compare this to all the other models in the study in the following subsection.
 |
Fig. 4 Migration history for all planets that get close to the observed orbit. The semi-major axis and eccentricity are scaled with the observed aobs and eobs, see Table 1. The grey area marks the success criterion, where the final parking position of the planet deviates by no more than 10% from the observed value, that is, Δap ∕ap,obs ≤ 10%. For the discs, we chose α = 10−4 and h = 0.04, plus one additional model for Kepler-38 using the stated values. |
Check-table indicating if a simulation for a given viscous α-value, aspect ratio, h, and planet mass reached the observed orbit.
 |
Fig. 5 Discs and planets of eight of the considered Kepler systems listed in Table 1 and shown in Fig. 3, here shown with the embedded planets. The quoted times are measured after insertion of the planets. The chosen aspect ratio, h, and viscosity, α, correspond to those models that most successfully could reproduce the observed planet orbits (see Table 2 below). The white dashed line marks the inner cavity edge and the light blue line the planet orbit. Top row: planets that correspond to our success criteria of reaching the observed orbit by ± 0.1aobs, while lower row: systems that did not reach the observed orbit, due to their eccentric discs. |
 |
Fig. 6 Argument of pericentre of the elliptic cavity and planet orbit for Kepler-413. The standard deviation of Δω = |ωp − ωcav| is 5.31 degree. |
 |
Fig. 7 Migration history for all planets that do not get close enough to the observed orbit. Semi-major axis and eccentricity are scaled with the observed aobs and eobs. The grey area marks the success criterion. |
3.3 Model results and best-fit parameter set
All simulation results are summarised in Table 2, where we make note whether a simulation has successfully reproduced the observational parameter of a given planet. The systems are sorted by the eccentricity of the host binary. With the exception of the heaviest planet, Kepler-38b, the α = 10−3 environment is not sufficient to explain the observations. Just by reducing the viscosity to α = 10−4, we find that for six out of the ten systems, the final semi-major axis deviates by no more than 10% from the observed value; for more, see the grey shaded region in Fig. 4.
To understand the reasons for the unsuccessful simulations, we have to analyse the differences in the systems. The first three binary systems have ebin ≤ 0.05. The next six systems have 0.10 ≤ ebin ≤ 0.21, while the last system has ebin = 0.52. The results can be split into these three regimes.
For the nearly circular binaries, it is difficult to match the observations. However, by reducing the disc scale height and the viscosity to α = 10−4 and h = 0.03, the planets are able to all migrate further inwards as they are more easily able to clear more of their orbit. In these systems, the effect of a two-fold planet mass increase is comparable to the impact of lowering the disc aspect ratio by 0.01. With the ten-fold mass increase, a planet of 0.5 mjup in the Kepler-47 system can migrate to the observed position. The other heavy planets with a ten-fold mass increase will migrate towards a less eccentric and closer-in position than the observed location and may potentially reach unstable orbits.
The second regime of intermediate eccentric binaries can easily be simulated with the set of α = 10−4 and h = 0.04. This is a good indication that the conditions in the disc should be comparable to this parameter set. In our previous study (Kley et al. 2019), we showed that in a viscously heated disc, the inner disc scale height is unflared and close to h = 0.04. Recent studies, observationally in the D-sharp survey (Dullemond et al. 2018) and theoretically (Flock et al. 2020) suggest that viscosities are α ≤ 10−3, and therefore our choice of a low viscosity is reasonable. The well-matched final planet orbits can be taken as an additional indicator forlow viscosities in protoplanetary discs.
The single observation with very high binary eccentricity Kepler-34 is hard to reproduce. With an increase in planet mass, the correct semi-major axis of the planet could be reached, however the eccentricity is lowered to values below the observed one and it is already too low in a system with a reduced scale height.
4 Discussion and summary
In this work, we perform 2D hydrodynamical simulations of circumbinary discs with embedded planets to explain the orbits of the observed sample of circumbinary planets. One simplification of the model is to use a locally isothermal disc. In a previous work (Kley et al. 2019), we explored viscously heated, radiatively cooled discs. The results showed a plateauing aspect ratio at 0.03< h < 0.05 for the inner 15 abin. According to those results, we chose a constant aspect ratio in this range, as this produced a reasonable and well-defined test disc.
In contrast to previous studies, where the planets typically were parked at overly large distances from the binary, our simulations show that we can explain the planetary orbits in systems which have a binary eccentricity between 0.05 to 0.3 by applying a simple locally isothermal model with a parameter set of a viscous α = 10−4, and a scale height of H∕r = 0.04. Variations in the binary mass ratio do not change the results in any significant way (as also found in Thun & Kley 2018). For these systems with intermediate binary eccentricity, planet-to-binary-star-mass ratios between 4.6 × 10−5 (Kepler-1661) and 30 × 10−5 (Kepler-38) are sufficient to carve out planetary gaps, move independently of the disc, and settle to closer orbits. Additionally, the small viscosity circularises the disc even when there is no planet, which allows for tighter orbits as well. Using this parameter set (α = 10−4, h = 0.04), we can reproduce the observed orbits of 6 of 10 Kepler circumbinary planets with hydrodynamical simulations and obtain a much closer agreement to the observations for the other four systems than in previous studies.
It is useful to compare our findings to the standard gap opening criteria derived for planets emdedded in discs around single stars. The mass of a planet required to open a gap can be estimated by a thermal and a viscous criterion. The thermal criterion requires the Hill radius to exceed the local pressure scale height, while the viscous criterion requires the gravitational torque to exceed the viscous one. In terms of the aspect ratio, the visocity α and the mass ratio, qp = mp∕Mbin, they read (Bryden et al. 1999):
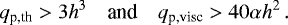 (1)
(1)
Up to factors of order unity, these values agree with other criteria (Crida et al. 2006; Ziampras et al. 2020).
For α = 10−4 and h = 0.04, we find qp,th ≈ 2 × 10−4 and qp,visc ≈ 6.4 × 10−6. While the viscous criterion is matched by all systems, the thermal one is only fulfilled clearly for Kepler-38b and marginally by Kepler-16b and Kepler-413b. This explains why a larger viscosity (α = 10−3) is still sufficient for the Kepler-38 system.
There have been a number of recent studies of the opening and structure of gaps attributed to the activity of planets around single stars (Crida et al. 2006; Duffell & MacFadyen 2013; Fung et al. 2014; Duffell & Dong 2015; Kanagawa et al. 2015, 2016). Given that circumbinary discs and planets become eccentric, planet-induced gap structures are likely to be different in this scenario. Undertaking a detailed study of this goes beyond the scope of this paper, but it would make an interesting topic for future work.
The systems that could not be matched that well were those with very small and large binary eccentricities. For both of these extreme cases, the inner cavity of the disc is most eccentric and the planets were not able to to ‘free’ themselves from the dynamical forcing of the disc given their masses are at most 0.2 Mjup. This might be due to the fact that for these eccentric discs higher planet masses are required to clear a gap. This is supported by simulations with artificially increased planet masses, where we observed orbital parameters in closer agreement with the observations. The close, eccentric orbit around the highly eccentric binary (Kepler-34) is still difficult to explain by this simple approach of planet migration within a disc because the presence of the disc damped the planet eccentricity below the observed value. The study of possible further (tidal) interactions following the dissipation of the disc, however, exceeds the scope of this work.
Even though the thermal mass is nearly reached by the planet for the low ebin Kepler-413 system, the final planet orbit is not in very good agreement with the observed one, which is probably due to the high disc eccentricity. In the other small ebin system Kepler-453, the planet has a very low mass and a relatively large orbit. So for this planet, it appears that the migration was halted by the disc earlier than for the comparable heavier planet in the low eccentricity binary (as in the case of Kepler-413b). Kepler-47 is the only observed multi-planet circumbinary system which may influence the migration.
The upper mass of close-in circumbinary planets in the observations is limited to ~ 0.4 Mjup. When we simulated the more massive planets, we observed that heavy planets migrate further in, so they might reach unstable orbits and suffer ejections, which is in agreement with Pierens & Nelson (2008).
The binary parameters may also change over time. However, to make a comparison with the existing systems, we kept them fixed in the initial disc simulation. As the binaries are close, 10 000 Tbin is less than 2000 yr. For the planetary evolution simulations, the binary orbit is also effected by the forces from the disc but changes in the binary parameters over this time frame are negligible, amounting to about 1% in 60 000 Tbin. The shrinkage of the binary orbit on longer time scales could be accounted for by starting the system at larger separations than observed today, but that would not be possible via direct hydrodynamical simulations and would lead to the same result eventually.
The reason why some of the systems are characterised by final orbits that remain too eccentric and too far out may also be the result of missing physics in the models. In our models, we neglected radiative transport vertically and within the disc’s plane and this could potentially reduce the disc eccentricity. We modelled the discs with 2D simulations but by moving to 3D, it might be possible to obtain better agreement for the systems because disc eccentricities and cavity sizes are different in 3D versus 2D. For example, in their 3D simulations, Pierens & Nelson (2018) found that the planet in the (difficult-to-match) system Kepler-413 indeed moved closer to the binary.
Possibly, multiple planets are present in some of the systems that are even slightly inclined, such that we see only one of the planets. In Penzlin et al. (2019), we showed that a secondary planet does not change the orbit of the first one significantly, hence, we did not include multi-planet simulations here.
It may also be possible to reduce the binary eccentricity through tidal interaction with the planet after the disc has been dispersed. Thereby, the low eccentric binaries may have been more eccentric during the planet formation phase and only lost the eccentricity after the planets reached stable orbits and were thus undisturbed by the outer disc (Zoppetti et al. 2019).
After all, the fact that all planets in systems where the circumbinary discs have an intermediate eccentricity could be matched well shows that the migration scenario of explaining short-period circumbinary planets is very likely to be valid. It is only those
systems with highly eccentric discs and large cavities that point towards missing physics or 3D effects to explain their properties.
Acknowledgements
A.P. was funded by grant KL 650/26 of the German Research Foundation (DFG). R.N. acknowledges support from STFC through the Consolidated Grants ST/M001202/1 and ST/P000592/1 and from the Leverhulme Trust through grant RPG-2018-418. The authors acknowledge support by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG. The plots in this paper were prepared using the Python library matplotlib (Hunter 2007).
References
- Bromley, B. C., & Kenyon, S. J. 2015, ApJ, 806, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Cuello, N., & Giuppone, C. A. 2019, A&A, 628, A119 [CrossRef] [EDP Sciences] [Google Scholar]
- Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Duffell, P. C., & Dong, R. 2015, ApJ, 802, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Duffell, P. C., & MacFadyen, A. I. 2013, ApJ, 769, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dvorak, R. 1986, A&A, 167, 379 [NASA ADS] [Google Scholar]
- Flock, M., Turner, N. J., Nelson, R. P., et al. 2020, ApJ, 897, 155 [CrossRef] [Google Scholar]
- Fung, J., Shi, J.-M., & Chiang, E. 2014, ApJ, 782, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2015, ApJ, 806, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2016, PASJ, 68, 43 [NASA ADS] [Google Scholar]
- Kley, W., & Haghighipour, N. 2014, A&A, 564, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Haghighipour, N. 2015, A&A, 581, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [Google Scholar]
- Kley, W., Thun, D., & Penzlin, A. B. T. 2019, A&A, 627, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostov, V. B., McCullough, P. R., Carter, J. A., et al. 2014, ApJ, 784, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kostov, V. B., Orosz, J. A., Feinstein, A. D., et al. 2020, AJ, 159, 253 [CrossRef] [Google Scholar]
- Lubow, S. H., & Martin, R. G. 2018, MNRAS, 473, 3733 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. V. 2019, MNRAS, 488, 3482 [CrossRef] [Google Scholar]
- Martin, R. G., & Lubow, S. H. 2017, ApJ, 835, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., & Papaloizou, J. C. B. 2003, ApJ, 588, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Meschiari, S. 2012, ApJ, 761, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mutter, M. M., Pierens, A., & Nelson, R. P. 2017, MNRAS, 469, 4504 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012a, ApJ, 758, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012b, Science, 337, 1511 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Orosz, J. A., Welsh, W. F., Haghighipour, N., et al. 2019, AJ, 157, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper,S.-J., Leinhardt, Z. M., Thébault, P., & Baruteau, C. 2012, ApJ, 754, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Penzlin, A. B. T., Ataiee, S., & Kley, W. 2019, A&A, 630, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Nelson, R. P. 2008, A&A, 483, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Nelson, R. P. 2013, A&A, 556, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Nelson, R. P. 2018, MNRAS, 477, 2547 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., McNally, C. P., & Nelson, R. P. 2020, MNRAS, 496, 2849 [CrossRef] [Google Scholar]
- Schwamb, M. E., Orosz, J. A., Carter, J. A., et al. 2013, ApJ, 768, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Silsbee, K., & Rafikov, R. R. 2015, ApJ, 808, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Socia, Q. J., Welsh, W. F., Orosz, J. A., et al. 2020, AJ, 159, 94 [CrossRef] [Google Scholar]
- Thun, D., & Kley, W. 2018, A&A, 616, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thun, D., Kley, W., & Picogna, G. 2017, A&A, 604, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, W. F., Orosz, J. A., Carter, J. A., et al. 2012, Nature, 481, 475 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Welsh, W. F., Orosz, J. A., Short, D. R., et al. 2015, ApJ, 809, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Ziampras, A., Ataiee, S., Kley, W., Dullemond, C. P., & Baruteau, C. 2020, A&A, 633, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoppetti, F. A., Beaugé, C., Leiva, A. M., & Folonier, H. 2019, A&A, 627, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Check-table indicating if a simulation for a given viscous α-value, aspect ratio, h, and planet mass reached the observed orbit.
All Figures
 |
Fig. 1 Surface density for discs around a Kepler-35 like binary for different α-values and an aspect ratio of 0.04. The dashed white line denotes a fitted ellipse (Thun & Kley 2018) which marks the edge of the inner cavity with the parameters displayed in the top left corner. |
| In the text | |
 |
Fig. 2 Discs for a Kepler-35 like system with different α-values with a planet embedded for 29 900 binary orbits. The dashed white line marks the edge of the inner cavity with the parameters displayed in the top right corner. The light blue line marks the orbits of the planet with the parameter displayed in the top left corner. |
| In the text | |
 |
Fig. 3 Surface density of eight modelled Kepler circumbinary systems, listed in Table 1, before the planet was embedded. The chosen h and α correspond to those models that eventually could reproduce the observed final planetary orbits best. The white dashed ellipse marks the inner cavity edge with the parameters shown in the top left. |
| In the text | |
 |
Fig. 4 Migration history for all planets that get close to the observed orbit. The semi-major axis and eccentricity are scaled with the observed aobs and eobs, see Table 1. The grey area marks the success criterion, where the final parking position of the planet deviates by no more than 10% from the observed value, that is, Δap ∕ap,obs ≤ 10%. For the discs, we chose α = 10−4 and h = 0.04, plus one additional model for Kepler-38 using the stated values. |
| In the text | |
 |
Fig. 5 Discs and planets of eight of the considered Kepler systems listed in Table 1 and shown in Fig. 3, here shown with the embedded planets. The quoted times are measured after insertion of the planets. The chosen aspect ratio, h, and viscosity, α, correspond to those models that most successfully could reproduce the observed planet orbits (see Table 2 below). The white dashed line marks the inner cavity edge and the light blue line the planet orbit. Top row: planets that correspond to our success criteria of reaching the observed orbit by ± 0.1aobs, while lower row: systems that did not reach the observed orbit, due to their eccentric discs. |
| In the text | |
 |
Fig. 6 Argument of pericentre of the elliptic cavity and planet orbit for Kepler-413. The standard deviation of Δω = |ωp − ωcav| is 5.31 degree. |
| In the text | |
 |
Fig. 7 Migration history for all planets that do not get close enough to the observed orbit. Semi-major axis and eccentricity are scaled with the observed aobs and eobs. The grey area marks the success criterion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


