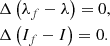| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 13 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202038946 | |
| Published online | 19 November 2020 | |
Nutation of the non-rigid Earth: Effect of the mass redistribution
1
Dept. of Sciences and Informatics, University Centre of Defence at the Spanish Air Force Academy, 30720 Santiago de la Ribera, Spain
e-mail: tomas.baenas@cud.upct.es
2
Dept. of Aerospace Engineering, University of León, 24071 León, Spain
3
Dept. of Applied Mathematics, University of Alicante, PO Box 99, 03080 Alicante, Spain
Received:
16
July
2020
Accepted:
14
September
2020
In this research, we computed the nutation of the figure axis for a non-rigid Earth model due to the mass redistribution resulting from the lunisolar attraction on the deformable Earth, thus extending our previous work on the precessional motion. The basic Earth model is a two-layer structure composed of a fluid core and an anelastic mantle. We used the Hamiltonian approach, leading to closed-form analytical formulae that describe the nutations in longitude and obliquity of the figure axis as a sum of Poisson and Oppolzer terms. Those formulae were evaluated assuming different Earth rheologies by means of the Love number formalism. In particular, we first computed the effect using the standard model of the International Earth Rotation and Reference Systems Service Conventions (2010) solid tides, and then the Love numbers computed by Williams and Boggs, accounting for the complete oceanic tide contribution, which should provide more consistent and updated values for the nutations. The main amplitudes correspond to the 18.6 yr nutation component and reach 201 μas and −96 μas in the in-phase components in longitude and obliquity, respectively. The obtained values differ greatly from those considered in the current nutation model, IAU2000, of the International Astronomical Union (IAU) – and later similar studies – which includes this effect under the denomination of non-linear terms and derives its numerical contribution on the basis of the Sasao, Okubo, and Saito framework. The differences are significant and reach more than 30 μas for some nutation amplitudes. They can be likely attributed to several factors: an incomplete modelling of the redistribution potential; a different treatment of the permanent tide; and the use of different oceanic tide models.
Key words: celestial mechanics / methods: analytical / reference systems
© ESO 2020
1. Introduction
The effects of the mass redistribution of the Earth on the precession of the equator were studied in two research works by Baenas et al. (2017a, 2019), who derived updated values of the precession rates in longitude and obliquity. Those values are a correction of the current ones adopted by the IAU2006 precession theory (Capitaine et al. 2003, 2005), which is included in that formulation among the second order components of the precession rates that were taken from previous results of several authors.
Although both studies tackled the contribution of the mass redistribution on the precession due to the lunisolar attraction, their nature was quite different. In Baenas et al. (2017a), the origin of the contributions was due to the derivation enhancement of the approximate analytical solution of the Earth rotation dynamic equations. Namely, they stemmed from extending that solution up to the second order in the sense of mathematical perturbation methods. In contrast, Baenas et al. (2019) – hereinafter referred to as Paper I – worked out the effects raised by the redistribution tidal potential, that is, the additional potential due to the Earth’s anelastic yielding resulting from the lunisolar attraction. Here, the same approach is extended in order to derive the nutations of the Earth’s figure axis.
The construction of the redistribution tidal potential, or the additional term of the gravitational potential energy of the system due to the tidal deformation, was comprehensively revisited in Paper I, where its treatment within the Hamiltonian formalism was also introduced. The Hamiltonian approach – used for the first time by Kinoshita (1977) to study the rotation of the rigid Earth, and generalized by the authors to treat the non-rigid Earth in a series of papers1 – makes it possible to apply an analytical perturbation theory for obtaining closed formulae that asymptotically approximate the effects of the redistribution potential on the Earth’s rotation, because the direct integration of the Hamiltonian equations to get exact analytical solutions is unfeasible.
Since the redistribution tidal potential causing the nutations is the same as in the precessional case, we can shorten the background and directly take the expression of the potential derived in Paper I. That is the sole perturbation considered in this work – to be added to the Hamiltonian of the two-layer Earth model (Getino & Ferrándiz 2001).
Afterwards, the Lie–Hori perturbation method (Hori 1966; Baenas et al. 2017b) is applied to derive the generating function of a canonical transformation allowing us to obtain the quasi-periodic solutions (nutations) of the Earth’s figure axis. In the present work, the procedure to build the first-order generating function is based on the work of Baenas et al. (2020), which extends that of Getino & Ferrándiz (2001).
The effects of the redistribution potential on the Earth nutations have been previously studied by Krasinsky (1999), Souchay & Folgueira (2000), Mathews et al. (2002; MHB2000 model, included in the IAU2000 nutation model), Escapa et al. (2003, 2004), Lambert & Capitaine (2004), Lambert & Mathews (2006, 2008), and Baenas (2014), among others. Souchay & Folgueira, Escapa et al., and Baenas’ works adhere to the Hamiltonian framework. They differ on the complexity of the Earth model and the terms of the redistribution potential considered, but all of them represent simpler models when compared with the current investigation.
The remaining references apply procedures closer to the Newtonian dynamics including a redistribution tidal torque: for instance, the modified Sasao, Okubo, and Saito (SOS) equations (Sasao et al. 1980) extended in the MHB2000 model. In its current formulation, such an approach does not provide analytical formulae, and therefore, only the comparison of the numerical results is possible.
This second group of research papers also contains significant simplifications, except the ones by Lambert & Mathews. That work is supposed to be closer to the current one regarding the features of the Earth model, although, as we show, significant discrepancies exist in their results relative to ours. A detailed comparison between this investigation and the former ones is given in Sect. 6 with the available numerical results.
The structure of this paper is the following. In Sect. 2, the canonical expression of the redistribution tidal potential is reiterated from Paper I and arranged in a convenient way to study nutations by perturbation methods. In Sect. 3, the calculation of the first-order generating function is performed, allowing the application of the Lie–Hori equations in Sect. 4. There, the analytical formulae for the nutations of the Earth’s figure axis are stated and suitably decomposed into the Poisson terms – nutations of the Earth’s angular momentum axis – and the Oppolzer terms – deviations of the Earth’s figure axis with respect to the angular momentum one.
Those formulae are evaluated for different Earth models, described through the Love number formalism, and the numerical results are provided in Sect. 5. The same three models used in Paper I are considered. Namely, Love numbers are specified by the spherical, non-rotating, elastic, and isotropic Earth (SNREI), IERS Conventions (2010) solid tides, and Williams & Boggs (2016) model for the Earth with oceans. In Sect. 6, the numerical results are discussed and compared with those of the aforementioned antecedents, pointing towards potential causes that might explain the large differences with Mathews et al. (2002) and Lambert & Mathews (2006, 2008) values – which for their part are respectively quite different in the various recalculations.
Some recommendations are suggested with the final report of the IAU/IAG Joint Working Group on theory of Earth rotation and validation (Ferrándiz et al. 2020) in mind; along with resolution number 5 of the International Association of Geodesy (IAG), adopted2 in the XXVII International Union of Geodesy and Geophysics (IUGG) General Assembly 2019; and the recent recommendations agreed for the next International Earth Rotation and Reference Systems Service (IERS) Conventions update (Gross et al. 2019). Finally, an Appendix includes mathematical proof of the cancellation of effects of the redistribution potential on the nutations in the case of an SNREI Earth where the permanent tide is included in the redistribution potential.
2. Expression of the redistribution potential in canonical variables
In Getino & Ferrándiz’s theory, an Andoyer-like canonical set of variables – firstly introduced by Getino (1995) – is used. This set is given by
where the lowercase Greek letters stand for coordinates and the capital ones for the conjugated momenta. The variables with no subscript are associated with the whole Earth, while those with c subscript refer to the fluid core.
For both of them, the canonical momenta have a clear dynamical meaning. Namely, M is the modulus of the total angular momentum vector of the Earth, M = ‖L‖, and Mc that of the FOC, Mc = ‖Lc‖; Λ and N are the projections of L onto the third (or zeta) axis of the celestial system (OXYZ) and the terrestrial (Oxyz) one, while Λc and Nc are the corresponding ones of Lc with respect to the fluid core system and the z axis of the terrestrial system, respectively. Thus, it is useful to introduce the auxiliary angles I, Ic, σ, and σc, through
Getino (1995), or more recently Baenas et al. (2017a), can be consulted for further details on this canonical set and its geometrical rendering.
The redistribution potential energy, 𝒱t, can be expressed in the Andoyer-like canonical set of variables of the Earth, following a similar procedure to that of Kinoshita (1977) for the tide-raising potential. This methodology is based on a Fourier expansion of the constituent spherical harmonics of the potential, using an analytical solution of the ephemeris of the perturbing bodies referred to in the celestial reference system. Considering the magnitude of both the gravitational interactions and the mass redistribution is only necessary to include the Moon and the Sun as perturbers. The details of such a mathematical procedure are shown in Paper I and references therein.
For convenience within this work, 𝒱t is split as a sum of 𝒱m, n components, m being the harmonic contribution (associated with the frequency band). Namely, zonal (long-period, m = 0), tesseral (diurnal, m = 1) sectorial (semidiurnal, m = 2), and n the truncation order in the auxiliary angle σ (n = 0, 1), whose magnitude is about 10−6 rad (Kinoshita 1977). Therefore, the decomposition
is considered. The explicit expression of the σ0 components are
whereas that of σ1 can be written as
The notations employed in those expressions are detailed in Paper I. However, it is expedient to recall the meaning of the most important symbols.
Regarding the summation indexes, i and j stand for the ith and jth orbital frequencies in the Fourier-like expansion of the orbital motion of the perturbed bodies – whose gravitational field is affected by the Earth deformation – and the perturbing ones – whose gravitational field induces the Earth deformation; τ and ϵ take the values ±1 from certain linear combinations of the fundamental arguments Θi and Θj; finally, p and q add on the perturbed and perturbing bodies: respectively the Moon (M) and the Sun (S) in both cases. Thus, the set of indexes {i,p,τ} applies to the perturbed bodies, and {j,q,ϵ} to the perturbers.
The i (and j) subscript is a 5-tuple of integers mki (k = 1, 2, …, 5) such that the fundamental argument Θi (and Θj) is given by
where l, g, and h are the Delaunay variables of the Moon, l′, g′, and h′ of the Sun, F = l + g, D = l + g + h − l′ − g′ − h′, and Ω = h − λ.
Complex Love functions, 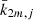 , appear through their modulus and phase, namely,
, appear through their modulus and phase, namely, 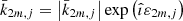 ,
, 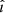 being the imaginary unit. It should be noted that these functions depend on the j-th frequency due to the fact that they describe the anelastic response of the Earth induced by the gravitational action of the perturbers. The kp and fq parameters are the defined as
being the imaginary unit. It should be noted that these functions depend on the j-th frequency due to the fact that they describe the anelastic response of the Earth induced by the gravitational action of the perturbers. The kp and fq parameters are the defined as
With respect to the Andoyer set, the tilde symbol on the variables is used when they correspond to the perturbing bodies, whose orbital motion is considered to be decoupled from the Earth’s rotational motion (see Paper I for further details). In other words, 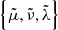 must be considered as explicit time functions. On the other hand, {μ,ν,λ} are the canonical coordinates of the perturbed bodies, entering in the derivation of the canonical equations. The fundamental argument, Θi, depends on the λ variable through Θi = Θ0i − m5iλ, while Θj does it with respect to
must be considered as explicit time functions. On the other hand, {μ,ν,λ} are the canonical coordinates of the perturbed bodies, entering in the derivation of the canonical equations. The fundamental argument, Θi, depends on the λ variable through Θi = Θ0i − m5iλ, while Θj does it with respect to 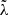 .
.
Finally, Bi; p, Ci; p, and Di; p – and their respective versions with j and q subscripts – stand for Kinoshita’s (Kinoshita 1977) orbital functions3. Strictly speaking, the i and j subscripts used in Kinoshita’s and Love’s functions are an abridged notation where the summation indexes, τ and ϵ, are not displayed, inasmuch as they participate in the different combinations of the fundamental arguments in the Fourier-like expansion. This abuse of notation is kept due to the absence of confusion in practice (as seen in Paper I), and to facilitate the reading of the formulae.
For the sake of simplicity, its is convenient to introduce the argument ϵij = τΘi − ϵΘj. Since the magnitude of the redistribution potential is small (Paper I, Sect. 3.1), its time derivative can be approximated by the constant,
ni and nj being the orbital frequencies related to the fundamental arguments, Θi and Θj. Hence, the summation over ϵij must be understood as the summation over the set {i,j,τ,ϵ}. When the condition ϵij ≠ 0 is indicated, it reads that the summation over {i,j,τ,ϵ} has the restriction τΘi − ϵΘj ≠ 0. In our notation, ϵij ≠ 0 and nij ≠ 0 are equivalent conditions.
3. First-order generating function
The nutations stemming from the disturbing tidal potential given by Eq. (3) are obtained by means of a standard perturbative procedure. As stated above, the Lie–Hori perturbation method (Hori 1966) is widely used, following the pioneering work by Kinoshita (1977) within the Earth rotation Hamiltonian framework. At the first order, the nutations are obtained after removing the secular component of the Hamiltonian, 𝒱t, per = 𝒱t − 𝒱t, sec, 𝒱t, sec being the time-averaged Hamiltonian, whose effect was studied in Paper I, which was devoted to the precession.
Then, a canonical transformation is performed by means of the first-order generating function,
defined by the path integration over UP, which provides the unperturbed trajectories of the two-layer Earth model (Getino & Ferrándiz 2001). This procedure was recently enhanced (Baenas et al. 2020) to remove some approximations made when tackling the dissipation at the core-mantle boundary (CMB).
The decomposition of the perturbation given by Eq. (3) induces a similar one into the generating function. Hence, using the same notation for the subscripts, the sum of terms,
is considered in order to perform the integration. The handling of the terms depends on their order with respect to the small angle σ, as is customary in this kind of approach4.
3.1. Terms of σ0 order
The 𝒱m, 0 terms can be split in two parts: 𝒱m, 0, sec and 𝒱m, 0, per. The 𝒱m, 0, sec part was considered in Paper I. Within our level of approximation, it is the only contribution needed to determine the precessional evolution (i.e. 𝒱t, sec ≃ Vm, 0, sec). The periodic part, 𝒱m, 0, per, is obtained by applying the nij ≠ 0 condition to the 𝒱m, 0 terms. The calculation is similar to that of the one-layer elastic Earth (see, e.g. Escapa et al. 2003, 2004, or Baenas 2014). The UP trajectories needed for the integration are given by λ = λ0, I = I0, μ + ν = ωEt + (μ0+ν0). The path integral leads to the following expressions:
3.2. Terms of σ1 order
The 𝒱m, 1 portions of the redistribution potential energy have no secular part. In order to perform the calculation of the 𝒲m, 1 terms, we rely on the integration procedure of Getino & Ferrándiz (2001, Sect. 6.1). This is based on the auxiliary integral,
where h = μ + ν − τΘi, and its frequency – time derivative over UP – is given by nh = ωE − τni. The explicit form of the Getino & Ferrándiz 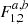 functions can be consulted in Ibid and in Baenas et al. (2020). Their argument depends on the nh frequency, which, for brevity, does not appear explicitly in the notation. In the current study, when the effects of the redistribution potential are included, h and nh are generalised by
functions can be consulted in Ibid and in Baenas et al. (2020). Their argument depends on the nh frequency, which, for brevity, does not appear explicitly in the notation. In the current study, when the effects of the redistribution potential are included, h and nh are generalised by
since Θi is now replaced by the combination ϵij of fundamental arguments (and the same happens with the ni and nij frequencies). The 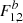 functions vanish when the dissipation processes in the CMB are not considered (Ibid).
functions vanish when the dissipation processes in the CMB are not considered (Ibid).
3.2.1. Zonal terms
By a direct application of Eqs. (12) and (13), the zonal component, 𝒲0, 1, acquires the form
where the elements in curly brackets are introduced to shorten the formulae, instead of witting the sum of their rows. Expanding h by means of Eq. (13), the arguments of the trigonometric functions can be rewritten as
The 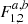 functions depend on frequencies ωE − nij, even if their argument is implicit in Eq. (14). In order to lighten the writing in the following, without the need to display the argument when a new frequency, ωE + nij, appears, the notation
functions depend on frequencies ωE − nij, even if their argument is implicit in Eq. (14). In order to lighten the writing in the following, without the need to display the argument when a new frequency, ωE + nij, appears, the notation 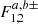 is employed. The ± superscript denotes the dependence of the F function with the frequency ωE ± nij. Therefore, Eq. (14) is as follows:
is employed. The ± superscript denotes the dependence of the F function with the frequency ωE ± nij. Therefore, Eq. (14) is as follows:
The 𝒲0, 1 zonal generating function is characterised by its amplitude dependent on the Bj; q Kinoshita orbital function of the perturbing body q.
3.2.2. Tesseral terms
In order to compute 𝒲1, 1, two types of terms coming from different products of the Kinoshita orbital functions must be considered: namely, Bi; pCj; q and Di; pCj; q, both involving the Cj; q orbital function of the perturber q. The generating function is then provided by means of the same integration procedure as the previous case,
3.2.3. Sectorial terms
Finally, the integration through Eq. (9) of the 𝒱2, 1 term, depending on the Dj; q orbital function of the perturbing bodies, results in the generating function
4. Nutation formulae
The nutations of the Earth’s figure axis are described through the angles λf and If – longitude and obliquity – which provide the longitude and the inclination of the equatorial plane relative to the celestial reference system5. Within the Hamiltonian formalism, it is customary to decompose them in two parts (Kinoshita 1977): the Poisson terms, Δλ and ΔI – or equivalently, the nutations in longitude and obliquity of the angular momentum axis, L/M, and the Oppolzer terms, Δ(λf−λ) and Δ(If−I) – or equivalently, the quasi-periodic components of the motion of the figure axis with respect to the angular momentum one. In this way, the nutations of the figure axis are the sum of both contributions:
As in Paper I, the final layout of the formulae has been adapted to follow the same sign convention for the phase ε2m, j as that used in Williams & Boggs (2016).
4.1. Poisson terms
The Poisson terms of the nutation due to the redistribution potential effects are obtained from the first-order equations of the Lie–Hori perturbation method. These ones, rendered in the Andoyer-like canonical set, are (Kinoshita 1977)
Once the derivatives in Eq. (20) have been performed, it is possible to identify the variables with and without tilde symbol (i.e. 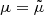 ,
, 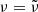 , and
, and 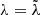 ), since they correspond to the same angles but play different roles (known time functions and canonical variables), and no further derivative has to be taken. In addition, it can be used that M ≃ N = CωE, Mc ≃ Nc = CcωE.
), since they correspond to the same angles but play different roles (known time functions and canonical variables), and no further derivative has to be taken. In addition, it can be used that M ≃ N = CωE, Mc ≃ Nc = CcωE.
In the computation of the Poisson terms, only the 𝒲i, 0 portions of the generating function have influence, inasmuch as the rest of the terms are finally proportional to sin σ or sin σc (about 10−6, Getino & Ferrándiz 2001) and since Eq. (20) do not include derivatives with respect to σ or σc. Therefore, the following expressions are obtained in a similar way to that of a one-layer elastic Earth (Escapa et al. 2003, 2004; Baenas 2014). The nutation formulae result in
where the following amplitude functions have been introduced
In the former expressions, δmk stands for the Kronecker delta symbol, which is entered because of the dependence of the Love number set with m.
4.2. Oppolzer terms
The calculation of the Oppolzer terms is performed through the following expressions, which are written in the Andoyer-like canonical set (Kinoshita 1977):
Now, the 𝒲i, 0 parts have no contribution due to their symmetry under the permutation of the μ and ν variables and their independence with respect to σ. Namely, it is clear that
The computation of the 𝒲i, 1 terms, in contrast, is cumbersome. After some algebra, it is possible to obtain the following analytical formulae:
where the functions 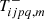 and
and 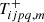 are defined as
are defined as
4.3. In-phase and out-of-phase amplitudes: Final nutation formulae
The nutation formulae provided by Eqs. (21) and (25) are conveniently rewritten by means of the trigonometric identities:
These allow the identification of the in-phase and out-of-phase amplitude functions in longitude and obliquity, as is normally done in nutational studies (e.g. Escapa et al. 2017).
Using Eq. (27), the Poisson terms given by Eq. (21) become
where the following amplitude functions have been introduced:
with superscript 1 denoting the Poisson terms.
In a similar way, the Oppolzer terms can be rewritten as
where, in turn, the corresponding amplitudes – with superscript 2 – have been defined:
supported by the following combinations of functions:
Equations (28) and (30) provide the contributions of the redistribution tidal potential to the nutations and represent one of the most important results of this paper. As in the case of the precessional motion (Paper I, Eqs. (40) and (41)), the analytical nature of our approach makes those relationships very valuable. For example, any update to the rheology model of the Earth can be automatically translated to the nutation series via a simple evaluation of the formulae derived in this study.
5. Redistribution nutations: Theoretical aspects and numerical results
In what follows, the nutation formulae of the Earth’s figure axis given by Eqs. (28) and (30) is evaluated. Those numerical results allow us to quantify the effect of the tidal redistribution potential on the Earth’s different rheologies, or more specifically, different Love number sets. We considered SNREI Earth, IERS Conventions (2010) solid tides, and Williams & Boggs (2016) Earth with oceans models. Particular details about those models can be found in Paper I.
The SNREI Earth is a simplified but expedient model, due to its theoretical features. In particular, the redistribution contributions to the Earth’s rotation must nullify for this model. It is characterised by a constant real Love number describing the elastic response of the Earth at all frequencies – including the zero one.
The IERS model is the current conventional standard, whose frequency-dependent Love numbers – due to the rotation and ellipticity of the Earth – include the solid Earth tides, corrected by the oceanic loading as described in IERS Conventions (2010, Chap. 6).
The model provided by Williams & Boggs (2016) offers a more recent and very complete description of the tidal deformation of the Earth, adding the direct oceanic effect, which complements the IERS solid Earth tides Love numbers.
For each of the former Earth models, the computations were performed using the constants and parameters shown in Table 1 of Paper I. The following Tables 1–3, display all the arguments whose total longitude or obliquity amplitude, in module, is larger than 0.5 μas for the SNREI model. Their periods are given in mean solar days.
Figure axis nutations.
The amplitudes in longitude, denoted as ℒin, out, and obliquity, 𝒪in, out, are provided by the sum over the indexes p, q, and m. The unit of nutation amplitudes is 1 μas. In Table 1, the contributions of the permanent tide6 are displayed in columns 7 and 12 as discussed below. In contrast, the amplitudes in Tables 2 and 3 were obtained without considering the permanent tide in the redistribution potential (i.e. skipping the term i = 0 in 𝒱0, 0).
Figure axis nutations: in-phase and out-of-phase amplitudes.
Figure axis nutations: in-phase and out-of-phase amplitudes.
This choice is consistent with the common practice of not considering the inertia moments as free-tide quantities7. In this way, the redistribution contribution to be added once again does not contain the time-independent part (IERS Conventions 2010, Chap. 6) included in the ordinary nutations. As pointed out in Burša (1995), this convention avoids the question of what is the appropriate Love number to be considered in the permanent tide (k2f), since its accurate value is uncertain.
For their widespread use in most of the theories and standards, the nutation amplitudes are given for the astronomical longitude and obliquity – ψ and ε – instead of Euler angles of the figure axis – λf and If, related by ψ = −λf and ε = −If. This criterion implies a change of sign in the Poisson and Oppolzer terms as defined previously.
It should be noted that 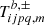 functions depend on the
functions depend on the 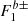 ones, which vanish if the CMB dissipation processes are neglected. In the current study, the Poisson terms do not depend on the CMB effects; in fact, they do not depend on the Earth layer structure at first order as seen in Eq. (21) and examples in Escapa et al. (2017). In turn, the dissipation effects are numerically negligible in the Oppolzer terms since the
ones, which vanish if the CMB dissipation processes are neglected. In the current study, the Poisson terms do not depend on the CMB effects; in fact, they do not depend on the Earth layer structure at first order as seen in Eq. (21) and examples in Escapa et al. (2017). In turn, the dissipation effects are numerically negligible in the Oppolzer terms since the 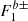 functions incorporate a factor about 10−6 (Baenas et al. 2020), whose effect on the nutation amplitudes is below 10−4 μas.
functions incorporate a factor about 10−6 (Baenas et al. 2020), whose effect on the nutation amplitudes is below 10−4 μas.
5.1. Cancellation of the redistribution effect in the SNREI Earth model
As stated above, SNREI Earth is an initial benchmark useful for validating our formulae and computational software. Specifically, based on physical grounds it can be seen that the effects of the redistribution potential – including the permanent tide – must cancel in an SNREI Earth, whatever approach had been used to model those effects. This fact is a consequence of the exact cancellation of the torque causing the redistribution effect (Krasinsky 1999; Baenas 2014), and therefore must be reproduced by the nutation formulae.
The SNREI Earth model is characterised by assuming that 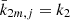 (m = 0, 1, 2), that is, a common real constant value for the Love number set. In such cases, the redistribution effects on the nutation are analytically cancelled out, in the same way as it happens with the precessional motion (see Paper I, Sect. 4.1, and references therein). Full proof of this result is included in Appendix A.
(m = 0, 1, 2), that is, a common real constant value for the Love number set. In such cases, the redistribution effects on the nutation are analytically cancelled out, in the same way as it happens with the precessional motion (see Paper I, Sect. 4.1, and references therein). Full proof of this result is included in Appendix A.
We remind the reader that the cancellation of the redistribution effect requires the inclusion of the permanent tide in the total sum of contributions, as seen in Table 1. Moreover, the fluid Love number, k2f (IERS Conventions 2010, Sect. 8.1), which describes the zonal time-independent elastic response, must be computed using the same value used for the rest of the harmonic components of the redistribution potential, k2f = k2, although that is not physically feasible (e.g. Lambeck 1980).
Table 1 displays the in-phase amplitudes of the figure axis nutations – in longitude and obliquity – in order to exemplify the numerical cancellation of the redistribution potential effects. A cut-off level of 10−2 μas was adopted for the table, but the aforementioned cancellation is exact to the degree of precision used in the numerical evaluation of the formulae. This is favoured if the parameter fq (Eq. (7)) is re-written as
where G denotes the constant of gravitation and fE = 15.9444 s. The numerical value of this parameter is obtained by taking the constants from IERS Conventions (2010) and Groten (2004), which are compatible with those used to compute the Love number sets employed in this work. In this way, kpfq = kqfp is numerically assured, which is a necessary condition for the exact cancellation (Appendix A).
The columns in Table 1 show the different harmonic contributions of the redistribution potential, respectively denoted by B0 (permanent with k2f = k2), B − B0 (zonal non-permanent), C (tesseral), and D (sectorial) – the permanent part just comes from the zonal contribution. The last two columns (Total) exhibit the totals resulting from the addition of the previous contributions either without considering the permanent part of the redistribution tidal potential (B − B0 + C + D) or considering it (B + C + D).
5.2. IERS Conventions (2010) frequency-dependent Love numbers
An extended conventional model for the solid Earth tides is described by means of the IERS Conventions (2010) frequency-dependent Love numbers set (see Paper I, Sect. 4.2.2, for more details)8. From a physical point of view, the related Love numbers take into account the effects of the mantle anelasticity and oceanic loads on the solid Earth tides. Joined to the rotation and ellipticity of the Earth, they make the Love numbers frequency dependent, including resonant processes due to the retrograde free core nutation (FCN), the Chandler wobble (CW), and the free inner-core nutation. With this model, the nutations due to the redistribution potential are numerically evaluated, and they are displayed in Table 2.
5.3. Williams & Boggs (2016) frequency-dependent Love numbers
The IERS Conventions (2010) solid Earth Love numbers were completed explicitly by Williams & Boggs (2016) who derived the direct contribution of the oceans (see Paper I, Sect. 4.3, for further explanation). Those authors computed the real and imaginary parts of the Love numbers, accounting for the direct oceanic effect from the ocean model FES2004 (Lyard et al. 2006). Table 3 shows the numerical results for this more complete model for the Earth with oceans.
As can be seen, there are significant differences with respect to the previous case that just took into account the Earth’s solid tides. Although they are present for the in-phase nutations, they are especially evident for the out-of-phase total longitude and obliquity, reaching 10.6 and 6.3 μas, respectively, for the main 6798.38 days period (18.6 yr) nutation component. It is related to the leading direct contribution of the ocean to the imaginary parts of the Love numbers (Williams & Boggs 2016).
Hence, it must be concluded that the effects of the direct oceanic contribution in the redistribution potential must be considered, since they provide contributions to the nutations of the figure axis well above the μas level for some amplitudes. It should be noted that a similar conclusion was reached in the study of the related precession rates (see Paper I, Sect. 5.4).
6. Discussion and conclusions
6.1. Figure axis redistribution nutations
The nutations of the figure axis of the Earth due to the redistribution potential are split in two parts: Poisson terms (Eq. (28)), that is, nutations of the angular momentum axis; and Oppolzer terms (Eq. (30)) providing the nutations of the figure axis relative to the angular momentum one.
The Poisson terms run parallel to the secular motion formulae of the figure axis derived in Paper I. The reason is twofold. First, both motions stem from the σ0 component of the redistribution tidal potential (Eq. (4)): one from its secular part – precession – and the other from the quasi-periodic one – nutation. Second, the amplitudes in the Fourier expansions of Eq. (4) are constant in the UP trajectories. It entails that they keep the same functional form when computing the generating function except by the presence of a divisor that depends on the constant orbital frequencies, nij.
As a consequence, the formulae providing the Poisson terms (Eq. (20)) and precessional rates (Paper I, Eq. (34)) lead to the same amplitude functions (Eq. (22) and Paper I, Eq. 41)9.
The Oppolzer terms have no equivalence in the precessional motion. They come from the σ1 component of the redistribution potential (Eq. (5)) and depend on the Earth’s interior modelling through the functions 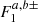 (Getino & Ferrándiz 2001; Baenas et al. 2020). In the ordinary theory of the nutations of the rigid Earth, the functions playing a similar role to
(Getino & Ferrándiz 2001; Baenas et al. 2020). In the ordinary theory of the nutations of the rigid Earth, the functions playing a similar role to 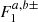 are about ni/ωE smaller than the corresponding Poisson amplitudes (Kinoshita 1977).
are about ni/ωE smaller than the corresponding Poisson amplitudes (Kinoshita 1977).
However, in the case of two-layer Earth models that ratio is affected by the FCN resonance and can be amplified in a significant way (e.g. Getino 1995). Hence, although the perturbing potential has a small magnitude as is the case for the redistribution tidal potential (Paper I), some Oppolzer terms might reach non-negligible amplifications. This fact cannot be ascertained easily from an a priori analysis, in consequence it is also necessary to compute the Oppolzer terms as performed in this work.
The analytical character of our theory makes it possible to evaluate the amplitudes for different Earth elastic responses numerically. One of them is that of Williams & Boggs (2016), which constitutes a relative complete Earth rheological model to study the redistribution effects. We computed the nutations of the figure axis in longitude and obliquity in Table 3 for the Love number set provided by those authors, which is labelled as WB2016.
For some terms, the resulting amplitudes are clearly above 1 μas. This threshold can be considered as the current precision target for individual terms of nutation theories (e.g. Escapa et al. 2017). The contributions of the 18.6 yr component are especially relevant: 201.11 μas and 10.60 μas for the longitude in-phase and out-of-phase amplitudes, and −96.04 μas and 6.26 μas for the obliquity ones. Those values, however, depend heavily on the particular Earth rheology model used in the computation (compare, for example, with Table 2).
The dominant part of the amplitudes is due to the Poisson terms for all the contributions. Nevertheless, some Oppolzer terms must be retained for the in-phase component of longitude and obliquity, since some periods reach magnitudes of about 1 μas. Consistently with the previous explanation, the out-of-phase Poisson terms are at least one order of magnitude smaller than the corresponding in-phase terms as shown in Table 3.
These computed contributions must be added to the ordinary ones of the nutation of the non-rigid Earth due to the tide-raising potential (e.g. Getino & Ferrándiz 2001; Mathews et al. 2002, etc.) to account for the observed values (besides other effects not considered here, like the second-order asymptotic perturbative solution).
6.2. Comparisons
Some previous research that addressed the study of the effects of the redistribution potential on the nutations were enumerated in the Introduction. It is interesting to discuss some of their features in order to gain insight into the underlying modelling of this complex problem. It also allows us to point out the pre-existing discrepancies, although some of them have been superseded by more complete treatments.
We considered the works of Souchay & Folgueira (2000), Mathews et al. (2002), Lambert & Capitaine (2004), and Lambert & Mathews (2006, 2008)10. Table 4 features the in-phase and out-of-phase nutation amplitudes for longitude and obliquity for the three main relevant nutation components provided in those references. The figures in the table are the final ones given by each study, regardless of the modelling differences that we note below and render the various results inhomogeneous.
Nutations of the redistribution potential: numerical comparison of the main amplitude terms.
Among the quoted research, there is the first group to have considered simplified sceneries to model the redistribution contributions. They are Souchay & Folgueira (2000), Mathews et al. (2002), and Lambert & Capitaine (2004). They present a limited utility from the perspective of the current precision needs. However, it is worth making some comparisons with the results derived in this work when applied to the SNREI Earth. Besides, since Mathews et al. (2002) gave raise to the IAU2000 nutation model, which is still in force, it is expedient to make explicit its limitations and drawbacks.
The article by Souchay & Folgueira (2000) uses the Hamiltonian formalism to calculate the influence of the zonal tides on the Poisson terms with a SNREI Earth model11. In view of the results of Table 1 (see also Escapa et al. 2003, 2004), the first simplification does not allow a suitable description of the effects of the redistribution potential, since the rest of the harmonic contributions – tesseral and sectorial – are not numerically negligible. In addition, at the 1 μ as level, it is also necessary to take into account the Oppolzer terms. Besides, the use of a more refined Earth model, both for its internal structure and its rheology, is currently unavoidable. In any case, the numerical values obtained by those authors (Table 4, SF1998) are in good agreement with those derived here when restricted to hold similar hypothesis.
The other results appearing on Table 4 were derived in the SOS (Sasao et al. 1980) framework introducing a torque accounting for the tidal redistribution. Due to the lack of complete analytical expressions in this research12, the comparison must be strictly numerical; apart from general considerations, it is not straightforward to make a comparison with the nutation formulae derived in this work (Eqs. (28) and (30)).
Mathews et al. (2002) and Lambert & Capitaine (2004) considered simplified cases with respect to the structure of the redistribution tidal torque, although the underlying Earth model and rheology represented a clear advance with respect to Souchay & Folgueira (2000) investigation.
Lambert & Capitaine (2004) restricted their computations to the zonal contributions of the redistribution torque for a deformable Earth with a fluid core. In contrast to Mathews et al. (2002), they did not take into account the effects of the anelasticity and ocean tide. Since they focused on the zonal contributions, the rheology of the model was borrowed from the IERS Conventions (2003) variations of the Earth’s rotation rate, which is given in chapter 8. They confirmed that the results of Mathews et al. (2002) presented some inaccuracies.
The numerical values determined by Lambert & Capitaine (2004) – Table 4, LC2004 – have the same order of magnitude as those given in Table 1 for the SNREI Earth – column B − B0, included in Table 4 under “This work (Zonal, SNREI)” – and also as those of Souchay & Folgueira (2000). The differences can be explained in terms of the more sophisticated Earth model and rheology considered by Lambert & Capitaine (2004). In particular, out-of-phase amplitudes are not present for the SNREI Earth, since its deformations are purely elastic (Paper I).
Specifically, Mathews et al. (2002) tackled the effects of the tidal redistribution by deriving the related torque for the zonal and sectorial tides. It led to the computation of what they refer to as “non-linear” terms13, although few details were provided. In that process, they performed some plausible simplifications about the Earth’s interior and rheology considered when constructing the MHB2000 model that, according to Lambert & Capitaine (2004), incorporated anelasticity and ocean tide effects.
The obtained numerical contributions for the nutations and the precession rate in longitude (Mathews et al. 2002, Table 7) were taken into account in calculating the final solution for their model, which led to the full IAU2000A precession-nutation model – Table 4, IAU2000A (MHB2000). Those contributions, however, were revised as stated in Lambert & Capitaine (2004)14. This recomputed zonal contribution was 194 μas and −10 μas for the in-phase longitude and obliquity of the 18.6 yr period nutation – Table 4, M2004 (LC2004).
The second group of works of Table 4 are those of Lambert & Mathews (2006, 2008). They are the most similar to the current study with respect to the general assumptions on the Earth model features and redistribution potential. In fact, the complete harmonic contributions of the tidal redistribution, in a two-layer Earth with fluid core and anelastic mantle plus oceanic contribution, are considered. In contrast, the framework used in the derivations are very different: the SOS approach versus the Hamiltonian formulation. Inasmuch as Lambert & Mathews (2006, 2008) do not provide analytical nutation formulae, we have to base our discussion on comparing the numerical nutation amplitudes, as already mentioned.
Lambert & Mathews (2006) followed a similar scheme to ours studying both an elastic Earth model (denoted as EL in Table 2 of this reference), and a more realistic one with anelasticity and ocean tide effects (denoted as EL+AE+OT). The first case is comparable with the SNREI Earth (Sect. 5.1). The second one was recomputed by the same authors in Lambert & Mathews (2008). For the sake of brevity, we only include the revised results from their later work (LM2008) in Table 4.
It should be noted that their harmonic contributions to the nutations, in terms of types of tides and potentials, are not split in the same way as ours. In order to have a rule of thumb that allows the comparison, it must be taken into account that, although these authors do not explicitly state the tidal system where the calculation has been performed, it seems that they kept the time-independent part of the redistribution tidal potential.
It explains the almost perfect cancellation of the redistribution nutations for their elastic Earth model. A circumstance only expected if the permanent tide is included within the redistribution potential, as was shown in Sect. 5.1. The inclusion of the permanent tide is a drawback of the numerical contributions obtained in Lambert & Mathews (2006, 2008) because it requires the use of a specific value for the fluid Love number, which is uncertain and about three times larger than the ordinary k2 (see, e.g. Burša 1995). Besides, it suffers from the potential inconsistency of counting the effect of the permanent tide twice.
Considering this fact, the nutations called “zonal potential on tesseral tides” in Lambert & Mathews’ works are comparable to the zonal non-permanent contributions in this paper (column B − B0 in Table 1). The “tesseral potential on zonal tides” plus the “tesseral potential on sectorial tides” would be coincident with our tesseral plus zonal permanent contributions (columns B0 plus C). And finally, their “sectorial potential on tesseral tides” would be comparable to our sectorial contributions (column D).
Using this rule, the nutation amplitudes in Table 2 of Lambert & Mathews (2006) for the elastic Earth model (columns EL) have the same order of magnitude as those in Table 1 of this paper with k2f taking the reference value 0.3. This is in spite of the different approaches both formulations seeming consistent when considering an elastic Earth model as far as the same tidal system is used.
Therefore, when adding the contributions of anelasticity and oceans (Lambert & Mathews 2008) to the Earth model, the comparison with this work can just be made effective by including the contribution of the permanent tide in the computed nutations. These results are also shown in Table 4 – “This work (B0 included, k2f = 0.3)” – where the fluid Love number has been set to 0.3, since there is no information about the particular value used in Lambert & Mathews (2006, 2008). However, it should be noted that the discrepancy is relevant: see, e.g. the in-phase amplitude in longitude of the 18.6 yr component, whose values are −39.0 μas and 1.0 μas for the “LM2008” and 33.5 μas and −6.7 μas for the “This work (B0 included, k2f = 0.3)” rows, respectively. Similar discrepancies were found in the calculation of the precession rates due to the redistribution potential (see Paper I, Sect. 5.4, for further details).
It is difficult to determine the source of these differences with certainty. Indeed, the particular k2f value employed has its relevance as pointed out above. Besides, the ocean model has an undoubted influence that can explain those magnitude variations. Specifically, the ocean model employed in Lambert & Mathews (2006) was CSR4.0 (University of Texas at Austin empirical model, Eanes 2002), while in this work the FES2004 (Lyard et al. 2006) is used through Williams & Boggs’ Love numbers, as previously stated.
There are relevant differences between the CSR4.0 and FES2004 ocean tide models. For instance, FES2004 uses higher spatial resolution (0.125° × 0.125°) than CSR4.0 (0.5° × 0.5°), and also comprises a higher number of tides (14 vs 8), among other different features (see, e.g. Ardalan & Hashemi’s chapter in Donner & Barbosa 2008). It should be noted that CSR4.0 is an empirical model, based on sea level observations and not the driving forces of the tides; while FES2004 is an hydrodynamic one, based on gravitational forces driving the tide phenomenon, as well as other effects like topography, ocean boundaries, and so on, by means of a finite element solution (FES). In this sense, FES2004 seems to be more suitable to tackle the forced tidal effect on the Earth rotation. In fact, FES2004 is the ocean tide model currently recommended in the IERS Conventions (2010, Chap. 6).
In this context, with the same oceanic model Lambert & Mathews (2008) offered a revised value of the obliquity rate of 1.84 cy−1 – replacing their previous 2006 value of 0.13 cy−1 –, closer to that of Williams (1994), 2.44 cy−1, as stated by the authors. However, Williams & Boggs (2016) explicitly corrected the previous value of the obliquity rate computed by Williams (1994) – explaining it was derived under incorrect assumptions – and gave a revised rate of 0.92 cy−1, which is in very good agreement with our value of 0.93 cy−1 (Paper I) for the precession in obliquity, thus providing a partial validation of our results on precession. This fact is closely related to the differences found in the out-of-phase terms of nutations, since the obliquity rate and the out-of-phase Poisson terms share a similar derivation within the theoretical background that we developed in Paper I and in this work.
7. Conclusions
In this research, the contributions to the nutations of the figure axis arising from the tidal redistribution potential were derived and computed. This paper thus completes the study of the redistribution effects on the precession and nutation initiated by the authors in Baenas et al. (2019).
The application of the Hamiltonian framework has allowed us to provide analytical nutation formulae, which support different Earth rheologies described by means of the Love number formalism. The comparison between the nutations obtained from the IERS Conventions (2010) Love number set – including solid tides and oceanic load – and those supplemented by Williams & Boggs (2016) – inserting the direct oceanic contribution – was performed. It showed that the role played by the direct oceanic effect cannot be neglected, since it contributes 49.4 and −16.5 μas in the in-phase longitude and obliquity, respectively, in the main nutation component.
The largest derived nutation amplitude corresponds to the 18.6 yr component, reaching 201.1 μas in the in-phase longitude, and −96.0 μas in the in-phase obliquity, for a two-layer (fluid core and anelastic mantle) Earth with oceans, computed with a complete second-degree redistribution tidal potential. Other significant nutation components and out-of-phase terms also exist, as shown in Table 4.
The derived values for redistribution nutation of the figure axis are quite different from those considered in Mathews et al. (2002) and related works (Lambert & Mathews 2006, 2008). In the first case, which is incorporated in the IAU2000A nutation model, the differences can be attributed to an incomplete modelling of the redistribution that lacks the tesseral part. In addition, the values provided in that work were later revised as indicated, for example, in Lambert & Capitaine (2004). Hence, this part of the IAU2000 model in its current status is incorrect and must be improved.
In the second group of previous works cited in the discussion, the main sources of the discrepancies are very likely due to the treatment of the permanent tide and the considered ocean tide model. It is necessary to recall that the effects of the permanent tide must not be counted twice. It entails that the redistribution tidal potential has to be free from its zero frequency terms, which are commonly accounted for in the ordinary nutation amplitudes (through the dynamical ellipticity Hd).
With regard to the oceanic model, and in view of the magnitude of its contribution, it is expedient to compute the redistribution nutation and precession due to available oceanic tide models and to establish an updated standard. For consistency, the selected ocean model used in the development of precession and nutation theories of the non-rigid Earth must be the same as those adopted in the IERS and GGOS Conventions and in data analysis.
Those recommendations fit in the conclusions presented in the final report of the IAU/IAG WG on the theory of Earth rotation and validation (Ferrándiz et al. 2020) and in Resolution 5 adopted by the IAG General Assembly in 2019. They should be taken into account within the discussions of the new IAU/IAG JWG on improving theories and models of the Earth’s rotation (ITMER) and in the future revision of the IERS Conventions, which is under development.
For instance, Getino & Ferrándiz (1990, 1991, 1995, 1997, 2001), Escapa et al. (2001), Efroimsky & Escapa (2007), and Escapa (2011).
The complete text of the resolution can be found at https://iag.dgfi.tum.de/fileadmin/IAG-docs/IAG_Resolutions_2019.pdf
Their explicit form can be consulted in Appendix A.
The general methodology of this procedure is explained, for example, in Ferraz-Mello (2007) or Baenas et al. (2017b). From a practical point of view, the integration process is similar to that performed to derive the main lunisolar nutations at the first order (Getino & Ferrándiz 2001).
The relations between λf and If with the Euler angles are provided, among others, in Kinoshita (1977) or, in greater detail, in Appendix A of Getino et al. (2010).
IERS Conventions (2010, Chap. 1) refer to the zero-tide and tide-free systems to specify how the permanent tide has been kept or removed in the modelling of the redistribution tidal potential. Paper I can also be consulted for further explanations on this topic.
Usually, this question is not explicitly addressed in Earth rotation studies and in what tide system the Hd value is given (Escapa et al. 2020a) is not indicated.
Concerning this Earth model, we detected a typo in Table 2 of Paper I, “Anelastic IERS 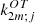 ” column – in fact, the third and fourth columns of the table are almost identical due to this erratum. The corrected values, quite close to those originally published, are 5.9222 and 0.1686 mas cy−1 for the longitude and obliquity rates in precession, respectively.
” column – in fact, the third and fourth columns of the table are almost identical due to this erratum. The corrected values, quite close to those originally published, are 5.9222 and 0.1686 mas cy−1 for the longitude and obliquity rates in precession, respectively.
We excluded the works by Escapa et al. (2003, 2004) from this comparison, since they are precursors of the theory developed in this research.
It is necessary to take into account the fact that there are some misprints in Souchay & Folgueira (2000). The most relevant is that the sign in their Eq. (5) must be reversed (see Eqs. (1-14), (1-17), and (3-399) in Moritz & Mueller 1986). It changes the sign of the nutation amplitudes derived by those authors.
That terminology is confusing since the mathematical solution is linear in the sense of perturbation methods. Truly non-linear theories require second-order methods (e.g. Escapa et al. 2020b).
References
- Baenas, T. 2014, Ph.D. Thesis (in Spanish), Universityof Alicante, Alicante, Spain [Google Scholar]
- Baenas, T., Ferrándiz, J. M., Escapa, A., Getino, J., & Navarro, J. F. 2017a, AJ, 153, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Baenas, T., Escapa, A., Ferrándiz, J. M., & Getino, J. 2017b, Int. J. NonLin. Mech., 90, 11 [CrossRef] [Google Scholar]
- Baenas, T., Escapa, A., & Ferrándiz, J. M. 2019, A&A, 626, A58 (Paper I) [CrossRef] [EDP Sciences] [Google Scholar]
- Baenas, T., Escapa, A., & Ferrándiz, J. M. 2020, Adv. Space Res., 66, 2646 [CrossRef] [Google Scholar]
- Burša, M. 1995, Earth Moon Planets, 69, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2003, A&A, 412, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2005, A&A, 432, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donner, R. V., & Barbosa, S. M. 2008, Nonlinear Time Series Analysis in the Geosciences (Berlin: Springer) [CrossRef] [Google Scholar]
- Eanes, R. 2002, The CSR4.0 Global Ocean Tide Model, http://download.csr.utexas.edu/pub/tide/ [Google Scholar]
- Efroimsky, M., & Escapa, A. 2007, Celest. Mech. Dyn. Astron, 98, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A. 2011, Celest. Mech. Dyn. Astron, 110, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2001, J. Geophys. Res., 106, 11387 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2003, in Book of Abstracts of the Journés 2003, Astrometry, Geodynamics and Solar System Dynamics: From Milliarcseconds to Microarcseconds, ed. A. Finkelstein (St. Petersburg, Russia: Institute of Applied Astronomy of Russian Academy of Science (IAARAS)), 17 [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2004, in Proceedings Journées 2004, ed. N. Capitaine (Paris: Observatoire de Paris), 70 [Google Scholar]
- Escapa, A., Getino, J., Ferrándiz, J. M., & Baenas, T. 2017, A&A, 604, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Escapa, A., Baenas, T., & Ferrándiz, J. M. 2020a, EGU General Assembly, EGU2020-21410 [Google Scholar]
- Escapa, A., Getino, J., Ferrándiz, J. M., & Baenas, T. 2020b, in Proc. Journées “Systèmes de Référence Spatio-temporels” 2019, ed. C. Bizouard (Observatoire de Paris), 221, https://syrte.obspm.fr/astro/journees2019/LATEX/JOURNEES2019.pdf [Google Scholar]
- Ferrándiz, J. M., Gross, R. S., Escapa, A., et al. 2020, International Association of Geodesy Symposia, https://doi.org/10.1007/1345_2020_103 [Google Scholar]
- Ferraz-Mello, S. 2007, Canonical Perturbation Theories: Degenerate Systems and Resonance (New York: Springer) [Google Scholar]
- Getino, J. 1995, Geophys. J. Int., 122, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1990, Celest. Mech. Dyn. Astron., 49, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1991, Celest. Mech. Dyn. Astron., 51, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1995, Celest. Mech. Dyn. Astron., 61, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1997, Geophys. J. Int., 130, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 2001, MNRAS, 322, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., Escapa, A., & Miguel, D. 2010, AJ, 139, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Gross, R. S., Heinkelmann, R., & Altamimi, Z. 2019, Report of the Unified Analysis Workshop 2019, Co-organized by IAG, GGOS, and IERS, http://www.ggos.org/en/unified-analysis-workshop-2019/general-uaw/ [Google Scholar]
- Groten, E. 2004, J. Geod., 77, 724 [CrossRef] [Google Scholar]
- Hori, G. I. 1966, PASJ, 18, 287 [Google Scholar]
- IERS Conventions 2003, in IERS Technical Note 32, eds. D. D. McCarthy, & G. Petit, 127 [Google Scholar]
- IERS Conventions 2010, in IERS Technical Note 36, eds. G. Petit, & B. Luzum, 179 [Google Scholar]
- Kinoshita, H. 1977, Celest. Mech. Dyn. Astron., 15, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Krasinsky, G. A. 1999, Celest. Mech. Dyn. Astron., 75, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Lambeck, K. 1980, The Earth’s Variable Rotation (London: Cambridge University Press) [CrossRef] [Google Scholar]
- Lambert, S. B., & Capitaine, N. 2004, A&A, 428, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, S. B., & Mathews, P. M. 2006, A&A, 453, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, S. B., & Mathews, P. M. 2008, A&A, 481, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyard, F., Lefevre, F., Letellier, T., & Francis, O. 2006, Ocean Dyn., 56, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, P. M., Herring, T. A., & Buffet, B. A. 2002, J. Geophys. Res., 107, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Moritz, H., & Mueller, I. 1986, Earth Rotation (New York: Frederic Ungar) [Google Scholar]
- Sasao, T., Okubo, S., & Saito, M. 1980, in Proc. IAU Symp., eds. E. P. Federvo, M. L. Smith, & P. L. Bender, 165 [Google Scholar]
- Souchay, J., & Folgueira, M. 2000, Earth Moon Planets, 81, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. G. 1994, AJ, 108, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. G., & Boggs, D. H. 2016, Celest. Mech. Dyn. Astr., 126, 89 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Exact cancellation of nutation formulae in the SNREI model with k2f = k2
In this appendix, the analytical cancellation of the nutation formulae describing the redistribution potential effect in the SNREI Earth (with k2f = k2) is proven. The demonstration is restricted to the Oppolzer terms for the sake of brevity, since the case of Poisson terms is analogous to the one-layer elastic Earth and can be consulted in Escapa et al. (2003, 2004), Baenas (2014, Sect. 6.3), and Paper I (Appendix B, since it is formally analogous to the case of precession formulae).
The nutation amplitudes 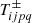 that appear in Eq. (30) are given by the combinations of Kinoshita’s orbital functions B, C, and D, provided in Eq. (26). It should be noted that the m subscript has been omitted from the T functions since in the SNREI Earth the Love numbers do not depend on it (i.e.
that appear in Eq. (30) are given by the combinations of Kinoshita’s orbital functions B, C, and D, provided in Eq. (26). It should be noted that the m subscript has been omitted from the T functions since in the SNREI Earth the Love numbers do not depend on it (i.e. 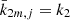 ). These orbital functions, in turn, depend on the
). These orbital functions, in turn, depend on the 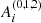 orbital coefficients, through their definition (Kinoshita 1977):
orbital coefficients, through their definition (Kinoshita 1977):
The 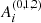 orbital coefficients verify the following conditions (see ibid and Paper I, Appendix B, for further details):
orbital coefficients verify the following conditions (see ibid and Paper I, Appendix B, for further details):
The application of those conditions yields a developed expression of the amplitudes in the following form, depending on the m5i value:
Here, hm5i are functions of obliquity whose explicit form is not relevant for the purpose of proof – they can be consulted in Baenas (2014, Sect. 6.4). It should be noted that only a permutation of τ and ϵ indexes exists between both expressions.
Considering Eqs. (25) and (A.5), the Oppolzer terms of the nutation can be written in the form
by means of introducing the following functions:
Regarding 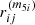 , the permutation between the i and j subscripts, denoted as Pi, j, is studied. It must be noted that Pi, j permutation also happens in the implicit argument ωE ± nij of the F± functions. In fact, since nij = τni − ϵnj = −(ϵnj−τni) (and the same happens for ϵij), taking into account that nij (and ϵij) appear under the summation over τ and ϵ (dummy indexes), it is possible to exchange the labels between τ and ϵ in such a way that the following transformations hold:
, the permutation between the i and j subscripts, denoted as Pi, j, is studied. It must be noted that Pi, j permutation also happens in the implicit argument ωE ± nij of the F± functions. In fact, since nij = τni − ϵnj = −(ϵnj−τni) (and the same happens for ϵij), taking into account that nij (and ϵij) appear under the summation over τ and ϵ (dummy indexes), it is possible to exchange the labels between τ and ϵ in such a way that the following transformations hold:
Therefore, 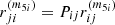 entails
entails
In other words, 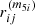 is an antisymmetric quantity under the permutation of their indexes. A very similar development is applicable to
is an antisymmetric quantity under the permutation of their indexes. A very similar development is applicable to 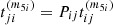 , also reaching the antisymmetry of
, also reaching the antisymmetry of 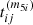 , that is,
, that is,
The case of 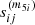 is somewhat different. Now the Pi, j permutation acts taking into account that the summation indexes are p and q. Hence,
is somewhat different. Now the Pi, j permutation acts taking into account that the summation indexes are p and q. Hence, 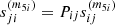 yields
yields
where dummy indexes, p and q, have interchanged their names in [1], and the identity fqkp = fpkq – from Eq. (33) – is used in [2]. Therefore, 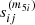 is a symmetric quantity under the permutation of their indexes.
is a symmetric quantity under the permutation of their indexes.
Finally, it is only necessary to observe in Eq. (A.6) that Δ(λf−λ) and Δ(If−I) are formed by the product between antisymmetric and symmetric quantities, added over their common indexes, and therefore, they are exactly zero:
All Tables
Nutations of the redistribution potential: numerical comparison of the main amplitude terms.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



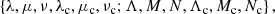
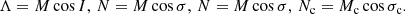
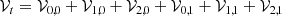
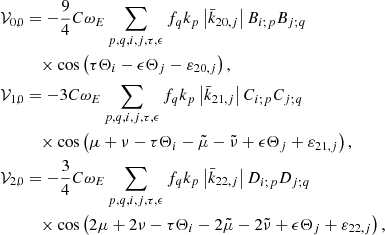
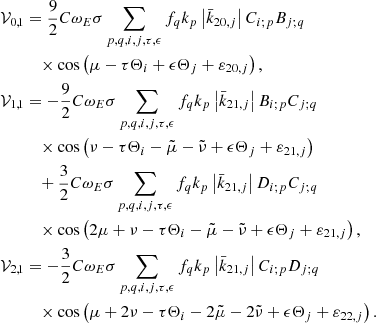
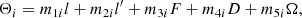
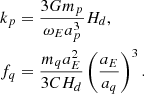
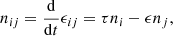
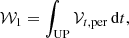
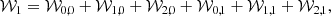
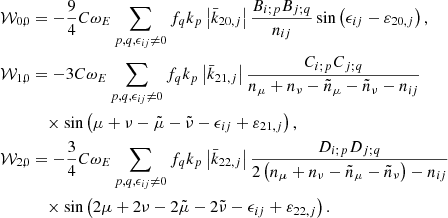
![$$ \begin{aligned} I_{1}&=\int _{\mathrm{UP}}M\sin \sigma \cos \left(\mu -\tau \Theta _{i}\right)\,\mathrm{d}t \nonumber \\&=M\sin \sigma \left[ F_{1}^{a}\sin \left(h-\nu \right) +F_{1}^{b}\cos \left(h-\nu \right) \right] \\&\quad +M_{\rm c}\sin \sigma _{\rm c}\left[ F_{2}^{a}\sin \left(h+\nu _{\rm c}\right) +F_{2}^{b}\cos \left(h+\nu _{\rm c}\right) \right], \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq17.gif)
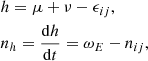
![$$ \begin{aligned} \mathcal{W} _{0,1}&=\frac{9}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k}_{20,j}\right|C_{i;p}B_{j;q} \nonumber \\&\quad \times \int _{\mathrm{UP}}M\sin \sigma \cos \left(\mu -\epsilon _{ij}+\varepsilon _{20,j}\right) dt \nonumber \\&=\frac{9}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k} _{20,j}\right|C_{i;p}B_{j;q} \\&\quad \times \left[ M\sin \sigma \left\{ \begin{array}{c} F_{1}^{a}\sin \left(h-\nu +\varepsilon _{20,j}\right) \\ F_{1}^{b}\cos \left(h-\nu +\varepsilon _{20,j}\right) \end{array}\right\} \right. \nonumber \\&\quad +\left. M_{\rm c}\sin \sigma _{\rm c}\left\{ \begin{array}{c} F_{2}^{a}\sin \left(h+\nu _{\rm c}+\varepsilon _{20,j}\right) \\ F_{2}^{b}\cos \left(h+\nu _{\rm c}+\varepsilon _{20,j}\right) \end{array}\right\} \right], \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq21.gif)
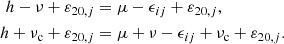
![$$ \begin{aligned} \mathcal{W} _{0,1}&=\frac{9}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k}_{20,j}\right|C_{i;p}B_{j;q} \nonumber \\&\quad \times \left[ M\sin \sigma \left\{ \begin{array}{c} F_{1}^{a-}\sin \left(\mu -\epsilon _{ij}+\varepsilon _{20,j}\right) \\ F_{1}^{b-}\cos \left(\mu -\epsilon _{ij}+\varepsilon _{20,j}\right) \end{array}\right\} \right. \\&\quad +\left. M_{\rm c}\sin \sigma _{\rm c}\left\{ \begin{array}{c} F_{2}^{a-}\sin \left(\mu +\nu -\epsilon _{ij}+\nu _{\rm c}+\varepsilon _{20,j}\right) \\ F_{2}^{b-}\cos \left(\mu +\nu -\epsilon _{ij}+\nu _{\rm c}+\varepsilon _{20,j}\right) \end{array}\right\} \right]. \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq25.gif)
![$$ \begin{aligned} \mathcal{W} _{1,1}&=-\frac{9}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k}_{21,j}\right|B_{i;p}C_{j;q} \nonumber \\&\quad \times \left[ M\sin \sigma \left\{ \begin{array}{c} -F_{1}^{a+}\sin \left(\nu -\tilde{\mu }-\tilde{\nu }-\epsilon _{ij}+\varepsilon _{21,j}\right) \\ F_{1}^{b+}\cos \left(\nu -\tilde{\mu }-\tilde{\nu }-\epsilon _{ij}+\varepsilon _{21,j}\right) \end{array}\right\} \right. \nonumber \\&\quad +\left. M_{\rm c}\sin \sigma _{\rm c}\left\{ \begin{array}{c} F_{2}^{a+}\sin \left(\nu _{\rm c}+\mu +\nu +\epsilon _{ij}+\varepsilon _{21,j}\right) \\ F_{2}^{b+}\cos \left(\nu _{\rm c}+\mu +\nu +\epsilon _{ij}+\varepsilon _{21,j}\right) \end{array} \right\} \right] \nonumber \\&\quad +\frac{3}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k} _{21,j}\right|D_{i;p}C_{j;q} \\&\quad \times \left[ M\sin \sigma \left\{ \begin{array}{c} F_{1}^{a-}\sin \left(2\mu +\nu -\tilde{\mu }-\tilde{\nu }-\epsilon _{ij}+\varepsilon _{21,j}\right) \\ F_{1}^{b-}\cos \left(2\mu +\nu -\tilde{\mu }-\tilde{\nu }-\epsilon _{ij}+\varepsilon _{21,j}\right) \end{array} \right\} \right. \nonumber \\&\quad +\left. M_{\rm c}\sin \sigma _{\rm c}\left\{ \begin{array}{c} F_{2}^{a-}\sin \left(2\mu +2\nu +\nu _{\rm c}\right) \\ F_{2}^{b-}\cos \left(-\tilde{\mu }-\tilde{\nu }-\epsilon _{ij}+\varepsilon _{21,j}\right) \end{array} \right\} \right]. \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq26.gif)
![$$ \begin{aligned} \mathcal{W} _{2,1}&=-\frac{3}{2}\sum _{p,q,\epsilon _{ij}}f_{q}k_{p}\left|\bar{k}_{22,j}\right|C_{i;p}D_{j;q} \\&\quad \times \left[ M\sin \sigma \left\{ \begin{array}{c} -F_{1}^{a+}\sin \left(\mu +2\nu -2\tilde{\mu }-2\tilde{\nu }-\epsilon _{ij}+\varepsilon _{22,j}\right) \\ F_{1}^{b+}\cos \left(\mu +2\nu -2\tilde{\mu }-2\tilde{\nu }-\epsilon _{ij}+\varepsilon _{22,j}\right) \end{array}\!\! \right\} \right. \nonumber \\&\quad +\left. M_{\rm c}\sin \sigma _{\rm c}\left\{ \begin{array}{c} F_{2}^{a+}\sin \left(\nu _{\rm c}-\mu -\nu +\nu _{\rm c}\right) \\ F_{2}^{b+}\cos \left(2\tilde{\mu }+2\tilde{\nu }+\epsilon _{ij}+\varepsilon _{22,j}\right) \end{array}\right\} \right]. \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq27.gif)
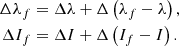
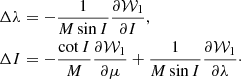
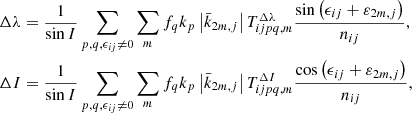
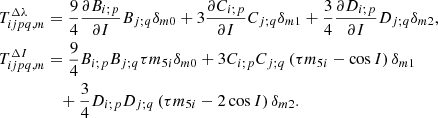
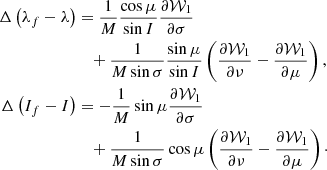
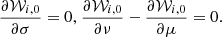
![$$ \begin{aligned} \Delta \left(\lambda _{f}-\lambda \right)&=-\frac{1}{\sin I} \sum _{p,q,\epsilon _{ij}}\sum _{m}f_{q}k_{p}\left|\bar{k} _{2m,j}\right|\nonumber \\&\quad \times \left[ T_{ijpq,m}^{-}\left\{ \begin{array}{c} F_{1}^{a-}\sin \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \\ -F_{1}^{b-}\cos \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \end{array}\right\} \right. \nonumber \\&\quad +\left. T_{ijpq,m}^{+}\left\{ \begin{array}{c} F_{1}^{a+}\sin \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \\ F_{1}^{b+}\cos \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \end{array}\right\} \right] \mathrm{,} \nonumber \\ \Delta \left(I_{f}-I\right)&=-\sum _{p,q,\epsilon _{ij}}\sum _{m}f_{q}k_{p}\left|\bar{k}_{2m,j}\right| \\&\quad \times \left[ T_{ijpq,m}^{-}\left\{ \begin{array}{c} F_{1}^{a-}\cos \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \\ F_{1}^{b-}\sin \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \end{array}\right\} \right. \nonumber \\&\quad +\left. T_{ijpq,m}^{+}\left\{ \begin{array}{c} F_{1}^{a+}\cos \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \\ -F_{1}^{b+}\sin \left(\epsilon _{ij}+\varepsilon _{2m,j}\right) \end{array}\right\} \right], \nonumber \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq37.gif)
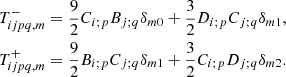
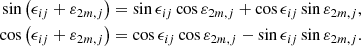
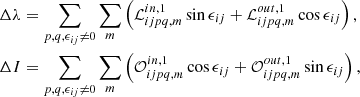
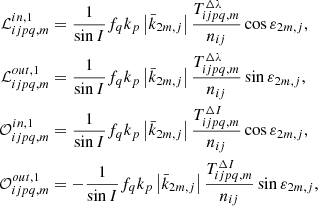
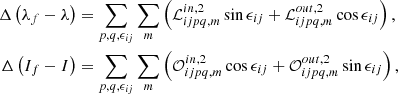
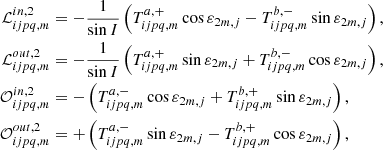
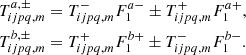
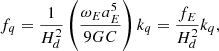
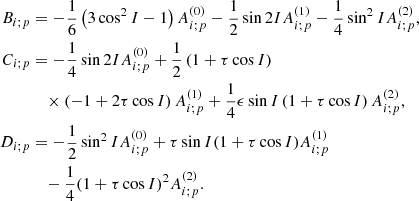
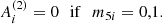
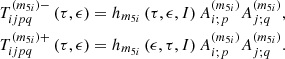
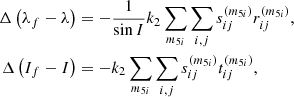
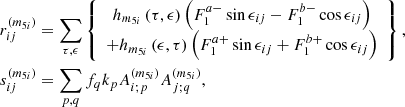
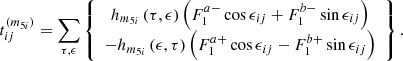
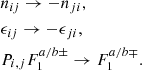
![$$ \begin{aligned} r_{ji}^{\left(m_{5i}\right) }&=\sum _{\tau ,\epsilon }\left\{ \begin{array}{c} h_{m_{5i}}\left(\tau ,\epsilon \right) \left(P_{i,j}F_{1}^{a-}\sin \epsilon _{ji}-P_{i,j}F_{1}^{b-}\cos \epsilon _{ji}\right) \\ +h_{m_{5i}}\left(\epsilon ,\tau \right) \left(P_{i,j}F_{1}^{a+}\sin \epsilon _{ji}+P_{i,j}F_{1}^{b+}\cos \epsilon _{ji}\right) \end{array}\right\} \nonumber \\&=\sum _{\tau ,\epsilon }\left\{ \begin{array}{c} h_{m_{5i}}\left(\epsilon ,\tau \right) \left[ F_{1}^{a+}\sin \left(-\epsilon _{ij}\right) -F_{1}^{b+}\cos \left(-\epsilon _{ij}\right) \right]\\ +h_{m_{5i}}\left(\tau ,\epsilon \right) \left[ F_{1}^{a-}\sin \left(-\epsilon _{ij}\right) +F_{1}^{b-}\cos \left(-\epsilon _{ij}\right) \right] \end{array}\right\} \nonumber \\&=\sum _{\tau ,\epsilon }\left\{ \begin{array}{c} h_{m_{5i}}\left(\epsilon ,\tau \right) \left[ -F_{1}^{a+}\sin \epsilon _{ij}-F_{1}^{b+}\cos \epsilon _{ij}\right] \\ +h_{m_{5i}}\left(\tau ,\epsilon \right) \left[ -F_{1}^{a-}\sin \epsilon _{ij}+F_{1}^{b-}\cos \epsilon _{ij}\right] \end{array}\right\} \nonumber \\&=-r_{ij}^{\left(m_{5i}\right) }\mathrm{.} \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq70.gif)
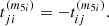
![$$ \begin{aligned} s_{ji}^{\left(m_{5i}\right) }&=\sum _{p,q}f_{q}k_{p}A_{j;p}^{\left(m_{5i}\right) }A_{i;q}^{\left(m_{5i}\right) }\overset{\left[ 1\right] }{=} \sum _{p,q}f_{p}k_{q}A_{j;q}^{\left(m_{5i}\right) }A_{i;p}^{\left(m_{5i}\right) }\overset{\left[ 2\right] }{=} \nonumber \\&=\sum _{p,q}f_{q}k_{p}A_{i;p}^{\left(m_{5i}\right) }A_{j;q}^{\left(m_{5i}\right) }=s_{ij}^{\left(m_{5i}\right) }\mathrm{,} \end{aligned} $$](/articles/aa/full_html/2020/11/aa38946-20/aa38946-20-eq77.gif)