| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | L20 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202038999 | |
| Published online | 26 October 2020 | |
Letter to the Editor
Orbital features of distant trans-Neptunian objects induced by giant gaseous clumps
Institute of Astronomy, Russian Academy of Sciences, Moscow 119017, Russia
e-mail: vvemel@inasan.ru
Received:
22
July
2020
Accepted:
6
October
2020
Context. The discovery of distant trans-Neptunian objects has led to heated discussions about the structure of the outer Solar System.
Aims. We study the dynamical evolution of small bodies from the Hill regions of migrating giant gaseous clumps that form in the outer solar nebula via gravitational fragmentation. We attempt to determine whether the observed features of the orbital distribution of distant trans-Neptunian objects could be caused by this process.
Methods. We consider a simple model that includes the Sun, two point-like giant clumps with masses of ∼10 Jupiter masses, and a set of massless objects initially located in the Hill regions of these clumps. We carry out numerical simulations of the motions of small bodies under gravitational perturbations from two giant clumps that move in elliptical orbits and approach each other. The orbital distribution of these small bodies is compared with the observed distribution of distant trans-Neptunian objects.
Results. In addition to the known grouping in longitudes of perihelion, we note new features for observed distant trans-Neptunian objects. The observed orbital distribution points to the existence of two groups of distant trans-Neptunian objects with different dynamical characteristics. We show that the main features of the orbital distribution of distant trans-Neptunian objects can be explained by their origin in the Hill regions of migrating giant gaseous clumps. Small bodies are ejected from the Hill regions when the giant clumps move in high-eccentricity orbits and have a close encounter with each other.
Conclusions. The resulting orbital distribution of small bodies in our model and the observed distribution of distant trans-Neptunian objects have similar features.
Key words: Kuiper belt: general / planet-disk interactions / methods: numerical
© ESO 2020
1. Introduction
The discovery of distant trans-Neptunian objects (TNOs) moving in orbits with semimajor axes a > 150 au and perihelion distances q > 30 au has provided unexpected information about the structure of the outer Solar System. Trujillo & Sheppard (2014) first suggested that there is a concentration of arguments of perihelion ω near the value ω = 0°. This value corresponds to one of the centers of the libration zones in the von Zeipel-Lidov-Kozai mechanism of secular perturbations (Von Zeipel 1910; Lidov 1962; Kozai 1962). Therefore, an assumption was made about the existence of a distant planet producing this effect. Later, Batygin & Brown (2016) noted that, to a greater extent, there is a grouping of longitudes of ascending nodes Ω and longitudes of perihelion π = ω + Ω, and this effect is associated with the combined action of orbital and secular resonances (Batygin & Morbidelli 2017). Although Lawler et al. (2017) and Shankman et al. (2017a) scrutinized observational bias in the Outer Solar System Origins Survey sample and concluded that there is no evidence of clustering in angular orbital element distributions (see also Bernardinelli et al. 2020; Clement & Kaib 2020; Trujillo 2002), Brown (2017) estimated a rather low probability for the observed sample of TNOs with a > 230 au to be drawn from a uniform population. Detailed studies have shown that the observed features in the distribution of angular elements for distant TNOs could be produced by a planet with a mass of ∼5−10 Earth masses moving in an orbit with a semimajor axis a ∼ 400−800 au, eccentricity e ∼ 0.2−0.5, and inclination i ∼ 15−25° (Batygin & Brown 2016; Batygin et al. 2019).
Although the dynamical arguments seem quite convincing (Batygin & Morbidelli 2017), the question of the actual existence of a ninth planet in the Solar System remains open. Despite ongoing searches, the planet has not yet been discovered. An explanation for the formation of such a massive and distant planet is also difficult to establish (Batygin et al. 2019). Shankman et al. (2017b) and Kavelaars et al. (2020) have found dynamical effects that a massive distant planet would have on the distant TNO population that were not highlighted in the initial published theory of Batygin & Brown (2016). Nesvorný et al. (2017) concluded that the inclination distribution of Jupiter-family comets is wider than the observed one in models with a ninth planet.
However, without existing additional perturbers, it is difficult to explain the observed clustering of the apsidal lines of distant TNOs. It has been suggested that a self-gravitating massive disk of TNOs, and not a ninth planet, may be sustaining the confinement of the longitudes of perihelion (Sefilian & Touma 2019; Zderic et al. 2020). This suggestion was criticized in Batygin et al. (2019). Their main objections concern the lack of material needed for the formation and existence of the massive disk of TNOs. The arguments discussed were based on the widespread “core accretion” theory of planet formation (e.g., Safronov 1991; Montmerle et al. 2006; Armitage 2018) and the classical “minimum mass solar nebula” model of the solar protoplanetary disk (e.g., Weidenschilling 1977; Hayashi 1981; Desch 2007; Crida 2009).
An alternative planet formation scenario is provided by the “gravitational instability” theory (see, for example, the reviews Kratter & Lodato 2016; Nayakshin 2017). The detection of exoplanets in wide orbits provides observational support for this theoretical scenario (e.g., Marois et al. 2008; Bohn et al. 2020). The gravitational instability of protoplanetary disks is envisioned to lead to the formation of self-gravitating clouds of gas and dust (the canonical gas-to-dust mass ratio is 100:1), called giant gaseous clumps. Recently, it has been shown that such clumps participate in a complex dynamical interaction with the disk, which notably leads to the migration of clumps (Mayer et al. 2002; Vorobyov & Basu 2005; Nayakshin 2010; Baruteau et al. 2011; Zhu et al. 2012; Stamatellos 2015; Vorobyov & Elbakyan 2018). Moreover, migrating clumps can experience close encounters with each other, which often lead to the ejection of objects into hyperbolic orbits (Terquem & Papaloizou 2002; Vorobyov & Elbakyan 2018). Emel’yanenko (2020) showed that the observed distribution of angular orbital elements of TNOs could be created by the perturbations of such clumps, based on the results of hydrodynamical simulations in Vorobyov & Elbakyan (2018).
In this Letter, we first discuss new features of the observed distant TNOs. Then we consider dynamical processes of migration and close encounters of giant gaseous clumps, motivated by the results of Vorobyov & Elbakyan (2018). We attempt to determine whether the observed orbital distribution of distant TNOs could be induced by such clumps moving in orbits with different inclinations to the ecliptic. For this purpose, we study the dynamical evolution of small bodies from the Hill regions of the giant clumps. In the numerical hydrodynamics simulations of Vorobyov & Elbakyan (2018), the first clump forms 60 kyr after the star formation, and no clumps are present in the protoplanetary disk at 0.5 Myr. Thus, our model relates to a very early stage in the evolution of the protoplanetary disk when the present-day planets were not yet formed.
2. Orbital features of the observed distant trans-Neptunian objects
We consider TNOs with q > 40 au, in contrast to many previous works (e.g., Trujillo & Sheppard 2014; Batygin & Brown 2016) that analyzed orbits with q > 30 au. This restriction seems more justified when studying dynamical mechanisms in the early stages of Solar System formation. Orbits with perihelia near the orbit of Neptune have changed significantly over the lifetime of the Solar System due to planetary perturbations. Moreover, the stronger restriction on perihelion distances allows us to take into consideration not only orbits with very large a, but also a population of detached TNOs with smaller a. The heliocentric orbital elements presented on the website of the Minor Planet Center1 on January 16, 2020, were used for objects observed in at least two oppositions. A list of these objects and their orbital elements are given in Appendix A.
Figure 1 shows the distribution of semimajor axes and inclinations for TNOs with q > 40 au and a > 60 au. All the objects with a < 160 au have i > 20°. Large inclinations are not very unusual because there are dynamical mechanisms, in particular resonances, by which TNOs can reach high-inclination orbits. Really surprising is the lack of low-inclination orbits for all objects with q > 40 au and a > 60 au. Objects with larger semimajor axes have lower inclinations on average, and all the objects with a > 400 au have i < 15°. Figure 2 shows the distribution of longitudes of perihelion and perihelion distances for TNOs with q > 40 au and a > 100 au. For q > 40 au, two concentrations of longitudes of perihelion are clearly visible, even for objects with a > 100 au. The first group of 12 objects has the mean value 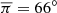 , and the second group of six objects has the mean value
, and the second group of six objects has the mean value 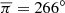 . The observed values of perihelion distances for these groups are different. For the first group, perihelion distances extend from 44 au to 80 au. Perihelion distances for the second group are smaller; they do not exceed 45 au. The orbits in these groups also differ in regards to the distribution of inclinations. While the inclinations for the first group are in the interval (4°, 20°) with the mean value i̅ = 15°, the inclinations for the second group spread from 14° to 48° with the mean value i̅ = 30°. The described features give us reason to suppose that we are observing two groups of objects with different dynamical characteristics. In this Letter, we assume that these features are inherent in the real distribution of distant TNOs and are not generated by observational biases.
. The observed values of perihelion distances for these groups are different. For the first group, perihelion distances extend from 44 au to 80 au. Perihelion distances for the second group are smaller; they do not exceed 45 au. The orbits in these groups also differ in regards to the distribution of inclinations. While the inclinations for the first group are in the interval (4°, 20°) with the mean value i̅ = 15°, the inclinations for the second group spread from 14° to 48° with the mean value i̅ = 30°. The described features give us reason to suppose that we are observing two groups of objects with different dynamical characteristics. In this Letter, we assume that these features are inherent in the real distribution of distant TNOs and are not generated by observational biases.
 |
Fig. 1. Distribution of semimajor axes and inclinations for observed multiple-opposition TNOs with q > 40 au and a > 60 au. |
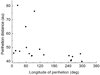 |
Fig. 2. Distribution of longitudes of perihelion and perihelion distances for observed multiple-opposition TNOs with q > 40 au and a > 100 au. |
3. Methods
We study a system of two interacting gaseous clumps surrounded by planetesimals in the Hill regions defined by the radius 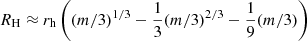 , where rh is the clump heliocentric distance and m is the clump mass in the astronomical system of units (e.g., Murray & Dermott 1999). This approach is based on the results from Vorobyov & Elbakyan (2018) regarding the dynamics of clumps. In this model, the outer object with a lower mass moves in an initial orbit with e ∼ 0.5. The inner object starts moving in a near-circular orbit with a ∼ 100 au. After a certain period of time, the objects approach each other. As a result of mutual perturbations, these objects enter into orbits with high eccentricities. The outer object is ejected to a near-parabolic or hyperbolic orbit. The inner object enters an orbit with q ∼ 30 au, and this orbit is quickly rounded off at such a distance due to interaction with the protoplanetary gas disk (see Fig. 17 in Vorobyov & Elbakyan 2018).
, where rh is the clump heliocentric distance and m is the clump mass in the astronomical system of units (e.g., Murray & Dermott 1999). This approach is based on the results from Vorobyov & Elbakyan (2018) regarding the dynamics of clumps. In this model, the outer object with a lower mass moves in an initial orbit with e ∼ 0.5. The inner object starts moving in a near-circular orbit with a ∼ 100 au. After a certain period of time, the objects approach each other. As a result of mutual perturbations, these objects enter into orbits with high eccentricities. The outer object is ejected to a near-parabolic or hyperbolic orbit. The inner object enters an orbit with q ∼ 30 au, and this orbit is quickly rounded off at such a distance due to interaction with the protoplanetary gas disk (see Fig. 17 in Vorobyov & Elbakyan 2018).
We assume that planetesimals exist in the Hill regions of giant clumps during their migration stage. According to the calculations in Vorobyov & Elbakyan (2018), the lifetimes of giant clumps in the protoplanetary disk do not exceed 0.5 Myr. Although the question of the formation of small bodies in such a short time period is open, there are many works that consider a very rapid formation of small bodies in the outer Solar System. For example, Wahlberg Jansson & Johansen (2014) claim that planetesimals of various sizes can be made at 40 au in their numerical experiments through the collapse of pebble clouds formed by the streaming instability in protoplanetary disks: more than ∼100 km in ∼25 years, 10 km in several hundred years, and 1 km in several thousand years. Boley et al. (2010), Nayakshin & Cha (2012), and Nayakshin (2017) argue that making solid bodies is more straightforward inside the giant gaseous clump regions than in circumstellar disks.
The main dynamical mechanism of creating the population of small bodies moving in distant heliocentric orbits is associated with a decrease in the size of the Hill region when the clump moves from aphelion to perihelion. Some bodies formed in the Hill region are outside this region at a certain time and are ejected from the vicinity of the clump.
Here we consider simple models in which the clump is treated as a point mass and the planetesimals are treated as massless particles. The particles are initially placed in the plane of the heliocentric motion of the clump. The planetesimal disk has the initial surface density profile of 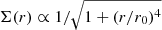 (Vorobyov & Elbakyan 2019), where r is the radius of a circular orbit around the center of the clump. According to the numerical simulations in Vorobyov & Elbakyan (2019), r0 is usually much less than R, where R is the clump radius; then, Σ(r) is approximately proportional to r−2 for r > R. For each r, the initial particles have a random uniform distribution along the orbit. We consider particles with initial r > R and prograde Keplerian velocities.
(Vorobyov & Elbakyan 2019), where r is the radius of a circular orbit around the center of the clump. According to the numerical simulations in Vorobyov & Elbakyan (2019), r0 is usually much less than R, where R is the clump radius; then, Σ(r) is approximately proportional to r−2 for r > R. For each r, the initial particles have a random uniform distribution along the orbit. We consider particles with initial r > R and prograde Keplerian velocities.
The integration of the equations of motion is based on the symplectic integrator for the N-body problem (Emel’yanenko 2007). To describe the changes of orbits during the migration of clumps, we applied a method used in Emel’yanenko (2011).
4. Numerical simulations
We consider a simple model that includes the Sun, two point-like massive clumps, and a set of particles initially located in the Hill regions of these clumps. To model the motion of clumps, we relied on the results of Vorobyov & Elbakyan (2018), but we carried out numerical simulations with different masses and orbits of clumps. Below we demonstrate variants for which the basic features of the simulated distribution are similar to those observed for distant TNOs. All the analyzed orbital elements are heliocentric.
In the first stage of our model, two clumps migrate slightly inward. The outer clump, with a mass of 12 Jupiter masses and radius R = 6.4 au, starts in the aphelion of the orbit with a = 187 au, q = 123 au, i = 30°, and π = 257°. The inner object, with a mass of 17 Jupiter masses and radius R = 7.2 au, starts in the orbit with a = 110 au, q = 100 au, i = 15°, and π = 98°. Near every clump, 1000 particles are initially distributed between R and RH at the aphelion distances of the clumps (37 au for the outer clump and 20 au for the inner clump). The dynamical evolution of the clumps is shown in Fig. B.1. The orbital distribution of particles in the first stage (after 2300 years) is described in Appendix C.
In our model, there is then a close encounter of the clumps. This encounter occurs near the perihelion of the outer clump and the aphelion of the inner clump. As a result, the inner clump evolves to have an orbit with q = 37 au. According to Vorobyov & Elbakyan (2018), the orbit quickly becomes near-circular at such a distance due to interaction with the protoplanetary gas disk, and the clump loses its mass. After that, this object weakly disturbs distant particles. Therefore, we consider the orbital distribution of particles near the moment of the perihelion passage of the inner clump.
Figure 3 shows the distribution of semimajor axes and inclinations for particles with 40 < q < 80 au and 100 < a < 1000 au (the observable region of distant TNOs). Only particles located outside the Hill regions of the clumps are included. Figure 4 shows the distribution of longitudes of perihelion and perihelion distances for the same particles. The main features of these distributions are consistent with those shown in Figs. 1 and 2. On average, the inclinations of the orbits decrease as the semimajor axes increase. There are two concentrations of particles in the distribution of longitudes of perihelion (applying the Kolmogorov–Smirnov statistical test to those presented in Fig. 4 shows that the hypothesis of a uniform distribution is rejected with a probability of more than 0.9999). We note that orbits of these two groups differ in inclinations (for example, the mean inclination of orbits with π < 180° is equal to 16.4°, while the mean inclination of orbits with π > 180° is equal to 28.7°).
 |
Fig. 3. Distribution of semimajor axes and inclinations for simulated particles with 40 < q < 80 au and 100 < a < 1000 au. |
 |
Fig. 4. Distribution of longitudes of perihelion and perihelion distances for simulated particles with 40 < q < 80 au and 100 < a < 1000 au. |
5. Discussion
We have studied a model in which two giant gaseous clumps approach each other and move into high-eccentricity orbits. In this Letter, we do not consider the possible further evolution of such clumps. According to Vorobyov & Elbakyan (2018), the inner clump is rapidly destroyed due to tidal effects. In the model discussed above, the final orbit of the outer object has q = 106 au and a = 544 au. It is natural to assume that this clump also gradually disperses in such an orbit, adding to the swarm of solid bodies in the distant Solar System. In some variants of our simulations, such a clump is ejected into a hyperbolic orbit, as in the work of Vorobyov & Elbakyan (2018).
The clustering of orbital elements is clearly discernible in our simulations. But this clustering should be sustained by some mechanism during the lifetime of the Solar System in order to be seen in the present observational data. For example, planetary perturbations are large enough to disperse the initial clustering of longitudes of perihelion throughout the lifetime of the Solar System, even for Sedna-type objects (e.g., Saillenfest et al. 2019). Sefilian & Touma (2019) propose that a self-gravitating disk of TNOs can maintain its orbital features throughout the lifetime of the Solar System. This scenario is very relevant for our model. Figure 5 shows the distribution of semimajor axes and perihelion distances for all particles with q > 30 au and positive a < 105 au. Obviously, it is not difficult to obtain the required mass of the disk of ∼10 Earth masses (Batygin et al. 2019; Sefilian & Touma 2019) if the initial giant clumps have masses of ∼10 Jupiter masses. We leave a detailed study of the orbital evolution of the disk population over the lifetime of the Solar System to a future paper.
 |
Fig. 5. Distribution of semimajor axes and perihelion distances for simulated particles with q > 30 au and positive a < 105 au. |
It is difficult to discuss in more detail the consistency of the suggested dynamical process and the observed distribution of distant TNOs. On the one hand, the number of detected distant TNOs is currently too small. On the other hand, it is evident that the process of the formation and migration of giant gaseous clumps is much more complicated than in our model. In particular, while we consider only two clumps on a relatively short timescale, numerical hydrodynamics simulations (e.g., Vorobyov 2013; Vorobyov & Pavlyuchenkov 2017; Vorobyov & Elbakyan 2018) show that the formation process of giant gaseous clumps continues for ∼0.5 Myr, with many clumps involved. It is actually surprising that the studied simple model describes the main features of the observed orbital distribution of distant TNOs so well.
In addition to the abovementioned features, Fig. 5 shows that there is a gap in the distribution of perihelion distances in the observable region for a > 170 au. A similar gap exists for the observed distant TNOs (although there are also no observed TNOs with q > 56 au for smaller semimajor axes). This figure also shows that our model produces many objects with 30 < q < 40 au and high eccentricities. Although modern theories relate the origin of such objects to the result of gravitational scattering by Neptune (the so-called scattered disk) (e.g., Morbidelli & Nesvorný 2020), our numerical simulations demonstrate that giant clumps migrating in the outer Solar System could play a significant role in creating this population of TNOs.
Future observations confirming the proposed dynamical process would have important implications for understanding the structure of the outer Solar System. We would like to note three points that were not explicitly discussed in the Letter but follow from the general approach of the considered model.
First, the solar protoplanetary disk was more extended than the classical minimum mass solar nebula model formulates. The theory of a massive, extended solar nebula has long existed, and it is supported by observations of massive disks around pre-main sequence and main sequence stars (e.g., Bailey 1994).
Second, there are many undiscovered small bodies with q > 80 au (see Fig. 5). A significant additional contribution can come from the disintegration of the outer clump.
Thirdly, Fig. 5 shows that many objects in our model reach high-eccentricity orbits located in both the inner core (103 < a < 104 au) (Hills 1981) and the outer component (a > 104 au) of the Oort cloud (Oort 1950). Therefore, the formation of the Oort cloud may be associated with the described process, although the main models relate the origin of the Oort cloud to the scattering of remaining planetesimals by the formed planets (e.g., Fernández 1980; Duncan et al. 1987; Dones et al. 2004; Emel’yanenko et al. 2007).
6. Conclusions
We have analyzed the orbital distribution of distant TNOs. We note several new features of the observed objects in addition to their known groupings in longitudes of perihelion. Although the number of detected objects is still too small to make final conclusions, the observed orbital distribution points to the existence of two groups of distant TNOs with different dynamical characteristics.
We have shown that the main features of the observed orbital distribution of distant TNOs can be explained by their origin in the Hill regions of migrating giant gaseous clumps that form in the outer solar nebula via gravitational fragmentation. In our model, two clumps with masses of ∼10 Jupiter masses interact gravitationally with the small bodies that surround them. The small bodies are ejected from the Hill regions when two giant clumps move in high-eccentricity orbits and have a close encounter with each other. The resulting orbital distribution of small bodies in our model and the observed distribution of distant TNOs have similar features.
Acknowledgments
The author acknowledges the support of the Large Scientific Project of the Russian Ministry of Science and Higher Education “Theoretical and experimental studies of the formation and evolution of extrasolar planetary systems and characteristics of exoplanets” (project No. 13.1902.21.0039). The calculations were carried out using the MVS-100K supercomputer of the Joint Supercomputer Center of the Russian Academy of Sciences. The author thanks an anonymous referee for helpful comments.
References
- Armitage, P. J. 2018, in Handbook of Exoplanets, eds. H. J. Deeg, & J. A. Belmonte, 135 [Google Scholar]
- Bailey, M. E. 1994, in Asteroids, Comets, Meteors 1993: Proceedings of the 160th Symposium of the International Astronomical Union, eds. A. Milani, M. Di Martino, & A. Cellino, 443 [CrossRef] [Google Scholar]
- Baruteau, C., Meru, F., & Paardekooper, S.-J. 2011, MNRAS, 416, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Brown, M. E. 2016, AJ, 151, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2017, AJ, 154, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Adams, F. C., Brown, M. E., & Becker, J. C. 2019, Phys. Rep., 805, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardinelli, P. H., Bernstein, G. M., Sako, M., et al. 2020, Planet. Sci. J., 1, 28 [CrossRef] [Google Scholar]
- Bohn, A. J., Kenworthy, M. A., Ginski, C., et al. 2020, ApJ, 898, L16 [CrossRef] [Google Scholar]
- Boley, A. C., Hayfield, T., Mayer, L., & Durisen, R. H. 2010, Icarus, 207, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E. 2017, AJ, 154, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Clement, M. S., & Kaib, N. A. 2020, AJ, 159, 285 [CrossRef] [Google Scholar]
- Crida, A. 2009, ApJ, 698, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J. 2007, ApJ, 671, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Dones, L., Weissman, P. R., Levison, H. F., & Duncan, M. J. 2004, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver, 153 [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Emel’yanenko, V. V. 2007, Celest. Mech. Dyn. Astron., 98, 191 [CrossRef] [MathSciNet] [Google Scholar]
- Emel’yanenko, V. V. 2011, Sol. Syst. Res., 45, 402 [CrossRef] [Google Scholar]
- Emel’yanenko, V. V. 2020, Sol. Syst. Res., 54, 64 [CrossRef] [Google Scholar]
- Emel’yanenko, V. V., Asher, D. J., & Bailey, M. E. 2007, MNRAS, 381, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, J. A. 1980, Icarus, 42, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hills, J. G. 1981, AJ, 86, 1730 [NASA ADS] [CrossRef] [Google Scholar]
- Kavelaars, J. J., Lawler, S. M., Bannister, M. T., & Shankman, C. 2020, in The Trans-Neptunian Solar System, eds. D. Prialnik, M. A. Barucci, & L. Young, 61 [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kratter, K., & Lodato, G. 2016, ARA&A, 54, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, S. M., Shankman, C., Kaib, N., et al. 2017, AJ, 153, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Sci, 322, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Quinn, T., Wadsley, J., & Stadel, J. 2002, Sci, 298, 1756 [Google Scholar]
- Montmerle, T., Augereau, J.-C., Chaussidon, M., et al. 2006, Earth Moon Planets, 98, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Nesvorný, D. 2020, in The Trans-Neptunian Solar System, eds. D. Prialnik, M. A. Barucci, & L. Young, 25 [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Nayakshin, S. 2010, MNRAS, 408, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2017, PASA, 34, e002 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S., & Cha, S.-H. 2012, MNRAS, 423, 2104 [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Dones, L., et al. 2017, ApJ, 845, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H. 1950, Bull. Astron. Inst. Neth., 11, 91 [Google Scholar]
- Safronov, V. S. 1991, Icarus, 94, 260 [CrossRef] [Google Scholar]
- Saillenfest, M., Fouchard, M., Ito, T., & Higuchi, A. 2019, A&A, 629, A95 [CrossRef] [EDP Sciences] [Google Scholar]
- Sefilian, A. A., & Touma, J. R. 2019, AJ, 157, 59 [CrossRef] [Google Scholar]
- Shankman, C., Kavelaars, J. J., Bannister, M. T., et al. 2017a, AJ, 154, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Shankman, C., Kavelaars, J. J., Lawler, S. M., Gladman, B. J., & Bannister, M. T. 2017b, AJ, 153, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D. 2015, ApJ, 810, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2002, MNRAS, 332, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, C. A. in The Trans-Neptunian Solar System, eds. D. Prialnik, M. A. Barucci, & L. Young, 79 [Google Scholar]
- Trujillo, C. A., & Sheppard, S. S. 2014, Nature, 507, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Von Zeipel, H. 1910, Astron. Nachr., 183, 345 [CrossRef] [Google Scholar]
- Vorobyov, E. I. 2013, A&A, 552, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, ApJ, 633, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Elbakyan, V. G. 2018, A&A, 618, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Elbakyan, V. G. 2019, A&A, 631, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Pavlyuchenkov, Y. N. 2017, A&A, 606, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahlberg Jansson, K., & Johansen, A. 2014, A&A, 570, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
- Zderic, A., Collier, A., Tiongco, M., & Madigan, A.-M. 2020, ApJ, 895, L27 [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Nelson, R. P., & Gammie, C. F. 2012, ApJ, 746, 110 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Orbital elements of distant multiple-opposition TNOs
Table A.1 gives the heliocentric orbital elements and their standard deviations for the TNOs with a > 100 au used in Sect. 2. These values were taken from the Jet Propulsion Laboratory website2 on September 2, 2020.
Heliocentric orbital elements of distant multiple-opposition TNOs at epoch 2020 May 31.0.
Appendix B: Dynamical evolution of the studied clumps
 |
Fig. B.1. Heliocentric distances of two clumps. |
Figure B.1 shows the heliocentric distances of two clumps as a function of time.
Appendix C: Orbital distribution of particles before a close encounter
 |
Fig. C.1. Distribution of longitudes of perihelion and semimajor axes for simulated particles with 40 < q < 80 au and a > 100 au after the first stage. |
After 2300 years of evolution, the outer clump reaches the orbit with a = 180 au and q = 107 au, and the inner clump moves in the orbit with a = 100 au and the aphelion distance Q = 107 au. Figure C.1 shows the distribution of longitudes of perihelion and semimajor axes for particles with 40 < q < 80 au and a > 100 au (the observable region of distant TNOs) at this time. Only particles located outside the Hill region are included. All these particles originate in the Hill region of the outer clump. The inner clump does not contribute to the observable region at this stage. The longitudes of perihelion of the particles are concentrated near the value of π of the outer clump.
All Tables
Heliocentric orbital elements of distant multiple-opposition TNOs at epoch 2020 May 31.0.
All Figures
 |
Fig. 1. Distribution of semimajor axes and inclinations for observed multiple-opposition TNOs with q > 40 au and a > 60 au. |
| In the text | |
 |
Fig. 2. Distribution of longitudes of perihelion and perihelion distances for observed multiple-opposition TNOs with q > 40 au and a > 100 au. |
| In the text | |
 |
Fig. 3. Distribution of semimajor axes and inclinations for simulated particles with 40 < q < 80 au and 100 < a < 1000 au. |
| In the text | |
 |
Fig. 4. Distribution of longitudes of perihelion and perihelion distances for simulated particles with 40 < q < 80 au and 100 < a < 1000 au. |
| In the text | |
 |
Fig. 5. Distribution of semimajor axes and perihelion distances for simulated particles with q > 30 au and positive a < 105 au. |
| In the text | |
 |
Fig. B.1. Heliocentric distances of two clumps. |
| In the text | |
 |
Fig. C.1. Distribution of longitudes of perihelion and semimajor axes for simulated particles with 40 < q < 80 au and a > 100 au after the first stage. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


