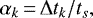| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A169 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202037624 | |
| Published online | 28 September 2020 | |
Spiral structure generated by major planets in protoplanetary disks
The role of periodic orbits near resonance
Kapteyn Astronomical Institute,
PO Box 800,
9700 AV
Groningen, The Netherlands
e-mail: sanders@astro.rug.nl
Received:
30
January
2020
Accepted:
28
May
2020
In this paper I describe numerical calculations of the motion of particles in a disk about a solar-mass object perturbed by a planet on a circular orbit with mass greater than 0.001 of the stellar mass. A simple algorithm for simulating bulk viscosity is added to the ensemble of particles, and the response of the disk is followed for several planet orbital periods. A two-arm spiral structure forms near the inner resonance (2–1) and extends to the planetary orbit radius (corotation). In the same way for gaseous disks on a galactic scale perturbed by a weak rotating bar-like distortion, this is shown to be related to the appearance of two perpendicular families of periodic orbits near the resonance combined with dissipation which inhibits the crossing of streamlines. Spiral density enhancements result from the crowding of streamlines due to the gradual shift between families. The results, such as the dependence of pitch-angle on radius and the asymmetry of the spiral features, resemble those of sophisticated calculations that include more physical effects. The morphology of structure generated in this way clearly resembles that observed in objects with well-defined two-arm spirals, such as SAO 206462. This illustrates that the process of spiral formation via interaction with planets in such disks can be due to orbital motion in a perturbed Keplerian field combined with kinematic viscosity.
Key words: protoplanetary disks / planet–disk interactions
© ESO 2020
1 Introduction
A striking result of recent high resolution near-infrared and submillimeter to millimeter observations of disks around young stars is the discovery of various structures (Perez et al. 2016, Avenhaus et al. 2018): rings, gaps, and spirals. These disks, on a scale of tens of astronomical units, are the sites of nascent planetary systems, and the observed structures may reflect, either as cause or effect, the formation of planets within the disks. Initially the detected structures were observed primarily in the polarized near-infrared scattered light that arises in the thin outer layers of the disks, and thus could essentially be a surface phenomenon (Dong et al. 2018). Detection of structure in CO line emission (e.g., Tang et al. 2017) is also relevant to the outer disk layers because of the large optical depth in these spectral lines. The more recent detection of structure in the thermal dust emission at millimeter wavelengths (Huang et al. 2018) more likely reflects the basic underlying structure of the disks implying that the structure is not merely surface phenomenon. This is significant because the mid-plane is the likely site of planet formation (a caveat is that the large grains responsible for millimeter wave emission are more susceptible to aerodynamic drag, and thus may not reflect the overall gas distribution; Andrews 2020).
For decades it has been known that satellites can sculpt the structure of planetary ring systems (like that of Saturn) by clearing gaps, forming rings, and exciting spiral structure (Goldreich & Tremaine 1979, 1980; Shu 1984). The new observations of protoplanetary disks (PPDs) may be evidence of a similar phenomenon on the scale of forming planetary systems, as explored in the work of Goodman & Rafikov (2001) and Ogilvie & Lubow (2002). Although most of the structure observed is essentially axisymmetric (rings, gaps), a non-trivial fraction, perhaps one-fifth to one-fourth, is of spiral form, in some cases even grand design two-arm spirals, as in galaxy disks (Dong et al. 2018). This suggests that the mechanisms for the generation of structure in PPDs are similar to those in galaxy disks: gravitational instability in the gaseous disk or the effect of pre-existing non-axisymmetric structure in the gravitational field (or some combination of the two). It is the second mechanism that I consider here.
In galaxies detailed structure is more evident in gas-rich disk systems than in spheroidal systems or early-type disks that are relatively deficient in gas. An aspect of this difference is due to star formation which, in effect, lights up the existing structure in the disk. But the argument has been made that the basic structure itself is due to the presence of a dissipative medium that responds in a highly non-linear way to weak perturbations in the axisymmetric potential of the dominant stellar component: a spiral or a bar form in the underlying stellar distribution, and hence in the gravitational field. For example, a weak bar distortion in the potential can excite conspicuous rings or spirals in the gaseous component (Sanders & Huntley 1976; Schwarz 1981). In this phenomenon periodic orbits play a primary role (van Albada & Sanders 1982) in forming the basis for gas streamlines.
The same must be true in PPDs, but in this case the non-axisymmetric distortion is due to forming or formed giant planets. As in the case of galaxy disks it is near the inner-Lindblad resonance (a test particle orbits twice as the planet orbits once) where periodic orbits far from the planet itself have the largest deviations from circular motion and have their dominant effect in initiating structure formation. However, there are obvious differences with general galactic disks: in the case of a planetary system the perturbation is one-sided, corresponding to an m = 1 distortion in a Fourier description, but the response of orbits at the inner resonance is bisymmetric, m = 2. Thus, the gas response near the resonance would be expected to reflect this symmetry. I argue here that the overlapping of two families of periodic orbits in a dissipative medium is the basic driver of two-arm spiral structure formation excited by planets in PPDs, although one would expect m = 1 variations about this bisymmetric structure near corotation where the planet is no longer a weak perturbation.
The formation of spirals in disks perturbed by massive planets has been demonstrated in earlier numerical hydrodynamical calculations,so this is not a new result (Dong et al. 2015; Zhu et al. 2015). These previous calculations are sophisticated, including effects such as three-dimensional structures, multi-components, and radiative transfer, whereas the simulations employed here are simple in comparison. The simulations are two-dimensional, where the zeroth-order axisymmetric force is the inverse square law due to the central star (on the order of one solar mass). This symmetry is broken by a planet of one-thousandth to several thousandths of the stellar mass (one to several Jupiter masses) on a circular orbit within the disk at a distance of several tens of astronomical units. The disk is represented by an ensemble of several thousand particles, and the effects of dissipation are simulated by giving each particle an interaction size on the order of twoastronomical units, an interaction which reduces the velocity differences between particles over this distance.
The goal is not primarily to model specific systems (although one specific system with a well-defined two-arm structure is considered), but to reduce the problem to its essential elements. The only physics entering the calculation is two-dimensional motion in a perturbed Keplerian potential including a crude mechanism for simulating viscosity. Nonetheless, with this brutalized approach the spiral structure revealed in more elaborate simulations is reproduced, and the basic anatomy of spiral structure generation in PPDs can be understood in terms of the response of sticky test particles at resonance. I do not mean to imply that this is the only, or even the primary, mechanism underlying the observed spirals in the astrophysical environment, but it may be a fundamental driver of this phenomenon.
These spiral arms are kinematic spirals; they are not dynamic self-gravitating structures, which would certainly be expected in cases where the disk mass is a substantial fraction of that of the central star (Dong et al. 2018). Nonetheless, the fact remains that massive planets do form in such disks and will, inevitably, have the effect of generating spiral structure via this mechanism within a sufficiently viscous surrounding gaseous disk.
2 Response of gas disks to a weak bisymmetric perturbation
The equation of hydrodynamics in Lagrangian form, neglecting pressure gradient forces and viscous stresses, is the equation of motion of a particle in the given gravitational potential. That is to say, in the absence of thermal, turbulent, viscous, or magnetic pressure forces, the motion of an element of gas is described by an orbit, and in steady-state gas stream lines correspond to simple non-intersecting periodic orbits. But a stronger statement can be made: given an ensemble of particles moving in a potential, filling the entire volume of phase space permitted by the Hamiltonian constraint, and allowing these particles to be “sticky” in the sense that over some finite interaction distance the relative radial velocities of neighboring particles are reduced (in effect adding a viscous force that resists compression of a fluid element), then we find that such viscous dissipation forces the motion onto periodic orbits; that is to say, periodic orbits arise as attractors in the phase space of the system and each orbit family has its basin Lake & Norman (1983), the region of phase space within which a particle will inevitably move toward the attractor.
Only a subset of such periodic orbits can represent streamlines: those that do not cross other period orbits (i.e., separate attractors with non-overlapping basins) and that are not self-looping. Otherwise hydrodynamical effects must intervene and the nature of the gas flow is altered, but often in way that is clearly related to the original periodic orbits. This was demonstrated more than 40 yr ago in Eulerian hydrodynamical simulations which followed the gas response in a galactic potential perturbed by a non-axisymmetric term (cos(2θ)) (Sanders & Huntley 1976). In these calculations the non-axisymmetric forcing is given a figure rotation such that all three principal resonances, inner-Lindblad (ILR), coronation, and outer-Lindblad (OLR), are present within the numerical grid. The assumed axisymmetric force law (r−1.5) assures that these resonances are equally spaced.
The principal families of simple periodic orbits (most nearly circular) near the inner resonance are elongated, but differ in orientation by 90°. These two stable families are designated X1 and X2 (Contopoulos & Mertzanides 1977), where X1 is dominant between the ILR and corotation and elongated parallel to the major axis of the bar-like distortion; X2 is elongated perpendicular to the distortion and is dominant within the ILR or between two ILRs. For particle orbits the amplitude of the deviation from circular motion increases near the resonance and the two perpendicular families intersect, but the hydrodynamical simulations demonstrate that the transition from X2 to X1 is gradual and results in a rotation of gas streamlines, which now crowd in the locus of a trailing two-arm spiral.
As a test I repeated this experiment using the Lagrangian sticky particle technique employed here. The details of this method have been described previously (Sanders 1998) and are briefly summarized here. The particles, in two dimensions, are disks all with radius σ. A particle i may be influenced by a second particle j at a separation rij < σ where that influence is weighted by a third-order polynomial w(x) (x = rij∕σ) with coefficients chosen such that the peak is at w(0) = 1.0 and w(x) falls smoothly to zero at x = 1 (w(x) = 1 − 3x2 + 2x3) At every time-step Δtk particle i adjust its velocity so as to reduce the velocity difference with each neighbor j, but only for approaching neighbors. If Vij is the component of the velocity difference along the line joining the two particles (Vij is a vector at the position of i pointing away from j), then over this time step particle i changes its velocity by an amount given by the vector sum
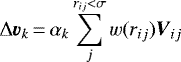 (1)
(1)
where ts is a dissipation timescale typically taken to be roughly a characteristic orbit timescale.
This method provides an explicit kinematic bulk viscosity that is proportional to the local velocity divergence, but only if that divergence is negative (converging flow). The method manifestly conserves linear momentum (the effect of particle j on particle i is equal but opposite that of particle i on particle j); angular momentum is also conserved to high precision in rotating viscous fluid in an axisymmetric potential. There is no explicit shear viscosity in this scheme, but because it is dissipational the method does not conserve energy. Consequently, there is some radial re-arrangement of the density of particles in an axisymmetric rotating fluid, but this happens slowly, on a timescale of 50 characteristic rotation periods.
In repeating the Sanders-Huntley experiment I took 6000 finite size particles initially uniformly covering a circular area with a radius of 40 distance units (one unit may be taken as 10 pc). For each particle σ = 3.5 units so that on average one particle overlaps 45 neighboring particles. The strength of the non-axisymmetric perturbation is initially zero, but grows to a maximum over one pattern rotation period corresponding to an azimuthal force of 0.05 of the axisymmetric force. The pattern speed is such that the three principal resonances are located at radii 15, 30, and 45. The setup and the results are shown in Fig. 1.
Figure 1a shows the principal periodic orbits in the perturbed potential near the inner resonance: the X1 family elongated parallel to the major axis of the bar distortion (along the X-axis), and the X2 family perpendicular to the bar distortion. These two families intersect near the resonance, and therefore cannot represent gas streamlines. Figure 1b illustrates the distribution of 6000 particles after five pattern rotation periods in the fully perturbed potential, but with no dissipation (this is a pure orbit calculation). We see the pattern of periodic orbits in the crowding of particles which gives rise to rings and gaps. Figure 1c is the distribution of 6000 dissipative particles in the complete non-axisymmetric potential after five bar rotation periods with the viscous force (Eq. (1)) in place. The trailing spiral structure is present throughout the radial range of the simulation and is similar (but not identical) to that found by Sanders-Huntley in the Eulerian scheme on a 40 × 40 cartesian grid; in the earlier simulation there is even a trace of the double spiral structure seen here. Figure 1d shows the paths of several particles near resonance taken from the full simulation (Fig. 1c). These are the gas streamlines; the gradual rotation of the streamlines by 90° between X2 and X1 is evident and results in the trailing spiral pattern.
Overall, the method applied here provides an acceptable solution for the gas distribution and flow in the perturbed potential in the highly supersonic limit.
3 Gas flow in a protoplanetary disk perturbed by a giant planet
The proposal is that the generation of spiral structure in a PPD containing a Jupiter-mass planet is fundamentally the same as in the perturbed galaxy disk considered above with respect to the role of periodic orbits. The origin of the inverse square force is at the center, and the source can be scaled to one solar mass. The planet is on a circular orbit at a radius of 32 units where one unit can be scaled to 1 AU. In the Keplerian potential, this places the ILR and OLR at 20 and 42 AU, respectively. Combined with a velocity unit of 1 km s−1, the distance scaling of 1 AU and a mass scale of one solar mass, the time unit is 4.75 yr. Scaling is straightforward in this gravitational central force problem with no additional physics; keeping GM fixed while scaling distance by a factor f is equivalent to scaling the time unit by a factor of f1.5.
Figure 2 illustrates the structure of several periodic orbits in the rotating frame of the planetary orbit near the ILR. The different panels correspond to four different values of the planetary mass: 0,001, 0.002, 0.004 and 0.006 in units of the central mass (1, 2, 4, and 6 Jupiter masses or MJ). The two perpendicular orbit families are evident in the perturbed Keplerian potential. In Fig. 2a (one Jupiter mass) these periodic orbits are seen to barely overlap, but for 2, 4, and 6 MJ the overlapping becomes more pronounced,as do deviations from m = 2 symmetry. From the above arguments this would imply that the spiral structure should be weak for the 1 MJ perturber, but increasingly conspicuous for the higher mass perturber, and indeed this is evident in the simulations including dissipation.
Figure 3 illustrates the response of the gas disk corresponding to these same planetary masses in the rotating frame. Again I take 6000 particles initially distributed with constant density in a disk with a radius of 40 AU. For every particle σ = 1.8, so initially the average number of interacting neighbors is 12. To avoid high accelerations an inner boundary is taken at 5 AU; particles crossing the inner boundary are reflected. The panels are snapshots showing the distribution of the ensemble of dissipatingparticles after four planet orbital periods (780 yr). In all cases, a quasi-steady state is reached after two rotation periods. To avoid shocking the system I have also run cases in which the planet mass builds up slowly, over one revolution period, but this makes no difference in the final gas distribution,
In the case of a one Jupiter mass perturber, a faint spiral structure is visible, as would be expected from the slight overlapping of periodic orbits, but as the mass of the perturber increases, the spiral response becomes stronger. There are two principal arms that wrap through roughly 200°. The breakdown from bisymmetry due to the planet is especially evident in the primary arm that connects to the planet at corotation. There is a cluster of particles about the planet in all cases; this corresponds to the Hill sphere within which particles are permanently trapped by the planet (radius of about 3.5 AU for the 4 MJ case).
The amplitude of the spiral response appears to be roughly proportional to the mass of the perturber over this range of planetary masses. This is illustrated in Fig. 4, which is a plot of the gas surface density (smearing particle mass by the smoothing function w(x) over σ) as a function of azimuthal angle at a radius of 20 AU for a planet masses of 2 MJ (solid curve) and 6 MJ (dashed curve). The amplitude of the response increases with the mass of the perturber, as does the asymmetry between the two principle arms. This is expected because of the increasing m = 1 signal with planet mass in the perturbed potential. This figure also illustrates an additional marker of the basic spiral structure: the angular separation between the primary and secondary arms. At 20 AU (r∕rp = 0.62) this varies from 140° (2 MJ) to 165° (6 MJ), which is broadly consistent with the results given by Bae & Zhu (2018b).
For both principal arms the pitch angle decreases moving inward from corotation; thus, the geometry of the arms is not described well by a logarithmic spiral. To estimate the run of pitch angle with radius it is best to consider the density distribution displayed in a polar map, as in Fig. 5 for the Mp = 6 MJ case (density contours shown in the θ-r space). The two principal arms (and a faint third arm) are evident in the figure, as is the deviation, most conspicuous for the primary arm from a constant pitch angle.
With this display one can determine the run of pitch angle via the relation ψ = d ln(r)∕dθ; the results are shown in Fig. 6 where the run of pitch angle is plotted against radius in terms of the semi-major axis of the 6 MJ planet. The results for the primary amd secondary inner arms are shown, as well as the outer arm, and are compared to the numerical simulations of Zhu et al. (2015). The form and range of the pitch angle dependence do not vary greatly with planetary mass, reflecting the fact that streamline rotation of 90° is the maximum possible over the range between ILR and corotation independent of planetary mass. It is also clear that the arms tend to wrap into a ring at about 0.4 rp, that is, within the inner resonance at 0.62 rp. In the higher resolution calculations of Bae & Zhu (2018b), the spirals continue to wrap within this radius.
These results on pitch angle, asymmetry, and arm separation are generally consistent with the sophisticated simulations of Zhu et al. This is significant because the only physics in the present calculation is orbital motion in the perturbed Newtonian potential with a crude algorithm for viscosity.
 |
Fig. 1 Particles and gas in weak rotating bar potential. (a) Periodic orbits in bar potential, (b) particle ensemble in bar potential, (c) ensemble in bar potential with viscosity, (d) gas orbits near resonance in full simulation. |
 |
Fig. 2 Periodic orbits in the rotating frame near inner resonance with various planet masses. Corotation is at r = 32 and the inner resonance at r = 20. (a) Mp = 1 MJ, (b) Mp = 2 MJ, (c) Mp = 4 MJ, (d) Mp = 6 MJ. |
 |
Fig. 3 Snapshots of the quasi-steady-state density distribution after 4.5 planet rotation periods in the fully dissipative gas of 6000 particles. (a) Mp = 1 MJ, (b) Mp = 2 MJ, (c) Mp = 4 MJ, (d) Mp = 6 MJ. |
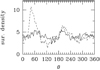 |
Fig. 4 Azimuthal distribution of gas surface density for 2 MJ (solid curve) and 6 MJ (dashed curve). |
 |
Fig. 5 Gas density distribution for the 6 MJ case in polar projection corresponding to panel 3d. |
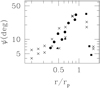 |
Fig. 6 Pitch angles as a function of radius scaled to planet radius for 6 MJ: circles and squares are the data points from the present calculations (triangles are secondary spirals); crosses are the data points from the simulations of Zhu et al. (2015). |
4 Role of dissipation
It should be noted that the mechanism described here for the role of viscous dissipation differs from most previous analyses of spiral structure generated in gaseous discs via interaction with planets. The seminal work on this subject is Goldreich & Tremaine (1979): in the linear limit spiral wakes in a gaseous disk perturbed by an orbiting planet are explained as a result of constructiveinterference among a set a wave modes propagating at the sound speed and having different azimuthal wave numbers. These linearcalculations are inviscid, but include self-gravity of the gaseous disk. A spiral wave is formed from the inner Lindblad resonance to corotation, and Goldreich and Tremaine emphasize that in the inviscid case no spiral waves propagate without some degree of self-gravity.
In the present simulations there is no self-gravity of the gas, but it is argued that the large-scale spiral structure results from trapping of gas on periodic orbits; near resonance these orbits intersect and dissipation intervenes to promote the gradual rotation of streamlines at resonance which crowd into a two-arm spiral pattern. Viscous dissipation is the only gas dynamical effect, and here it plays a critical role in the formation of coherent structure. The question arises: how do these two descriptions relate to one another: are they separate explanations or the same mechanism?
In the simulations the dissipation is promoted by an artificial bulk viscosity that inhibits the crossing of streamlines. For a disk initiallyin pure rotational motion, the finite size particles jostle one another due to the differential rotation, and a random velocity appears that initially grows until the energy loss rate becomes equal to the energy gain. In the simulations with σ = 1.8 and a viscous timescale of 1 AU kms−1 this equilibrium velocity is ΔV ≈ 0.03 km s−1 at rp = 32. This could be taken as the effective signal speed in the system; a disturbance is propagated from the center to corotation on a timescale rp ∕ΔV or roughly 30 planetary revolution periods. But in the simulations the structure develops on the much shorter dynamical (orbit) timescale, which is relevant to the trapping on periodic orbits.
It can be shown that for this algorithm (Eq. (1)) the resultant kinematic (bulk) viscosity in units of rp Vp at the radius of the planet is given by 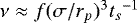 , where f is a factor (1/8 to 1/16) correcting σ to an effective particle size, and ts is the dissipation timescale in the adopted units (1 AU km−1 s−1). This amounts to
, where f is a factor (1/8 to 1/16) correcting σ to an effective particle size, and ts is the dissipation timescale in the adopted units (1 AU km−1 s−1). This amounts to 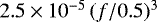 at rp.
at rp.
Previous discussions of viscosity in this context (Kley 1999; Bryden et al. 2000) have primarily focused on the longer timescale problem of accretion onto the forming planet rather than the role with respect to structure formation. Kley in particular considered separately an artificial kinematic bulk viscosity as well as shear, and his scaled viscosity coefficient was approximately that derived above. It is interesting that the spiral structure that developed was also similar to that described here. Like several cases considered by Kley, the present simulations do not contain an explicit shear viscosity; only the radially approaching components of the relative velocity of finite size gas particles are considered, so it is not meaningful to discuss these simulations in terms of the α disk assumption. Explicit shear viscosity could have been included in Eq. (1), but this was not relevant because the essential role of viscous dissipation in structure formation is to inhibit streamline crossing. The sound speed is effectively zero and gas elements can only communicate with one another via the bulk viscosity with the signal speed.
Bae & Zhu (2018b) demonstrated that in the linear limit (Goldreich & Tremaine 1979; Ogilvie & Lubow 2002) and in the absence of self-gravity and dissipative processes the phase of spiral arms agree with hydrodynamic simulations; moreover, they point out kinematic viscosity is not explicitly included in the simulations. In their case disturbances communicate with the explicit sound speed, whereas in the present simulations, the sound speed is effectively zero. The results here would appear to be relevant to a cold disk with vanishing disk thickness. In other words, the mass of the planet is much higher than the thermal mass (that at which the Hill or accretion radius is equal to the vertical scale height), even if we take the sound speed to be the signal speed with bulk viscosity. The implication is that within this limit the discussion in terms of periodic orbits should be valid.
To demonstrate the effect of bulk viscous dissipation I have run a set of simulations where the dissipation timescale, ts (Eqs. (1) and (2)) is varied. This parameter determines the strength of the viscous interaction with larger values implying a smaller effect of dissipation. Figure 7 shows the results of these simulations; panels a to d correspond respectively to a dissipation timescale of 0.2, 1, 5. 25 time units (one unit is scaled to 1 AU/1 km s−1 or 4.75 yr for the 4 MJ case). For the strongest dissipation (case a) the spiral structure is present, but the arms are rather diffuse and broad. Case b (ts = 1), the level of dissipation is that considered in the previous simulations (Fig. 3) and in case c the dissipation is much weaker (ts = 5). Here we see the arm connecting to the planet is less conspicuous, but a third arm with lower pitch angle is more prominent. Finally, in case d (ts = 25) the spiral structure consists of two tightly wound arms just inside the inner resonance and begins to resemble a complete ring. In the limit of vanishing dissipation the structure is that of ring-gap rather than spirals. These simulations illustrate, at least in this limit of cold thin disks, that the kinetic bulk viscosity is necessary for the development of a spiral structure excited by a massive planet, and that the properties of the arms depend upon the magnitude of the viscosity.
 |
Fig. 7 Effect of the dissipation timescale on the morphology of structure. The sequence a–d is in the sense of decreasing viscous dissipation. |
 |
Fig. 8 Particle and gas distribution for disks extending beyond the outer resonance (r = 42). (a) Dissipationless particle distribution, (b) Corresponding gas density distribution. |
5 Extended disks and non-circular planetary orbits
In all of the examples considered above, the radius of the circular planetary orbit was near the outer edge of the gaseous disk (rp = 32, Rd = 40). Here I consider the response of the gas when the planet is more deeply embedded within the disk. Such a case is shown in Fig. 8 where Rp = 28 and Rd = 50, and where Mp = 4; the disk extendsbeyond the outer-Lindblad resonance at a radius of 37.
In the first panel (Fig. 8a) we see the response of the ensemble of 6000 particles with no dissipation (pure dynamical orbits) after five planetary rotation periods. This reflects the basic structure of the periodic orbits; in particular we see a set of rings and gaps (particularly obvious at the location of the OLR) that is characteristic of the ballistic simulations. Figure 8b illustrates the response when dissipation is added via Eq. (1). Within the orbit of the planet the spiral pattern is that seen in the previous simulation (Fig. 3c), but beyond corotation a second almost disconnected two-arm spiral is evident; the principal arm is the extension of the planetary wake beyond corotation, and the secondary arm appears completely disconnected from the inner structure. This could be viewed as a prediction. For a disk extending well beyond the circular planetary orbit of a major planet, two separate spiral patterns should be observed.
The properties of the double-spiral system are more obvious on a polar density map, as shown in Fig. 9. It is particularly clear in this plot that the run of pitch angles for arms beyond the planet orbit radius differs from that within corotation in the sense that the pitch angles become smaller with increasing radius. Moving away from corotation in either direction, the arms wrap up. This could be useful in identifying the location of the planet with respect to the spirals (see also Bae & Zhu 2018b).
A second issue concerns deviations from a pure circular orbit. What is the form of the spiral pattern excited by a planet on a more general elliptical orbit? Figure 10 illustrates the effect of such deviations for the 4 MJ example. In both cases the elliptical orbit is broken down into the circular motion of the guiding center and the epicycle. In panel a of Fig. 10, the radius of the guiding center is 35 AU and the eccentricity is 0.1. In panel b of Fig. 10, the guiding center is at 38.7 AU and the eccentricity is 0.21.
The basic spiral pattern is essentially identical to that excited by the planet on the circular orbit at the guiding center, but the structure of the primary arm that connects to the planet differs and is transient. This is also generally true for more eccentric orbits (eccentricity of 0.4 for example), but additional transient structures appear at corotation. I have not pursued this further because of the certainty of secular evolution of the planetary orbit due to gravitational interactions with the excited structure (orbital decay), but the conclusion is that the basic spiral pattern generated is almost independent of deviations from circular motion, expected because the basic pattern of underlying periodic orbits depends on the radius of the guiding center.
 |
Fig. 9 Gas surface density distributions in polar projection for disk extending beyond the outer resonance (Fig. 7a). |
 |
Fig. 10 Gas density distribution for 4 MJ planets on non-circular orbits. The epicycle about the guiding center is shown in both cases. (a) Eccentricity = 0.1. (b) Eccentricity = 0.21. |
 |
Fig. 11 Left panel: structure observed in SAO 206462 in the J-band polarized continuum with r2 scaling (with permission of Stolker et al. 2016). The small bar on the lower left shows a linear scale of 28 AU at the assumed distance to the object of 140 pc. Right panel: snapshots of the distribution of 6000 sticky particles in orbits about a 1.7 M⊙ star perturbed by a 0.0068 M⊙ planet on orbit with semi-major axis of nearly 85 AU and an eccentricity of 0.061. |
6 Direct comparison with observations
As emphasized above, with respect to the observable characteristics of the generated spiral structure the results here are generally consistent with the sophisticated simulations that include more physical effects. Therefore, one could say that insofar as the previous calculations (such as those of Zhu et al. 2015) agree with the observations, so do these simplified simulations. Nonetheless,detailed comparisons of the results here with the observed spiral structure in actual PPDs, particularly with respect to morphology, remain of interest. How well do the shapes of the spirals formed by overlapping of periodic orbits in the presence of dissipation agree with observations?
Here I consider one specific case, SAO 206462 (HD 135344B), because it presents a reasonably clean two-arm spiral with low inclination to the line of sight (on the order of 11°), and it is clearly a case where the mass of the PPD is much less than that of the central star; self-gravity of the disk probably plays no role in exciting or maintaining the observed structure (van der Marel et al. 2016). Moreover, the spiral structure has the general characteristics (Fig. 6) typical of objects of this kind. The spirals sweep through about 200° covering a radial range of 30–80 AU and the mass of the central star is estimated to be 1.7 M⊙. To produce a spiral of this scale requires a planetary orbit having a semi-major axis of roughly 80 AU and a planetary mass in excess of 0.002 that of the star (0.0034 M⊙). I have simulated several such cases with these properties for three rotation periods over a range of orbital eccentricities. One of these is shown in Fig. 10 along with the observed system in the near-infrared J band (Stolker et al. 2016).
The simulation is for a planet of 0.004 M* (0.0068 M⊙) on an elliptical orbit (eccentricity of 0.061) at a distance of 85 AU to the star. Figure 11 is a snapshot after approximately three planetary rotations. The simulation provides a reasonable representation of the observed structure. In particular it demonstrates that the spiral arms wrap into a ring at about 0.4 times the planet orbital semi-major axis and that the bisymmetry is broken by the arm connecting to the spiral. In general this two-dimensional simulation with orbital motion in the presence of a simple scheme for viscosity adequately describes the phenomenon.
7 Conclusions
In an axisymmetric potential perturbed by a weak rotating bisymmetric distortion two families of periodic orbits elongated perpendicular to one another appear near the inner-Lindblad resonance. These orbits intersect and therefore cannot represent gas stream lines; viscosity forces gas flow onto gradually rotating stream lines, and the resulting density distribution is spiral in form, hence the appearance of spiral structure in a pure bar-like potential.
The same effect occurs in a disk rotating in a Keplerian potential perturbed by a planet even though the perturbation is not bisymmetric. This occurs because the same two orbit families arise near the inner resonance (2–1 resonance) and the overlap of these families becomes significant when the mass of the satellite is more than 1/1000 of the central mass. Hence, the appearance of a spiral structure is inevitable in a sufficiently dissipative gas and dust disk about a solar mass star perturbed by a planet of one Jupiter mass or higher.
In the calculations described here the only physical effects included are two-dimensional orbital motion in a perturbed Keplerian potential combined with a simple mechanism for an artificial bulk viscosity. This is all that is necessary for the generation of spiral structure in the thin disk environment of the forming planetary system. There is no radiative transfer, no third dimension, no two-fluid hydrodynamics, no shadowing, and no self-gravity of the disk. That is not to say that such effects are absent or play no role, but that the form of the periodic orbits near resonance provides the essential ingredient for the spiral response of a dissipative medium in a perturbed point-mass field. This sort of insight can be lost in more complicated calculations that do include these additional effects. The principal goal of the present work has been to gain some understanding of the underlying mechanism of spiral structure generation in planet-disk interactions, to elucidate periodic orbits as the foundation of such a structure. In that sense, this work is essentially a “proof of concept”.
I cannot claim that all spiral structure observed in PPDs is solely due to this mechanism of streamline crowding at resonances. The maximum pitch angle is limited to roughly 25° which may be exceeded in some observed systems. The total range of wrapping is restricted to about 200°, and there will inevitably be a breaking of bisymmetry in the observed spiral structure particularly near the perturbing planet. In some systems, particularly those with disk masses approaching that of the central star, a non-Keplerian potential as well as self-gravity in the disk will certainly play a role in exciting and shaping the observed structure, with or without the presence of a massive planet, but it seems to be the case that in many PPDs the disk mass is a small fraction of the stellar mass and that the disks are likely to stable against the self-gravitational formation of structure (Kama et al. 2020). Even if these conditions are met, it may require a cold, very thin disk to generate the observed structure via this mechanism.
Massive planets do form in such disks and they have the effect of exciting spiral structure. When the extent of the disk exceeds the outer-Lindblad resonance, there may even be the appearance of a second set of apparently disconnected spiral arms as in Fig. 8. The inner spiral should wrap into a circular ring at about 40% of the planetary orbit radius; that is to say, the planet would be found at a distance of roughly 2.5 the ring radius near the maximum extension of the strongest arm with the largest pitch angle. The acid test for this mechanism would be the actual observation of the perturbing (proto)planet at this location.
Acknowledgements
I am grateful to Renzo Sancisi for very useful comments on an earlier version of this manuscript and to Tomas Stoker for permission to use the near-infrared map of SAO 206462 as well as a useful comment on the broken 180° symmetry of the observed spiral structure. I also acknowledge numerous very helpful remarks from an anonymous referee, in particular suggesting evaluating of the significance of viscosity by simulations with various dissipation timescales (Fig. 7).
References
- Andrews, S. 2020, ARA&A, 58, 1 [Google Scholar]
- Avenhaus, H., Quanz, S., Antonio, G., et al. 2018, ApJ, 683, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Bae, J., & Zhu, Z. 2018b, ApJ, 259, 119B [CrossRef] [Google Scholar]
- Bryden, G., Różyczka, M., Lin, D. N. C., & Bodenheimer, P. 2000, ApJ. 540, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G., & Mertzanides, C. 1977, A&A, 61, 477 [NASA ADS] [Google Scholar]
- Dong, R., Zhao, Z., Rafikov, R., & Stone, J. M. 2015, ApJ, 809, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Najita, J. R., & Brittain, S. 2018, ApJ, 862, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
- Goodman, J., & Rafikov, R. R. 2001, ApJ, 552, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., Andrews, S. M., Perez, L. M., et al. 2018, ApJ, 869, 43 [Google Scholar]
- Kama, M., Trapman, L., Fwedele, D., et al. 2020, A&A 634, A88 [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Lake, G., & Norman, C. 1983, ApJ, 270, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lubow, S. H. 2002, MNRAS, 330, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, L. M., Carpenter, J. M., Andrews, S. M., et al. 2016 Science, 253, 6307 [Google Scholar]
- Sanders, R. H. 1998, MNRAS, 294, 35S [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R., & Huntley, J. 1976, ApJ, 209, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, M. P. 1981, ApJ, 247, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. 1984, Planetary Rings (A85-34401 15-88) (Tucson, AZ: University of Arizona Press), 513 [Google Scholar]
- Stolker, T., Dominik, C., Avenhuis, H., et al. 2016, A&A, 595, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, Y-W., Guilloteau, M., Dufrey, A., et al. 2017, ApJ, 840, 32 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S., & Sanders, R. H. 1982, MNRAS, 201, 303 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., Cazoletti, P., Pinilla, P., & Garafi, A. 2016, ApJ, 832, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Dong,R., Stone, J. M., & Rafikov, R. R. 2015, ApJ, 813, 88 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Particles and gas in weak rotating bar potential. (a) Periodic orbits in bar potential, (b) particle ensemble in bar potential, (c) ensemble in bar potential with viscosity, (d) gas orbits near resonance in full simulation. |
| In the text | |
 |
Fig. 2 Periodic orbits in the rotating frame near inner resonance with various planet masses. Corotation is at r = 32 and the inner resonance at r = 20. (a) Mp = 1 MJ, (b) Mp = 2 MJ, (c) Mp = 4 MJ, (d) Mp = 6 MJ. |
| In the text | |
 |
Fig. 3 Snapshots of the quasi-steady-state density distribution after 4.5 planet rotation periods in the fully dissipative gas of 6000 particles. (a) Mp = 1 MJ, (b) Mp = 2 MJ, (c) Mp = 4 MJ, (d) Mp = 6 MJ. |
| In the text | |
 |
Fig. 4 Azimuthal distribution of gas surface density for 2 MJ (solid curve) and 6 MJ (dashed curve). |
| In the text | |
 |
Fig. 5 Gas density distribution for the 6 MJ case in polar projection corresponding to panel 3d. |
| In the text | |
 |
Fig. 6 Pitch angles as a function of radius scaled to planet radius for 6 MJ: circles and squares are the data points from the present calculations (triangles are secondary spirals); crosses are the data points from the simulations of Zhu et al. (2015). |
| In the text | |
 |
Fig. 7 Effect of the dissipation timescale on the morphology of structure. The sequence a–d is in the sense of decreasing viscous dissipation. |
| In the text | |
 |
Fig. 8 Particle and gas distribution for disks extending beyond the outer resonance (r = 42). (a) Dissipationless particle distribution, (b) Corresponding gas density distribution. |
| In the text | |
 |
Fig. 9 Gas surface density distributions in polar projection for disk extending beyond the outer resonance (Fig. 7a). |
| In the text | |
 |
Fig. 10 Gas density distribution for 4 MJ planets on non-circular orbits. The epicycle about the guiding center is shown in both cases. (a) Eccentricity = 0.1. (b) Eccentricity = 0.21. |
| In the text | |
 |
Fig. 11 Left panel: structure observed in SAO 206462 in the J-band polarized continuum with r2 scaling (with permission of Stolker et al. 2016). The small bar on the lower left shows a linear scale of 28 AU at the assumed distance to the object of 140 pc. Right panel: snapshots of the distribution of 6000 sticky particles in orbits about a 1.7 M⊙ star perturbed by a 0.0068 M⊙ planet on orbit with semi-major axis of nearly 85 AU and an eccentricity of 0.061. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.