| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 5 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202038451 | |
| Published online | 21 August 2020 | |
The catalogue of cometary orbits and their dynamical evolution⋆
1
Centrum Badań Kosmicznych Polskiej Akademii Nauk (CBK PAN), Bartycka 18A, Warszawa 00-716, Poland
e-mail: mkr@cbk.waw.pl
2
Astronomical Observatory Institute, Faculty of Physics, A.Mickiewicz University, Słoneczna 36, Poznań, Poland
Received:
19
May
2020
Accepted:
23
June
2020
We present the CODE catalogue, the new cometary catalogue containing data for almost 300 long-period comets that were discovered before 2018. This is the first catalogue containing cometary orbits in the five stages of their dynamical evolution and covering three successive passages through the perihelion, with the exception of the hyperbolic comets which are treated in a different manner. Non-gravitational orbits are given for about 100 of these long-period comets, and their orbits obtained while neglecting the existence of non-gravitational acceleration are included for comparison. For many of the presented comets, different orbital solutions, based on the alternative force models or various subsets of positional data, are also provided. The preferred orbit is always clearly indicated for each comet.
Key words: comets: general / Oort Cloud
This catalogue (the CODE catalogue) is publicly available at https://pad2.astro.amu.edu.pl/comets
© ESO 2020
1. Introduction
The knowledge of orbits is crucial in many research areas related to the origin and the evolution of comets and their populations. In particular, the orbits of long-period comets (LPCs) are needed for studies on individual comets, as well as for the Oort Cloud dynamical evolution and its origin as a whole population; see, for example, Rickman (2014) and Dones et al. (2015) for reviews of the current unsolved problems.
We present the Catalogue of Cometary Orbits and their Dynamical Evolution (CODE catalogue). This is the first orbital catalogue showing the orbital evolution of LPCs during three consecutive perihelion passages – previous, observed, and future – and covering their dynamical evolution over a period of typically 1–10 million years. This is implemented by recording five snapshots of osculating orbits: previous, original, observed, future, and next. The positions of these snapshots along the trajectory are shown schematically in Fig. 1; we show as an example the orbit evolution of C/2012 T7 LINEAR. This particular plot describes the orbital changes of C/2002 T7 projected on its original orbit plane, where the five snapshots are indicated.
 |
Fig. 1. Orbital changes of C/2002 T7 projected on its original orbit plane that are described by five snapshots in CODE catalogue. Red line depicts the past motion of this comet while the blue line depicts its future evolution. Five epochs (snapshots) when orbital elements are recorded are marked: 1– osculating heliocentric orbit near the centre of the observational interval (typically near the perihelion); 2– original barycentric orbit recorded in past at 250 au from the Sun; 3– future barycentric orbit recorded in future at 250 au from the Sun; 4– previous orbit, recorded at the previous perihelion; 5– next orbit, in this case recorded at the escape border at 120 000 au from the Sun, but for many other comets recorded in the next perihelion. |
The CODE catalogue currently offers orbital solutions for a near-complete sample of comets discovered during the period 1885–2017 with an original semi-major axis greater than 10 000 au for a purely gravitational orbit. In this paper, we call these objects the Oort spike comets. Fewer than 20 Oort spike comets with q < 3.1 au discovered during the period 2013–2017 are missing, and they will be added in the near future.
As of May 2020, the CODE catalogue includes orbital solutions for 277 LPCs. Most of these comets were described in various dynamical aspects in a series of our previous papers; the most recent are Królikowska & Dybczyński (2017, KD2017) and Królikowska (2020, K2020). Some others (over 50 Oort spike comets have been discovered since 2012) will be analysed in our next paper, currently in preparation.
In the next section, we describe the procedure of determining the osculating orbit from the positional data and provide Snapshot 1. The method of obtaining Snapshots 2 and 3, that is original and future orbits, is described in Sect. 3. The previous and next orbit calculations (Snapshots 4 and 5) are sketched out in Sect. 4. Section 5 is devoted to the description of the CODE database content and its online interface. An example of a multi-threaded approach to orbit determination in several different variants is presented in Sect. 6, in the context of the comet C/2002 T7 with non-gravitational (NG) effects that are difficult for modelling. Some statistics of the CODE catalogue content is provided in Sect. 7, and future plans are laid out in the last section.
2. Osculating orbit determination: Snapshot 1
All osculating orbits of comets in the CODE catalogue were determined from the positional data using the same method of orbit determination and a model of the Solar System that was used in our previous papers (see, for example, Królikowska & Dybczyński 2010, KD2010; Królikowska 2014, K2014), including the procedure of data selection and weighting (Sect. 2 in KD2010). Only the aspects related to the NG acceleration are briefly discussed below.
This homogeneity of methods and models used in the CODE catalogue is essential for statistical considerations of comet orbits, particularly when trying to determine the shape of the Oort spike maximum (that is the original 1/a-distribution).
2.1. Non-gravitational orbits
Over one-third of the LPCs presented in the CODE catalogue exhibit detectable NG accelerations in their orbital motion. In the subsample of small perihelion distance comets (q < 3.1 au), NG orbits are determined for over 60 percent of objects. We present an NG orbit solution for all these comets, along with their purely gravitational orbit for the sake of comparison.
To determine the NG orbit, we rely on the widely used formalism described by Marsden et al. (1973). Here, the three orbital components of the NG acceleration acting on a comet nucleus are proportional to the g(r)-like function, which is symmetric relative to a perihelion,
where F1, F2, and F3 represent radial, transverse, and normal components of the NG acceleration, respectively, and the radial part is defined as positive outwards along the Sun-comet line.
However, for some comets we applied different sets of coefficients m, n, k, the distance scale r0, and the normalisation constant α (fulfilling the condition: g(1 au) = 1). Generally, for comets with q ≤ 3.1 au, the standard values dedicated to a water sublimation were used, whereas for q ≥ 3.1 au we often took the values more adequate for a CO-sublimation (see Table 1). In a few cases, we managed to apply an even more dedicated approach, as in the case of comets C/2001 Q4 NEAT or C/2002 T7 LINEAR.
Moreover, it was also possible to determine the fourth NG parameter, which describes the shift of a maximum of g(r)-function relative to the moment of perihelion passage, for some comets (Yeomans & Chodas 1989; Sitarski 1994); see, for example, asymmetric NG solutions for C/1956 R1 Arend-Roland, C/1959 Y1 Burnham, C/1990 K1 Levy, C/1996 E1 NEAT, C/1993 A1 Mueller, C/1998 P1 Williams, C/2002 T7 LINEAR, C/2007 W1 Boattini, and others (see also K2020). However, such asymmetric solutions can not always be considered as the preferred ones; this is, for example, the case of C/2002 T7 (see Sect. 6).
It should be stressed that in all cases the NG parameters were obtained together with the osculating orbital elements. This was done in an iterative process of NG orbit determination based on positional observations (more details are available in KD2010).
In cases where the assumption of constant NG parameters (see Eq. (1)) operating within the entire data arc is not adequate (due to an unexpected variable comet activity for any reason), it was worthwhile using another dedicated approach, particularly in the context of studying the past or future evolution of analysed LPCs. Therefore, in such a situation when NG acceleration seems to be significantly different before and after perihelion passage, we also present separate orbit solutions based on observations taken separately before and after the perihelion passage, or give a solution based on data taken only at large heliocentric distances; see, for example, different orbital solutions for: C/1993 A1 Mueller, C/2001 Q4 NEAT, C/2002 T7 LINEAR, C/2003 K4 LINEAR, C/2007 W1 Boattini, C/2008 A1 McNaught, and others.
In the sample of LPCs with small perihelion distances, especially for those with q ≤ 1 au, sudden outbursts and/or split events were often observed (Sekanina 2019). For these cases, we derived the orbit (gravitational or NG orbit) on the basis of data restricted to the period prior to the detected sudden activity of a given comet; see, for example, C/1999 S4 LINEAR, C/2010 X1 Elenin, C/2002 O4 Hönig, C/2002 O7 LINEAR, C/2012 S1 ISON, and others.
As a result of different possible force models and alternative approaches to available positional data, a set of various orbital solutions is presented for many comets in the CODE catalogue, with an indication of the preferred orbit; for more details, see K2020. The case of C/2002 T7 is a representative example of various solutions presented in the CODE catalogue (see Sect. 6). In total, at the moment of this writing, we present 508 different orbital solutions for 277 individual LPCs.
2.2. Division of comets into four groups
Each comet in the CODE catalogue is classified into one of four groups to indicate the various impact of NG effects on positional data fitting (for more details, see Sect. 5 of K2020). These groups are listed below in order of decreasing impact of NG effects on a comet’s trajectory. Membership to a specific group is indicated by one of the following descriptions.
One: “Comet lost close to perihelion or split comet”. This group consists of split comets or those lost soon after perihelion, and the NG orbit is determined using some part of the data (see, for example, comets C/2002 Q4, C/2002 Q7, and 2012 S1). At the moment, there are about a dozen such comets in the catalogue. For these comets, large NG effects are often derived using the standard g(r) formula (see Eq. (1)), but the effects should be physically interpreted as a sudden change in the comet’s activity, sometimes occurring long before the main split event (e.g. in the form of outbursts). Therefore, the NG orbit should be determined using Eq. (1) from a shorter data arc for which there are no reports of such violent activities.
Two: “Comet with NG effects strongly manifested in positional data fitting”. At the moment, about 20 comets qualify for this group (see, for example, C/1956 R1, C/1959 Y1, C/1998 P1, C/2001 Q4, C/2002 T7, C/2007 W1, and C/2008 A1).
Three: “Comet with determinable NG orbit”. This group consists of all remaining comets with determinable NG effects. This is one of the two largest groups, containing several dozen comets.
Four: “NG effects not determinable”. These are comets with indeterminable NG effects using only the positional observations. It is the largest group of comets. Also included in this group are C/2010 X1 and C/2012 T5 with preferred GR orbits (see Group [1]).
A card describing the purely gravitational orbit is shown for each comet in the CODE catalogue. This card contains a block named “solution description” (left-hand side of the screen). There is an information about the “detectability of NG effects in the comet’s motion” including one of four possibilities described above.
3. Original and future cometary orbits: Snapshots 2 and 3
For the past and future dynamical evolution of a given comet, a swarm of 5001 virtual comets (VCs), including the nominal orbit, were constructed according to the Monte Carlo method proposed by Sitarski (1998). This approach allowed us to determine the uncertainties of all orbital elements at any epoch covered by a numerical integration to the previous perihelion passage, as well as to the subsequent perihelion passage.
Next, the dynamical evolution of each swarm of VCs was numerically followed backwards and forwards in time until each VC reached 250 au from the Sun, that is, a distance where planetary perturbations are already negligible. At this stage we also switched from a heliocentric to a barycentric reference frame. These swarms of orbits are called original (Snapshot 2) and future (Snapshot 3) and are available for download as described in Sect. 5.1.
An interesting example is C/2002 T7 LINEAR, as various approaches were used to determine its orbit (Królikowska et al. 2012, K2020, and Sect. 6). The trajectory of this comet is shown in Fig. 1; the position of the observed perihelion is indicated in an inset by a green point with the label “1”, while positions corresponding to the original and future snapshots are given by green points with the labels “2” and “3”, respectively. Due to a small perihelion distance of 0.615 au, the perihelion point merges with the position of the Sun in this plot.
4. Previous and next cometary orbits: Snapshots 4 and 5
Original and future swarms of the orbits of LPCs were next followed numerically, taking Galactic and stellar perturbations into account. We used the models and methods described in detail in Dybczyński & Berski (2015). In short, we numerically integrated each VC with the Sun and several hundred nearby stars under the overall Galactic potential.
Our current list of potential stellar perturbers includes 643 stars or stellar systems that can appear closer than 4 pc from the Sun during the studied time intervals (typically 10 Myr into the past or into the future). The detailed description of this list and of the publicly available database of stellar perturbers1 can be found in Wysoczańska et al. (2020).
To obtain Snapshots 4 and 5, we generally stopped our calculation at the previous (when numerically integrating an orbit backwards in time) or next perihelion (when a comet orbit is integrated forwards in time). However, for hyperbolic or extremely elongated elliptic orbits in a swarm of VCs, we applied the so-called “escape limit” of 120 000 au; see Snapshot 5 in Fig. 1. We call the final orbits obtained from these calculations “previous” (Snapshot 4) and “next” (Snapshot 5). In the catalogue, we call a comet (or, more precisely, each individual VC) “returning” [R] if it goes (backwards or forwards in time) no further than 120 000 au from the Sun. All other VCs are generally named “escaping” [E]; however, in this group we separately count a number of hyperbolic [H] orbits.
In many cases a variety of the dynamical behaviour among VCs within a particular swarm of orbits enforced the use of individual rules of stopping the numerical integration. We decided to treat each swarm of orbits as uniformly as possible; thus, we distinguish between the following three cases.
One: When all VCs of a particular comet were returning, they were stopped in two ways. They were either stopped at the previous (or next) perihelion (a basic variant) or stopped simultaneously at the moment when the nominal VC reached the previous or next perihelion (a synchronous variant).
Two: When all VCs were escaping, the calculation was stopped synchronously at the moment when the fastest VC crossed the escape limit. This was usually very close to a heliocentric distance of 120 000 au.
Three: When a swarm of VCs consisted of both returning and escaping VCs, we decided to stopped them in two ways. The returning part was stopped at the previous or next perihelion and the rest (escaping ones) were stopped when the fastest escaping VC crossed the escape limit (mixed variant). All VCs (both returning and escaping) were stopped at the moment when the fastest VC crossed the escape limit (synchronous variant). The synchronous variant is used to examine more homogeneously constructed orbital element distributions, that is when all VCs were stopped exactly at the same epoch.
In the CODE catalogue, we describe parameters of the previous and/or next orbit of a comet using statistics of basic or synchronous variants depending on an individual swarm structure. It means that for previous and next orbits we present: a number of returning [R], escaping [E], and hyperbolic [H] (among the escaping) VCs in a swarm. We mark in which of these three parts of VCs the nominal orbit can be found. We also present the reciprocal of the semi-major axis, an aphelion distance, and a time interval to the previous or next perihelion.
The last three parameters are presented in two variants. In the case when their distribution in the swarm is close to the Gaussian, we present the mean value and its standard deviation. If the distribution of a particular parameter is far from being a normal one, we present three deciles: the first (10 percent of distribution), the fifth (median), and the ninth (90 percent). We additionally present statistics of the previous or next perihelion distance, showing the percentage of its values smaller than 10 au, between 10 and 20 au, and greater than 20 au. For previous orbits, we interpret these value ranges as defining whether the particular comet is dynamically old, has an uncertain status, or is dynamically new, respectively (more details are available in KD2017).
The example of C/2002 T7 in Fig. 1 demonstrates how the above rules work. According to the preferred solution, this comet passed its previous perihelion at a distance of about 150 au (see the green point labelled “4”). However, this Oort spike comet escapes from the planetary zone on a hyperbolic orbit. Therefore, Snapshot 5 was taken at the moment when the comet reached 120 000 au from the Sun in our dynamical calculations of its future motion (currently this comet is less than 40 au from the Sun).
5. CODE database usage
There are two main ways to view the CODE database interface: “Browse” and “Search”. The former allows the user to browse through all the orbital solutions available in the database, including the osculating, original, future, previous, and next orbits described in the preceding sections.
The Search screen allows a user to search through the data by narrowing almost all parameter intervals. Below, we briefly describe both of these functionalities.
An anonymous user has access to a slightly narrowed subset of data; for example, objects currently under additional study might be partially embargoed. Logged users can access some additional objects or individual orbits. Log-in credentials can be obtained from the authors via e-mail in well-founded cases.
5.1. Browsing the CODE database
Browse is the default view of the CODE database, available immediately after opening the website’s main page in a browser. It shows all comets with their designations, names, observational material characteristics, and osculating orbit elements (presented in lowered precision). In this view, we present only one preferred orbit for each comet. The user can narrow the visible list of comets by using a filtering box (located at the upper-left corner). Any string entered in this box will automatically be matched against a comet designation and/or its name. Moreover, clicking on any column heading will sort the tables according to the chosen parameter.
Clicking on the comet designation presented in the leftmost column allows the user to enter a “comet presentation screen”. A comet description is available in the upper section and a clickable list of orbital solutions is shown (the preferred one is presented by default and written in green).
Five cards are available for each orbital solution, which describe the five orbital snapshots in a more detailed manner and with greater precision: osculating, original, future, previous, and next. They are presented from left to right in chronological order. In most cases, additional graphics are also presented.
As mentioned in Sect. 3, we constructed a swarm of 5001 VCs, including the nominal osculating orbit for each of the orbital solutions in the database. By propagating in time each of these VCs to the previous or next perihelion, we can estimate the uncertainties for all presented orbital parameters. For those who intend to perform similar investigations, but for example on much longer time scales, we offer a downloadable text file consisting of all 5001 VCs at the original or future orbit stages; see the appropriate cards marked “Original” or “Future” orbit.
5.2. Searching the CODE database
After entering the Search view, the user has the possibility of choosing a subset of orbital solutions available in CODE by narrowing the intervals of nearly all the parameters. By default, the Search screen begins the search among osculating orbits, but it can be switched to the other four types of snapshots. By checking an appropriate box (located on the right), the user can limit the search to only the preferred orbits.
Orbital elements are selected by defining an interval of interest, and a simple check of correctness of the entered data is performed dynamically. A special treatment is performed for four elements: a perihelion distance, an aphelion distance, an eccentricity, and a semi-major axis. Since these elements are not independent, the user can enter the preferred interval of any two of them and the rest are automatically blocked. When selecting an interval of the perihelion passage epoch, the user can set different limitations for: a year, a year+month, or a year+month+day. In the lower part of the screen, a selection can be done basing on the observational data characteristics or on an orbital solution type.
Performing a search amongst previous and next orbits takes a slightly different form. However, it is adapted to the information presented for these types of orbits.
After clicking the Submit button, the user obtains a list of matching orbital solutions in a form identical to the Browse screen, which can be filtered further by comet designation or name. There is only one important difference: the search results can be downloaded as a simple text file, with all the data presented in full precision together with their uncertainties.
6. C/2002 T7: the example case description
The C/2002 T7 comet belongs to the group of comets with NG effects strongly manifested in positional data fitting (see Sect. 2.2). Additionally, this comet was discovered at a large heliocentric distance and was followed for a long time. Thus, in this case, a satisfactory fit to the data for the NG model of motion (based on the g(r)-formula adequate for water ice sublimation) can be obtained without great loss of the orbital accuracy when positional data around the perihelion are neglected or when we try to derive the orbit from data taken before the perihelion for past dynamical evolution (or data taken only after perihelion for future dynamical studies).
For this comet, not even an asymmetric NG model fits the whole data set satisfactorily because some trends in observed minus calculated (O−C) residuals in right ascension and/or declination are visible (see the database). The better data fitting is obtained when positional data around the perihelion are neglected; such an NG model based on DIST- type data (solution “d6”; see the database or K2020) is chosen as the preferred model when we want to find a general orbital solution for this comet.
In Fig. 2 we present the past and future evolution of the nominal orbit of C/2007 T7 (the preferred solution d6) using the dynamical model adopted for the CODE catalogue. The thick lines describe the past (to the previous perihelion) and future (to the escape limit crossing) orbit evolutions under the simultaneous Galactic and stellar perturbations. The list of the potential stellar perturbers collected for the CODE catalogue calculations is described in Wysoczańska et al. (2020). For the sake of comparison, an evolution with all stellar perturbations omitted is also shown (thin lines).
 |
Fig. 2. Dynamical evolution of the nominal orbit of C/2002 T7 LINEAR (d6 solution) under the simultaneous Galactic and stellar perturbations. The left vertical axis describes a heliocentric distance plot (thin blue lines) and a perihelion distance (green lines that turn black if e ≥ 1.0). The right vertical axis describes the angular elements (with respect to the Galactic disc plane): an inclination (fuchsia line) and an argument of perihelion (red line). Thin lines describe the dynamics when all stellar perturbations are omitted. |
It is clear that the previous perihelion is well outside the planetary zone. Therefore, we classified this comet as a dynamically new one.
However, there are also other satisfactory solutions based on pre-perihelion data. Fortunately, all NG models that represent different approaches to data give a very similar original orbit for this comet, with 1/aori ranging from 17.75 in units of 10−6 au−1 (NG solution: p6, based on pre-perihelion data) to 28.93 in the same units (asymmetric NG solution: n6, entire data set). In all of the solutions, we conclude that this comet is a dynamically new one by obtaining its previous perihelion distance (Snapshot 4). The preferred model (d6) with 21.65 ± 0.86 is in the middle of this range.
We also include one solution in the CODE catalogue based on the g(r)-like function describing CO-sublimation. Such a solution (named “pc” and based on pre-perihelion data only) gives a significantly different value of 1/aori = 53.21 ± 3.63 in units of 10−6 au−1. This solution leads to the result that C/2002 T7 was at a distance of about 5–7 au from the Sun at the previous perihelion passage. In this case, we should classify this object as a dynamically old comet. However, a comet that is dynamically old but still sublimating mainly CO is rather unlikely.
7. Some statistics
At the moment, the CODE catalogue contains data for 277 Oort spike comets. Since different orbital solutions are presented in the database for some of them, we show a total of 508 different orbits; however, the preferred orbit is always indicated for each comet. In the case where it was possible to obtain an NG orbit, two types of orbits are always given: NG and purely gravitational. This approach allows us to independently examine this sample of comets from various points of view; for example, to study the impact of NG effects on the change of the osculating orbit, etc. We had previously done many similar statistical analyses for smaller samples of Oort spike comets. Here, we present the result of one such analysis that can be performed based on the original orbits for solutions indicated as preferred in this database.
Figure 3 displays the 1/aori distribution of the whole sample of all comets currently available in the CODE catalogue. This histogram was constructed using the full swarms of preferred orbits; see Dybczyński & Królikowska (2016) for a detailed description of this technique. Thus, this distribution is the sum of individual Gaussian distributions of 1/aori, where the dispersion of each Gaussian reflects the individual uncertainties of 1/aori of each comet. All of these individual distributions are also available in the database (see Sect. 5.1).
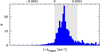 |
Fig. 3. Distribution of 1/aori based on the preferred orbits for the whole sample of LPCs available in the CODE catalogue; about one-third have NG solutions. The light grey vertical band indicates the region occupied by Oort spike comets. |
8. Future plans
In the near future, we plan to investigate the Oort spike comets with q < 3.1 au discovered during the period 2013–2017 (about 20 objects). Once these objects are added, the CODE catalogue will contain a complete sample of Oort spike comets2 from the period 1885–2017, with the exception of a few comets discovered long ago. These comets require a special and time-consuming approach, which includes completing positional data from highly dispersed sources; see the case of C/1890 F1 (Królikowska & Dybczyński 2016).
When the observations are finished and the data set is fixed, the osculating orbit(s) of a particular comet can be treated as “definitive”, except for situations when we deal with the original old positional data based on old stellar catalogues. An example of such a recent correction to the definitive comet orbit obtained long ago can found in Królikowska & Dybczyński (2016).
The situation is slightly different in the case of original and future orbits. Once the existence of the hypothetical planet nine is unambiguously documented, it cannot be ruled out that certain original and future orbits may experience some, probably minor or slight, modifications.
However, the previous and next orbit calculations strongly depend on our detailed knowledge of the Galactic neighbourhood of the Solar System. Our current list of stellar perturbers (Wysoczańska et al. 2020), based on the Gaia DR2 catalogue (Gaia Collaboration et al. 2018), still contains several problematic objects that have to be examined further when new data becomes available. These uncertain perturbers can affect both past and future cometary motion, so previous and next orbits of many LPCs included in the CODE catalogue might be changed in the future releases. Therefore, this catalogue provides orbital data based on the current state of our knowledge about the Solar System and its surroundings.
We also plan to enrich the database interface with more graphical capabilities, including an application that will allow users to obtain a picture of the dynamical evolution of orbits under Galactic and stellar perturbations over a time scale of about ±10 million yr.
Acknowledgments
We are thankful to the referee, Giovanni Valsecchi for his useful comments that have improved the description of the CODE Catalogue. This research was partially supported by the project 2015/17/B/ST9/01790 founded by the National Science Centre in Poland.
References
- Dones, L., Brasser, R., Kaib, N., & Rickman, H. 2015, Space Sci. Rev., 197, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczyński, P. A., & Berski, F. 2015, MNRAS, 449, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczyński, P. A., & Królikowska, M. 2016, P&SS, 123, 77 [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M. 2014, A&A, 567, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M. 2020, A&A, 633, A80 [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2010, MNRAS, 404, 1886 [NASA ADS] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2016, MNRAS, 460, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2017, MNRAS, 472, 4634 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., Dybczyński, P. A., & Sitarski, G. 2012, A&A, 544, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Rickman, H. 2014, Meteorit. Planet. Sci., 49, 8 [Google Scholar]
- Sekanina, Z. 2019, ArXiv e-prints [arXiv:1903.06300] [Google Scholar]
- Sitarski, G. 1994, Acta Astron., 44, 91 [NASA ADS] [Google Scholar]
- Sitarski, G. 1998, Acta Astron., 48, 547 [NASA ADS] [Google Scholar]
- Wysoczańska, R., Dybczyński, P. A., & Polińska, M. 2020, A&A, in press https://doi.org/10.1051/0004-6361/202037876 [Google Scholar]
- Yeomans, D. K., & Chodas, P. W. 1989, AJ, 98, 1083 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Orbital changes of C/2002 T7 projected on its original orbit plane that are described by five snapshots in CODE catalogue. Red line depicts the past motion of this comet while the blue line depicts its future evolution. Five epochs (snapshots) when orbital elements are recorded are marked: 1– osculating heliocentric orbit near the centre of the observational interval (typically near the perihelion); 2– original barycentric orbit recorded in past at 250 au from the Sun; 3– future barycentric orbit recorded in future at 250 au from the Sun; 4– previous orbit, recorded at the previous perihelion; 5– next orbit, in this case recorded at the escape border at 120 000 au from the Sun, but for many other comets recorded in the next perihelion. |
| In the text | |
 |
Fig. 2. Dynamical evolution of the nominal orbit of C/2002 T7 LINEAR (d6 solution) under the simultaneous Galactic and stellar perturbations. The left vertical axis describes a heliocentric distance plot (thin blue lines) and a perihelion distance (green lines that turn black if e ≥ 1.0). The right vertical axis describes the angular elements (with respect to the Galactic disc plane): an inclination (fuchsia line) and an argument of perihelion (red line). Thin lines describe the dynamics when all stellar perturbations are omitted. |
| In the text | |
 |
Fig. 3. Distribution of 1/aori based on the preferred orbits for the whole sample of LPCs available in the CODE catalogue; about one-third have NG solutions. The light grey vertical band indicates the region occupied by Oort spike comets. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&F_{i}=A_{i} \> g(r), \quad A_{i}=\mathrm{~const.~~for}\quad {i}=1,2,3,\nonumber \\&g(r)=\alpha (r/r_{0})^{m}[1+(r/r_{0})^{n}]^{k}, \end{aligned} $$](/articles/aa/full_html/2020/08/aa38451-20/aa38451-20-eq1.gif)