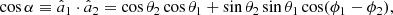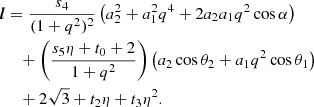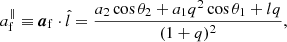| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | L20 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202038427 | |
| Published online | 21 August 2020 | |
Letter to the Editor
Formation of low-spinning 100 M⊙ black holes
1
Nicolaus Copernicus Astronomical Centre of the Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
e-mail: chrisbelczynski@gmail.com
2
Helmholtz-Instituts für Strahlen- und Kernphysik, Nussallee 14-16, 53115 Bonn, Germany
3
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
Received:
15
May
2020
Accepted:
2
August
2020
Aims. It is speculated that a merger of two massive stellar-origin black holes in a dense stellar environment may lead to the formation of a massive black hole in the pair-instability mass gap (∼50−135 M⊙). Such a merger-formed black hole is expected to typically have a high spin (a ∼ 0.7). If such a massive black hole acquires another black hole it may lead to another merger detectable by LIGO/Virgo in gravitational waves. Acquiring a companion may be hindered by gravitational-wave kick/recoil, which accompanies the first merger and may quickly remove the massive black hole from its parent globular or nuclear cluster. We test whether it is possible for a massive merger-formed black hole in the pair-instability gap to be retained in its parent cluster and have low spin. Such a black hole would be indistinguishable from a primordial black hole.
Methods. We employed results from numerical relativity calculations of black hole mergers to explore the range of gravitational-wave recoil velocities for various combinations of merging black hole masses and spins. We compared merger-formed massive black hole speeds with typical escape velocities from globular and nuclear clusters.
Results. We show that a globular cluster is highly unlikely to form and retain a ∼100 M⊙ black hole if the spin of the black hole is low (a ≲ 0.3). Massive merger-formed black holes with low spins acquire high recoil speeds (≳ 200 km s−1) from gravitational-wave kick during formation that exceed typical escape speeds from globular clusters (∼ 50 km s−1). However, a very low-spinning (a ∼ 0.1) and massive (∼100 M⊙) black hole could be formed and retained in a galactic nuclear star cluster. Even though such massive merger-formed black holes with such low spins acquire high speeds during formation (∼ 400 km s−1), they may avoid ejection since massive nuclear clusters have high escape velocities (∼ 300−500 km s−1). A future detection of a massive black hole in the pair-instability mass gap with low spin would therefore not be proof of the existence of primordial black holes, which are sometimes claimed to have low spins and arbitrarily high masses.
Key words: black hole physics / gravitational waves
© ESO 2020
1. Introduction
By the beginning of 2020 the LIGO/Virgo collaboration had published ten black hole–black hole (BH–BH) mergers from the first two (O1/O2) observational runs (Abbott et al. 2019a), and more than 50 BH–BH merger alerts from their recently concluded third observing run1 (O3). The origin of these BH–BH mergers is still unknown.
Numerous formation scenarios and sites have been proposed in the literature to explain LIGO/Virgo BH–BH merger detections. The two most prominent proposals are the classical isolated binary evolution channel in galactic fields (Tutukov & Yungelson 1993; Lipunov et al. 1997; Voss & Tauris 2003) and dynamical formation in dense clusters (Miller & Hamilton 2002; Portegies Zwart et al. 2004; Gültekin et al. 2006). Triple stars are also proposed as BH–BH merger formation sites (Antonini et al. 2018), or isolated binaries with very rapid rotation leading to homogeneous evolution (Marchant et al. 2016). First generation of stars is yet another potential formation site Bond & Carr (1984).
Massive stars are subject to pair instabilities (Bond et al. 1984) and are not expected to form BHs with masses of ∼100 M⊙. We note that typically this pair-instability mass gap is adopted to be broad, namely ∼50−135 M⊙, but recently it was claimed that the range may be narrower: ∼90−125 M⊙ (Farmer et al. 2020). The stellar-origin BHs are claimed to form with low spins a ≲ 0.2 from single massive stars (Fuller et al. 2019; Belczynski et al. 2020). Mergers of two massive BHs in dense clusters can produce ∼100 M⊙ BHs, but such BHs will typically have large spin a ∼ 0.7 (Gerosa & Berti 2017; Fishbach et al. 2017). Therefore, it seems that astrophysical channels that invoke stars, at least initially, to produce BHs cannot form BHs of ∼100 M⊙ with low spins. This inference could be potentially used to distinguish stellar-origin BHs from primordial BHs.
Primordial BHs were proposed to form from density fluctuations in the very early Universe by Hawking (1971). These primordial BHs are sometimes employed to explain LIGO/Virgo BH–BH mergers, that is if they catch a companion BH (Clesse & García-Bellido 2017). Although in principle primordial BHs could have an arbitrary mass, various observational constraints exclude most possibilities, nevertheless allowing masses in the range ∼10−100 M⊙ (Carr & Silk 2018). Primordial BHs are usually argued to have very low spins a ∼ 0.01 (De Luca et al. 2019).
It may appear that the detection of a 100 M⊙ BH with low spin (e.g., by LIGO/Virgo) would point to the primordial formation scenario. However, there are several alternative astrophysical scenarios. It has been proposed in the past that numerous consecutive mergers of a seed BH with lighter companions (either other BHs or stars) with randomly oriented spins (so they cancel out in the final merger product) would not increase the spin of the seed BH (Miller 2002; Hughes & Blandford 2003; Antonini et al. 2019). Consecutive (runaway) mergers of stars in young stellar clusters were claimed to lead to the formation of quasi-stellar objects massive enough to form ∼100 M⊙ BHs (Portegies Zwart & van den Heuvel 2007; Fujii & Portegies Zwart 2013; Di Carlo et al. 2019). However, it is not clear how such a quasi-stellar object would avoid pair-instability explosion (no BH formation) or what the spin would be of a BH if pair instability was avoided somehow.
Here we investigate the validity of a different astrophysical scenario. We test the possibility that a merger of two massive stellar-origin BHs can produce a ∼100 M⊙ BH with low spin and with such spatial velocity that it could be retained in its parent globular or nuclear cluster. Such a BH could catch another BH and produce a merger detectable by LIGO/Virgo.
2. Calculations
We explore a range of mass ratios of BH–BH mergers, leading to a BH of ≈100 M⊙, by considering three combinations of component masses, namely (M1, M2) = (50.0 M⊙, 50.0 M⊙), (70.0 M⊙, 35.0 M⊙), and (70.0 M⊙, 20.0 M⊙). These choices are motivated by the range of mass ratios in BH–BH mergers observed to date (≈0.3 − ≈1.0; Abbott et al. 2019b). For each combination, we consider two extreme cases, namely both component BHs are maximally spinning, i.e., their dimensionless spin magnitudes are (a1, a2) = (1.0, 1.0) or both components are not spinning, i.e., (a1, a2) = (0.0, 0.0). For each (M1, M2),(a1, a2) combination, we perform 105 evaluations of the final merged BH’s dimensionless spin vector, af, and the recoil kick velocity, vk, due to the anisotropic radiation of GW during the merger assuming that the component BH spins are uncorrelated and oriented isotropically with respect to the orbital angular momentum. We note that the energy carried away by the GW emission will result in the final BHs’ mass, Mf, being smaller than M1 + M2. Since this discrepancy is at most a few percent (but depends, in a complex manner, on the BH–BH binary mass ratios and spin vectors as numerical-relativity calculations suggest (Hughes 2009; Sperhake 2015), we ignore it for the present purpose and assign Mf ≈ M1 + M2.
The vectors vk and af of the merged BH were obtained using numerical relativity (NR) calculations for a wide range of mass ratio and spin configurations of the merging BHs (Pretorius 2005; Campanelli et al. 2007; Baker et al. 2008; van Meter et al. 2010) and fitting formulae exist that well reproduce the NR outcomes. In general, if the spins of the merging BHs are zero, vk will lie on the orbital plane and be aligned along the line joining the BHs just before the merger. Its magnitude, vk, is zero (small) for equal-mass (extreme-mass-ratio) components and maximizes to ≈ 170 km s−1 at the mass ratio of ≈1/2.9. If the merging BHs have spins, then depending on the magnitudes and orientations of the spins, vk will also have an in-plane component perpendicular to the mass axis and a component perpendicular to the orbital plane. For (near-) maximally spinning BHs, this off-plane component of the merger recoil typically dominates and can well exceed 500 km s−1 (Baker et al. 2008; van Meter et al. 2010); for certain configurations, it can reach ≈ 3000 km s−1 (Campanelli et al. 2007). In this work, we use the NR-based fitting formulae of van Meter et al. (2010) for the components of vk, which incorporate cases where the spins of the BHs are inclined with respect to the orbital angular momentum and would therefore undergo spin-orbit precession during the in-spiral and merger phases of the BH–BH. These formulae agree with NR outcomes within 5%.
If the spins of the merging BH components are zero, then the only source of angular momentum of the merged BH is the BH–BH orbital angular momentum. Accordingly, the dimensionless spin of the merged BH, af, will be aligned with the orbital angular momentum, L, and, for equal-mass components, will have the magnitude af ≈ 0.7 (Pretorius 2005). When the merging BHs have finite, misaligned spins, af is generally misaligned relative to L and its magnitude is augmented (suppressed) with respect to the nonspinning-merger value if the spins are pro-aligned (anti-aligned). For most configurations, L dominates the angular momentum budget of the BH–BH system (Rezzolla et al. 2008) and hence the angle between af and L is typically < 10°. In this work, we use the NR-based fitting functions of Rezzolla et al. (2008) to compute af for each of the randomly chosen component-spin orientations. The NR-based fitting formulae used in this work are described in Appendix A.
For each combination, (M1, M2),(a1, a2), of the merging BH masses and dimensionless spin magnitudes (see above), we perform 105 evaluations of af and vk. Each evaluation proceeds as follows: the inclinations and the azimuths of the component BH spins, (θ1, θ2), (ϕ1, ϕ2), with respect to the orbital angular momentum, L, are chosen randomly and independently of each other from a uniform distribution within the range (0, 2π). Next, the NR fitting formulae, as described in Appendix A, are applied to evaluate the in-plane and off-plane components of the vector, vk, of the merger recoil kick and the magnitude of the final spin, af. We used dedicated numerical routines for this purpose, in which the formulae in Appendix A are implemented to evaluate the vk-components and af (and θf) simultaneously. Given the pure analytical nature and medium complexity of these expressions, each evaluation sequence takes less than a second; 105 iterations typically take < 3 h on a single ∼3 Ghz processor. That way, the distributions of vk and af for each (M1, M2),(a1, a2) combination are obtained for isotropic and uncorrelated orientations of the spins of the merging BHs. As explained in Appendix A, the effect of the undetermined angles on the fitting formulae is automatically cancelled out by the choice of a large number of isotropically distributed spin orientations. Therefore, the distributions of vk and af depend only on the (M1, M2),(a1, a2) combination.
Figure 1 shows the probability, P, that af < af,crit as a function of af,crit, with af,crit being a chosen threshold value of af, for the three component-mass combinations and for a1 = a2 = 1.0. The fractions plotted in this figure are out of 105 trials (see above). Because of the dominance of L, the final angular momentum of the BH–BH system can be significantly suppressed only for strongly anti-aligned spin orientations of the merging BHs. Accordingly, the fraction of configurations that suppress the system’s angular momentum to produce af below a certain af,crit decreases strongly with af,crit, as Fig. 1 demonstrates. Only mergers with the most dissimilar BH masses (70.0 M⊙, 20.0 M⊙) can yield af < 0.1, and that too with a very small probability (P ≈ 0.05). Equal-mass, maximally spinning BHs cannot yield af below ≈0.35 and, with the mass ratio of 0.5, the lower limit of af is ≈0.2.
 |
Fig. 1. Probability, P(af < af,crit), that the dimensionless spin magnitude, af, of a merged BH is less than the value af,crit, as a function of af,crit. Each curve corresponds to a particular mass combination of the maximally spinning components of the merging BH–BH, as indicated in the legend. The probabilities are obtained out of 105 trials of random and uncorrelated orientations of the spins of the BH components. |
On the other hand, when a1 = a2 = 0.0 the orbital angular momentum, which is necessarily perpendicular to the orbital plane, is the only resource of angular momentum of the merging BH–BH system. In that case, both af and vk are unique and depend only on the mass ratio of the merging BHs, as determined by the NR fitting formulae employed here. Therefore, P(af < af,crit) is a step function jumping from zero to unity at the value of af,crit that is equal to the unique af for the chosen mass ratio. This is demonstrated in Fig. 2. With nonspinning BHs, the lowest af obtained here is ≈0.5 for mergers with the smallest mass ratio (≈0.3).
Since our focus here is the low-spinning BH–BH merger products, it would be worth considering the GW recoil kick magnitudes, vk, such merged BHs would receive as a result of the merger. This is shown in Fig. 3. Here, the distributions of vk are shown for those a1 = a2 = 1.0 mergers that lead to af < 0.1, 0.3, and 0.4 for the mass ratios ≈0.3, 0.5, and 1.0, respectively (for a1 = a2 = 0.0, we have af > 0.5; see above). As evident, the strongly anti-aligned mergers that yield af < 0.1 have a relatively narrow range of recoil kicks, 200 km s−1 ≲ vk ≲ 700 km s−1, and their distribution is strongly peaked at vk ≈ 400 km s−1. For af,crit = 0.3 and 0.4 and mass ratios ≳0.5, the vk distributions are peaked at smaller values but have tails extending up to 1600 km s−1. Qualitatively, any BH–BH configuration (out of spinning BH components) that leads to a small af would emit GW relatively symmetrically leading to a relatively low recoil. But due to the required low mass ratio (see Fig. 1), the configuration just before the merger is still asymmetrical leading to recoils of typically 400 km s−1.
 |
Fig. 3. Distributions of GW recoil kick magnitudes, vk, for those mergers of maximally spinning BHs that yield a low-spinning merged BH with af < af,crit. The BH-mass combinations and the correspondingly chosen af,crit are indicated in the legend. |
3. Discussion and conclusions
We have shown that a merger of two rapidly spinning (a1 ≈ a2 ≈ 1) and unequal mass (q ≲ 0.3) BHs can produce a ∼100 M⊙ BH with low spin and sufficiently low spatial velocity (from GW kick) for it to be retained in a nuclear cluster. Such a BH, under the assumption that it catches another BH, can manifest itself in high-frequency GW observations (LIGO/Virgo).
So far, (O1/O2) LIGO/Virgo observations seem to indicate that the detected BH–BH mergers have component BHs with low spins (Abbott et al. 2019b; see also Belczynski et al. 2020; Banerjee 2020), with the exception of GW170729 and GW190412 which are consistent with a moderately spinning BH (Abbott et al. 2019b; The LIGO Scientific Collaboration & The Virgo Collaboration 2020). This was explained in terms of Tayler-Spruit magnetic dynamo (Spruit 2002; Fuller et al. 2019) which efficiently removes angular momentum from massive stars and leads to the formation of low-spinning BHs in BH–BH mergers (Belczynski et al. 2020; Bavera et al. 2020). If this applies to all first-generation BHs, then the only way to produce a merger of two highly spinning BHs is to have a merger of two second-generation BHs, as these will typically have large spin (Gerosa & Berti 2017; Fishbach et al. 2017). Alternatively, it seems that nature can produce rapidly spinning BHs, as these are observed in Galactic and extra-galactic high-mass X-ray binaries (HMXRBs): Cyg X-1: a = 0.98, LMC X-1: a = 0.92, and M33 X-7: a = 0.84 (Miller & Miller 2015). The apparent tension between LIGO/Virgo BHs and those in HMXRBs can be understood if the specific evolutionary scenarios are different for both populations (e.g., Qin et al. 2019). Whether or not the tension is fully understood (which is still debated), it is clear that nature can produce both slow- and rapidly spinning BHs, and if the rapidly spinning BHs merge they are the potential candidates for our scenario.
Stars can possibly form BHs massive enough to satisfy the total mass requirement and the uneven mass ratio limit. As noted in Sect. 1, stars can possibly form BHs (first generation) as massive as ∼90 M⊙ and still avoid pair-instability pulsation mass loss. Such a massive BH would then need to dynamically pair with a ∼20−30 M⊙ BH in a dense stellar cluster, which is possible as Monte Carlo and direct N-body computations show (Rodriguez et al. 2019; Di Carlo et al. 2019; Banerjee 2020). As we demonstrate here, the formation of a low-spinning ∼100 M⊙ BH induces a strong GW recoil kick that accelerates the merged BH to a high speed of ∼ 400 km s−1. This removes all such BHs from globular clusters (mass ∼105 − 106 M⊙, size ∼ pc; Harris 1996; Baumgardt & Hilker 2018), which have typical central escape velocities of ≲ 70 km s−1 (e.g., Georgiev et al. 2009). However, such BHs can potentially be retained in nuclear clusters (mass ∼106 − 108 M⊙, size ∼ pc; Schödel et al. 2014) that typically have much higher central escape velocities of ∼ 300−500 km s−1 (Georgiev et al. 2016, 2009; Schödel et al. 2014; Miller & Lauburg 2009).
We note that current LIGO/Virgo observations do not provide spin magnitude measurements of merging BHs. These observations provide measurements of the BH–BH effective spin parameter, which is a projection of both BH spins weighted by BH mass on the binary’s orbital angular momentum vector. This means that if the effective spin is low then the BH spins are low; the spin vectors are facing in opposite directions causing them to cancel out; or the spin vectors are in the orbital plane. However, future observations may provide large numbers of massive BHs and this may allow for statistical assessment of BH spin magnitudes. Alternatively, there is hope for measuring spin precession in the inspiral waveform in future. This would also allow the spin magnitudes of merging BHs to be estimated.
In future work, we intend to explore the effect of more recent NR results (e.g., Lousto & Zlochower 2013; Hofmann et al. 2016) and the mass–spin dependence of BHs as obtained from stellar-evolutionary calculations (Belczynski et al. 2020). Also, the formation rate estimate of the proposed scenario would require careful analysis of nuclear cluster evolution folded with detailed stellar and binary evolution. Such an estimate is beyond the scope of this paper.
Here, we simply point out (proof-of-principle) the possibility of the formation of a 100 M⊙, low-spinning BH of astrophysical origin. This adds to existing scenarios of a seed BH growing in mass by accretion of lower mass stars or light BHs (Miller 2002; Hughes & Blandford 2003) and BH formation from a runaway stellar merger product (Portegies Zwart & van den Heuvel 2007; Fujii & Portegies Zwart 2013; Di Carlo et al. 2019). These astrophysical scenarios are to be contrasted with any claims that such BHs (if they exist and are detected) must be of primordial origin. Despite the fact that the channel pointed out here is potentially of lower probability than the other channels, it follows from basic physics (numerical relativity) and requires only a specific astrophysical site (nuclear cluster), of which there are many in the Universe.
Acknowledgments
We thank the anonymous referee for constructive comments and useful suggestions that have helped to improve the manuscript. KB acknowledges support from the Polish National Science Center (NCN) grant Maestro (2018/30/A/ST9/00050). SB acknowledges the support from the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) through the individual research grant “The dynamics of stellar-mass black holes in dense stellar systems and their role in gravitational-wave generation” (BA 4281/6-1; PI: S. Banerjee). The authors thank Cole Miller and Mirek Giersz for useful comments and criticisms that have helped to improve the manuscript. They acknowledge the hospitality of the National Astronomical Observatories of China (NAOC), Beijing where a good part of this work has been done.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019a, ApJ, 882, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019b, Phys. Rev. X, 9, 031040 [Google Scholar]
- Antonini, F., Rodriguez, C. L., Petrovich, C., & Fischer, C. L. 2018, MNRAS, 480, L58 [Google Scholar]
- Antonini, F., Gieles, M., & Gualandris, A. 2019, MNRAS, 486, 5008 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, J. G., Boggs, W. D., Centrella, J., et al. 2007, ApJ, 668, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, J. G., Boggs, W. D., Centrella, J., et al. 2008, ApJ, 682, L29 [Google Scholar]
- Banerjee, S. 2020, ArXiv e-prints [arXiv:2004.07382] [Google Scholar]
- Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [NASA ADS] [CrossRef] [Google Scholar]
- Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [CrossRef] [EDP Sciences] [Google Scholar]
- Blanchet, L., Qusailah, M. S. S., & Will, C. M. 2005, ApJ, 635, 508 [Google Scholar]
- Bond, J. R., & Carr, B. J. 1984, MNRAS, 207, 585 [Google Scholar]
- Bond, J. R., Arnett, W. D., & Carr, B. J. 1984, ApJ, 280, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Campanelli, M., Lousto, C., Zlochower, Y., & Merritt, D. 2007, ApJ, 659, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B., & Silk, J. 2018, MNRAS, 478, 3756 [Google Scholar]
- Clesse, S., & García-Bellido, J. 2017, Phys. Dark Univ., 15, 142 [Google Scholar]
- De Luca, V., Desjacques, V., Franciolini, G., Malhotra, A., & Riotto, A. 2019, J. Cosmol. Astropart. Phys., 2019, 018 [CrossRef] [Google Scholar]
- Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, R., Renzo, M., de Mink, S., Fishbach, M., & Justham, S. 2020, ApJ, submitted [arXiv:2006.06678] [Google Scholar]
- Favata, M., Hughes, S. A., & Holz, D. E. 2004, ApJ, 607, L5 [Google Scholar]
- Fishbach, M., Holz, D. E., & Farr, B. 2017, ApJ, 840, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Fitchett, M. J. 1983, MNRAS, 203, 1049 [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2013, MNRAS, 430, 1018 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Georgiev, I. Y., Hilker, M., Puzia, T. H., Goudfrooij, P., & Baumgardt, H. 2009, MNRAS, 396, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Georgiev, I. Y., Böker, T., Leigh, N., Lützgendorf, N., & Neumayer, N. 2016, MNRAS, 457, 2122 [Google Scholar]
- Gerosa, D., & Berti, E. 2017, Phys. Rev. D, 95, 124046 [NASA ADS] [CrossRef] [Google Scholar]
- González, J. A., Sperhake, U., Brügmann, B., Hannam, M., & Husa, S. 2007, Phys. Rev. Lett., 98, 091101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Gültekin, K., Miller, M. C., & Hamilton, D. P. 2006, ApJ, 640, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hawking, S. 1971, MNRAS, 152, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, F., Barausse, E., & Rezzolla, L. 2016, ApJ, 825, L19 [Google Scholar]
- Hughes, S. A. 2009, ARA&A, 47, 107 [Google Scholar]
- Hughes, S. A., & Blandford, R. D. 2003, ApJ, 585, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Kidder, L. E. 1995, Phys. Rev. D, 52, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Lipunov, V. M., Postnov, K. A., & Prokhorov, M. E. 1997, Astron. Lett., 23, 492 [NASA ADS] [Google Scholar]
- Lousto, C. O., & Zlochower, Y. 2013, Phys. Rev. D, 87, 084027 [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, M. C. 2002, ApJ, 581, 438 [Google Scholar]
- Miller, M. C., & Hamilton, D. P. 2002, MNRAS, 330, 232 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Miller, M. C., & Lauburg, V. M. 2009, ApJ, 692, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., & Miller, J. M. 2015, Phys. Rep., 548, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morawski, J., Giersz, M., Askar, A., & Belczynski, K. 2018, MNRAS, 481, 2168 [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Portegies Zwart, S. F., & van den Heuvel, E. P. J. 2007, Nature, 450, 388 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Pretorius, F. 2005, Phys. Rev. Lett., 95, 121101 [Google Scholar]
- Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Barausse, E., Dorband, E. N., et al. 2008, Phys. Rev. D, 78, 044002 [Google Scholar]
- Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Feldmeier, A., Kunneriath, D., et al. 2014, A&A, 566, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sperhake, U. 2015, Classical Quantum Gravity, 32, 124011 [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- The LIGO Scientific Collaboration, & The Virgo Collaboration 2020, ArXiv e-prints [arXiv:2004.08342] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675 [NASA ADS] [CrossRef] [Google Scholar]
- van Meter, J. R., Miller, M. C., Baker, J. G., Boggs, W. D., & Kelly, B. J. 2010, ApJ, 719, 1427 [Google Scholar]
- Voss, R., & Tauris, T. M. 2003, MNRAS, 342, 1169 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Numerical relativity fitting formulae
Fitting formulae based on NR are used to calculate the GR merger recoil kick and final spin of the merged BH, as discussed in Sect. 2. The recoil kick, vk, is computed using the fitting formulae as given in van Meter et al. (2010). These formulae are based on NR calculations of BH–BH mergers (Baker et al. 2008; van Meter et al. 2010) where the component BH spins are generally inclined with respect to the orbital axis, resulting in spin-orbit precession (i.e., precession of the BHs’ spin vectors and the orbital axis around the total angular momentum vector of the BH–BH system) of the merging BH–BH.
The GR merger recoil kick is given by
Here, v⊥m is the mass-ratio-determined recoil, v⊥s is the in-orbital-plane spin-determined recoil, v∥ is the off-plane (parallel to the orbital axis) spin-determined recoil, e1 and e3 are the unit vectors along the directions of the BHs’ separation and the orbital axis just before the merger, respectively, and e2 ≡ e1 × e3. ξ = 215° is a constant as obtained in the NR fitting by Baker et al. (2008).
The expressions for the in-plane and off-plane recoils are to some extent motivated by post-Newtonian treatments (Fitchett 1983; Kidder 1995; Favata et al. 2004; Blanchet et al. 2005; Baker et al. 2007; González et al. 2007; Campanelli et al. 2007) and are given by
In Eqs. (A.2)–(A.4), A, B, H, K2, K3, and Ks are constants as obtained by NR fitting, q ≡ m1/m2 (m1 ≤ m2) is the mass ratio of the merging BHs with dimensionless spin magnitudes (a1, a2), η ≡ q/(1 + q)2, (θ1, θ2) are the inclination angles that the BHs’ spins project to orbital axis, (ϕ1, ϕ2) are the azimuth angles that the spins project to the separation axis, and (Φ1, Φ2) are phase angles depending on q and the initial separation of the merging BHs’ (Baker et al. 2008; van Meter et al. 2010). Since, in this work, the BHs’ spins are assumed to be uncorrelated and randomly oriented (i.e., θ1, θ2, ϕ1, ϕ2 are random in the range 0° − 360°) over a large number of trials (see Sect. 2), the terms cos(ϕ1 − Φ1) and cos(ϕ2 − Φ2) will average out in Eq. (A.4). Hence, Φ1 = Φ2 = 0 is assumed, as also done in Morawski et al. (2018). The fitting constants are A = 1.35×104 km s−1, B = −1.48, H = 7540 km s−1 (Baker et al. 2008) and K2 = 32 092 km s−1, K3 = 108 897 km s−1, Ks = 15 375 km s−1 (van Meter et al. 2010).
The final spin magnitude of the merged BH, af, and its tilt angle with respect to the orbital axis (orbital angular momentum) at a large separation of the binary, θf, are obtained using the NR-fitting formulae of Rezzolla et al. (2008). The final spin is given by
with (see also, Morawski et al. 2018)
where l is a vector which is parallel to the orbital angular momentum at a large binary separation (Rezzolla et al. 2008) and whose magnitude is given by
Here, the fitting constants are s4 = −0.129, s5 = −0.384, t0 = −2.686, t2 = −3.454, and t3 = 2.353.
The component of the final spin vector parallel to the direction of the (large-separation) orbital angular momentum is
so that the tilt angle of the final spin is given by 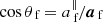 .
.
We note that in Eqs. (A.5)–(A.8), the inclination and azimuthal angles of the BH spins are, θ1, θ2, ϕ1, and ϕ2, are with respect to the binary’s orbit and its axis (i.e., the direction of the orbital angular momentum) at a sufficiently large binary separation, on which the ansatz for the final spin is based (Rezzolla et al. 2008). On the other hand, the angles in the GR recoil kick formulae, as given by Eqs. (A.2)–(A.4), are with respect to the instantaneous orbital plane just before the merger which would be oriented differently from the large-separation orbital plane if the merging BH–BH system undergoes spin-orbit precession (see above). However, since, in this work, the spins of the BHs are assumed to be uncorrelated and randomly oriented over a large number of trials (Sect. 2), the angles can in effect be used synonymously in both sets of equations.
Also, all of the above equations are expressed following the convention m1 ≤ m2 as often employed in NR and as they are implemented in the subroutines used in this work. The usual precautionary measures are taken to ensure this convention in these subroutines. However, in the main text of this paper, the astrophysical convention of M1 ≥ M2 is followed.
All Figures
 |
Fig. 1. Probability, P(af < af,crit), that the dimensionless spin magnitude, af, of a merged BH is less than the value af,crit, as a function of af,crit. Each curve corresponds to a particular mass combination of the maximally spinning components of the merging BH–BH, as indicated in the legend. The probabilities are obtained out of 105 trials of random and uncorrelated orientations of the spins of the BH components. |
| In the text | |
 |
Fig. 2. Same plot as Fig. 1 but for nonspinning BH components. |
| In the text | |
 |
Fig. 3. Distributions of GW recoil kick magnitudes, vk, for those mergers of maximally spinning BHs that yield a low-spinning merged BH with af < af,crit. The BH-mass combinations and the correspondingly chosen af,crit are indicated in the legend. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



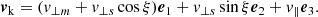
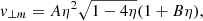
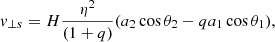
![$$ \begin{aligned}&{v}_\Vert = \frac{K_2\eta ^2+K_3\eta ^3}{q + 1}\nonumber \\&\times \left[q a_1\sin \theta _1\cos (\phi _1-\Phi _1) - a_2\sin \theta _2\cos (\phi _2-\Phi _2)\right] \nonumber \\&+ \frac{K_s(q-1)\eta ^2}{(q+1)^3} \nonumber \\&\times \left[q^2a_1\sin \theta _1\cos (\phi _1-\Phi _1) + a_2\sin \theta _2\cos (\phi _2-\Phi _2)\right]. \end{aligned} $$](/articles/aa/full_html/2020/08/aa38427-20/aa38427-20-eq4.gif)
![$$ \begin{aligned} \boldsymbol{a}_{\rm f}&= \frac{1}{(1+q)^2}\left[a_2^2 + a_1^2q^4 + 2a_1a_2q^2\cos \alpha \right.\nonumber \\&\quad +\left. 2(a_2\cos \theta _2+a_1q^2\cos \theta _1)lq + l^2q^2 \right]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2020/08/aa38427-20/aa38427-20-eq5.gif)