| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202038177 | |
| Published online | 21 July 2020 | |
The millimeter-wave spectrum and astronomical search for ethyl methyl sulfide⋆
1
Instituto de Física Fundamental (IFF-CSIC). Group of Molecular Astrophysics, C/ Serrano 123, 28006 Madrid, Spain
e-mail: carlos.cabezas@csic.es
2
Observatorio de Yebes (IGN), Cerro de la Palera s/n, 19141 Yebes, Guadalajara, Spain
3
Observatorio Astronómico Nacional (OAN-IGN), C/ Alfonso XII 3, 28014 Madrid, Spain
Received:
15
April
2020
Accepted:
9
June
2020
Context. Sulfur-containing molecules constitute only 8% of the molecules observed in the interstellar medium (ISM), in spite of the fact that sulfur has been shown to be an abundant element in the ISM. In order to understand the chemical behavior of the ISM and specific cases like the missing sulfur reservoir, a detailed chemical molecular composition in the ISM must be mapped out.
Aims. Our goal is to investigate the rotational spectrum of ethyl methyl sulfide, CH3CH2SCH3, which seems to be a potential candidate for observation in the ISM since the simpler analogs, CH3SH and CH3CH2SH, have already been detected. Rotational spectrum of ethyl methyl sulfide has been observed before, but its experimental rotational parameters are not precise enough to allow its detection in the ISM.
Methods. The rotational spectrum of ethyl methyl sulfide in the frequency range 72−116.5 GHz was measured using a broadband millimeter-wave spectrometer based on radio astronomy receivers with fast Fourier transform backends. The spectral searches and identification of the vibrational excited states of ethyl methyl sulfide was supported by high-level ab initio calculations on the harmonic and anharmonic force fields.
Results. The rotational spectra for the trans and gauche conformers of ethyl methyl sulfide was analyzed, and a total of 172 and 259 rotational transitions were observed for each one, respectively. The observation of A − E internal rotation splittings allowed the experimental determination of the V3 hindered internal rotation barrier height for both trans and gauche species. In addition, the vibrational excited states, resulting from the lowest frequency vibrational mode ν30 were identified for both conformers. The new experimental rotational parameters were employed to search for ethyl methyl sulfide in the warm and cold molecular clouds Orion KL, Sgr B2(N), B1-b and TMC-1, using the spectral surveys captured by IRAM 30 m at 3 mm and 2 mm.
Key words: ISM: molecules / methods: laboratory: molecular / molecular data / line: identification
Lists of the measured and predicted frequencies are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/639/A129
© ESO 2020
1. Introduction
Sulfur is the tenth most abundant element in the Galaxy, (1.23 × 10−5NH; Asplund et al. 2005). However, in molecular clouds and star-forming regions, its cosmic abundance is drastically reduced from the gas-phase molecular inventory. Many sulfur-bearing species have already been detected, but they only account for ∼0.1% of its estimated cosmic abundance (Tieftrunk et al. 1994). Several hypotheses have been proposed about where the missing sulfur is located. It has been suggested that it is locked onto the icy mantles of dust grains (Ruffle et al. 1999), but until now only OCS (Geballe et al. 1985; Palumbo et al. 1995) and SO2 (Boogert et al. 1997) have been firmly detected in icy grain mantles toward high-mass protostars. A very recent physical model (Laas & Caselli 2019) predicts that most of the “missing” sulfur is in the form of sulfur-bearing species that are trapped on grains. Thus, if these species are released from the grains into the gas phase, they would become a potential sink of astronomical sulfur. Therefore, observations aiming to detect interstellar sulfur-bearing molecules are of interest in the search for the missing sulfur reservoir and to understand the chemistry occurring in the ISM and star-forming regions, since these species could act as chemical clocks (Hatchell et al. 1998; van der Tak et al. 2000) to obtain information about these regions.
Among all the molecular species (around 200) detected so far in the ISM or circumstellar shells1, the family of sulfur-containing molecules represents approximately 8% (17 species). This group of molecules mainly consists of diatomic and triamotic molecular species, 12 of them to be precise, including NS (Gottlieb et al. 1975), NS+ (Cernicharo et al. 2018), SH+ (Menten et al. 2011), HS2 (Fuente et al. 2017), and HCS/HSC (Agúndez et al. 2018). Four of these species are formed by four and six atoms, C3S (Yamamoto et al. 1987), H2CS (Sinclair et al. 1973), CH3SH (Linke et al. 1979), and C5S (Agúndez et al. 2010), while the remaining one is the largest sulfur molecule detected so far, CH3CH2SH (Kolesniková et al. 2014). Ethyl methyl sulfide (EMS, CH3CH2SCH3), seems to be a potential candidate for observation in the ISM since the simpler analogs, CH3SH and CH3CH2SH, have already been detected. In addition, the analog molecule containing oxygen, CH3CH2OCH3, ethyl methyl ether, was detected in Orion KL by Tercero et al. (2018) using the ALMA science verification data2 and a line survey of this source with the IRAM 30 m telescope (Tercero et al. 2010).
The rotational spectrum of EMS has been studied before by Hayashi et al. (1981) and Adachi et al. (1982) in the centimeter wave range up to 35 GHz, using a Stark modulation spectrometer. In these works, the two conformations that EMS can adopt in the gas phase, trans and gauche, were identified. The spectra of the 34S substituted isotopologues in natural abundance were also observed, together with those of the chemically singly substituted 13C and deuterium isotopologues. The measurements for the parent isotopologue included rotational transitions with J ≤ 10 and Ka ≤ 2. In final fits, the rotational and the quartic distortion constants, only one for the trans conformer, were determined with large uncertainties. The astronomical search for EMS at the observational frequency ranges of the radio telescopes becomes difficult with the predictions obtained with these rotational and centrifugal distortion parameters. Hence, a more accurate spectral modeling of EMS with spectral measurements extended into the millimeter-wave region constitutes the first scenario for a well-based astronomical detection.
In the present work, new spectroscopic measurements for both conformers of EMS have been performed in the 72–116.5 GHz frequency range using a new broadband millimeter-wave spectrometer based on radio astronomy receivers with fast Fourier transform (FFT) backends (Cernicharo et al. 2019; Cabezas et al. 2019). The analysis of the new data, involving 250 and 350 new torsion–rotation transitions for the trans and gauche conformers, respectively, allowed us to more accurately determine the rotational and the internal rotation parameters needed to provide more reliable predictions to support astronomical observations of EMS. In addition, we report the identification of low-lying vibrational excited states for both the trans and gauche conformers. Finally, the rotational parameters for the ground state have been used to search for EMS in the warm and cold molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1, using the spectral surveys captured by IRAM 30 m at 3 mm and 2 mm.
2. Quantum chemical calculations
Although quantum chemical calculations are not strictly necessary for the conformational identification, since previous rotational data for EMS have been reported, we carried out ab initio calculations in order to estimate the conformational stability and the parameters necessary to the internal rotation analysis. We optimized the molecular structure for both the trans and gauche conformers (see Fig. 1) of EMS at the coupled cluster with singles and doubles excitations with the Dunning’s correlation consistent polarized valence triple-ζ (CCSD/cc-pVTZ) level of theory (Dunning 1989) using the Molpro 2018.1 ab initio program package (Werner et al. 2018). In addition, harmonic and anharmonic frequency calculations were done out at the CCSD/cc-pVTZ and MP2/cc-pVTZ (Müller–Plesset perturbation theory) levels of theory, using the Molpro 2018.1 and Gaussian16 (Frisch et al. 2016) program packages, respectively. We found a small energy difference of only 2 cm−1 between the trans and gauche conformers, the former conformation being the most stable one. This energy difference increases up to 33 cm−1 when the Gibbs free energies are considered. The relative energies of the conformers are listed in Table 1 together with the rest of molecular parameters, rotational and centrifugal distortion constants, and internal rotation parameters, calculated for each of the EMS conformers.
 |
Fig. 1. Schematic visualization of four lowest frequency normal vibrational modes of trans (left) and gauche (right) conformers of EMS ν30, ν29, ν28, and ν27 obtained from ab initio calculations. |
Theoretical and experimental molecular constants for the EMS conformers.
3. Experimental
The experimental measurements were conducted using the broadband high-resolution rotational spectrometer GACELA (GAS CEll for Laboratory Astrophysics) constructed at the Yebes Observatory (Spanish National Geographic Institute (IGN)) within the context of the ERC synergy project NANOCOSMOS. The spectrometer is equipped with radio receivers similar to those used in the radio telescopes to search for molecular emission in space. The receivers are equipped with 16 × 2.5 GHz FFTs, with a spectral resolution of 38.14 kHz allowing the observation of the rotational transitions in the Q (31.5–50 GHz) and W bands (72–116.5 GHz). Cernicharo et al. (2019) gave a detailed description of the spectrometer.
The EMS sample (purity > 99%), purchased from Sigma Aldrich, was placed into a PyrexTM vacuum Schlenk which was connected directly to the spectrometer’s cell, which consists of a stainless steel cylinder of 890 mm in length and 490 mm in diameter. The vapor pressure of EMS was sufficient to measure the rotational spectrum at room temperature in a flow mode. Prior to the sample introduction, the pressure inside the vacuum chamber was 2.0 × 10−4 mbar and during the experiment the pressure was kept at 7.0 × 10−3 mbar, because higher pressures produce undesirable line broadenings. With the selected working pressure, the rotational lines of EMS have a half width at half maximum (HWHM) of 0.3−0.45 MHz, which is well adapted to measuring frequencies with a high level of accuracy. In all these experiments, a frequency switching (of two seconds) with a throw of 25 MHz was selected as the observing procedure. It has previously been confirmed as the most suitable mode since the lines are observed twice and the noise is improved by a factor square root of two, allowing us to derive accurate line profiles and intensities for lines of up to 2 MHz full width at half maximum (FWHM; Cernicharo et al. 2019).
4. Rotational spectrum and analysis
The rotational spectrum obtained for EMS shows a complex pattern that can be attributed to two intense species: the trans and the gauche conformers. According to the previous experimental results, the trans conformer belongs to the Cs point symmetry group and only shows b-type rotational spectra (μb = 1.559 D) (Hayashi et al. 1981). In contrast, the gauche conformer does not contain any element of symmetry, thus it belongs to the C1 point symmetry group, and it will show a-, b- and c-type spectra (Adachi et al. 1982). The identification of the rotational transitions of both conformers of EMS in the 72 to 116.5 GHz was achieved using the rotational and distortion constants previously reported by Hayashi et al. (1981) and Adachi et al. (1982). The uncertainties in the predictions for the trans conformer using the previous data provided by Hayashi et al. (1981) were relatively large because only rotational constants and the centrifugal distortion constant ΔJ were determined by these authors. Several R-branch transitions were identified and fit using the SPFIT/SPCAT (Pickett 1991) program with the A-reduction of the Watson’s Hamiltonian in Ir representation (Watson 1977). The initial fit provided a set of refined experimental constants that were used for new spectral predictions that allowed in turn the identification of b-type Q-branch transitions with Ka values ranging from four to seven. As previously reported by Hayashi et al. (1981), some of the rotational transitions of the trans conformer of EMS exhibit doublet structures with small splitting due the internal rotation of the S-CH3 group. Hayashi et al. (1981) found that the V3 internal rotation barrier height for the trans conformer of EMS was 692 (19) cm−1. The magnitude of the expected splittings, estimated using this experimental value, is of about tenths of kHz for most of the rotational transitions, which is irresolvable in our spectrum since the splittings are smaller than the experimental broadening of the lines. However, for some of the b-type Q-branch transitions, we were able to observe the A − E splittings, which were no larger than 4 MHz (see Fig. 2). In total, we observed 172 rotational transitions for the trans conformer (given in Table A.1 available at the CDS), which were included in a least-squares fit, together with those observed by Hayashi et al. (1981), using the XIAM program (Hartwig & Dreizler 1996) that it is based on the combined axis method introduced by Woods (1996). The analysis rendered the experimental rotational constants and the internal rotation parameters shown in Table 1.
 |
Fig. 2. Left: section of the rotational spectrum of EMS showing the 190, 19–181, 18 and 162, 15–152, 14 rotational transitions for trans and gauche conformers, respectively. For these transitions, the A − E splittings are irresolvable since they are smaller than the experimental broadening of the lines. The negative features marked with an asterisk are produced by the folding of the frequency-switched data and appear at ±25 MHz of each rotational transition. Middle: 363, 33–362, 34b-type Q-branch rotational transition for the trans conformer of EMS where the A − E splittings can be observed. Right: 335, 28–334, 29b-type Q-branch rotational transition for the gauche conformer of EMS with the A − E internal rotation components indicated. |
We analogously predicted the rotational transition frequencies for the gauche conformer using the experimental rotational constants and the V3 internal rotation barrier height reported by Adachi et al. (1982). In the case of the gauche conformer, the determined V3 value is smaller than that of the trans conformer, and thus the expected A − E splittings are larger (see Fig. 2). Consequently, we observed most of the R- and Q-branch rotational transitions of the gauche conformer split in A − E components due to the internal rotation of the S-CH3 group. Finally, a total of 259 rotational transitions (given in Table A.2, available at the CDS), including a- and b-types with J ≤ 62 and Ka ≤ 13, were observed for the gauche conformer and included, together with those reported by Adachi et al. (1982), in a least-squares fit using the XIAM program (Hartwig & Dreizler 1996). The rotational and centrifugal distortion constants derived from the fit together with the internal rotation parameters are shown in Table 1.
Around each ground state line for both the trans and gauche conformers, some satellite lines attributable to pure rotational transitions in excited vibrational states were observed. In order to interpret the vibrational pattern, ab initio calculations at the MP2/cc-pVTZ level of the theory using the Gaussian16 program package were carried out to estimate harmonic frequencies of the lowest normal vibrational modes. The vibrational contributions to the rotational constants were modeled on the basis of calculated first-order vibration-rotation constants αi that define the vibrational dependence of rotational constants Bν = Be − ∑iαi(νi + 1/2), where Bν and Be substitute all three rotational constants in a given excited state and in equilibrium, respectively, and νi is the vibrational quantum number. The four lowest-frequency modes, lying below 300 cm−1, are schematically visualized in Fig. 1.
Using the estimated rotational constants for the vibrationally excited states, we identified the rotational transitions for the vibrational mode ν30 for both the trans and gauche conformers. In addition, for the trans conformation we also identified the second quanta of ν30, which could not be observed for the gauche conformer. As can be seen in Fig. 1, the ν30 vibrational mode is a skeletal torsion with a frequency of 79 and 83 cm−1 for the trans and gauche conformers, respectively. Most of the assigned rotational transitions in ν30 state of the trans conformer showed characteristic A − E splittings with similar magnitude to that found in the trans ground state spectrum. A total of 61 components (given in Table A.3, available at the CDS) were included in the final fit for this species and the derived parameters are provided in Table 2. For the 2ν30 state, only 17 rotational transitions (given in Table A.4, available at the CDS) were observed and no evidence of the A − E splitting was found in these measured lines. Hence, these transitions were analyzed using a Watson’s semirigid-rotor Hamiltonian and the spectroscopic constants obtained are shown in Table 2. Likewise, the rotational transitions observed for the excited state ν30 state of the gauche conformer (given in Table A.5, available at the CDS) did not show A − E splitting. Next, all 43 of these rotational transitions were also analyzed using a Watson’s semirigid-rotor Hamiltonian. Results from this analysis are depicted in Table 2.
Spectroscopic constants for the vibrationally excited states of the EMS conformers.
5. Discussion
The rotational parameters obtained in this work and those predicted ab initio are shown in Table 1 together with the previously data reported by Hayashi et al. (1981) and Adachi et al. (1982) for trans and gauche conformers, respectively. For the trans conformer, the accuracy of the rotational parameters from our analysis, including all the quartic and the sextic ΦK distortion constants, has been increased compared to those reported by Hayashi et al. (1981), who only determined the rotational and ΔJ centrifugal distortion constant. The new set of experimental values agree reasonably well with those from Hayashi et al. (1981) and with those calculated ab initio. In the case of the gauche conformer, our rotational constants are similar to those determined by Adachi et al. (1982). However, the distortion constant values from our fit are completely different to those determined by Adachi et al. (1982). The reason for these discrepancies comes from the different type of analysis performed in each case and the number of rotational transitions included in fits. We carried out a global fit including a- and b-types with J ≤ 62 and Ka ≤ 13 of both A and E states, while Adachi et al. (1982) performed the analysis only for the A substate transitions, and then it was possible for the internal rotation perturbations to be included in the centrifugal distortion constants. Our experimental constants agree very well with those estimated by ab initio calculations. With these new sets of rotational constants, we can predict the rotational spectrum of each of the EMS conformers up to 200 GHz with accuracies of a few kHz for the 72–116.5 GHz domain, around 100 kHz between 120 and 150 GHz, ∼500 kHz between 150–200 GHz, and ∼1 MHz in the 1 mm domain. The frequency predictions for trans and gauche conformers up to 200 GHz calculated at T = 300 K are given in Tables A.6 and A.7, respectively, available at the CDS. The rotational and vibrational partition functions used in these predictions, at different temperatures, are listed in Table 3.
Rotational, vibrational and conformational partition functions for both conformers of EMS at different temperatures.
The analysis of the internal rotation splittings allowed us to determine the internal rotation barrier heights, V3, for both the trans and gauche conformers, with better accuracy than Hayashi et al. (1981) and Adachi et al. (1982), due to the larger number of rotational transitions analyzed in this work. The discrepancies between the present values for V3 and those reported before are smaller than the (3 σ), indicating a good agreement too. We estimated the V3 values using quantum chemical calculations for both the trans and gauche conformers by optimizing the transition state of the CH3-S rotation motion at the CCSD/cc-pVTZ level of theory. In spite of the fact that the results shown in Table 1 indicate that our ab initio calculations overestimate the V3 barrier heights for both EMS conformers, the obtained values are compatible.
The experimental V3 values can be compared to those previously obtained for similar molecular systems such as ethyl methyl ether, CH3CH2OCH3, the analog EMS molecule containing oxygen. For ethyl methyl ether, only the V3 barrier height for the trans conformer has been experimentally determined: 893 (7) cm−1 (Hayashi & Kuwada 1975). This larger value, compared to that of 683.28 (60) cm−1 found for the trans conformer of EMS, can be explained by the shorter bond distance between the CH3-O in the ethyl methyl ether compared to the CH3-S distance in the EMS. This shorter distance, or higher bond order, produces a large hindrance for the methyl top rotation. Similar behavior has been observed between equivalent molecular systems like S-methyl thioformate (Caminati et al. 1981) and O-methyl formate (Curl 1959), for which V3 values are 146.3 (25) and 416 (14) cm−1, respectively. Hence, as a general rule, CH3-S tops possess smaller internal rotation barrier height than their equivalent CH3-O tops, with exception of the particular case of methanol (De Lucia et al. 1989) and methyl mercaptan (Sastry et al. 1986) where the associate V3 is smaller for the CH3-O top.
All the previous experimental investigations on EMS using rotational (Hayashi et al. 1981; Adachi et al. 1982), vibrational (Hayashi et al. 1957; Nogami et al. 1975; Sakakibara et al. 1977), and electron diffraction (Oyanagi & Kuchitsu 1978) spectroscopy reported that the gauche conformer was the most stable species, being up to three times more abundant than the trans one. However, Durig et al. (1991) calculated the energy difference between the trans and gauche conformers and found that the trans species was more stable than the gauche one by more than 130 cm−1. This statement was experimentally confirmed by far-infrared spectral measurements (Durig et al. 1991). To gain some insight into these inconsistencies, we evaluated the relative abundance of each EMS conformer in two different ways. The concentration of each conformer in the gas phase can be estimated by relative intensity measurements of their rotational transitions. It is assumed that the intensity of the rotational transitions is proportional to the number density of each conformer and the square value of the corresponding component of the electric dipole moment, 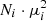 . From our measurements, using several b-type rotational transitions, we found an approximate population ratio of 1:2, with the gauche conformer being the most abundant species. In addition, conformational abundances were estimated and our ab initio calculations predict that the trans conformer is energetically more stable than the gauche one. However, the expected populations indicate that gauche species is 1.7 times more abundant in the gas phase. These populations have been calculated using the Gibbs free energies and considering that the gauche conformer has its equivalent (isoenergetic) counterpart differing in the sign of the ∠CCCS dihedral angle and, thus, its concentration is statistically favored by a factor of two. This is not the case for the trans conformer due to the planarity of its backbone. Hence, our calculations and the relative abundances derived from the spectrum are in good agreement and both indicate that in spite of the fact that trans conformer is energetically more favorable, the concentration of the gauche one is larger in the gas phase at the temperature of the gas in our experiments (300 K).
. From our measurements, using several b-type rotational transitions, we found an approximate population ratio of 1:2, with the gauche conformer being the most abundant species. In addition, conformational abundances were estimated and our ab initio calculations predict that the trans conformer is energetically more stable than the gauche one. However, the expected populations indicate that gauche species is 1.7 times more abundant in the gas phase. These populations have been calculated using the Gibbs free energies and considering that the gauche conformer has its equivalent (isoenergetic) counterpart differing in the sign of the ∠CCCS dihedral angle and, thus, its concentration is statistically favored by a factor of two. This is not the case for the trans conformer due to the planarity of its backbone. Hence, our calculations and the relative abundances derived from the spectrum are in good agreement and both indicate that in spite of the fact that trans conformer is energetically more favorable, the concentration of the gauche one is larger in the gas phase at the temperature of the gas in our experiments (300 K).
This conformational behavior is in sharp contrast with that found for the analog molecule ethyl methyl ether for which the trans conformer is the most abundant species. The trans ethyl methyl ether molecule has been fully characterized by rotational spectroscopy (Hayashi & Kuwada 1975; Adachi et al. 1982; Fuchs et al. 2003), while the gauche conformation has not been observed so far. Just for comparison, we carried out ab initio calculations for both isomers of ethyl methyl ether at the CCSD/cc-pVTZ level of theory and found that the gauche conformer is 479 cm−1 less stable than the trans conformation. This change in the stability trends in EMS and ethyl methyl ether molecules can be attributed to the different atomic sizes between S and O atoms and their influence in the balance of intramolecular interactions. A similar trend in the conformational stability is observed between ethyl mercaptan and ethanol. In ethyl mercaptan, the gauche conformation is lower in energy by 162 cm−1 (Senent et al. 2014), while for ethanol, the trans isomer is the most stable species, by 41 cm−1 (Pearson et al. 1994).
6. Searching for ethyl methyl sulfide in space
As discussed before, we found that the gauche conformer is two times more abundant than the trans conformer in spite of the fact that the trans species is predicted to be more stable than the gauche species. Therefore, the astronomical searches for both the gauche and trans conformers of EMS were carried out using the rotational parameters obtained in this work, Table 1, and the MADEX code (Cernicharo 2012).
We used data from different molecular line surveys collected with the IRAM 30 m telescope. We focused on two high-mass star-forming regions: Orion KL (public data provided by Tercero et al. 2010) and Sagittarius (Sgr) B2 (public data of Sgr B2(N) provided by Belloche et al. 2013), on a starless core in the Taurus Molecular Cloud (TMC-1; data from Marcelino et al. 2007), and in the cold dark cloud Barnard 1 (B1-b; data from Marcelino et al. 2007; Cernicharo et al. 2012). Owing to our frequency predictions are sufficiently reliable up to 200 GHz, we examined data at 3 mm (∼80 − 115 GHz) and 2 mm (∼130 − 178 GHz) for Orion KL, and data at 3 mm for the rest of the sources. Although we expected that EMS could arise as the product of dust mantle evaporation in hot cores, we extended our search to cold clouds since methyl mercaptan (CH3SH) has been detected in both hot and cold environments (Linke et al. 1979; Cernicharo 2012; Belloche et al. 2013; Kolesniková et al. 2014).
After spectral searches in all these sources, we did not find rotational signatures of any of two conformers of EMS above the detection limit of these data. To provide upper limits to the column density for the two conformers of EMS, we used the MADEX code assuming local thermodynamic equilibrium (LTE) to derive their synthetic spectrum in these sources. The assumed physical parameters for the different models (Table 4) are those of CH3SH derived by Kolesniková et al. (2014) for the hot core of Orion KL, those of CH3CH2OCH3 derived by Tercero et al. (2015) for the compact ridge of Orion KL, and those of CH3SH derived by Belloche et al. (2013) for Sgr B2(N). For B1-b and TMC-1, we limited the search for transitions with upper-level energies below 30 K and we assumed the same physical parameters adopted by Marcelino et al. (2007) and Cernicharo et al. (2012). Figure 3 shows selected frequencies of these data together with the model derived by MADEX that demonstrates the lack of gauche and trans EMS lines. Table 5 lists the spectroscopic parameters of the lines shown in Fig. 3.
 |
Fig. 3. Observed data of Orion KL, Sgr B2, B1-1, and TMC-1 taken with the IRAM 30 m telescope (histogram black spectra), together with the synthetic spectra of gauche-CH3CH2SCH3 (red thin curve) and trans-CH3CH2SCH3 (blue thin curve) obtained using MADEX and the physical parameters shown in Table 4. The synthetic total model for the 30 m data of Orion KL (see Cernicharo et al. 2016) and Sgr B2(N) (see Belloche et al. 2013) is overlaid in green. Radial velocities (vLSR) of +9.0 km s−1, +64.0 km s−1, +6.7 km s−1, and +6.0 km s−1 are assumed for Orion KL, Sgr B2, B1-b, and TMC-1, respectively. |
Physical parameters of the considered cloud cores in the astronomical search of EMS.
Both the large partition function of gauche and trans EMS for energies above 100 K and the high level of blending and line confusion in the IRAM 30 m surveys of Orion KL and Sgr B2 lead to very high values for the upper limits to the column densities of both EMS conformers in these regions. In fact, they are of the same order of magnitude as the column densities derived for CH3SH (Belloche et al. 2013; Kolesniková et al. 2014). This limitation prevents a realistic discussion about abundance ratios with related species. Only interferometric data, which drastically reduce the line blending caused by the emission of different spatial components in these sources, could provide further insights about the presence of EMS.
7. Conclusions
This paper presents an extensive laboratory study of the rotational spectrum of EMS in its ground and vibrationally excited states, extending the earlier knowledge on the spectroscopic properties of this molecule. The measurements have been performed in the 72–116.5 GHz frequency region using a broadband millimeter-wave spectrometer to collect 172 and 259 new rotational transitions for the trans and gauche conformers, respectively. Many transitions show resolvable internal rotation splittings that were analyzed to determine the corresponding internal rotation parameters. The optimised values of all the spectroscopic constants are in good agreement with those predicted by quantum chemical calculations. The newly obtained set of rotational parameters allowed us to obtain frequency predictions sufficiently reliable up to 200 GHz. With these data, we searched for EMS in the warm and cold molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1, using the spectral surveys captured by IRAM 30 m at 3 mm and 2 mm. We did not find EMS above the detection limit of these data and provided upper limits to the column density for the two conformers of EMS.
CDMS 2020, The Cologne Database for Molecular Spectroscopy: Molecules in the Interstellar Medium or Circumstellar Shells (as of 02/2020), https://cdms.astro.uni-koeln.de/classic/molecules
Acknowledgments
We thank the European Research Council for funding support under Synergy Grant ERC-2013-SyG, G.A. 610256 (NANOCOSMOS). CB thanks to Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva postdoctoral fellowship (FJCI-2016-27983). This work was also based on observations carried out with the IRAM 30-meter telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
References
- Adachi, M., Nakagawa, J., & Hayashi, M. 1982, J. Mol. Spectr., 91, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2010, A&A, 570, A45 [Google Scholar]
- Agúndez, M., Marcelino, N., Cernicharo, J., & Tafalla, M. 2018, A&A, 611, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogert, A. C. A., Schutte, W. A., Helmich, F. P., Tielens, A. G. G. M., & Wooden, D. H. 1997, A&A, 317, 929 [NASA ADS] [Google Scholar]
- Cabezas, C., Bermúdez, C., Gallego, J. D., et al. 2019, A&A, 629, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminati, W., van Eijck, B. P., & Lister, D. G. 1981, J. Mol. Spectr., 90, 15 [CrossRef] [Google Scholar]
- Cernicharo, J. 2012, in ECLA-2011: Proc. of the European Conference onLaboratory Astrophysics, eds. C. Stehl, C. Joblin, & L. d’Hendecourt (Cambridge: Cambridge Univ. Press), EAS Pub. Ser., 251, https://nanocosmos.iff.csic.es/?pageid=1619 [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Kisiel, Z., Tercero, B., et al. 2016, A&A, 587, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Gallego, J. D., López-Pérez, J. A., et al. 2019, A&A, 626, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curl, R. F. 1959, J. Chem. Phys., 30, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, F. C., Herbst, E., Anderson, T., & Helminger, P. 1989, J. Mol. Spectr., 134, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Durig, J. R., Rollins, M. S., & Phan, H. V. 1991, J. Mol. Spectr., 263, 95 [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., & Schlegel, H. B. 2016, Gaussian 16, Revision A.03 [Google Scholar]
- Fuchs, U., Winnewisser, G., Groner, P., De Lucia, F. C., & Herbst, E. 2003, ApJS, 144, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Goicoechea, J. R., Pety, J., et al. 2017, ApJ, 851, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., Baas, F., Greenberg, J. M., & Schutte, W. 1985, A&A, 146, L6 [NASA ADS] [Google Scholar]
- Gottlieb, C. A., Ball, J. A., Gottlieb, E. W., Lada, C. J., & Penfield, H. 1975, ApJ, 200, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwig, H., & Dreizler, H. 1996, Z. Naturforsch., 51a, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&A, 338, 713 [Google Scholar]
- Hayashi, M., & Adachi, M. 1982, J. Mol. Spectr., 78, 53 [NASA ADS] [Google Scholar]
- Hayashi, M., & Kuwada, K. 1975, J. Mol. Spectr., 28, 147 [NASA ADS] [Google Scholar]
- Hayashi, M., Shimanouchi, T., & Mizushima, S. 1957, J. Chem. Phys., 26, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Adachi, M., & Nakagawa, J. 1981, J. Mol. Spectr., 86, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kolesniková, L., Tercero, B., Cernicharo, J., et al. 2014, ApJ, 784, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Laas, J. C., & Caselli, P. 2019, A&A, 624, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linke, R. A., Frerking, M. A., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Wyrowski, F., Belloche, A., et al. 2011, A&A, 525, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogami, N., Sugeta, H., & Miyazawa, T. 1975, Bull. Chem. Soc. Jpn., 48, 3573 [CrossRef] [Google Scholar]
- Oyanagi, K., & Kuchitsu, K. 1978, Bull. Chem. Soc. Jpn., 51, 2243 [CrossRef] [Google Scholar]
- Palumbo, M. E., Tielens, A. G. G. M., & Tokunaga, A. T. 1995, ApJ, 449, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Sastry, K. V. L. N., Herbst, E., & De Lucia, F. C. 1994, J. Mol. Spectr., 175, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, JMoSp, 148, 371 [NASA ADS] [Google Scholar]
- Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Sakakibara, M., Matsuura, H., Harada, I., & Shimanouchi, T. 1977, Bull. Chem. Soc. Jpn., 50, 111 [CrossRef] [Google Scholar]
- Sastry, K. V. L. N., Herbst, E., Booker, R. A., & Lucia, F. C. D. 1986, J. Mol. Spectr., 116, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Senent, M. L., Puzzarini, C., Domínguez Gómez, R., Carvajal Zaera, M., & Hochlaf, M. 2014, J. Chem. Phys., 140, 124302 [NASA ADS] [CrossRef] [Google Scholar]
- Sinclair, M. W., Fourikis, N., Ribes, J. C., et al. 1973, Aust. J. Phys., 26, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cernicharo, J., López, A., et al. 2015, A&A, 582, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cuadrado, S., López, A., et al. 2018, A&A, 620, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tieftrunk, A., Pineau des Forets, G., Schilke, P., & Walmsley, C.M. 1994, A&A, 289, 579 [Google Scholar]
- van der Tak, F. F. S., Boonman, A. M. S., Braakman, R., & van Dishoeck, E. F. 2000, A&A, 361, 327 [Google Scholar]
- Watson, J. K. G. 1977, in Vibration Spectra and Structure, ed. J. Durig (Amsterdam: Elsevier), 1977 [Google Scholar]
- Werner, H.J., Knowles, P.J., & Knizia, G. 2018, MOLPRO, version 2018.1 [Google Scholar]
- Woods, R. C. 1996, J. Mol. Spectr., 21, 4 [Google Scholar]
- Yamamoto, S., Saito, S., Kawaguchi, K., et al. 1987, ApJ, 317, L119 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectroscopic constants for the vibrationally excited states of the EMS conformers.
Rotational, vibrational and conformational partition functions for both conformers of EMS at different temperatures.
Physical parameters of the considered cloud cores in the astronomical search of EMS.
All Figures
 |
Fig. 1. Schematic visualization of four lowest frequency normal vibrational modes of trans (left) and gauche (right) conformers of EMS ν30, ν29, ν28, and ν27 obtained from ab initio calculations. |
| In the text | |
 |
Fig. 2. Left: section of the rotational spectrum of EMS showing the 190, 19–181, 18 and 162, 15–152, 14 rotational transitions for trans and gauche conformers, respectively. For these transitions, the A − E splittings are irresolvable since they are smaller than the experimental broadening of the lines. The negative features marked with an asterisk are produced by the folding of the frequency-switched data and appear at ±25 MHz of each rotational transition. Middle: 363, 33–362, 34b-type Q-branch rotational transition for the trans conformer of EMS where the A − E splittings can be observed. Right: 335, 28–334, 29b-type Q-branch rotational transition for the gauche conformer of EMS with the A − E internal rotation components indicated. |
| In the text | |
 |
Fig. 3. Observed data of Orion KL, Sgr B2, B1-1, and TMC-1 taken with the IRAM 30 m telescope (histogram black spectra), together with the synthetic spectra of gauche-CH3CH2SCH3 (red thin curve) and trans-CH3CH2SCH3 (blue thin curve) obtained using MADEX and the physical parameters shown in Table 4. The synthetic total model for the 30 m data of Orion KL (see Cernicharo et al. 2016) and Sgr B2(N) (see Belloche et al. 2013) is overlaid in green. Radial velocities (vLSR) of +9.0 km s−1, +64.0 km s−1, +6.7 km s−1, and +6.0 km s−1 are assumed for Orion KL, Sgr B2, B1-b, and TMC-1, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


