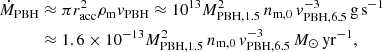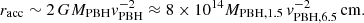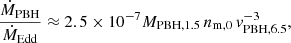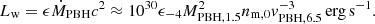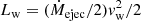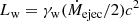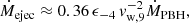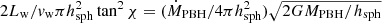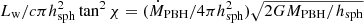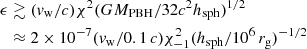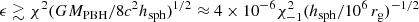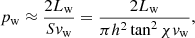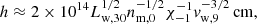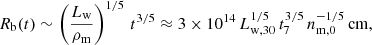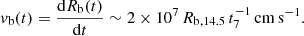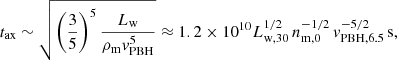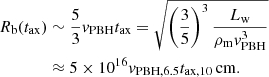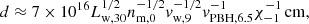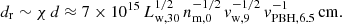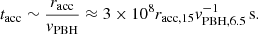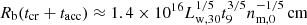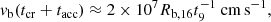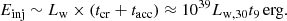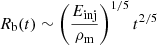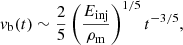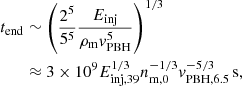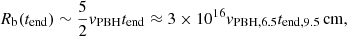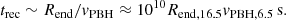© ESO 2020

1. Introduction

The first gravitational waves detected by LIGO-Virgo were produced by the merger of two heavy stellar-mass black holes (BHs; Abbott et al. 2016). These detections revived the idea that primordial black holes (PBHs; Zel’dovich & Novikov 1967; Hawking 1971; Carr & Hawking 1974; Chapline 1975) may be an important component of dark matter (Bird et al. 2016; Sasaki et al. 2016; Clesse & García-Bellido 2017), particularly with regard to those with masses around 10−100 M_⊙. Among the different astrophysical and cosmological consequences of PBH existence (see, e.g., Sasaki et al. 2018, and references therein), the radiation produced by PBH accretion could have left a detectable imprint on the cosmic microwave background (CMB; Ricotti et al. 2008; Ali-Haïmoud & Kamionkowski 2017; Poulin et al. 2017; Bernal et al. 2017; Nakama et al. 2018) and the 21 cm hydrogen signal (Bernal et al. 2018; Hektor et al. 2018; Mena et al. 2019; Hütsi et al. 2019) and could be producing detectable radio and X-ray emission in our galaxy (Gaggero et al. 2017; Manshanden et al. 2019).

The characterization of accreting PBHs is based on a number of assumptions that have not been fully tested yet. The robustness of PBH abundance constraints, coming from CMB, 21 cm signal, and galactic emission, depends significantly on those assumptions. In particular, one important aspect of PBH accretion-emission physics that has been rarely discussed in the literature concerns the indirect impact on accretion of outflows, winds and (or) jets, produced by the PBHs themselves. This effect, known as mechanical feedback, consists of a reduction of gas accretion caused by outflows sweeping the medium away, as this leaves only diluted and hot gas to accrete. Mechanical feedback is, in fact, an important astrophysical process in general, and has been discussed for instance in the context of heavy stellar-mass BHs as those detected by LIGO (Ioka et al. 2017), supermassive BHs growth (see, e.g., Levinson & Nakar 2018; Zeilig-Hess et al. 2019, and references therein), and other astrophysical objects such as stars, galaxies and clusters (e.g., Soker 2016; Gruzinov et al. 2020; Li et al. 2020).

The aim of the present work is to estimate for the first time, using analytical and numerical tools, the potential reduction of the accretion rate, hence in the associated radiation, caused by the production of outflows in a moving PBH. Li et al. (2020) already tentatively explored, through a numerical study, the impact of mechanical feedback on Bondi-Hoyle-Lyttleton accretion in different astrophysical contexts. Here we consider the PBH case due to its far-reaching astrophysical and cosmological consequences. Thus, we focus on the case in which a PBH moves with a supersonic speed through an almost homogeneous medium, similar to that of the Universe at high redshift, when non-linear structures had not yet formed, both before and after hydrogen recombination. Therefore the results of this work can be applied both to existing CMB constraints and to future 21 cm constraints, but they also hold relevance for PBH (and isolated BHs in general) detectability in the present-day Universe.

The paper is structured as follows: first we provide an analytical characterization of the impact of outflows on the accretion process (Sects. 2 and 3). Then, we present the results of numerical simulations to complement the analytical characterization (Sect. 4). Finally, we conclude with a summary and a discussion of our findings (Sect. 5). Throughout this work, we adopt the convention Q_b = Q/10^b, where Q is any physical quantity measured in cgs units¹, unless indicated otherwise. Also, the symbol ∼ indicates an order of magnitude estimate, whereas the symbol ≈ is used when we provide an approximate numerical estimate of a given quantity.

2. Basics of accretion and outflow physics

2.1. Accretion

We consider a PBH of mass M_PBH that moves with supersonic speed v_PBH through an almost homogeneous medium with density ρ_m = ⟨m⟩n_m, number density n_m, and average particle mass ⟨m⟩ ∼ m_H ≈ 1.7 × 10⁻²⁴ g (i.e., the hydrogen atom mass). We assume as reference case a PBH with mass M_PBH = 30 M_⊙ moving with a speed of v_PBH = 3 × 10⁶ cm s⁻¹ in a medium with number density n_m = 1 cm⁻³ (i.e., M_PBH, 1.5 ≈ 1, v_PBH, 6.5 ≈ 1, n_m, 0 = 1).

As proposed in Ali-Haïmoud & Kamionkowski (2017), if PBHs are all the dark matter, their typical speed is approximately constant before hydrogen recombination, with v_PBH ≈ 3 × 10⁶ cm s⁻¹ (Dvorkin et al. 2014), and v_PBH ∝ (1 + z) afterwards (Tseliakhovich & Hirata 2010), where z is the redshift. Since PBHs move supersonically with respect to baryons until relatively low redshift (z ≈ 20), our set-up roughly captures both pre- and (early) post-recombination scenarios. The reference value taken for the number density of the medium, n_m = 1 cm⁻³, corresponds to the baryon number density n_b(z) = n_b0(1 + z)³ at redshift z ≈ 150, where n_b0 ∼ Ω_b0ρ_0c/m_H ≈ 3 × 10⁻⁷ cm⁻³ is the present-day baryon number density, Ω_b0 ≈ 0.05 the baryon fractional abundance at present time, and ρ_0c ≈ 10⁻²⁹ g cm⁻³ the present-day critical density².

A supersonic PBH accretes approximately at the Bondi-Hoyle-Lyttleton accretion rate (Hoyle & Lyttleton 1939; Bondi & Hoyle 1944):

$$\begin{array}{cc}\hfill {\dot{M}}_{\mathrm{PBH}}& \approx \pi r_{\mathrm{acc}}^2{\rho }_{\mathrm{m}}{v}_{\mathrm{PBH}}\approx {10}^{13}{M}_{\mathrm{PBH},1.5}^2{n}_{\mathrm{m},0}{v}_{\mathrm{PBH},6.5}^{-3}\mathrm{g}{\mathrm{s}}^{-1}\hfill \\ \hfill & \approx 1.6\times {10}^{-13}{M}_{\mathrm{PBH},1.5}^2{n}_{\mathrm{m},0}{v}_{\mathrm{PBH},6.5}^{-3}{M}_{\odot }{\mathrm{yr}}^{-1},\hfill \end{array}$$(1)

where the effective accretion radius r_acc, which defines the PBH sphere of influence radius, is given by:

$$\begin{array}{c}\hfill r_{\mathrm{acc}}\sim 2G{M}_{\mathrm{PBH}}{v}_{\mathrm{PBH}}^{-2}\approx 8\times {10}^{14}{M}_{\mathrm{PBH},1.5}{v}_{\mathrm{PBH},6.5}^{-2}\mathrm{cm}.\end{array}$$(2)

In the case where the PBH moves with subsonic speed, we have to substitute v_PBH in Eq. (2) with the sound speed of the medium (Bondi 1952). In that situation, accretion would be closer to the spherical case, at least on scales ≲r_acc (but not necessarily in the close vicinity of the PBH; Waters et al. 2020). This would be the case, for instance, at redshift z ≲ 20, but we do not investigate that epoch here due to its high complexity, as it coincides with the formation of the first structures.

Processes in the PBH vicinity may reduce the accretion rate in that region. Typically, they are accounted for by defining the real accretion rate as Ṁ = λṀ_PBH, where Ṁ_PBH is the accretion rate defined in Eq. (1), and the parameter λ ≲ 1 encloses the physical effects of pressure, viscosity, radiation feedback and other processes on scales close to the PBH gravitational radius (r_g = GM_PBH/c² ≈ 5 × 10⁶ cm for M_PBH = 30 M_⊙). In fact, λ captures the presence of gravitationally unbounded flows of any type. In particular, the production of fast winds or jets can significantly reduce the accretion rate on those scales (i.e., λ ≪ 1; see, e.g., Tsuna et al. 2018; Bu & Yang 2019, in the context of isolated stellar-mass and supermassive BHs). Here, since we are interested only on mechanical feedback on scales comparable to r_acc, any process that reverts accretion close to the PBH is phenomenologically treated as outflow on larger scales. Thus, our reference value for the accretion rate is Ṁ_PBH, that is, we take λ = 1.

Relatively far from the PBH, accretion takes place through a column that forms behind the accretor, as schematically drawn in Fig. 1. In the case of a perfectly homogeneous medium, accretion is axisymmetric, and matter is channeled by this gravitationally bounded gas column straight to the accretor. However, it is expected that small perturbations, which would be certainly present in a cosmological context, would lead to a break of the axisymmetry of the accretion process, which can be then enhanced by instability growth. This can lead to the accretion of some angular momentum (see, e.g., Foglizzo et al. 2005; Lora-Clavijo et al. 2015; see also Waters et al. 2020 for the spherical case). In fact, density inhomogeneities accreted with different impact parameters will already provide some angular momentum. In these contexts, even if the average angular momentum accreted in the long-term is very small, it is possible to form a short-lived small disk close to the PBH (see, e.g., Agol & Kamionkowski 2002, and references therein).

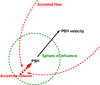Fig. 1. Sketch of the no-outflow case, where the PBH is moving supersonically through a medium, and it is accreting material from its sphere of influence through a gas column forming opposite to the direction of motion. Sketch not to scale.

To further characterize accretion in the vicinity of the PBH, it is informative to compare the BH accretion luminosity to the Eddington luminosity. Accounting only for Thomson scattering on ionized hydrogen, the Eddington luminosity is given by L_Edd ≈ 3.8 × 10³⁹ M_PBH, 1.5 erg s⁻¹. Defining here the Eddington accretion rate as Ṁ_Edd = 10L_Edd/c², we obtain the ratio of the PBH accretion rate to the Eddington rate given by:

$$\begin{array}{c}\hfill \frac{{\dot{M}}_{\mathrm{PBH}}}{{\dot{M}}_{\mathrm{Edd}}}\approx 2.5\times {10}^{-7}{M}_{\mathrm{PBH},1.5}{n}_{\mathrm{m},0}{v}_{\mathrm{PBH},6.5}^{-3},\end{array}$$(3)

which shows that, for a very broad range of parameter values, Ṁ_PBH/Ṁ_Edd ≪ 0.1. Such a low Eddington accretion fraction implies that in our scenario the accreted gas will not cool efficiently on scales ≳r_g, leading to the formation of a faint and hot (virialized) accretion structure close to the PBH (see, e.g., Shakura & Sunyaev 1973). As we will see, such a configuration is prone to outflow formation.

Observational cosmology is unable to establish whether inhomogeneities lead to net angular momentum accretion because of the small spatial scales involved. The key quantities that regulate angular momentum accretion are amplitude and spatial scale of the inhomogeneities. Regarding the former, we note that the development of instabilities in the inner accretion structure can help to amplify rather smooth inhomogeneities. Concerning the latter, by characterizing the inhomogeneity scale as l_inh, one can estimate the duration of net angular momentum accretion: t_l ∼ l_inh/v_PBH. For inhomogeneities to be important, it is required that: (i) t_l ≫ r_g/c, that is, t_l is larger than the wind formation time scale; and (ii) t_l ≲ r_acc/v_PBH, that is, t_l is smaller than the PBH sphere of influence crossing time. Otherwise, (i) the wind will not have time to form, or (ii) the gradients may be too small to accrete a non-negligible amount of net angular momentum. Given the random nature of the inhomogeneities, both in amplitude and in l_ihn, it is expected that the outflow will change orientation on a time ∼t_l. Given that the evolution timescale of the whole system is expected to be longer than any relevant t_l (see below), the outflow could effectively act, on average, as a very broad wind at large scales.

2.2. Outflows

A bipolar outflow (wind and– or –jet) from an accreting PBH can affect its own energetics, and the radiation from accretion, by sweeping away medium gas on scales ∼r_acc. Nevertheless, the launch of such an outflow requires: (i) a strong magnetic field of specific geometry; and (or) (ii) an excess of thermal energy in some of the accreted gas, that is, positive energy gas that turns into a wind.

Regarding (i), we must note first that the magnetic field in the accreted primordial gas is expected to be very small, although the Biermann battery mechanism may alleviate this problem in the accretion flow, and the magnetorotational instability could produce an enhancement of magnetization and turbulence, thereby generating the viscosity needed for accretion (see, e.g., Safarzadeh 2018)³. However, the magnetic field seed generated by the Biermann battery is toroidal, whereas jet launching requires some vertical magnetic flux (see, e.g., the discussion in Sotomayor Checa & Romero 2019). Nevertheless, if enough vertical flux is present close to the PBH, the inner accretion region can efficiently launch a collimated, supersonic bipolar outflow (Blandford & Payne 1982). In addition, if the PBH is spinning fast, relativistic, highly collimated jets can be also produced in the PBH ergosphere through the Blandford-Znajek (Blandford & Znajek 1977) mechanism (even if accretion is quasi-spherical, as discussed, for example, in Barkov & Khangulyan 2012; Barkov et al. 2012).

In the case of (ii), regardless of the presence of jets, a weakly accreting, geometrically thick disk can form winds through thermal pressure gradients (see, e.g., Sądowski et al. 2016, where jets are also shown to form if the BH is spinning). Such (less collimated) outflows, produced by an excess of thermal energy in the accretion structure, are less dependent on the details of the magnetic field. Thus, to be conservative, hereafter we assume that the outflow has a thermal origin, and carries only a small fraction ϵ of the rate of accreted energy ∼ Ṁ_PBHc². The power of each constituent of the bipolar supersonic outflow can be characterized as:

$$\begin{array}{c}\hfill L_{\mathrm{w}}=ϵ{\dot{M}}_{\mathrm{PBH}}{c}^2\approx {10}^{30}{ϵ}_{-4}{M}_{\mathrm{PBH},1.5}^2{n}_{\mathrm{m},0}{v}_{\mathrm{PBH},6.5}^{-3}\mathrm{erg}{\mathrm{s}}^{-1}.\end{array}$$(4)

Alternatively, we can write

$$\begin{array}{c}\hfill L_{\mathrm{w}}=({\dot{M}}_{\mathrm{ejec}}/2)v_{\mathrm{w}}^2/2\end{array}$$(5)

or

$$\begin{array}{c}\hfill L_{\mathrm{w}}={\gamma }_{\mathrm{w}}({\dot{M}}_{\mathrm{ejec}}/2)c^2\end{array}$$(6)

in the non-relativistic and the highly relativistic (cold outflow) case, respectively, where v_w is the outflow speed, Ṁ_ejec the total ejected mass, and γ_w the outflow Lorentz factor. Equations (4) and (5) imply

$$\begin{array}{c}\hfill {\dot{M}}_{\mathrm{ejec}}\approx 0.36{ϵ}_{-4}{v}_{\mathrm{w},9}^{-2}{\dot{M}}_{\mathrm{PBH}},\end{array}$$(7)

which shows that 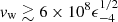$v_{\mathrm{w}}\gtrsim 6\times {10}^8{ϵ}_{-4}^{1/2}$ cm s⁻¹ to ensure that Ṁ_ejec < Ṁ_PBH (i.e., large ϵ values require highly relativistic outflows).

We can also estimate a minimum ϵ for the outflow to escape the vicinity of the PBH: The outflow propagation should proceed roughly unimpeded if accretion is rather equatorial, away from the outflow close to the PBH. However, beyond some distance, hard to ascertain but prescribed here by the parametric length h_sph, the inflowing gas could be quasi-isotropic. If such a region were present within the PBH sphere of influence, the supersonic outflow should have enough ram pressure to overcome that of the inflowing gas, if distances > r_acc are to be reached. One can estimate when it is the case assuming that accretion is roughly spherical above h_sph from the PBH, that the gas flows inwards at free fall velocity, and then deriving a constraint on ϵ by equating the outflow and medium ram pressures, p_w = p_m at h_sph:

$$\begin{array}{c}\hfill 2L_{\mathrm{w}}/v_{\mathrm{w}}\pi h_{\mathrm{sph}}^2{tan}^2\chi =({\dot{M}}_{\mathrm{PBH}}/4\pi h_{\mathrm{sph}}^2)\sqrt{2G{M}_{\mathrm{PBH}}/h_{\mathrm{sph}}}\end{array}$$(8)

or

$$\begin{array}{c}\hfill L_{\mathrm{w}}/c\pi h_{\mathrm{sph}}^2{tan}^2\chi =({\dot{M}}_{\mathrm{PBH}}/4\pi h_{\mathrm{sph}}^2)\sqrt{2G{M}_{\mathrm{PBH}}/h_{\mathrm{sph}}}\end{array}$$(9)

for the non-relativistic and the highly relativistic case, respectively; χ is the outflow half opening angle. Thus, the outflow will escape if:

$$\begin{array}{cc}\hfill ϵ& \gtrsim (v_{\mathrm{w}}/c){\chi }^2{(G{M}_{\mathrm{PBH}}/32c^2{h}_{\mathrm{sph}})}^{1/2}\hfill \\ \hfill & \approx 2\times {10}^{-7}(v_{\mathrm{w}}/0.1c){\chi }_{-1}^2{(h_{\mathrm{sph}}/{10}^6{r}_{\mathrm{g}})}^{-1/2}\hfill \end{array}$$(10)

or

$$\begin{array}{c}\hfill ϵ\gtrsim {\chi }^2{(G{M}_{\mathrm{PBH}}/8c^2{h}_{\mathrm{sph}})}^{1/2}\approx 4\times {10}^{-6}{\chi }_{-1}^2{(h_{\mathrm{sph}}/{10}^6{r}_{\mathrm{g}})}^{-1/2}\end{array}$$(11)

for the non-relativistic and the highly relativistic case, respectively, where tanχ has been approximated as χ (valid for χ ≪ 1).

3. Mechanical feedback: analytical estimates

In this section, we characterize analytically the interaction of the outflow with the surrounding medium in its early (Sect. 3.1) and long-term (Sects. 3.2 and 3.3) stages of evolution. We discuss the effect of the relative orientation between the outflow and the PBH velocity, corresponding to different values of the angle θ shown in Fig. 2. We investigate the cases when the outflow and the PBH velocities are orthogonal (θ = π/2; Sect. 3.2), and when they are aligned (θ = 0; Sect. 3.3). In the long-term evolution, the value of the half-opening angle χ is expected to be also important for mechanical feedback; we discuss two qualitatively distinct cases: collimated outflows with χ ≪ 1 (see Sects. 3.2 and 3.3) versus non-collimated outflows with χ ∼ 1 (see Sect. 3.3). In this section we consider as reference case a conical outflow with half-opening angle χ = 10⁻¹, velocity of the outflow v_w = 10⁹ cm s⁻¹, and luminosity L_w = 10³⁰ erg s⁻¹, corresponding to ϵ ≈ 10⁻⁴ (see Eq. (4)) for our choice of parameters. Nevertheless we note that our predictions will not be very sensitive to the actual parameter values (with the clear exception of χ) as long as L_w is large enough to allow the outflow front to escape the PBH sphere of influence.

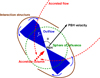Fig. 2. Sketch of the early stage of the outflow-medium interaction, including the formation of a diluted and hot gas bubble that ultimately engulfs the PBH sphere of influence. Sketch not to scale.

3.1. Early interaction

After leaving the region close to the compact object, the front of the supersonic outflow is eventually slowed down by the ram pressure of the gas surrounding the PBH. Since the medium sound speed is significantly smaller than v_w, the medium ram pressure in the outflow reference frame is 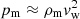$p_{\text{m}}\approx {\rho }_{\text{m}}{v}_{\text{w}}^2$. The ram pressure of the outflow front in the medium frame is:

$$\begin{array}{c}\hfill p_{\mathrm{w}}\approx \frac{2L_{\mathrm{w}}}{S{v}_{\mathrm{w}}}=\frac{2L_{\mathrm{w}}}{\pi h^2{tan}^2\chi v_{\mathrm{w}}},\end{array}$$(12)

in the non-relativistic case, where S = πh²tan²χ is the outflow front surface at the distance h from the PBH. For typical values of the parameters we have that the outflow and medium pressures become comparable at a height:

$$\begin{array}{c}\hfill h\approx 2\times {10}^{14}{L}_{\mathrm{w},30}^{1/2}{n}_{\mathrm{m},0}^{-1/2}{\chi }_{-1}^{-1}{v}_{\mathrm{w},9}^{-3/2}\mathrm{cm},\end{array}$$(13)

where tanχ ∼ χ. If the outflow velocity were highly relativistic, then 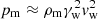$p_{\text{m}}\approx {\rho }_{\text{m}}{\gamma }_{\text{w}}^2{v}_{\text{w}}^2$ and p_w ≈ L_w/(Sv_w), turning h into $h^{\mathrm{rel}}=h/({\gamma }_{\mathrm{w}}\sqrt{2})$.

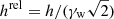Approximately at the distance h from the PBH, where pressure equilibrium is reached, the front of the supersonic outflow significantly slows down and the material reaching the front gets shocked. Then, this shocked material is directed sideways and then backwards, and inflates a bubble of hot adiabatic gas surrounded by a shell of shocked medium. The outflow is initially freely expanding, but at some point the bubble pressure balances the lateral pressure of the outflow, point at which the latter acquires a cylindrical geometry. This leads to the self-similar evolution of the bubble, in which the bubble dynamics depends on its energy content and the accumulated medium mass (see, e.g., Alexander 2006, in an extragalactic context). The bubble evolution is thus not very sensitive to how collimated or relativistic the initial outflow was. This process is illustrated in Fig. 2.

The self-similar bubble expansion can be approximated as adiabatic and symmetric, fed by a steady source of energy; thus, its evolution can be approximately characterized by the Sedov-Taylor equation in the continuous regime (see, e.g., Blandford & McKee 1976 and references therein; see also Kaiser & Alexander 1997; Alexander 2006 in the context of extragalactic jets), according to which the bubble radius R_b evolves in an approximate self-similar fashion as:

$$\begin{array}{c}\hfill R_{\mathrm{b}}(t)\sim {\left(\frac{L_{\mathrm{w}}}{{\rho }_{\mathrm{m}}}\right)}^{1/5}{t}^{3/5}\approx 3\times {10}^{14}{L}_{\mathrm{w},30}^{1/5}{t}_7^{3/5}{n}_{\mathrm{m},0}^{-1/5}\mathrm{cm},\end{array}$$(14)

with forward velocity:

$$\begin{array}{c}\hfill v_{\mathrm{b}}(t)=\frac{\mathrm{d}{R}_{\mathrm{b}}(t)}{\mathrm{d}t}\sim 2\times {10}^7{R}_{\mathrm{b},14.5}{t}_7^{-1}{\mathrm{cm}\mathrm{s}}^{-1}.\end{array}$$(15)

Thus, for some time the bubble is expanding forward significantly faster than the PBH moves, for v_PBH = 3 × 10⁶ cm s⁻¹. Here, for simplicity, we assume that the bubble is approximately spherical, although the lateral expansion can be a factor of a few slower (see, e.g., Kaiser & Alexander 1997), which should be accounted for in a more detailed treatment of the problem.

If the pressure equilibrium distance is larger than the effective accretion radius, that is, h >  r_acc, the bubble will start to form after a time t_h ∼ h/v_w, and once the outflow front has already left the PBH sphere of influence. In this case, the time required by the front to cross the sphere of influence t_cr roughly corresponds to the time needed to reach a distance r_acc from the PBH: t_cr ∼ 10⁶ r_acc, 15/v_w, 9s (< t_h). Vice versa, if h <  r_acc, the crossing time will be 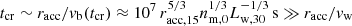$t_{\mathrm{cr}}\sim r_{\mathrm{acc}}/v_{\mathrm{b}}(t_{\mathrm{cr}})\approx {10}^7{r}_{\mathrm{acc},15}^{5/3}{n}_{\mathrm{m},0}^{1/3}{L}_{\mathrm{w},30}^{-1/3}\mathrm{s}\gg r_{\mathrm{acc}}/v_{\mathrm{w}}$. In either case, after a time ≳max[t_h, t_cr], the bubble filled with hot gas will engulf the PBH sphere of influence and accretion is expected to be affected. Only if v_b becomes ≲v_PBH before the bubble reaches out of the PBH sphere of influence (i.e., an extreme case plus the condition h <  r_acc), bubble growth will be overcome by gravity, and the outflow will not be able to prevent accretion.

3.2. Quasi-perpendicular outflow

Once outside the PBH sphere of influence, the bubble slows down until its expansion velocity and the PBH velocity become comparable, that is, v_b ∼ v_PBH. At that moment and for θ ∼ 1, the bubble is already far from symmetric because the medium ram pressure is mostly acting on one side of the bubble. The typical timescale of the previous axisymmetric expansion t_ax can be derived from Eq. (15):

$$\begin{array}{c}\hfill t_{\mathrm{ax}}\sim \sqrt{{\left(\frac{3}{5}\right)}^5\frac{L_{\mathrm{w}}}{{\rho }_{\mathrm{m}}{v}_{\mathrm{PBH}}^5}}\approx 1.2\times {10}^{10}{L}_{\mathrm{w},30}^{1/2}{n}_{\mathrm{m},0}^{-1/2}{v}_{\mathrm{PBH},6.5}^{-5/2}\mathrm{s},\end{array}$$(16)

and the bubble size at time t_ax is:

$$\begin{array}{cc}\hfill R_{\mathrm{b}}(t_{\mathrm{ax}})& \sim \frac{5}{3}{v}_{\mathrm{PBH}}{t}_{\mathrm{ax}}=\sqrt{{\left(\frac{3}{5}\right)}^3\frac{L_{\mathrm{w}}}{{\rho }_{\mathrm{m}}{v}_{\mathrm{PBH}}^3}}\hfill \\ \hfill & \approx 5\times {10}^{16}{v}_{\mathrm{PBH},6.5}{t}_{\mathrm{ax},10}\mathrm{cm}.\hfill \end{array}$$(17)

Therefore, for the system under consideration, we have that after t ∼ t_ax ≈ 400 yr the bubble will reach a typical size of ∼60 r_acc (see Eqs. (2) and (17)). At that point, the bubble is already getting compressed in the direction of the PBH motion, and tends to expand in the opposite direction, as shown in Fig. 3 (see also, e.g., Yoon et al. 2011 for simulations of jets from a BH microquasar moving in the interstellar medium, and Li et al. 2020 for a simulation of a case more similar to ours).

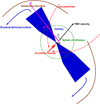Fig. 3. Long-term outflow-medium interaction in the quasi-perpendicular case. Sketch not to scale.

The strong bubble asymmetry makes the two constituents of the bipolar outflow deflect away from the PBH motion direction. The typical scale d at which the outflow deflection is significant can be derived from equating the medium ram pressure in the PBH reference frame, 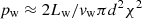$p_{\text{w}}\approx 2L_{\text{w}}/v_{\text{w}}\pi d^2{\chi }^2$, with the outflow ram pressure, p_w ≈ 2L_w/v_wπd²χ² in the non-relativistic case:

$$\begin{array}{c}\hfill d\approx 7\times {10}^{16}{L}_{\mathrm{w},30}^{1/2}{n}_{\mathrm{m},0}^{-1/2}{v}_{\mathrm{w},9}^{-1/2}{v}_{\mathrm{PBH},6.5}^{-1}{\chi }_{-1}^{-1}\mathrm{cm},\end{array}$$(18)

where we assume that χ ≪ 1. In the highly relativistic case, for which p_w ≈ L_w/cπ(d^rel)²χ², this distance turns into 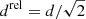$d^{\mathrm{rel}}=d/\sqrt{2}$. The deflection distance d turns out to be much larger than the PBH sphere of influence; for the parameters considered in this work: d ∼ 70 r_acc. This scale also characterizes the typical size of the section of the interaction structure perpendicular to the PBH motion.

For θ = π/2 (and χ ≪ 1), free sidewards expansion of the outflow propagating within the asymmetric bubble is stopped on the side on which the medium ram pressure acts, on a distance d_r <  d from the PBH. Assuming for simplicity that the outflow is very cold, outflow asymmetric reconfinement occurs at the distance where the medium and outflow lateral ram pressures are equal, 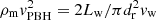${\rho }_{\text{m}}{v}_{\text{PBH}}^2=2L_{\text{w}}/\pi d_{\text{r}}^2{v}_{\text{w}}$ in the non-relativistic case:

$$\begin{array}{c}\hfill d_{\mathrm{r}}\sim \chi d\approx 7\times {10}^{15}{L}_{\mathrm{w},30}^{1/2}{n}_{\mathrm{m},0}^{-1/2}{v}_{\mathrm{w},9}^{-1/2}{v}_{\mathrm{PBH},6.5}^{-1}\mathrm{cm}.\end{array}$$(19)

In the highly relativistic case, where 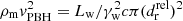${\rho }_{\mathrm{m}}{v}_{\mathrm{PBH}}^2=L_{\mathrm{w}}/{\gamma }_{\mathrm{w}}^{2}c\pi {(d_{\mathrm{r}}^{\mathrm{rel}})}^2$, this distance becomes 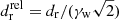$d_{\mathrm{r}}^{\mathrm{rel}}=d_{\mathrm{r}}/({\gamma }_{\mathrm{w}}\sqrt{2})$. Within d_r, the outflow is expected to be ballistic, at ∼d_r it starts to deflect, and at d, it has significantly deviated. The tail described above is in fact made of shocked deflected outflow heavily mixed with shocked medium, as the outflow-medium contact discontinuity is prone to hydrodynamical instability growth (see, e.g., Sect. 4).

As shown by Li et al. (2020), for θ = π/2 the surrounding medium gas can penetrate into the sphere of influence and reach the PBH on the directions perpendicular to the outflow, because the bubble pressure is the lowest there. Thus, accretion may only be moderately affected by mechanical feedback. Nevertheless we note that for χ ≪ 1 and θ <  π/2 (but still ∼1), the outflow can suffer a stronger, oblique shock that can widen the outflow front. This situation might turn into a case where we effectively have χ ∼ θ, which is closer to the quasi-parallel case reported in Sect. 3.3.

So far we have assumed that the evolution of the outflow-medium interaction structure was adiabatic. However, according to the cooling rates for low metallicities in Sutherland & Dopita (1993) and the timescale of the problem (≳t_ax) close the recombination epoch the medium was dense enough (n_m(z_rec ≈ 1100)≈400 cm⁻³) to make the bubble-driven shock in the medium radiative. This affects the dynamics of the bubble; in particular, it enhances the growth of instabilities at the outflow-medium contact discontinuity. A fully disrupted contact discontinuity would make an analytical treatment of the studied scenario more speculative. At this stage, we leave for future work a more detailed analysis of the radiative bubble case.

3.3. Quasi-parallel outflow

When the outflow is roughly aligned with the direction of motion (see Fig. 4), accretion onto the PBH sphere of influence is expected to be almost halted once the hot and diluted bubble gas fully occupies that region, keeping out the external gas (as shown in Sect. 4, and also in Li et al. 2020). As already mentioned, this could occur also for non-negligible values of θ if the outflow is non-collimated, that is, χ ∼ 1. Under these circumstances, significant outflow production can last only until the remaining material within the sphere of influence has been accreted.

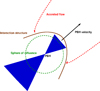Fig. 4. Long-term outflow-medium interaction in the quasi-parallel case. Sketch not to scale.

The typical timescale of accretion of the remaining medium gas is of order of the free-fall timescale at r_acc:

$$\begin{array}{c}\hfill t_{\mathrm{acc}}\sim \frac{r_{\mathrm{acc}}}{v_{\mathrm{PBH}}}\approx 3\times {10}^8{r}_{\mathrm{acc},15}{v}_{\mathrm{PBH},6.5}^{-1}\mathrm{s}.\end{array}$$(20)

After a time ∼t_cr + t_acc from the formation of the outflow, only diluted hot matter should be present around the PBH and accretion should be very weak. The bubble size and expansion speed at this stage are given by Eqs. (14) and (15), and they read as:

$$\begin{array}{c}\hfill R_{\mathrm{b}}(t_{\mathrm{cr}}+t_{\mathrm{acc}})\approx 1.4\times {10}^{16}{L}_{\mathrm{w},30}^{1/5}{t}_9^{3/5}{n}_{\mathrm{m},0}^{-1/5}\mathrm{cm}\end{array}$$(21)

and

$$\begin{array}{c}\hfill v_{\mathrm{b}}(t_{\mathrm{cr}}+t_{\mathrm{acc}})\approx 2\times {10}^7{R}_{\mathrm{b},16}{t}_9^{-1}\mathrm{cm}{\mathrm{s}}^{-1},\end{array}$$(22)

respectively. Therefore, even after having expanded up to ∼20 r_acc, the bubble expansion speed is still significantly faster than the PBH, for v_PBH = 3 × 10⁶ cm s⁻¹.

When both accretion and ejection stop, energy injection into the bubble stops as well. At that point, the outflow has injected an energy of:

$$\begin{array}{c}\hfill E_{\mathrm{inj}}\sim L_{\mathrm{w}}\times (t_{\mathrm{cr}}+t_{\mathrm{acc}})\approx {10}^{39}{L}_{\mathrm{w},30}{t}_9\mathrm{erg}.\end{array}$$(23)

Once the energy injection stops, for t ≫ (t_cr + t_acc) the bubble will expand adiabatically with size and velocity approximated as (see, e.g., Blandford & McKee 1976, for the adiabatic and impulsive regime):

$$\begin{array}{c}\hfill R_{\mathrm{b}}(t)\sim {\left(\frac{E_{\mathrm{inj}}}{{\rho }_{\mathrm{m}}}\right)}^{1/5}{t}^{2/5}\end{array}$$(24)

and

$$\begin{array}{c}\hfill v_{\mathrm{b}}(t)\sim \frac{2}{5}{\left(\frac{E_{\mathrm{inj}}}{{\rho }_{\mathrm{m}}}\right)}^{1/5}{t}^{-3/5},\end{array}$$(25)

respectively.

The time needed for the bubble velocity v_b to reach the PBH velocity v_PBH reads as:

$$\begin{array}{cc}\hfill t_{\mathrm{end}}& \sim {\left(\frac{2^5}{5^5}\frac{E_{\mathrm{inj}}}{{\rho }_{\mathrm{m}}{v}_{\mathrm{PBH}}^5}\right)}^{1/3}\hfill \\ \hfill & \approx 3\times {10}^9{E}_{\mathrm{inj},39}^{1/3}{n}_{\mathrm{m},0}^{-1/3}{v}_{\mathrm{PBH},6.5}^{-5/3}\mathrm{s},\hfill \end{array}$$(26)

and the bubble final size after a time t_cr + t_acc + t_end ∼ t_end is:

$$\begin{array}{c}\hfill R_{\mathrm{b}}(t_{\mathrm{end}})\sim \frac{5}{2}{v}_{\mathrm{PBH}}{t}_{\mathrm{end}}\approx 3\times {10}^{16}{v}_{\mathrm{PBH},6.5}{t}_{\mathrm{end},9.5}\mathrm{cm},\end{array}$$(27)

which is somewhat smaller than the value obtained in Eq. (18) for the quasi-perpendicular case, but still much larger than the PBH sphere of influence.

Once v_b gets ≲v_PBH, the ram pressure of the medium becomes dominant over that of the shocked outflow, and the material starts re-approaching the PBH as the latter moves, reaching it in an accretion recovery time:

$$\begin{array}{c}\hfill t_{\mathrm{rec}}\sim R_{\mathrm{end}}/v_{\mathrm{PBH}}\approx {10}^{10}{R}_{\mathrm{end},16.5}{v}_{\mathrm{PBH},6.5}\mathrm{s}.\end{array}$$(28)

As (t_rec + t_end)≫(t_cr + t_acc), the stage in which the PBH neither accretes nor ejects largely dominates the duration of the whole on-off accretion cycle, and so the time-average accretion rate should be much lower than the Bondi-Hoyle-Lyttleton one. For the typical values derived here, we find an average reduction in Ṁ_PBH by a factor (t_cr + t_acc)/(t_rec + t_end)∼0.1 (see Sect. 4), but lower and higher values are also possible given the large plausible parameter space.

The maximum, temporary section radius of the outflow-medium interaction structure in the quasi-parallel case can be identified with the bubble radius R_b(t_end). If otherwise accretion and outflow production were constant, the structure section radius would be also constant and characterized by Eq. (18).

4. Mechanical feedback: numerical calculations

In Sect. 3.2 we have seen that a perpendicular, well-collimated outflow may leave the PBH sphere of influence without strongly affecting the gas accretion from directions away from the outflow, allowing the gas to reach the PBH. On the other hand, even in the perpendicular case, accretion could be reduced if high-pressure, shocked outflow material were more homogeneously distributed inside the PBH sphere of influence, more effectively preventing the external medium from entering that region. As noted, this could be the case for more oblique and (or) broad outflows, but even collimated (χ ≪ 1) perpendicular outflows may in principle divert enough momentum sideways due to instability growth closer to the PBH, leading to a situation closer to that discussed in Sect. 3.3. Unfortunately, finding the value range of θ and χ for which accretion is inhibited by mechanical feedback requires a number of expensive 3-dimensional (3D) hydrodynamical simulations, as they should include spatial scales both ≪ r_acc and ≳d; for typical parameter values this spans several orders of magnitude. Adaptive mesh refinement can be useful to reduce the computational time, but we note that highly turbulent flows, as expected in the studied scenario, are sometimes challenging for this technique (see, e.g., Bosch-Ramon et al. 2015).

The computing time needed for a simulation is proportional to the number of computing cells of the grid, times the number of simulation time steps: T_sim ∝ N_cells × N_steps, where N_cells ∝ (d/r_acc)^D ∝ (v_w/v_PBH)^D/2, with D being the dimensionality, and N_steps ∝ t_phys/Δt_phys, where t_phys ∝ d/v_PBH is the total simulated time, and Δt_sim ∝ d/v_w the simulated time step. This yields T_sim ∝ (v_w/v_PBH)^D/2 + 1. To make the problem more tractable, one can choose parameter values to reduce T_sim, although one still requires that d/r_acc ≫ 1 to capture at least qualitatively the main features of the system. This additional constraint makes a 3D simulation quite demanding. On the other hand, a 2D simulation, which is realistic in the parallel outflow case because of axisymmetry, becomes more affordable.

For this work, as a test of the case in which accretion is strongly reduced due to mechanical feedback, we carried out axisymmetric hydrodynamical simulations for θ = 0. We adopted values for v_PBH and v_w that allow us to probe a moderately large range of spatial scales d/r_acc, and that reduce significantly N_steps. An intermediate value of the outflow half-opening angle was obtained by adopting a Mach number of M_ch = 2.5, which yields shortly after injection, already in the supersonic regime, a χ ≈ 1/M_ch = 0.4; but we note that trials with χ = 0.1 (not shown here) yielded similar results.

4.1. Properties of the simulation

We performed axisymmetric hydrodynamical simulations of the interaction between a collimated outflow with v_w = 10⁹ cm s⁻¹ and initial M_ch = 2.5, and a moving medium with v_PBH = 5 × 10⁷ cm s⁻¹ and Mach number of 3. The medium density was fixed to ρ_m = 1.7 × 10⁻²⁴ cm⁻³ (i.e., n_m ≈ 1 cm⁻³), and the power of each constituent of the bipolar outflow to 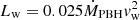$L_{\mathrm{w}}=0.025{\dot{M}}_{\mathrm{PBH}}{v}_{\mathrm{w}}^2$, corresponding to ϵ ≈ 10⁻⁴, which is the reference value used for our analytical estimates above. The grid size was chosen such that the interaction structure remained in the computational grid for the duration of the simulation. We note that exploratory trials done with a higher ϵ-value suggested that results should not change significantly.

The cell size of the simulation was fixed to 10¹¹ cm. The size of the grid in the radial 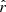$\widehat{r}$- and the vertical 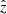$\widehat{z}$-directions are 250 cells (2.5 × 10¹³ cm) and 500 cells (5 × 10¹³ cm), respectively. The source of the gravitational potential is assumed to be point-like, with mass M_PBH = 30 M_⊙, but the grid region where matter is accreted and leaves the grid (i.e., the accretor in the context of the numerical simulation) is modeled as a spherical region of low density and pressure, with a radius of 10 cells and centred at the origin. The outflow is injected in the 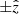$\pm \widehat{z}$-directions through a cylindrical inlet with a height and radius of 20 and 5 cells, respectively, and centred also at the origin, occupying thus a fraction of the accretion sphere. Any material crossing the accretor spherical surface but at the outflow inlet boundaries immediately disappears from the grid. Outside the outflow inlet and the accretor region, reflection conditions are imposed at the vertical axis (r = 0: left grid boundary), outflow conditions⁴ at the upper and right grid boundaries, and inflow conditions (i.e., the medium) at the bottom grid boundary. The motion of the medium in the PBH reference frame is in the 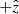$+\widehat{z}$-direction. The accretion rate is computed on the cells right outside the boundary of the accretor (i.e., excluding the outflow inlet). In this specific set-up the sphere of influence has approximately a radius of 30 cells (3 × 10¹² cm). Trials carried out with better resolution by a factor ≈1.9, and a slightly smaller accretor radius, ≈26% instead of 30%, yielded very similar results to those presented here.

The code used to solve the hydrodynamics equations is the same as the one used in de la Cita et al. (2017): third order in space (Mignone et al. 2005); second order in time; and using the Marquina flux formula (in the non-relativistic case, Donat & Marquina 1996). Both the outflow and medium fluids were simplified as non-relativistic mono-atomic gases with adiabatic index 5/3. We neglect the effects of ionization and gas abundances, which are not relevant on the simulated scales (≫r_g), on which gravity and ram pressure dominate the dynamics of an adiabatic flow. Any magnetic field should be affected by the flow evolution, but here we are assuming that the role of the magnetic field is purely subsidiary to the collisionless gas hydrodynamical approximation, and so of no dynamical importance. The accretor gravitational force was appropriately included in the hydrodynamical equations as a source term (see, e.g., Toro 2009).

4.2. Results

We show in Fig. 5 the accretion rate of two cases: when the mechanical feedback mechanism due to the outflow is present and when it is not. When there is no feedback, the long-term accretion rate converges to a value within a factor of 2 from Ṁ_PBH ≈ 3 × 10⁻¹⁷ M_⊙ yr⁻¹ predicted by Eq. (1). On the other hand, when outflows are launched, our simulations indicate that matter reaches the PBH only indirectly, through filamentary structures related to hydrodynamical instabilities in the contact discontinuity between the outflow and the medium. Thus, accretion is on average one order of magnitude lower (Ṁ_PBH ≈ 3 × 10⁻¹⁸ M_⊙ yr⁻¹) than in the case without outflow, but presents strong fluctuations with respect to that average value. It is worth indicating the presence of filamentary material entering the grid from the top for t ≳ 15 t_acc. This backflow is a numerical artifact associated to the boundary conditions and the presence of subsonic material in the upper boundary. The subsonic material in the boundary can induce the flow to bounce back, sending waves into the grid. However, we have checked with additional simulation trials that imposing a positive velocity at the boundary (i.e., the flow is forced to leave the grid), of modulus 5 × 10⁷ cm s⁻¹, quantitatively yields very similar results. The simulation was run until it presented repetitive patterns of the flow, a sort of quasi-steady state. Our results are quite similar to those obtained by Li et al. (2020) for θ = 0.

Fig. 5. Evolution of the accretion rate with (blue curve) and without outflow (green curve). Time is measured in units of the accretion dynamical timescale tacc = 6 × 104 s. Orange crosses are located at the times of the eleven density maps with outflow of Fig. 6.

We also present in Fig. 6 the density maps showing the evolution of the outflow structure for approximately 50 times the accretion dynamical timescale t_acc (t_acc ≈ 6 × 10⁴ s, according to Eq. (20)). The time of each snapshot in Fig. 6 is marked with a cross at its corresponding location in the accretion rate curve of Fig. 5. These density maps can be compared to the no-outflow simulation, run for a very similar amount of time, and shown in the bottom right panel of Fig. 6. Both Figs. 5 and 6 are illustrative of the strong non-linear nature of the outflow-medium interaction structure, and reminiscent of the intermittent nature of accretion predicted in Sect. 3.

Fig. 6. Color density maps of the outflow-medium interaction structure after (from left to right, and top to bottom) t ≈ 0, 5, 10; 15, 20, 25; 30, 35, 40; 45, 50 tacc. The bottom right density map corresponds to the case without outflow after t ≈ 50 tacc. The arrows illustrate the accreted gas trajectories. The injector-accretor region is located at (0, 0). The axis scales are normalized to racc, and the color scale is normalized to the medium density. The medium motion in the PBH reference frame is upwards.

4.3. A toy-model for θ = π/2

Despite the difficulty of studying the quasi-perpendicular case numerically, we still made a toy simulation in 2D of the case θ ∼ 1 by introducing an additional gravitational potential with a velocity dispersion σ, and with the medium initially at rest (as under the presence of a dark matter halo; see, e.g., Zeilig-Hess et al. 2019, for a calculation in the supermassive black-hole case). We ran test simulations of that scenario in the context of a PBH of 30 M_⊙ and σ = 30 km s⁻¹ and of a BH of 10⁸ M_⊙ and σ = 300 km s⁻¹, and obtained similar results in both cases to those of Zeilig-Hess et al. (2019) for the second case, that is, the accretion rate tended to a value a factor of a few smaller than the Bondi value without additional gravitational potential⁵. This result cannot be overstressed as it is not 3D, but shows the robustness of our numerical scheme. Moreover, the derived reduction in the accretion rate is similar to that found by Li et al. (2020) when computing a case in actual 3D similar to the one discussed in Sect. 3.2. This similarity is likely related to the fact that in both cases, 3D supersonic accretion with outflow and θ = π/2, and 2D subsonic accretion with outflow and adding a dark-matter-like potential, there is a characteristic medium velocity (v_pbh and σ, respectively) leading to reduced but steady accretion on the directions away from the outflow.

5. Discussion and conclusions

The effect of mechanical feedback is expected to reduce accretion onto a moving massive object, but quantifying this effect is difficult. In this work, we show that the angle between the outflow direction and the PBH motion, θ, is likely to determine how far below the Bondi rate the PBH accretion is. A numerical study of a similar but more general scenario by Li et al. (2020) reaches results in line with those presented here in the context of PBH. The half-opening angle χ is also expected to play an important role, as broader outflows are expected to have larger solid angles for which accretion is halted. As our analytical estimates and simulations show, an outflow do not need to be strong in order to reduce accretion; it is enough that the outflow effectively heats and dilutes all the gas in the PBH surroundings on scales ≳r_acc.

Assessing the level of accretion as a function of θ and χ is challenging due to the complexity of the outflow-medium interaction, and its intrinsic 3D nature in general. Nevertheless, we can already predict that accretion is expected to be significantly smaller than Bondi-Hoyle-Lyttleton accretion, with the presence of strong fluctuations, at least for values of θ ≲ χ. For θ ≫ χ, analytical and numerical calculations seem to indicate that the reduction may still be non-negligible, but with accretion proceeding more steadily. Nevertheless, the larger the ratio v_w/v_PBH, the larger the region affected by the outflow, in which case there is more room for some redirection of outflow momentum and energy, caused, for instance, by instability growth on the outflow walls. This might lead to the formation of a more effective barrier for accretion on scales similar to r_acc, even for θ ≈ π/2 and χ ≪ 1. In addition, θ may change with time, as explained at the end of Sect. 2.1, which could effectively lead to a time-averaged χ ∼ 1. For all this, knowing the effect of the time-averaged values of θ and χ of a PBH, and their statistical distribution in the PBH population(s), is crucial to estimate the effects of their accretion and related emission.

It is clear that the inclusion of mechanical feedback on a PBH population has a direct impact on PBH abundance constraints, as they depend on the energy injected by the PBH population into the primordial medium. This can be exemplified by the following. In the case of CMB constraints (Ricotti et al. 2008; Ali-Haïmoud & Kamionkowski 2017; Poulin et al. 2017; Bernal et al. 2017; Nakama et al. 2018), the injected energy density rate scales as 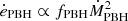${\dot{e}}_{\mathrm{PBH}}\propto f_{\mathrm{PBH}}{\dot{M}}_{\mathrm{PBH}}^2$, where f_PBH is the fraction of dark matter made up of PBHs. Fixing ė_PBH and assuming for simplicity the same M_PBH and Ṁ_PBH for all PBH, a decrease of an order of magnitude in Ṁ_PBH would allow an increase of two orders of magnitude in f_PBH. This would largely relax the present constraints on f_PBH in the 10−100 M_⊙ mass range. In addition to CMB constraints, constraints derived from galactic emission (Gaggero et al. 2017; Manshanden et al. 2019) could be also affected by mechanical feedback.

We have not discussed here the effects on the medium of the non-thermal radiation directly generated by the PBH outflows, because in our case outflows are rather weak, that is, ϵ ≪ 1. Notwithstanding, outflows from PBHs may have ϵ ≈ 1 and high radiative efficiency, in which case their high-energy radiation could contribute to heat, excite, and ionize the medium in addition to direct accretion emission. This would make the constraints on PBH abundance tighter, so such an effect should be considered in the future. In fact, radio (Gaggero et al. 2017; Manshanden et al. 2019) and high-energy emission from outflows produced by PBHs, located in dense regions of our galaxy, may be important enough to be detectable at galactic distances. This idea has been already explored in Barkov et al. (2012) in the case of isolated stellar BHs.

Acknowledgments

We thank the anonymous referee for constructive and useful comments that helped to improve the manuscript. We acknowledge Núria Torres-Albà, Edgar Molina, Licia Verde, and Alexander James Mead for useful comments and discussions. V.B-R. acknowledges support by the Spanish Ministerio de Economía y Competitividad (MINECO/FEDER, UE) under grant AYA2016-76012-C3-1-P, with partial support by the European Regional Development Fund (ERDF/FEDER), MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”), and the Catalan DEC grant 2017 SGR 643. NB is supported by the Spanish MINECO under grant BES-2015-073372.

References

All Figures

	Fig. 1. Sketch of the no-outflow case, where the PBH is moving supersonically through a medium, and it is accreting material from its sphere of influence through a gas column forming opposite to the direction of motion. Sketch not to scale.
In the text

	Fig. 2. Sketch of the early stage of the outflow-medium interaction, including the formation of a diluted and hot gas bubble that ultimately engulfs the PBH sphere of influence. Sketch not to scale.
In the text

	Fig. 3. Long-term outflow-medium interaction in the quasi-perpendicular case. Sketch not to scale.
In the text

	Fig. 4. Long-term outflow-medium interaction in the quasi-parallel case. Sketch not to scale.
In the text

	Fig. 5. Evolution of the accretion rate with (blue curve) and without outflow (green curve). Time is measured in units of the accretion dynamical timescale tacc = 6 × 104 s. Orange crosses are located at the times of the eleven density maps with outflow of Fig. 6.
In the text

Fig. 6. Color density maps of the outflow-medium interaction structure after (from left to right, and top to bottom) t ≈ 0, 5, 10; 15, 20, 25; 30, 35, 40; 45, 50 tacc. The bottom right density map corresponds to the case without outflow after t ≈ 50 tacc. The arrows illustrate the accreted gas trajectories. The injector-accretor region is located at (0, 0). The axis scales are normalized to racc, and the color scale is normalized to the medium density. The medium motion in the PBH reference frame is upwards.

In the text