| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202037902 | |
| Published online | 21 May 2020 | |
Liverpool-Maidanak monitoring of the Einstein Cross in 2006–2019⋆
I. Light curves in the gVrRI optical bands and microlensing signatures
1
Departamento de Física Moderna, Universidad de Cantabria, Avda. de Los Castros s/n, E-39005 Santander, Spain
e-mail: goicol@unican.es
2
Sternberg Astronomical Institute, Lomonosov Moscow State University, Universitetsky pr. 13, 119992 Moscow, Russia
e-mail: bartamon@mail.ru
3
O.Ya. Usikov Institute for Radiophysics and Electronics, National Academy of Sciences of Ukraine, 12 Acad. Proscury St., UA-61085 Kharkiv, Ukraine
e-mail: vshal@ukr.net
4
Institute of Astronomy of V.N. Karazin Kharkiv National University, Svobody Sq. 4, UA-61022 Kharkiv, Ukraine
5
Institute of Radio Astronomy of the National Academy of Sciences of Ukraine, 4 Mystetstv St., UA-61002 Kharkiv, Ukraine
6
Ulugh Beg Astronomical Institute of the Uzbek Academy of Sciences, Astronomicheskaya 33, 100052 Tashkent, Uzbekistan
7
National University of Uzbekistan, Department of Astronomy and Atmospheric Physics, 100174 Tashkent, Uzbekistan
Received:
6
March
2020
Accepted:
3
April
2020
Quasar microlensing offers a unique opportunity to resolve tiny sources in distant active galactic nuclei and study compact object populations in lensing galaxies. We therefore searched for microlensing-induced variability of the gravitationally lensed quasar QSO 2237+0305 (Einstein Cross) using 4374 optical frames taken with the 2.0 m Liverpool Telescope and the 1.5 m Maidanak Telescope. These gVrRI frames over the 2006–2019 period were homogeneously processed to generate accurate long-term multi-band light curves of the four quasar images A–D. Through difference light curves, we found strong microlensing signatures. We then focused on the analytical modelling of two putative caustic-crossing events in image C, finding compelling evidence that this image experienced a double caustic crossing. Additionally, our overall results indicate that a standard accretion disc accounts reasonably well for the brightness profile of UV continuum emission sources and for the growth in source radius when the emission wavelength increases: Rλ ∝ λα, α = 1.33 ± 0.09. However, we caution that numerical microlensing simulations are required before firm conclusions can be reached on the UV emission scenario because the VRI-band monitoring during the first caustic crossing and one of our two α indicators lead to a few good solutions with α ≈ 1.
Key words: techniques: photometric / methods: data analysis / gravitational lensing: strong / gravitational lensing: micro / quasars: individual: QSO 2237+0305
Tables 4–8 and 10–14 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/637/A89
© ESO 2020
1. Introduction
Analysis of multiply imaged quasars (which undergo strong gravitational lensing) reveals the structure and composition of tiny regions in distant active galactic nuclei, halos of intervening galaxies, and intergalactic space (e.g. Schneider et al. 1992, 2006). For a given gravitationally lensed quasar, multi-band optical light curves of its multiple images sometimes show phases of chromatic microlensing activity. This activity is related to microlenses (stars) that affect each continuum-emitting region differently and to a different extent, so that more compact (bluer) sources are expected to suffer stronger effects (e.g. Mosquera & Kochanek 2011, and references therein). Therefore multi-band photometric monitorings of microlensing episodes in lensed quasars are used, among other things, to probe the relationship between source radius and emission wavelength λ. Although some multi-band light curves only provided evidence that bluer sources are smaller (e.g. Vakulik et al. 2004), several studies indicated that microlensing-induced chromatic variations are fully or marginally consistent with radii that grow as λα, α = 4/3 (standard disc model; e.g. Shalyapin et al. 2002; Anguita et al. 2008; Eigenbrod et al. 2008; Poindexter et al. 2008; Hainline et al. 2013; Blackburne et al. 2015; Muñoz et al. 2016).
QSO 2237+0305 (the Einstein Cross; zs = 1.695) consists of four quasar images (A, B, C, and D) that are arranged like a cross around the nucleus of a nearly face-on spiral galaxy at zl = 0.039 (Huchra et al. 1985; Yee 1988). Although the light of this quadruply imaged quasar passes through four different regions in the bulge of the lensing spiral galaxy, time delays between images are extraordinarily short (typical values range from a few hours to a few days; e.g. Schneider et al. 1988; Vakulik et al. 2006). As a result of these short delays, magnitude differences between any two images exclusively include microlensing variations because intrinsic variations are removed (Irwin et al. 1989). Taking advantage of this fact, Eigenbrod et al. (2008) used the chromaticity of A − B to robustly constrain the power-law index α. They analysed a three-year spectroscopic monitoring at the European Southern Observatory (ESO) by removing the broad emission lines and the iron pseudo-continuum from quasar spectra in 39 epochs and by focusing on the continuum for λ values in the 1500–3000 Å interval. Each spectral distribution of the continuum was then integrated in six independent 250 Å bands to construct multi-band light curves. The six brightness records for A and B, along with the well-sampled V-band light curves of both images from the Optical Gravitational Lensing Experiment (OGLE; Woźniak et al. 2000; Udalski et al. 2006), led to α = 1.2 ± 0.3, in good agreement with a standard accretion disc. This result agrees with that of Muñoz et al. (2016) from a follow-up in six narrow bands in six epochs (α ≈ 1.0 ± 0.3), which is only marginally consistent with a standard disc, however.
In addition to the growth of the source radius with increasing emission wavelength, the surface brightness profile of sources at different wavelengths is a key piece to understand the accretion disc structure. While it has been proved that the shape of this profile does not play a relevant role in accounting for microlensing effects away from (micro)caustics (e.g. Mortonson et al. 2005), well-sampled light curves of QSO 2237+0305 are sensitive to the size and shape of emission regions when these regions cross caustic folds (e.g. Shalyapin et al. 2002; Gil-Merino et al. 2006; Koptelova et al. 2007a; Abolmasov & Shakura 2012; Mediavilla et al. 2015), favouring the standard disc profile or its relativistic version. Except for the Gravitational Lenses International Time Project (GLITP) observations in the R band (Alcalde et al. 2002), the only finely sampled light curves of the Einstein Cross that have been deeply interpreted are those of the GLITP and OGLE collaborations in the V band (source emitting at λ∼ 2000 Å). These V-band records provided not only constraints on the source geometry, but also information on physical properties of the lensing galaxy (fraction of mass in stars, mean stellar mass, and transverse velocity; e.g. Kochanek 2004; Gil-Merino et al. 2005). Even former poorly sampled light curves (Irwin et al. 1989; Corrigan et al. 1991; Østensen et al. 1996) led to interesting physical constraints (e.g. Wyithe et al. 1999, 2000a,b). Therefore, new well-sampled multi-band light curves of QSO 2237+0305 are promising tools for improving our knowledge of the distant active galactic nucleus and the local intervening spiral galaxy.
This paper describes a collaborative project that analysed optical frames of the Einstein Cross in a homogeneous way (using the same photometric method), built accurate multi-band light curves of the four quasar images throughout the last 14 years (2006–2019), and searched for new microlensing-induced variations. The project relied on a large set of gVrRI frames taken from two telescopes in the northern hemisphere: the 2.0 m Liverpool Telescope (LT; using gr Sloan filters) and the 1.5 m telescope at the Maidanak Observatory (hereafter MT; using VRI Bessell filters). In Sect. 2 we present the 14-year multi-band monitoring with the LT and the MT, outline main photometric tasks required to extract quasar fluxes, and show new and updated light curves of A, B, C, and D. In Sect. 3 we discuss microlensing signatures in difference light curves and focus on a possible double caustic-crossing event (DCCE) in C. Our conclusions are summarised in Sect. 4.
2. Observations and data reduction
First VRI photometric observations of QSO 2237+0305 with the MT were performed in 1995 (Vakulik et al. 1997), and VRI light curves over the first monitoring decade have been described in several previous papers (e.g. Vakulik et al. 2004; Koptelova et al. 2007b). Here, we present new MT observations from 2006 to 20191. An important upgrade of the telescope occurred in 2006 by installing the SNUCAM camera, which uses a CCD detector with a 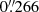 pixel−1 scale (Im et al. 2010). Although this camera is still working on the MT, we used the FLI MicroLine CCD with a pixel scale of
pixel−1 scale (Im et al. 2010). Although this camera is still working on the MT, we used the FLI MicroLine CCD with a pixel scale of 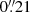 in 2012 and 2017. During the new observing period, we collected frames in VRI Bessell passbands. This translates into a follow-up of sources emitting at effective wavelengths λV = 2002 Å, λR = 2398 Å, and λI = 3113 Å. Before quasar fluxes were extracted, basic instrumental reductions were applied to all MT frames. This incorporated bias subtraction, dark frame subtraction (only for FLI MicroLine data), trimming of the overscan regions, flat fielding, and cosmic-ray cleaning. Moreover, we mapped pixel instrumental locations to their positions in the World Coordinate System, inserting sky coordinates into frame headers.
in 2012 and 2017. During the new observing period, we collected frames in VRI Bessell passbands. This translates into a follow-up of sources emitting at effective wavelengths λV = 2002 Å, λR = 2398 Å, and λI = 3113 Å. Before quasar fluxes were extracted, basic instrumental reductions were applied to all MT frames. This incorporated bias subtraction, dark frame subtraction (only for FLI MicroLine data), trimming of the overscan regions, flat fielding, and cosmic-ray cleaning. Moreover, we mapped pixel instrumental locations to their positions in the World Coordinate System, inserting sky coordinates into frame headers.
Additionally, the monitoring with the LT in gr Sloan bands started in 2006, soon after the commencement of science operations for this robotic telescope (Steele et al. 2004), and Gil-Merino et al. (2018) have shown r-band light curves over two four-year periods. In this paper, we describe the full database between 2006 and 2019, including new LT observations in the g band, as well as an extended (updated) set of frames in the r band. Frames in 2006–2009 were taken with the RATCam CCD camera (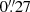 pixel−1 scale), whereas we used the IO:O CCD camera (
pixel−1 scale), whereas we used the IO:O CCD camera (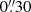 pixel−1 scale) from 2013 onwards. Regarding effective wavelengths in the quasar rest frame, we have λg = 1779 Å and λr = 2296 Å. In addition to basic pre-processing tasks included in the LT pipelines, we cleaned cosmic rays and interpolated over bad pixels using bad-pixel masks. Many LT frames of QSO 2237+0305 were already incorporated into the Gravitational LENses and DArk MAtter (GLENDAMA) database2 (Gil-Merino et al. 2018), and the next update of this archive will allow us to add all available LT-MT data of the Einstein Cross. The summary of LT-MT observations is shown in Table 1.
pixel−1 scale) from 2013 onwards. Regarding effective wavelengths in the quasar rest frame, we have λg = 1779 Å and λr = 2296 Å. In addition to basic pre-processing tasks included in the LT pipelines, we cleaned cosmic rays and interpolated over bad pixels using bad-pixel masks. Many LT frames of QSO 2237+0305 were already incorporated into the Gravitational LENses and DArk MAtter (GLENDAMA) database2 (Gil-Merino et al. 2018), and the next update of this archive will allow us to add all available LT-MT data of the Einstein Cross. The summary of LT-MT observations is shown in Table 1.
Liverpool-Maidanak monitoring of QSO 2237+0305 in 2006–2019.
Point-spread function (PSF) fitting photometry is particularly useful to extract fluxes of closely spaced quasar images. This photometric method relies on the assumption that all point-like sources can be represented by the same PSF, which is well traced by an analytical function or a field star (e.g. Howell 2006). We performed PSF-fitting photometry on the Einstein Cross using the 2D profile of a field star as empirical PSF (see details on field stars in Table 2). The brightest star (γ) was used as PSF in most frames. However, when γ was saturated or had defective pixels, we took the PSF of the star α. The α star also served for estimating the signal-to-noise ratio (S/N) in each frame, and to calculate magnitude zero-points. PSF-fitting photometry on the β star was used to verify that the quasar variability is real.
Stars around QSO 2237+0305.
In the crowded region containing the four images of QSO 2237+0305 (QSO subframes), the photometric model consisted of a constant background, four point-like sources, and a de Vaucouleurs profile convolved with the PSF (Alcalde et al. 2002; Gil-Merino et al. 2018). This last ingredient accounts for the light distribution of the lensing galaxy bulge. Taking the position of image A as a reference for astrometry, and setting the relative positions of B-D and the centre of the galaxy to those obtained from Hubble Space Telescope (HST) data in the H band (e.g. Table 1 of Alcalde et al. 2002), we fitted the model to each QSO subframe using the IMFITFITS software3 (McLeod et al. 1998). Our initial model had 11 free parameters: 2D position of A, sky background, galaxy structural parameters (flux, effective radius, axis ratio, and orientation) and four quasar fluxes. It was only applied to a large set of good frames in terms of seeing and S/N. Results from this initial iteration allowed us to determine the inner structure of the galaxy (see Table 3). In a second iteration, we applied IMFITFITS to all frames, setting relative positions and galaxy parameters. A number of individual frames produced anomalous photometric results (outliers). These are characterised by a poor image quality and were therefore removed from the final database. Additionally, we used the simplest photometric model (point-like source plus constant background) to extract fluxes of the β control star.
Structural parameters of the lensing galaxy.
Detailed photometric results for all individual frames are available in Tables 4 (g band), 5 (V band), 6 (r band), 7 (R band), and 8 (I band) at the CDS: Cols. 1–12 list the civil date and frame number on that date (yymmdd_number), the observing epoch (MJD-50 000), the exposure time (s), FWHM (″), the PSF ellipticity, S/N, A (mag), B (mag), C (mag), D (mag), β (mag), and the reduced chi-square (χ2/d.o.f., where “d.o.f.” denotes the degrees of freedom) value when IMFITFITS was applied on the QSO subframe, respectively. Column 13 contains an asterisk for removed poor-quality frames or is empty for selected (non-removed) frames. Results for selected frames were combined on a nightly basis to obtain magnitudes at 203 (g band), 180 (V band), 253 (r band), 445 (R band), and 179 (I band) epochs (see Table 1). To estimate mean photometric errors in the light curves of A–D and β, we calculated deviations between adjacent magnitudes that are separated from each other by no more than 2.5 d. For each optical band, the number of pairs used and the mean deviations are displayed in Table 9. The typical uncertainties in quasar magnitudes range from ∼1% for the brightest (A) image to ∼2–5% for the generally faintest (C) image. For a given band, errors at every epoch were then computed by weighting mean values by the ⟨S/N⟩/S/N ratio (e.g. Howell 2006).
Mean magnitude errors of the quasar and control star.
The final light curves of A–D and β are shown in Fig. 1, and they are provided in tabular format at the CDS4: Tables 10 (g band), 11 (V band), 12 (r band), 13 (R band), and 14 (I band). These five machine-readable ASCII files are structured in the same manner. Column 1 includes the observing epoch (MJD-50 000), while Cols. 2–3, 4–5, 6–7, 8–9, and 10–11 display the magnitudes and magnitude errors of A, B, C, D, and β, respectively. In Appendix A we compare our V-band magnitudes in 2006–2008 with those obtained through a different photometric technique and the OGLE data at the same epochs.
 |
Fig. 1. Liverpool-Maidanak light curves of QSO 2237+0305. The quasar variability is measured at effective rest-frame wavelengths in the UV region (∼1780–3110 Å) over a 14-year period. |
3. Difference light curves: new tools for microlensing studies
As discussed in Sect. 1, the chromatic microlensing variability of QSO 2237+0305 can be analysed by obtaining magnitude differences between image pairs in several optical bands. Additionally, for this lens system, the source radius crossing and Einstein radius crossing timescales are 0.23 and 8.11 years, respectively (Mosquera & Kochanek 2011). In view of the timescales involved, multi-band follow-up observations during 14 years might prove very useful for finding strong chromatic microlensing effects. To gain insight into the origin of variations in the quasar images that are most affected by microlensing, it is also convenient to use the light curves of the least variable image as reference records (e.g. Mediavilla et al. 2015). Thus, we constructed difference light curves A − B − ⟨A − B⟩, C − B − ⟨C − B⟩, and D − B − ⟨D − B⟩ in the gVrRI bands. These difference curves are depicted in Fig. 2.
 |
Fig. 2. Difference light curves of the Einstein Cross from the Liverpool-Maidanak brightness records in the gVrRI bands. To construct these difference curves, the multi-band brightness records of B have been subtracted from those of A (top left panel), C (top right panel), and D (bottom panel). In addition to subtracting the records of the least variable image, the resulting difference curves are shifted in magnitude to show variations around the zero level. |
As expected, Fig. 2 shows significant microlensing variability in the difference curves for A (top left panel), C (top right panel), and D (bottom panel). Although the variability in A − B and D − B has a total amplitude of ∼1 mag, it is not as strong as in C − B. Chromaticity is also detected in these difference curves. For example, D − B exhibits an oscillating global behaviour with an amplitude less than 1 mag in the I band and more than 1 mag in the g band. Moreover, C − B include two sharp chromatic variations that occurred in the periods 2012–2013 and 2015–2016. Although the whole set of difference curves can be used to probe the accretion disc structure and the composition of the lensing galaxy at relatively small impact parameters (e.g. Kochanek 2004; Eigenbrod et al. 2008), here we focus on the two prominent features of C − B. These resemble DCCE peaks seen in microlensing simulations, when sources enter regions interior to caustics (first crossing of a fold caustic) and later exit from them (second caustic crossing; see e.g. Figs. 10 and 11 of Wambsganss 1998). Based on this, each sharp variation of C − B is thought to be due to a caustic crossing event in image C. The association between prominent variations in observed light curves and caustic crossings is sometimes justified by detailed numerical simulations (e.g. Gil-Merino et al. 2006; Anguita et al. 2008).
To demonstrate that the putative DCCE is a powerful tool for studying the accretion disc structure, we considered the corrected flux ratio (C/B)corr over the 2009–2018 period for each optical band, that is, after removing a long-term microlensing gradient from C/B (see Fig. 3). Our procedure is discussed in depth and placed in perspective in Appendix B. We analysed the two individual caustic-crossing events in a separate way. Unfortunately, we cannot draw the 2012–2013 event in the g and r bands because there is a long gap between days 5200 and 6400 in these passbands. Therefore, only the caustic-crossing induced variations in the VRI bands were independently fitted to the three-parameter model μcaustic = 1 + (cJ/c0)J[(t − t0)/Δt] for three different source profiles giving rise to analytical functions J(z) (sources enter the caustic region; see Appendix B). In general, the p = 3/2 power-law profile (Shalyapin 2001) leads to the best fits in terms of χ2/d.o.f. values, and the best-fit curves for p = 3/2 power-law sources are shown in Fig. 3 (solid lines). In Table 15 we also compare results for p = 3/2 power-law sources and those for Gaussian sources. In each optical band, a Δt (Gaussian) ∼2 × Δt (p = 3/2 power law) relationship is expected if both sources have the same half-light radius and move with the same velocity perpendicular to the caustic line (Shalyapin et al. 2002).
 |
Fig. 3. Corrected flux ratio (C/B)corr in the gVrRI bands. Each sharp monochromatic variation is fitted to the microlensing model μcaustic for a p = 3/2 power-law source (see Appendix B), yielding the solid and dashed lines (best-fit curves) associated with the caustic crossing events in 2012–2013 and 2015–2016, respectively. |
Results from fitting caustic-crossing induced variations in 2012–2013.
Data in 2015–2016 make it possible to study the corresponding caustic-crossing event in all five bands. The microlensing model is now μcaustic = 1 + (cJ/c0)J[−(t − t0)/Δt], which should provide Δt > 0 values if sources actually exit from the caustic region. In order to improve results for a given source profile, we initially fit the best-sampled variation (in the R band) to the model instead of performing five fits with three free parameters each. We then obtained Δt and cJ/c0 in the gVrI bands, setting t0 to that derived from R-band data. We reasonably assumed that all variations in (C/B)corr are characterised by the same value of t0. The lowest values of χ2/d.o.f. were again obtained by using the p = 3/2 power-law profile (see the dashed lines in Fig. 3 and results in Table 16). Consequently, our global results favour a surface brightness profile close to that of the standard accretion disc. As a general rule, profiles that most appreciably depart from the standard profile produce the worst fits, that is p = 5/2 power law and Gaussian models. The global analysis also indicates that a DCCE most likely occurred.
Results from fitting caustic-crossing induced variations in 2015–2016 using p = 3/2 power-law sources.
In addition, each of the two caustic crossings allows us to probe the relationship between source radius and emission wavelength. As a first indicator, we studied the correlation between Δt and observed wavelength λ0, where Δt and λ0 are proportional to Rλ and λ, respectively (see Appendix B). For the first caustic crossing event in 2012–2013, we considered solutions of Δt for p = 3/2 power law and Gaussian source models. In addition to the results through (C/B)corr (see Table 15), new solutions were inferred from (C/A)corr. This complementary analysis is useful to determine the influence of the choice of smoothly varying reference records on the Δt − λ0 relationship. For the second caustic crossing event in 2015–2016, we only used the results via (C/B)corr in Table 16 (p = 3/2 power-law sources).
Figure 4 displays the chromatic behaviour of Δt, along with power-law fits. These fits inform us about the power-law index α in Rλ ∝ λα (see Table 17). The 2015–2016 event leads to radii of sources at five emission wavelengths that are consistent with a standard accretion disc (α = 4/3), although both χ2/dof and the scatter in α values are relatively high. This measure (α = 1.34 ± 0.23) confirms but does not improve a previous result through ESO-OGLE multi-band light curves of QSO 2237+0305 (α = 1.2 ± 0.3; Eigenbrod et al. 2008). When we consider our best power-law fits to radii at three wavelengths for the event in 2012–2013 (χ2/d.o.f. ≤ 1), the index is measured to ∼10% precision: α = 1.0 ± 0.1. The new measurement is more accurate than previous estimates based on chromatic variations of the Einstein Cross (e.g. Eigenbrod et al. 2008; Muñoz et al. 2016), suggesting that as the emission wavelength increases, the source radius grows more smoothly than the standard disc radius.
 |
Fig. 4. Chromatic behaviour of the source radius crossing time during the 2012–2013 and 2015–2016 microlensing events in image C. The Δt values for Gaussian sources are reduced by a factor of about 2 for comparison purposes, and the five lines decribe power-law fits (see main text). |
Power-law index of the radius-wavelength relation Rλ ∝ λα via the chromaticity of Δt.
In principle, we can use a second α indicator. The relative caustic strength is proportional to 1/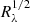 , and the chromaticity of cJ/c0 therefore provides complementary information on α. As shown in Fig. 5, the residuals from power-law fits are very large, yielding uncomfortable χ2/d.o.f. values ≥10. Therefore we did not include these values in Table 18 and do not try to discuss results individually. However, the set of measures of cJ/c0 indicates that the relative caustic strength really decreases as the radius (wavelength) increases, and we considered all estimates of α in Tables 17 and 18, ignoring differences in errors and χ2/d.o.f. values, to compute the mean and its standard deviation: 1.33 ± 0.09. This statistical approach clearly favours a standard accretion disc.
, and the chromaticity of cJ/c0 therefore provides complementary information on α. As shown in Fig. 5, the residuals from power-law fits are very large, yielding uncomfortable χ2/d.o.f. values ≥10. Therefore we did not include these values in Table 18 and do not try to discuss results individually. However, the set of measures of cJ/c0 indicates that the relative caustic strength really decreases as the radius (wavelength) increases, and we considered all estimates of α in Tables 17 and 18, ignoring differences in errors and χ2/d.o.f. values, to compute the mean and its standard deviation: 1.33 ± 0.09. This statistical approach clearly favours a standard accretion disc.
 |
Fig. 5. Chromatic behaviour of the relative caustic strength during the 2012–2013 and 2015–2016 microlensing events in image C. The five lines represent power-law fits (see main text). |
Power-law index of the radius-wavelength relation Rλ ∝ λα via the chromaticity of cJ/c0.
4. Conclusions
Within the framework of a collaboration between the GLENDAMA team and several groups operating the Maidanak Observatory, we analysed a joint database of the quadruply imaged quasar QSO 2237+0305. This large database contains optical frames in the gVrRI bands in the period 2006–2019, which were used to extract fluxes of the four quasar images A-D in a homogeneous way. Our 14-year multi-band light curves are expected to appreciably contribute to a better knowledge of the structure of the accretion disc around the central supermassive black hole, as well as the composition of the lensing galaxy bulge (e.g. Kochanek 2004; Eigenbrod et al. 2008). We concentrated on two sharp chromatic microlensing events that appear in the difference light curve C − B. These prominent features in 2012–2013 and 2015–2016 were tentatively associated with two consecutive caustic-crossing events in image C.
We studied the two putative caustic-crossing events in a separate way, considering three different models for the brightness profile of involved sources: the widely used Gaussian model, and the p = 5/2 and p = 3/2 power-law models (Shalyapin et al. 2002). This choice allowed us to probe the behaviour of source profiles close to that of the standard accretion disc (p = 3/2), profiles that noticeably depart from it (Gaussian), and intermediate profiles (p = 5/2). Our global results favour the p = 3/2 power-law profile. The global analysis also supports our initial hypothesis of a double caustic-crossing event in image C. While previous studies reported isolated strong-microlensing episodes in images of the Einstein Cross (e.g. Mediavilla et al. 2015, and references therein), the Liverpool-Maidanak light curves suggest that image C has been affected by a double caustic crossing between 2012 and 2016. More specifically, our results are consistent with a standard accretion disc entering a region interior to a caustic and then exiting from it. However, we note that despite these encouraging conclusions, a final confirmation of the DCCE requires a description of the full microlensing event (including its central part) through numerical simulations (e.g. Wambsganss 1998; Kochanek 2004). Such detailed modelling is beyond the scope of this paper (see below).
We also probed the relationship between source radius and emission wavelength: Rλ ∝ λα at λ ∼ 1780 − 3110 Å, using two α indicators. For these sources of UV radiation, α is unfortunately not as well constrained as would be desirable. The statistical result based on ten solutions from both indicators contradicts the measurement based on the two best solutions with χ2/d.o.f. ≤ 1. This last measurement of α (1.0 ± 0.1) relies on only one indicator and VRI data during the 2012–2013 event. On the other hand, the statistical result from both indicators (α = 1.33 ± 0.09) takes into account VRI data during the first event and gVrRI data over the second event, although most individual solutions have χ2/d.o.f. > 1. This estimate is fully consistent with a standard accretion disc (α = 4/3), and it is probably more representative (unbiased) than the other. Again we need to perform numerical microlensing simulations to robustly constrain the value of α, which has been measured from microlensing-induced chromatic variations to ∼25–30% precision (Eigenbrod et al. 2008; Muñoz et al. 2016), or to ∼10% formal precision, but in an ambiguous way (this paper).
A deep analysis of the Liverpool-Maidanak light curves with the aid of detailed microlensing simulations will be presented in a subsequent paper. The future paper will focus on, among other things, providing a probabilistic confirmation of the DCCE in image C, discussing the brightness profile of UV continuum sources, and constraining the size and structure of the accretion disc. When we were completing this paper, the COSmological MOnitoring of GRAvItational Lenses (COSMOGRAIL) collaboration reported ESO R-band light curves of QSO 2237+0305 that cover the period 2010–2013 (see Fig. B.11 of Millon et al. 2020). Although these COSMOGRAIL light curves are not yet publicly available and were obtained using a photometric approach different from ours, they might play a role in the future analysis through numerical microlensing simulations.
Observations in 2006–2008 have previously been presented in an Ukrainian journal (Dudinov et al. 2010).
See also https://grupos.unican.es/glendama/q2237.htm for updated results.
OGLE photometry is available at http://ogle.astrouw.edu.pl/
Acknowledgments
This paper is based on observations made with the Liverpool Telescope (LT) and the AZT-22 Telescope at the Maidanak Observatory (MT). The LT is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias with financial support from the UK Science and Technology Facilities Council. We thank the staff of the LT for a kind interaction before, during and after the observations. The Maidanak Observatory is a facility of the Ulugh Beg Astronomical Institute (UBAI) of the Uzbekistan Academy of Sciences, which is operated in the framework of scientific agreements between UBAI and Russian, Ukrainian, US, German, French, Italian, Japanese, Korean, Taiwan, Swiss and other countries astronomical institutions. We thank O. Ye. Kochetov and V. V. Konichek for performing some observations with the MT. We also used data taken from the Sloan Digital Sky Survey (SDSS) web site (http://www.sdss.org/), and we are grateful to the SDSS collaboration for doing that public database. This research has been supported by the MINECO/AEI/FEDER-UE grant AYA2017-89815-P, the University of Cantabria, and the Ministry of Innovative Development of Uzbekistan grants F2-FA-F026 and VA-FA-F-2-010.
References
- Abolmasov, P., & Shakura, N. I. 2012, MNRAS, 423, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Aguado, D. S., Ahumada, R., Almeida, A., et al. 2019, ApJS, 240, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Alard, C., & Lupton, R. H. 1998, ApJ, 503, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalde, D., Mediavilla, E., Moreau, O., et al. 2002, ApJ, 572, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Alexandrov, A. N., & Zhdanov, V. I. 2011, MNRAS, 417, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Anguita, T., Schmidt, R. W., Turner, E. L., et al. 2008, A&A, 480, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackburne, J. A., Kochanek, C. S., Chen, B., Dai, X., & Chartas, G. 2015, ApJ, 798, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Corrigan, R. T., Irwin, M. J., Arnaud, J., et al. 1991, AJ, 102, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Dudinov, V. N., Smirnov, G. V., Vakulik, V. G., Sergeev, A. V., & Kochetov, A. E. 2010, Radio Phys. Radio Astron., 15, 387. [in Russian] [NASA ADS] [Google Scholar]
- Eigenbrod, A., Courbin, F., Meylan, G., et al. 2008, A&A, 490, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fluke, C. J., & Webster, R. L. 1999, MNRAS, 302, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudi, B. S., & Petters, A. O. 2002, ApJ, 574, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Merino, R., Wambsganss, J., Goicoechea, L. J., & Lewis, G. F. 2005, A&A, 432, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil-Merino, R., González-Cadelo, J., Goicoechea, L. J., Shalyapin, V. N., & Lewis, G. F. 2006, MNRAS, 371, 1478 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Merino, R., Goicoechea, L. J., Shalyapin, V. N., & Oscoz, A. 2018, A&A, 616, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hainline, L. J., Morgan, C. W., MacLeod, C. L., et al. 2013, ApJ, 774, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2006, Handbook of CCD Astronomy (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Huchra, J., Gorenstein, M., Kent, S., et al. 1985, AJ, 90, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Ko, J., Cho, Y., et al. 2010, JKAS, 43, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Webster, R. L., Hewitt, P. C., Corrigan, R. T., & Jedrzejewski, R. I. 1989, AJ, 98, 1989 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2004, ApJ, 605, 58 [Google Scholar]
- Koptelova, E., Shimanovskaya, E., Artamonov, B., & Yagola, A. 2007a, MNRAS, 381, 1655 [NASA ADS] [CrossRef] [Google Scholar]
- Koptelova, E. A., Artamonov, B. P., Shimanovskaya, E. V., et al. 2007b, ARep, 51, 797 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, B. A., Bernstein, G. M., Rieke, M. J., & Weedman, D. W. 1998, AJ, 115, 1377 [NASA ADS] [CrossRef] [Google Scholar]
- Mediavilla, E., Jiménez-Vicente, J., Muñoz, J. A., & Mediavilla, T. 2015, ApJ, 814, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Millon, M., Courbin, F., Bonvin, V., et al. 2020, A&A, submitted [arXiv:2002.05736] [Google Scholar]
- Moreau, O., Libbrecht, C., Lee, D.-W., & Surdej, J. 2005, A&A, 436, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortonson, M. J., Schechter, P. L., & Wambsganss, J. 2005, ApJ, 628, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Mosquera, A. M., & Kochanek, C. S. 2011, ApJ, 738, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, J. A., Vives-Arias, H., Mosquera, A. M., et al. 2016, ApJ, 817, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Refsdal, S., Stabell, R., et al. 1996, A&A, 309, 59 [NASA ADS] [Google Scholar]
- Poindexter, S., & Kochanek, C. S. 2010, ApJ, 712, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Poindexter, S., Morgan, N., & Kochanek, C. S. 2008, ApJ, 673, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Weiss, A. 1987, A&A, 171, 49 [NASA ADS] [Google Scholar]
- Schneider, D. P., Turner, E. L., Gunn, J. E., et al. 1988, AJ, 96, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lensing (Berlin: Springer) [Google Scholar]
- Schneider, P., Kochanek, C. S., & Wambsganss, J. 2006, in Gravitational Lensing: Strong, Weak & Micro, Proc. of the 33rd Saas-Fee Advanced Course, eds. G. Meylan, P. Jetzer, & P. North (Berlin: Springer) [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shalyapin, V. N. 2001, AstL, 27, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Shalyapin, V. N., Goicoechea, L. J., Alcalde, D., et al. 2002, ApJ, 579, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Steele, I. A., Smith, R. J., Rees, P. C., et al. 2004, Proc. SPIE, 5489, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymański, M. K., Kubiak, M., et al. 2006, Acta Astronomica, 56, 293 [NASA ADS] [Google Scholar]
- Vakulik, V. G., Dudinov, V. N., Zheleznyak, A. P., et al. 1997, AN, 318, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Vakulik, V. G., Schild, R. E., Dudinov, V. N., et al. 2004, A&A, 420, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vakulik, V., Schild, R., Dudinov, V., et al. 2006, A&A, 447, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wambsganss, J. 1998, Living Rev. Relat., 1, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Weisenbach, L., Schechter, P., & Wambsganss, J. 2019, MNRAS, 488, 3452 [NASA ADS] [CrossRef] [Google Scholar]
- Woźniak, P. R., Udalski, A., Szymański, M., et al. 2000, ApJ, 540, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Wyithe, J. S. B., Webster, R. L., & Turner, E. L. 1999, MNRAS, 309, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Wyithe, J. S. B., Webster, R. L., & Turner, E. L. 2000a, MNRAS, 315, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Wyithe, J. S. B., Webster, R. L., Turner, E. L., & Mortlock, D. J. 2000b, MNRAS, 315, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C. 1988, AJ, 95, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Yonehara, A. 2001, ApJ, 548, L127 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Magnitudes of quasar images using different photometric techniques and telescopes
Here, we compare our MT V-band data at 19 epochs in 2006–2008 with MT V-band magnitudes at the same epochs derived from a different photometric approach (Dudinov et al. 2010, henceforth D10), and also with concurrent OGLE data5. The OGLE collaboration monitored QSO 2237+0305 in the V band from 1997 to the first half of 2009, using a photometric technique different from ours and a telescope in the southern hemisphere (Woźniak et al. 2000; Udalski et al. 2006). Briefly, we used the software IMFITFITS (McLeod et al. 1998) to perform PSF-fitting photometry, modelling the lensing galaxy bulge as a de Vaucouleurs profile convolved with the PSF and taking HST astrometric constraints into account (see Sect. 2). Vakulik et al. (2004) introduced another flux-extraction technique that was also applied to MT frames in the period of interest (D10). In this alternative PSF photometry, for instance, the lensing galaxy is described as the sum of three elliptical Gaussian functions. Additionally, the OGLE light curves rely on the so-called image subtraction method (e.g. Alard & Lupton 1998). After the OGLE team obtained differences between individual frames and a reference stacked image, differential quasar fluxes were measured through PSF-fitting photometry with HST astrometric constraints (e.g. Udalski et al. 2006).
In Fig. A.1 we display the measures in this paper (circles; see Table 11), MT data from a flux extraction technique different to ours (squares; D10), and OGLE light curves (triangles). MT magnitudes from both photometric approaches are remarkably similar for the brightest images (see Table A.1). However, there are significant magnitude offsets with respect to OGLE data, in particular for the faintest images. We note that the comparison in this appendix can be particularly useful for studying 25-year V-band records of the four quasar images because MT and OGLE observations cover the period 1995–2019.
 |
Fig. A.1. Comparison of V-band magnitudes in 2006–2008 using different photometric approaches and telescopes. Our MT data (circles), MT data from an alternative flux extraction technique (squares), and OGLE brightness records (triangles). |
Mean magnitude offsets.
Appendix B: Analysis of caustic crossing events in image C of QSO 2237+0305
When the continuum source emitting at λ crosses a fold caustic for a given quasar image, the observed flux of such an image at λ0 = λ(1 + zs) changes dramatically over time. Because the accretion disc of QSO 2237+0305 is seen face-on (e.g. Poindexter & Kochanek 2010), it is reasonable to consider an axisymmetric source to model this flux variation during the caustic-crossing event. Moreover, the fold caustic is generally assumed to be a straight line, so that the theoretical microlensing curve can be primarily built by convolving the axisymmetric intensity profile with the straight-fold magnification (e.g. Schneider & Weiss 1987; Shalyapin et al. 2002). However, there are a number of caveats concerning this simple approximation, which does not work properly in some cases. For example, Fluke & Webster (1999) noted that the model is only correct when the source size is much smaller than that of the fold caustic, while Gaudi & Petters (2002) incorporated a slowly (linearly) varying background term (see also Yonehara 2001). Very recently, Weisenbach et al. (2019) have also discussed the magnification of a source near a fold caustic using higher order approximations and numerical simulations. Interestingly, higher order approximations were required to accurately fit a caustic-crossing flux variation (V band) in image C of the Einstein Cross that occurred in 1999 (Alexandrov & Zhdanov 2011). For a Gaussian brightness profile, the χ2/d.o.f. value decreased from 1.35 to 0.9–1 when suitable corrections to the straight-fold model were taken into account.
Whereas Alexandrov & Zhdanov (2011) have neglected possible intrinsic variations in image C, Mediavilla et al. (2015) have removed intrinsic fluctuations of images A and C by dividing their V-band caustic-crossing flux variations by flux records of the least variable images. Mediavilla et al. (2015) also showed that the global shape of these flux ratios (associated with three caustic-crossing events occurring before 2006 or ending in 2006) can be reasonably fitted by the straight-fold model plus a linearly varying background contribution. In more detail, when the intensity profile of the standard thin disc is used (Shakura & Sunyaev 1973), the χ2/d.o.f. values are ∼1.5–3.6. Although these fits can be easily improved by considering a more realistic magnification pattern for the image undergoing the caustic crossing (Alexandrov & Zhdanov 2011), a microlensing magnification gradient for the image with the smoothest variability and/or a different source profile (e.g. including relativistic effects; Abolmasov & Shakura 2012; Mediavilla et al. 2015), they are enough to prove the great potential of the Einstein Cross light curves.
We focused on two new caustic-crossing events in image C of QSO 2237+0305, which occurred in 2012–2013 and 2015–2016 (see Sect. 3). When the difference curves C − B are used to build the flux ratio C/B in the gVrRI bands over the 2009–2018 period, it is apparent that this ratio contains a long-term microlensing gradient (see the top right panel of Fig. 2). This gradient originates in the image that experiences caustic crossings (C; e.g. Gaudi & Petters 2002) or in the least variable image B. In the first scenario, each caustic-crossing induced variation in C/B was modelled as
where c0 + cJJ[(t − t0)/T] results from the convolution of the source profile with the straight-fold magnification (straight-fold model; see, e.g., Fig. 1 and Eq. (13) in Shalyapin et al. 2002). In Eq. (B.1), c0 and c1 are the constant background and slope of the linear gradient for image C (t1 is an epoch in the 2009–2018 period that can be conveniently fixed), cJ is related to the caustic strength, t0 is the time of caustic crossing by the source centre, T = ±Δt (the plus indicates that the source enters the caustic region, while the minus denotes that the source exits from it; Δt = Rλ/V⊥ is the source radius crossing time, and Rλ and V⊥ are the typical radius of the source profile and source velocity perpendicular to the caustic line), and b0 is the constant term for image B (we implicitly assume that B does not suffer a time-varying microlensing magnification).
For the second scenario, instead of Eq. (B.1), we used
where b1 is the slope of the linear gradient for B. Equations (B.1) and (B.2) show that both models have the same number of parameters. We considered three axisymmetric shapes for the source profiles that produce analytical functions J(z). These are the Gaussian model, and the p = 5/2 and p = 3/2 power-law models introduced by Shalyapin (2001). As shown in Fig. 4 of Shalyapin et al. (2002), the p = 3/2 power-law profile closely mimics the behaviour of the standard accretion disc, and the Gaussian profile departs more strongly from the standard behaviour. After some initial tests, we realised that the second secenario, that is, Eq. (B.2), fits the caustic-crossing induced variations in C/B better. We therefore chose to present results for this theoretical microlensing model. The reference epoch t1 was set to 1 January 2014, and the C/B values in the 2009–2010 and 2017–2018 periods (when sources are presumably not affected, or very weakly affected, by the caustic region and the J function becomes zero or negligible) were used to determine c0/b0 and b1/b0 (see Table B.1). After these parameters that are not related to caustic effects are derived, the key idea is to remove the long-term microlensing gradient by computing the corrected flux ratio (C/B)corr = (C/B){[1 + (b1/b0)(t − t1)]/(c0/b0)} in the gVrRI bands, and then fit each caustic-crossing induced variation in (C/B)corr to the microlensing law μcaustic = 1 + (cJ/c0)J[(t − t0)/T] (see Sect. 3). In addition to Δt ∝ Rλ, it is straightforward to show that 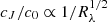 .
.
Long-term microlensing gradient in C/B.
All Tables
Results from fitting caustic-crossing induced variations in 2015–2016 using p = 3/2 power-law sources.
Power-law index of the radius-wavelength relation Rλ ∝ λα via the chromaticity of Δt.
Power-law index of the radius-wavelength relation Rλ ∝ λα via the chromaticity of cJ/c0.
All Figures
 |
Fig. 1. Liverpool-Maidanak light curves of QSO 2237+0305. The quasar variability is measured at effective rest-frame wavelengths in the UV region (∼1780–3110 Å) over a 14-year period. |
| In the text | |
 |
Fig. 2. Difference light curves of the Einstein Cross from the Liverpool-Maidanak brightness records in the gVrRI bands. To construct these difference curves, the multi-band brightness records of B have been subtracted from those of A (top left panel), C (top right panel), and D (bottom panel). In addition to subtracting the records of the least variable image, the resulting difference curves are shifted in magnitude to show variations around the zero level. |
| In the text | |
 |
Fig. 3. Corrected flux ratio (C/B)corr in the gVrRI bands. Each sharp monochromatic variation is fitted to the microlensing model μcaustic for a p = 3/2 power-law source (see Appendix B), yielding the solid and dashed lines (best-fit curves) associated with the caustic crossing events in 2012–2013 and 2015–2016, respectively. |
| In the text | |
 |
Fig. 4. Chromatic behaviour of the source radius crossing time during the 2012–2013 and 2015–2016 microlensing events in image C. The Δt values for Gaussian sources are reduced by a factor of about 2 for comparison purposes, and the five lines decribe power-law fits (see main text). |
| In the text | |
 |
Fig. 5. Chromatic behaviour of the relative caustic strength during the 2012–2013 and 2015–2016 microlensing events in image C. The five lines represent power-law fits (see main text). |
| In the text | |
 |
Fig. A.1. Comparison of V-band magnitudes in 2006–2008 using different photometric approaches and telescopes. Our MT data (circles), MT data from an alternative flux extraction technique (squares), and OGLE brightness records (triangles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} f_{\lambda } = \frac{c_0 + c_1(t - t_1) + c_{{J}}J[(t - t_0)/T]}{b_0}, \end{aligned} $$](/articles/aa/full_html/2020/05/aa37902-20/aa37902-20-eq6.gif)
![$$ \begin{aligned} f_{\lambda } = \frac{c_0 + c_{{J}}J[(t - t_0)/T]}{b_0 + b_1(t - t_1)} , \end{aligned} $$](/articles/aa/full_html/2020/05/aa37902-20/aa37902-20-eq7.gif)