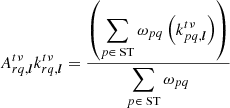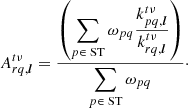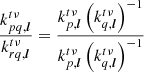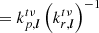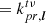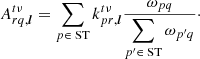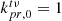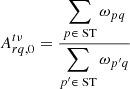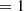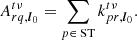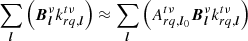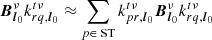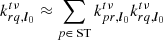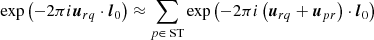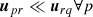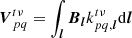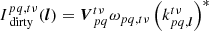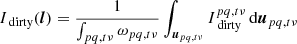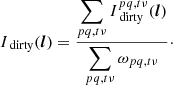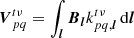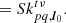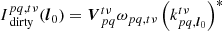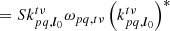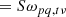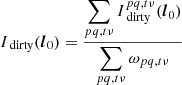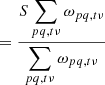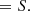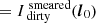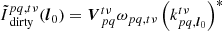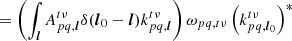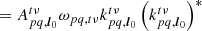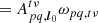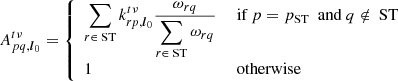| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202037486 | |
| Published online | 13 May 2020 | |
Decoherence in LOFAR-VLBI beamforming
1
Universita di Bologna, Via Zamboni 33, 40126 Bologna, Italy
e-mail: etienne.bonnassieux@unibo.it
2
INAF, Instituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
3
Centre for Extragalactic Astronomy, Department of Physics, Durham University, Durham DH1 3LE, UK
Received:
13
January
2020
Accepted:
13
March
2020
We show that the use of a superstation (a phased array created using multiple stations of an interferometric array) created in post-processing for LOFAR-VLBI observations introduces a direction-dependent loss of signal in the image. We show this effect using simulations and real data. Using the RIME formalism, we characterise it fully, and give limits under which this signal loss is negligible. Finally, we show that we are able to fully predict this effect. We close with guidelines for interferometric observers to avoid this effect in their observations, and a discussion of techniques which could limit this effect or do away with it entirely. The latter in particular will be relevant to the SKA should its long baselines be used to their fullest potential.
Key words: techniques: high angular resolution / techniques: interferometric / methods: analytical / methods: observational / methods: data analysis
© ESO 2020
1. Introduction
The new generation of Square Kilometer Array (SKA) pathfinder instruments is pushing the boundaries of what has previously been achievable with radio interferometers. The LOw Frequency ARray LOFAR (van Haarlem et al. 2013), in particular, is in full science-production mode, mapping the sky at very low frequencies and high resolution. However, the instrument is not yet used to its fullest extent as a matter of course: in particular, the use of LOFAR-VLBI (i.e. LOFAR with its international, or European, stations – as opposed to using only the stations in the Netherlands) is still an ongoing and active area of technical development, with great strides still being made (e.g. Jackson et al. 2016; Varenius et al. 2015, 2016; Morabito et al. 2016; Kappes et al. 2019, with further scientific papers scheduled for the near future year).
One aspect of interferometric technique in the LOFAR-VLBI regime is that it blurs the conceptual boundaries between traditional interferometry and very long baseline interferometry (henceforth VLBI). Although the two disciplines share common ancestry and common techniques, the specific case of VLBI has histoircally allowed for a set of simplifications to the general problem of interferometry, at the cost of certain constraints and limitations. In particular, VLBI focused on small fields of view (FoV), extremely high resolutions, and single-object observations. This freed it from the direction-dependent effects which require correcting for modern standard interferometric observations, such as the Dutch LOFAR’s Two-meter Sky Survey (LOTSS) fields (Shimwell et al. 2019). Because VLBI focuses on single-object pointings, it also did not need to account for effects such as time or frequency smearing (see Smirnov 2011a, and companion papers), which increase signal loss as a function of angular distance from phasing centre; the angular distances for VLBI observations are typically very small.
LOFAR-VLBI aims to use the full LOFAR array, which includes baselines exceeding 1000 km (van Haarlem et al. 2013) and therefore lies squarely within the limit of VLBI as understood from an instrumental perspective. However, it also aims to take advantage of the tremendous opportunities offered by the LOFAR-VLBI FoV of 1.15° (the full width at half-maximum, or FWHM, of the primary beam quoted in van Haarlem et al. 2013) – allowing for multiple objects to be detected simultaneously, at sub-arcsecond angular resolutions. This places LOFAR-VLBI outside the scope of traditional VLBI because it introduces additional constraints: we now have to properly account for direction-dependent effects and smearing if we wish to take advantage of the wide FoV by imaging away from phase centre.
In many cases, one bottleneck to LOFAR data reduction in the sheer size of the data. The LOFAR-VLBI pipeline therefore performs post-processing beamforming of all the core LOFAR stations (i.e. the 24 LOFAR stations closest to the central core). This results in an 80% reduction in data size, making its reduction much more tractable. It also increases the sensitivity of the baselines pointing from this superstation to the international stations by a factor of 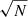 , with N the number of stations being beamformed, which is necessary to calibrate the long baselines. However, this comes at a cost: should the astronomer’s science target be somewhat extended, this drastic superstation formation will inevitably result in direction-dependent flux suppression. For example, we show the exact amount of suppression resulting from using all core LOFAR stations as a single superstation (which is standard practice with LOFAR-VLBI at the time of writing) later in the paper, in Fig. 4. This figure is referred to out of order so as to preserve the paper’s throughline, and thus its clarity.
, with N the number of stations being beamformed, which is necessary to calibrate the long baselines. However, this comes at a cost: should the astronomer’s science target be somewhat extended, this drastic superstation formation will inevitably result in direction-dependent flux suppression. For example, we show the exact amount of suppression resulting from using all core LOFAR stations as a single superstation (which is standard practice with LOFAR-VLBI at the time of writing) later in the paper, in Fig. 4. This figure is referred to out of order so as to preserve the paper’s throughline, and thus its clarity.
For most science cases, the source of interest may either not be at phase centre or may be mildly extended. In such cases, even 30′ away from phase centre (which, to give an idea of scale, corresponds to 6 pixels in LOTSS images1, Shimwell et al. 2019), scientists can expect an extinction factor of about 40%. This will have major effects on the fidelity of their source modelling, on the quality of their calibration solutions, and on the reliability and the veracity of their scientific work. Worse, this may not be immediately apparent to the astronomer.
The aim of this paper is to explain the source of this flux suppression, the regime in which it occurs, and how to avoid it. Although much of the discussion here is quite technical and targets a specialist audience, we have taken care to make it as accessible as possible to astronomers by explaining the practical consequences of our results throughout the paper.
The paper structure is as follows: in Sects. 2 and 3, the scientific context for post-processing superstation formation is discussed. In Sect. 4, a full mathematical development of this technique and its effect on interferometric measurement is given. This development is the cornerstone of this paper, and the foundation on which we build our analysis. In Sect. 5, we show that we not only correctly model the way current suites of LOFAR data reductions perform post-processing superstation formation, but that our analytical conclusions are valid; this is done by creating a simulated dataset. In Sect. 6, we perform the same analysis using real data. We close with a general discussion and practical guidelines for astronomers on how to avoid the issue outlined in this paper.
2. LOFAR, VLBI, and superstation beamforming
Good telescopes are designed for their resolution to be diffraction-limited. The very long wavelength of radio frequencies means that, to obtain resolutions comparable to what is routinely achieved in the optical regime, extremely large antennas are necessary. Historically, this has led to two relatively divergent paths: monolithic antennas (e.g. the Effelsberg 100 m Radio Telescope or the Green Bank Telescope) and aperture synthesis (which can be further broken down into phased arrays and interferometric arrays). For the remainder of this paper, we consider only the second family of instruments.
The difference between the two types of aperture synthesis array lies in the way in which signal from their constituent antennas is combined: phased arrays rely on a sum operation (and are hence also known as ∑ arrays) while interferometric arrays rely on a multiplication operation (and are hence also known as Π arrays). LOFAR is exceptional (but not unique) in that it is an interferometer made up of phased arrays. This allows it to reach very high sensitivity and resolution at a low cost.
Very long baseline interferometry is an interferometric technique that consists of combining the signal from multiple telescopes at very large distances from each other, forming baselines greater than 106 wavelengths in length as a single interferometer. This introduces technical constraints on observations (e.g. very accurate clocks are needed to combine the signals from different instruments properly (and offline), the extremely sparse uv coverage leads to worse conditioning for calibration and imaging inverse problems, geometric correlator model needs high accuracy) but is an extremely powerful method for reaching very high resolutions in instances where the diffraction limit of the component stations would otherwise forbid it, by creating a sparse interferometer with them.
At the very high spatial frequencies (i.e. very high resolution) that the instrument probes, the morphological structure of sources often become resolved and there is no guarantee that much signal is present in a given baseline. Consequently, VLBI calibration is often limited by the signal-to-noise ratio (henceforth S/N) of a given observation. Because signal calibration effects are functions of time and frequency, one approach sometimes used to improve S/N and therefore calibration is the post-processing beamforming of nearby central antennas, with the benefits outlined above (improvement of 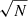 in sensitivity, with N the number of antennas combined into a superstation). Using central stations, rather than outlying ones, helps further constrain calibration by increasing sensitivity on similar spatial frequencies multiple times.
in sensitivity, with N the number of antennas combined into a superstation). Using central stations, rather than outlying ones, helps further constrain calibration by increasing sensitivity on similar spatial frequencies multiple times.
If the distance between these central antennas is sufficiently small compared to the distance between these antennas and others, then instead of probing N slightly different spatial frequencies once (with N the number of central antennas), these individual samples can be approximated as probing the same spatial frequency N times, thereby decreasing the noise associated with that spatial frequency by a factor of 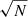 . The question then becomes: for LOFAR, under what limits can this be done, and what constraints does this technique impose?
. The question then becomes: for LOFAR, under what limits can this be done, and what constraints does this technique impose?
3. Decoherent phasing in LOFAR beamforming
The main difference between standard VLBI superstation forming and LOFAR is that in VLBI, one has access to the voltage information (i.e. analog signal) of individual stations prior to visibility formation, whereas in the case of LOFAR, the superstation formation is done after visibility formation (i.e. we only have access to the correlated signal). This is why we refer specifically to post-processing superstation beamforming in the case of LOFAR. In this section, we will highlight the problem this introduces in terms of signal coherence, which is the quantity that is actually measured by interferometers.
We begin by considering the case of traditional (pre-processing) superstation beamforming from the antenna voltages. This simply reduces to creating a phased array using the stations that are beamformed: a phase factor is applied to the voltages so as to have fully coherent combination at the phase centre, the voltages are then averaged together, and this new voltage is then used to form visibilities with other stations. In other words, the order of operations is as follows:
where r is the index of the superstation being formed, vp is the voltage measurement associated with antenna p, R is the set of NR antennas used to form r, q ∉ R is some remote antenna, ϕp is the phase correction for antenna p, and δt and δν are the correlator dump time and channel bandwidth respectively. We assume here that all visibilities have equal weight. Equation (2) is the equation for the formation of visibilities from antenna voltages: it is this operation that the correlator performs. The point here is that, in this case, the sum over p is done prior to correlation.
In post-processing, however, we no longer have access to the information prior to correlation. For LOFAR, this means that we no longer have access to the voltage information of the antennas that constitute each station, but only to the station-level information: the beamforming is done with each station acting as a single antenna, rather than by phasing up every physical antenna in the set of stations that is beamformed. The phasing must therefore be done from visibilities:
where  is the post-processing estimate of Vrq. The sum over p in Eq. (3) is performed before averaging over time and frequency, while it is performed after the fact in Eq. (5). In other words, this summation is done before correlation in the first case, and afterwards in the second. These two operations will only be equivalent if the variables being correlated are independent random variables. If this is not the case, some amount of signal coherence will inevitably be lost.
is the post-processing estimate of Vrq. The sum over p in Eq. (3) is performed before averaging over time and frequency, while it is performed after the fact in Eq. (5). In other words, this summation is done before correlation in the first case, and afterwards in the second. These two operations will only be equivalent if the variables being correlated are independent random variables. If this is not the case, some amount of signal coherence will inevitably be lost.
It should be noted that this effect or a similar one has been noted over the course of developing the LOFAR-VLBI pipeline by its working group (Morabito, priv. comm.). However, this effect was not fully understood or modelled at the time. Understanding and thus mitigating it is therefore of immediate interest: by characterising it fully, we can ensure that it does not bias our existing pipelines and associated results.
The mathematical framework used thus far, however, is not well suited to analysing this problem in depth. For this reason, we will pursue the same line of reasoning using a more appropriate framework: the radio interferometer’s measurement equation, or RIME.
4. Analytical framework: the RIME approach
In this section, we give an analytical development of what post-processing superstation beamforming entails using the RIME (see Smirnov 2011a,b,c,d, and references therein). This allows us to find a quantitative estimate for a baseline-dependent error factor, and thus to predict the overall decoherence introduced by this operation for a point source at a given distance from phase centre.
4.1. Predicting decoherence for a single visibility
We begin by writing what the operation of superstation beamforming entails by considering the creation of one superstation visibility pointing to antenna q from superstation r, formed with a set of antennas p. We allow for the presence of weights. The uvw coordinates and weights of our superstation are thus the following:
where ST is the set of stations that are beamformed into the superstation, (upq, vpq, wpq) are the uvw coordinates associated with visibility Vpq, and ωpq is the associated weight, accounting for data flagging. In the measurement sets used in this paper, the averaged uvw coordinates of Eq. (6) are actually stored as (uqr, vqr, wqr) because the new visibilities are added after the existing visibilities, and not before. This introduces a factor of −1 to the stored coordinates because urq = −uqr. This has no impact on imaging, and thus only appears within the dataset. The weights ωrq are unaffected.
The calculated visibilities of our beamformed superstation, meanwhile, are given by:
that is to say, the visibility between superstation r and antenna q is simply the weighted average of all visibilities from the antennas used to form the superstation and antenna q. The hat denotes that this is an estimation. 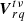 is a 2 × 2 complex matrix. Using the RIME, we can write
is a 2 × 2 complex matrix. Using the RIME, we can write 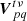 as
as
where 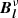 is the brightness distribution matrix at position l = (l, m, n − 1) (where (l, m, n) are cardinal angles and we make the small-angle approximation that
is the brightness distribution matrix at position l = (l, m, n − 1) (where (l, m, n) are cardinal angles and we make the small-angle approximation that  ) and frequency ν,
) and frequency ν, 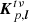 is a scalar Jones matrix that encodes which point in uv-space antenna p contributes to sampling, and
is a scalar Jones matrix that encodes which point in uv-space antenna p contributes to sampling, and 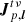 is the Jones matrix associated with antenna p and direction l. This Jones matrix encodes the propagation effects that affect the signal as it travels between its source, located at l, and the final measurement at the end of the instrumental chain. All of these matrices are complex 2 × 2 matrices.
is the Jones matrix associated with antenna p and direction l. This Jones matrix encodes the propagation effects that affect the signal as it travels between its source, located at l, and the final measurement at the end of the instrumental chain. All of these matrices are complex 2 × 2 matrices.  and
and 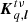 are scalar matrices,
are scalar matrices,
and they therefore commute with all other Jones matrices.
We now make a simplifying hypothesis, and assume that we are unaffected by propagation signals: 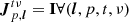 , where I is the 2 × 2 unit matrix. This is equivalent to assuming that we have perfectly corrected all calibration effects, including direction-dependent ones. In this limit, Eq. (9) can be written as
, where I is the 2 × 2 unit matrix. This is equivalent to assuming that we have perfectly corrected all calibration effects, including direction-dependent ones. In this limit, Eq. (9) can be written as
where 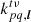 now becomes the Fourier kernel that determines the mapping between the brightness matrix and the visibility. We can now rewrite Eq. (8) as:
now becomes the Fourier kernel that determines the mapping between the brightness matrix and the visibility. We can now rewrite Eq. (8) as:
Within the limit of perfect calibration, we can also analytically predict the expected value of the superstation visibility 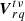 because we know its associated urq coordinates exactly. With the definitions above, we can show straightforwardly that it can be written as:
because we know its associated urq coordinates exactly. With the definitions above, we can show straightforwardly that it can be written as:
If Eq. (14) is exact, then it should give the same result as Eq. (15). We therefore equate them with a proportionality factor. If this proportionality factor is unity, then Eq. (14) is exact. Otherwise, this proportionality factor gives us an indication of some error factor introduced by the post-processing superstation beamforming. We define our proportionality factor as A. We assume it is a scalar and function of the same parameters as 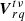 , and therefore a function of (r, q, t, ν) at least. We can now write
, and therefore a function of (r, q, t, ν) at least. We can now write
where we have used the commutation properties of scalars to factorise 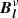 . For Eq. (18) to hold, the two terms in the brackets must be equal for all values of l.
. For Eq. (18) to hold, the two terms in the brackets must be equal for all values of l. 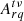 must therefore be a function of l in addition to the previous parameters. We therefore write
must therefore be a function of l in addition to the previous parameters. We therefore write
We can simplify the expression above by decomposing the Fourier kernels into their individual parts,
where we have used the property that 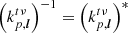 . Plugging this back into Eq. (20), we finally find
. Plugging this back into Eq. (20), we finally find
This result tells us that the loss of information caused by incoherent beamforming manifests as a baseline-dependent loss factor – that is to say, dependent on the exact baseline formed between two stations at a given time and frequency, not just on the length of this baseline. In other words, in the image plane, incoherent beamforming results in a convolution of the true sky brightness distribution with some position-dependent decoherence point-spread function (PSF). The peak of this position-dependent decoherence PSF gives a measure of how much the measured signal is affected, and its width gives a measure of how widely the signal is smeared in the sky.
4.2. Interpreting our result
The decoherence factor calculated for a single superstation visibility, given in Eq. (24), depends on a few parameters. Firstly, and most importantly, it is a function of l the angular distance between the position that is considered in the sky and the phase centre for the data. Secondly, it is a function of the distance between the superstation’s u coordinates and those of the stations used to create it. Finally, it is a function of the visibility weighting.
We consider the limits in which the decoherence is negligible, that is, within which 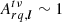 . Firstly, if l = 0 (i.e. when the source is at phase centre), we have
. Firstly, if l = 0 (i.e. when the source is at phase centre), we have
and so we are unaffected by this beamforming decoherence, regardless of any other factors.
Secondly, assuming we are interested in a source located elsewhere than phase centre, we consider the limit in which we can beamform stations into the superstation at a negligible cost in decoherence. This is particularly relevant for LOFAR, because we might in principle synthesise a superstation out of all LOFAR core stations, decreasing the thermal noise in the relevant visibilities by a factor of nearly 7 if we phased up up all the core Dutch stations and used the dual mode (where there are two HBA sub-stations per station). If our FoV includes only a single source at position l0 ≠ 0, and if we assume unit weights (ωpq = const.), the decoherence factor becomes:
This quantity obviously tends towards unity as urq → 0. This is a trivial limit, however: it simply states that as the difference between the superstation coordinates and its phased antenna coordinates vanishes, so does the decoherence. What interests us, however, is the limit in which the impact of decoherence becomes negligible for a given baseline with an antenna q that is neither part of the antennas that are phased up nor of the superstation. In other words, what interests us is the limit in which
which, with the approximations above, becomes
which is satisfied when
that is, when the uvw distance between the antennas that are beamformed and the resultant superstation is negligible compared to the distance between the superstation uvw coordinates and those of the antennas q ∉ ST. This condition is always met by standard VLBI arrays, but LOFAR-VLBI can be an edge case: this limit tells us that, for example, phasing up the Superterp may be fine, but phasing up all core Dutch stations would bring problems (because the distance between the nearest core station to a remote station and the distance between the Superterp and this core station could be comparable).
It should be noted that traditional VLBI satisfies both of these conditions, but large-scale interferometers such as LOFAR and the future SKA may not. If these instruments still wish to make use of VLBI techniques, understanding the exact limits of their applicability will be very useful.
4.3. Predicting decoherence for a full observation
We begin by formalising the relationship between visibilities and images made from them. Because the decoherence factor is a scalar quantity, we proceed with unpolarised emission from here on out, and therefore reduce our framework to a scalar one. All correlations (and therefore all Stokes images) experience the effects described from here on out. A visibility is simply the Fourier transform of the sky brightness distribution sampled at a specific point in Fourier space, which is a function of the uvw coordinates of the antennas forming the baseline. In other words
where 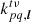 encodes both the forward Fourier transfer function and the Fourier sampling function. The contribution of this visibility to the position l on a dirty image is then the inverse Fourier transform of the above. The integral can be thought of as being performed over a series of fringes
encodes both the forward Fourier transfer function and the Fourier sampling function. The contribution of this visibility to the position l on a dirty image is then the inverse Fourier transform of the above. The integral can be thought of as being performed over a series of fringes 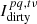 , each associated with a single visibility,
, each associated with a single visibility,
where ωpq, tν is the weight associated with that fringe. Equivalently, this can be written in discrete form as
By iterating over the cardinal sine coordinates of all the pixels in our image, we can now recreate the so-called dirty map of an observation analytically from the visibilities.
After writing the relationship between a set of visibilities for an observation and the resulting dirty image, we consider the case of an empty sky with a single point source of brightness S at some position l0. This gives us
The value of the dirty map at coordinates l0 is then
By placing our point source through our forward and backward operators, we therefore correctly recover the flux of the source at its known coordinates. We can thus use this formalism, combined with the result of Eq. (24), to estimate the peak of the position-dependent decoherence PSF at a given point in the sky.
For a source with unit brightness at position l0, B = δ(l − l0) and the decoherence factor can be written as:
where the denominator vanishes because we have set S = 1 in this case. To develop this further, we explicitly write an expression for the smeared value of 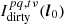 , denoted as
, denoted as 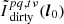
where, from Eq. (24) (changing mute indices),
and where ST is the set of antennas that are beamformed into superstation antenna pST. Now, to determine the proper decoherence factor, we must discard all visibilities with (p, q)∈ST, and use in their stead the visibilities associated with pST. Using this method, we can now estimate the suppression factor at any coordinates in the sky as a function of the choice of beamforming stations and the angular distance between these coordinates and phase centre.
5. Simulations
In this section, we verify the results given in Sect. 4 on a simulated dataset. This dataset is created by slicing 30 min of observation from an 8 h LOFAR HBA observation made in HBA_DUAL_INNER mode, resulting in 48 core stations and 14 remote stations. No international stations are present. This allows us to obtain realistic uvw coordinates and frequency coverage.
With this information, we then simulate the visibilities for a sky consisting of a single 1 Jy point source at (l = −0.3, m = 0.3). We then use the NDPPP StationAdder function (van Haarlem et al. 2013) to create a beamformed superstation using all the core stations. This results in a set of visibilities with 63 antennas: the original 62, and one superstation where we expect to see decoherence in the simulated point source. We henceforth refer to this set of visibilities as the averaged visibilities, even though only some of them are affected: this is in contrast to the control visibilities. These are created by simulating the point source exactly as it ought to be seen for all 63 antennas. There is no noise introduced in this simulation.
5.1. Simulated dataset
The observation considered was taken on July 28, 2014, from 1300 h to 1400 h. We took 30 min and a single subband for our tests, starting from 13 h 30 min. This gave us a bandwidth of 2 kHz centred on 134.86 MHz and 20 channels. The core and remote stations were present, in HBA_DUAL_INNER mode (see Shimwell et al. 2019). The uv coverage is shown in Fig. 1.
 |
Fig. 1. uv coverage of the dataset chosen to perform our simulations. Quantities are dimensionless. |
5.2. Verifying that beamforming is correctly modeled
Here, our aim is to show that the equations given in Sect. 4, Eqs. (6), (7), and (8), correctly model the behaviour of the LOFAR post-processing beamforming software, specifically the NDPPP StationAdder function. To this end, we took the weights, uvw coordinates and control visibilities for the beamformed antennas pointing to individual remote antennas at a given time, applied Eqs. (6), (7) and (8), and compared these visibilities with those of the averaged visibilties for that baseline. The values of the residual uvw coordinates are given in Figs. 2a–2c, while the weights are shown in Fig. 2d and the visibility phase and amplitude in Figs. 2e and 2f, respectively. These are all relative residuals, meaning that they are normalised by the measured values. In other words, if the residual xr between a value x and its measure xm is xr = x − xm, we plot 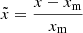 . This removes patterns in the residuals that are due to varying amplitudes in the values that are computed, rather than to systemic errors.
. This removes patterns in the residuals that are due to varying amplitudes in the values that are computed, rather than to systemic errors.
 |
Fig. 2. Values for various quantities for baselines pointing towards the beamformed superstation, calculated with NDPPP and by the authors. The residuals below the plots are relative residuals, meaning that they have been normalised by the associated quantity value. |
As these residual figures show, we calculated the same values as NDPPP for all quantities of interest, up to machine noise (i.e. up to the precision of the averaging function of either python or NDPPP). The loss of coherence outlined in Sect. 4 (and starkly visible in Fig. 2e) therefore applies to any sources away from phase centre in observations that use the NDPPP StationAdder routine to form a superstation. Furthermore, the simulations in this section accurately depict this loss of coherence.
5.3. Predicting the impact of decoherence on simulated data
The visibilities averaged in the previous section are the simulated visibilities corresponding to a single 1 Jy point source away from phase centre. The amplitude of these visibilities is expected to be unity for all measurements. We can immediately see the impact of simple averaging in post-processing superstation beamforming visibilities by inspecting Fig. 2e: while we expect the visibility amplitude to be 1 at all points of measurement, we instead find constant suppression.
However, although this decoherence is immediately obvious in visibility space, its impact in image space is of greater interest. To characterise it, we simulated a single point source at increasing distances from phase centre. We then created two dirty images from each simulated set of visibilities. One includes the beamformed superstation formed using all LOFAR core stations (and therefore affected by decoherence), flagging all core stations during imaging. The other does not include the beamformed superstation, but uses all the core stations. Both are then effectively two similar images of the source, but one is affected by smearing.
We begin by verifying that our simulations show the predicted behaviour when the NDPPP post-processing beamforming routine is used on our simulated visibilities, but not when we simulate the visibilities directly into the superstation. This is shown in Fig. 3. The dirty maps made without the superstation are equivalent, but the dirty maps made using the superstation differ: the small spatial scales are suppressed when the post-processing beamforming is used. This accounts for the presence of a cross-shaped artefact in Fig. 3b, which disappears in Fig. 3d: this artefact is in fact the high spatial frequencies of the PSF, precisely that which is suppressed by our post-processing averaging. Although it is hard to see, this results in reducing the peak flux in Fig. 3d to only 57% of what it is in all other images.
 |
Fig. 3. Dirty maps of a single point source simulated into the visibilities. The images on the left are made using the simulated visibilities directly. The images on the right are made using the superstation visibilities: at the top they are simulated directly, and at the bottom they result from post-processing beamforming. The higher spatial frequencies are suppressed: this accounts for the absence of the x-shaped artefact in panel d: this artefact is in fact the part of the PSF that corresponds to our high spatial frequencies. The peak flux values are: 1.77 Jy in panel a, 1.77 Jy in panel b, 1.74 Jy in panel c, and 1.09 Jy in panel d. |
We created one such set of four images for a range of l values, keeping m zero. For each such set of images, we determined the pixel with the highest flux value in the dirty map that was created using the core stations. For this pixel, we then determined the flux value in the image that was created using the superstation. This is the measured decorrelation factor, df.
We then created an inverse Fourier kernel for the associate (l, m)-values, and computed the value expected in both cases at the exact position of the source. This was done analytically, without using any imager package.
Finally, we plot these two decorrelation factors as functions of l in Fig. 4. The two curves are in agreement, to within a few percent. The source of the disparity is very likely found in the quantisation of the Fourier kernel that is necessary for imaging packages: the imager does not calculate the values of the sky brightness distribution at every l, m value, but only at those on its grid. This probably is the reason for the tendency of the residuals to show the same values after about 12′, for every four values of l.
 |
Fig. 4. Decorrelation function as a function of distance from phase centre, for a point source located at that position and with a given set of antennas chosen to form a superstation. Here, the residuals are absolute residuals, not relative residuals. This is to show the quantisation in the residuals. l is in units of arcminutes. |
Decorrelation becomes very strong very fast: this is because we chose to use every single core LOFAR station for our beamformed superstation, which exaggerates the strength of the decorrelation. LOFAR observations that use only the Superterp (usually formed with the six innermost core stations) will be much less affected by this behaviour. However, it has become standard practice in LOFAR-VLBI to use all core stations to form a superstation, which is still referred to as the Superterp. In the context of LOFAR-VLBI at the time of writing, this decorrelation plot is therefore representative of the signal loss that might be expected in real observations that do not use the international stations. This signal loss has yet to be characterised and will depend on the international stations being used, but assuming that signal can be calibrated and recovered on those international baselines, they are expected to suffer less decorrelation because they are closer to the limit of negligibility given in Eq. (33).
The structure in the residuals is likely due to sky coordinates that are quantised in images; the overall error never rises above 1% of the prediction, however, and is therefore negligible. The bump around l ∼ 12′ is discussed further in Sect. 7.
In conclusion, Fig. 4 conclusively shows that the decoherence introduced by post-processing beamforming is not only analytically understood, but accurately modelled by our predictions.
6. Application to real data
In this section, we take a single subband of the full 8 h of observations from which a slice was taken to create the simulations shown in Sect. 5. This dataset is then calibrated and imaged with certain constraints in order to confirm that the behaviour described in Sect. 5 applies to real data as well. We begin with a description of the observation itself, and then explain the choices we made to confirm the presence of source suppression. This entails explaining our calibration and imaging procedures, along with certain flagging choices made to ensure we compare like to like.
6.1. Description of observation & data reduction
The dataset we used here was a single subband (ν0 = 128.3188 MHz, Δν = 195.3 kHz, split into eight channels of 24.4 kHz each) of an 8 h LOFAR HBA observation of the Extended Groth Strip, pointing at (α, δ) = (14:17:00.00,6+52.30.00.00) and taken on September 29, 2014, from noon to 8 pm, UTC. The observation was made in HBA_DUAL_INNER configuration, where the core stations (which are usually made up of 48 beamformed antennas) are split into two phased arrays with 24 antennas each. The visibilities were averaged to one measurement per 2 s per baseline.
We began by calibrating the dataset using killMS (Smirnov & Tasse 2015). One calibration solution was found per four channels and per 8 s. Calibration was made using the best high-resolution model of 3C295 currently available at LOFAR frequencies (Bonnassieux et al., in prep.). This dataset was then used to create two new ones using the LOFAR new default pre-processing pipeline (NDPPP: cf. van Haarlem et al. 2013). Specifically, one dataset was created by reading the calibrated visibilities and writing them into a new dataset, while forming a superstation from all the core stations in the original dataset and flagging out the international stations (along with two remote stations that were found to have poor-quality calibration solutions during calibration, RS210 and RS509). The other dataset was formed by keeping only core-remote, remote-core and remote-remote baselines (excluding, once again, RS210 and RS509).
The international stations were removed because the model we used for calibration is not yet good enough to ensure that their calibration solutions are correct because they resolve the brightest sources out. They thus lead us beyond the scope of our formalism. By flagging them, we ensure that the calibrator can be considered as a point source, and thus that our calibration solutions are reliable. We removed core-core baselines because autocorrelations are not preserved for LOFAR imaging. Thus, when the superstation is formed from all core stations, all core-core baselines are removed because all core stations are now one station, every baseline between different core stations is treated as an autocorrelation and therefore discarded. As a consequence, flagging the core-core baselines is necessary to ensure that the comparison between our datasets is valid. Without it, the first dataset has far more visibilities and the observation therefore has a different sensitivity and the comparison becomes invalid because the signal loss that is specifically due to decoherent superstation formation is of interest to us here. Our final dataset therefore includes no core-core baselines at all.
6.2. Source extinction
Each dataset was imaged using the same imaging parameters: a cell size of 1″, 15 k × 15 k pixels, an inner uv cut of 10 km (thereby excluding the shortest baselines to ensure consistency between our calibration and imaging) and Briggs weighting with a robust parameter value of 2 (Briggs 1995). The only differences between the imaging runs were the output names and dataset. The dirty maps (Figs. 5a and 5c) are simply the inverse Fourier transform of the visibilities, and therefore map the sky brightness distribution convolved with the instrument response, or PSF. The restored maps (Figs. 5b and 5d) are the result of running the dirty maps through a deconvolution algorithm, stopped in both cases by running out of major iterations (20). The most prominent sidelobes of the brightest sources are reduced, allowing fainter sources to appear.
 |
Fig. 5. Dirty and restored maps of the sky showing the impact of incoherent post-processing superstation beamforming. These images show apparent flux, not intrinsic flux. Colour scales and pixel coordinates are matched in all images, and all units are Jy bm−1. 3C295 is the very prominent, very bright source that dominates the field. While the PSF changes as a result (which is an expected and normal outcome), signal is also lost: this can be seen most clearly in the two north-eastern sources in panels a and b (dirty and restored maps made without the superstation respectively) that vanish from panels c and d (dirty and restored maps made with the superstation, respectively). |
Figure 5 requires some further explanation. Firstly, the difference in source morphology between Figs. 5a and 5c is due to the different uv coverage in both observations, which leads to different PSFs. This is normal and expected.
Secondly, the deconvolution did not give equivalent results in the two cases. While some artefacts remain around 3C295 (which is the brightest source in the field by far) in Fig. 5b, the shift from Figs. 5a and 5b is what is expected from comparing dirty and restored maps: sources in the field that were previously hidden in the sidelobes become apparent. The shift from Figs. 5c and 5d, however, gives no such improvement. The deconvolution appears to deteriorate the image rather than improve it. This is in fact expected. The signal loss introduced by decoherent superstation beamforming does not manifest itself simply as a flux loss: it manifests as a baseline-dependent extinction factor. In other words, it manifests itself as a modulation of the PSF, which the deconvolution algorithm does not take into account. It then attempts to deconvolve with an incorrect PSF, resulting in overall deterioration. This is particularly obvious in this image because 3C295 is so very bright, but is expected to occur, less obviously but no less problematically, for all sources in the field. This deconvolution issue likely accounts for the aliasing effect visible in Fig. 5c. As a consequence of this, a fair comparison between the images ought to be made using the dirty maps rather than the restored maps.
Thirdly, then, we can note one very interesting fact by visual inspection of Figs. 5a and 5c. In the first, two sources are present in the north-east corner (top left). They are absent in the second. These two sources are also detected in Fig. 5b, which means that they are not just some kind of strange resonance: they are physical sources. In other words, we have firsthand, visible evidence that superstation formation results in source suppression, all other things being equal. By taking the ratio of the highest pixel values in the two dirty images, we calculate a measured decoherence factor for 3C295: df, m = 20.77%. In other words, the brightest pixel in the image made using the superstation is only about 20% of that in the image using the core stations (without the core-core baselines).
7. Conclusion and future work
Thus far, we focused on a demonstration of the effects of an interferometric technique. Ultimately, however, the purpose of techniques is to be used, and used wisely. We therefore wish to provide scientists with guidelines to help them make the most out of this technique while mitigating, or at least recognising, potential negative consequences on their scientific analysis.
Our conclusion therefore consists of two discussions. The first aims to help recognise and avoid negative effects from superstation formation, providing practical advice for scientists who are literate in radio interferometry but not specialised in its techniques. The second is more appropriate to an audience of specialists who may wish to take this effect into account in their pipelines or data reduction software, and discusses possible paths forward to do so.
7.1. Avoiding decoherence
The first and most obvious conclusion of this paper is also the most important: if you seek to improve your S/N on long baselines, where signal is scarcer, by performing post-processing beamforming, you will systematically lose signal if currently-existing data reduction suites are used. This signal loss will be greater as distance from the phase centre increases. Accordingly, should this be the approach chosen to reduce an interferometric dataset, care must be taken to rephase the observation onto the target source before forming the superstation.
This effect is negligible if the distance between the stations that are beamformed is negligible compared to the distance between these stations and others in the array, as expressed in Eq. (33). For a single baseline, the exact expression is given in Eq. (24). It is also negligible near the phase centre at which the beamforming was made. This effect is therefore expected to be negligible for standard VLBI, which is usually only concerned with a single target at phase centre, and where the distances between the stations that are beamformed into a superstation is neglibible compared to the distance between these stations and more distant stations. The LOFAR-VLBI pipeline is also largely unaffected because it takes care to rephase around each source, average, combine stations, and then calibrate.
When a naive approach is used to create a widefield image with a beamformed superstation, the impact of decoherence will manifest itself as artefacts around sources (caused by the deconvolution of a source with the incorrect, unsmeared PSF), and for point sources, in a net loss in integrated flux. This can be handled in the same way as the beam in apparent-flux images: by predicting the expected decoherence at the positions of the sources in a field, the true flux may be recovered. For LOFAR, assuming that all core stations are used to form the superstation, and that the observation includes no international stations, this will result in the decoherence factors as a function of distance from phase centre given in Fig. 4.
For standard widefield observations with international stations, it is therefore not recommended to form up the Superterp in this way at the time of writing if any emission from the source of interest lies farther than 1′ away from phase centre (either because of the size of the source or because of its location relative to phase centre). This will ensure that signal suppression remains below ∼5%. After the methods described in the section below are implemented, it may become safe to form the Superterp from core stations. The best way to ensure that the scientific analysis is not negatively affected remains performing the same test as shown here: image the same dataset with and without superstation beamforming. This can be done with a small subset of the overall dataset without negatively impacting the test.
Finally, in the specific case of LOFAR-VLBI in the LBA regime (i.e. at the lowest frequencies), this problem of superstation beamforming will likely be solved in the near future through NenuFAR (new extension in nancay upgrading LOFAR – cf. Zarka et al. 2012, 2015, and in prep.). NenuFAR is a compact array of 19 tiles of 96 LWA-like antennas (Hicks et al. 2012). These are much more sensitive than LOFAR LBA antennas out of a narrow spectral range centered at 58 MHz, the peak response of LBA antennas, and are laid out within a diameter of 400 m. It can operate in several modes, notably as a LOFAR superstation created by connecting the 96 tiles of 19 antennas to the LOFAR-FR606 receivers. The beamforming of the entire LOFAR core prior to correlation with LOFAR stations is expected to provide a superstation with > 19 times the sensitivity of a standard international LOFAR station, without any of the drawbacks described in the present paper. It might therefore naturally serve all the purposes that a superstation can (anchoring the calibration solutions for the longest baselines) without the current superstation formation cost of losing the core–core visibilities when solving for international station gains (which can also serve to anchor the core station gains, and thus contribute to anchoring the international station gains in turn). However, because it is located on the outskirts of the array, it would not be a good substitute for the core superstation, but is expected to provide a fantastic additional anchor. NenuFAR is therefore expected to be very beneficial to LOFAR-VLBI observations at the lowest frequencies after it becomes operational as an alternative to the French LOFAR station.
7.2. Correcting decoherence
Because decoherence due to post-processing beamforming can be predicted, it can in principle be modelled away. The most obvious way to do this is the method proposed above: simply predict the extent of coherence lost at the position of the sources in the sky model that is used for calibration, and apply the appropriate decorrelation correction factor at each position. If the sky model consists of unresolved point sources, this is an equivalent approach to applying the interferometric array beam response to the model, and it is expected to give equivalent results in correcting for its associated effect. Creating such a script is the subject of future work. The main issue here is that the decoherence will depend on the dataset: its uv coverage, the choice of stations to beamform, etc. will all have an impact. This script is therefore not entirely trivial to create in a user-friendly way.
Furthermore, in the presence of diffuse emission, this approach will not be sufficient. We have shown that the decoherence not only introduced some decoherence factor, but also changed the local PSF. This is very significant: it means that decoherence will necessarily introduce deconvolution artefacts around sources (because the deconvolution will be performed with an incorrect PSF). This will have much greater consequences for diffuse emission because these artefacts will accumulate and further bias the deconvolved map. An ideal solution would therefore be performing much the same operation as DDFacet (Tasse et al. 2018) uses with baseline-dependent averaging to model away time or frequency smearing: apply the decoherence directly to the PSF, and deconvolve with the smeared PSF. Making this an option in DDFacet is part of our expected future work.
In continuation with this notion of baseline-dependent averaging, we can propose one final solution to this issue, which would be the ideal one. Post-processing beamforming introduces decoherence because it uses, effectively, a tophat function for its averaging. This explains the odd bump seen in Fig. 4: compare it with smearing functions shown in Atemkeng et al. (2018). It is simply the image-space consequence of using a tophat averaging function in Fourier-space: it introduces a sinc smearing in image-space. Therefore, if baseline-dependent averaging were to be used during superstation formation, as explained in Atemkeng et al. (2018), this issue could be resolved by simply specifying a desired FoV (which the cited paper refers to as “FoV shaping”), which determines the period of the baseline-dependent averaging sinc function used to create the visibilities during superstation formation. Implementing this application of FoV shaping in existing software is beyond the scope of this paper. Proving that this method corrects for the problem and implementing it in existing astronomy software is the subject of future work.
Acknowledgments
The authors thank the LOFAR Surveys KSP Primary Investigators for allowing us to use their data for our tests and images in this paper. We also wish to thank Philippe Zarka for his help in seeing the relevance of this paper in the context of NenuFAR’s “international station” mode. Etienne Bonnassieux & Annalisa Bonafede acknowledge support from the ERC-ERG grant DRANOEL, n.714245. ACE acknowledges support from STFC grant ST/P00541/1.
References
- Atemkeng, M., Smirnov, O., Tasse, C., et al. 2018, MNRAS, 477, 4511 [NASA ADS] [CrossRef] [Google Scholar]
- Briggs, D. S. 1995, Bull. Am. Astron. Soc., 27, 1444 [Google Scholar]
- Hicks, B. C., Paravastu-Dalal, N., Stewart, K. P., et al. 2012, PASP, 124, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, N., Tagore, A., Deller, A., et al. 2016, A&A, 595, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kappes, A., Perucho, M., Kadler, M., et al. 2019, A&A, 631, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morabito, L. K., Deller, A. T., Röttgering, H., et al. 2016, MNRAS, 461, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M. 2011a, A&A, 527, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M. 2011b, A&A, 527, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M. 2011c, A&A, 527, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M. 2011d, A&A, 531, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M., & Tasse, C. 2015, MNRAS, 449, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Tasse, C., Hugo, B., Mirmont, M., et al. 2018, A&A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varenius, E., Conway, J. E., Martí-Vidal, I., et al. 2015, A&A, 574, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varenius, E., Conway, J. E., Marti-Vidal, I., et al. 2016, VizieR Online Data Catalog, J/A+A/593/A86 [Google Scholar]
- Zarka, P., Girard, J. N., Tagger, M., & Denis, L. 2012, in SF2A-2012: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. S. Boissier, P. de Laverny, N. Nardetto, et al., 687 [Google Scholar]
- Zarka, P., Tagger, M., Denis, L., et al. 2015, in International Conference on Antenna Theory and Techniques (ICATT) (Karkiv, Ukraine, 13 [Google Scholar]
All Figures
 |
Fig. 1. uv coverage of the dataset chosen to perform our simulations. Quantities are dimensionless. |
| In the text | |
 |
Fig. 2. Values for various quantities for baselines pointing towards the beamformed superstation, calculated with NDPPP and by the authors. The residuals below the plots are relative residuals, meaning that they have been normalised by the associated quantity value. |
| In the text | |
 |
Fig. 3. Dirty maps of a single point source simulated into the visibilities. The images on the left are made using the simulated visibilities directly. The images on the right are made using the superstation visibilities: at the top they are simulated directly, and at the bottom they result from post-processing beamforming. The higher spatial frequencies are suppressed: this accounts for the absence of the x-shaped artefact in panel d: this artefact is in fact the part of the PSF that corresponds to our high spatial frequencies. The peak flux values are: 1.77 Jy in panel a, 1.77 Jy in panel b, 1.74 Jy in panel c, and 1.09 Jy in panel d. |
| In the text | |
 |
Fig. 4. Decorrelation function as a function of distance from phase centre, for a point source located at that position and with a given set of antennas chosen to form a superstation. Here, the residuals are absolute residuals, not relative residuals. This is to show the quantisation in the residuals. l is in units of arcminutes. |
| In the text | |
 |
Fig. 5. Dirty and restored maps of the sky showing the impact of incoherent post-processing superstation beamforming. These images show apparent flux, not intrinsic flux. Colour scales and pixel coordinates are matched in all images, and all units are Jy bm−1. 3C295 is the very prominent, very bright source that dominates the field. While the PSF changes as a result (which is an expected and normal outcome), signal is also lost: this can be seen most clearly in the two north-eastern sources in panels a and b (dirty and restored maps made without the superstation respectively) that vanish from panels c and d (dirty and restored maps made with the superstation, respectively). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



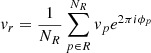
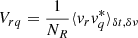
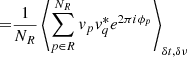
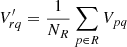
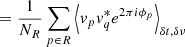
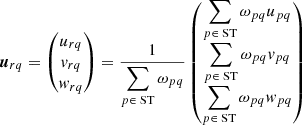
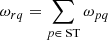
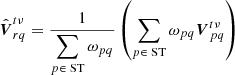

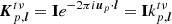
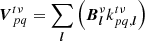
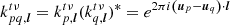
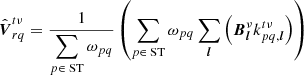
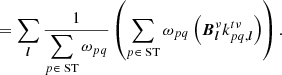
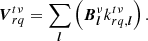
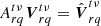
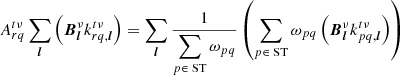
![$$ \begin{aligned}&0 = \sum _{{\boldsymbol{l}}} \left[{{\boldsymbol{B}}}_{{\boldsymbol{l}}}^{\nu }\left( {{A}}_{rq}^{t\nu } k_{rq,{\boldsymbol{l}}}^{t\nu } - \frac{ \left(\displaystyle \sum _{p\in \text{ ST}} \omega _{pq} \left(k_{pq,{\boldsymbol{l}}}^{t\nu } \right) \right) }{\displaystyle \sum _{p\in \text{ ST}} \omega _{pq}} \right)\right] \end{aligned} $$](/articles/aa/full_html/2020/05/aa37486-20/aa37486-20-eq34.gif)