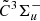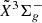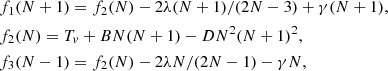| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202037448 | |
| Published online | 19 May 2020 | |
High-resolution laser spectroscopy of the linear SiC2Si molecule and its astrophysical implications
Hefei National Laboratory for Physical Sciences at the Microscale, and Department of Chemical Physics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
e-mail: dzhao@ustc.edu.cn
Received:
6
January
2020
Accepted:
28
March
2020
Small silicon-carbon clusters are important gas-phase constituents of stellar atmospheres, and are thought to play a role as potential seeds of the interstellar dusts formed in the envelopes of evolved carbon stars. Here we present the high-resolution optical spectra of the linear SiC2Si molecule (l-Si2C2) studied via laboratory experiments. The l-Si2C2 molecules are generated in a supersonically expanding planar plasma by discharging a silane-acetylene-argon gas mixture. The optical absorption spectra in the 5000−5300 Å region are recorded using sensitive pulsed cavity ring-down spectroscopy. In total, five optical absorption bands belonging to the 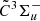 –
– 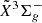 electronic transition system of l-Si2C2 are measured with fully resolved spin splitting fine structures in individual rotational transitions. Accurate spectroscopic constants for both
electronic transition system of l-Si2C2 are measured with fully resolved spin splitting fine structures in individual rotational transitions. Accurate spectroscopic constants for both 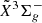 and
and 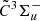 states of l-Si2C2, including the spin-spin interaction constants and spin-rotation interaction constants, are determined from the experimental spectra, which can be used to simulate these optical bands with different temperatures. Using the determined spectroscopic constants, optical spectra of l-Si2C2 simulated with different rotational excitation temperatures are compared to the stellar spectra of evolved carbon stars V Hya and IRAS 12311−23509, where the triatomic SiC2 are known to be abundant. Tentative assignments of the l-Si2C2 spectral features in the stellar spectra are discussed.
states of l-Si2C2, including the spin-spin interaction constants and spin-rotation interaction constants, are determined from the experimental spectra, which can be used to simulate these optical bands with different temperatures. Using the determined spectroscopic constants, optical spectra of l-Si2C2 simulated with different rotational excitation temperatures are compared to the stellar spectra of evolved carbon stars V Hya and IRAS 12311−23509, where the triatomic SiC2 are known to be abundant. Tentative assignments of the l-Si2C2 spectral features in the stellar spectra are discussed.
Key words: molecular data / ISM: molecules / ISM: lines and bands / stars: carbon
© ESO 2020
1. Introduction
Small silicon-carbon clusters of the form SinCm have been the topic of many observational and laboratory experimental studies. These small silicon-bearing molecules are thought to be important gas-phase constituents of stellar atmospheres and to be potential seeds of the interstellar dust formed in the envelopes of carbon-rich asymptotic giant branch (AGB) stars (McCarthy et al. 2019; Gobrecht et al. 2017; Mackay & Charnley 2010). A number of molecules, such as SiC, SiC2, Si2C, and the cyclic SiC3, have been detected by radio astronomy in the dust formation and growth zone of the evolved carbon-star IRC+10216 (Cernicharo et al. 1989, 2015; Wienkoop 1997; Thaddeus et al. 1984; Patel et al. 2011; Apponi et al. 1999). In the atmospheres of cool carbon stars, the Merrill-Sanford (MS) band system of the SiC2 molecule, arising from its 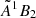 –
– 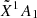 electronic transition in the blue-green optical region (Merrill 1926; Sanford 1926; Sarre et al. 1996, 2000; Lloyd Evans et al. 2000), has also been widely observed, and is used as a useful probe of the prevailing conditions.
electronic transition in the blue-green optical region (Merrill 1926; Sanford 1926; Sarre et al. 1996, 2000; Lloyd Evans et al. 2000), has also been widely observed, and is used as a useful probe of the prevailing conditions.
Due to the observed high abundances of tri-atomic SiC2 and Si2C molecules, the tetra-atomic Si2C2 is likely one of the detectable chemical intermediates that ultimately lead to the formation of the silicon carbide dust. Quantum chemistry calculations have shown that two isomers of Si2C2, the rhombic D2h structure (D2h, r-Si2C2) and the linear SiC2Si (D∞h, l-Si2C2) structure (see Fig. 1), are nearly isoenergetic (Rintelman & Gordon 2001; Presilla-Márquez et al. 1995; Fitzgerald & Bartlett 1990; Lammertsma & Guner 1988). Density functional theory calculations predicted the r-Si2C2 structure to be the most stable form, while the l-Si2C2 structure lies only ∼0.01 eV higher. Such a small energy difference will lead to the co-existence of both isomers in reactive environments. However, because of the lack of a permanent dipole moment in such centro-symmetric molecules, an observational search via pure rotational transitions by radio astronomy is challenging (Sonnentrucker et al. 2007). Alternatively, their electronic or vibrational transition spectra can provide an additional approach in astronomical observations. On the laboratory side, an early mid-infrared spectroscopic study in rare gas matrix has led to the identification of two vibrational modes of r-Si2C2 and one tentatively assigned vibrational mode for l-Si2C2. The only gas-phase laboratory study on Si2C2 was performed by Steglich & Maier (2015), where electronic transition spectra for both r- and l-Si2C2 isomers were tentatively assigned based on quantum chemistry calculations. Of particular interest in that study are several strong narrow bands near 5165 Å, which are assigned as the 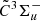 –
– 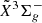 electronic transition of l-Si2C2. Theoretical calculations predict this transition system to have an oscillator strength as large as f = 0.25, which may be potentially used in optical observational studies. However, the relatively low spectral resolution and signal-to-noise ratio (S/N) level in the experimental spectra by Steglich & Maier (2015) prohibited an accurate determination of spectroscopic constants that are needed in calculating spectral profiles with different environmental temperatures.
electronic transition of l-Si2C2. Theoretical calculations predict this transition system to have an oscillator strength as large as f = 0.25, which may be potentially used in optical observational studies. However, the relatively low spectral resolution and signal-to-noise ratio (S/N) level in the experimental spectra by Steglich & Maier (2015) prohibited an accurate determination of spectroscopic constants that are needed in calculating spectral profiles with different environmental temperatures.
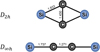 |
Fig. 1. Ground-state geometries of the rhombic (upper) and linear (lower) isomers of Si2C2. Structural parameters are taken from Steglich & Maier (2015). |
Here, we present a high-resolution laboratory study on the 5165 Å band system of l-Si2C2. The fully rotationally resolved experimental spectra allow us to accurately determine the spectroscopic constants that can be used to simulate this electronic transition system with different temperatures, making the linear Si2C2 accessible in the optical region to observers. Using the new molecular constants, we compare the simulated l-Si2C2 spectra with optical spectra of evolved carbon stars where strong MS bands of SiC2 have been observed, and tentative coincidences of the l-Si2C2 spectral features are discussed.
2. Experimental methods
The experiment setup is described in Zhang et al. (2017) and Zhao et al. (2011). In brief, small silicon-carbon clusters are produced by discharging a SiH4:C2H2:Ar (∼5:2:1000) gas mixture using a slit discharge nozzle that is constructed following the design by Motylewski & Linnartz (1999). Silicon and carbon in the precursor gas mixture are in their natural abundances, i.e., 28Si:29Si:30Si ≈ 1:0.05:0.03, and 12C:13C ≈ 1:0.01. The gas mixture with a backing pressure of ∼6 bar is supersonically expanded into a vacuum chamber through a 200 μm × 32 mm nozzle slit. A pair of radio-frequency (RF) high voltage pulses (1.8 MHz, 3000 V peak-to-peak voltage, ∼30 μs duration) with opposite phases is applied to the two jaw electrodes and the gas mixture is discharged. Direct absorption spectra of the plasma expansion are recorded using highly sensitive pulsed cavity ringdown spectroscopy. The 58 cm optical cavity consists of two plano-concave mirrors (LayerTec, reflectivity > 99.995% at 520 nm). The tunable light source is a pulsed dye laser pumped by the third harmonic output (355 nm) of a Nd:YAG laser. To record the fully resolved spectrum of l-Si2C2, the output bandwidth of the dye laser is reduced to ∼0.035 cm−1 by modifying the dye laser oscillator with one of the 1800 l mm−1 gratings working at its second-order diffraction. Experiments are operated at 10 Hz, which is determined by the pulsed laser system. The RF voltage, as well as the time sequence among the gas pulse, the discharge pulse, and the pulsed ringdown event, are optimized by maximizing the l-Si2C2 band intensity while minimizing the C2 Swan band intensity in the same wavelength region. The laser wavelength (or frequency) is calibrated online using a wavelength meter (High Finesse, WS7-60), providing an accuracy of resolved transition line positions better than 0.003 Å (or 0.01 cm−1). In our high-resolution experimental spectra, the full widths at half maximum (FWHMs) of individual transition lines are found to be ∼0.035 cm−1 (or ∼0.01 Å), nearly identical to the dye laser bandwidth used in the experiment.
3. Experimental results and analysis
Steglich & Maier (2015) has assigned four bands to the 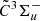 –
– 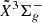 electronic transition of l-Si2C2 based on a mass-selective but low-resolution spectrum. This has guided the experimental search for the absorption spectral features of l-Si2C2 in the 5000−5300 Å range in this work. An overview of our experimental spectrum is shown in Fig. 2. Only three of the four bands reported by Steglich & Maier (2015) are detected in our experiment, located at ∼19358, 19487, and 19705 cm−1, respectively, labeled A–C in Fig. 2. These bands exhibit very similar profiles to each other at high resolution. Band A at ∼19358 cm−1 (5164 Å), assigned as the 0
electronic transition of l-Si2C2 based on a mass-selective but low-resolution spectrum. This has guided the experimental search for the absorption spectral features of l-Si2C2 in the 5000−5300 Å range in this work. An overview of our experimental spectrum is shown in Fig. 2. Only three of the four bands reported by Steglich & Maier (2015) are detected in our experiment, located at ∼19358, 19487, and 19705 cm−1, respectively, labeled A–C in Fig. 2. These bands exhibit very similar profiles to each other at high resolution. Band A at ∼19358 cm−1 (5164 Å), assigned as the 0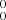 electronic origin band by Steglich & Maier (2015), is the strongest of the three. In addition, two weak bands at ∼19190 (D) and 19303 cm−1 (E) on the red side of the 0
electronic origin band by Steglich & Maier (2015), is the strongest of the three. In addition, two weak bands at ∼19190 (D) and 19303 cm−1 (E) on the red side of the 0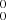 origin band are found to exhibit similar band profiles, and are also identified as l-Si2C2 absorption features following the rotational analysis, as discussed below. The two bands are likely hot band transitions involving excitation of low-frequency vibrations in the ground state of l-Si2C2. In the mass-selective spectrum presented by Steglich & Maier (2015) we found that a number of weak features in the red wing of the strong 0
origin band are found to exhibit similar band profiles, and are also identified as l-Si2C2 absorption features following the rotational analysis, as discussed below. The two bands are likely hot band transitions involving excitation of low-frequency vibrations in the ground state of l-Si2C2. In the mass-selective spectrum presented by Steglich & Maier (2015) we found that a number of weak features in the red wing of the strong 0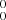 band seem recognizable, and two of them reasonably agree with the positions of bands D and E in our spectrum. All five bands (A–E) cannot be detected when only using SiH4 or C2H2 as the precursor gas (see the SiH4 plasma spectrum in Fig. 3 and the C2H2 spectrum in Zhao et al. 2011). The band at ∼19442 cm−1 mentioned by Steglich & Maier (2015), which is not detectable in our jet-cooled plasma, may be other hot band transitions for which the ground-state vibrational level cannot be efficiently populated in our jet-cooled plasma.
band seem recognizable, and two of them reasonably agree with the positions of bands D and E in our spectrum. All five bands (A–E) cannot be detected when only using SiH4 or C2H2 as the precursor gas (see the SiH4 plasma spectrum in Fig. 3 and the C2H2 spectrum in Zhao et al. 2011). The band at ∼19442 cm−1 mentioned by Steglich & Maier (2015), which is not detectable in our jet-cooled plasma, may be other hot band transitions for which the ground-state vibrational level cannot be efficiently populated in our jet-cooled plasma.
 |
Fig. 2. Medium-resolution experimental spectrum of the plasma jet-spectra of l-Si2C2. The five bands assigned to the l-Si2C2
|
As shown in Fig. 2, all the l-Si2C2 bands are contaminated to varying degrees by absorption lines of other small molecules produced in the plasma, such as C2 and SiH2. Specifically, the (0, 0) Swan bandhead of C2 is heavily blended with the 0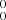 band at ∼5165 Å. To reduce the spectral congestion, we carefully optimized the experimental conditions. As shown in Fig. 3, the C2 Swan band intensity can be significantly reduced by increasing the SiH4:C2H2 concentration ratio in the gas mixture. Additional test experiments show that increasing the RF discharge voltage and carefully optimizing the experimental timing sequence can further optimize the l-Si2C2 production yield. All the experimental spectra used in the high-resolution analysis below are recorded under the optimal experimental settings.
band at ∼5165 Å. To reduce the spectral congestion, we carefully optimized the experimental conditions. As shown in Fig. 3, the C2 Swan band intensity can be significantly reduced by increasing the SiH4:C2H2 concentration ratio in the gas mixture. Additional test experiments show that increasing the RF discharge voltage and carefully optimizing the experimental timing sequence can further optimize the l-Si2C2 production yield. All the experimental spectra used in the high-resolution analysis below are recorded under the optimal experimental settings.
 |
Fig. 3. Experimental spectra of l-Si2C2, C2, and SiH2 in the 5165 Å region recorded using different precursor gas mixtures: (a) SiH4(0.2%)/C2H2(0.2%)/Ar; (b) SiH4(0.4%)/C2H2(0.2%)/Ar; (c) SiH4(0.5%)/C2H2(0.2%)/Ar; (d) SiH4(0.6%)/Ar. |
In Fig. 4, the high-resolution spectrum of the 0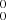 origin band is shown. Here, l-Si2C2 is a linear centro-symmetric molecule with a statistical weight 1:0 for symmetric and assymmetric rotational levels. As a consequence, only odd-N rotational levels (N the rotational quantum number) in the
origin band is shown. Here, l-Si2C2 is a linear centro-symmetric molecule with a statistical weight 1:0 for symmetric and assymmetric rotational levels. As a consequence, only odd-N rotational levels (N the rotational quantum number) in the 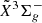 ground state can be populated. In both ground
ground state can be populated. In both ground 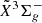 and excited
and excited 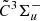 states, each N-rotational level is split into three fine spin structure levels that are defined by the total angular momentum quantum number J with J = N + 1 (f1), N (f2), and N − 1 (f3), except for N = 0 where only f1 (J = 1) exists. In our experimental spectra, the FWHMs of individual transition lines is ∼0.035 cm−1. As depicted by the spin-rotation assignments for a zoomed-in part of the 0
states, each N-rotational level is split into three fine spin structure levels that are defined by the total angular momentum quantum number J with J = N + 1 (f1), N (f2), and N − 1 (f3), except for N = 0 where only f1 (J = 1) exists. In our experimental spectra, the FWHMs of individual transition lines is ∼0.035 cm−1. As depicted by the spin-rotation assignments for a zoomed-in part of the 0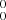 band spectrum (see Fig. 5, inset) the present spectral resolution has allowed us to fully resolve most spin-spliting fine structures in the
band spectrum (see Fig. 5, inset) the present spectral resolution has allowed us to fully resolve most spin-spliting fine structures in the 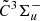 –
– 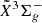 electronic transition. It should be noted that, in addition to the assigned transitions in Figs. 4 and 5, there are still some unassigned weak features slightly above the noise level of the experimental spectrum. These weak features are likely due to the 28Si-isotopologue transitions, as we used the SiH4 precursor with natural isotope abundances of silicon.
electronic transition. It should be noted that, in addition to the assigned transitions in Figs. 4 and 5, there are still some unassigned weak features slightly above the noise level of the experimental spectrum. These weak features are likely due to the 28Si-isotopologue transitions, as we used the SiH4 precursor with natural isotope abundances of silicon.
 |
Fig. 4. Experimental (upper black trace) and simulated (lower red trace) high-resolution spectra of l-Si2C2 |
 |
Fig. 5. Zoomed-in l-Si2C2 |
Least-squares fits of the high-resolution band spectra were made by using the Pgopher software (Western 2016) and a Hamiltonian for a typical 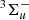 –
– 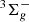 electronic transition. In the fits, individual rotational level energies with inclusion of spin-splitting effects in a 3Σ state are described by
electronic transition. In the fits, individual rotational level energies with inclusion of spin-splitting effects in a 3Σ state are described by
where B and D are rotational and centrifugal distorsion constants, respectively; λ the spin-spin interaction constant; and γ the spin-rotation interaction constant.
For the 0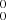 origin band, which is recorded with the highest S/N, in total about 200 spin-resolved rotational transitions are unambiguously assigned, and are fitted to the 3Σ Hamiltonian using PGOPHER. The overall root mean square (rms) of the fit is less than 0.003 cm−1, which is substantially smaller than the spectral resolution and the absolute frequency accuracy in our experiment. The resulting spectroscopic constants for both
origin band, which is recorded with the highest S/N, in total about 200 spin-resolved rotational transitions are unambiguously assigned, and are fitted to the 3Σ Hamiltonian using PGOPHER. The overall root mean square (rms) of the fit is less than 0.003 cm−1, which is substantially smaller than the spectral resolution and the absolute frequency accuracy in our experiment. The resulting spectroscopic constants for both 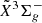 and
and 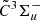 vibrational origin states are summarized in Table 1. Independent combination difference fits for
vibrational origin states are summarized in Table 1. Independent combination difference fits for 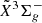 and
and 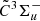 states are also performed, and this results in spectroscopic constants with differences of less than one standard deviation compared to those in Table 1. This is indicative for negligible correlations between the derived ground
states are also performed, and this results in spectroscopic constants with differences of less than one standard deviation compared to those in Table 1. This is indicative for negligible correlations between the derived ground 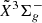 and excited
and excited 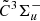 state constants listed in Table 1. Compared to the suggested values in Steglich & Maier (2015), both quantities and signs of the spin-spin interaction constants (λ), and also the magnitude of the spin-rotation interaction constants (γ), are substantially corrected by the present high-resolution data.
state constants listed in Table 1. Compared to the suggested values in Steglich & Maier (2015), both quantities and signs of the spin-spin interaction constants (λ), and also the magnitude of the spin-rotation interaction constants (γ), are substantially corrected by the present high-resolution data.
Spectroscopic constants of the ground 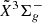 and
and 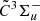 excited states of l-Si2C2.
excited states of l-Si2C2.
Bands B and C at ∼5120 and 5071 Å, respectively, are analyzed in the same way. The resulting lower state constants for both bands are nearly identical to the values obtained from the 0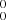 origin band. This indicates that the two bands are due to transitions from the same ground origin state, but to different vibrational levels in the upper
origin band. This indicates that the two bands are due to transitions from the same ground origin state, but to different vibrational levels in the upper 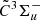 state. Therefore, in the final analysis of the two bands, we fixed the lower state constants to the values derived from the high-quality 0
state. Therefore, in the final analysis of the two bands, we fixed the lower state constants to the values derived from the high-quality 0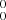 band. The resulting upper state constants are also summarized in Table 1.
band. The resulting upper state constants are also summarized in Table 1.
Band D at ∼5210 Å is the second strongest of the five observed bands. From a rotational analysis of this band, both lower and upper state levels are found to be somewhat perturbed, yielding a larger rms (0.013 cm−1) of the least-squares fit. The resulting lower state rotational constant, B″ = 0.05357 cm−1, is slightly larger than that obtained from the 0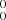 band, which is indicative of excitation of a bending vibrational mode in the ground state. For the weakest band E at ∼5180 Å, a detailed rotational analysis including the spin-splitting effect is failed due to a poorer S/N. However, a rotational contour fit on the band profile yields a set of spectroscopic constants (see Table 1) that allow us to classify this band as a hot band transition of l-Si2C2.
band, which is indicative of excitation of a bending vibrational mode in the ground state. For the weakest band E at ∼5180 Å, a detailed rotational analysis including the spin-splitting effect is failed due to a poorer S/N. However, a rotational contour fit on the band profile yields a set of spectroscopic constants (see Table 1) that allow us to classify this band as a hot band transition of l-Si2C2.
Based on the vibrational mode symmetries and the theoretically predicted vibrational frequencies (Rintelman & Gordon 2001; Presilla-Márquez et al. 1995; Fitzgerald & Bartlett 1990; Lammertsma & Guner 1988), bands B (5120 Å) and C (5071 Å) are tentatively assigned to the 5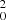 and 2
and 2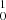 vibronic transitions, respectively. This results in the
vibronic transitions, respectively. This results in the 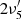 (overtone of the symmetric bending mode) and
(overtone of the symmetric bending mode) and 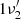 (symmetric Si-C stretching mode) vibrational level energies in the upper
(symmetric Si-C stretching mode) vibrational level energies in the upper 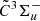 state to be 129.3 and 347.5 cm−1, respectively, both of which are significantly smaller than the theoretically predicted ground-state values (256 and 460 cm−1, respectively, in Rintelman & Gordon 2001). It should be noted that, following our assignment, the low-frequency bending vibration (
state to be 129.3 and 347.5 cm−1, respectively, both of which are significantly smaller than the theoretically predicted ground-state values (256 and 460 cm−1, respectively, in Rintelman & Gordon 2001). It should be noted that, following our assignment, the low-frequency bending vibration (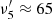 cm −1) in the
cm −1) in the 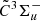 state is a quite floppy mode, very similar to the ground-state bending vibration of C3 (Schmuttenmaer et al. 1990; Schröder et al. 2018). As discussed for the case of C3 (Schröder et al. 2018), such a low-frequency bending mode will challenge high-precision theoretical calculations of the potential energy surfaces, as well as theoretical predictions of anharmonic vibrational frequencies and vibration-rotation interaction constants. As a consequence, vibrational assignments for the hot bands D (5210 Å) and E (5180 Å) cannot be made here. Even for the B (5
state is a quite floppy mode, very similar to the ground-state bending vibration of C3 (Schmuttenmaer et al. 1990; Schröder et al. 2018). As discussed for the case of C3 (Schröder et al. 2018), such a low-frequency bending mode will challenge high-precision theoretical calculations of the potential energy surfaces, as well as theoretical predictions of anharmonic vibrational frequencies and vibration-rotation interaction constants. As a consequence, vibrational assignments for the hot bands D (5210 Å) and E (5180 Å) cannot be made here. Even for the B (5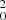 ) and C (2
) and C (2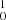 ) bands, the present assignments also need further support from theory.
) bands, the present assignments also need further support from theory.
4. Astrophysical implications
The spectroscopic constants determined from high-resolution experimental spectra allow us to reproduce the spectra of l-Si2C2 with various temperatures, which is necessary to search for possible l-Si2C2 features in the optical spectra of evolved carbon stars. We note that the spectroscopic constants are determined from the jet-cooled experimental spectra at ∼45 K, and in applications of high-temperature spectra the uncertainty of calculated transition line position may dramatically increase with increasing rotational quantum number J. For example, using the standard deviations of the spectroscopic constants in Table 1, we estimate that uncertainties of transition lines with J ∼ 120, which are the most intense lines in a 2000 K spectrum, to be ∼0.5 Å. Although the high-J transition lines are much less accurate than the experimentally measured J < 50 transitions, the calculated high-temperature spectra can be used to reproduce the band contours without rotationally resolved structures. However, we note that the l-Si2C2
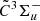 –
– 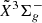 system is located in the same optical region of the MS bands of SiC2 and the Swan bands of C2, both of which are usually strong. Specifically, of the five bands recorded in the present experiment, only the weak 5181 Å band does not overlap with known SiC2 and C2 spectral features. For the others, the strongest 5164 Å band and weaker 5122 Å bands of l-Si2C2 overlap with the (0, 0) and (1, 1) bandheads of the Swan system of C2, respectively, while the 5072 Å and 5202 Å bands coincide with hot band transitions of the MS system of SiC2. As a consequence, an observational search for l-Si2C2 in this optical region could be challenging. On the other hand, the high oscillator strength for the l-Si2C2
system is located in the same optical region of the MS bands of SiC2 and the Swan bands of C2, both of which are usually strong. Specifically, of the five bands recorded in the present experiment, only the weak 5181 Å band does not overlap with known SiC2 and C2 spectral features. For the others, the strongest 5164 Å band and weaker 5122 Å bands of l-Si2C2 overlap with the (0, 0) and (1, 1) bandheads of the Swan system of C2, respectively, while the 5072 Å and 5202 Å bands coincide with hot band transitions of the MS system of SiC2. As a consequence, an observational search for l-Si2C2 in this optical region could be challenging. On the other hand, the high oscillator strength for the l-Si2C2
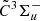 –
– 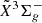 transition, f = 0.25, is approximately one order of magnitude higher than that for the MS system of SiC2 (f = 0.018) (Steglich & Maier 2015) and the Swan system of C2 (f = 0.031) (Brooke et al. 2013), making a careful search in the optical spectra of evolved carbon stars still worthwhile.
transition, f = 0.25, is approximately one order of magnitude higher than that for the MS system of SiC2 (f = 0.018) (Steglich & Maier 2015) and the Swan system of C2 (f = 0.031) (Brooke et al. 2013), making a careful search in the optical spectra of evolved carbon stars still worthwhile.
In Figs. 6 and 7, the simulated spectral features of l-Si2C2, and those of SiC2 and C2, are compared to the optical spectra of V Hya and IRAS 12311−23509, respectively. Both observational data sets are obtained by directly digitizing the spectra presented by Sarre et al. (2000) and Lloyd Evans et al. (2000), and have been known to contain strong MS band features of SiC2.
 |
Fig. 6. Comparison of the l-Si2C2A, D, and E bands (red dashed curves) with the spectrum of V Hya (N) (thick black curve; see Sarre et al. 2000). The simulated spectra of SiC2 and C2 bands (thin black curves) are also plotted. A rotational temperature of ∼1300 K is used in the spectral simulations of l-Si2C2, SiC2, and C2. |
 |
Fig. 7. Comparison of the l-Si2C2A–E bands (red dashed curves) with the reduced optical spectrum of IRAS 12311−3509 (see Lloyd Evans et al. 2000). The simulated spectra of SiC2 and C2 bands (thin black curves) are also plotted, with the 2 |
In Fig. 6, the spectrum of V Hya is dominated by the absorption bands of SiC2 and C2. Due to the saturated absorption of the C2 Swan band system, there is almost no photon flux at wavelengths shorter than 5165 Å. In the simulated absorption spectra of l-Si2C2, SiC2, and C2, a rotational temperature of ∼1300 K and a spectral resolution of ∼2 Å are used. The chosen temperature of 1300 K has been used by Sarre et al. (2000) to reproduced the MS band profiles of SiC2 in a similar N-type star Y Hya. It can be seen from Fig. 6 that the 5210 Å band of l-Si2C2 fully overlaps with the 5200 Å band of SiC2, where the latter is slightly saturated. For the other two l-Si2C2 bands in the shadowed region of Fig. 6, tentative coincidences can be found. Despite the strong 0 band of l-Si2C2 at 5165 Å heavily blends with the (0, 0) Swan band of C2, the red-degraded absorption wing in the 5165−5185 Å region agrees reasonably well with the 0
band of l-Si2C2 at 5165 Å heavily blends with the (0, 0) Swan band of C2, the red-degraded absorption wing in the 5165−5185 Å region agrees reasonably well with the 0 band profile of l-Si2C2. Meanwhile, a blended weak absorption feature at ∼5185 Å also tentatively matches the weak 5181 Å band of l-Si2C2.
band profile of l-Si2C2. Meanwhile, a blended weak absorption feature at ∼5185 Å also tentatively matches the weak 5181 Å band of l-Si2C2.
Similar comparisons can be made with the emission spectrum of IRAS 12311−23509. The spectrum of IRAS 12311−23509 in Fig. 7 is adopted from Lloyd Evans et al. (2000), which has been reduced by subtracting a scaled spectrum of a reference carbon star HD 98767 (with negligible SiC2) from IRAS 12311−23509 to emulate the removal of the contribution from the underlying star (see Lloyd Evans et al. 2000 for details). For the simulated emission spectra of l-Si2C2, SiC2, and C2 here, a rotational temperature of ∼300 K and a spectral resolution of ∼2 Å are chosen based on the discussion on the SiC2 MS bands by Lloyd Evans et al. (2000). As seen in the shaded region of Fig. 7, the red-degraded wing of the 5165 Å feature and the weak 5180 Å feature also tentatively match the simulated l-Si2C2 bands. In addition, a careful comparison shows that the emission feature at 5131 Å slightly deviates from the (1, 1) bandhead of C2 (5129 Å), but better matches the l-Si2C2 band at this position (see the vertical solid and dashed lines in Fig. 7). Both the 5165 and 5131 Å features in the reduced spectrum of IRAS 12311−23509 are slightly red-degraded, which is not reproducible by the C2 Swan bands. Considering that the C2 features should be weakened by subtracting the reference spectrum of HD 98767, the 5165 and 5131 Å features may be partially contributed by l-Si2C2 emission bands.
It should be noted that the laboratory spectrum in the present experiment is recorded in a supersonic jet condition, and only two weak hot bands are measurable due to the jet-cooling condition. In the stellar atmospheres of evolved carbon stars where the excitation temperature of SiC2 is found to range from 102 to 103 K, vibrational hot bands of small molecules can exhibit comparative intensities. For example, the excitation temperature of SiC2 have been interpreted as ∼1300 K in the spectrum of N-type stars. The low-lying vibrational modes of l-Si2C2, ν2, ν4, and ν5, are predicted by ab initio calculations at the MBPT(2)/6-311G* level of theory (Presilla-Márquez et al. 1995) as ∼493 cm−1, ∼278 cm−1, and 117 cm−1, respectively. These low-lying modes, and their combination modes, must be efficiently excited with an environmental temperature of 1300 K in such typical stellar atmospheres. As a consequence, if the tentative assignments of l-Si2C2 spectral features above are correct, there will be a series of additional hot band transitions with considerable intensities in the 5000−5300 Å wavelength region. Further laboratory experimental studies with higher excitation temperatures and high-level theoretical calculations on the l-Si2C2 hot band transitions will help to search and classify additional spectral features in the stellar atmospheres of carbon-rich stars.
5. Conclusions
The high-resolution laboratory spectra of the l-Si2C2
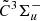 –
– 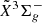 electronic transition system has allowed us to fully resolve the spin-splitting fine structures in individual rotational transitions. As a consequence, accurate spectroscopic constants including the spin-spin interaction constants and spin-rotation interaction constants are determined for both
electronic transition system has allowed us to fully resolve the spin-splitting fine structures in individual rotational transitions. As a consequence, accurate spectroscopic constants including the spin-spin interaction constants and spin-rotation interaction constants are determined for both 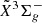 and
and 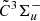 states. Using the determined spectroscopic constants, calculated optical spectra with different rotational excitation temperatures are compared to the stellar spectra of evolved carbon stars where the triatomic SiC2 are known to be abundant. Because of the heavily overlapped SiC2 and C2 bands, only some tentative coincidences with the l-Si2C2 bands can be found. Further laboratory studies on additional hot band transitions of l-Si2C2, as well as high-level theoretical calculations, will help find an unambiguous identification of l-Si2C2 in stellar atmospheres of carbon-rich stars.
states. Using the determined spectroscopic constants, calculated optical spectra with different rotational excitation temperatures are compared to the stellar spectra of evolved carbon stars where the triatomic SiC2 are known to be abundant. Because of the heavily overlapped SiC2 and C2 bands, only some tentative coincidences with the l-Si2C2 bands can be found. Further laboratory studies on additional hot band transitions of l-Si2C2, as well as high-level theoretical calculations, will help find an unambiguous identification of l-Si2C2 in stellar atmospheres of carbon-rich stars.
Acknowledgments
The author is grateful for the financial support from National Natural Science Foundation of China (21773221 and 21827804), the National Key R&D program of China (2017YFA0303502), and the Fundamental Research Funds for the Central Universities of China (WK2340000078). Prof. Linnartz (Leiden, the Netherlands) made the slit discharge nozzle available in the present experiment.
References
- Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 1999, ApJ, 516, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Brooke, J. S., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spectr. Radiat. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Gottlieb, C., Guélin, M., Thaddeus, P., & Vrtilek, J. 1989, ApJ, 341, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., McCarthy, M. C., Gottlieb, C. A., et al. 2015, ApJ, 806, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, G. B., & Bartlett, R. J. 1990, Int. J. Quantum Chem., 38, 121 [Google Scholar]
- Gobrecht, D., Cristallo, S., Piersanti, L., & Bromley, S. T. 2017, ApJ, 840, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Lammertsma, K., & Guner, O. F. 1988, J. Am. Chem. Soc., 110, 5239 [CrossRef] [Google Scholar]
- Lloyd Evans, T., Hurst, M. E., & Sarre, P. J. 2000, MNRAS, 319, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. D. S., & Charnley, S. B. 2010, MNRAS, 302, 793 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Gottlieb, C. A., & Cernicharo, J. 2019, J. Mol. Spect., 356, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1926, PASP, 38, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Motylewski, T., & Linnartz, H. 1999, Rev. Sci. Instrum., 70, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Young, K. H., Gottlieb, C. A., et al. 2011, ApJS, 193, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Presilla-Márquez, J. D., Gay, S. C., Rittby, C. M. L., & Graham, W. R. M. 1995, J. Chem. Phys., 102, 6354 [NASA ADS] [CrossRef] [Google Scholar]
- Rintelman, J. M., & Gordon, M. S. 2001, J. Chem. Phys., 115, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Sanford, R. F. 1926, PASP, 38, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P. J., Hurst, M. E., & Evans, T. L. 1996, ApJ, 471, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P., Hurst, M., & Evans, T. 2000, MNRAS, 319, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schmuttenmaer, C., Cohen, R., Pugliano, N., et al. 1990, Science, 249, 897 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schröder, B., Doney, K. D., Sebald, P., Zhao, D., & Linnartz, H. 2018, J. Chem. Phys., 149, 014302 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Welty, D. E., Thorburn, J. A., & York, D. G. 2007, ApJS, 168, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Steglich, M., & Maier, J. P. 2015, ApJ, 801, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Thaddeus, P., Cummins, S., & Linke, R. 1984, ApJ, 283, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Western, C. 2016, J. Quant. Spectr. Radiat. Transf., 186, 221 [Google Scholar]
- Wienkoop, M., Mürtz, P., Schumann, P.-C., Havenith, M., & Urban, W. 1997, Chem. Phys., 225, 17 [CrossRef] [Google Scholar]
- Zhang, Q., Zhu, B., Zhang, D., et al. 2017, Rev. Sci. Instrum., 88, 126108 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D., Haddad, M. A., Linnartz, H., & Ubachs, W. 2011, J. Chem. Phys., 135, 044307 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Ground-state geometries of the rhombic (upper) and linear (lower) isomers of Si2C2. Structural parameters are taken from Steglich & Maier (2015). |
| In the text | |
 |
Fig. 2. Medium-resolution experimental spectrum of the plasma jet-spectra of l-Si2C2. The five bands assigned to the l-Si2C2
|
| In the text | |
 |
Fig. 3. Experimental spectra of l-Si2C2, C2, and SiH2 in the 5165 Å region recorded using different precursor gas mixtures: (a) SiH4(0.2%)/C2H2(0.2%)/Ar; (b) SiH4(0.4%)/C2H2(0.2%)/Ar; (c) SiH4(0.5%)/C2H2(0.2%)/Ar; (d) SiH4(0.6%)/Ar. |
| In the text | |
 |
Fig. 4. Experimental (upper black trace) and simulated (lower red trace) high-resolution spectra of l-Si2C2 |
| In the text | |
 |
Fig. 5. Zoomed-in l-Si2C2 |
| In the text | |
 |
Fig. 6. Comparison of the l-Si2C2A, D, and E bands (red dashed curves) with the spectrum of V Hya (N) (thick black curve; see Sarre et al. 2000). The simulated spectra of SiC2 and C2 bands (thin black curves) are also plotted. A rotational temperature of ∼1300 K is used in the spectral simulations of l-Si2C2, SiC2, and C2. |
| In the text | |
 |
Fig. 7. Comparison of the l-Si2C2A–E bands (red dashed curves) with the reduced optical spectrum of IRAS 12311−3509 (see Lloyd Evans et al. 2000). The simulated spectra of SiC2 and C2 bands (thin black curves) are also plotted, with the 2 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.