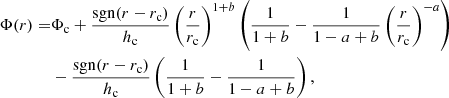EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 635 (March 2020) A&A, 635 (2020) L9 Full HTML
Free Access
Issue
A&A
Volume 635, March 2020
Article Number L9
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202037682
Published online 11 March 2020

© ESO 2020

1. Introduction

Recent high-resolution observations revealed a great diversity of protoplanetary disk morphologies, in which multiple rings or gaps, cavities, and spirals appear as common features (e.g., Andrews et al. 2011, 2018; ALMA Partnership 2015; Avenhaus et al. 2018; Long et al. 2018, 2019). Although alternative mechanisms have been proposed, such as gravitational instability in massive disks (e.g., Nelson et al. 1998; Dong et al. 2015a), gravitational perturbation by stellar or substellar companion or pressure variations induced by shadowing effects (Montesinos et al. 2016), disk substructures are usually interpreted as indirect evidence of embedded planets (Dong et al. 2015b). Spiral structures in circumstellar disks around young stars have first been discovered in the scattered light emission of submicron grains (e.g., Fukagawa et al. 2004; Muto et al. 2012) and in submillimeter thermal dust emission (e.g., Pérez et al. 2016; Dong et al. 2018; Huang et al. 2018). Observations of spirals in a gas tracer (CO) remain very rare, the more famous examples being AB Aur (Tang et al. 2012, 2017), HD142527 (Christiaens et al. 2014), MWC758 (Boehler et al. 2018), TW Hya (Teague et al. 2019), and HD100453 (Rosotti et al. 2019).

In this context, GG Tau A is a very peculiar system. Located at 150 pc (Gaia Collaboration 2016, 2018), GG Tau A is considered as the prototype of the young T Tauri multiple system. The system consists of a single star GG Tau Aa and a close-binary star GG Tau Ab1/Ab2 with separations of 35 au and 4.5 au in the plane of the sky, respectively (Di Folco et al. 2014). The triple star is surrounded by a Keplerian outer disk (hereafter the circumbinary or CB disk), tidally truncated at an inner radius of ∼180 au, which consists of a dense gas and dust ring extending from about 180 au up to 260 au, and an outer disk extending out to ∼800 au (Dutrey et al. 1994). This disk is the most massive of the Taurus region with a total mass of ∼0.15 M⊙ (∼10% of the stellar mass). At the outer edge of the dense ring, a remarkable “hot spot” has been reported with ALMA observations by Dutrey et al. (2014) as additional CO emission, with a temperature Tb = 40 K that is twice as high as that of the surrounding gas in the ring. Tang et al. (2016) have also shown that several dips in the radial profile of CO emission could represent unresolved partial gaps (or spiral patterns) in the outer disk between about 250 au and 400 au.

In this Letter, we present new ALMA CO(2–1) observations of the environment of GG Tau A revealing large spirals out to 5−6″ that seem to be physically connected to the hot spot. After we describe the observation and data reduction in Sect. 2, the results are presented in Sect. 3. We then discuss the presence of embedded planet(s) in the CB disk of GG Tau A in Sect. 4.

2. Observations and data reduction

ALMA observations of project 2018.1.00532.S (PI Denis Alpizar) were carried on November 8, 13, and 18, 2018, with 44 to 47 useful antennas in four scheduling blocks. The projected baselines range from 15 m to 1398 m, and the total time on source is about three hours. Data were calibrated in the CASA1 software (Version 5.4.0) using the pipeline. Quasars J0510+1800 and J0423−0120 were used for flux and bandpass calibration. Phase and amplitude calibration was made using J0440+1437. The calibrated data were regrided in velocity to the LSR frame using the “cvel” task, and exported through UVFITS format to the GILDAS2 package for further data processing.

Proper motion corrections were applied using values derived from Gaia release 2. GG Tau A is a multiple star whose proper motions are inaccurate in Gaia. However, Gaia provides accurate parallax and proper motions (μRA = 12.67 ± 0.19 mas yr−1 and μDec = −20.40 ± 0.11 mas yr−1) for GG Tau Ba, the brightest star of the GG Tau B binary located 10″ south. The Gaia parallax indicates a distance of D = 150.1 ± 2.2 pc. We assumed that the proper motions and distance of GG Tau A are those of GG Tau Ba. The reference of the coordinates, which corresponds to the GG Tau ring center, are RA = 04:32:30.3448 and Dec = 17:31:40.59 at epoch J2000.0.

Imaging and deconvolution was made using the IMAGER program in GILDAS, with robust weighting. Amplitude and phase self-calibration was performed on the continuum signal, and the derived corrections were applied to the spectral line data. Deconvolution was made using the a multiscale hogbom-like Clean algorithm, and the images were cleaned down to the rms noise level. The channel spacing is 0.079 km s−1, and the effective spectral resolution is 0.16 km s−1. The angular resolution is 0.31″ × 0.25″ at PA 26.7°. The rms noise level is 1.35 mJy beam−1, or 0.40 K at this resolution.

3. Results

Figure 1 shows the maps of the brightness of continuum emission, the integrated area, the peak brightness, and its radial variation after deprojection and azimuthal averaging of the CO(2–1) emission. The observations reveal at least two broad spiral arms connecting the material of the ring to the outer disk, and possibly extending inward down to the central cavity. The brighter and longer arm (northwest, hereafter NW) is more clearly seen between 1.7″ and 2.7″ (255−400 au), with a peak emission in the NW region Tb, peak = 16−18 K and a mean contrast of about 50% with respect to the interarm values (10−12 K). It seems to vanish at PA ∼ 30°. The southeast (hereafter SE) spiral arm is dimmer and shallower, and extends out to about 3.5″ (530 au), with a maximum brightness temperature Tb, peak = 14−16 K and an average contrast of about 35%. Lower level spiral patterns are also visible out to 5.4″ with Tb, peak = 8−9 K.

thumbnail Fig. 1.

Upper panel: maps of the continuum brightness temperature (left) and integrated brightness of CO(2–1) (right). Lower panel: map of the peak brightness temperature of CO(2–1) (left) and its radial dependence on the plane of the disk (right). The white ellipses indicate the approximate inner and outer edge of the dust ring at 180 au and 260 au, respectively. The beam size is 0.31″ × 0.25″, and PA = 27° is shown in the lower left corners. Vertical lines mark the brightness at 1.9″, 3.0″ and 4.1″, respectively. The error bars indicate the azimuthal dispersion of the brightness (the high values near 1.8″ are due to the hot spot).

We note that spirals are better seen in the peak brightness image than in the integrated area. The CO(2–1) emission being optically thick, the peak brightness is representative of the gas temperature while the integrated area is more complex to interpret. This suggests that the observed spirals correspond to warmer gas located well above the mid-plane (at 2 to 3 scale heights, as directly observed in the “Flying Saucer” by Dutrey et al. 2017). An increase in surface density, as occurs in the spiral density waves created by a planet, will result in a higher CO opacity, and thus in the τ = 1 layer located at higher altitude, where the temperature is higher because of the moderate vertical temperature gradient (Phuong et al. 2020).

The inner main spiral may take its origin near the location of the CO(6–5) hot spot that Dutrey et al. (2014) interpreted as resulting from hot gas that is accreted onto an unseen protoplanet. The hot spot is also detected in our CO(2–1) image at the same location and with the same brightness (40 K).

To confirm a planetary origin for this spiral pattern, we used the prescription of a spiral wave from Rafikov (2002) and Muto et al. (2012). This spiral wake is derived under the hypothesis of linearity or a weakly nonlinear regime,

Φ ( r ) = Φ c + sgn ( r − r c ) h c ( r r c ) 1 + b ( 1 1 + b − 1 1 − a + b ( r r c ) − a ) − sgn ( r − r c ) h c ( 1 1 + b − 1 1 − a + b ) , $$ \begin{aligned} \Phi (r) = &\Phi _{\rm c}+\frac{\mathrm{sgn}(r-r_{\rm c})}{h_{\rm c}}\left(\frac{r}{r_{\rm c}}\right)^{1+b}\left(\frac{1}{1+b}-\frac{1}{1-a+b}\left(\frac{r}{r_{\rm c}}\right)^{-a}\right) \nonumber \\&-\frac{\mathrm{sgn}(r-r_{\rm c})}{h_{\rm c}}\left(\frac{1}{1+b}-\frac{1}{1-a+b}\right), \end{aligned} $$(1)

where a and b are the exponents of disk rotation and sound speed radial profiles, and hc is the disk aspect ratio at the location of the planet (rc, Φc). This method has been applied on near-IR (NIR) observations (see, e.g., Benisty et al. 2015, who applied this method to fit the NIR spiral arms observed in MWC758).

Figure 2 displays our results. We superimposed our optimum model of the inner and outer arm spirals on the CO(2–1) peak brightness image. The planet, hereafter GG Tau Ac, was assumed to be at the hot spot position (PA = 125°, and a deprojected radial distance of rc = 1.93″ or 290 au). The disk is in Keplerian rotation (a = 3/2) and the temperature was found to fall as ∼r−1 beyond the ring edge, and slightly flatter inside (see Dutrey et al. 2014; Phuong et al. 2020). As a compromise, b, the exponent of the radial dependence of the sound speed Cs, was thus taken to be 0.45. We used a scale height Hc(r) = 17 × (r/200 au)+1 as derived from the CO analysis by Phuong et al. (2020) (this value corresponds to a kinetic temperature of 15 K), which leads to a constant disk aspect ratio hc = Hc/r of 0.085. The only free parameter in our spiral fit was therefore the height of the τ = 1 layer in CO in scale height units along the spiral, X. We assumed that X is independent of r. The apparent shape of the spirals was derived by rotating the theoretical spiral pattern from the disk PA of 7°, and correcting for the height of the emitting layer above the disk plane.

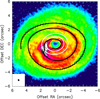thumbnail Fig. 2.

Best inner and outer spirals associated with the putative planet (hot spot) observed by Dutrey et al. (2014). The origin of the spirals is given by the CO(2–1) maximum peak brightness. The best spiral is obtained by assuming that the CO emission arises from 2.5 scale height above the mid-plane. The white ellipses indicate the approximate inner and outer edge of the dust ring. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.

We found the shape to be sensitive to the value of X, but rather insensitive to those of b and to the exact position of the planet. Figure 3 presents the effect of the altitude of the CO layer on the shapes of the spiral wakes. X = 2.5 provides an excellent match to the spine of the NW spiral arm. However, the SE arm is more marginally reproduced.

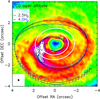thumbnail Fig. 3.

Dependence on scale height of the spiral induced by the planet 1 (GG Tau Ac), assuming the planet is at 290 au. The white ellipses indicate the approximate inner and outer edge of the dust ring at 180 au and 260 au, respectively. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.

4. Discussion

Since the first observations of the GG Tau A system, two major points have remained unexplained. So far, there is no satisfactory model that explains the presence of a ring that is both narrow (width of about 80 au) and very massive (about 0.12 M⊙, a factor 3 to 5 more than most of T Tauri disks). Modeling the 13CO(1–0) observations of the Plateau de Bure Interferometer (PdBI), Dutrey et al. (1994) reported that the best representation is obtained by mimicking the ring with a Gaussian of width ∼80 au followed by a tail of CO gas distribution extending up to 800 au with a volume density radial index of 2. At a radius of 260 au (outer edge of the ring), the density contrast with the ring maximum is at least a factor of 10. These results were confirmed by Guilloteau et al. (1999) using higher angular resolution 13CO(2–1) observations.

Using a sympletic code, Beust & Dutrey (2005, 2006) analyzed the dynamics and evolution of the whole hierarchical system GG Tau A and GG Tau B with the circumbinary disk. Located at 10″ in the plane of sky of GG Tau A, GG Tau B is also a binary of total mass ∼0.17 M⊙ and projected separation 1.48″ (White et al. 1999). Beust & Dutrey (2006) found that a few possible orbital configurations exist for the two binaries that peal out the outer part of the large CB disk orbiting GG Tau A due to periastron tidal interactions. Although this study may explain the radial shape of the gas and dust distribution (namely a ring and a shallow outer disk), it does not explain why the ring remains impressively massive, because the distribution results from mass erosion at each periastron passage.

A confinement mechanism would provide a better explanation. One possibility would be the confinement by a (proto-)planet located at the outer edge of the ring. Dutrey et al. (2014) suggested that the CO(6–5) hot spot located near the outer edge of the ring was due to such an accreting planet. Their observations (at a resolution of ∼0.25″ or 37 au), confirmed by those of Tang et al. (2016) in CO(3–2), however, rule out a large gap opened by a massive planet, as is observed in some cases around stars (the case of HD142527 by Boehler et al. 2017, being one of the most obvious). Based on the limited angular resolution (which can still hide an unresolved gap), Dutrey et al. (2014) found that the mass of the putative planet cannot be significantly higher than the mass of Neptune.

The theory of planet migration in CB disks reveals that gap opening depends on several parameters including the planet mass, but also the disk aspect ratio and its viscosity. Only a planet of the mass of Neptune or lower tends to open a partial gap similar to what is observed in CO images. In presence of a Neptune-mass planet, it is also expected that the dynamical evolution is stable, with the planet orbiting near the edge of the cavity formed by the binary (Pierens & Nelson 2008). The possible evolution outcomes of a Neptune-mass planet migrating in a CB disk are presented as a function of disk parameters in Pierens & Nelson (2013). For a disk with constant aspect ratio (as seems to be the case for GG Tau A, see Phuong et al. 2020) and a viscous parameter α ∼ 0.001, Pierens & Nelson (2008) reported halting of inward migration due to the formation of a narrow ring located in between the edge of the central cavity and the planet orbit. This can occur provided the migration rate is higher than the viscous drift rate, which therefore requires the planet to not open a deep gap. The high density in the ring resulting from the disk material being confined from both the inner and outer sides can significantly increase the positive contribution to the wave torque exerted by the disk material located within the planet orbit. As migration proceeds, the positive inner Lindblad torque continuously increases until the inner and outer torques are in balance, at which point migration is halted. In the context of the GG tau A, this scenario would be clearly consistent with (i) the confinement of the ring and (ii) the fact that the hot spot is located at the outer edge of the ring. A situation like this was also found by Pierens & Nelson (2013) in the case of Kepler 16 simulations.

Pierens & Nelson (2008) reported that in case of a more massive object, for example, a Jupiter-like planet, this cannot occur. The planet would tend to orbit within a large cavity corresponding to the cavity formed by the binary plus the gap formed by the planet. This would lead to the continuous inward migration of the planet until it becomes trapped in a mean motion resonance with the binary. The evolution of circumbinary planets that open such a deep gap is thought to be dynamically unstable.

Alternative scenarii for explaining the stopping of inward migration that involve either the corotation torque or Lindblad torque reversal once the planet eccentricity has reached a sufficiently high value would rather predict a final planet position located at the inner edge of the ring. The spiral wave model of GG Tau Ac, at the location of the hot spot, is a nice confirmation of the scenario of confinement presented above. However, Fig. 1 also reveals CO spirals beyond the outer spiral generated by GG Tau Ac, with a particularly prominent SE pattern at the distance of 3.3″, and a shallower arm in the southwest (hereafter SW) quadrant at about 5″.

We therefore propose an explanation of these additional spirals by considering first another planet in the system, GG Tau Ad. A good model, using the same parameters as for GG Tau Ac except for the planet position, is obtained by locating GG Tau Ad at radius of ∼3.0″ (450 au) and PA of ∼118°, as illustrated by Fig. 4. In this configuration, we note that GG Tau Ad is close to the 2:1 mean motion resonance compared to GG Tau Ac, reinforcing the dynamical stability of the system. This configuration is already observed in the case of PDS 70 (Haffert et al. 2019), where simulation of the system suggests that the two planets are likely in 2:1 mean motion resonance (Bae et al. 2019).

thumbnail Fig. 4.

Spirals induced by the three putative planets, GG Tau Ac (black), GG Tau Ad (cyan), and GG Tau Ae (blue). The white ellipses indicate the approximate inner and outer edge of the dust ring. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.

Similarly, the outer SW spiral may be nicely explained by a third planet (GG Tau Ae) located around 4.0″ (600 au) and PA of ∼215°, near the 3:1 mean motion resonance with GG Tau Ac. Although first-order resonances are expected to be much stronger than second-order ones to balance the inner disk torque and are therefore more efficient in halting inward migration, the stability of GG Tau Ae may nevertheless be reinforced by the 3:2 resonance with the second planet GG Tau Ad. This resonance is by far the most frequent resonant configuration observed among Kepler multiple exoplanet systems (Fabrycky et al. 2014).

Pierens & Nelson (2013) also reported that a planetary configuration similar to the observed one is stable only if the outer planet(s) are less massive than the inner one. The lack of clear gaps in the gas distribution at radii of 450 au and 600 au is also compatible with this constraint.

In conclusion, GG Tau A appears as an extraordinary hierarchical system surrounded by one or more CB planets in resonant orbits. Such a complex and rich system might partially result from gravitational instabilities and clearly opens many questions about planet formation in multiple systems at large distance from the central star.

Acknowledgments

Anne Dutrey and Stéphane Guilloteau thank Mike Simon who initiated GG Tau studies a long time ago using the (3 antennas) IRAM array. This work was supported by “Programme National de Physique Stellaire” (PNPS) and “Programme National de Physique Chimie du Milieu Interstellaire” (PCMI) from INSU/CNRS. This research made use of the SIMBAD database, operated at the CDS, Strasbourg, France. This Letter makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00532.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea) in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. N. T. Phuong and P. N. Diep acknowledge financial support from World Laboratory, Rencontres du Viet Nam, the Odon Vallet fellowships, and Vietnam National Space Center. This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.99-2018.325.

References

  1. ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
  4. Avenhaus, H., Quanz, S. P., Garufi, A., et al. 2018, ApJ, 863, 44 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bae, J., Zhu, Z., Baruteau, C., et al. 2019, ApJ, 884, L41 [NASA ADS] [CrossRef] [Google Scholar]
  6. Benisty, M., Juhasz, A., Boccaletti, A., et al. 2015, A&A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Beust, H., & Dutrey, A. 2005, A&A, 439, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Beust, H., & Dutrey, A. 2006, A&A, 446, 137 [Google Scholar]
  9. Boehler, Y., Weaver, E., Isella, A., et al. 2017, ApJ, 840, 60 [NASA ADS] [CrossRef] [Google Scholar]
  10. Boehler, Y., Ricci, L., Weaver, E., et al. 2018, ApJ, 853, 162 [Google Scholar]
  11. Christiaens, V., Casassus, S., Perez, S., van der Plas, G., & Ménard, F. 2014, ApJ, 785, L12 [Google Scholar]
  12. Di Folco, E., Dutrey, A., Le Bouquin, J.-B., et al. 2014, A&A, 565, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dong, R., Zhu, Z., & Whitney, B. 2015a, ApJ, 809, 93 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dong, R., Zhu, Z., Rafikov, R. R., & Stone, J. M. 2015b, ApJ, 809, L5 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dong, R., Najita, J. R., & Brittain, S. 2018, ApJ, 862, 103 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dutrey, A., Guilloteau, S., & Simon, M. 1994, A&A, 286, 149 [NASA ADS] [Google Scholar]
  17. Dutrey, A., di Folco, E., Guilloteau, S., et al. 2014, Nature, 514, 600 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dutrey, A., Guilloteau, S., Piétu, V., et al. 2017, A&A, 607, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fukagawa, M., Hayashi, M., Tamura, M., et al. 2004, ApJ, 605, L53 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Guilloteau, S., Dutrey, A., & Simon, M. 1999, A&A, 348, 570 [NASA ADS] [Google Scholar]
  24. Haffert, S. Y., Bohn, A. J., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Huang, J., Andrews, S. M., Pérez, L. M., et al. 2018, ApJ, 869, L43 [NASA ADS] [CrossRef] [Google Scholar]
  26. Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17 [NASA ADS] [CrossRef] [Google Scholar]
  27. Long, F., Herczeg, G. J., Harsono, D., et al. 2019, ApJ, 882, 49 [NASA ADS] [CrossRef] [Google Scholar]
  28. Montesinos, M., Perez, S., Casassus, S., et al. 2016, ApJ, 823, L8 [NASA ADS] [CrossRef] [Google Scholar]
  29. Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
  30. Nelson, A. F., Benz, W., Adams, F. C., & Arnett, D. 1998, ApJ, 502, 342 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pérez, L. M., Carpenter, J. M., Andrews, S. M., et al. 2016, Science, 353, 1519 [NASA ADS] [CrossRef] [Google Scholar]
  32. Phuong, N. T., Dutrey, A., Diep, P. N., et al. 2020, ArXiv e-prints [arXiv:2001.08147] [Google Scholar]
  33. Pierens, A., & Nelson, R. P. 2008, A&A, 483, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Pierens, A., & Nelson, R. P. 2013, A&A, 556, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Rafikov, R. R. 2002, ApJ, 569, 997 [NASA ADS] [CrossRef] [Google Scholar]
  36. Rosotti, G. P., Tazzari, M., Booth, R. A., et al. 2019, MNRAS, 486, 4829 [NASA ADS] [CrossRef] [Google Scholar]
  37. Tang, Y. W., Guilloteau, S., Piétu, V., et al. 2012, A&A, 547, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Tang, Y.-W., Dutrey, A., Guilloteau, S., et al. 2016, ApJ, 820, 19 [NASA ADS] [CrossRef] [Google Scholar]
  39. Tang, Y.-W., Guilloteau, S., Dutrey, A., et al. 2017, ApJ, 840, 32 [NASA ADS] [CrossRef] [Google Scholar]
  40. Teague, R., Bae, J., Huang, J., & Bergin, E. A. 2019, ApJ, 884, L56 [NASA ADS] [CrossRef] [Google Scholar]
  41. White, R. J., Ghez, A. M., Reid, I. N., & Schultz, G. 1999, ApJ, 520, 811 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Upper panel: maps of the continuum brightness temperature (left) and integrated brightness of CO(2–1) (right). Lower panel: map of the peak brightness temperature of CO(2–1) (left) and its radial dependence on the plane of the disk (right). The white ellipses indicate the approximate inner and outer edge of the dust ring at 180 au and 260 au, respectively. The beam size is 0.31″ × 0.25″, and PA = 27° is shown in the lower left corners. Vertical lines mark the brightness at 1.9″, 3.0″ and 4.1″, respectively. The error bars indicate the azimuthal dispersion of the brightness (the high values near 1.8″ are due to the hot spot).
In the text
thumbnail Fig. 2.

Best inner and outer spirals associated with the putative planet (hot spot) observed by Dutrey et al. (2014). The origin of the spirals is given by the CO(2–1) maximum peak brightness. The best spiral is obtained by assuming that the CO emission arises from 2.5 scale height above the mid-plane. The white ellipses indicate the approximate inner and outer edge of the dust ring. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.
In the text
thumbnail Fig. 3.

Dependence on scale height of the spiral induced by the planet 1 (GG Tau Ac), assuming the planet is at 290 au. The white ellipses indicate the approximate inner and outer edge of the dust ring at 180 au and 260 au, respectively. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.
In the text
thumbnail Fig. 4.

Spirals induced by the three putative planets, GG Tau Ac (black), GG Tau Ad (cyan), and GG Tau Ae (blue). The white ellipses indicate the approximate inner and outer edge of the dust ring. The peak brightness has been multiplied by r $ \sqrt{r} $ and the color scale is saturated to optimize the visibility of spiral patterns. Contours are given where the color is saturated.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.