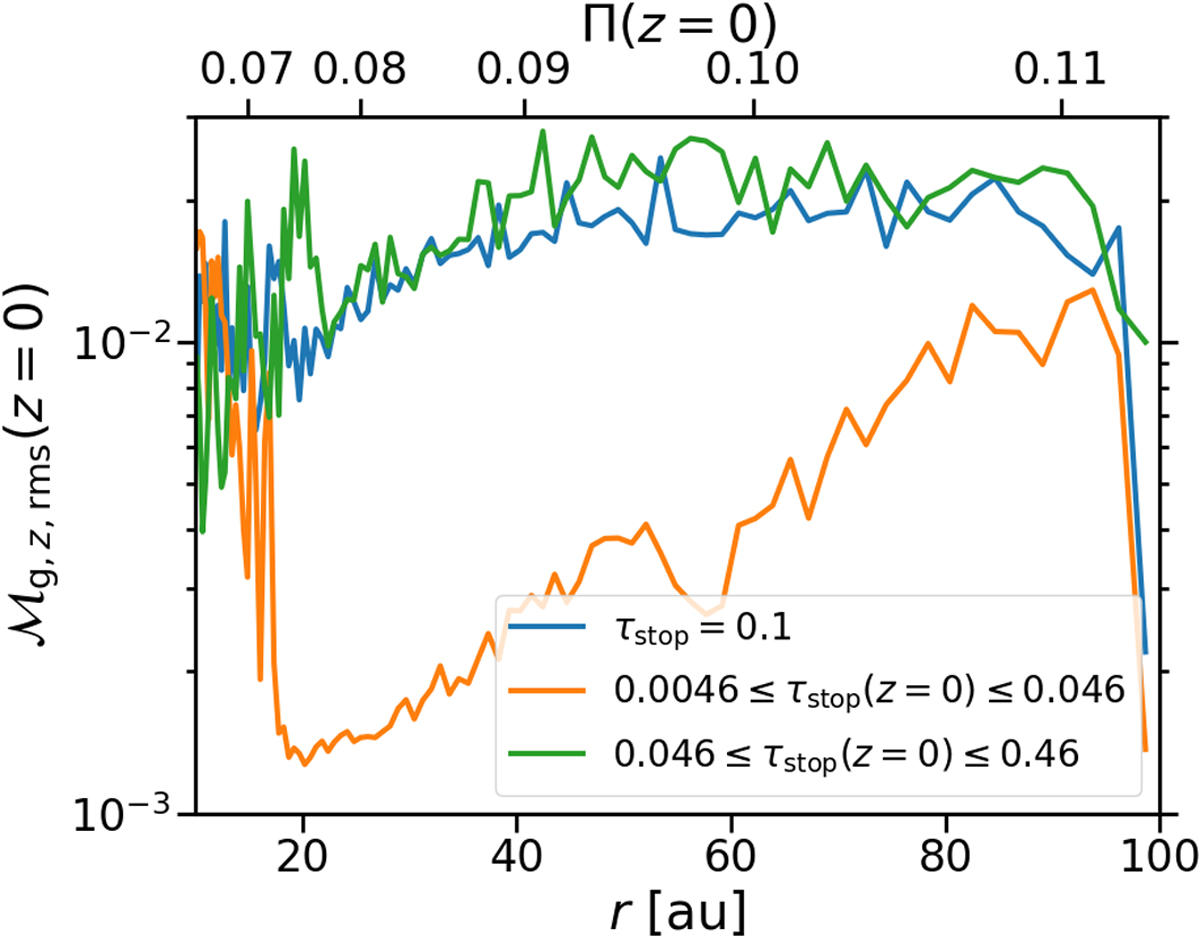
Rootmean square of in the midplane as a function of r (lower abscissa) and the dimensionless gas pressure gradient parameter Π in the midplane (upper abscissa). The root mean square is calculated using the mass-weighted mean over 500 yr after an equilibrium value of the dust scale height is reached. In the simulation adi_Z=0.02_Lr=90au_taustop=0.1 (blue line), in which the dimensionless dust stopping time τ_stop is fixed at 0.1, the Mach number increases with the pressure gradient parameter if Π ≲ 0.09, but is approximately constant if the pressure gradient is stronger. The Mach number in this one and the simulation adi_Z=0.02_Lr=90au (green line), in which the stopping time increases from 0.046 to 0.46, is comparable at all radii. That is, the turbulent strength does not depend significantly on the stopping time in this stopping time regime. The Mach number is lower overall, but depends more strongly on the radius in the simulation adi_Z=0.02_Lr=90au_a=3mm (orange line) in which the stopping time ranges from 0.0046 to 0.046. In this regime, the turbulent strength increases with both the strength of the pressure gradient and the stopping time.