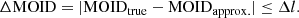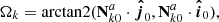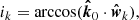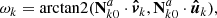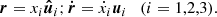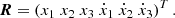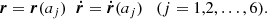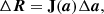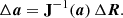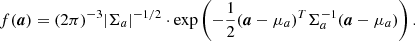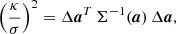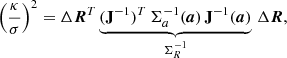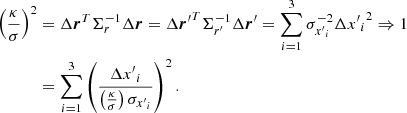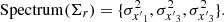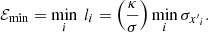| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201936502 | |
| Published online | 23 December 2019 | |
Minimum orbital intersection distance: an asymptotic approach
1
Space Dynamics Group, ETSIAE, Technical University of Madrid, Pza. Cardenal Cisneros 3, 28040 Madrid, Spain
e-mail: josemanuel.hedo@upm.es
2
Aerospace Engineering Department, Khalifa University of Science and Technology, PO Box 127788, Abu Dhabi, UAE
e-mail: elena.fantino@ku.ac.ae
Received:
13
August
2019
Accepted:
6
October
2019
The minimum orbital intersection distance (MOID) is used as a measure to assess potential close approaches and collision risks between astronomical objects. Methods to calculate this quantity have been proposed in several previous publications. The most frequent case is that in which both objects have elliptical osculating orbits. When at least one of the two orbits has low eccentricity, the latter can be used as a small parameter in an asymptotic power series expansion. The resulting approximation can be exploited to speed up the computation with negligible cost in terms of accuracy. This contribution introduces two asymptotic procedures into the SDG-MOID method for the computation of the MOID developed by the Space Dynamics Group (SDG) of the Technical University of Madrid and presented in a previous article, it discusses the results of performance tests and their comparisons with previous findings. The best approximate procedure yields a reduction of 40% in computing speed, without degrading the accuracy of the determinations. This result suggests that some benefits can be obtained in applications involving massive distance computations, such as in the analysis of large databases, in Monte Carlo simulations for impact risk assessment, or in the long-time monitoring of the minimum orbital intersection distance between two objects.
Key words: minor planets / asteroids: general / methods: numerical / celestial mechanics
© ESO 2019
1. Introduction
The minimum orbital intersection distance (MOID) at a given epoch between two objects orbiting a common primary is the distance between the closest points of their osculating orbits. The problem of computing the MOID is as old as Kepler’s laws. However, the need for a quick and accurate solution has increased as its role in several branches of Celestial Mechanics and Astrodynamics has become more and more prominent. Nowadays, the MOID is used primarily to provisionally discard objects from large space debris catalogs when collisions with a given target can be excluded (Hoots et al. 1984; Woodburn et al. 2009; Casanova et al. 2014), and to predict possible close encounters of asteroids and comets with the planets (mainly, Earth and Mars for the asteroids, and Jupiter for the comets) prior to the study of their dynamics (Milani et al. 1989, 2000; Harris & Bailey 1998; Wlodarczyk 2013). Regarding the space debris problem, according to Gorno (2019), “the ever-growing population of space debris (or space junk), especially in the LEO zone, is posing serious issues to the survival of man-made objects in space. Every mission planner has to take into account the possibility of the satellite colliding with relatively small pieces of debris, which, traveling at orbital speeds, could jeopardize the survival of the mission”. The Center for Space Standards and Innovation (CSSI) offers the Satellite Orbital Conjunction Reports Assessing Threatening Encounters in Space (SOCRATES) service (Kelso & Alfano 2006), intended to help satellite operators avoid undesired close approaches through advanced mission planning. According to Kelso & Alfano (2006), “hundreds of conjunctions within one kilometer occur every week, with little or no intervention, putting billions of dollars of space hardware at risk, along with their associated missions”. As for the close planetary encounters, the MOID between the asteroid and Earth turns out to be one of the most important parameters when assessing the impact risk (Sitarski 1968).
The calculation of the MOID involves two Keplerian orbits, represented by their classical orbital elements. The orbital elements change over time as a result of perturbations. In the case of the asteroids, for example, Sekhar et al. (2016) show that Einstein’s General Theory of Relativity predicts a significant orbital precession if the object has both a moderately low perihelion and a small semimajor axis, and observe that the effect “could play an important role in the calculations pertaining to MOID and close-encounter scenarios in the case of certain small solar system bodies (depending on their initial orbital elements)”. Due to the time evolution of the orbital elements, the MOID itself is a function of time. Thus, understanding the evolution of the MOID over long time frames is important for impact risk assessment. In the case of asteroids, such MOID monitoring makes it possible to better assess the risk of a possible impact with Earth. Recently, Monte Carlo methods have been implemented to calculate the impact probability of an asteroid with Earth (Rickman et al. 2014).
The orbit of an asteroid is known with an uncertainty that depends on the quality of the observations and that reflects in the uncertainty of the MOID. For its assessment, the covariance matrix must be propagated, with the inherent requirement to explicitly compute the derivatives of the MOID with respect to some variables. Bonanno (2000) uses an approximate analytical expression to obtain the required partial derivatives of the MOID. Alternatively, the differentiation can be carried out numerically, in which case, it is beneficial to employ fast, accurate, and safe algorithms to calculate the MOID without increasing the uncertainty brought by the observational data. In this respect, it is worth remembering that a singularity appears in the computation of the uncertainty of the MOID in the orbit-crossing case. This problem was studied and solved by Gronchi & Tommei (2007).
Using models currently accepted for the long-term dynamical evolution of the Solar System, the MOID computation makes it possible to determine the cometary impact rates on the Moon and on the terrestrial planets during the late heavy bombardment (Rickman et al. 2017). Fast MOID computation is in high consideration and demand also to facilitate the analysis of large catalogs of objects. Obviously, accuracy is also a key issue. Here, the latter is meant to encompass both precision (low random errors) and trueness (low systematic errors) (ISO Central Secretary 1994).
In summary, a fast and accurate MOID computation method is an asset in several common problems. Many methods for computing the MOID have been published in the literature over the past seven decades. The majority are approximate numerical methods (Sitarski 1968; Dybczinski et al. 1986). However, more recently, algebraic (Kholshevnikov & Vassiliev 1999; Gronchi 2005) and analytical (Bonanno 2000; Armellin et al. 2010) approaches have been established, and some hybrid methods have appeared (see, e.g., Derevyanka 2014).
The Space Dynamics Group (SDG) of the Technical University of Madrid developed a fast and accurate numerical method for the computation of the MOID. This method is called SDG-MOID (Hedo et al. 2018) and is based on two algorithms. Algorithm 1 determines the distance between a point and an ellipse in three-dimensional space by composing two orthogonal distances: the distance from the point to its orthogonal projection onto the plane of the ellipse and the distance from the ellipse to the projected point. The former is trivial to determine, whereas the latter (which, for the sake of brevity, will be referred to as the in-plane distance) can be obtained in closed form with elementary functions only under specific circumstances1, the general scenario requiring application of an iterative method to the solution (as accurate as desired) of a transcendental equation. Algorithm 2 calculates the minimum distance between two confocal ellipses in the following way: one of the two ellipses is discretized in a finite set of points by means of a uniform partition of the interval [0, 2π], where its eccentric anomaly is defined – see Eqs. (3) and (4) below– and the corresponding distances to the other ellipse are computed by means of Algorithm 1: this yields a discrete function approximation of the distance. Then, the partition intervals containing the local minima of the distance are identified, the distance function in these intervals is minimized using the golden-section search, and the minimum minimorum is selected.
This work considers asymptotic expansions for the computation of the in-plane distance component in Algorithm 1 of the SDG-MOID method. These asymptotic procedures are tested to assess the gain in computing speed, the corresponding accuracy loss, and hence the benefits of their introduction: they are worth adopting if a positive balance between advantages and disadvantages is achieved. Our tests employed the NEODyS (Near Earth Object – Dynamics Site) catalog (NEODyS Consortium 2011) for MJD 58600 to compute the position uncertainty and the Earth MOID of NEOs (Near Earth Objects). Improvements of Algorithm 2 are also being undertaken: the aim is to preserve accuracy by decreasing the resolution of the discretization, and by limiting it to the vicinity of the minimum minimorum. However, these enhancements are under development and out of the scope of this contribution.
The paper is structured as follows. Section 2 features an illustration of the mathematical foundations of the two asymptotic expansions, here proposed as approximate procedures to compute the in-plane distance component. These methods constitute one-parameter families of procedures, the parameter being the number of terms retained in the expansions. Section 3 gives an assessment of the minimum MOID accuracy (trueness) needed in order not to deteriorate the total uncertainty of the starting orbital data. Section 4 presents the results of the accuracy and computing speed tests on the two families of asymptotic expansions and compares them with the performance of the exact in-plane distance determination carried out with SDG-MOID. The family exhibiting the best performance was tested for accuracy and computing speed on the Earth MOID of NEOs, and the results were compared with the SDG-MOID determinations. Section 5 features the benefits that the asymptotic expansions can bring when applied to the time monitoring of the MOID through the presentation of an application to the space debris problem. The paper closes (Sect. 6) with a summary and a discussion of the relevance of the results.
2. Mathematical foundations
This section summarizes the theory of asymptotic expansions in powers of a small parameter. It describes in detail the application of two such methods to the determination of the in-plane distance component.
2.1. Asymptotic expansions in powers of a small parameter
Given the function f : ℝn + 1 ↦ ℝ, and
with x ∈ ℝ : x ≪ 1 the independent variable, z ∈ ℝ the dependent variable, and yk ∈ ℝ (k = 1, 2, …, n) a set of parameters, the asymptotic expansion of z in powers of x is defined as:
where N is the order of the expansion, meaning, the highest power of x among the terms that appear in the expansion, and ci ∼ O(1) (i = 0, 1, 2, …, N) are the functional coefficients. N is used to control the accuracy of the asymptotic expansion. The advantages of the truncation of the expanded function are a higher speed of the computation of the approximate function compared with the original function, and a more treatable mathematical expression for algebraic manipulation and computation. The main drawback consists of the introduction of truncation errors, meaning, the expansion only provides an approximation to true values. The smaller the value of x and the higher the value of N, the better the approximation of z obtained from the corresponding truncation. The procedure is useful if the improvement in computing speed compensates for the inherent loss of accuracy.
Several choices for the asymptotic expansion exist. In this paper, we consider the two most suitable options, meaning, an expansion in the critical eccentric anomaly, and an expansion in the minimum distance. They are described here below.
2.2. Expansion in the critical eccentric anomaly
Let 𝔢 be an ellipse in the standard Cartesian parametric representation relative to its symmetry axes:
where u is the eccentric anomaly, a is the semi-major axis, and e ≪ 1 is the eccentricity. Let P be a coplanar point with Cartesian coordinates (α, β) in the previous axes. Find the eccentric anomaly u* that minimizes the distance d(P, E):E ∈ 𝔢, defined as
This problem was addressed as part of the presentation of the SDG-MOID method (Hedo et al. 2018). The main conclusions of that study can be summarized as follows:
-
d(u) is 2π-periodic, and, therefore, it has an even number of extreme points. All global maxima and minima are always critical points.
-
The critical points u* of Eq. (5) (equivalent to the critical points of its square) must satisfy the transcendental equation
Equation (6) admits a minimum of two and a maximum of four solutions in the interval [0, 2π) (including, in the latter case, a possible double root resulting from the coincidence between one maximum and one minimum). Solving Eq. (6) is equivalent to solving a polynomial equation of degree four. The latter admits exact solutions, but, as pointed out in Hedo et al. (2018), the loss of precision due to the rounding errors may change their character, for example, from real to complex. Since the interest is in real solutions, this approach cannot be employed.
-
The minima must also satisfy the condition
The geometric study showed that the absolute minimum (and the absolute maximum) always exists. Let ℳ = {ui, i = 1, 2, …, m} be the set of eccentric anomalies corresponding to the minima (they satisfy Eqs. (6) and (7)). Then,
-
the eccentric anomaly u* yielding the minimum distance in ℳ is
The symbol ≤ takes into account the case in which multiple u*s are associated with the same minimum distance.
The results can be summarized as follows:
-
If e = 0 (circular orbit), the solution is simply u* = arctan(β/α).
-
If e > 0 and α = 0 or β = 0 (P on a symmetry axis of 𝔢), closed-form solutions for u* always exist.
-
If e > 0, α ≠ 0 and β ≠ 0, numerical techniques constitute the only method to solve the equation, with the additional requirement that u* be in the same quadrant as P. In particular, iterative methods offer the best results (i.e., the fastest and the most accurate), and a suitable seed for such numerical approximations is u0 = arctan(β/α).
Equation (6) defines an implicit function u*(a, e, α, β); and, when e ≪ 1, a truncated series expansion in powers of e is convenient:
The parameter N ∈ ℕ controls the finite number of terms in the truncated series, whereas the ci(a, α, β) coefficients must be computed to approximate the critical eccentric anomaly.
Substituting u* as given by Eq. (9) into Eq. (6) yields the expansion in powers of e. Since 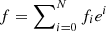 must satisfy Eq. (6), the ci’s can be calculated by successive cancellation of the fi’s in increasing order. This problem was solved for N up to 6 using the MAPLE 2017.3 math software. The result is:
must satisfy Eq. (6), the ci’s can be calculated by successive cancellation of the fi’s in increasing order. This problem was solved for N up to 6 using the MAPLE 2017.3 math software. The result is:
After substituting Eqs. (10)–(14) into Eq. (9), the Euclidean distance function (Eq. (5)) with 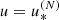 yields the following parametric family of procedures for the approximate computation of the minimum distance:
yields the following parametric family of procedures for the approximate computation of the minimum distance:
in which N = 0, 2, 4, 6 is the parameter. The selection of N is a trade-off between efficiency and accuracy: the lower its value, the more mathematically treatable the final expression contained in Eq. (5), but the lower the accuracy of the resulting distance approximation.
2.3. Minimum distance expansion
Following (Hedo et al. 2018), an alternative approach to the computation of the critical points of the distance function consists of solving the following system of two algebraic equations:
If e = 0, the solution corresponding to the minimum distance is trivial:
If 0 < e ≪ 1, let us consider the following decomposition:
Substituting Eqs. (20) and (21) with Eqs. (18) and (19) into Eqs. (16) and (17) leads to a system of two equations to be solved with respect to ξ and η:
Hence, the square of the distance function (Eq. (5)) can be written as:
A truncated series expansion in powers of e of this function2 is
in which the di(a, α, β) coefficients need to be specified. In this contribution, the di(a, α, β)s were computed for N up to six using the MAPLE 2017.3 math software:
The distance approximation can then be computed by substituting the required number of terms up to N = 0, 2, 4, 6 in Eq. (25). Again, the lower the order N, the more mathematically treatable the final expression (Eq. (24)), and the lower the accuracy obtained for the distance.
3. Accuracy assessment
The original SDG-MOID method introduces negligible errors in the distance computation, meaning, it does not increase the uncertainty of the original orbital data. For an approximate MOID, like the one provided by the methods presented here, the accuracy should not be lower than the minimum uncertainty of the data, the best performance in terms of computing speed being achieved when the former is close to the latter.
The uncertainty of the state vector is usually expressed by its six-dimensional confidence ellipsoid. However, since only the position accuracy is relevant here, we limited our attention to the corresponding three-dimensional confidence (or uncertainty) ellipsoid. Its major axis is aligned very closely with the velocity vector (its direction is tangent to the trajectory), whereas the other two axes define the plane that is normal to the orbit.
The proposed methods were tested on the computation of the Earth MOIDs of Near Earth Objects. In this case, Earth is the primary object, and its orbital eccentricity constitutes the small parameter. Since the Earth’s position vector is known with the highest possible precision (Gronchi et al. 2006), the uncertainty of the MOID is entirely determined by the uncertainty of the orbit of the NEO, expressed by its covariance matrix (Milani et al. 1989).
The space objects of interest are tracked by dedicated observatories, and their data are systematically computed and recorded in catalogs. Each entry has an associated uncertainty (affecting both position and velocity) due to several factors, such as instrument precision, shortage of measurements, truncations, round-off errors (Gronchi et al. 2006). The orbit determination of NEOs is carried out through either radar tracking or optical observations. The former technique is characterized by low measurement errors, but it is applicable to a limited number of objects. The majority of NEOs are monitored by optical observations, which are affected by larger errors owing to the more limited visibility conditions. The NEOs whose orbits are determined by radio telescopes are associated with the smallest position uncertainties, at the level of 100 m, whereas optical determinations are affected by much larger (by at least two orders of magnitude) position uncertainties.
The minimum accuracy required by the approximate algorithm must be greater than the smallest uncertainty in the position vector. Therefore, the smallest error in length (maximum tolerance) is the size of the shortest semiaxis of the 1σ position’s confidence ellipsoids obtained for the subset of NEOs observed with radar tracking. These values were calculated from the covariance matrix data in equinoctial elements of the first 281 radar-tracked Near Earth Asteroids (NEAs)3 of the NEODyS catalogue using the algorithm illustrated in Appendix A. The results are the lengths of the three semiaxes of each 1σ position’s confidence ellipsoid. On the other hand, the geometric mean of the two smallest semiaxes is the radius of a circle whose area is equal to that of the section (ellipse) of the ellipsoid with the plane containing the two shortest axes. This holds because the minimum distance line is in this plane, but its exact orientation is a priori not known. It should be noted that the longest axis – corresponding to the maximum uncertainty due to instability in the sense of Lyapunov – is tangent to the orbit, whereas the MOID always corresponds to a line that is normal to both orbits.
Table 1 is a statistical summary of the data. The several rows contain the minimum, the average, and the maximum values of the sets formed by the three semiaxis lengths (i.e., shortest, intermediate, and longest) of the position’s confidence ellipsoids, and by the geometric mean of the shortest and intermediate semiaxes.
Summary of the statistical properties of the 1σ position’s confidence ellipsoids of the first 281 radar-tracked NEAs published in the NEODyS database.
The minimum of the shortest is 6.711 × 10−10 au (∼100 m). Therefore, Δl = 6.711 × 10−10 au is the tolerance to be used to assess the level of trueness for the approximate computation of the Earth MOIDs of all the objects of the NEODyS database:
4. Tests
4.1. Approximate computation of the in-plane distance for low-eccentricity ellipses
The two families of procedures proposed here for the computation of the distance between a low-eccentricity ellipse and a coplanar point, meaning, 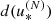 (Eq. (15)) and
(Eq. (15)) and 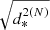 (Eq. (25)), respectively, were coded and tested. Simulations were run on an Intel® Core™ I7-8750H at 2.2 GHz processor with 32 MiB of RAM. Accuracy and computing speed tests were executed on an ellipse with unit semimajor axis (a = 1) and eccentricity close to that of Earth’s orbit (e = 1.671022 × 10−2), and a set of 616 points evenly distributed in the first quadrant and belonging to a family of concentric circles with radii respectively larger, equal to and smaller than the semimajor axis of the ellipse. The center of the circles coincides with the center of the ellipse. The points form a grid with polar coordinates
(Eq. (25)), respectively, were coded and tested. Simulations were run on an Intel® Core™ I7-8750H at 2.2 GHz processor with 32 MiB of RAM. Accuracy and computing speed tests were executed on an ellipse with unit semimajor axis (a = 1) and eccentricity close to that of Earth’s orbit (e = 1.671022 × 10−2), and a set of 616 points evenly distributed in the first quadrant and belonging to a family of concentric circles with radii respectively larger, equal to and smaller than the semimajor axis of the ellipse. The center of the circles coincides with the center of the ellipse. The points form a grid with polar coordinates 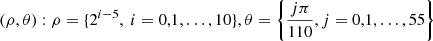 .
.
4.1.1. Numerical errors
Table 2 gives a summary of the basic statistical properties, meaning, the minimum, the average, and the maximum value, of the absolute error of the in-plane distances from the selected elliptical orbit to each of the 616 test points (see text). The in-plane distances were obtained with the two families of approximate algorithms at different expansion orders. We observe that the 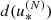 algorithm is far more accurate than
algorithm is far more accurate than 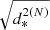 at the same N. With only two terms, it introduces no appreciable error; the
at the same N. With only two terms, it introduces no appreciable error; the 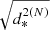 algorithm requires four terms to reach a comparable performance.
algorithm requires four terms to reach a comparable performance.
Basic statistical properties (minimum, average, and maximum) of the in-plane distance error ϵ of the two approximate algorithms, meaning, 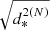 and
and 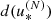 , at different expansion orders.
, at different expansion orders.
4.1.2. Execution speed
Table 3 features results and statistics regarding the execution times for the test cases described above. We observe that the two approximate methods are at least ten times faster than the exact distance determination, there are no appreciable differences in execution time between the two approximate algorithms (neither by family nor by number of terms), and the computing speed is inversely proportional to the expansion order.
Execution times per in-plane distance determination as obtained with the approximate algorithms 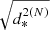 and
and 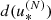 at different expansion orders (Cols. 2–9) and the computing time required by the exact distance determination d (Col. 10).
at different expansion orders (Cols. 2–9) and the computing time required by the exact distance determination d (Col. 10).
4.2. Approximate computation of the MOID for low-eccentricity ellipses
The 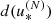 algorithms exhibit similar execution times but better accuracy than the
algorithms exhibit similar execution times but better accuracy than the 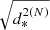 methods. For this reason, the former one-parameter family, with the expansion order as the parameter, is the method of choice to replace the exact in-plane distance computation method in SDG-MOID. Tests were performed to assess accuracy and execution speed of this method relative to the exact SGD-MOID determination. The simulations consist of the computation of the Earth MOID of objects belonging to the NEODyS database.
methods. For this reason, the former one-parameter family, with the expansion order as the parameter, is the method of choice to replace the exact in-plane distance computation method in SDG-MOID. Tests were performed to assess accuracy and execution speed of this method relative to the exact SGD-MOID determination. The simulations consist of the computation of the Earth MOID of objects belonging to the NEODyS database.
4.2.1. Numerical errors for the approximate SDG-MOID
Table 4 reports the most significant statistical properties of the results of the accuracy tests, meaning, the minimum, the average, and the maximum absolute error of the MOID computed using the 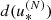 algorithm at different expansion orders. The high accuracy (trueness) obtained with N = 2 is the most remarkable outcome.
algorithm at different expansion orders. The high accuracy (trueness) obtained with N = 2 is the most remarkable outcome.
Basic statistical properties (minimum, average, and maximum) of the Earth MOID error ϵ resulting from application of the 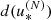 family of approximate algorithms at different expansion orders relative to the exact Earth SDG-MOID for objects in the NEODyS database.
family of approximate algorithms at different expansion orders relative to the exact Earth SDG-MOID for objects in the NEODyS database.
4.2.2. Execution speed for the approximate SDG-MOID
Table 5 shows the average execution times per distance computation resulting from several determinations – both exact and approximate – of Earth MOID of NEODyS objects, as well as some descriptive statistics and relevant ratios. On average, the 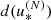 algorithm with N = 2 is 40% faster than the exact SDG-MOID. This result constitutes a remarkable enhancement.
algorithm with N = 2 is 40% faster than the exact SDG-MOID. This result constitutes a remarkable enhancement.
Average execution times per distance determination of the complete NEODyS database as obtained with the exact SDG-MOID (first column) and with the 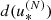 algorithm at N = 6, 4, 2, 0 (remaining columns).
algorithm at N = 6, 4, 2, 0 (remaining columns).
5. Application: time monitoring of the MOID
The first application of the algorithms described in this paper was within a numerical tool called DROMOID (Gorno 2019) that monitors the MOID of two LEO objects (e.g., a satellite and a space debris object) over time. DROMOID implements the DROMO orbital propagator (Urrutxua et al. 2016)4 and the SDG-MOID algorithm. The evolution of the two orbits over a selected time period and at a given sampling resolution was computed using DROMO. Then, the osculating classical orbital elements of the two objects were obtained at each sampling time and used to determine the evolution of the MOID. One of the advantages of the tool is that in input it accepts the space debris ephemerides of NASA’s Two-Line-Element (TLE) database, which are always accessible and are considered the most reliable public source of orbital data. The time performance of DROMOID depends on the time resolution. However, the 2-weeks propagation of 19 664 valid TLE ephemerides at a sampling resolution of 1 h takes only 9.5 h on an I5 processor. DROMOID can efficiently predict close encounters, as shown by the following example, for the detailed analysis of which the reader is referred to Gorno (2019). According to SOCRATES, the Space Technology EXperiments (STEX) satellite and a debris from the CBERS 1 satellite had a close approach with a minimum range of 0.638 km on June 21st 2019 at 18:57:58.129 UTC.
The two orbits were propagated with DROMOID over a period of seven days starting at noon on June 16 2019 (58 650.5 MJD) and using a sampling interval of one minute. The resulting MOID is smaller than three kilometers during the whole propagation period, and it oscillates very rapidly between zero and three kilometers, the amplitude of the variations getting smaller (below two kilometers) approximately between day two and day six, and the oscillations reaching the highest frequency between day five and day six (see Fig. 1). When the MOID is zero, the two orbits are crossing each other, but this does not necessarily correspond to a collision, because the latter requires time coincidence5. Hence, SDG-MOID can be reliably employed as part of the first processing stage of a more complex tool for the real-time monitoring of thousands of space debris in the determination of the risk of collision with a spacecraft.
 |
Fig. 1. MOID between STEX and CBERS 1 between day five and day six after 12 p.m. on June 16 2019 (58650.5 MJD). Simulations made with DROMOID. |
6. Conclusions
Two families of algorithms for the approximate computation of the distance from an ellipse to a coplanar point are proposed for the case of low-eccentricity ellipses: they consist of asymptotic expansions in terms of eccentricity, respectively, of the critical eccentric anomaly and the squared distance. The family based on the critical eccentric anomaly (Sect. 2.2, Eq. (15)) is more accurate (at the same expansion order). Since the speeds of execution are very similar for the two families, this method has been chosen for further tests involving the computation of the MOID. The algorithm was implemented in the SDG-MOID software and tested against the exact Earth MOID of NEOs. When N = 2, the absolute Earth MOID error is always smaller than 6.4 × 10−11 au = 9.53 m, meaning, ten times smaller than the assumed tolerance. The speed improvement over the exact Earth MOID is 40%.
This remarkable result makes the method based on the critical eccentric anomaly the ideal choice for all the applications in which a fast and accurate MOID computation is required. For the processing of large catalogs of objects, for the long-term monitoring of the MOID between two objects in the presence of perturbations, for the assessment of the impact probability through Monte Carlo simulations, and for the propagation of the uncertainty of the observational data.
NEAs have perihelion below 1.3 au and aphelion above 0.983 au. Some NEAs are classified as Potentially Hazardous Asteroids (PHAs), i.e., asteroids whose MOID is lower than 0.05 au, and whose absolute magnitude is 22 or brighter (see also Novaković 2013). PHAs are associated with a higher probability of experiencing a close encounter with Earth.
Acknowledgments
The work of J. M. Hedo, E. Fantino and J. Peláez has been funded by Khalifa University of Science and Technology’s internal grants FSU-2018-07 and CIRA-2018-85. Additionally, the authors acknowledge the support provided by the project entitled Dynamical Analysis of Complex Interplanetary Missions with reference ESP2017-87271-P, sponsored by Spanish Agencia Estatal de Investigación (AEI) of Ministerio de Economía, Industria y Competitividad (MINECO), and by European Fund of Regional Development (FEDER).
References
- Armellin, R., Lizia, P. D., Berz, M., & Makino, K. 2010, Celest. Mech. Dyn. Astron., 107, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Arsenault, J. L., Ford, K. C., & Koskela, P. E. 1970, AIAA J., 8, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, C. 2000, A&A, 360, 411 [NASA ADS] [Google Scholar]
- Broucke, R. 1970, A&A, 6, 173 [NASA ADS] [Google Scholar]
- Casanova, D., Tardioli, C., & Lemaître, A. 2014, MNRAS, 442, 3235 [NASA ADS] [CrossRef] [Google Scholar]
- Danielson, D. A., Sagovac, C. P., Neta, B., & Early, L. W. 1995, Semianalytic Satellite Theory, Tech. rep., Naval Postgraduate School [CrossRef] [Google Scholar]
- Derevyanka, A. E. 2014, J. Samara State Tech. Univ., Ser. Phys. Math. Sci., 4, 144 [Google Scholar]
- Dybczinski, P. A., Jopek, T. J., & Serafin, R. A. 1986, Celest. Mech. Dyn. Astron., 345 [CrossRef] [Google Scholar]
- Gorno, M. 2019, Master’s Thesis, ETSI Aeronáutica y del Espacio, Universidad Politécnica de Madrid [Google Scholar]
- Gronchi, G. F. 2005, Celest. Mech. Dyn. Astron., 93, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Gronchi, G. F., & Tommei, G. 2007, Discrete Contin. Dyn. Syst. Ser. B, 7, 755 [CrossRef] [Google Scholar]
- Gronchi, G. F., Tommei, G., & Milani, A. 2006, Proc. Int. Astron. Union, 2, 3 [CrossRef] [Google Scholar]
- Harris, N., & Bailey, M. 1998, MNRAS, 297, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Hedo, J. M., Ruíz, M., & Peláez, J. 2018, MNRAS, 479, 4108 [CrossRef] [Google Scholar]
- Hoots, F. R., Crawford, L. L., & Roehrich, R. L. 1984, Celest. Mech. Dyn. Astron., 33, 143 [CrossRef] [Google Scholar]
- ISO Central Secretary 1994, Accuracy (trueness and precision) of Measurement Methods and Results, Standard ISO 5725–1:1994(en) (Geneva, Switzerland: International Organization for Standardization) [Google Scholar]
- Kelso, T., & Alfano, S. 2006, in Modeling, Simulation, and Verification of Space-based Systems III, Int. Soc. Opt. Photon., 6221, 622101 [CrossRef] [Google Scholar]
- Kholshevnikov, K. V., & Vassiliev, N. N. 1999, Celest. Mech. Dyn. Astron., 75, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Carpino, M., Hahn, G., & Nobili, A. 1989, Icarus, 78, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Chesley, S. R., & Valsecchi, G. B. 2000, Planet. Space Sci., 48, 945 [NASA ADS] [CrossRef] [Google Scholar]
- NEODyS Consortium 2011, NEODyS-2 Near Earth Objects – Dynamic Site, https://newton.spacedys.com/neodys/, last accessed July 2019 [Google Scholar]
- Novaković, B. 2013, Asteroids (Berlin: Springer), 45 [CrossRef] [Google Scholar]
- Rickman, H., Wiśniowski, T., Wajer, P., Gabryszewski, R., & Valsecchi, G. 2014, A&A, 569, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickman, H., Wiśniowski, T., Gabryszewski, R., et al. 2017, A&A, 598, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sekhar, A., Werner, S., Hoffmann, V., et al. 2016, AAS/Division for Planetary Sciences Meeting Abstracts, 48 [Google Scholar]
- Sitarski, G. 1968, Acta Astron., 18, 171 [NASA ADS] [Google Scholar]
- Urrutxua, H., Sanjurjo-Rivo, M., & Peláez, J. 2016, Celest. Mech. Dyn. Astron., 124, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesel, W. E. 2003, Modern Orbit Determination, (Beavercreek: Aphelion Press), 2652 [Google Scholar]
- Wlodarczyk, I. 2013, MNRAS, 434, 3055 [NASA ADS] [CrossRef] [Google Scholar]
- Woodburn, J., Coppola, V., & Stoner, F. 2009, Adv. Astronaut. Sci., 135, 1157 [Google Scholar]
Appendix A: Estimation of the positional uncertainty
A.1. Keplerian and Equinoctial elements
Let  be the Barycentric Celestial Reference Frame (BCRF). Let k be the index associated with an object orbiting the Sun, and ak, ek, Ωk, ik, ωk, Mk its Keplerian orbital elements with respect to the BCRF (Table A.1). The size and shape of the orbit are defined by the semi-major axis ak and the eccentricity ek, respectively, whereas the elements of the set {Ωk, ik, ωk} are the three Euler angles defining the orientation of the perifocal reference frame
be the Barycentric Celestial Reference Frame (BCRF). Let k be the index associated with an object orbiting the Sun, and ak, ek, Ωk, ik, ωk, Mk its Keplerian orbital elements with respect to the BCRF (Table A.1). The size and shape of the orbit are defined by the semi-major axis ak and the eccentricity ek, respectively, whereas the elements of the set {Ωk, ik, ωk} are the three Euler angles defining the orientation of the perifocal reference frame  in the BCRF. Mk is the mean anomaly that serves to position the object on the orbit at the epoch (temporary data). The basis
in the BCRF. Mk is the mean anomaly that serves to position the object on the orbit at the epoch (temporary data). The basis 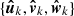 of the perifocal reference frame as well as the rotation matrix [Qk0] (which is formed by the components of these unit vectors) are functions of the elements of the triple {Ωk, ik, ωk}, and they can be easily computed.
of the perifocal reference frame as well as the rotation matrix [Qk0] (which is formed by the components of these unit vectors) are functions of the elements of the triple {Ωk, ik, ωk}, and they can be easily computed.
Keplerian orbital elements.
Let 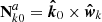 be the vector to the ascending node of object k relative to the Fx0y0 plane in the BCRF. The angles in Table A.1 are defined as
be the vector to the ascending node of object k relative to the Fx0y0 plane in the BCRF. The angles in Table A.1 are defined as
where t0 is the epoch, τk is the epoch of pericenter passage, μ is the gravitational parameter of the Sun, and arctan2(y, x) is the angle measured in counterclockwise direction from 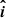 to
to 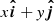 and defined in the interval [0, 2π].
and defined in the interval [0, 2π].
When sin ik = 0, Ωk is undefined, because so is the nodal line. When ek = 0, ωk is undefined, because so is the pericenter. The singularities that arise in many applications, for example, orbit determination and orbit propagation, under these circumstances are well known (Broucke 1970). Given the high frequency of occurrences of low-inclination and/or low-eccentricity orbits in the Solar System, an alternative set of elements are often employed with respect to which the above equations and expressions are non-singular. It is the set of so-called equinoctial elements ai (i = 1, 2, …, 6) (Arsenault et al. 1970) (see Table A.2). Every orbit can be associated with an equinoctial reference frame 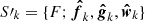 , where
, where 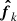 and
and 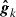 define the orbital plane, and the angle between
define the orbital plane, and the angle between 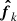 and
and 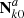 is the longitude of ascending node. The first and the sixth equinoctial elements are the semimajor axis and the mean longitude, respectively. The second and the third are the components of the eccentricity vector (
is the longitude of ascending node. The first and the sixth equinoctial elements are the semimajor axis and the mean longitude, respectively. The second and the third are the components of the eccentricity vector (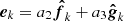 ) in the equinoctial reference frame, whereas the fourth and the fifth are the components of the ascending node vector (
) in the equinoctial reference frame, whereas the fourth and the fifth are the components of the ascending node vector (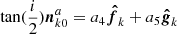 ).
).
Equinoctial elements (tensor and two common notations N1 and N2) and their relation with the Keplerian elements.
A.2. Positional uncertainty from the equinoctial covariance matrix
In the following, we present the positional uncertainty estimation of an object given its set of equinoctial elements and the corresponding covariance matrix. The velocity uncertainty estimation must be computed as well, but it is not relevant for the MOID problem. Knowing the positional uncertainties of the two objects makes it possible to select the appropriate accuracy in their MOID computation. As a matter of fact, requiring a higher accuracy than that of the input data slows down the computations without any benefit.
Let r, ṙ be the position and velocity vectors of the center of mass of a given object (here the index k has been omitted for the sake of brevity) in a quasi-inertial frame of reference – for example, the BCRF for objects orbiting the Sun. The former vectors can be expressed as linear combinations of basis unit vectors 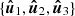 of the reference frame
of the reference frame
Here, we adopt Einstein summation convention, and the dot symbol above a variable represents time differentiation. When the latter is applied to a vector, it is done in a quasi-inertial reference frame. The state vector R is defined as
The position and velocity vectors can be written as functions of the equinoctial elements ai (i = 1, 2, …, 6) (Danielson et al. 1995):
Introducing the vector a = (a1a2 … a6)T of equinoctial elements allows to express Eq. (A.7) as a vector-valued function of a vector variable:
Differentiation yields
where J ∈ 𝕄6 × 6 is the Jacobian matrix of 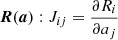 . Solving Eq. (A.8) with respect to Δa (which is possible if, and only if, J is regular) provides
. Solving Eq. (A.8) with respect to Δa (which is possible if, and only if, J is regular) provides
Under the usual assumption that a ∼ 𝒩6(μa, Σa), the probability density function f(a) of the equinoctial elements is (Wiesel 2003)
In order for the integral of f (which gives the probability) to be convergent, 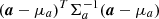 must be non-negative. This requires
must be non-negative. This requires 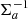 (the precision or normal matrix) and its inverse Σa (the covariance matrix) to be positive definite. The precision matrix defines a quadratic form (Gronchi & Tommei 2007) used to calculate the sum of the squares of the residuals Δa = a − μa. This quantity can be employed as the objective function of an optimization problem. The locus of the points with identical probability is a six-dimensional ellipsoid centered in the nominal orbit (six-dimensional point). The ellipsoid corresponding to a significance level p is
(the precision or normal matrix) and its inverse Σa (the covariance matrix) to be positive definite. The precision matrix defines a quadratic form (Gronchi & Tommei 2007) used to calculate the sum of the squares of the residuals Δa = a − μa. This quantity can be employed as the objective function of an optimization problem. The locus of the points with identical probability is a six-dimensional ellipsoid centered in the nominal orbit (six-dimensional point). The ellipsoid corresponding to a significance level p is
where σ is the standard deviation, κ is the radius of the probability interval (usually expressed in σ’s), and the non-dimensional parameter 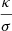 is the square root of the quantile p of a χ2 distribution of 6 degrees of freedom, because Δa ∼ 𝒩6(0, I) if it is properly rotated and scaled. 0 is the six-dimensional null vector, and I is the six-dimensional unit matrix. Introducing Eq. (A.9) into Eq. (A.11) yields
is the square root of the quantile p of a χ2 distribution of 6 degrees of freedom, because Δa ∼ 𝒩6(0, I) if it is properly rotated and scaled. 0 is the six-dimensional null vector, and I is the six-dimensional unit matrix. Introducing Eq. (A.9) into Eq. (A.11) yields
which shows that the matrix 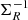 is a tensor of rank two. Besides,
is a tensor of rank two. Besides, 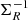 and ΣR are regular, symmetric, and positive definite.
and ΣR are regular, symmetric, and positive definite.
Since we are interested in positional errors only, we are going to limit our attention to the 3 × 3 principal sub-matrix of ΣR involving exclusively positional covariances (Σr). In its principal axis (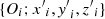 ), the corresponding matrix
), the corresponding matrix 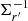 is diagonal, and the ellipsoid takes the canonical form
is diagonal, and the ellipsoid takes the canonical form
in which 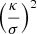 is the quantile p of a χ2 distribution of 3 degrees of freedom, and
is the quantile p of a χ2 distribution of 3 degrees of freedom, and 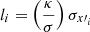 is the ith semi-axis length.
is the ith semi-axis length.
In conclusion, by solving the spectral problem for Σr, we obtain the eigenvalues of the covariance matrix, which are the critical variances:
Then, by adopting a conservative approach, the minimum error ℰmin associated with a positional uncertainty is
where 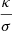 is a function of p. It is usually set to 1, which implies that for a 3D ellipsoid p ≈ 0.2.
is a function of p. It is usually set to 1, which implies that for a 3D ellipsoid p ≈ 0.2.
All Tables
Summary of the statistical properties of the 1σ position’s confidence ellipsoids of the first 281 radar-tracked NEAs published in the NEODyS database.
Basic statistical properties (minimum, average, and maximum) of the in-plane distance error ϵ of the two approximate algorithms, meaning, 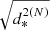 and
and 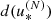 , at different expansion orders.
, at different expansion orders.
Execution times per in-plane distance determination as obtained with the approximate algorithms 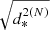 and
and 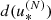 at different expansion orders (Cols. 2–9) and the computing time required by the exact distance determination d (Col. 10).
at different expansion orders (Cols. 2–9) and the computing time required by the exact distance determination d (Col. 10).
Basic statistical properties (minimum, average, and maximum) of the Earth MOID error ϵ resulting from application of the 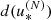 family of approximate algorithms at different expansion orders relative to the exact Earth SDG-MOID for objects in the NEODyS database.
family of approximate algorithms at different expansion orders relative to the exact Earth SDG-MOID for objects in the NEODyS database.
Average execution times per distance determination of the complete NEODyS database as obtained with the exact SDG-MOID (first column) and with the 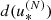 algorithm at N = 6, 4, 2, 0 (remaining columns).
algorithm at N = 6, 4, 2, 0 (remaining columns).
Equinoctial elements (tensor and two common notations N1 and N2) and their relation with the Keplerian elements.
All Figures
 |
Fig. 1. MOID between STEX and CBERS 1 between day five and day six after 12 p.m. on June 16 2019 (58650.5 MJD). Simulations made with DROMOID. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




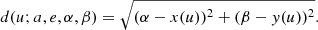
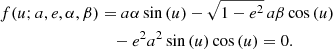
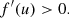
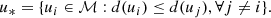
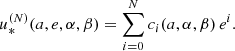
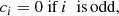
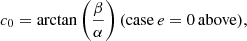
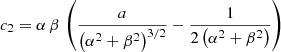
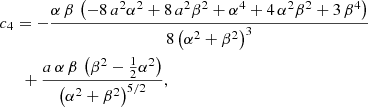
![$$ \begin{aligned}&c_6 = \frac{\alpha \beta }{\left(\alpha ^2+\beta ^2\right)^{4}} \left[ -\frac{\alpha ^6}{16} - \alpha ^4 \left( \frac{a^2}{2} +\frac{13 \beta ^2}{48} \right)\right. \nonumber \\&\quad ~~ + \left. {\alpha }^{2} \left( 4\,{a}^{2}{\beta }^{2} - \frac{25{\beta }^{4}}{48} \right) - \frac{3}{2}\,{a}^{2}{\beta }^{4} -\frac{5{\beta }^{6}}{16} \right] \nonumber \\&\quad ~~ + \frac{a\,\alpha \,\beta }{\left( \alpha ^2+ \beta ^2 \right)^{9/2}} \left[ -\frac{\alpha ^6}{8} + \alpha ^4\left(a^2 - \frac{9\beta ^2}{8} \right) \right. \nonumber \\&\quad ~~ - \left.\frac{23{a}^{2}{\alpha }^{2}{\beta }^{2}}{6} + a^2 \beta ^4+ \beta ^6 \right]. \end{aligned} $$](/articles/aa/full_html/2020/01/aa36502-19/aa36502-19-eq15.gif)
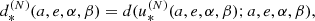
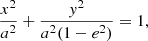
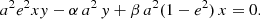
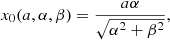
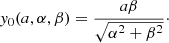
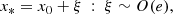
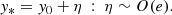
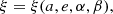
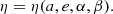
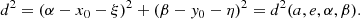
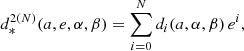
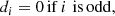
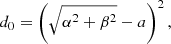
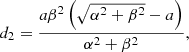
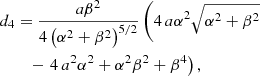
![$$ \begin{aligned} d_6&= \frac{a^2 \alpha ^2 \beta ^{2} \left[ {\alpha }^{2}\left( {\beta }^{2} -{a}^{2} \right) +{a}^{2}{\beta }^{2}+{\beta }^{4} \right]}{\left( {\alpha }^{2}+{\beta }^{2} \right) ^{4}} \nonumber \\&\quad - \frac{3 a \beta ^{2} \left[ -\frac{2}{3} {a}^{2}{\alpha }^{4}+ {\alpha }^{2}\left( {a}^{2}{\beta }^{2}- \frac{{\beta }^{4}}{12} \right) -\frac{{\beta }^{6}}{12} \right]}{ 2 \left( {\alpha }^{2}+{\beta }^{2} \right) ^{7/2}}\cdot \end{aligned} $$](/articles/aa/full_html/2020/01/aa36502-19/aa36502-19-eq32.gif)