| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201936316 | |
| Published online | 14 January 2020 | |
Non-gravitational effects change the original 1/a-distribution of near-parabolic comets★
Space Research Centre of Polish Academy of Sciences,
Bartycka 18A,
Warszawa,
Poland
e-mail: mkr@cbk.waw.pl
Received:
15
July
2019
Accepted:
13
November
2019
Context. The original 1∕a-distribution is the only observational basis for the origin of long-period comets (LPCs) and the dynamical properties of the Oort Cloud. Although they are very subtle in the motion of these comets, non-gravitational effects can cause major changes in the original semimajor axis, 1∕aori.
Aims. We obtained reliable non-gravitational orbits for as many LPCs with small perihelion distances of q < 3.1 au as possible, and determined the corresponding shape of the Oort spike.
Methods. We determined the osculating orbits of each comet using several data-processing methods, and selected the preferred orbit using a few specific criteria. The distribution of 1∕aori for the whole comet sample was constructed using the individual Gaussian distribution we obtained for the preferred solution of each comet.
Results. The derived distribution of 1∕aori for almost all known small-perihelion Oort spike comets was based on 64% of the non-gravitational orbits. This was compared with the distribution based on purely gravitational orbits, as well as with 1∕aori constructed earlier for LPCs with q > 3.1 au. We present a statistical analysis of the magnitudes of the non-gravitational acceleration for about 100 LPCs.
Conclusions. The 1∕aori-distribution, which is based mainly on the non-gravitational orbits of small-perihelion Oort spike comets, is shifted by about 10 × 10−6 au−1 to higher values of 1∕aori compared with the distribution that is obtained when the non-gravitational effects on comet motion are ignored. We show the differences in the 1∕aori-distributions between LPCs with q < 3.1 au and those with q > 3.1 au. These findings indicate the important role of non-gravitational acceleration in the motion and origin of LPCs and in the formation of the Oort Cloud.
Key words: comets: general / Oort Cloud
Full Tables 1, 3, and A.1–A.4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/633/A80
© ESO 2020
1 Introduction
Seven decades ago, Oort (1950) postulated the existence of a huge cloud built from billions of kilometer-sized bodies or larger. His hypothesis was based on a very small number of near-parabolic comets that visit the inner part of the Solar System. Since then, the number of such detected comets has increased tenfold, but we still know very little about the number and distribution of the objects that constitute the Oort Cloud. A comprehensive review of the current knowledge about the Oort Cloud, which may be the largest small-body reservoir in our Solar System, can be found in Rickman (2014) and Dones et al. (2015).
Our knowledge of the Oort cloud is poor, largely because so few parameters can be derived from the observational data. The only relatively reliable information we have is a distribution of the original 1∕a for the near-parabolic comets discovered so far. Moreover, to interpret this distribution realistically, we need to be able to dynamically separate new comets (that visit the inner Solar System for the first time) from the dynamically old comets because the latter have distorted orbits as a result of the earlier passages through the planet zone, in which planetary perturbations changed their semi-major axes; see for example Dybczyński (2001) and Królikowska & Dybczyński (2010, KD10) for more details.
Królikowska & Dybczyński (2017, KD17) investigated the dynamical evolution of Oort spike comets (original semimajor axes1 greater than 10 000 au) with perihelion distances exceeding 3.1 au. This selection minimized the potential effects of non-gravitational (NG) forces on the comet motion. In the sample of 100 such objects (KD17), only 16% of the comets showed some deviation from the purely gravitational (GR) motion within the observed arc. The large perihelion distances allowed us to assume that the NG effects were negligible in the remaining cases. The shape and position of the original 1∕a-distribution based on mixed orbit types (NG in 16% of the comet sample and purely GR in the remaining 84%) does not differ significantly from the original 1∕a-distribution that was based entirely on the purely GR orbits (see Fig. 6 in KD17).
However, in the motion of the Oort spike comets with small perihelion distances (q < 3.1 au, hereafter “small-perihelion comets”) the NG acceleration is important because of the increased water-ice sublimation when the comet approaches the Sun (Marsden et al. 1973, MSY), and can substantially change the original 1∕a of these comets (see, e.g., Królikowska 2001; and Table 1 in KD10). Studies of NG effects in these comets have so far been limited to relatively small samples. The main purpose of the present investigation was to construct the original 1∕a-distribution for as large a sample of small-perihelion Oort spike comets as possible, based on as many NG orbits as possible. To realize this task, it is crucial to determine the NG effects in the motion of each studied comet.
A simple NG model of three constant components of NG forces (MSY) was used. This model allows us to determine the NG effects in the motion of the majority of the investigated comets; however, it represents a simplified description of the NG phenomenon. Therefore, where the NG effects seemed to be variable within the data arc, a dedicated approach was introduced to determine the NG orbit locally, for example, only before perihelion. As a result of different possible approaches to available data, a set of 1∕aori values was presented for many of the studied comets, with an indication of the preferred value2 in the context of this research. These values were then used for further statistical analysis.
Furthermore, an important goal of the present research was to estimate a range of NG-acceleration amplitudes acting on nuclei of the Oort spike comets. Similar analyses have been performed earlier for various cometary populations.Almost 50 yr ago, MSY determined the NG forces using constant radial and transverse parameters A1 and A2 based on a standard g(r) function (Sect. 3). They estimated that the amplitude of NG forces is roughly 10−5 times the solar attraction at 1 au for the short-period comets (on the basis of 23 comets) and about 5–10 times greater for the long-period comets (LPCs; on the basis of 7 comets). Thirty years later, Królikowska (2004) derived a very similar result based on the NG effects determined for 19 LPCs, including 6 Oort spike comets. Here, a similar analysis is performed using a much richer sample of 78 NG orbits determined for the Oort spike comets. This time, the sample size is sufficiently rich to postulate a statistical relationship between the NG forces and perihelion distances, where the latter is an orbital element that evolvesduring the long-term dynamical evolution of Oort spike comets over many revolutions around the Sun.
The intention of this work was also to share some experience in how to determine the comet orbit when the NG acceleration plays an important role. We also establish the main focus in calculating the NG orbits based on positional data.
A short description of the LPC sample is given in Sect. 2. In Sect. 3 we discuss how the present NG model works, and why occasionally it is worthwhile using some part of the data arc to determine the NG orbit locally, for example, only in the period when the comet moves along the in-going leg of its orbit. In Sect. 4 the magnitude of the NG accelerations obtained for the Oort spike comets is subjected to simple statistical analysis.
Based on the diverse impact of the NG effects on the orbital fitting to the positional data, the division of the whole sample of the LPCs into four subgroups is proposed in Sect. 5. Then, three subgroups of the LPCs with NG orbits are discussed in detail in Sects. 7 and 8. These sections contain descriptions of various aspects of the most spectacular cases of the NG behavior.
In addition, to provide a wider context for the effects of the data selection (and data weighting) on amplitudes of the original 1∕a, we compare the values of 1∕aori presented here with two other widely known and publicly available sources of comet orbits, for which original semimajor axes are also given, that is, the Minor Planet Center3 (MPC) and Nakano Notes4. In Tables A.1–A.4, we provide a brief description of the data that these two sources use to determine the osculating orbits, and present values of the original and derived future semimajor axes. For a few selected examples (Sects. 7 and 8), we try to explain the difference between the three approaches to determining the orbit from the positional data.
Finally, the distribution of the original 1∕a for the small-perihelion LPCs is presented in Sect. 9 and are compared with the distribution constructed for the large-perihelion LPCs in KD17. The main results are summarized in Sect 10.
2 LPC sample and orbit determinations
2.1 General information
We consider here a sample of 122 LPCs with small perihelion distances (q < 3.1 au) with original 1∕aori < 0.000100 au−1 for purely GR orbits. They form an almost complete sample of such objects discovered in the period 1885–2012. About 50 of them were studied previously by KD10, Królikowska et al. (2012, 2014), and Królikowska & Dybczyński (2016), and all the LPCs ( ~20) of this type that were discovered during the period 2006–2010 were examined by Królikowska & Dybczyński (2013, hereafter KD13). The orbits of the majority of these comets were presented by Królikowska (2014, hereafter K14).
Positional observations of comets discovered before 1980 were mostly collected from the original papers, see also Królikowska et al. (2014). However, positional measurements for comets discovered after 1980 were taken from the MPC.
New orbits from the positional data were determined using the same method of orbit determination as in previous papers (see, e.g., KD10 and K14), including the procedure of data selection and weighting (Sect. 2 in KD10). Only aspects related to the NG acceleration are therefore discussed in detail in the next section. This homogeneity of methods and models is essential for statistical considerations of comet orbits, particularly in the investigations of the original 1∕a-distribution.
New orbits for some previously studied comets were obtained for the purpose of the present analysis using the greater number of observations that is available now in the MPC. In justified cases, however, only some subsets of the data were taken into account for a preferred solution (e.g., data only before perihelion). The information relevant to the NG effects on positional data for all the comets considered here is summarized in Tables A.1–A.4 (see Sect. 5). References to the original and future 1∕a used in the present paper are given in Col. [12] of Table A.1 and Col. [13] of Tables A.2–A.4. The 1∕a-values derived in the present study are marked as “new”.
2.2 Details of the comet list
All 122 Oort spike comets investigated in the paper are listed in Table 1. The new orbital solutions are shown in bold. In this table, the preferred solutions are selected and are indicated by “YES” in Col. [15] of Tables A.2–A.4.
Part A of Table 1 consists of comets discovered before 1901. In this group, only the solution for comet C/1990 F1 Brooks can be treated as the “final” solution because the orbit of this comet is based on positional observations recalculated using modern catalogs (Królikowska & Dybczyński 2016). Currently, a similar analysis has been started for C/1885 X1 Fabry and C/1885 X2 Barnard, but the results may not be published before 2021. Therefore, we decided to use existing 1∕aori-values for all eight comets (listed in Part A) for the current statistical study.
Part B of Table 1 shows Oort spike comets from the period 1901–1950 that were analyzed in Królikowska et al. (2014). This is a complete sample of Oort spike comets discovered in this period and consistsof 32 small-perihelion objects, where only 13 comets have detectable NG effects based on positional data. These results were taken without any new recalculations to analyze the shape of the original 1∕a-distribution. They are not presented in Tables A.1 and A.4 because all characteristics have previously been published in Tables A.1 and C.1 in Królikowska et al. (2014).
Part C of Table 1 concerns comets discovered after 1950. In this last group, new solutions were obtained for more than 50% of the LPCs because new types of solutions have now been derived for many previously studied comets, both in terms of other g(r)-like functions and selection of data subsets that are more suitable to study the past and/or future dynamical evolution (see next section).
Table 1 also presents the orbital quality classes obtained for the studied small-perihelion Oort spike comets according tothe modified method described in KD13. This method of quality assessment is more restricted than the standard method developed by Marsden et al. (1978, MSE), and introduces a new class of 1a+ type of orbital quality (best orbits). The necessity of introducing this diversification and sharper quality assessment of orbits can be seen in the study of large-perihelion Oort spike comets, where the new method designates 31 comets as class 1a+ and 46 as class 1a out of a sample of 100 LPCs (Królikowska & Dybczyński 2018), while the MSE method designates over 85 comets as class 1A using the same orbital solutions.
Statistically speaking, we study the orbits of the small-perihelion Oort spike comets that are with significantly poorer quality than the large-perihelion comets, for three basic reasons: a lower accuracy of a single measurement is due to more strongly blurred comet images when the comet is closer to the Sun, on average, for a shorter arc of data, and many NG orbits (additional NG parameters for determination cause an even lower accuracy of the orbital elements). As a result, the currently studied sample of small-perihelion Oort spike comets is designated as follows: 12 comets are class 1a+, 22 comets are class 1a, 46 comets are class 1b, 26 comets are class 2a, and 16 comets are class 2b or lower (3a, 3b).
Analyzed sample of small-perihelion Oort spike comets.
3 Modeling NG effects
The formalism described in 1973 by MSY was applied to determine an NG orbit from positional data. In this approach, the three orbital components of the NG acceleration acting on a comet are proportional to the g(r)-like function, which is symmetric relative to perihelion,
![\begin{eqnarray*} F_{i}=A_{ i} \> g(r),& A_{i}=\textrm{const\, for}\quad{i}=1,2,3,\nonumber\\ & \quad g(r)=\alpha(r/r_{0})^{m}[1+(r/r_{0})^{n}]^{k},\end{eqnarray*}](/articles/aa/full_html/2020/01/aa36316-19/aa36316-19-eq1.png) (1)
(1)
where F1, F2, and F3 represent the radial, transverse, and normal components of the NG acceleration, respectively. The radial component is defined as positive outward along the Sun–comet line, whereas the unit vector of transverse acceleration is directed normal to r∕r, in the orbit plane, and in the general direction of the cometary motion.
The perihelion distances of all comets analyzed here are smaller than 3.1 au. Therefore, we expect that the standard g(r)-function based on water-ice sublimation usually is an adequate approximation. For water-ice sublimation, Table 2 lists the exponential coefficients m, n, and k, the distance scale, r0, and the normalization constant, α (fulfilling the condition: g(1 au) = 1). This type ofsolution is also described as the standard NG solution here, when the asymmetric (relative to the moment of perihelion passage) g(r(t − τ)) rather than the g(r(t)) function is assumed (Yeomans & Chodas 1989; Sitarski 1994). Four NG parameters were determined based on this last case: A1, A2, A3, and τ. Here τ is the time shift of the maximum of the g(r) function with respect to the moment of perihelion passage.
The NG parameters A1, A2, and A3 (and τ) were obtained together with orbital elements in the iterative process of NG orbit determination using positional observations (more details in KD10). Equation (1) is the most commonly used formula for NG accelerations that act on the comet nucleus. Because of its simplicity, it allows determining the NG acceleration in the motion of most near-parabolic comets (single-apparition) with a small perihelion distance that have been analyzed to date. For short-period comets (many apparitions), more complicated models of NG acceleration can be constructed.
The asymmetric NG model fits the orbit significantly better to positional data than the symmetrical model for several previously analyzed LPCs (KD10, KD13). The most spectacular case is for C/1959 Y1 Burnham (KD10), where the root mean square (RMS) decreases from 3.′′0 (standard NG orbital solution) to 1.′′6 (asymmetricstandard NG-solution), and this last orbital solution is preferred here. A decrease in RMS is also observed for comet C/1993 A1 Mueller (decrease of about 0.′′ 04 for the more preferred solutions compared with the symmetric NG). A similar decrease is found for standard as well as g(r)-like functions for C/1998 P1 Williams (0.′′ 12; preferred solution) and C/2007 W1 Boattini (0.′′ 59, preferred solution). All four of these asymmetric solutions are marked with an asterisk in Col. [11] of Table A.3. Asymmetric standard NG solutions for 11 other comets with very small or negligible decrease in RMS are also given in the appendix. All these asymmetric models can be determined with reasonable NG-parameters and seem to be as adequate as symmetric NG models, but sometimes they are notthe preferred solutions (see models marked with an asterisk in Col. [11] of Tables A.2–A.4 for comets C/1956 R1 Arend-Roland, C/1990 K1 Levy, C/1996 E1 NEAT, C/2002 T7LINEAR, C/2003 K4 LINEAR, C/2007 N3 Lulin, C/2007 Q3 Siding Spring, C/2008 A1 McNaught, C/2011 R1 McNaught, C/2012 K1 PANSTARRS, and C/2012 T5 Bressi).
Similarly as in KD10, we assume that in general NG effects can be determined using the positional data if the solutions satisfy at least one of the following relationships:
- (i)
a decrease in RMS for the NG solution compared with the GR orbit;
- (ii)
smaller trends in the time distribution of observed minus calculated (O−C) residuals in right ascension and/or declination for NG-orbit compared with GR orbit;
- (iii)
an O−C distribution closer to Gaussian for the NG orbit than the GR orbit.
In the analyzed sample, 78 comets met at least two of these criteria (almost always the first and third criteria, often all three). This indicates that an NG orbit could be obtained for about 64% of the small-perihelion Oort spike comets. About half of the comets with determinable NG-orbits have been discussed earlier in previous research (see Sect. 2 and Table 1).
NG solutions based on entire data sets are described in Tables A.2–A.4 compared with GR solutions for each analyzed comet. However, in many cases, orbits based on the standard g(r)-function seem to be imperfect, which is manifested by still visible trends in the time distribution of residuals in right ascension and/or declination (hereafter described as the O−C diagram). We then tested other forms of the g(r) function, so-called g(r)-like functions. It has been concluded that in rare cases, it is possible to find a dedicated g(r)-like function (using the nonstandard exponents m, n, and k) based on positional data alone (Królikowska 2004; Królikowska et al. 2012) because the values of m, n, and k are not strongly sensitive to the quality of positional data fitting. It was also shown that the improved fit to the positional data can be obtained using the nonstandard value of the distance scale, r0, (Królikowska 2004). For example, Królikowska (2004) obtained best fit to data assuming r0 = 1.5 au for three comets (C/1999 H1 Lee, C/1995 O1 Hale-Bopp, and C/1999 J3 LINEAR) and r0 = 4 au for another four comets (C/1996 B2 Szczepanski, C/1990 K1 Levy, C/1998 P1 Williams, and C/1993 A1 Mueller). This first group consists of small-perihelion LPCs with a semimajor axis smaller than 1000 au, whereas three of the four comets from the second group are Oort spike comets. We here confirm all of these previous findings. A small improvement in the orbital fitting in the sense of (i) and (ii) was obtained for some comets for the g(r)-like function reflecting the CO sublimation features, where a large r0 = 10 au was assumed (see Table 2). The differences in shapes of g(r) for water-ice sublimation and g(r)-like function used here for CO sublimation are shown in Fig. 1 in KD17.
When undesirable trends in the O−C diagram were still present, we used the approach of determining the orbit from a certain type of data-sequence alone, using three basic types of data selection: (a) data before perihelion, (b) data at large distances from the Sun, and (c) data after perihelion (see Sect. 7). The type of data selection is indicated in Tables A.1–A.4 (as “PRE”, “DIS”, “POS”, respectively) in Col. [13] or [14]).
Table 3 presents NG parameters for all comets with detectable NG forces using their positional data. For 15 of the 78 comets with detectable NG effects, it was possible to determine the time shift of maximum g(r) relative to the moment of perihelion passage (last column in this table). However, for 5 other comets (all discovered before 1950), only the radial component of NG force could be determined using positional measurements (see part C of Table 3).
NG parameters derived assuming NG effects in the motion of small-perihelion Oort spike comets.
4 Magnitude of the NG acceleration
The NG acceleration reaches its maximum value at perihelion, which can be expressed by
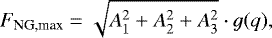 (2)
(2)
which estimates the strength of NG acceleration acting on cometary nucleus.
Figure 1 shows FNG,max as a function of perihelion distance, q, for almost 100 Oort spike comets in which NG effects can be detected using positional data. Vertical error bars show the maximum errors estimated using Eq. (2). The open red dot represents the only comet for which the uncertainty of FNG,max is higher than its value (C/1895 W1). The small-perihelion comets presented in Fig. 1 are indicated by 7 green squares, 18 magenta triangles, and 53 red dots, which represent the preferred NG solutions based on the standard g(r) function provided in Tables A.2–A.4, respectively. The 2 cyan dots illustrate NG-solutions for C/2012 S1 and C/2002 O7 based on the CO-driven formula and can be compared with the individual green squares representing models based on water-ice sublimation. The three black dotted curves exemplify the 10−3, 10−4, and 10−5 of F⊙ (r), where F⊙ (r) is a solar gravitational acceleration calculated using F⊙(r) = 0.59 ⋅ r−2, in units of cm s−2 if r is given in au.
Values of FNG,max∕F⊙(q) for Oort spike comets cover more than two orders of magnitude, and usually are in the range of (0.15−41) × 10−5, where the three comets with the highest values of FNG,max∕F⊙ are excluded (C/2002 O7 and C/2012 S1 with values of 120 × 10−5 and 80 × 10−5, respectively, and C/1998 P1 with a value of 64 × 10−5, see Fig. 1). Figure 1 shows a wider range of FNG,max∕F⊙(q) than that previously obtained for the sample of 16 LPCs in KD17 ((2−30) × 10−5).
The mean values of 6.19 × 10−5, 8.34× 10−5, and 34.8× 10−5 were then derived for FNG,max∕F⊙(q) for comets with “typical” NG effects (52 LPCs from Table A.4 and Królikowska et al. 2014, excluding C/1895 W1, indicated by red points in Fig. 1), peculiar or erratic NG effects (18 LPCs, Table A.3; magenta triangles in the plot), and split or disintegrated comets (7 of 9 LPCs given in Table A.2). For this last group, solutions based on the standard g(r) function were used for direct comparison with the previous two mean values (green squares in the figure).
For solutions based on the CO-ice formula instead of water ice for two comets from the group of split or disintegrated objects (C/2002 O7 LINEAR and C/2012 S1 ISON; cyan dots in the figure), a slightly lower mean value of 25.6× 10−5 is obtained, but it remains four to five times higher than the mean values for the remaining two groups of Oort spike comets. Values of FNG,max for these seven comets might be overestimated because of a progressive disintegration that may even have started long before perihelion was reached, although the positional data sequences for orbit determination were truncated before an outburst event was first detected in these objects (more details are given in Sect. 6).
To improve the level of detail we present, we introduce in Fig. 2 a horizontal axis that covers a smaller range of periheliondistances than in Fig. 1; thus C/2012 S1 is now omitted. All points in this figure are the same as in Fig. 1 (C/1895 W1, and the other two comets shown by two blue points representing NG solutions with g(r)-like function reflecting CO-sublimation are excluded) and all are shown in light red. Figure 2 might be useful for finding a method that includes the NG forces to simulate dynamical evolution of Oort spike comets over many revolutions around the Sun (e.g., see Wiegert & Tremaine 1999). During one revolution, q is almost the same; but over many subsequent revolutions, it can change substantially due to perturbations from galactic tides and passing stars. Figure 2 indicates that it is incorrect to maintain a constant A1 and A2 (or A1, A2 and A3) during this q-evolution because q decreases between successive passages around the Sun can often lead to unrealistically high values of FNG,max (compare the blue curves with the diagonal belt that is covered with points representing real comets), which may even become comparable with F⊙ (r). As a result, the assumption that the NG force can be treated as a perturbation breaks down for small q. For large q, it seems that the NG forces do not become negligible so fast with growing q as suggested by the blue curves (compare the blue curves and points for q > 3.0 au). However, Fig. 2 shows that it is possible to model the NG force in these long-term dynamical simulations over many revolutions around the Sun simply to assume a fixed value of FNG,max∕F⊙(q) (red dotted lines in the figure) as a function of changing q.
 |
Fig. 1 Strength of NG acceleration acting on cometary nuclei at perihelion for the sample of Oort spike comets. Solutions obtained in KD17 are shown by light red (NG orbit based on the standard g(r) function) and blue dots (g(r)-like function adequate for CO-sublimation). The solutions presented here are shown by green squares, magenta triangles, and red dots, all of which represent preferred solutions based on the standard g(r)-function. The two solutions marked as cyan dots represent models for C/2012 S1 and C/2002 O7 based on the CO-driven formula. |
 |
Fig. 2 Comparison between derived values of NG forces operating at perihelion and curves representing constant parameter A1 and the assumed ratio of A2∕A1 = 0.1 (and A3 = 0); see text for more details. |
5 NG effects deduced from positional data
Because the effect of NG on positional data fitting is so diverse, we divided the sample of studied comets into four groups. These groups are listed below in the order of decreasing impact of NG effects on a comet trajectory.
- [I]
Split comets or those that are lost soon after perihelion (see Table A.2). The sample contains 9 such comets, 7 of which have q < 1.0 au (see Sect. 6). For 2 of these 9 comets (C/2010 X1 and C/2012 T5), purely GR orbits (based on pre-perihelion data obtained a long time before perihelion passage) are selected as preferred solutions.
- [II]
Comets in which NG effects are strongly manifest in positional data fitting (see Table A.3). Eighteen comets qualified for this group, three of which have q > 2.0 au (see Sect. 7).
- [III]
Other comets with determinable NG effects using positional measurements (see Table A.4 and Appendix A in Królikowska et al. 2014). This is the largest group, containing 53 comets, 8 of which have q > 2.0 au. All 13 comets with NG orbits from Królikowska et al. (2014) are included in this group.
- [IV]
Comets with indeterminable NG effects using positional observations alone (see Table A.1 and Appendix A in Królikowska et al. 2014). For these 44 comets (36% of all investigated small-perihelion LPCs), we were unable to determine NG orbits. Of these, 20 comets have q > 2.0 au. C/2010 X1 and C/2012 T5 are also included in this group (see Group [I]).
In Tables A.1–A.4, the original and future values of 1∕a resulting from the solutions we analyzed here (and used in Sect. 9) are compared with results available at MPC and Nakano Notes, except for 32 comets that were discovered in the period 1901–1950, for which GR and NG orbits are discussed and arranged in Table C.1 of Królikowska et al. (2014). In the following sections we describe the first three groups of comets in detail.
6 Split comets or comets lost soon after perihelion: Group [I]
This group contains nine comets (Table A.2), all discovered since 1999. The positions for the majority of these comets wereonly measured until perihelion passage. The others were lost a few days after perihelion (C/1999 S4, C/2006 VZ13), or a month later (C/2012 T5).
Three of these comets (C/2006 VZ13, C/2009 R1,and C/2010 X1) were also analyzed in KD13, who presented a more detailed discussion of these cases. We here supplement the sets of previously published solutions with a new NG orbital solution based on a shorter arc than those discussed before for C/2010 X1 and with an asymmetric NG orbit for C/2006 VZ13.
For all these comets, nucleus disintegration was either observed close to perihelion or considered to be very likely. Seven of the comets (C/1999 S4, C/2002 O4, C/2002 O7, C/2009 R1, C/2010 X1, C/2012 S1, and C/2012 T5) were described by Sekanina (2019) as Oort Cloud comets that did not survive the observed perihelion passage, and these comets are described in the last column of Table A.2 as “perished” using Sekanina’s original terminology.
C/1999 S4 LINEAR is one of the most spectacular cases because it was the first Oort Cloud comet to have been captured by the Hubble Space Telescope during its spectacular fragmentation process. Nucleus decay started around 5-6 July 2000 after the comet first brightened because of its violent outburst, and many chunks were then observed along its orbit. Around 20 July, the comet brightened once again, and the main component finally started to disintegrate three days later. Thus, the NG orbit based on data up to 5 July is indicated here as the preferred solution, and it results in 1∕aori = 6.24 ± 1.67 in units of 10−6 au−1.
Similarly, the preferred orbits of all remaining comets were obtained using the data arc for which there were no reports of breakup events or strange light-curve behavior. Below we describe three more interesting cases.
C/2012 S1 ISON was a comet with an extremely small perihelion distance of 0.0125 au (about 3 solar radii). It was intensely followed by numerous observers until its decay. Sekanina & Kracht (2014) studied the disintegration process of C/2012 S1 in detail, suggesting that the comet fully disintegrated hours before perihelion passage. The first minor outburst occurred 16 days before perihelion (beginning of November) at a distance of 0.7 au from the Sun. However, an unforeseeable fading of the originally very active comet was reported by observers many weeks before this event. Therefore, two orbits are proposed here as the most probable, both based on data taken at large heliocentric distances (more than ~3.4 au from the Sun) and before the two-month gap starting from 9 June 2013. The first orbit is purely GR and gives 1∕aori as nearly zero, whereas the second one is an NG orbit obtained using the g(r)-like formula describing CO sublimation. This last NG orbit results in 1∕aori = 22.4 ± 12.6 in units of 10−6 au−1.
Observers reported that C/2002 O4 Hönig started to disintegrate a few days before perihelion and then faded very rapidly prior to perihelion passage. In mid-October 2002, it was no longer possible to see C/2002 O4 (Kadota et al. 2002). Sekanina (2002) speculated that the comet was undergoing a major outburst near the time of its discovery (27 July 2002) and that a major loss of mass triggered by this episode was completed in mid-August. The data arc for this comet is extremely short (two months), but NG effects can easily be detected in its motion. The NG orbit obtained from the full data arc gives negative 1∕aori, whereas the NG orbit derived using a shorter data arc (see preferred orbit in Table A.2) results in a closed original orbit with 1∕aori = (244 ± 133) × 10−6 au−1, indicating that the orbit of this comet is poorly known. In addition, the assumptions that NG acceleration is constant along the data arc is very rough in light of Sekanina’s speculation. Therefore, all orbits of C/2002 O4 presented in the literature should be treated with great caution, especially in the context of the origin of this comet.
C/2002 O7 LINEAR was discovered two days after the discovery of C/2002 O4, but it passed perihelion almost a year later on 22 September 2003. Mattiazzo et al. (2003) reported that C/2002 O7 was disrupted five days after perihelion, and a month later, the comet could no longer be found. Table A.2 presents two NG orbits based on a full data arc for the standard g(r) function and the g(r)-like function with r0 = 10 au. This second orbit fits the data with a slightly smaller RMS than the first orbit, but it results in a hyperbolic original orbit. Similarly, two other NG orbits of C/2002 O7 were based on a shorter arc of data that was limited to measurements taken in heliocentric distances larger than 2.44 au. However, these two orbits of C/2002 O7 match the data equally, and both were thus chosen as preferred solutions in this study (dedicated to water ice and CO sublimation, respectively).
7 Comets in which NG effects strongly manifest in positional data: Group [II]
A total of 18 comets were included in this group. Almost all of them (except for C/2012 K1) have been analyzed before in our previous papers; however, richer sets of solutions are presented here for most of them. These new solutions are marked as “new” in Col. [13] of Table A.3. The following two characteristic features are observed in all these comets:
- (i)
pure GR solutions give clear trends in the residuals of right ascension and/or declination in the O−C diagram;
- (ii)
NG solutions show a substantial RMS decrease and reduction or disappearance of the trends described in (i).
Figures 3–7 show a comparison between GR and NG solutions for several selected comets. The first group of illustrations shows the cases for which the NG solution gives a satisfactory O−C diagram (see Sect. 7.1), while the second group presents cases in which the O−C diagram for the NG solution based on the entire data arc still reveals the existence of time trends in the residuals (see Sect. 7.2).
7.1 Standard approach to NG orbit determination using the entire data-arc span
This analysis included seven comets (C/1956 R1 Arend-Roland, C/1959 Y1 Burnham, C/1986 P1 Wilson, C/1989 Q1 Okazaki-Levy-Rudenko, C/1996 E1 NEAT, C/1997 J2 Meunier-Dupouy, C/1998 P1 Williams, and C/1999 Y1 LINEAR), of which three were chosen to discuss the characteristic behaviors of this group. For all comets of this subgroup, NG solutions based on a complete data arc do not seem to show any unusual trends in the O−C diagram.
Comet C/1998 P1 Williams represents a rare case that reveals a huge decrease in RMS from 1.′′ 46 for the GR solution to 0.′′ 78 for the symmetric NG solution, and the asymmetric NG model gives a further drop in RMS to 0.′′ 66, togetherwith a better orbital fit than the symmetric NG model. Figure 3 (lowest panel) shows that the pure GR solution reveals large-amplitude trends in the O−C diagram both in right ascension and declination, which strongly indicates NG forces at work in the motion of this comet. This unfit GR orbit gives a hyperbolic original orbit (1∕aori < 0), whereas both NG solutions give the original orbit definitely inside the Oort Cloud with 1∕aori > 200 in units 10−6 au−1. Much the same result is presented in the MPC, where the symmetric NG orbit is calculated based on a data arc that is shorter by one month (see Table A.3).
Similar features are observed for comet C/1959 Y1 Burnham (left panel of Fig. 4). The reduction of RMS for the NG solution is almost double that of the purely GR solution. We have a data arc almost half of that for C/1998 P1, but also half the perihelion distance; but the number of observations is five times smaller. As a result, the derived orbit is only of 2b class. Nonetheless, the asymmetrical NG model is firmly determined, giving a slightly smaller RMS than the symmetrical model. In this case, the GR orbit gives a hyperbolic original orbit (1∕aori < 0), whereas the asymmetric nominal NG solution gives a marginally elliptical original orbit with a large uncertainty (1∕aori = (2 ± 126) × 10−6 au−1). It is worth noting here that the NG orbit in the MPC is based on fewer data (the arc is the same) and gives a hyperbolic original orbit with 1∕aori = −519.6 × 10−6 au−1. However, 1∕aori uncertainties are not given by the MPC, and it is therefore difficult to assess the differences between the solutions given here and in the MPC. When we assume, however, that the solution given in the MPC is subject to similar uncertainty levels as that given here, it can be estimated that the differences do not exceed the combined 3σ level.
The third illustrated example is C/1997 J2 Meunier-Dupouy, with q = 3.05 au and a much longer observation data arc than in the previous two examples. Here, we can also see clear trends in the O−C diagram (see the bottom right panel of Fig. 4) for a purely GR solution; but the relative decrease in RMS for the NG solution is smaller than in previous cases. Symmetric NG models give quite satisfactory and indistinguishable O−C diagrams for both the standard form of g(r) (corresponding to the sublimation of water) and the g(r)-like form, assuming a large r0 (corresponding to CO sublimation). However, orbital solutions adequate for CO sublimation result in much lower values of 1∕aori (see Table A.3), which suggests considerably different past orbital evolution, resulting in a dynamically new comet. It is unfortunately impossible to indicate which orbital solution reflects the reality based on positional data alone. Therefore, we should also look elsewhere to study the backward evolution, for example, for spectroscopic observations. However, it is not known whether water ice or CO sublimation is mainly responsible for the NG activity in this comet. It is worth noting that the MPC gives only a pure GR solution for this comet based on data until 10 July 1999 (four months after perihelion, three months before the last position measurement), whereas the Nakano Notes presents GR orbit using the full data arc.
Comet C/1999 Y1 LINEAR, with a perihelion distance also of ~3 au, represents a similar case to C/1997 J2. The MPC presents a pure GR orbit based on data that extend until seven months after perihelion (about 1.7 yr before the last positional measurement). The Nakano Notes also give the GR orbit, but it was determined using a longer data arc that extended to 11 May 2003 (more than two years after perihelion, two months before the last measurements). However, the NG orbit given here is well determined with a smaller RMS than that in a case of GR orbit. Furthermore, unlike the GR orbit, the NG orbit produces no trends in the O−C diagram. In addition, NG solutions based on standard g(r) function and g(r)-like function reflecting CO sublimation are also presented here.
The results for C/1996 E1 NEAT deserve particular attention. In the MPC, a GR orbit for this comet is given using a full data arc covered by observations. Similarly to our results here, the original orbit in a purely GR model is hyperbolic. However, the NG model gives a substantial decrease in RMS (KD10 and Table A.3), the disappearance of trends in the O−C diagram, and a closedoriginal orbit.
 |
Fig. 3 Data span and O−C residuals for comet C/1998 P1 Williams. Upper panel: time distribution of heliocentric (red dots) and geocentric distance (green dots) for all measurements that were taken into account to determine the orbit. The moment of perihelion passage and its heliocentric distance are indicated by vertical and horizontal dotted black lines, respectively. The following three panels show the time distribution of the O−C residuals for the respective orbital solutions, where residuals in right ascension are displayed by magenta dots and those in declination are represented by blue dots. Gray vertical bands show the area where residuals are below 1σ uncertainty of orbit determination. The asymmetric NG solution (preferred, second panel from the top) is compared with the symmetric NG solution (third panel) and pure GR solution (lowest panel). |
 |
Fig. 4 Same as in Fig. 3 for comet C/1959 Y1 Burnham (left panels) and comet C/1997 J2 Meunier-Dupouy (right panels). The preferred NG solutions are presented in the middle panels, and pure GR solutions are shown in the lowest panels. |
7.2 Dedicated approach to NG orbit determination
Ten such comets are given in Table A.3. They can be divided into three subgroups based on the slightly different behavior of NG effects in the positional data:
-
Comets C/2001 Q4 NEAT, C/2002 T7 LINEAR, C/2003 K4 LINEAR, and C/2007 Q3 Siding Spring were discovered at large heliocentric distances and were followed for a long time. The NG orbits obtained using the whole data arcs still give clear trends in residuals in the O−C diagram, especially around perihelion. For these comets, a satisfactory fit to the data for the NG model can be obtained without great loss of orbital accuracy when positional data around perihelion are neglected. In addition, it is often possible to separately obtain satisfactory NG models for data before and after perihelion. This group often allows several solutions of similar quality, and it is therefore difficult to indicate one preferred model for each individual comet. We therefore distinguish between the preferred model for the full data-arc covered with observations (“YES/YOS” in Col. [15] in Table A.3, depending on whether the standard NG model is assumed or the model based on the g(r)-like function), and two separate preferred models based on standard g(r) function describing the cometary motion before and after perihelion (“YE1” and “YE2” in Col. [15]).
Comets C/2007 W1 Boattini and C/2008 A1 McNaught were both discovered closer to the Sun (3–4 au from the Sun) than those from the previous subgroup and were observed for the relatively shorter time of one and two years, respectively. However, a very large decrease in RMS for the NG orbit compared to the GR orbit was obtained, and clearly different NG accelerations for the two parts of the data arcs (before and after perihelion).
In the case of comets C/1990 K1 Levy, C/1993 A1 Mueller, C/2007 N3 Lulin, and C/2012 K1 PANSTARRS, marginally observable trends in the O−C diagram for the NG model based on the standard approach to data are visible. However, the NG model can still be considered satisfactory. In contrast to the cases described in Sect. 7.1, orbits obtained using only pre- or post-perihelion data arcs (“PRE” or “POS”) give local solutions with an acceptable accuracy for the orbital elements and/or a marginally better time distribution of residuals.
Comets C/2001 Q4 and C/2002 T7 (first subgroup) have been discussed in detail in Królikowska et al. (2012, KDS12), where the grid of g(r)-like functions was considered for various data-arc selections (Tables 3 and 4 in KDS12). Figure 4 in KDS12 shows the O−C diagram for standard NG models for these two comets. Model “w5” for C/2001 Q4 given in Table A.3 represents an NG model that is consistent with the water production rates obtained by Combi et al. (2009) (see Table 3 in KDS12). We only list those solutions that seemed the most physical in Table A.3.
In KDS12, “PRE” (only data before perihelion are used for orbit determination) solutions were based on the full arc of data taken before perihelion for C/2002 T7 (here the NG model marked as p6 is the only such solution given in Table A.3). In addition, other “PRE” solutions based on data arcs that are about one year shorter than the previous solutions are given (observations until 12 April 2003, which is limited to data taken well before the perihelion passage to the heliocentric distance of 2.5 au). This approach on the one hand allowed a reduction in the undesired effects associated with possible outburst events in this comet, and on the other hand allowed maintaining a very good quality orbit (quality reduction from class 1a+ to 1a). The purely GR orbit based on these pre-perihelion data obtained at large heliocentric distance (marked as “p8”) similarly fits the data taken into account as NG orbit based on the full pre-perihelion data arc (“p6”).
The approach taken for both of these comets is different between the MPC and the Nakano Notes. For C/2001 Q4, orbits based on the full data arc are given in both of these sources. The Nakano value of 1∕aori is almost the same as that for the “w5” solution presented in Table A.3. For C/2002 T7 both sources neglected some part of the data after perihelion; however, observations reaching no more than two months after perihelion are used for NG orbit determination in the MPC, whereas in the Nakano Notes, data up to 7 March 2006 are included in the NG orbit determination (almost a full data arc). This results in large differences in 1∕aori values between the two sources.
It was also difficult to indicate the preferred model for comet C/2007 Q3. Therefore, in Table A.3, two global NG models are given using the asymmetric g(r) function dedicated to water sublimation (“n9” solution) and the g(r)-like function dedicated to CO (“dc” solution based on data taken at large heliocentric distances). In addition,there are two further solutions: NG orbit for pre-perihelion arc of data (g(r)-like function consistent with CO) dedicated for past orbital evolution, and a GR orbit based on post-perihelion data taken at heliocentric distances starting from 3.5 au and dedicated to future evolution. From the dynamical perspective, all preferred models give a fairly precise range of original 1∕a values from 28 to 41 in units of 10−6 au−1. The solution given in the Nakano Notes (NG orbit) is also placed inside this range of 1∕aori, but the MPC solution (GR orbit) results in a slightly lower value of 1∕aori.
C/2003 K4 is the least spectacular representative of the first subgroup. This comet was observed in five oppositions during 3.5 yr (upper panel in Fig. 5). The NG model based on data obtained only at large distances from the Sun does not reveal substantial trends in residuals in the O−C diagram for this comet (lowest panel). In particular, residuals in right ascension from the end of 2005 (and since last opposition in declination) are more randomly spread around zero (lowest panel in Fig. 5) compared with the NG model based on a full data arc (the second panel from the top in Fig. 5).
Time distributions of residuals in right ascension and declination (O−C diagrams) for various NG models for comet C/2008 A1 are shown in KD13. The authors reported that trends in O−C residuals are still visible for the NG orbit that is determined using full data arc. Thus, separate NG solutions were obtained for data before and after perihelion. The conclusion was that the magnitude of NG accelerations seems to be different for pre- and post-perihelion data (see also Table 3). In the MPC and the Nakano Notes, NG orbits were obtained using data up to 10 December 2008 (almost 2.5 months after perihelion passage) and 1 May 2009 (7 months after perihelion) while positional observations were continued to 17 January 2010 (Table A.3).
Comet C/2007 W1 was also analyzed in KD13. For this comet, a considerable decrease in RMS for the symmetric NG model compared with purely GR model was observed (see Table A.3), as well as a clear improvement in the amplitude of tendencies in right ascension and declination (compare the second and third panel from the top in Fig. 6). A further substantial decrease in RMS occurs when an asymmetrical NG model is used to determine the orbit (lowest panel in Fig. 6). The largest decrease in RMS between thesymmetrical and asymmetrical NG model for an analyzed sample was found for this comet, as previously mentioned in Sect. 3. Despite this improved data match, some trends in the O−C diagram can still be recognized in the asymmetrical NG model based on the full data arc (lowest panels in Figs. 6 and 7). In the next step, two separate NG orbits were therefore obtained for the cometary motion on the in- and out-going trajectory legs. The middle panel in Fig. 7 shows the O−C diagram for the NG orbit determined using pre-perihelion data alone, where some further reduction in trends is noticeable. A similar situation was also found for the post-perihelion NG orbit. The NG parameters for both NG solutions are listed in Part B of Table 3 and reveal that on average, the magnitude of NG acceleration obtained using positional data seems to be considerably greater after perihelion than before perihelion. A similar approach was applied earlier by Nakano for C/2007 W1, but not for C/2008 A1 (see Table A.3).
We include C/1990 K1 in the third subgroup. The decrease in RMS is very large between the GR and NG orbits, and large magnitude trends in the O−C diagram almost disappeared for the NG solution, except for the small tendency to negative residuals in right ascension and declination starting from November 1991 (data after the largest gap, see Fig. 8). Unfortunately, the NG orbit obtained using pre-perihelion data also shows some trends before perihelion. It is interesting that the NG orbit based on the entire dataset shows fewer trends in the O−C diagram within the pre-perihelion part of the observations compared with the orbit obtained using pre-perihelion data alone. All NG orbits (STD and PRE) result in 1∕aori greater than 100 × 10−6 au−1. The MPC value of 1∕aori is about 70 × 10−6 au−1.
Comet C/2007 N3 is slightly different: here both NG solutions (STD and PRE) are almost identical according to the O−C diagrams. However, all obtained orbits give a very narrow range of (29−33) × 10−6 au−1 for 1∕aori and the orbits are 1a+ or 1a class. The MPC also gives a 1∕aori value inside this range. In contrast, only the lower value of 1∕aori is presented in the Nakano Notes (see Table A.3).
Comet C/1993 A1 represents a more interesting case because its orbit obtained using g(r)-like function with r0 = 10 au has a slightly smaller RMS than the NG orbits based on the standard g(r) function. It is interesting that 1∕aori is 3 × 10−6 au−1 for this first solution (probably dynamically new comet), whereas 1∕aori is in the range (48−64) × 10−6 au−1 for NG orbits (STD or PRE data selection) based on water–ice sublimation (probably a dynamically old comet). This first fact (together with the moderately large perihelion distance of 1.9 au) suggests that sublimation might be caused by CO in this comet. This is just a suggestion because a solution based on r0 = 10 au and using the pre-perihelion data arc gives almost the same value of RMS as that of the NG solution based on standard r0.
 |
Fig. 6 Same as in Fig. 3 for comet C/2007 W1 Boattini, where the asymmetric NG solution (lowest panel) is compared with the symmetric NG solution (second panel from the top) and the pure GR solution (third panel). |
 |
Fig. 7 Same as in Fig. 6, where the asymmetric NG solution from the lowest panel of Fig. 6 is now compared with the NG solution based on pre-perihelion data only (middle panel). |
 |
Fig. 8 Same as in Fig. 3 for comet C/1990 K1. The symmetric NG solution based on the entire data arc is given in the middle panel. |
8 Other comets with detectable NG effects using positional data: Group [III]
Comets with determinable NG orbits but with weaker NG effects in the motion than those described in the two previous sections form the largest group of 53 objects. Eight comets discovered in this century alone were also given orbits based on a shorter data arc than in the standard approach (PRE, DIS, or POS) when we found that these solutions slightly improve the O−C diagram. This is sometimes also reflected in the fact that the cometary orbits are presented in the MPC or Nakano Notes using shorter data arcs than available (see, e.g., the Nakano result for C/2012 CH17 cited in Table A.4).
8.1 Comets with hyperbolic GR orbits
The most interesting of the comets included here are those with orbits giving negative values of 1∕aori when NG effects are neglected. This behavior is observed for 16 comets from group [III] (C/1885 X1, C/1892 Q1,C/1895 W1, C/1899 E1, C/1906 B1, C/1911 S3, C/1921 E1, C/1940 R2, C/1946 U1, C/1952 W1, C/1971 E1, C/1975 V2, C/1975 X1, C/1991 X2, C/2011 L2, and C/2011 Q2 and several more are includedin groups [I]–[II] and were discussed earlier). The MPC presents purely GR orbits with negative 1∕aori for most of them, except for comet C/1885 X1, where the NG orbit is presented with positive 1∕aori, and two other cases (C/1921 E1 and C/1940 R2), in which the GR orbits have positive 1∕aori. However, NG orbits can be obtained for all 16 of these comets. Moreover, in 14 cases, the resulting values of 1∕aori are positive, including 6 cases giving orbits with 1∕aori > 100 × 10−6 au−1. It can therefore be concluded that the GR orbits in these last cases incorrectly reflect the actual comet orbits. NG orbits still give negative values of 1∕aori for comets C/1899 E1 and C/1952 W1, but the excess of energy does not exceed the 1σ uncertainty of the 1∕aori value. These two comets can therefore also be considered as Solar System objects.
It is worth noting that most comets in this group were discovered long ago; only two were observed in this century. Moreover, only 4 out of these 16 cases of NG orbits (C/1899 E1, C/1940 R2, C/1946 U1, and C/2011 L2) include good-quality orbits (1b-class), and the remaining NG orbits are second-quality class or lower. In these four cases, the differences in 1∕aori between NG and GR solutions are relatively moderate. In eight other cases (C/1895 W1, C/1896 V1, C/1906 B1, C/1911 S3, C/1971 E1, C/1975 V2, C/1975 X1, and C/2008 C1) the change in the orbital elements between NG and GR orbits is sufficiently large to give an original nominal orbit with semimajor axis smaller than 10 000 au (1∕aori > 100 × 10−6 au−1).
Comet C/2011 Q2 is a useful example case to show how weighting (and selection) can affect the change in orbital elements when we only have a small number of observations. In this case, 106 measurements have been carried out, including one outlier. This number is close to the limit of 100 measurements below which the weighting procedure is usually not applied for orbit determination in current research. When weighting was applied during the orbit determination procedure, the resulting value of 1∕aori was less negative than in the case without data weighting. For comet C/2011 L2, only about 60 observations were available, which means that the weighting procedure was turned off.
The opposite situation was only in one isolated case (comet C/2003 T3), in which the GR orbit based on full data arc gives positive 1∕aori. The original NG orbit based on the same data arc is only slightly negative, however.
For comet C/1995 Y1 Hyakutake, the situation is slightly differnt: the NG orbit with nonzero radial component only (for A2 = A3 = 0 assumption) gives positive 1∕aori, whereas an NG orbit with nonzero radial and transverse components gives negative 1∕aori and significant decrease in RMS from 0.′′ 82 to 0.′′ 68. A very similar NG solution assuming two nonzero components of NG acceleration and giving 1∕aori < 0 is presentedin the MPC for this comet (see Table A.4). The use of the g(r)-like function with large r0 does not improve this situation.
8.2 Comets with a negative radial component of NG acceleration
The NG orbits with a negative radial component of NG acceleration (A1 < 0) (directed toward the Sun) also deserve attention. This was shown for a subgroup of comets. The MPC and the Nakano Notes also contain several examples of similar NG solutions. These solutions may indicate a specific geometry of the cometary rotation axis and the active area position on the surface of the comet, which gives, after averaging over the surface of the cometary nucleus and time, the observed effect in this simple modeling of NG acceleration applied here.
In the model based on sublimation of water ice, the negative A1 was obtained only for 8 out of the 78 comets with determinable NG effects: C/1896 V1, C/2002 Q5, C/2003 T3, C/2005 E2, C/2006 HW51, C/2006 L2, C/2008 T2, and C/2012 CH17 (Table 3). In the MPC, all these comets have GR orbits only, whereas the Nakano Notes include two comets with negative radial components of NG acceleration (C/2005 E2 and C/2008 T2). However, in Marsden & Williams (2008) a negative A1 was given for several other comets.
We decided to place all these cases within group III, although some of them (e.g., C/2003 T3) have almost as clearly visible NG effects as comets in group II, as discussed in Sect. 7. These solutions with negative A1 should be treated with some caution as they may be strongly approximating the unknown reality. However, the GR orbit of a small-perihelion comet should generally be treated as even more incongruent with reality.
In this group, it was possible to obtain NG solutions based on PRE type of data only for comets C/2003 T3 and C/2012 CH17, which gave a positive and high value of the radial acceleration component, even though it was at the expense of a clear drop the orbital quality from the first class to the second (see Table A.4). Here, it is worth noting that the NG orbit of C/2012 CH17 based on PRE data gives a similar value of 1∕aori as the GR orbit for the same data arc. Conversely, for C/2003 T3 we have so distinct a nominal NG orbit that it gives a definitely different value 1∕aori, although this is compatible with 1∕aori obtained using an NG orbit based on a full data arc within the combined 3σ error. This last example shows, however, that NG solutions with a negative radial component should be treated with caution because it may indicate the need to use a more complicated NG model in these cases, perhaps because of the highly variable cometary activity or activity that is limited to a small area of the cometary surface.
In turn, purely GR solutions based on PRE data are also shown for comets C/2006 HW51 and C/2008 T2 in Table A.4. The NG solution obtained for C/2008 T2 is the only one showing a slight increase in RMS and is included because it is possible to note a decrease in the trends in the O−C diagram compared with those visible for the GR solution. The NG solution is also presented in the Nakano Notes for this comet.
9 Shape of the Oort maximum for small-perihelion LPCs
The richer sample of comets with determinable NG effects enables obtaining a shape of the Oort maximum that is based on NG orbits alone. Now as many as 64% of the small-perihelion LPCs have NG orbits, suggesting that there is now a representative sample of such objects. This is in contrast to the sample of large-perihelion LPCs, where only 16% of the comets have determinable NG orbits.
 |
Fig. 9 Distribution of 1∕aori for small-perihelion LPCs (q < 3.1 au) with determinable NG orbits. Upper panel: shape of the Oort spike for preferred NG orbits; 78 comets were included. For comparison, the 1∕aori distribution using purely GR orbits is presented in the lower panel. Light green distributions in both panels represent the sample of comets with GR orbits of class 2 or lower. The positions of some comets with hyperbolic original orbits are labeled. |
9.1 NG effects on the shape of the original 1/a
The distribution of 1∕aori for the 78 small-perihelion LPCs based solely on NG orbits is shown in the upper panel of Fig. 9 in dark green, and the distribution for comets with orbits of the second quality class and lower is plotted in light green. For comparison, the distribution for the same sample of comets neglecting NG acceleration in their motion is shown in the bottom panel, using the same rules of color-coding, where as many as five comets are beyond the left border of this figure (C/1971 E1, C/1975 X1,C/1991 X2, C/2002 O4, and C/2007 W1) and only one of these five has an NG orbit of class 1 (C/2007 W1).
The two distributions shown in Fig. 9 were constructed using swarms of 5001 virtual comets (including nominal orbit, see KD17 for a detailed description of this technique). This method allows including the uncertainties of the original semimajor axes when the 1∕aori distribution is obtained. This means that each comet is represented with a Gaussian distribution, with the mean and standard deviation taken from Tables A.2–A.4 for the preferred orbits. It is revealed that a single Gaussian for an individual comet with the orbit of second class is scattered in the range of 1∕aori which is comparable to or larger than the width of the classical Oort spike (gray vertical band in the figures). Therefore, in practice, orbits of this class give some low level of fluctuating background in the 1∕aori distribution;see the light green distributions in the two panels of Fig. 9.
First of all, Fig. 9 reveals that several comets give hyperbolic original orbits (1∕aori < 0) in a purely GR model of motion (27 comets, including 16 objects with orbits of class 2, see also Sect. 8.1) and a substantial reduction of such solutions (7 comets) when NG acceleration in the motion of a comet is considered. In this group of 7 comets with hyperbolic original NG orbits, one has an elliptical original GR orbit and a marginally negative 1∕aori = (−1.81 ± 4.85) × 10−6 au−1 for the NG orbit (C/2003 T3, see also Sect. 8), and two other comets have NG orbits of class 2 (C/1952 W1 and C/2002 O7). C/2007 W1 Boattini has a value of 1∕aori for the NG orbit of class 1 that is negative at a statistically significant level, which results in a steep peak that protrudes from the background of other LPCs with more dispersed individual 1∕aori distributions (upper panel of Fig. 9). Comet C/1995 Y1 represents another example of negative 1∕aori for the NG orbit at a statistically significant level. This is an unusual situation because the NG solution assuming only a nonzero radial acceleration component gives positive 1∕aori (see Table A.4).
These changes in 1∕aori between GR and NG orbits arise because NG effects produce a large systematic effect in the shape of original orbits for LPCs: the inferred original semimajor axis before the comet enters the planetary region is almost always smaller than that resulting from a purely GR orbit. A qualitative explanation of this systematic effect, aori, NG < aori, GR, is given by Rickman (2014, see page 11) and is as follows:
A jet force acting mostly in the outward radial direction will decelerate the comet on the preperihelion branch and accelerate it after perihelion. This will slightly decrease the normal Keplerian trend for the speed of motion to increase with decreasing heliocentric distance, and the way to emulate this effect in a gravitational solution is to increase the orbital eccentricity, that is, to decrease the value of 1∕a without affecting the well-determined value of q.
Numerical orbital calculations show that we also have a tiny systematic effect in q, that is, qori, NG < qori, GR for about 90% of LPCs with NG orbits. These differences in the values of qori, NG and qori, GR never exceeded 10−4 au (Dybczyński & Królikowska, in prep.).
This systematic effect in 1∕aori has been known for a long time, see for example Marsden et al. (1973), Królikowska (2001, 2006), Yeomans et al. (2004), Królikowska & Dybczyński (2013), and Rickman (2014). The question of how NG effects may change the orbit of near-parabolic comets was investigated even earlier by Squires & Beard (1961). They estimated that parabolic comets with perihelia close to 1 au may experience positive shift in 1∕a of even as much as 500 × 10−6 au−1. However, Bolatto et al. (1995) argued that NG forces alone cause changes in energy (hereafter Δ1∕aori) no greater than 100 × 10−6 au−1 for comets with perihelia grater than 0.25 au and typical values of about 10−8 au day−2 for the NG force magnitude. However, the NG acceleration magnitudes for LPCs can be greater than those postulated by Bolatto et al. (1995); see Fig. 2 and Table 3.
Figure 7 in KD13 shows changes in 1∕aori between the NG and GR solutions for 48 previously analyzed LPCs. In some specific cases, these differences can be considerably larger than 100 × 10−6 au−1. In the present sample, we have such a situation for C/2002 O4 (perished comet, NG orbit of class 2b); 5 comets with NG effects that are strongly manifest in the positional data (C/1956 A1, C/1959 Y1, C/1998 P1, C/2007 W1, and C/2008 A1,all asymmetric NG models and NG orbits of classes 1b, 2b, 1b, 1a, and 1a, respectively); and 11 comets withnormal NG effects (C/1892 Q1, C/1895 W1, C/1896 V1, C/1911 S3, C/1914 F1, C/1937 N1, C/1971 E1, C/1975 V2, C/1975 X1, C/1991 X2, and C/2000 W1, all NG orbits of class 2 or lower). This indicates that for 11 of the 17 comets with GR orbits of class 2 or worse in the analyzed sample, we have Δ1∕aori > 100 × 10−6 au−1 for nominalorbits. However, in these cases, the uncertainties of the 1∕aori values are typically greater than 50 × 10−6 au−1. When all these second-quality orbits are not taken into account, this is reduced to 6 cases with Δ1∕aori > 100 × 10−6 au−1, 4 of which are comets with strong NG effects. Thus, it seems that this large difference in Δ1∕aori is rather rare in the case of orbits of class 1.
For the nominal orbits alone, distributions of the original 1∕a for NG and GR models of motion can also be compared using the Kolmogorov-Smirnov test (hereafter K-S), where the null hypothesis is that these two 1∕aori samples are drawn from one distribution. Figure 10 shows the cumulative distributions, Fi, for the analyzed samples (i = 1, 2, where the first represents the 1∕aori sample based on nominal GR orbits and the second represents the 1∕aori sample based on nominal NG orbits). Here, the K-S statistic is given by
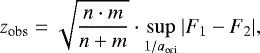
where n = m = 78 and zobs = 3.36 at 1∕aori = 40.3 in units of 10−6 au−1. The K-S statistics tables indicate that if the observed difference zobs is greater than 1.95, the hypothesis is rejected at a significance level of 10−3. Thus, our high value of zobs implies that these two tested distributions are statistically different at a very high confidence level (significantly greater than 0.999). It is important to stress here that when we ignored comets with GR orbits of class 2 or lower (the light green histograms in Fig. 9 show their distribution using full swarms of virtual comets), a similarly high value of zobs = 2.96 was obtained. This significant difference between these two 1∕aori distributions (Figs. 9 and 10) clearly shows that ignoring the NG accelerations for the small-perihelion LPCs leads to an unrealistic shape and position of the maximum of the 1∕aori distribution.
 |
Fig. 10 Cumulative distribution, F, of 1∕aori for the same sample of LPCs as in Fig. 9. The red distribution represents NG nominal orbits, and the blue distribution corresponds to pure GR solutions. |
9.2 Full sample of 122 small-perihelion comets
The upper panel in Fig. 11 shows the 1∕aori distribution for the full sample of small-perihelion LPCs analyzed here, where NG solutions make up 64% of all orbits. There is a clear difference between the distribution mostly based on NG orbits relative to that based on GR orbits (lower panel). It is difficult to estimate the magnitude of this shift because the two histograms have different shapes, but a sharp decline in the upper distribution starts for 1∕aori ≥ 50 × 10−6 au−1 (original semimajor axis smaller than 20 000 au), whereas in a lower panel of Fig. 11 this sharp decrease is for 1∕aori ≥ 40 × 10−6 au−1 (original semimajor axis smaller than 25 000 au). This suggests that the actual maximum of distribution of small-perihelion LPCs is located about 10 000 au closer to the Sun than it would be if the result were based on purely GR orbits.
A comparison of 1∕aori distributions between small-perihelion and large-perihelion LPCs is presented in Fig. 12. Because the strength of the NG effects decreases with osculating perihelion distance, q (see bottom panel of Fig. 7 in KD13), and in the light of the results presented in KD17 (see Fig. 6 therein), we can expect that the 1∕aori distribution of large-perihelion LPCs is little affected by the fact that for 84% of this sample the NG orbits cannot be determined. We therefore conclude that there is a difference in the actual 1∕aori distributions for both LPC samples (small and large perihelion). In particular, the dip at the semimajor axis of about 30 000–40 000 au for large-perihelion LPCs (associated with a separation of dynamically new and old comets in KD17) is not visible for small-perihelion LPCs.
 |
Fig. 11 Upper panel: distribution of 1∕aori based on preferred orbits for the whole sample of small-perihelion LPCs (q < 3.1 au), where 64% are NG orbits. For comparison, lower panel: 1∕aori distribution for purely GR orbits. |
 |
Fig. 12 Upper panel: distribution of 1∕aori based on preferred orbits for the whole sample of small-perihelion LPCs (q < 3.1 au). Middle panel: 1∕aori distribution for large-perihelion LPCs given in KD17, and lowest panel: sum of the two panels shown above. |
10 Summary and perspective
This study shows that it can be a difficult and delicate task to determine NG orbits in the motion of near-parabolic comets. This is because on the one hand, there is a sequence of position data that is limited to a very short period compared with the orbital period of the studied comet, which in practice allows a reasonable determination of only a small number of NG parameters (four in the best case) together with orbital elements. On the other hand, these tiny NG effects on the cometary motion can be variable, which means that the model becomes oversimplified.
In situations when the assumption of constant NG parameters operating within the entire data arc is not adequate (Sect. 3), it is therefore worthwhile to use a dedicated approach for studying the past or future orbital evolution of these comets and for determining separate orbits before and after perihelion. When this is still insufficient, a further process can be conducted, such as limiting the study to an even shorter arc of observations that are taken only at large distances from the Sun. Of course, determining the orbit from a shorter data arc reduces the accuracy of the obtained orbit, so that this should be made only when necessary. Numerous examples of how this approach works in practice are shown in Sects. 7 and 8.
In addition, the standard form of the g(r) function corresponding to water-ice sublimation may not be appropriate, especially when the comet first penetrates the planetary zone of our Solar System. Unfortunately, NG effects are so subtle in the motion of a comet that it is impossible to determine a larger number of NG parameters, such as additional exponents m, n, k, and/or r0 (see Sect. 3). Moreover, the change in these exponents in their sensible range does in most cases not translate into noticeable changes in the RMS or O−C diagram. Thus, it is difficult to indicate the most suitable set of exponents using positional data. A better approach is to study the influence of r0 on the quality of the data fitting. Therefore, based on the results of earlier studies, two different forms of g(r) were used in this investigation, the standard (corresponding to sublimation of water ice) and the g(r)-like function, with r0 = 10 au corresponding to sublimation of CO ice (see Eq. (1) and Table 2).
As a result of this approach, NG orbits for 78 small-perihelion LPCs were obtained. The statistical analysis of magnitudes of NG accelerations for all LPCs considered here and in KD17 gives a mean value of 6.19 × 10−5, 8.34 × 10−5, and 34.8 × 10−5 for FNG,max∕F⊙(q) for LPCs with “typical” NG effects (52 LPCs), peculiar or erratic NG effects (18 LPCs), and split or disintegrated comets (7 LPCs), respectively. Figure 1 shows the range of maximum values of NG accelerations operating at perihelion for all considered LPCs. A method was proposed for modeling the change in NG accelerations as a function of perihelion distance change over long timescales because of galactic tides and perturbations from passing stars (Sect. 4).
By obtaining a sufficiently large sample of NG orbits for small-perihelion LPCs, it was possible to construct a distribution of 1∕aori for an almost complete sample of these comets, 64% of which were based on NG orbits. The resulting distribution lies at higher values of 1∕aori than the distribution that is solely determined using GR orbits (Fig. 11). The magnitude of this shift is estimated at about 5000 au in a semimajor axis using the decreasing branch of the 1∕aori distribution.
Some differences in the 1∕aori distributions between small-perihelion and large-perihelion LPCs are shown (Fig. 12). However, in order to properly interpret the postulated differences in the two distributions, the dynamically new LPCs first need to be separated from the dynamically old ones. This was already done for large-perihelion LPCs in KD17. Similarly, it will be done in the near future for small-perihelion comets, where orbits of small-perihelion LPCs (osculating, original, and future) will be presented in tabular forms for public use. In addition, all orbits of Oort spike comets will be published in the online database of the near-parabolic comets, which is now in preparation.
The approach described here can be improved. Our conclusion is that the most promising new approach will be to obtain numerical and/or analytical forms of NG functions using light curves for as many LPCs as possible. On this basis, a new phenomenological NG function(s) should be developed that is dedicated to near-parabolic comets. The new NG function(s) can then be used to determine NG orbits for all Oort spike comets and to construct the 1∕aori distribution.
Acknowledgements
The comparison of comet solutions presented in this research with solutions obtained by other authors was possible thanks to the regular updating of the orbits (primarily original 1∕a discussed here) of the newly discovered comets by the Minor Planet Center (https://minorplanetcenter.net/db_search) and Syuichi Nakano (http://www.oaa.gr.jp/~oaacs/nk.htm) for which the author is extremely grateful. I would like to thank Andrzej M. Sołtan for valuable help in statistical considerations and Piotr A. Dybczyński for important critical remarks that made possible to improve this paper. I also thank the anonymous reviewer for all the critical comments. This research was partially supported by the project 2015/17/B/ST9/01790 founded by the National Science Centre in Poland.
Appendix A Description of observational material and orbital quality assessment for LPCs with perihelion <3.1 au
Small-perihelion Oort spike comets discovered in 1885–1900 and 1951–2012 and only with pure gravitational orbits determinable.
Near-parabolic comets split when they were close to perihelion, or objects that have ceased to be observed soon after perihelion passage.
References
- Bolatto, A. D., Fernández, J. A., & Carballo, G. F. 1995, Planet. Space Sci., 43, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Combi, M. R., Mäkinen, J. T. T., Bertaux, J.-L., Lee, Y., & Quémerais, E. 2009, AJ, 137, 4734 [NASA ADS] [CrossRef] [Google Scholar]
- Dones, L., Brasser, R., Kaib, N., & Rickman, H. 2015, Space Sci. Rev., 197, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczyński, P. A. 2001, A&A, 375, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kadota, K., Nakano, S., & Ezaki, Y. 2002, IAU Circ., 7995, 4 [NASA ADS] [Google Scholar]
- Królikowska, M. 2001, A&A, 376, 316 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M. 2004, A&A, 427, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M. 2006, Acta Astron., 56, 385 [NASA ADS] [Google Scholar]
- Królikowska, M. 2014, A&A, 567, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2010, MNRAS, 404, 1886 [NASA ADS] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2013, MNRAS, 435, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2016, MNRAS, 460, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2017, MNRAS, 472, 4634 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2018, MNRAS, 477, 2393 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., Dybczyński, P. A., & Sitarski, G. 2012, A&A, 544, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Królikowska, M., Sitarski, G., Pittich, E. M., et al. 2014, A&A, 571, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, B. G., & Williams, G. V. 2008, Catalogue of Cometary Orbits, 17th edn. (Cambridge: Smithsonian Astrophysical Observatory) [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Everhart, E. 1978, AJ, 83, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Mattiazzo, M., Tozzi, G. P., Boehnhardt, H., et al. 2003, IAU Circ., 8250 [Google Scholar]
- Oort, J. H. 1950, Bull. Astron. Inst. Nether., 11, 91 [NASA ADS] [Google Scholar]
- Rickman, H. 2014, Meteorit. Planet. Sci., 49, 8 [Google Scholar]
- Sekanina, Z. 2002, Int. Comet Q., 24, 223 [Google Scholar]
- Sekanina, Z. 2019, ArXiv e-prints [arXiv:1903.06300] [Google Scholar]
- Sekanina, Z., & Kracht, R. 2014, ArXiv e-prints [arXiv:1404.5968] [Google Scholar]
- Sitarski, G. 1994, Acta Astron., 44, 91 [NASA ADS] [Google Scholar]
- Squires, R. E., & Beard, D. B. 1961, ApJ, 133, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, P., & Tremaine, S. 1999, Icarus, 137, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Yeomans, D. K., & Chodas, P. W. 1989, AJ, 98, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Yeomans, D. K., Chodas, P. W., Sitarski, G., Szutowicz, S., & Królikowska, M. 2004, Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson, AZ: University of Arizona Press), 137 [Google Scholar]
All Tables
NG parameters derived assuming NG effects in the motion of small-perihelion Oort spike comets.
Small-perihelion Oort spike comets discovered in 1885–1900 and 1951–2012 and only with pure gravitational orbits determinable.
Near-parabolic comets split when they were close to perihelion, or objects that have ceased to be observed soon after perihelion passage.
All Figures
 |
Fig. 1 Strength of NG acceleration acting on cometary nuclei at perihelion for the sample of Oort spike comets. Solutions obtained in KD17 are shown by light red (NG orbit based on the standard g(r) function) and blue dots (g(r)-like function adequate for CO-sublimation). The solutions presented here are shown by green squares, magenta triangles, and red dots, all of which represent preferred solutions based on the standard g(r)-function. The two solutions marked as cyan dots represent models for C/2012 S1 and C/2002 O7 based on the CO-driven formula. |
| In the text | |
 |
Fig. 2 Comparison between derived values of NG forces operating at perihelion and curves representing constant parameter A1 and the assumed ratio of A2∕A1 = 0.1 (and A3 = 0); see text for more details. |
| In the text | |
 |
Fig. 3 Data span and O−C residuals for comet C/1998 P1 Williams. Upper panel: time distribution of heliocentric (red dots) and geocentric distance (green dots) for all measurements that were taken into account to determine the orbit. The moment of perihelion passage and its heliocentric distance are indicated by vertical and horizontal dotted black lines, respectively. The following three panels show the time distribution of the O−C residuals for the respective orbital solutions, where residuals in right ascension are displayed by magenta dots and those in declination are represented by blue dots. Gray vertical bands show the area where residuals are below 1σ uncertainty of orbit determination. The asymmetric NG solution (preferred, second panel from the top) is compared with the symmetric NG solution (third panel) and pure GR solution (lowest panel). |
| In the text | |
 |
Fig. 4 Same as in Fig. 3 for comet C/1959 Y1 Burnham (left panels) and comet C/1997 J2 Meunier-Dupouy (right panels). The preferred NG solutions are presented in the middle panels, and pure GR solutions are shown in the lowest panels. |
| In the text | |
 |
Fig. 5 Same as in Fig. 3 for comet C/2003 K4 LINEAR; see text in Sect. 7.2 for more explanations. |
| In the text | |
 |
Fig. 6 Same as in Fig. 3 for comet C/2007 W1 Boattini, where the asymmetric NG solution (lowest panel) is compared with the symmetric NG solution (second panel from the top) and the pure GR solution (third panel). |
| In the text | |
 |
Fig. 7 Same as in Fig. 6, where the asymmetric NG solution from the lowest panel of Fig. 6 is now compared with the NG solution based on pre-perihelion data only (middle panel). |
| In the text | |
 |
Fig. 8 Same as in Fig. 3 for comet C/1990 K1. The symmetric NG solution based on the entire data arc is given in the middle panel. |
| In the text | |
 |
Fig. 9 Distribution of 1∕aori for small-perihelion LPCs (q < 3.1 au) with determinable NG orbits. Upper panel: shape of the Oort spike for preferred NG orbits; 78 comets were included. For comparison, the 1∕aori distribution using purely GR orbits is presented in the lower panel. Light green distributions in both panels represent the sample of comets with GR orbits of class 2 or lower. The positions of some comets with hyperbolic original orbits are labeled. |
| In the text | |
 |
Fig. 10 Cumulative distribution, F, of 1∕aori for the same sample of LPCs as in Fig. 9. The red distribution represents NG nominal orbits, and the blue distribution corresponds to pure GR solutions. |
| In the text | |
 |
Fig. 11 Upper panel: distribution of 1∕aori based on preferred orbits for the whole sample of small-perihelion LPCs (q < 3.1 au), where 64% are NG orbits. For comparison, lower panel: 1∕aori distribution for purely GR orbits. |
| In the text | |
 |
Fig. 12 Upper panel: distribution of 1∕aori based on preferred orbits for the whole sample of small-perihelion LPCs (q < 3.1 au). Middle panel: 1∕aori distribution for large-perihelion LPCs given in KD17, and lowest panel: sum of the two panels shown above. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


