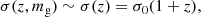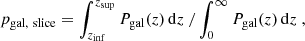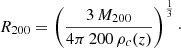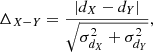| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935394 | |
| Published online | 26 November 2019 | |
Pre-processing of galaxies in cosmic filaments around AMASCFI clusters in the CFHTLS
1
Sorbonne Université, CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98bis Bd Arago, 75014 Paris, France
e-mail: florian.sarron@iap.fr
2
Aix Marseille Université, CNRS, Laboratoire d’Astrophysique de Marseille, Marseille, France
3
Sub-department of Astrophysics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
Received:
4
March
2019
Accepted:
8
September
2019
Context. Galaxy clusters and groups are thought to accrete material along the preferred direction of cosmic filaments. These structures have proven difficult to detect because their contrast is low, however, and only a few studies have focused on cluster infall regions.
Aims. We detect cosmic filaments around galaxy clusters using photometric redshifts in the range 0.15 < z < 0.7. We characterise galaxy populations in these structures to study the influence of pre-processing by cosmic filaments and galaxy groups on star formation quenching.
Methods. We detected cosmic filaments in the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS) T0007 data, focusing on regions around clusters of the AMASCFI CFHTLS cluster sample. The filaments were reconstructed with the discrete persistent structure extractor (DISPERSE) algorithm in photometric redshift slices. We show that this reconstruction is reliable for a CFHTLS-like survey at 0.15 < z < 0.7 using a mock galaxy catalogue. We split our galaxy catalogue into two populations (passive and star forming) using the LePhare spectral energy density fitting algorithm and worked with two redshift bins (0.15 < z ≤ 0.4 and 0.4 < z < 0.7).
Results. We showed that the AMASCFI cluster connectivity (i.e. the number of filaments that is connected to a cluster) increases with cluster mass M200. Filament galaxies outside R200 are found to be closer to clusters at low redshift, regardless of the galaxy type. Passive galaxies in filaments are closer to clusters than star-forming galaxies in the low redshift bin alone. The passive fraction of galaxies decreases with increasing clustercentric distance up to d ∼ 5 cMpc. Galaxy groups and clusters that are not located at nodes of our reconstruction are mainly found inside cosmic filaments.
Conclusions. These results give clues for pre-processing in cosmic filaments that could be due to smaller galaxy groups. This trend could be further explored by applying this method to larger photometric surveys such as the Hyper Suprime-Cam Subaru Strategic Program (HSC-SPP) or Euclid.
Key words: galaxies: clusters: general / large-scale structure of Universe / galaxies: evolution / galaxies: statistics / methods: data analysis
© F. Sarron et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Matter in the Universe is not distributed uniformly, but rather tends to aggregate into a complex structure in which rich and poor galaxy clusters are connected by filaments and sheets that surround regions that are almost devoid of galaxies, known as cosmic voids. This network of structures forms the so-called cosmic web.
This structure was first observed using spectroscopic redshifts with the pioneering work of de Lapparent et al. (1986). Since then, this galaxy distribution has been observed in great detail by many surveys, either shallow (i.e. limited to low redshifts) but on large portions of the sky (e.g. 2 degree Field Galaxy Redshift Survey (2dRGRS) Colless et al. 2001; and the Sloan Digital Sky Survey (SDSS) York et al. 2000), or deeper (i.e. probing higher redshifts) but limited to smaller regions (e.g. the VIMOS Very Large Telescope Deep Survey (VVDS) Le Fèvre et al. 2005). Recent efforts to probe higher redshifts in significant areas of the sky have been made (e.g. VIMOS Public Extragalactic Redshift Survey (VIPERS) Guzzo et al. 2014).
Numerical simulations of dark matter particles (e.g. Springel et al. 2005) have led to similar results. These simulations allow us to grasp the dynamical aspect of the formation and evolution of these structures. Dark matter is shown to aggregate in a bottom-up fashion forming increasingly larger structures throughout cosmic time (from galaxies to rich clusters). In this process, matter is expelled from the voids and aligns itself to the sheets or walls, where it is accreted in filaments. If clusters at the nodes of the cosmic web are believed to form mostly at z > 1, they keep accreting galaxies along the preferential direction of the filaments they are connected to at lower redshift (Bond et al. 1996).
These galaxy clusters host a population of quiescent galaxies (the so-called red sequence) that formed at z > 1 (e.g. Mullis et al. 2005; Mei et al. 2006; Eisenhardt et al. 2008; Kurk et al. 2009; Hilton et al. 2009; Papovich et al. 2010) and continue to be enriched at lower redshift (e.g. Rudnick et al. 2009; Zhang et al. 2019; Martinet et al. 2017; Sarron et al. 2018). The formation and evolution of this “red and dead” galaxy population implies that some physical processes are at play that quench star formation in galaxies.
The mechanisms that are responsible for this quenching are still poorly constrained, however. While it is now well established that the environment density plays a role in star-formation quenching (the fraction of quiescent galaxies steadily increases with environment density, e.g. Baldry et al. 2004; Bamford et al. 2009; Peng et al. 2010; Moutard et al. 2018), the efficiency of quenching in mildly dense environments (groups or filaments) is still unclear, as are the specific physical processes in these environments that may cause the high quiescent fraction observed in clusters. In the hierarchical structure formation paradigm described above, galaxies are indeed found to first cluster in small groups inside the filaments that later collapse into massive clusters (e.g. Contini et al. 2016).
In this context, groups and filaments could be favourable environments for galaxies to be quenched before they enter clusters, a phenomenon that is referred to as “pre-processing” (Fujita 2004). This is a vibrant topic in the field of galaxy evolution because understanding where environmental quenching occurs is crucial to determining the physical mechanisms that are responsible for it.
Pre-processing by galaxy groups has been extensively studied in recent years based on numerical simulations (e.g. De Lucia et al. 2012; Taranu et al. 2014) and observations (e.g. Smith et al. 2012; Roberts & Parker 2017; Bianconi et al. 2018; Olave-Rojas et al. 2018). The specific role of cosmic filaments in pre-processing began to be explored more recently using spectroscopic surveys. Various teams have reported a colour or type gradient of galaxies towards filaments (e.g. Martínez et al. 2016; Malavasi et al. 2017; Chen et al. 2017; Kuutma et al. 2017; Kraljic et al. 2018).
These reconstructions of the cosmic web are all based on spectroscopic redshifts, which allow tracing filaments in three dimensions. It is unclear whether the effect of filaments can be traced based on photometric redshifts. Malavasi et al. (2016) explored the effect of the photo-z error on the ability of assigning the correct environment densities to galaxies. They concluded that an uncertainty σz ≲ 0.01 × (1 + z) provides a good reconstruction of the environment. This was confirmed by Laigle et al. (2018), who showed that this reconstruction is possible with very good photometric redshifts (σz ∼ 0.008 × (1 + z)) by recovering similar stellar mass and colour-type gradients as previously mentioned studies (e.g. Malavasi et al. 2017) in the redshift range 0.5 < z < 0.9.
In this work, we first explore the ability of such a method of recovering filaments in the infall regions of clusters based on the less accurate (σz ∼ 0.03 × (1 + z)) photometric redshifts of the Canada France Hawaii Telescope Legacy Survey (CFHTLS). We aim at understanding whether the environmental quenching of faint galaxies observed in Sarron et al. (2018) occurred inside the cluster region, or if these galaxies have been pre-processed before they entered the clusters. To do this, we use our cosmic filament reconstruction to study galaxies that are located in the cosmic filaments that feed galaxy clusters. This question has been relatively unexplored so far. Martínez et al. (2016) studied filaments between galaxy groups in the SDSS up to z = 0.15. They found in particular that filaments play a specific role in quenching galaxies when compared to isotropic infall onto the groups. The method was very recently applied to the VIPERS data in the redshift range 0.43 ≤ z ≤ 0.89 (Salerno et al. 2019), where similar results were found that confirmed the important role played by filaments in quenching up to z ∼ 0.9. Darragh-Ford et al. (2019) also studied the role of filaments in feeding galaxy groups in the Cosmic Evolution Survey (COSMOS; Scoville et al. 2007) up to z = 1 by studying the dependence of group properties on cluster connectivity (i.e. the number of connected cosmic filaments).
In this paper we focus on the study of filaments in the infall regions of clusters in the CFHTLS survey up to z = 0.7 based on the cluster catalogue assembled with the Adami, Mazure, and Sarron cluster finder AMASCFI reported in Sarron et al. (2018) and on the detection of filaments based on photometric redshifts with a method adapted from Laigle et al. (2018). In Sect. 2 we present our data and our method to detect cosmic filaments. In Sect. 3 we use mock data to quantify the ability of our method to recover 3D cosmic filaments, particularly in the infall region of clusters. The method is then applied in Sect. 4 to the CFHTLS T0007 data to study quenching in the filaments that feed AMASCFI clusters. The results are discussed in Sect. 5. We use AB magnitudes throughout the paper and assume a flat ΛCDM cosmology with ΩM = 0.3 and h = 0.7.
2. Data sets and method
Before we focus on the distribution of galaxies in and around the projected 2D cosmic web, we first describe the data. These are the CFHTLS T0007 data set and mock data taken from the lightcones of Merson et al. (2013). We also describe our method for reconstructing the cosmic web in these data sets.
2.1. CFHTLS and mock data
2.1.1. CFHTLS T0007
The photo-z catalogue was obtained from the CFHTLS data release T00071. CFHTLS T0007 photo-zs were computed in the 154 deg2 sky coverage of the CFHTLS from multicolour images in the u*g′r′i′z′ filters of MegaCam at the CFHT.
The photo-zs were obtained with the LePhare software (Arnouts et al. 1999; Ilbert et al. 2006). Details of the method are given in Coupon et al. (2009). Briefly, the photo-zs were computed using 62 templates obtained after four templates from Coleman et al. (1980) and two starburst templates from Kinney et al. (1996) were optimised. Ilbert et al. (2006) linearly interpolated between them to better sample the colour-redshift space using the VVDS spectroscopic sample (e.g. Le Fèvre et al. 2005). A particularly crucial step of the process is the calibration of the zero-points using spectroscopic samples that help in removing biases. The resulting statistical errors on photo-zs depend on the redshifts and magnitudes of the galaxies.
Following the photo-z catalogue based on the CFHTLS T0007 data release, we define the dispersion as
which is the normalised median absolute deviation (NMAD) estimator defined in Ilbert et al. (2006), with Δzphot = zphot − zs, where zphot and zs are the photometric and spectroscopic redshifts, respectively. The catastrophic failure rate η is set as the proportion of objects with |Δz| ≥ 0.15 × (1 + zs).
In our analysis, we only considered galaxies that are outside the masks provided with the CFHTLS T0007 release. These masks are located around bright stars or artefacts, and mark regions of lower photometric quality. Thus photo-zs in these regions would be of poorer quality than those outside the masked regions.
To estimate the photo-z uncertainty at a given magnitude and redshift, we used the median of the errors obtained using spectral energy density (SED) fitting binned in magnitude and redshift2. This is useful for comparing the photo-z uncertainties of galaxies of the same absolute magnitude at different redshifts, and thus to have slices that encompass the same galaxy population at every redshift.
We considered a Bruzual & Charlot (2003) single stellar population calibrated with the field galaxy luminosity function (GLF) of Ramos et al. (2011) to compute the apparent GLF knee magnitude at redshift z: 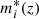 . This allowed us to obtain the redshift evolution of the photo-z uncertainty at fixed absolute magnitude. We used this information to choose the photo-z slice thickness in the CFHTLS (see Sect. 2.3.3).
. This allowed us to obtain the redshift evolution of the photo-z uncertainty at fixed absolute magnitude. We used this information to choose the photo-z slice thickness in the CFHTLS (see Sect. 2.3.3).
2.1.2. CFHTLS passive versus star-forming classification
In Sect. 4 we split the CFHTLS galaxy sample into two populations to study pre-processing in cosmic filaments: passive and star-forming galaxies. CFHTLS T0007 photo-zs were computed using LePhare. The algorithm uses 62 templates (see Sect. 2) and allows for dust reddening in the star-forming galaxy templates. The best photometric redshift is taken as the median of the maximum likelihood distribution. To classify galaxies as passive or star-forming, we used the LePhare best-fit template at this redshift. Because LePhare templates are built from the four templates from Coleman et al. (1980) and two starburst templates from Kinney et al. (1996), we classified the templates corresponding to the elliptical template of Coleman et al. (1980) as passive. Other templates were classified as star forming (with or without dust reddening).
There is a known degeneracy between the colours of passive galaxies and dusty star-forming galaxies that necessarily affects a classification based on SED fitting such as ours. Moreover, the effect may depend on redshift. At higher redshifts, the observed part of the rest-frame spectrum is shifted towards the blue, where the effect of dust cannot be properly estimated.
To test this, we compared our classification scheme to the more precise NUVrK colour–colour diagram of Arnouts et al. (2013), which allows efficiently separating passive and dusty star-forming galaxies. In this scheme, galaxies are classified as either quiescent, green valley, or star-forming galaxies. The comparison was made using the Vipers-MLS survey (Moutard et al. 2016), which covers most of the W1 and W4 fields of the CFHTLS. Through its near-ultraviolet (GALEX NUV band) and near-infrared (WIRCam Ks band) observations, it allows using the NUVrK diagram at z < 0.7.
We were thus able to directly compare the two classifications for each galaxy that is in common. We first matched galaxies in the two catalogues using their positions and a matching distance of 0.1″ on the sky. In total, we find 784 736 galaxies in common, out of which 349 447 have a redshift in the range 0.10 < z < 0.75 in the CFHTLS T0007. To assess the quality of our classification, we compared the classifications for galaxies with similar photometric redshifts and absolute magnitudes in the two samples. We selected a subsample for which the difference between the photometric redshift was Δz < 0.05 × (1 + zCFHTLS) and with 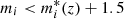 , where
, where 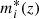 was computed using Bruzual & Charlot (2003) single stellar population models calibrated with the field GLF of Ramos et al. (2011). Our final common sample contains 127 145 galaxies.
was computed using Bruzual & Charlot (2003) single stellar population models calibrated with the field GLF of Ramos et al. (2011). Our final common sample contains 127 145 galaxies.
Over the full redshift range 0.10 < z < 0.75, 55% of our passive galaxies are quiescent in the Moutard et al. (2016) catalogue, 29% are green valley galaxies, and 16% are star forming. Conversely, 93% of the quiescent, 76% of the green valley, and 6% of the star-forming galaxies in Moutard et al. (2016) are passive in our classification.
When we split in redshift at 0.10 < z ≤ 0.40, only 5% of our passive galaxies are classified as star forming in the Moutard et al. (2016) catalogue, while 64% are classified as quiescent and 31% are green valley galaxies. Conversely, 95% of the quiescent, 73% of the green valley, and only 2% of the star-forming galaxies in Moutard et al. (2016) are passive in our classification at these redshifts.
At 0.40 < z < 0.75, 20% of our passive galaxies are classified as star forming in the Moutard et al. (2016) catalogue, while 51% are classified as quiescent and 29% are green valley galaxies. Conversely, 92% of the quiescent, 78% of the green valley, and only 7% of the star-forming galaxies in Moutard et al. (2016) are passive in our classification at these redshifts.
Our definition of passive galaxies therefore roughly corresponds to the combined quiescent and green valley galaxies in the Moutard et al. (2016) classification, with some contamination by dusty star-forming galaxies. This contamination seems to be higher (by ∼15%) at higher redshift (in the range 0.4 < z < 0.75 vs. 0.1 < z < 0.4), as expected. When we separately analysed the W1 and W4 fields, we observed variations of ∼5% from one field to another, which mitigates the difference we observed between the two redshift bins. Nevertheless, this caveat should be kept in mind when the redshift evolution of the properties of our galaxy populations is considered (see Sect. 4).
2.1.3. Mock data
To quantify the quality of the cosmic-web reconstruction from photometric redshifts, we used a modified lightcone based on a 100 deg2 Deep EUCLID lightcone3 produced following Merson et al. (2013). The number counts in this lightcone are ∼25% lower than the CFHTLS T0007 data at all apparent magnitudes (mi < m* + 1.5). This might affect the contrast of cosmic-web structures, including cosmic filaments, in the mock compared to the real data. However, this should not be a problem because the AMASCFI cluster finder has been shown to behave similarly in this mock and in the CFHTLS T0007 data (Sarron 2018).
We converted the SDSS i-band magnitudes of the mock to obtain the CFHTLS Megacam i band magnitudes as in Sarron et al. (2018) following
We added realistic noise to the redshift of each galaxy in the mock using the median CFHTLS T0007 uncertainty computed in bins of magnitude and redshift. We refer to Sarron et al. (2018) for a detailed description of the procedure.
From this information, we computed a redshift probability distribution function (PDZ) Pg(z) for each galaxy in the mock. This was made following the formalism presented in Castignani & Benoist (2016),
where mg, zp, g, and σ(z, mg) are the magnitude, photo-z, and photo-z uncertainty of the galaxy, respectively. While Castignani & Benoist (2016) took the simplified prescription
here we used our discrete sampling of σ(z, mg). For a given galaxy, mg and zp, g were fixed, but σ(z, mg) is a function of z, so that the PDZ was not simply a Gaussian centred at zp, g. We refer to Castignani & Benoist (2016) for a more detailed discussion of this topic.
Finally, the masks due to bright stars in the CFHTLS T0007 catalogue might affect the quality of our reconstruction of cosmic filaments, therefore we added masks that are representative of the CFHTLS T0007 masks on the mock to make it more realistic. Thus, the effect of the masks are directly included in our validation analysis.
2.2. Cluster catalogue
To study cosmic filaments feeding galaxy clusters in the CFHTLS, we considered the cluster catalogue from Sarron et al. (2018). This catalogue was obtained by running the AMASCFI algorithm on the CFHTLS T0007 data. We refer to Sarron et al. (2018) for a full description of the algorithm as well as for detailed properties of the cluster catalogue.
Briefly, candidate clusters are detected based on photometric redshifts by cutting the galaxy catalogue into redshift slices and detecting peaks in 2D density maps in each slice. Individual detections closer than 1 Mpc on the sky and Δz = 0.06 are then merged through a minimal spanning tree (MST, see e.g. Adami et al. 2010).
Sarron et al. (2018) computed the selection function of the algorithm in the CFHTLS. The mean purity and completeness at z < 0.7 and cluster mass M200 > 1014 M⊙ are ∼90% and ∼70%, respectively.
Each candidate cluster in the final catalogue has a position, a photometric redshift (with uncertainty σz = 0.018 × (1 + z)), a richness estimate, and a mass estimate (M200). Cluster masses M200 were inferred through a scaling with richness. This scaling relation was obtained for a subsample of AMASCFI candidate clusters whose X-ray masses were taken from Gozaliasl et al. (2014) and Mirkazemi et al. (2015). We refer to Sarron et al. (2018) for details on this procedure. The typical uncertainty on the cluster mass estimate M200 is ∼0.20 − 0.25 dex.
2.3. Cosmic filament reconstruction method
Our reconstruction of the cosmic web from photometric redshifts is based on the discrete persistent structure extractor (DISPERSE, Sousbie 2011), a software that extracts the cosmic-web filaments as ridges of the density field from discrete point distributions in either 3D or 2D. The extraction is naturally scale free and robust to noise.
The software is based on discrete Morse theory and theory of persistence. We refer to Sousbie (2011) for a detailed description of the theoretical grounds of the algorithm as well as its implementation. Application of the software to astrophysical data can also be found in Sousbie et al. (2011). Here we briefly present the main features of the algorithm with specific details of our 3D and 2D use in the relevant sections.
2.3.1. Cosmic-web extraction with DISPERSE
DISPERSE computes the density field from the discrete distribution of points (i.e. galaxy distribution in our application) by computing the Delaunay tessellation of the points. This is done with the Delaunay tessellation field estimator (DTFE, Schaap & van de Weygaert 2000; Cautun & van de Weygaert 2011), which computes the density at each galaxy position considering the area (2D) or volume (3D) of the tessellation cells.
Discrete Morse theory then enables the algorithm to find critical points of the density field, i.e. the points where the gradient of the field vanishes (minima, saddle points, and maxima). The skeleton (Pogosyan et al. 2009) is computed as the field lines joining saddle points to maxima. It is defined as a set of segments that trace the ridges of the distribution (i.e. the filaments of the cosmic web).
From there, DISPERSE allows filtering only robust structures using the persistence as a criterion. This is defined as the ratio of the density value at each point of a pair of critical points. In the context of filament (skeleton) extraction, the pairs of interest are the saddle-maximum pairs.
This ratio (the persistence) quantifies the strength of the pair, that is, how robust the topological component of this pair is to local modification of the field value. Thus it allows quantifying how significant a structure is by knowing the noise level in the data. In the case of a discrete data set such as a galaxy distribution, DISPERSE can accomodate Poisson noise and quantify the robustness of structures in numbers of σ.
2.3.2. 3D cosmic-web extraction
Here, the 3D skeleton extraction was performed on the Merson et al. (2013) lightcone with DISPERSE. As we detail in Sect. 3, this was done to assess the reliability of the 2D reconstruction.
Ideally, the 2D reconstruction would be compared to a reference skeleton obtained from the dark matter particle distribution in the lightcone because galaxies are a biased tracer of the underlying dark matter distribution (see e.g. Laigle et al. 2018, for a discussion). Here we chose to work with a lightcone with a large field of view in order to have meaningful statistics regarding filaments around clusters of different masses, and to be able to trace filaments on large scales. The chosen lightcone (Merson et al. 2013) only allows accessing the mock galaxy distribution. However, because we do not focus on quantifying the bias of using galaxies as a tracer of the cosmic web, but rather on the ability of recovering the 3D density field obtained from galaxies with photometric redshifts, this choice is not penalising. Moreover, reconstruction of the cosmic web from the galaxy distribution in 3D has been shown to trace the underlying properties of the density field and its specific geometry (see e.g. Malavasi et al. 2017; Kraljic et al. 2018).
To choose our reference skeleton, two parameters need to be tuned. As explained in Sect. 2.3.1, the skeleton changes as the detection threshold is modified. It also depends on the stellar mass limit of the sample. Up to z = 1, the Merson et al. (2013) lightcone is complete down to M* ∼ 2.5 × 108 M⊙.
The aim of this work is to detect and study filaments of galaxies around galaxy clusters based on photometric redshifts. As detailed in Sect. 2.3.3, the photometric redshift uncertainty prevents us from detecting the leaves and leaflets of the cosmic web. We thus need to choose both the stellar mass and the significance cut in 3D appropriately to allow for a meaningful comparison.
Working only with the most massive galaxies, we might miss some fainter filaments, but decreasing the mass limit will include more faint filaments that we will not be able to recover in 2D. For our reference 3D skeleton, we chose to work with a stellar mass cut M* > 109 M⊙ and a significance threshold set to 5.5σ. We verified on subsamples of the mock data that our results are not too sensitive to the exact choice of these parameters.
2.3.3. 2D cosmic-web extraction
To identify cosmic filaments in the CFHTLS from photometric redshifts, we applied the method outlined in Laigle et al. (2018) with two main modifications. As in Laigle et al. (2018), the galaxy catalogue was cut along the redshift dimension in slices of constant co-moving size. This ensured that the quality of the cosmic-web reconstruction is the same at all redshifts and thus avoided possible systematics due to increased slice thickness at higher redshifts.
Galaxies belong to the slice corresponding to their photo-z. To compute the density field in 2D from these galaxies, we used the DTFE in two dimensions, each galaxy being weighted by its probability to be in the slice pgal, slice:
where zinf, zsup are the limits of the redshift slice.
To deal with boundary conditions, we added a surface of “guard particles” outside the bounding box by interpolating the actual density at the boundary. Galaxies in masked areas were removed from the catalogue. We did not fill these regions with fake particles as is sometimes done (e.g. Aragón-Calvo et al. 2015). After the density was computed, we extracted the skeleton using DISPERSE with a persistence threshold of 2σ as in Laigle et al. (2018). The two main modifications of the method in this work are listed below.
− Galaxies in each slice were selected following an absolute magnitude cut rather than a stellar mass cut as in Laigle et al. (2018). Here, we selected galaxies with 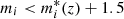 , where
, where 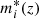 was computed using Bruzual & Charlot (2003) single stellar population models calibrated with the field GLF of Ramos et al. (2011). This cut ensures a good sampling while limiting the photo-z uncertainty.
was computed using Bruzual & Charlot (2003) single stellar population models calibrated with the field GLF of Ramos et al. (2011). This cut ensures a good sampling while limiting the photo-z uncertainty.
− Because our study focuses on cosmic filaments around galaxy clusters, the centring of the slices is different. Here, the skeleton around each cluster was reconstructed from a slice centred at the cluster redshift. This ensured an optimal reconstruction because the bias from photo-zs is minimised.
3. Validation of the connectivity measurement and filament extraction on mocks
The aim of this section is to quantify the ability of photo-zs of accurately tracing the cosmic web in the CFHTLS data. Laigle et al. (2018) showed that high-quality photo-zs obtained by Laigle et al. (2016) in the COSMOS survey (Scoville et al. 2007) allow probing the cosmic-web effect on galaxies up to high redshift (z ∼ 0.9). Their sample has a typical photo-z uncertainty of σz = 0.008 × (1 + z) at z < 0.9.
The photo-z uncertainty in the CFHTLS is ∼0.03 × (1 + z) (at 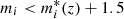 , z < 0.7). Because the photo-z uncertainty drives the slice width, slices were chosen to be thicker in the CFHTLS than in COSMOS. We chose a fixed width of 300 co-moving Mpc (cMpc) in the CFHTLS rather than 75 cMpc in COSMOS (Laigle et al. 2018). This choice is justified in Table 1. Considering the increased slice width, we needed to ensure that applying the Laigle et al. (2018) method to the CFHTLS data allowed us to obtain a fair reconstruction of cosmic filaments around clusters.
, z < 0.7). Because the photo-z uncertainty drives the slice width, slices were chosen to be thicker in the CFHTLS than in COSMOS. We chose a fixed width of 300 co-moving Mpc (cMpc) in the CFHTLS rather than 75 cMpc in COSMOS (Laigle et al. 2018). This choice is justified in Table 1. Considering the increased slice width, we needed to ensure that applying the Laigle et al. (2018) method to the CFHTLS data allowed us to obtain a fair reconstruction of cosmic filaments around clusters.
Redshift uncertainties σz and how they drive the choice of the slice thickness.
To do so, we worked on our modified CFHTLS-like (Merson et al. 2013) lightcone to test the quality of the skeleton reconstruction with CFHTLS-like photo-zs. After we chose the slices, we applied the method described in Sect. 2.3.3 to extract the skeleton at the 2σ level. We first considered the global skeleton reconstruction in the slice as in Laigle et al. (2018) (Sect. 3.1). We then focused on the reconstruction around clusters studying the connected filaments (Sect. 3.2).
3.1. Global skeleton
3.1.1. Distances between skeletons
To quantify the quality of the photometric reconstruction in the CFHTLS, we computed the distribution of the distances between the segments of the 2D skeleton and the projected 3D skeleton (Sousbie et al. 2008). We computed for each segment of the 2D skeleton the minimum distance to a segment of the 3D skeleton. This operation can be reversed to compute the distance of the projected 3D skeleton to the 2D skeleton.
Following Laigle et al. (2018), we define the purity as the proportion of 2D segments that are closer than 1.5 cMpc from a projected 3D segment. Inversely, the completeness is the proportion of projected 3D segments that are closer than 1.5 cMpc from a 2D segment.
The results are summarised in Table 2, where we list the completeness and the purity as well as the median of the distance distributions. The full distributions of the distances are shown in Fig. 1c.
Statistics of the distances between the 2D and 3D skeletons detected at 2σ and 5.5σ, respectively.
 |
Fig. 1. Top: 100 × 100 cMpc part of a slice centred at z = 0.42 in the mock data. The background distribution logδ is the logarithm of the DTFE obtained from the galaxy distribution in the slice (with photo-zs). Red circles show the positions of halos in the lightcone with redshifts 0.41 < z < 0.43. The radius of the circle is equal to 2 × R200 for display purposes. Panel a: black lines are the 3D projected skeleton. Panel b: green lines are the 2D skeleton. Bottom: distribution of the distances between skeletons. The distance from the 2D skeleton to the 3D (projected) skeleton is shown in yellow. The distance from the 3D (projected) skeleton to the 2D skeleton is shown in blue. Top panel: PDF and bottom panel: CDF. The vertical lines and associated error bars in the top panel are the median and error on the median of each distribution. |
We note that with the thresholds chosen in 3D (5.5σ) and in 2D (2σ), there are about twice as many 3D projected filaments than 2D filaments when the 3D skeleton is projected in the redshift slices. This affects our selection function by biasing results towards higher purity and lower completeness compared with the case where Nfil, 2D ≡ Nfil, 3D. When we chose a higher significance threshold in 3D, however, it was clear from visual inspection that some filaments with a counterpart at 5.5σ were considered as false detections, thus biasing our purity towards lower values.
3.1.2. Stellar mass gradients towards filaments
We have shown that the 2D skeleton is a good tracer of the projected 3D structures. However, to use the 2D skeleton in real data to infer filament properties, we need to confirm that we can trace signals that actually exist in 3D from our reconstruction. Here, we considered the stellar mass gradient towards filaments observed in 3D by Malavasi et al. (2017) and Kraljic et al. (2018). Laigle et al. (2018) showed that this gradient is recovered by the 2D reconstruction given the COSMOS precision. Here, we determined whether we recover it in our CFHTLS-like mock.
As in Laigle et al. (2018) and Kraljic et al. (2018), we removed the contribution of nodes by removing galaxies that lie too close to nodes in order to compute the effect of filaments alone. The stellar mass gradient towards nodes is known (i.e. clusters and groups), and we do not wish to account for it here. We therefore stress that the stellar mass gradients we detect are valid at a given scale.
Stellar mass gradients were measured in three stellar mass bins: 9.5 < log M*/M⊙ ≤ 10, 10 < log M*/M⊙ ≤ 11, and 11 < log M*/M⊙ ≤ 12. In each bin, we measured the distance of all galaxies to their closest filaments, as illustrated in Fig. 2.
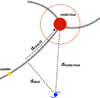 |
Fig. 2. Schematic view of the cosmic web as traced by DISPERSE that defines the different distances used in this chapter. The grey lines are the filaments. The red and yellow points are a node and saddle point, respectively. The red dashed circle shows the exclusion radius around the node. dskel is the distance to the skeleton, dnode/clus the distance to the node, and dclus, fil the distance to the cluster along the filament. |
In 3D we removed all galaxies that were closer than 3.5 cMpc from a node. This is a rather conservative choice. This value is higher than ∼2 R200 for the most massive halo in the lightcone. We took the 5.5σ skeleton as our reference skeleton for the 3D measurement. We tested that when the significance threshold was lowered, the distances of galaxies to filaments increased because fainter groups were classified as nodes and thus removed. The inverse was true when the detection threshold was increased because the less massive halos were no longer detected, so that their galaxies were included in the distance to filament statistics. The results are shown in Fig. 3. A significant stellar mass gradient towards filaments is detected in 3D: more massive galaxies lie closer to filaments.
 |
Fig. 3. Stellar mass gradients towards filaments detected in 3D at 5.5σ in the lightcone (left) and in 2D at 2σ in the CFHTLS-like mock (right). We split the galaxy catalogue into three mass bins for which we compute the distribution of the galaxy distances to the skeleton after removing galaxies close to nodes (see text for details). Red is for 11 < log M*/M⊙ < 12, yellow for 10 < log M*/M⊙ < 11, and blue for 9.5 < log M*/M⊙ < 10. In each panel, the top distribution is the PDF of the distances to the skeleton. The filled areas around the curves represent the 68% confidence limits computed from 1000 bootstrap re-samplings of the distributions. The bottom panels show the CDF. The vertical lines and associated error bars are the median and error on the median of each distribution. |
In 2D we adopted a projected exclusion radius of 1 cMpc. This is less conservative. However, adopting a higher value would drastically reduce the available statistics, while a smaller radius increases the influence of the nodes in the measurement. This makes the 1 cMpc choice a good compromise. The results are presented in Fig. 3. The stellar mass gradient towards filaments can still be observed in 2D even though it is dimmer than the 3D signal. The median values of the PDF for the different mass bins and different cases are reported in Table 3.
Median values of the galaxy distances to the skeleton in three mass bins, in the original 3D lightcone and in the three toy-model mocks considered in this work.
3.2. Reconstruction around clusters
3.2.1. Cluster connectivity
The quality of the reconstruction in the infall regions of clusters can also be assessed by studying the cosmic connectivity κ of clusters at the nodes of the cosmic web, that is, the number of cosmic filaments connected to a cluster. Cosmic connectivity is expected to scale with cluster mass; more massive clusters are more strongly connected (see e.g. Aragón-Calvo et al. 2010; Gouin et al. 2017; Codis et al. 2018; Darragh-Ford et al. 2019), but with large intrinsic scatter (see in particular Aragón-Calvo et al. 2010). Finding such a correlation from our 2D filaments would independently confirm our skeleton reconstruction quality, particularly in cluster infall regions.
In the lightcone, we computed the connectivity considering the 3D skeleton. The same measurement was carried out in our CFHTLS-like mock data using the 2D reconstruction.
In the skeleton extracted with DISPERSE, all nodes are linked to one or several saddle points through filaments, such that one node may be connected to several filaments. Formally, in the skeleton extracted by DISPERSE, two filaments leading to the same node can become infinitely close but still be counted separately because they are both topologically robust. However, they represent only a single filament, physically speaking. To avoid double counting, they are therefore merged into a single filament and a bifurcation point is added where they diverge. Our measure of a node connectivity is then the number of physical filaments departing from the node and crossing the sphere (3D) or circle (2D) of radius 1.5 cMpc centred on the node. This definition is slightly different from that of Darragh-Ford et al. (2019), who took a radius of 1.5 × R200. This is because our CFHTLS candidate cluster mass estimates have higher uncertainties (∼0.20 − 0.25 dex) than theirs. If we were to take the value of R200 computed from our estimated M200, it would introduce noise in our connectivity measurement.
To compute the number of filaments connected to a given cluster, we first matched the cluster to the nodes detected by DISPERSE and chose the node that was closest to the cluster. When no node was found at a distance smaller than the cluster R200, the cluster was marked as unmatched and not considered in the analysis. Here R200 was computed from the halo mass M200 following
We then defined the connectivity of a given cluster as the connectivity of the node it was matched with. The expected increase of connectivity with cluster mass is recovered, as shown in Fig. 4. Error bars are the standard error on the mean. The standard deviation of the distribution in each bin is much larger because of the large intrinsic scatter in the κ − log M200 scaling relation. We performed a Spearman correlation test to formally determine a correlation between connectivity and mass. In each case, we found a weak but strongly significant correlation. Results are reported in Table 4.
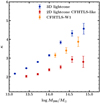 |
Fig. 4. Mean connectivity κ in bins of halo mass log M200 in 3D in the Merson et al. (2013) lightcone (blue) and in 2D in the CFHTLS-like mock (red) and in the CFHTLS (yellow). Error bars are standard errors on the mean. |
Results of the Spearman correlation test for κ vs. M200 in the three cases: 3D mock data, 2D CFHTLS-like mock data, and CFHTLS-W1.
This comparison highlights that the 2D connectivity is biased towards lower values than the 3D connectivity. The reason might be that some of the 3D filaments lie along the line of sight and cannot be recovered in 2D. It might also be that faint filaments become blurred into the noise (due either to the slice thickness or to the photo-z uncertainty). Moreover, this test seems to indicate that the bias is slightly dependent on halo mass, the slopes of the 2D and 3D scaling relations being different.
We note that in both cases we failed to find any redshift evolution of the connectivity in the range 0.1 < z < 0.7. This is compatible with measures by Codis et al. (2018), where an evolution was only found between z = 0 and z = 1.3.
3.2.2. Distance between skeletons in cluster infall regions
To proceed beyond connectivity and determine whether the 2D cosmic filaments connected to clusters are representative of the 3D connected cosmic filaments, we computed the distances between these filaments in the mocks. This allowed us to check if their directions agree statistically, which we were unable to assess based on the connectivity measurement.
We extracted connected filaments as in Sect. 3.2.1. The distances between the 3D and 2D connected filaments were computed as in Sect. 3.1.1. Results are displayed in Fig. 5.
 |
Fig. 5. Left: zoom on the most massive halo in the mock. The red circle shows the radius we used to compute the connectivity (1.5 cMpc). We show only the filaments of the skeleton connected to the cluster according to the 3D reconstruction (black) and 2D reconstruction (green). The background distribution logδ is the logarithm of the DTFE obtained from the galaxy distribution in the slice (with photo-zs). Right: distribution of the distances between skeletons. Solid lines show the distribution for the filaments connected to clusters (M200 > 1014 M⊙). The distribution for the global skeleton is shown in the background as thin transparent lines. Top panel: PDF and bottom panel: CDF. The vertical lines and associated error bars in the top panel correspond to the median and error on the median of each distribution. |
The median of distances between 2D and 3D filaments is higher with this method than when the global skeletons are compared (see Fig. 1c) because projection effects exist in the global method: Some filaments that may be in the background or in the foreground and are thus not connected to the clusters are included in the global reconstruction. Our results are not affected by these projections here. On the other hand, the median of distances between 3D and 2D filaments is lower because fewer 3D filaments have no counterpart in 2D.
This is reflected in the purity of the reconstructed filaments (computed as in Sect. 3.1.1, matching segments closer than 1.5 cMpc). This drops to 66%, meaning that about two-thirds of the reconstructed connected filaments correspond to actual 3D filaments that feed the clusters. The analysis of Sect. 3.1.1 then indicates that about 20% of the reconstructed filaments correspond to 3D filaments that appear in the slice because of projection effects, and 10% are false detections due to projection effects in the galaxy distribution and photometric redshift errors. On the other hand, the reconstruction allows us to detect ∼70% of true 3D connected filaments.
3.3. Caveats and limitations of the method
One main limitation of our reconstruction method is obviously the fact that because we work in 2D, we are sensitive to projection effects. If DISPERSE deals with Poisson noise and should thus clean spurious alignments properly, our results may be affected by coherent projection effects due to walls or filaments that are oriented in the direction of the slicing. The former might then be detected as a filament and the latter as a node.
The amplitude of this effect is difficult to quantify, but it might play a role when the stellar mass gradient towards filaments in 2D is computed. Figure 3 shows that the behaviours in 3D and 2D are not the same. Massive galaxies in the 3D skeleton present a pronounced gradient that does not appear as clear in 2D. The reason may be that, as shown by Kraljic et al. (2018), in addition to the stellar mass gradient towards filaments, there is also a stellar mass gradient towards walls as well, which we pick up in our 2D analysis.
Despite this limitation, we reach a rather high purity in our 2D filament detection at the CFHTLS accuracy (∼90% in the global skeleton reconstruction and ∼70% for filaments connected to clusters). We can thus use our filament reconstruction on the CFHTLS T0007 data to study how filaments affect galaxy properties.
4. Cosmic filaments around AMASCFI clusters in the CFHTLS
We then proceeded to study the properties of cosmic filaments around AMASCFI clusters in the CFHTLS T0007 data. We particularly focused on the role that filaments may play in environmental quenching by pre-processing galaxies that infall in galaxy clusters by comparing the properties of passive and star-forming galaxies. To this aim, we reconstructed the filaments using the technique described in Sect. 2.3.3. The ability of this technique to statistically trace the true 3D cosmic web at the CFHTLS precision was demonstrated in Sect. 3.
4.1. Galaxy cluster connectivity
To compute the connectivity of AMASCFI clusters, we used the same method as in Sect. 3.2.1. The difference is that here we did not know the exact position of the cluster but rather its estimate as computed by AMASCFI. This therefore probably introduces some bias in our connectivity measurement. The same is true for the mass. The cluster R200 was computed from the AMASCFI mass estimate following Eq. (6).
We investigated the scaling between the connectivity and cluster mass in the CFHTLS-W1 field from AMASCFI clusters considering three mass bins: 14 < log M200/M⊙ ≤ 14.3, 14.3 < log M200/M⊙ ≤ 14.6, and log M200/M⊙ > 14.6, as in Sarron et al. (2018).
We did recover the expected connectivity increase with cluster mass, as shown in Fig. 4 (yellow points). A scaling like this was also found in lower mass groups in the COSMOS survey by Darragh-Ford et al. (2019). In this figure, the error bars are standard errors on the mean. The standard deviation of the distribution in each bin is actually much larger, because of the large intrinsic scatter in the κ − log M200 scaling relation. We note that the mean connectivity at a given mass is higher in the CFHTLS data than the value obtained in the lightcone. The reason might be the difference in number counts between the mock and the data mentioned in Sect. 2.
4.2. Galaxy-type gradients towards clusters
Because galaxies fall along filaments onto clusters, we might expect to see a redshift dependence of their median distance to clusters along filaments. If galaxies are quenched inside filaments in their fall towards clusters, we then expect to see a colour-type gradient toward clusters inside filaments.
DISPERSE allows one to carry out such a measurement because the connecting filaments are well defined for each cluster (see Sect. 3.2.1). Moreover, we showed in Sect. 3.2.2 that the 2D reconstructed filaments are a good tracer of the actual 3D filaments that feed clusters (∼70% completeness and purity). We can therefore compute the distribution of the distances to AMASCFI clusters along their connecting filaments.
Galaxies at a distance dskel < 1 cMpc are considered filament members. This definition is coherent with that of Tempel et al. (2014; who took a radius of 0.5 h−1 (physical) Mpc at z < 0.15, which corresponds to 1 cMpc at z = 0.4) and more restrictive than that of Martínez et al. (2016), who considered a radius of 1.5 h−1 (physical) Mpc at z < 0.15.
This definition of the comoving radial size was fixed for all filaments connected to the AMASCFI clusters. We plotted the radial profile (without background subtraction) of these filaments as a function of several parameters. In particular, we checked the dependency of the radial profile as a function of the cluster redshift, cluster mass M200, and distance to the cluster along the filament. We found no redshift evolution or dependence on cluster mass (no significant difference between the distributions). The radial profiles show no significant variation at dclus, fil > 1.5 cMpc. At dclus, fil ≤ 1.5 cMpc, filaments become significantly more concentrated, showing that the influence of the cluster on the filaments becomes significant at this distance alone, which approximately corresponds to the virial radius.
We computed the distance to the connected cluster along the filament axis dclus, fil for these galaxies. We did not account for dskel in the measurement (see Fig. 2 for the distance definitions). Because we are interested in the role played by cosmic filaments in quenching, we removed all galaxies at a distance dclus < R200 from the cluster.
This measurement was made for passive and star-forming galaxies separately. We selected the two populations according to the SED classification given by LePhare at the galaxy best photo-z (see Sect. 2.1.1). We also split our cluster sample into two redshift bins 0.15 < z ≤ 0.4 and 0.4 < z < 0.7.
In the following, we compare the distribution of dclus, fil for the two galaxy populations (passive and star-forming) and redshift bins (low redshift and high redshift). The stellar-mass distributions of passive and star-forming galaxies are in general different: passive galaxies dominate the high-mass end. Because stellar mass and star formation rate are anti-correlated (e.g. Peng et al. 2010), we thus need to ensure that a potential difference in the distance distribution of the different types is not due to different stellar mass functions of the samples. In the CFHTLS, we do not have access to a stellar-mass estimate of galaxies, therefore we used the absolute magnitude as a proxy. To prevent the mentioned bias, we built 20 absolute magnitude-matched samples in each redshift bin using a method similar to that described by Cucciati et al. (2017). This allowed us to assess the effect of the filament environment.
The matched samples were built by cutting the two samples to the same minimum and maximum absolute magnitude. The population with the smallest number of galaxies was taken as the reference (always the passive population in our case), and we extracted 20 samples with the same absolute magnitude distribution as the reference in the larger population (star-forming galaxies here), allowing for repetition in the sampling. In practice, for each galaxy in the reference sample, we randomly selected a galaxy with absolute magnitude m, such that mref − Δm < m < mref + Δm with Δm = 0.1. If no such galaxy could be found, the galaxy was removed from the reference sample.
To compare the distance distributions, we considered the estimated medians of each distribution and compared them. We formally compared the distributions by performing a Kolmogorov–Smirnov (KS) test on the cumulative distribution functions (CDFs) with 1000 bootstraps. For each bootstrap realisation we tested the null hypothesis that the samples were drawn from the same parent distribution. The significance of the difference between the samples was then quantified through the fraction of bootstrap realisations for which the null hypothesis was rejected (KS p-value < 0.01).
Results are presented in Fig. 6, where we show the distributions of dclus, fil for passive galaxies and star-forming galaxies in the low (left) and high (right) redshift bins and in Fig. 7, where we show the distributions of dclus, fil for passive galaxies (left) and star-forming galaxies (right) in the two redshift bins. In these two figures we display the same four distributions, but Fig. 6 focuses on the galaxy-type difference at a given redshift, while Fig. 7 focuses on the redshift evolution for a given galaxy type.
 |
Fig. 6. Distances to AMASCFI clusters along filaments of passive galaxies (red) and star-forming galaxies (blue) at low redshift 0.15 < z ≤ 0.4 (left) and high redshift 0.4 < z < 0.7 (right) for absolute magnitude-matched samples. The top distribution is the PDF of the distances to the skeleton. The filled areas around the curves represent the 68% confidence limits computed from 1000 bootstrap re-samplings of the distribution. The vertical lines and associated error bars are the median and error on the median of each distribution. The bottom panel shows the CDF. |
Figure 6 shows that there is no difference in the distance distribution between passive galaxies and star-forming galaxies at high redshift (the KS null hypothesis cannot be rejected at the 99% confidence level in ∼97% of the bootstrap resamplings, see Fig. A.1b). On the other hand, passive galaxies are slightly closer to clusters at low redshift (the KS null hypothesis can be rejected at the 99% confidence level in ∼81% of the bootstrap resamplings and at the 95% confidence level in ∼94% of the bootstrap resamplings, see Fig. A.1a). If interpreted in the context of the colour-density relation (e.g. Cooper et al. 2007), the difference at low redshift confirms that by applying DISPERSE with photo-zs, we are able to recover a density increase along filaments up to AMASCFI clusters outside R200.
Figure 7 shows that the distances to clusters along filaments decrease with decreasing redshift for both galaxy populations, but the trend is stronger for passive galaxies. The difference between the distributions is significant in both cases (the KS null hypothesis can be rejected at the 95% confidence level in > 93% of the bootstrap resamplings, see Fig. A.2).
 |
Fig. 7. Distances to AMASCFI clusters along filaments of passive galaxies (left) and star-forming galaxies (right) at high (dark) and low (light) redshift. See Fig. 6 for details of the symbols. |
Values and differences of the distribution medians are reported in Table 5, where
Median values of the PDF of the filament galaxy distances to AMASCFI clusters along filaments for absolute magnitude-matched passive and star-forming galaxies in different redshift bins.
with dX and dY the distances (or their medians) and σdX and σdY the associated uncertainties. These results are discussed in Sect. 5.
4.3. Passive fraction
If quenching is efficient in cosmic filaments, we might expect to see an increased fraction of passive galaxies in their galaxy population compared to the field. To determine this, we computed the passive fraction in filament galaxies. Filament galaxies were selected and split between passive and star-forming galaxies as in Sect. 4.2.
To ensure that we probed the specific effect of cosmic filaments on the passive fraction, we proceeded in a similar way as Martínez et al. (2016). We chose as a reference sample galaxies in the infall region of clusters (dclus > R200) but outside filaments. For each cluster, we selected galaxies whose closest projected node in the slice is the cluster and that are not located in filaments (dskel > 1 cMpc). As in Martínez et al. (2016), we refer to these as isotropically falling galaxies or isotropic galaxies. As shown in Sect. 3.1.2, there is a stellar-mass gradient towards filaments such that the stellar mass function of galaxies in filaments is expected to differ from that of galaxies outside filaments. To ensure that we probed the effect of the filament environment on the passive fraction, we therefore needed to cancel out the effect of stellar mass. For this, we proceeded as in Sect. 4.2 and built absolute magnitude-matched samples. With these samples, we find that the passive fraction in filaments is fpassive, fil = 0.370 ± 0.006, while the passive fraction of isotropic galaxies is fpassive, iso = 0.301 ± 0.007.
We then computed the passive fraction of filament galaxies as a function of their distance to the cluster along filaments over the full redshift range 0.15 < z < 0.7. Results are shown in Fig. 8 (in red). Error bars and shaded areas are the 68% confidence intervals for binomial population proportions computed following Cameron (2011).
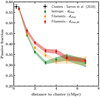 |
Fig. 8. Galaxy passive fraction as a function of the distance to the cluster in comoving Mpc. Red points are galaxies in filaments connected to the clusters, whose clustercentric distance is computed along the filaments. The results for galaxies in filaments connected to the clusters but with clustercentric Cartesian distance are plotted in yellow. In green we plot galaxies in annuli around the clusters, which are considered to fall on the cluster isotropically. The yellow and green distributions are built from absolute magnitude-matched samples. |
To assess the relevance of the filament environment on this effect, we compared the distributions for filament and isotropic galaxies. We needed to take two biases into account. First, when we computed the distance to the cluster along the filaments dclus, fil, we might introduce a bias compared to the isotropic sample because filaments twist on their way to the cluster. To cancel this effect, we therefore computed the Cartesian distance to the cluster for galaxies in filaments in the same way as for isotropic galaxies.
Once again, the stellar-mass functions of filament and isotropic galaxies are expected to be different according to Sect. 3.1.2. We therefore built 20 absolute magnitude-matched samples in each clustercentric distance bin with Δm = 0.1 (see Sect. 4.2). The passive fractions of the absolute magnitude-matched filament and isotropic galaxy samples as a function of clustercentric (Cartesian) distance are plotted in Fig. 8 in yellow and green, respectively.
For filament and isotropic galaxies, the passive fraction decreases as a function of increasing clustercentric distance. The value at dclus < 1 cMpc is compatible with the passive fraction observed in clusters by Sarron et al. (2018).
The passive fraction remains higher in filaments as the distance from the cluster increases up to dclus ∼ 4 − 5 cMpc, which roughly corresponds to (2.5 − 3) R200. The excess of passive galaxies remains between 2 and 4 cMpc when the Cartesian distance to the cluster is considered. These results are discussed in Sect. 5.
4.4. Galaxy groups inside filaments
As already mentioned, according to Libeskind et al. (2018), on large scales most filament finders tend to locate groups of M200 ∼ 1013.5 M⊙ inside cosmic filaments rather than at the nodes of the cosmic web. If groups are indeed located in filaments, then they may play a role in the observed gradient towards clusters observed in Sect. 4.2 and in the passive fraction observed in Sect. 4.3.
As mentioned in Sect 4.1, when the connectivity was computed, some halos were not matched to DISPERSE nodes. The proportion of unmatched halos is a function of halo mass. This is shown in Fig. 9, where we plot the histogram of matched and unmatched halos as a function of log M200/M⊙ in CFHTLS-W1. Most massive clusters are all matched to a node from the skeleton reconstruction. Many low-mass AMASCFI candidate clusters and groups are not matched to a node, however.
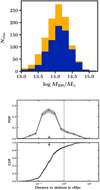 |
Fig. 9. Top: histogram of groups and clusters matched (blue) and unmatched (gold) with DISPERSE nodes as a function of their M200 in the CFHTLS-W1 field. The two histograms are stacked on top of each other so that their sum is the total number of groups and clusters in the mass bin. Bottom: distribution of the distances to the skeleton of groups that is not located at a node in CFHTLS-W1. The dashed line is the chosen radius for filaments (r = 1 cMpc). See Fig. 6 for details of the symbols. |
We therefore computed the distances of these unmatched groups to the filaments that were traced by DISPERSE to determine their location with respect to the filaments of the cosmic web. The distances were computed in two dimensions, in the slice centred at the cluster redshift.
Results are displayed in Fig. 9. The CDF shows that more than 80% of the groups are located in filaments (dskel < 1 cMpc). These results have implications on the interpretation we can give to the galaxy-type gradient towards clusters along filaments that we observed in Sect. 4.2 and to the observed passive fraction in filaments observed in Sect. 4.3, as discussed in Sect. 5.
5. Discussion
In Sect. 4.2 we showed that the median distance to clusters along filaments of both passive and star-forming galaxies is slightly higher at high redshift than at low redshift. While the trend is faint, a KS test confirmed that it is significant (see Figs. A.1 and A.2). This would agree with a picture where galaxies follow filaments towards the cluster potential well in the redshift range 0.15 < z < 0.7.
When we compared the distributions of passive and star-forming galaxies in the two redshift bins separately (see Fig. 6), we observed a galaxy-type gradient towards clusters inside filaments in the low-redshift bin alone (0.15 < zclus ≤ 0.4), passive galaxies being located in the regions closer to clusters along filaments than star-forming galaxies. At high redshift (0.4 < zclus < 0.7), the distributions are the same for passive galaxies and star-forming galaxies. This means that passive galaxies in filaments are located closer to clusters in the low-redshift bin but not in the high-redshift bin. The trend, while faint, was again confirmed to be significant by a KS test.
Moreover, we showed in Sect. 4.3 that over the full redshift range (0.15 < z < 0.7), the fraction of passive galaxies in filaments is higher than in regions around clusters outside of filaments (that we referred to as isotropic regions), and the fraction of passive galaxies in filaments decreases with increasing clustercentric distance. This agrees with the findings of Martínez et al. (2016) at z < 0.15 and Salerno et al. (2019) at 0.43 ≤ z ≤ 0.89, while exploring redshifts intermediate between these two studies. This is also in agreement with the findings of Kraljic et al. (2018) in the Galaxy And Mass Assembly (GAMA) survey in the range 0.03 ≤ z ≤ 0.25, who found that the red fraction depends simultaneously on the distance to the filament and on the distance to nodes.
We recall that our results are based on the classification of passive and star-forming galaxies using SED fitting. This classification is statistically correct but is not extremely robust for individual galaxies when five optical bands are used, as is the case in the CFHTLS. Some galaxies may thus be incorrectly classified as passive or star forming, which introduces noise in our galaxy-type gradient and passive fraction measurements.
Finally, we showed in Sect. 4.4 that some low-mass clusters and groups in the AMASCFI catalogue are not located at nodes as detected by our skeleton reconstruction. When we examined the distances of these unmatched groups to the skeleton, we found that most of them (∼80%) are located in filaments. This is in agreement with the scenario of hierarchical structure formation, in which clusters continue to accrete smaller groups in the redshift range 0.15 < z < 0.7 (e.g. Contini et al. 2016).
These results can be interpreted in two ways. First, we can assume that passive galaxies fall faster in the potential well than star-forming galaxies. This would explain why passive galaxies are closer to clusters than star-forming galaxies in the low-redshift bin. The increased falling speed might be caused by a higher radial speed along the filament because passive galaxies are located closer to the filament spine (Laigle et al. 2018; Kraljic et al. 2018). One way to understand this is also by thinking of passive galaxies as being located preferentially in galaxy groups, which we showed to be mainly located closer to the filament spines, and they may therefore fall faster onto clusters than isolated galaxies. In this case, the fact that we do not observe a significant difference in the distance distributions of passive and star-forming galaxies in our high-redshift bin would be coherent with a picture where most of the collapse of groups into clusters occurred at z < 0.7 (Contini et al. 2016).
On the other hand, the results can also be interpreted by quenching that occurred in the filaments. This would require that the quenching mechanism is more efficient when galaxies in the filament are located closer to the cluster. This could fit in a scenario where galaxies during their journey along the filaments have a higher probability of colliding or entering a group as satellites, and even more so when they approach the cluster. Both phenomena (merger and group accretion) are known to be responsible for quenching. Moreover, in our redshift range, filaments continue to accrete field galaxies from the walls or voids in the saddle-point regions. Because most of these galaxies should be star forming (e.g. Kraljic et al. 2019), this would tend to increase the median distance of star-forming galaxies to clusters.
Even though our results cannot assess which physical processes might be at play in the filament quenching, it is interesting to note in this second scenario that we also found groups that were located close to the filament spines. This might indicate that filament quenching is due to pre-processing by galaxy groups through strangulation, as argued by De Lucia et al. (2012) or Peng et al. (2015). We lack conclusive evidence to draw firm conclusions, however, and this calls for further investigation.
6. Conclusions
We presented a method for detecting the cosmic web filaments based on photometric redshifts. We showed the ability of the method, which has been applied to the COSMOS field by Laigle et al. (2018), of statistically reconstructing the filament distribution. In particular, we focused here on the infall regions around clusters, where we showed that the scaling of connectivity with cluster mass is recovered, and found a completeness of ∼70% and a purity of ∼66% for the connected filament reconstruction.
We then applied the method to the CFHTLS T0007 data to study filaments of galaxies around AMASCFI clusters (Sarron et al. 2018). We also analysed the cosmic filaments that are connected to each cluster.
Studying galaxy properties in these filaments that are connected to clusters, we find that galaxies are located closer to clusters in the redshift range 0.15 < z ≤ 0.4 than in the redshift range 0.4 < z < 0.7. In the low-redshift bin, we observed a galaxy-type gradient towards clusters, that is, passive galaxies are located closer to clusters than star-forming galaxies. No such gradient exists in our high-redshift bin. In the full redshift range, we showed that the fraction of passive galaxies is higher in our filaments than in istropically selected regions around clusters and that the passive fraction in filaments decreases with increasing distance to the cluster up to dclus ∼ 5 cMpc.
We proposed that this might be interpreted as quenching that occurs in the filaments before galaxies reach the cluster virial radius, the so-called pre-processing. Because we found that a large portion of groups not located at the nodes of the reconstructed cosmic web are in fact inside filaments (80% of groups at dskel < 1 cMpc), we postulated that this pre-processing might occur in galaxy groups during the hierarchical growth of structures, in agreement with previously proposed quenching models (e.g. Wetzel et al. 2013; Moutard et al. 2018).
We plan on building upon this proof-of-concept study by studying the passive and star-forming GLF of our filaments. This will enable us to better interpret the trends observed in the cluster GLFs and to determine the physical processes at play in quenching star-formation in dense environments.
This method is promising because it uses photometric redshifts with an accuracy typical of what is expected for future wide surveys such as Euclid and the LSST. Surveys like this will allow exploring cosmic filaments at even higher redshifts with more statistics.
Acknowledgments
We give special thanks to Didier Vibert for the development of the Python module we used in the analysis with DISPERSE. We also thank Thibaud Moutard for his help with the Vipers-MLS catalogue. We thank the referee for raising interesting questions. We acknowledge long-term financial support from CNES.
References
- Adami, C., Durret, F., Benoist, C., et al. 2010, A&A, 509, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aragón-Calvo, M. A., van de Weygaert, R., & Jones, B. J. T. 2010, MNRAS, 408, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Aragón-Calvo, M. A., van de Weygaert, R., Jones, B. J. T., & Mobasher, B. 2015, MNRAS, 454, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Le Floc’h, E., Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Bianconi, M., Smith, G. P., Haines, C. P., et al. 2018, MNRAS, 473, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. R., Kofman, L., & Pogosyan, D. 1996, Nature, 380, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Castignani, G., & Benoist, C. 2016, A&A, 595, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cautun, M. C., & van de Weygaert, R. 2011, Astrophysics Source Code Library [record ascl:1105.0370] [Google Scholar]
- Chen, Y.-C., Ho, S., Mandelbaum, R., et al. 2017, MNRAS, 466, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Codis, S., Pogosyan, D., & Pichon, C. 2018, MNRAS, 479, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, E., De Lucia, G., Hatch, N., Borgani, S., & Kang, X. 2016, MNRAS, 456, 1924 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Coil, A. L., et al. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Davidzon, I., Bolzonella, M., et al. 2017, A&A, 602, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darragh-Ford, E., Laigle, C., Gozaliasl, G., et al. 2019, MNRAS, 489, 5695 [Google Scholar]
- de Lapparent, V., Geller, M. J., & Huchra, J. P. 1986, ApJ, 302, L1 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Weinmann, S., Poggianti, B. M., Aragón-Salamanca, A., & Zaritsky, D. 2012, MNRAS, 423, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhardt, P. R. M., Brodwin, M., Gonzalez, A. H., et al. 2008, ApJ, 684, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y. 2004, PASJ, 56, 29 [NASA ADS] [Google Scholar]
- Gouin, C., Gavazzi, R., Codis, S., et al. 2017, A&A, 605, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gozaliasl, G., Finoguenov, A., Khosroshahi, H. G., et al. 2014, A&A, 566, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilton, M., Stanford, S. A., Stott, J. P., et al. 2009, ApJ, 697, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kraljic, K., Arnouts, S., Pichon, C., et al. 2018, MNRAS, 474, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraljic, K., Pichon, C., Dubois, Y., et al. 2019, MNRAS, 483, 3227 [NASA ADS] [CrossRef] [Google Scholar]
- Kurk, J., Cimatti, A., Zamorani, G., et al. 2009, A&A, 504, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuutma, T., Tamm, A., & Tempel, E. 2017, A&A, 600, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., Pichon, C., Arnouts, S., et al. 2018, MNRAS, 474, 5437 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libeskind, N. I., van de Weygaert, R., Cautun, M., et al. 2018, MNRAS, 473, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Malavasi, N., Pozzetti, L., Cucciati, O., Bardelli, S., & Cimatti, A. 2016, A&A, 585, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malavasi, N., Arnouts, S., Vibert, D., et al. 2017, MNRAS, 465, 3817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinet, N., Durret, F., Adami, C., & Rudnick, G. 2017, A&A, 604, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez, H. J., Muriel, H., & Coenda, V. 2016, MNRAS, 455, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Holden, B. P., Blakeslee, J. P., et al. 2006, ApJ, 644, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Merson, A. I., Baugh, C. M., Helly, J. C., et al. 2013, MNRAS, 429, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Mirkazemi, M., Finoguenov, A., Pereira, M. J., et al. 2015, ApJ, 799, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Moutard, T., Arnouts, S., Ilbert, O., et al. 2016, A&A, 590, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutard, T., Sawicki, M., Arnouts, S., et al. 2018, MNRAS, 479, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- Mullis, C. R., Rosati, P., Lamer, G., et al. 2005, ApJ, 623, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Olave-Rojas, D., Cerulo, P., Demarco, R., et al. 2018, MNRAS, 479, 2328 [Google Scholar]
- Papovich, C., Momcheva, I., Willmer, C. N. A., et al. 2010, ApJ, 716, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Maiolino, R., & Cochrane, R. 2015, Nature, 521, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Pogosyan, D., Pichon, C., Gay, C., et al. 2009, MNRAS, 396, 635 [CrossRef] [Google Scholar]
- Ramos, B. H. F., Pellegrini, P. S., Benoist, C., et al. 2011, AJ, 142, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, I. D., & Parker, L. C. 2017, MNRAS, 467, 3268 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, G., von der Linden, A., Pelló, R., et al. 2009, ApJ, 700, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Salerno, J. M., Martínez, H. J., & Muriel, H. 2019, MNRAS, 484, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Sarron, F. 2018, Ph. D. Thesis, Sorbonne Université, thése de doctorat en Astrophysique dirigée par Durret, Florence et Adami, Christophe [Google Scholar]
- Sarron, F., Martinet, N., Durret, F., & Adami, C. 2018, A&A, 613, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaap, W. E., & van de Weygaert, R. 2000, A&A, 363, L29 [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., Price, J., Hudson, M. J., & Phillipps, S. 2012, MNRAS, 419, 3167 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., Pichon, C., Colombi, S., Novikov, D., & Pogosyan, D. 2008, MNRAS, 383, 1655 [Google Scholar]
- Sousbie, T., Pichon, C., & Kawahara, H. 2011, MNRAS, 414, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taranu, D. S., Hudson, M. J., Balogh, M. L., et al. 2014, MNRAS, 440, 1934 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Tempel, E., Stoica, R. S., Martínez, V. J., et al. 2014, MNRAS, 438, 3465 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., Conroy, C., & van den Bosch, F. C. 2013, MNRAS, 432, 336 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zhang, Y., Miller, C. J., Rooney, P., et al. 2019, MNRAS, 488, 1 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: KS tests on distance distributions
As mentioned in Sect. 4.2, we determined whether the distributions of distances to clusters of galaxies in filaments are different for passive and star-forming galaxies in the low- (0.15 < z ≤ 0.4) and high- (0.4 < z < 0.7) redshift bins through Kolmogorov–Smirnov (KS) tests on 1000 bootstrap realisations of the absolute magnitude-matched samples. The same was done for passive and star-forming galaxies.
The distributions of the p-values of these KS tests are presented in Figs. A.1 and A.2.
 |
Fig. A.1. p-value histograms of 1000 bootstrap realisations of KS tests on the distributions of Fig. 6 at low redshift 0.15 < z ≤ 0.4 (top) and high redshift 0.4 < z < 0.7 (bottom). |
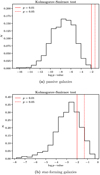 |
Fig. A.2. p-value histograms of 1000 bootstrap realisations of KS tests on the distributions of Fig. 7 for passive (top) and star-forming (bottom) galaxies. |
All Tables
Statistics of the distances between the 2D and 3D skeletons detected at 2σ and 5.5σ, respectively.
Median values of the galaxy distances to the skeleton in three mass bins, in the original 3D lightcone and in the three toy-model mocks considered in this work.
Results of the Spearman correlation test for κ vs. M200 in the three cases: 3D mock data, 2D CFHTLS-like mock data, and CFHTLS-W1.
Median values of the PDF of the filament galaxy distances to AMASCFI clusters along filaments for absolute magnitude-matched passive and star-forming galaxies in different redshift bins.
All Figures
 |
Fig. 1. Top: 100 × 100 cMpc part of a slice centred at z = 0.42 in the mock data. The background distribution logδ is the logarithm of the DTFE obtained from the galaxy distribution in the slice (with photo-zs). Red circles show the positions of halos in the lightcone with redshifts 0.41 < z < 0.43. The radius of the circle is equal to 2 × R200 for display purposes. Panel a: black lines are the 3D projected skeleton. Panel b: green lines are the 2D skeleton. Bottom: distribution of the distances between skeletons. The distance from the 2D skeleton to the 3D (projected) skeleton is shown in yellow. The distance from the 3D (projected) skeleton to the 2D skeleton is shown in blue. Top panel: PDF and bottom panel: CDF. The vertical lines and associated error bars in the top panel are the median and error on the median of each distribution. |
| In the text | |
 |
Fig. 2. Schematic view of the cosmic web as traced by DISPERSE that defines the different distances used in this chapter. The grey lines are the filaments. The red and yellow points are a node and saddle point, respectively. The red dashed circle shows the exclusion radius around the node. dskel is the distance to the skeleton, dnode/clus the distance to the node, and dclus, fil the distance to the cluster along the filament. |
| In the text | |
 |
Fig. 3. Stellar mass gradients towards filaments detected in 3D at 5.5σ in the lightcone (left) and in 2D at 2σ in the CFHTLS-like mock (right). We split the galaxy catalogue into three mass bins for which we compute the distribution of the galaxy distances to the skeleton after removing galaxies close to nodes (see text for details). Red is for 11 < log M*/M⊙ < 12, yellow for 10 < log M*/M⊙ < 11, and blue for 9.5 < log M*/M⊙ < 10. In each panel, the top distribution is the PDF of the distances to the skeleton. The filled areas around the curves represent the 68% confidence limits computed from 1000 bootstrap re-samplings of the distributions. The bottom panels show the CDF. The vertical lines and associated error bars are the median and error on the median of each distribution. |
| In the text | |
 |
Fig. 4. Mean connectivity κ in bins of halo mass log M200 in 3D in the Merson et al. (2013) lightcone (blue) and in 2D in the CFHTLS-like mock (red) and in the CFHTLS (yellow). Error bars are standard errors on the mean. |
| In the text | |
 |
Fig. 5. Left: zoom on the most massive halo in the mock. The red circle shows the radius we used to compute the connectivity (1.5 cMpc). We show only the filaments of the skeleton connected to the cluster according to the 3D reconstruction (black) and 2D reconstruction (green). The background distribution logδ is the logarithm of the DTFE obtained from the galaxy distribution in the slice (with photo-zs). Right: distribution of the distances between skeletons. Solid lines show the distribution for the filaments connected to clusters (M200 > 1014 M⊙). The distribution for the global skeleton is shown in the background as thin transparent lines. Top panel: PDF and bottom panel: CDF. The vertical lines and associated error bars in the top panel correspond to the median and error on the median of each distribution. |
| In the text | |
 |
Fig. 6. Distances to AMASCFI clusters along filaments of passive galaxies (red) and star-forming galaxies (blue) at low redshift 0.15 < z ≤ 0.4 (left) and high redshift 0.4 < z < 0.7 (right) for absolute magnitude-matched samples. The top distribution is the PDF of the distances to the skeleton. The filled areas around the curves represent the 68% confidence limits computed from 1000 bootstrap re-samplings of the distribution. The vertical lines and associated error bars are the median and error on the median of each distribution. The bottom panel shows the CDF. |
| In the text | |
 |
Fig. 7. Distances to AMASCFI clusters along filaments of passive galaxies (left) and star-forming galaxies (right) at high (dark) and low (light) redshift. See Fig. 6 for details of the symbols. |
| In the text | |
 |
Fig. 8. Galaxy passive fraction as a function of the distance to the cluster in comoving Mpc. Red points are galaxies in filaments connected to the clusters, whose clustercentric distance is computed along the filaments. The results for galaxies in filaments connected to the clusters but with clustercentric Cartesian distance are plotted in yellow. In green we plot galaxies in annuli around the clusters, which are considered to fall on the cluster isotropically. The yellow and green distributions are built from absolute magnitude-matched samples. |
| In the text | |
 |
Fig. 9. Top: histogram of groups and clusters matched (blue) and unmatched (gold) with DISPERSE nodes as a function of their M200 in the CFHTLS-W1 field. The two histograms are stacked on top of each other so that their sum is the total number of groups and clusters in the mass bin. Bottom: distribution of the distances to the skeleton of groups that is not located at a node in CFHTLS-W1. The dashed line is the chosen radius for filaments (r = 1 cMpc). See Fig. 6 for details of the symbols. |
| In the text | |
 |
Fig. A.1. p-value histograms of 1000 bootstrap realisations of KS tests on the distributions of Fig. 6 at low redshift 0.15 < z ≤ 0.4 (top) and high redshift 0.4 < z < 0.7 (bottom). |
| In the text | |
 |
Fig. A.2. p-value histograms of 1000 bootstrap realisations of KS tests on the distributions of Fig. 7 for passive (top) and star-forming (bottom) galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



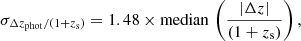
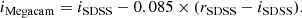
![$$ \begin{aligned} P_{\rm g}(z) = \frac{1}{\sigma (z,m_{\rm g})} \ \mathrm{exp} \left[ - \frac{(z - z_{\rm p,g})^2}{2 \sigma (z,m_{\rm g})^2} \right], \end{aligned} $$](/articles/aa/full_html/2019/12/aa35394-19/aa35394-19-eq6.gif)