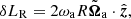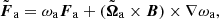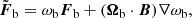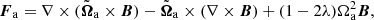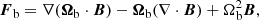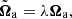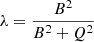| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A162 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201936433 | |
| Published online | 15 November 2019 | |
Testing magnetohydrostatic extrapolation with radiative MHD simulation of a solar flare
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: zhu@mps.mpg.de
Received:
1
August
2019
Accepted:
7
October
2019
Context. On the sun, the magnetic field vector is measured routinely solely in the photosphere. By using these photospheric measurements as a boundary condition, we developed magnetohydrostatic (MHS) extrapolation to model the solar atmosphere. The model makes assumptions about the relative importance of magnetic and non-magnetic forces. While the solar corona is force-free, this is not the case with regard to the photosphere and chromosphere.
Aims. The model has previously been tested with an exact equilibria. Here we present a more challenging and more realistic test of our model with the radiative magnetohydrodynamic simulation of a solar flare.
Methods. By using the optimization method, the MHS model computes the magnetic field, plasma pressure and density self-consistently. The nonlinear force-free field (NLFFF) and gravity-stratified atmosphere along the field line are assumed as the initial conditions for optimization.
Results. Compared with the NLFFF, the MHS model provides an improved magnetic field not only in magnitude and direction, but also in magnetic connectivity. In addition, the MHS model is capable of recovering the main structure of plasma in the photosphere and chromosphere.
Key words: Sun: magnetic fields / Sun: chromosphere / Sun: photosphere
© X. Zhu and T. Wiegelmann 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The nonlinear force-free field (NLFFF; Wiegelmann & Sakurai 2012; Guo et al. 2017) is considered a state-of-the-art model of the solar coronal magnetic field thanks to the low plasma β (Gary 2001) in the corona. This, however, is not the case in the photosphere and chromosphere, where plasma β is close to or even larger than unity. By calculating the net Lorentz force of AR7216, Metcalf et al. (1995) find that the magnetic field is not force-free in the photosphere. Zhu et al. (2016, 2017) derive the magnetic field configuration of active regions using the magnetohydrodynamic (MHD) relaxation approach. They find the force-free assumption fails beneath a height of 1.8 Mm. In order to study the magnetic field in the non-force-free region, a magnetohydrostatic (MHS) extrapolation should be used.
The MHS extrapolation is introduced on the basis of the MHS equilibria assumption, which is supposed to be a better approximation in the low layers of the Sun than the force-free assumption. The governing equations of the MHS equilibria can be written as
where B, p and ρ are the magnetic field, plasma pressure and plasma density, respectively. We note that the equations above have been normalized using the following constants: ρ0 = 2.7 × 10−1 g cm−3 (density), T0 = 6 × 103 K (temperature), g = 2.7 × 104 cm s−2 (gravitational acceleration), 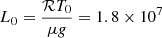 cm (length),
cm (length), 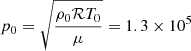 dyn cm−2 (plasma pressure), and
dyn cm−2 (plasma pressure), and 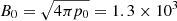 G (magnetic field). Low (1985, 1991, 1992) and Neukirch & Rastätter (1999) found the MHS equations can be linearized when the current consists of a linear component parallel to the magnetic field and another component perpendicular to gravity. Using this so-called linear MHS model, Aulanier et al. (1998, 1999) derived the magnetic field and plasma distribution of AR7722 and AR7986. More recently, Wiegelmann et al. (2015, 2017) use this model to extrapolate the MHS equilibria by SUNRISE/IMaX magnetogram. The unprecedented resolution (40 km pixel−1) of IMaX enabled the model to resolve the thin non-force-free layer with several tens of grids. However, the linear MHS model excludes the high concentration of electric currents and Lorentz forces. This is somewhat similar to the well-known limitations of linear force-free field in modeling the corona.
G (magnetic field). Low (1985, 1991, 1992) and Neukirch & Rastätter (1999) found the MHS equations can be linearized when the current consists of a linear component parallel to the magnetic field and another component perpendicular to gravity. Using this so-called linear MHS model, Aulanier et al. (1998, 1999) derived the magnetic field and plasma distribution of AR7722 and AR7986. More recently, Wiegelmann et al. (2015, 2017) use this model to extrapolate the MHS equilibria by SUNRISE/IMaX magnetogram. The unprecedented resolution (40 km pixel−1) of IMaX enabled the model to resolve the thin non-force-free layer with several tens of grids. However, the linear MHS model excludes the high concentration of electric currents and Lorentz forces. This is somewhat similar to the well-known limitations of linear force-free field in modeling the corona.
A few methods have been developed to solve the MHS equations in the general case numerically. Hu & Dasgupta (2006, 2008) propose an approach for deriving the non-force-free field by superposing one potential field and two linear force-free fields. The Grad-Rubin iteration procedure is extended by Gilchrist & Wheatland (2013), Gilchrist et al. (2016) to compute the MHS equilibria. The MHD relaxation method, which applies an “evolution technique”, is capable of yielding the MHS solution (McClymont & Mikic 1994; Jiao et al. 1997; Zhu et al. 2013). Wiegelmann & Inhester (2003), Wiegelmann & Neukirch (2006) and Wiegelmann et al. (2007) use the optimization method to treat the MHS equations without gravity in different coordinates systems. We extend the optimization method to model the system with a gravity force in Zhu & Wiegelmann (2018, hereafter Paper I). In that work, we test our model using a perfect MHS equilibria (Low 1985, 1991). However, the actual Sun is very dynamic and a lot more complex. Here we aim to investigate whether the MHS extrapolation functions in a realistic situation.
In this paper, we apply our numerical code to reconstruct a snapshot of the solar flare simulation. The simulation includes 3D radiative transfer in the convection zone and photosphere, optically thin radiation and field-aligned heat conduction in the corona, etc. These features set the simulation into a realistic environment. The organization of the paper is as follows. In Sect. 2, we briefly describe the simulation and assess the physical state of the reference snapshot. In Sect. 3, we introduce the optimization method for the MHS model and the numerical setup to extrapolate the reference snapshot. In Sect. 4, we evaluate the results through several metrics. In Sect. 5, we discuss a few factors that can impact the ability of our model to reconstruct the magnetic field and plasma. Concluding remarks are presented in Sect. 6.
2. The active region in the radiative MHD simulation
Cheung et al. (2019) carry out a radiative MHD simulation of a solar flare. They use the Max-Planck-Institute for Aeronomy/University of Chicago Radiation Magneto-hydrodynamics (MURaM) code, which allows for simulations spanning from the upper convection zone into the solar corona (Vögler et al. 2005; Rempel 2017). The initial setup consists of bipolar sunspots. After the thermally relaxed equilibra are reached, they impose the emergence of another twisted bipolar flux system at the bottom boundary. The accumulation of the magnetic energy finally leads to an abrupt relaxation which powers coronal mass ejection and a flare.
Among all the snapshots that are available for download1, we choose the last one (at about 8 minutes after the flare) as the reference model for our test. The original data spans ±49.152 and ±24, 576 Mm in the x- and y-axes, respectively. In the z-axis, the data spans from 7.5 Mm beneath the photosphere to 41.6 Mm above. The grid spacing is 192 (64) km in the horizontal (vertical) direction. In this study, we focus on the MHS equilibrium in the lower atmosphere. For this purpose, the data from photosphere to 8.192 Mm above are extracted. The photosphere is cut at the average geometrical height corresponding to optical depth unity. This is done by using “hgcr_hslice.pro” with input parameter “k = 116” which is suggested in “readme.txt”. Both “hgcr_hslice.pro” and “readme.txt” can be downloaded from the above data link. Photospheric magnetogram and the magnetic field lines in the sub-volume are illustrated in Fig. 1.
 |
Fig. 1. Panel a: magnetogram at height where ⟨τ⟩=1, used as the boundary input. The “hgcr_hslice.pro” from the data link is used to derive the MHD quantities sampled at constant height. For photosphere where ⟨τ⟩ = 1, set input parameter k = 116. Panel b: magnetic field line patterns in the box outlined in panel a. Purple/green lines represent open/closed field lines. |
The system continues to develop the entire time over the course of the simulation. However, Fig. 2a shows, at the moment we are considering, that the time-varying term is smaller than other terms in the momentum equation. The reference snapshot is not strictly static (see panel b). Part of the velocity comes from the violence of the flare eruption. To see how the moving fluid affects the magnetic field and plasma, we look at the momentum equation in a steady state.
 |
Fig. 2. Panel a: planar averaged value of each term in momentum equation. Panel b: planar averaged velocity varies along height. |
where ρ, p, v and B are mass density, pressure, velocity and magnetic field, respectively. The inertial term (Pv = ρv2), plasma pressure (Pg = p) and magnetic pressure(Pb = B2/2) in the above equation compensate for one another. Figure 3 shows the influence of these three terms. We see from panel a that: (1) plasma pressure affects the magnetic field significantly near the photosphere; (2) the magnetic field dominates the three terms above 300 km. Panel b shows that the strength of inertial term is stronger than that of plasma pressure in the layer 1 Mm < z < 2 Mm. We deduce that in the extrapolation: (1) plasma pressure should be taken into account near the photosphere; (2) excluding the inertial term has limited effects on the pattern of the magnetic field; (3) excluding the inertial term has significant impact on the plasma distribution above 1 Mm. We conclude that this snapshot is suitable, albeit imperfect, to test the MHS extrapolation.
 |
Fig. 3. Panel a: horizontal averages for reference model in sub-volume outlined in Fig. 1a. The inertial term |
3. The magnetohydrostatic extrapolation
3.1. Method
The optimization method used to solve the MHS equations in this study is described in detail in Paper I. Here we give a short outline and its recent improvements. The method involves the minimization of the functional
with
where ωa and ωb the weighting functions and ν the Lagrangian multiplier. W is a diagonal matrix to incorporate the measurement error of the magnetic field and gas pressure. [Bopt popt ρopt] and [Bobs pobs ρobs] are the optimized and observed quantities in the photosphere respectively. The weighting functions and slow boundary injection are found to be capable of improving the results (Wiegelmann 2004; Wiegelmann et al. 2012). Here, for simplicity, we set the weighting function to unity over the whole region and use a fixed lower boundary. We note that in Eqs. (5) and (6), the denominator (B2 + p) is different than that of the previous code (B2). We make the change in order to avoid nonphysically large contribution to the functional L from the weak magnetic field region. Then, the solution of the MHS equations can be optimized by
with p = Q2 and ρ = R2 which ensure the positive p and ρ.
The gradient descent method is used to find the minimum:
where δLB, δLQ and δLR (see Appendix A) are the functional derivatives respect to function B, Q and R, respectively. μB, μQ and μR control the step length.
In Paper I, pressure distribution on the photospheric pressure was derived by solving the following Poisson’s equation
where fph is the 2D horizontal Lorentz force on the photosphere,  ,
,  is the 2D Laplacian. In this study, however, the Poisson method does not work effectively because of the dynamics in the simulation. Instead, a simple vertical magnetic flux tube is assumed to derive the pressure distribution from the force balance condition. That is:
is the 2D Laplacian. In this study, however, the Poisson method does not work effectively because of the dynamics in the simulation. Instead, a simple vertical magnetic flux tube is assumed to derive the pressure distribution from the force balance condition. That is:
where pquiet is the plasma pressure in the quiet Sun where the magnetic field is extremely weak. We set p = 10−3pquiet when negative pressure appeared from Eq. (12).
3.2. Apply to a MURaM snapshot
Based on a photospheric vector magnetogram from the MURaM simulation, we extrapolate the magnetic field, plasma pressure and density on 512 × 256 × 128 grid points. The grid spacing (192/64 km in horizontal/vertical direction) is the same as the one in the simulation. The procedure shown below to perform the MHS extrapolation is slightly different from the one presented in Paper I:
1. Calculate a NLFFF model (Wiegelmann 2004; Wiegelmann et al. 2006).
2. Distribute the pressure in the photosphere by using 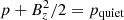 . Calculate the pressure along the magnetic field line with the gravity-stratified assumption (see 1D temperature profile in Fig. 4). Calculate the density in the computational box by using ideal gas with a 1D temperature model.
. Calculate the pressure along the magnetic field line with the gravity-stratified assumption (see 1D temperature profile in Fig. 4). Calculate the density in the computational box by using ideal gas with a 1D temperature model.
 |
Fig. 4. Temperature profile of the equilibrium atmosphere in the initial condition. |
3. Iterate for B, Q and R by Eqs. (8)–(10). This step is repeated until L reaches its minimum.
4. Result
4.1. Plasma solution
The MHS model computes the plasma in the computational box, which is an important advantage over the NLFFF model. Figures 5 and 6 compare the pressure and density of the two models at different levels. At the bottom boundary, the plasma of the MHS model is very similar to that of the reference model, which denotes that 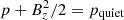 does indeed make sense. Above the bottom boundary, the MHS model is able to recover the main structures of the plasma in the photosphere and lower chromosphere (below 1 Mm). For example: the depletion of pressure and density in the strong field region, the spiral structure (indicated by arrows in Figs. 5 and 6) in the new emerging region, and the “tentacle” around the spots as well. From another perspective, Fig. 7 illustrates pressure and density in a vertical plane. We clearly see the main structures below 1 Mm are recovered well. Above 1 Mm, however, a large deviation appears. As we did not use the temperature data in the modeling, the plasma cannot be determined precisely. Another reason for the inaccurate plasma result comes from the dynamic nature of the atmosphere.
does indeed make sense. Above the bottom boundary, the MHS model is able to recover the main structures of the plasma in the photosphere and lower chromosphere (below 1 Mm). For example: the depletion of pressure and density in the strong field region, the spiral structure (indicated by arrows in Figs. 5 and 6) in the new emerging region, and the “tentacle” around the spots as well. From another perspective, Fig. 7 illustrates pressure and density in a vertical plane. We clearly see the main structures below 1 Mm are recovered well. Above 1 Mm, however, a large deviation appears. As we did not use the temperature data in the modeling, the plasma cannot be determined precisely. Another reason for the inaccurate plasma result comes from the dynamic nature of the atmosphere.
 |
Fig. 5. Pressure distribution of reference (left) and MHS model (right) in different planes. |
 |
Fig. 6. Density distribution of reference (left) and MHS model (right) in different planes. |
 |
Fig. 7. Vertical slice along cut indicated in Fig. 5. Panels a,b: pressure from reference/MHS model. Panels c,d: density from reference/MHS model. |
4.2. 3D magnetic structure in the models
Figure 8 shows the differences in the flux tube, which is widely studied in solar activity events. The field lines of different models start from the same seeds where the vertical electric current is strong. The comparison signifies that the MHS model is superior to the NLFFF model in reconstructing long twisted field lines. This leads not only to a different amount of twist, but also to the connectivity of the magnetic field. As illustrated in Fig. 9, the left footpoint is connected to another footpoint far away in the twin emerging spot in both the reference and MHS model. In the NLFFF, however, it connects to the closer side of the untwisted spot. The NLFFF line simply fails to bend up before it touches the photosphere, which results in a large difference in connectivity. It is worth noting that the vector magnetogram used in NLFFF extrapolation is preprocessed to smooth and fulfill the force-free conditions. Without preprocessing the photospheric boundary, the data are inconsistent with the force-free assumption and consequent force-free computations do not converge (which is not shown here). There have been some studies reporting that the preprocessing improves the extrapolation considerably (Wiegelmann et al. 2006; Metcalf et al. 2008).
 |
Fig. 8. Selected field lines of magnetic flux tube. |
 |
Fig. 9. Sample field lines of reference/MHS/NLFFF model from above (left) and south (right). Vertical scale of the right panel has been expanded. |
To quantify how well each is extrapolation performed, we use 6 metrics as noted in Schrijver et al. (2006) and Barnes et al. (2006) to compare vector field b (our results) and B (the reference MHD model):
where Cvec, CCS, EN, EM and Ee are vector correlation, Cauchy-Schwarz inequality, normalized vector error, mean vector error and magnetic energy metric, respectively. N is the number of grid points in the computation box. In addition, the field line divergence (FLD) metric measures how well the magnetic connectivity is recovered. For both the simulation and extrapolations, a score can be given to any point, where the field line is closed, by the distance between the endpoints divided by the length of the field line. A single score is assigned by the fraction of the area at the lower boundary that has an FLD below 20% (10%, as adopted in Barnes et al. 2006 and Metcalf et al. 2008).
The domain of comparison (within a grid size of 210 × 180 × 64) has the same field-of-view (FOV) as Fig. 1b, extending upward to the height of 4.1 Mm.
A quantitative evaluation of the two models is given in Table 1. The MHS model scores better than NLFFF in all metrics. It is not clear, based on the minute difference between Cvec and CCS, MHS extrapolation is a significant improvement over the NLFFF extrapolation. However, for the metric 1 − Em, the MHS extrapolation scores 0.65, which is an improvement over the NLFFF’s score of 0.57. It should be noted that Cvec and CCS are sensitive to differences in angle between the two vectors that are being compared, whereas En and Em are sensitive to both angle and norm differences. The FLD is the most rigorous metric among the six we used. It also indicates that the MHS model performs better than the NLFFF model.
Metrics for two extrapolations applied to vector magnetogram of simulation.
We also present a comparison of the first four metrics in every plane along the height (see Fig. 10). Again, the MHS extrapolation scores better. It is worth noting that the weak field region can contribute significantly to the metrics of CCS and EM (see Eqs. (14) and (16)). That is the reason why the two metrics drop dramatically in the layers near the photosphere. The scores of two different extrapolations get closer as height increases, which indicates that the influence of the plasma effect decreases as height increases.
 |
Fig. 10. Magnetic field metrics vary along height. |
4.3. Magnetic twist and quasi-separatrix layers (QSLs) in the models
Finally, we compare the magnetic twist numbers Tw, Tg and squashing factor Qs for different models. Tw and Tg are defined by Berger & Prior (2006) as the twist number of one magnetic field line about the neighboring line and the axis, respectively. They are different in most situations. The self-helicity which could be measured by local twist Tw is negligible for a large number of flux tube (Demoulin et al. 2006). In this study, Tg is applicable to evaluate the twist since only one flux rope with finite size exists. Tw and Tg are given as:
where T(s) is the unit tangent vector to the axis curve, V(s) is a unit vector normal to T(s) and points to the secondary curve, J∥ is the parallel component of the electric current. The integration is carried out along the specific field line. QSLs are the generalized topological structures (Demoulin et al. 1996) which are the regions with high squashing factor Qs. Qs is defined by mapping the field line (Titov et al. 2002):
where (x1, y1) and (x2, y2) are the two footpoints of one field line. Both indexes are important in studying the 3D magnetic structure. We used the code developed by Liu et al. (2016) to calculate Tw and Qs. To compute Tg, we first have to locate the axis. We assume as the axis any one of a number of magnetic field lines that penetrate the vertical square (4 × 4 Mm, thick black line from the top view shown in the left panel of Fig. 11) and a score can be assigned to this line based on the average Tg of the surrounding lines. Then we define the axis as the field line whose score is the greatest (see the axis and sample surrounding field lines in Fig. 11). A similar approach is used in Guo et al. (2010). For each model, the axis is determined by the same way. As a result, the average Tg about the axes of the reference, MHS and NLFFF model is 0.95, 0.94 and 0.88, respectively. The twists of the field lines close to the axis are sufficiently reconstructed by the MHS model.
 |
Fig. 11. Axis and surrounding field lines of reference model. Left: axis (purple) determined by average Tg of surrounding field lines. Black/dotted contours denote positive/negative polarity. Right: sample field lines of flux rope. |
The twist number Tw is illustrated in Fig. 12a–f. The white ellipses represent the central area that is mainly recovered, whereas the black ellipses show the mismatched areas. We can see a similar mismatch in the two extrapolations since the MHS model uses the NLFFF solution as the initial condition. If we look to some Tw structures with small size, the MHS model includes more of them that exist in the reference model. That is because the MHS model uses the unpreprocessed magnetogram while the NLFFF model uses the preprocessed one. Without preprocessing, NLFFF does not converge because the data are inconsistent with the force-free assumption. Preprocessing makes the data force-free consistent, but it also naturally removes structures related to finite Lorentz-forces.
The QSLs represent the layers which separate magnetic systems with different topologies. We can see the QSLs, which are indicated by the white arrow (Fig. 12j), mainly divide the central area into two topological parts. However, there are additional QSLs in the two extrapolations which divide the same area into three parts. So we should be very careful to use the QSLs result from extrapolation.
5. Discussion
The inability to generate an MHS model that sufficiently recovers the reference model is rather disappointing. This has led us to examine the new extrapolation in order to distinguish certain factors that impact out ability to produce a robust model.
5.1. Choice of free parameters and initial conditions
The three parameters μB, μp and μρ control the step length when the Eq. (4) is minimizing. μB is computed at every step by the line search method. We assume μp = μB because Q has the same dimension as B. We further assume μρ = ϵμB. Table 2 shows the case study with ϵ varied between 0.1 and 10. We find the functional L decreases with increasing ϵ. However, the most accurate magnetic field generated by the code when ϵ = 5. Figure 13 shows how the free parameter ϵ affect the pressure and density result. The density is much more affected than the pressure by ϵ. A larger ϵ leads to a stronger contrast of the density because of the higher weight introduced by ϵ. From the above case studies, we set ϵ = 5 as the optimized value for the extrapolation.
Metrics for various ϵ.
 |
Fig. 13. Pressure and density at height of 0.96 Mm with different ϵ. ϵ = 5a represents case with potential field as the initial condition. |
The choice of the initial condition of magnetic field has significant influence on the results (Wiegelmann 2004; Schrijver et al. 2006; Zhu & Wiegelmann 2018). We ran an additional test of ϵ = 5 with potential field as the initial condition. The test is named as 5a in Table 2 and Fig. 13. It shows that the MHS extrapolation with the initial potential field has lower scores for the magnetic field evaluation and less accurate plasma distribution.
5.2. All variables in the bottom boundary provided
Table 1 also compares the magnetic field of reference model with the result for case “MHS(a)” for which the pressure and density in the bottom boundary is provided. We observe a limited increase in the metrics for the magnetic field comparison. Figures 14 and 15 show the plasma distribution at the extremely low height (≤0.32 Mm) benefits from the application of the accurate bottom boundary condition. Above 1 Mm, however, the plasma result shows no improvement.
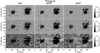 |
Fig. 14. Pressure comparison at different levels. |
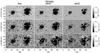 |
Fig. 15. Density comparison at different levels. |
The increasing dynamics at the higher atmosphere make the result resistant to the choice of the plasma boundary condition at the bottom. Nevertheless, the simplest boundary condition with the plasma uniformly distributed is not able to yield a satisfactory result. So, the plasma boundary described in Sect. 3.1 remains an adequate choice.
6. Conclusions
In this work, we applied the MHS extrapolation code to model an active region that serves as a snapshot of the flare simulation. The magnetic field, plasma pressure, and density are computed consistently by the model.
The MHS model is capable of reconstructing the main structures of pressure and density in the photosphere and lower choromosphere (below 1 Mm). As we did not use the temperature data to constrain the plasma, the plasma solution above 1 Mm cannot be relied on. The deviation gets larger as the height increases.
Generally, the magnetic field solution is improved compared with the NLFFF not only in terms of magnitude and direction, but magnetic connectivity as well. As to the flux tube, which is of vital importance for eruptive events, the twists of the field lines are constructed well. However, some twist structures derived outside the active region are incorrect. It is worth noting that even right inside the active region, the extrapolated QSLs could be unrealistic. The Qs value is computed by tracing the field lines from which the high nonlinearity is introduced. A tiny deviation shown in Fig. 9 near the bald patch area results in a large difference in connectivity.
Paper I developed the MHS extrapolation and tested the model using a semi-analytic MHS solution. In this work, we present a more challenging test of our model with a radiative MHD simulation of a solar flare. The next activity planned is an application for the IMaX magnetogram (Martínez Pillet et al. 2011) on board the SUNRISE balloon-borne solar observatory (Barthol et al. 2011; Berkefeld et al. 2011) during its second flight (Solanki et al. 2017).
Acknowledgments
We appreciate the constructive comments from the anonymous referee. This work was supported by DFG-grant WI 3211/4-1.
References
- Aulanier, G., Démoulin, P., Schmieder, B., Fang, C., & Tang, Y. H. 1998, Sol. Phys., 183, 369 [Google Scholar]
- Aulanier, G., Démoulin, P., Mein, N., et al. 1999, A&A, 342, 867 [NASA ADS] [Google Scholar]
- Barnes, G., Leka, K. D., & Wheatland, M. S. 2006, ApJ, 641, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Barthol, P., Gandorfer, A., Solanki, S. K., et al. 2011, Sol. Phys., 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, M. A., & Prior, C. 2006, J. Phys. A Math. Gen., 39, 8321 [NASA ADS] [CrossRef] [Google Scholar]
- Berkefeld, T., Schmidt, W., Soltau, D., et al. 2011, Sol. Phys., 268, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Chintzoglou, G., et al. 2019, Nat. Astron., 3, 160 [Google Scholar]
- Demoulin, P., Henoux, J. C., Priest, E. R., & Mandrini, C. H. 1996, A&A, 308, 643 [NASA ADS] [Google Scholar]
- Demoulin, P., Pariat, E., & Berger, M. A. 2006, Sol. Phys., 233, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gilchrist, S. A., & Wheatland, M. S. 2013, Sol. Phys., 282, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gilchrist, S. A., Braun, D. C., & Barnes, G. 2016, Sol. Phys., 291, 3583 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ding, M. D., Schmieder, B., et al. 2010, ApJ, 725, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Cheng, X., & Ding, M. 2017, Sci. China Earth Sci., 60, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., & Dasgupta, B. 2006, Res. Lett., 33, L15106 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., & Dasgupta, B. 2008, Sol. Phys., 247, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Jiao, L., McClymont, A. N., & Mikic, Z. 1997, Sol. Phys., 174, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., Kliem, B., Titov, V. S., et al. 2016, ApJ, 818, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 1985, ApJ, 293, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 1991, ApJ, 370, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 1992, ApJ, 399, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- McClymont, A. N., & Mikic, Z. 1994, ApJ, 422, 899 [Google Scholar]
- Metcalf, T. R., Jiao, L., McClymont, A. N., Canfield, R. C., & Uitenbroek, H. 1995, ApJ, 439, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., De Rosa, M. L., Schrijver, C. J., et al. 2008, Sol. Phys., 247, 269 [Google Scholar]
- Neukirch, T., & Rastätter, L. 1999, A&A, 348, 1000 [NASA ADS] [Google Scholar]
- Rempel, M. 2017, ApJ, 834, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., De Rosa, M. L., Metcalf, T. R., et al. 2006, Sol. Phys., 235, 161 [Google Scholar]
- Solanki, S. K., Riethmüller, T. L., Barthol, P., et al. 2017, ApJs, 229, 2 [Google Scholar]
- Titov, V. S., Hornig, G., & Démoulin, P. 2002, J. Geophys. Res. (Space Phys.), 107, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Inhester, B. 2003, Sol. Phys., 214, 287 [Google Scholar]
- Wiegelmann, T., & Neukirch, T. 2006, A&A, 457, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., & Sakurai, T. 2012, Liv. Rev. Sol. Phys., 9, 5 [Google Scholar]
- Wiegelmann, T., Inhester, B., & Sakurai, T. 2006, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Neukirch, T., Ruan, P., & Inhester, B. 2007, A&A, 475, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Thalmann, J. K., Inhester, B., et al. 2012, Sol. Phys., 281, 37 [NASA ADS] [Google Scholar]
- Wiegelmann, T., Neukirch, T., Nickeler, D. H., et al. 2015, ApJ, 815, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Neukirch, T., Nickeler, D. H., et al. 2017, ApJS, 229, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X., & Wiegelmann, T. 2018, ApJ, 866, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X. S., Wang, H. N., Du, Z. L., & Fan, Y. L. 2013, ApJ, 768, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X., Wang, H., Du, Z., & He, H. 2016, ApJ, 826, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, X., Wang, H., Cheng, X., & Huang, C. 2017, ApJ, 844, L20 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Variable definitions
The variables in Eqs. (8)–(10) are defined as
where 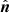 is the inward unit vector on the surface S.
is the inward unit vector on the surface S.
All Tables
All Figures
 |
Fig. 1. Panel a: magnetogram at height where ⟨τ⟩=1, used as the boundary input. The “hgcr_hslice.pro” from the data link is used to derive the MHD quantities sampled at constant height. For photosphere where ⟨τ⟩ = 1, set input parameter k = 116. Panel b: magnetic field line patterns in the box outlined in panel a. Purple/green lines represent open/closed field lines. |
| In the text | |
 |
Fig. 2. Panel a: planar averaged value of each term in momentum equation. Panel b: planar averaged velocity varies along height. |
| In the text | |
 |
Fig. 3. Panel a: horizontal averages for reference model in sub-volume outlined in Fig. 1a. The inertial term |
| In the text | |
 |
Fig. 4. Temperature profile of the equilibrium atmosphere in the initial condition. |
| In the text | |
 |
Fig. 5. Pressure distribution of reference (left) and MHS model (right) in different planes. |
| In the text | |
 |
Fig. 6. Density distribution of reference (left) and MHS model (right) in different planes. |
| In the text | |
 |
Fig. 7. Vertical slice along cut indicated in Fig. 5. Panels a,b: pressure from reference/MHS model. Panels c,d: density from reference/MHS model. |
| In the text | |
 |
Fig. 8. Selected field lines of magnetic flux tube. |
| In the text | |
 |
Fig. 9. Sample field lines of reference/MHS/NLFFF model from above (left) and south (right). Vertical scale of the right panel has been expanded. |
| In the text | |
 |
Fig. 10. Magnetic field metrics vary along height. |
| In the text | |
 |
Fig. 11. Axis and surrounding field lines of reference model. Left: axis (purple) determined by average Tg of surrounding field lines. Black/dotted contours denote positive/negative polarity. Right: sample field lines of flux rope. |
| In the text | |
 |
Fig. 12. Tw and Qs comparisons at different levels according to FOV of Fig. 1b. |
| In the text | |
 |
Fig. 13. Pressure and density at height of 0.96 Mm with different ϵ. ϵ = 5a represents case with potential field as the initial condition. |
| In the text | |
 |
Fig. 14. Pressure comparison at different levels. |
| In the text | |
 |
Fig. 15. Density comparison at different levels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



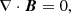
![$$ \begin{aligned} \nabla \cdot \left[\rho \boldsymbol{v}\boldsymbol{v}-\boldsymbol{B}\boldsymbol{B}+\left(\frac{B^{2}}{2}+p\right)\boldsymbol{I}\right] =0, \end{aligned} $$](/articles/aa/full_html/2019/11/aa36433-19/aa36433-19-eq6.gif)
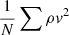
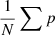
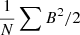
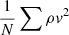
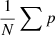
![$$ \begin{aligned} \begin{aligned} L(\boldsymbol{B},p,\rho )&=\int _{V}\omega _{\rm a}B^{2}\Omega _{\rm a}^{2}+\omega _{\rm b}B^{2}\Omega _{\rm b}^{2}\mathrm{d}V\\&\quad +\nu \int _{\rm S}([\boldsymbol{B}_{\rm opt}\ p_{\rm opt}\ \rho _{\rm opt}]-[\boldsymbol{B}_{\rm obs}\ p_{\rm obs}\ \rho _{\rm obs}])\cdot \\&\qquad \mathbf W \cdot ([\boldsymbol{B}_{\rm opt}\ p_{\rm opt}\ \rho _{\rm opt}]-[\boldsymbol{B}_{\rm obs}\ p_{\rm obs}\ \rho _{\rm obs}])\mathrm{d}^{2}S, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2019/11/aa36433-19/aa36433-19-eq12.gif)
![$$ \begin{aligned} \boldsymbol{\Omega _{\rm a}}&= \left[(\nabla \times \boldsymbol{B})\times \boldsymbol{B}-\nabla p - \rho {\hat{\boldsymbol{z}}}\right]/(B^2+p), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36433-19/aa36433-19-eq13.gif)
![$$ \begin{aligned} \boldsymbol{\Omega _{\rm b}}&= [(\nabla \cdot \boldsymbol{B})\boldsymbol{B}]/(B^2+p), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36433-19/aa36433-19-eq14.gif)
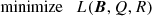
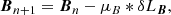
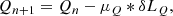
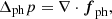
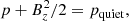
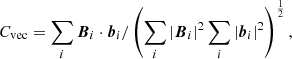
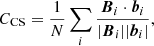
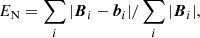
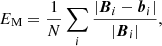
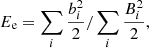
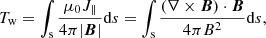
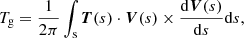
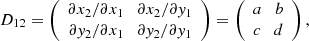
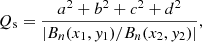
![$$ \begin{aligned} \delta L_{\rm Q}&=2[\lambda (\omega _{\rm a}\Omega _{\rm a}^{2}+\omega _{\rm b}\Omega _{\rm b}^{2})-\nabla \cdot (\boldsymbol{\omega _{\rm a}\tilde{\Omega }_{\rm a}})]Q,\end{aligned} $$](/articles/aa/full_html/2019/11/aa36433-19/aa36433-19-eq35.gif)