| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201936206 | |
| Published online | 31 October 2019 | |
Active minimization of non-common path aberrations in long-exposure imaging of exoplanetary systems
LESIA, Observatoire de Paris, Université PSL, CNRS, Université de Paris, Sorbonne Université, 5 Place Jules Janssen, 92195 Meudon, France
e-mail: garima.singh@obspm.fr
Received:
28
June
2019
Accepted:
13
September
2019
Context. Spectroscopy of exoplanets is very challenging because of the high star-planet contrast. A technical difficulty in the design of imaging instruments is the noncommon path aberrations (NCPAs) between the adaptive optics (AO) sensing and the science camera, which induce planet-resembling stellar speckles in the coronagraphic science images. In an observing sequence of several long exposures, quickly evolving NCPAs average out and leave behind an AO halo that adds photon noise to the planet detection. Static NCPA can be calibrated a posteriori using differential imaging techniques. However, NCPAs that evolve during the observing sequence do not average out and cannot be calibrated a posteriori. These quasi-static NCPAs are one of the main limitations of the current direct imaging instruments such as SPHERE, GPI, and SCExAO.
Aims. Our aim is to actively minimize the quasi-static speckles induced in long-exposure images. To do so, we need to measure the quasi-static speckle field above the AO halo.
Methods. The self-coherent camera (SCC) is a proven technique which measures the speckle complex field in the coronagraphic science images. It is routinely used on the THD2 bench to reach contrast levels of < 10−8 in the range 5 − 12 λ/D in space-related conditions. To test the SCC in ground conditions on THD2, we optically simulated the residual aberrations measured behind the SPHERE/VLT AO system under good observing conditions.
Results. We demonstrate in the laboratory that the SCC can minimize the quasi-static speckle intensity in the science images down to a limitation set by the AO halo residuals. The SCC reaches 1σ raw contrast levels below 10−6 in the region 5 − 12 λ/D at 783.25 nm in our experiments.
Conclusions. The results presented in this article reveal an opportunity for the current and future high-contrast imaging systems to adapt the SCC for real-time measurement and correction of quasi-static speckles in long-exposure science observations from the ground.
Key words: instrumentation: high angular resolution / instrumentation: adaptive optics / techniques: high angular resolution
© G. Singh et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
One of the goals of the Extremely Large Telescopes (ELTs) is to study the composition and chemistry of the exoplanetary atmospheres using direct imaging. Such a challenge requires the star-planet light to be separated. Exoplanets are 104–1010 times fainter than their host stars at only a fraction of an arcsecond, and a device called a coronagraph is required to reduce the stellar flux without affecting the light from the planet. The efficiency with which a coronagraph can reject the starlight depends on how well a high-contrast imaging (HCI) instrument deals with the optical aberrations of various natures (atmospheric turbulence and optical defects; Guyon 2005; Guyon et al. 2006). The atmosphere of Earth introduces dynamic wavefront errors creating quickly varying speckles in coronagraphic science images obtained by the ground-based HCI instruments. The adaptive optics (AO) systems compensate most of these fast wavefront errors, but the AO correction is not perfect. Servo lag errors and noncommon path aberrations (NCPAs) between the sensing and the science channel degrade the performance of AO systems (Racine et al. 1999; Bloemhof et al. 2001; Roddier 2004). Despite using the best AO systems (Poyneer et al. 2016; Fusco et al. 2016), speckle patterns appear in coronagraphic images and readily imitate signals from exoplanets (Beuzit et al. 1997; Oppenheimer et al. 2001; Boccaletti et al. 2003, 2004).
In a typical long exposure, the AO-induced quickly varying speckles (due to servo lag errors) average out and create a low spatial frequency halo that adds photon noise when looking for point-like sources such as exoplanets. Static speckles in an observing sequence of such exposures can be calibrated post-observation using differential imaging techniques (Racine et al. 1999; Marois et al. 2006; Martinez et al. 2013, 2012). Quasi-static speckles however evolve from one exposure to another with the slowly changing aberrations (thermal changes and gravity flexures). They can partially be calibrated a posteriori by differential imaging techniques, however the residuals left behind limit all the current HCI instruments such as SPHERE (Beuzit et al. 2006, 2019), GPI (Macintosh et al. 2014), and SCExAO (Jovanovic et al. 2015). In conclusion, the long-exposure coronagraphic images coming out of these instruments have three main visible features: a smooth halo, static speckles that remain unchanged in all images of a science sequence, and quasi-static speckles that vary slowly during the sequence. While we consider in our paper that the lifetime of static and quasi-static speckles is longer than the exposure time (typically a few seconds), it is assumed that the evolving time of quasi-static speckles is shorter than the length of the observing sequence (typically one hour). Our focus is therefore to address the quasi-static speckles that remain static for a few images but vary along the complete sequence of observations.
With a priori knowledge of speckle evolution lifetime (Milli et al. 2016), more evolved a posteriori algorithms may well calibrate the speckle pattern. However, any such method can directly benefit from an active technique that minimizes the static or quasi-static speckles in each science image during an observation. Active suppression of these speckles requires measurement of the electric field associated with the speckles directly from a coronagraphic image using a focal plane wavefront sensor (FPWFS). Several FPWFSs have been proposed such as phase diversity (Bordé & Traub 2006; Give’on et al. 2007; Sauvage et al. 2012) and the self-coherent camera (SCC; Baudoz et al. 2006, 2012). Once the electric field is measured, one or several deformable mirrors (DM) can then be used to minimize the speckle intensity in a region of the image called the dark hole (Malbet et al. 1995). Very encouraging laboratory results have been obtained on the coronagraphic testbeds simulating the space-related environment. The stellar speckle intensity is shown to be reduced by a factor of up to 105 (Belikov et al. 2007; Trauger et al. 2011, 2012; Mazoyer et al. 2013, 2014) which would enable the detection of planets 1010 times fainter than their host star. Several attempts on ground-based Extreme-AO instruments have been performed with moderate results. The stellar speckle intensity has been suppressed by only a factor of up to ten (Savransky et al. 2012; Martinache et al. 2014; Bottom et al. 2017; Matthews et al. 2017; Wilby et al. 2017; Vigan et al. 2019; Galicher et al. 2019) reaching contrast levels of roughly 10−6. Most of these techniques temporally modulate the speckle intensity to measure their phase and at least three images are needed for each estimation of the electric field. The quasi-static speckles that evolve faster than every four images cannot be correctly estimated and therefore set a limitation for the speckle estimation. Addressing this concern, our team proposed the SCC that spatially modulates the speckle intensity so that the associated complex electric field can be measured in every science image. The drawback is that a finer sampling of the coronagraphic image is required as compared to the temporal modulation techniques. The SCC has been developed and rigorously tested in space-related environments on the THD2 bench at the Paris Observatory (Baudoz et al. 2018).
This paper presents the laboratory performance of the SCC in ground-based conditions. In Sect. 2, we first define the expression of the averaged electric field that can be measured in a long-exposure coronagraphic science image given any FPWFS. Section 3 presents numerical simulations showing the expected level of quasi-static aberrations that can be measured on THD2 for a given exposure time. In Sect. 4, the components of the THD2 bench and the installation of a subsystem that mimics SPHERE AO residuals under good observing conditions are described. Section 5 reiterates the concept of SCC and describes how the sensor estimates the complex electric field from a long-exposure coronagraphic image. Section 6 presents the closed-loop laboratory performance and contrast results.
2. Expression of the complex electric field in long exposure
In this section, we establish an expression of the electric field in long-exposure images of a typical coronagraphic system as shown in Fig. 1. The star is assumed to be a monochromatic unresolved source centered on the optical axis. The starlight goes through the entrance pupil and is diffracted by a coronagraphic mask at the focal plane. This scattered starlight downstream of the mask is blocked by a Lyot stop. In the case of aberrations, part of the scattered starlight leaks through the Lyot stop and creates speckles at the final focal plane where a science detector is placed. For simplicity, we do not focus on deriving a classical expression of the complex electric field at each step of a coronagraphic system. Instead, we are interested in the electric field at the Lyot plane that can be linked to aberrations in the entrance pupil.
 |
Fig. 1. Optical layout of a typical coronagraphic system. |
During an exposure time t, the electric field Ψ(ξ, t) at the entrance pupil in Fig. 1 in the presence of static aberrations ϕ0 and independently evolving aberrations ϕ1(t) with a lifetime of t1 can be represented as
where P0 describes the entrance geometrical pupil and ξ is the position in the pupil plane. Here, a perfect coronagraph is considered, which completely rejects the starlight and contributes to the null electric field inside the Lyot pupil in the absence of aberrations. In the case of static aberrations (ϕ0) only, the field ΨS(ξ) at a position ξ in the pupil plane downstream of a perfect coronagraph (Cavarroc et al. 2006, and Appendix A.3) can be represented as
where 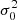 is the spatial variance of ϕ0. It has been demonstrated in numerical simulations and in the laboratory that this equation can be used to estimate and control the static aberrations ϕ0 in short exposures (Galicher et al. 2010; Mazoyer et al. 2013, 2014).
is the spatial variance of ϕ0. It has been demonstrated in numerical simulations and in the laboratory that this equation can be used to estimate and control the static aberrations ϕ0 in short exposures (Galicher et al. 2010; Mazoyer et al. 2013, 2014).
Our objective is to measure ϕ0 from a long-exposure. We assume that during this exposure, a part of the aberration called ϕ1(t) evolves quickly, with a lifetime t1 (post-AO residuals for example). In such a case, the instantaneous field ΨS in the pupil plane after a perfect coronagraph at a time t can then be written as
where  is the spatial variance of ϕ1(ξ, t), which is considered constant over time. For an infinite exposure time, the electric field is the mathematical expectation of ΨS over time (see Appendix A.4). It is represented as
is the spatial variance of ϕ1(ξ, t), which is considered constant over time. For an infinite exposure time, the electric field is the mathematical expectation of ΨS over time (see Appendix A.4). It is represented as
Here, it is assumed that the variance of ϕ1 over time is equal to the variance over space. The expression in Eq. (4) is the same as in the case of static errors only (Eq. (2)) multiplied by a constant factor  . The Eq. (4) interprets that the evolving aberration ϕ1 averages out and the static aberrations ϕ0 can be measured from an infinite exposure.
. The Eq. (4) interprets that the evolving aberration ϕ1 averages out and the static aberrations ϕ0 can be measured from an infinite exposure.
For a finite exposure which is  times longer than the aberration lifetime t1, the field
times longer than the aberration lifetime t1, the field  is the average over
is the average over  independent ϕ1 aberrations and can be written as
independent ϕ1 aberrations and can be written as
If  tends to infinity, the above equation is equal to E[ΨS(ξ, t)]. If
tends to infinity, the above equation is equal to E[ΨS(ξ, t)]. If  is a finite number, the part of the field that is not averaged is given by the variance of
is a finite number, the part of the field that is not averaged is given by the variance of  over time (see Appendix A.8):
over time (see Appendix A.8):
We note here that the lifetime t1 of ϕ1 can be different for each spatial frequency. A comprehensive formalism that includes this assertion will be presented in a future publication. Here, we focus on the aberration ϕ1 which is dominated by two spatial frequencies: 20 cycles per pupil diameter (AO cut-off) and less than 2 cycles per pupil diameter (see Sect. 3 and appendix).
We consider small aberrations in the experiments presented in this paper and rewrite Eqs. (4) and (5) as follows:
In other words, the averaged electric field at the Lyot plane is
where  is a complex random function that follows a Gaussian distribution of variance
is a complex random function that follows a Gaussian distribution of variance  . If a FPWFS can measure
. If a FPWFS can measure  , the averaged phase
, the averaged phase  can be estimated directly from Eq. (6). The longer the exposure, the more accurate the estimation of ϕ0.
can be estimated directly from Eq. (6). The longer the exposure, the more accurate the estimation of ϕ0.
3. Numerical simulations
As stated above, the goal is to estimate the static aberrations ϕ0 in long exposure in the presence of evolving aberrations ϕ1. We assume here that a system is able to estimate ψS that averages as described in Sect. 2. In the following sections, we first simulate the post-AO residuals using the assumptions that reproduce the laboratory conditions presented in Sect. 4. We then determine what level of static aberrations can be measured for a given exposure time and what level of contrast is achievable in the corresponding coronagraphic images.
3.1. Assumptions
For the experimental demonstration, we optically simulate the post-AO residuals using a rotating phase plate on the THD2 bench (more details about the practical implementation are given in Sect. 4). The simulated version of the phase plate is shown in Fig. 2. In the coronagraphic system as shown in Fig. 1, we consider the entrance pupil to be 8.23 mm in diameter and to be located at 40 mm from the center of the rotating phase plate. The plate can rotate around its center with 12 000 steps in total at a speed set to 300 steps per second. This corresponds to a linear velocity of 6.28 mm s−1, or 6.10 m s−1 when scaled to an 8m telescope. The power spectral density (PSD) of the simulated aberrations in Fig. 2 is similar to what is measured behind the AO system of SPHERE (Fusco et al. 2006) in the infrared. The PSD follows a power law as f−4/3 for spatial frequencies lower than 20 cycles per pupil and as f−11/3 for higher spatial frequencies. The standard deviation of the aberration is assumed to be 40 nm (in visible) inside the pupil mainly distributed in spatial frequencies below 2 cycles per pupil diameter and around the cut-off of 20 cycles per pupil diameter. Though such a level of aberration is optimistic for the current version of SPHERE (Beuzit et al. 2019, submitted), it represents a good estimation of the performance of an upgraded SPHERE.
 |
Fig. 2. Simulated map of the phase function that is induced by the phase plate. The entrance pupil of the THD2 bench is represented by a white circle. The phase plate is rotated around its center to mimic post-AO residual turbulence. |
We simulate the rotation of the post-AO phase plate around its center and extract 12 000 individual phase screens ϕ1(t) generated by the plate in the entrance pupil of 8.23 mm as shown in Fig. 2. These extracted phase screens are shown in Fig. 3.
 |
Fig. 3. (a) snapshot of one individual phase screen seen through the THD2 pupil. (b) cube of 12 000 phase screens used in the simulation. |
3.2. Accuracy versus exposure time
In the next step, we calculate the average of the phase screens as  with
with  increasing from 1 to 12 000. Figure 4 presents the standard deviation of the averaged phases
increasing from 1 to 12 000. Figure 4 presents the standard deviation of the averaged phases  as a function of
as a function of  . The plotted data give the level of aberrations for a finite long exposure in the absence of static aberrations. In other words, whatever the FPWFS, the best accuracy on the measured static aberrations from a finite long exposure is given by Fig. 4 for the simulated AO system. For example, for a plate rotation of 162° (see Sect. 6), the entrance pupil sees 5400 simulated phase screens (
. The plotted data give the level of aberrations for a finite long exposure in the absence of static aberrations. In other words, whatever the FPWFS, the best accuracy on the measured static aberrations from a finite long exposure is given by Fig. 4 for the simulated AO system. For example, for a plate rotation of 162° (see Sect. 6), the entrance pupil sees 5400 simulated phase screens ( ) pass by, and the standard deviation of the post-AO residuals is ∼1 nm. It is therefore expected that a FPWFS on the assumed experimental bench (Sect. 4) should be able to measure aberrations with an accuracy of ∼1 nm for an exposure time corresponding to a 162° rotation of the phase plate.
) pass by, and the standard deviation of the post-AO residuals is ∼1 nm. It is therefore expected that a FPWFS on the assumed experimental bench (Sect. 4) should be able to measure aberrations with an accuracy of ∼1 nm for an exposure time corresponding to a 162° rotation of the phase plate.
 |
Fig. 4. Simulated standard deviation within the pupil of the phase aberration averaged over |
More generally, we find that the standard deviation of the averaged phases  decreases as the square root of the number of individual screens considered in the range
decreases as the square root of the number of individual screens considered in the range  . For
. For  , the standard deviation decreases at a rate slower than
, the standard deviation decreases at a rate slower than  because the phase screens are not completely uncorrelated. There are mainly two regimes for
because the phase screens are not completely uncorrelated. There are mainly two regimes for  : residuals decreasing very slowly for
: residuals decreasing very slowly for  and a bit faster for
and a bit faster for  . The pupil beam of diameter 8.23 mm hits the simulated post-AO phase plate at 40 mm from its center as shown in Fig. 2. For
. The pupil beam of diameter 8.23 mm hits the simulated post-AO phase plate at 40 mm from its center as shown in Fig. 2. For  , the rotation of the post-AO phase plate is less than
, the rotation of the post-AO phase plate is less than  mm, which is equivalent to a movement of the plate by less than ∼1/40 of the pupil diameter. From the design of the phase plate (Sect. 4), most of the energy in the PSD of ϕ1 is close to the cut-off at 20 cycles per pupil. It is therefore expected that the standard deviation of
mm, which is equivalent to a movement of the plate by less than ∼1/40 of the pupil diameter. From the design of the phase plate (Sect. 4), most of the energy in the PSD of ϕ1 is close to the cut-off at 20 cycles per pupil. It is therefore expected that the standard deviation of  decreases at a rate slower for
decreases at a rate slower for  than for
than for  . Furthermore,
. Furthermore,  corresponds to a spatial frequency of two cycles per pupil, which is where the rest of the energy lies in the PSD of ϕ1. For
corresponds to a spatial frequency of two cycles per pupil, which is where the rest of the energy lies in the PSD of ϕ1. For  , we observe variations because the variance of the two independent phase screens is not exactly the same.
, we observe variations because the variance of the two independent phase screens is not exactly the same.
3.3. Coronagraphic images
To simulate long-exposure images under the post-AO residuals, we compute one coronagraphic image per individual phase screen (frozen aberrations) following the optical layout of Fig. 1. We assume a monochromatic light at 783.25 nm at the entrance pupil and a four-quadrant phase mask (FQPM; Rouan et al. 2000) as a focal plane mask (FPM). Only the post-AO aberrations without any static errors are considered (ϕ0 = 0). The intensities of the  individual images are then averaged to obtain a long-exposure coronagraphic image. Figure 5a represents a science image obtained for a short exposure (
individual images are then averaged to obtain a long-exposure coronagraphic image. Figure 5a represents a science image obtained for a short exposure ( ) where AO residuals are frozen. Figures 5b and c show how the AO halo averages when the exposure time (
) where AO residuals are frozen. Figures 5b and c show how the AO halo averages when the exposure time ( and 5400) is increased. The darker area in all the images represents a region controlled by the simulated AO system. The cut-off is at 20 λ/D (40 actuators across the pupil in the SPHERE instrument). We notice that even for
and 5400) is increased. The darker area in all the images represents a region controlled by the simulated AO system. The cut-off is at 20 λ/D (40 actuators across the pupil in the SPHERE instrument). We notice that even for  averaged images, speckles are still visible in the controlled area. They are induced by the ∼1 nm rms residual aberrations found in Fig. 4 and they vary from one long exposure to another. The dark cross that is visible in the images is due to the transitions of the FQPM. All the images are normalized by the maximum of the non-coronagraphic image.
averaged images, speckles are still visible in the controlled area. They are induced by the ∼1 nm rms residual aberrations found in Fig. 4 and they vary from one long exposure to another. The dark cross that is visible in the images is due to the transitions of the FQPM. All the images are normalized by the maximum of the non-coronagraphic image.
 |
Fig. 5. Focal plane coronagraphic images simulated with the FQPM coronagraph under the post-AO wavefront errors representing the residual level seen by SPHERE when atmospheric conditions are favorable. No additional static aberrations are added. (a) short exposure freezing the AO wavefront ( |
Figure 6 represents the azimuthal standard deviation profiles (1σ contrast) associated with the images of Fig. 5. At small angular separations (< 3 λ/D), starlight leaks due to low spatial frequency aberrations are visible. When speckles are frozen (red curve), the raw contrast reaches the level of ∼10−5 between 5 and 18 λ/D. This contrast roughly corresponds to what is measured behind the SPHERE AO system at the VLT (Vigan et al. 2019). For longer exposure, the quickly varying speckles average out and the contrast deepens. By choosing a realistic exposure time (N = 5400, which also corresponds to 18 s exposure at the VLT), the contrast level reaches below 3 × 10−6 in the range 5 − 18 λ/D (blue curve). Therefore, for an exposure of 18 s under the simulated AO residuals, the contrast of ∼6 × 10−7 is the best level that can be reached after the expected correction of quasi-static aberrations by any FPWFS.
 |
Fig. 6. Simulated profiles showing azimuthal standard deviation as a function of angular separation for focal plane images presented in Fig. 5. The red profile shows the contrast curve of a short-exposure image depicting what is obtained by SPHERE under good observing conditions. The contrast in the range 5 − 18 λ/D mostly stays around 10−5. For a realistic long exposure, the blue profile is mostly below 3 × 10−6 in the range 5 − 18 λ/D. |
4. THD2 bench in a glance
For our practical experiments, we used the THD2 bench. The detailed description of THD2 optical components can be found in Baudoz et al. (2018). In this section, we briefly recall the main components of THD2 and a sub-system that optically simulates the post-AO residuals. With a growing collaboration all over the world, the THD2 bench became a unique research and development platform for HCI in Europe. The main objective is to optimize the design of future exoplanet imaging instruments by comparing several HCI techniques under the same environmental conditions. Though the THD2 bench is not in a vacuum tank, the stabilization of temperature and humidity already enabled the testing of HCI techniques under steady conditions similar to those in space.
The optical representation of the THD2 bench is shown in Fig. 7, which follows the coronagraphic layout of Fig. 8.
 |
Fig. 7. Optical diagram of the THD2 bench. The post-AO residual subsystem containing a rotating phase plate is situated immediately after the entrance pupil. |
 |
Fig. 8. Optical layout of the SCC as used on the THD2 bench. The Lyot stop has a classical on-axis diaphragm and a reference pupil for the SCC. The aberrated starlight that goes through the on-axis diaphragm combines with the reference starlight to spatially modulate the speckle intensity in the science image. |
To simulate starlight, a single-mode optical fiber injects light at the entrance of the bench. In this paper, the source is a laser diode emitting at λ = 783.25 nm. The starlight is collimated towards a tip-tilt mirror (TTM), which is used to control the pointing. The beam after the correction of tip-tilt errors meets a circular unobscured entrance pupil, the diameter of which is set to 8.23 mm in this paper. The beam is then reflected by two DMs from Boston Micromachine Corporation (BMC). The first, DM1, has 952 actuators and is set in a collimated beam at 26.9 cm from the pupil plane. The second, DM3, has 1024 actuators and is conjugated to the pupil plane. There are 27 actuators of each DM across the pupil. After DM3, the beam is focused onto a transmissive FPM with a f-number of 110. In this paper, the FPM is a FQPM coronagraph. In the following pupil plane, a Lyot stop filters the starlight that is scattered by the FPM outside the geometrical pupil. The diameter of the Lyot diaphragm DL is 8.00 mm for our experiments. An off-axis hole of 0.5 mm in diameter is also used to create the SCC reference channel (Sect. 5). Finally, the coronagraphic image is recorded by an Andor camera with a readout noise of 3.2 e− rms per pixel. The science images are 400 × 400 pixels with the resolution element sampled by 7.6 pixels (λ/DL).
To prepare new ground-based imaging instruments or propose upgrades to the existing ones, an optical subsystem has been installed on THD2 to mimic post-AO residual aberrations in visible. The simulated post-AO phase plate is shown in Fig. 2 and its specifications are explained briefly in Sect. 3. It is composed of a transmissive (> 99% between 600 and 800 nm) rotating phase plate with a diameter of 100 mm and a thickness of 1.5 mm. The aberrations introduced on THD2 have a PSD following a power law as f−4/3 and f−11/3 for lower (< 20 cycles per pupil) and higher spatial frequencies, respectively. The specified standard deviation of the aberration is 40 nm inside the pupil. The plate was fabricated by the Zeiss company using ion-etching. The etched part of the plate starts at 18.6 mm from its center and continues until 45 mm. The lateral resolution of the etched phase function is 10 μm. Figure 9 presents the curves of a theoretical and measured PSD of the phase plate. The measured PSD is calculated using the images provided by an interferometric microscope with a field of view of 6.98 mm × 5.24 mm and a pixel size of 0.64 μm. These images are recorded on eight areas evenly distributed on the edge of the phase plate. Both a theoretical and measured phase map for a small area of 3.49 mm × 2.62 mm are also shown in Fig. 9. The plate sits immediately after the entrance pupil (green component in Fig. 7). It can rotate around its center, thus continuously changing the phase errors in the 8.23 mm entrance pupil (white circle in Fig. 2). The encoder that controls the position of the plate uses 12 000 steps for a full round. In the experiments presented here, the plate rotates by 300 steps per second and the beam that goes through the pupil hits the phase plate at 40 mm from its center.
 |
Fig. 9. Theoritical (black profile) and measured (red dashed line) PSD of the phase plate shown in Fig. 3. The images of theoretical and measured phase maps are extracted within the area of 3.49 mm × 2.62 mm on the phase plate. |
5. Focal-plane wavefront estimation in long exposure
The two main assets of THD2 bench for wavefront measurement are the Lyot-stop low-order wavefront sensor (LLOWFS; Singh et al. 2017) and a FPWFS. The former is used to stabilize the tip-tilt at < 100 Hz and the latter stabilizes all the other spatial frequencies up to the DM cut-off (13.5 λ/D). As for the focal plane wavefront sensing and correction, we can either use pair-wise plus electric field conjugation (Potier et al., in prep.) or the SCC. In the experiments presented in Sect. 6, we used both the LLOWFS and the SCC to control the wavefront errors.
The SCC principle has already been described in several papers (Galicher et al. 2010; Delorme et al. 2016). The SCC uses a modified Lyot stop as shown in Fig. 8. The on-axis diaphragm is the classical Lyot stop that filters out the stellar light rejected by the coronagraphic FPM. Part of the starlight goes through the diaphragm because of aberrations, which induce speckles on the science detector. We use AS to refer to the electric field of these speckles. The off-axis reference hole selects part of the rejected starlight at a distance ξ0 from the center of the on-axis diaphragm. Doing so, the stellar speckles are spatially modulated by Fizeau fringes on the detector. If we consider that the aberrations in the system are static during the exposure time, the intensity I(x) at a position x in the science image can be written as
where  is the conjugate of the electric field in the science image associated with the off-axis hole of the Lyot stop and, ℛ is the real part of a complex number. It has been demonstrated that
is the conjugate of the electric field in the science image associated with the off-axis hole of the Lyot stop and, ℛ is the real part of a complex number. It has been demonstrated that  can be extracted from I and that minimizing I− also minimizes the speckle electric field AS in the controlled area. To estimate I−, one selects the lateral peak in the Fourier transform of Eq. (7). The expression of this peak is
can be extracted from I and that minimizing I− also minimizes the speckle electric field AS in the controlled area. To estimate I−, one selects the lateral peak in the Fourier transform of Eq. (7). The expression of this peak is
where  is the conjugate of the electric field in the off-axis hole of the Lyot stop, ΨS is the field inside the on-axis diaphragm, and denotes the convolution product. If the wavefront aberrations are not too large or the diameter of the off-axis hole is small enough, it can be assumed that ΨR does not depend on the wavefront aberrations (Galicher et al. 2010; Baudoz et al. 2012). On the contrary, ΨS strongly depends on the aberrations upstream of the coronagraph. As shown in Sect. 2, the SCC can retrieve the static aberrations ϕ0 from the estimation of
is the conjugate of the electric field in the off-axis hole of the Lyot stop, ΨS is the field inside the on-axis diaphragm, and denotes the convolution product. If the wavefront aberrations are not too large or the diameter of the off-axis hole is small enough, it can be assumed that ΨR does not depend on the wavefront aberrations (Galicher et al. 2010; Baudoz et al. 2012). On the contrary, ΨS strongly depends on the aberrations upstream of the coronagraph. As shown in Sect. 2, the SCC can retrieve the static aberrations ϕ0 from the estimation of  measured from a long exposure coronagraphic image.
measured from a long exposure coronagraphic image.
6. Laboratory performance
In this section, we demonstrate that in the laboratory the SCC can be used to compensate static errors down to the fundamental level set by the averaged AO residuals described in Sect. 3. Before beginning our experiments, we first minimized the speckle level at < 10−8 contrast using the SCC with no AO phase plate in the beam. We then recorded a series of long-exposure SCC images by choosing a realistic exposure of 18 s while the phase plate that optically simulates the optimistic level of SPHERE post-AO residuals rotated at 300 steps per second. One such image is shown in Fig. 10a. It sets the fundamental level of AO residuals for 18 s exposure for the simulated AO system. The corresponding 1σ contrast curve is plotted in blue (dashed line) in Fig. 11. Figure 10a is similar to the numerically predicted coronagraphic image shown in Fig. 5c. The simulated AO cut-off is at 20 λ/D and the distribution of energy (blue dashed curves) as a function of spatial frequencies in Fig. 11 is also similar to the blue curve in Fig. 6. There are two small differences however: First, the laboratory image is brighter close to the star center. Even though the tip-tilt loop was closed, additional low-order aberrations were introduced by the plate itself that added up with the etched errors. Second, there are a few speckles outside the 13 λ/D × 13 λ/D area, which are brighter in the laboratory image. They are uncontrolled static aberrations on the THD2 bench and cannot be compensated as the cut-off of THD2 DMs is 13 λ/D.
 |
Fig. 10. Laboratory SCC science images obtained at an exposure of 18 s on the THD2 bench: (a) under the effect of post-AO aberrations only and (b, c, d) under the effect of both post-AO aberrations and static aberrations. b: 0th iteration of the SCC correction loop (starting point). (c) and (d) obtained after five iterations of the SCC correction loop when controlling speckles inside a full dark hole within a 25 λ/D × 25 λ/D region and a half dark hole going from −12.5 λ/D to 12.5 λ/D in one direction and from 2 λ/D to 12.5 λ/D in the other direction. |
In the next step, both phase and amplitude static aberrations were added to the system using the DM1 (inducing 1 nm rms of phase and 0.4% of amplitude) and DM3 (inducing 5 nm rms of phase only). The spectral density function of these aberrations varies as the inverse of the spatial frequency (f−1). This level of static aberrations is similar to what SPHERE can achieve after compensating the NCPA on the internal source. After applying these static aberrations in our system, we let the post-AO phase plate rotate. In the mean time, the science camera continuously recorded images, each acquired with an exposure of 18 s. One such aberrated image of 18 s exposure is presented in Fig. 10b. The associated contrast curve is plotted in red dot-dash in Fig. 11. As expected, static speckles limit the contrast performance. At each exposure, the SCC was then used to estimate and control the aberrations by using DM3 which is conjugated to the pupil plane. We note that the interaction matrix of the SCC was recorded under no post-AO residuals, which is similar to what would be done at the telescope using the internal source of the instrument.
 |
Fig. 11. Azimuthal standard deviations (i.e., 1 σ contrast detection) of the 18 s exposure images of Fig. 10. The blue dashed curves represent the post-AO aberrations if no static aberrations are added. The red dot-dash ones show the post-AO aberrations after adding static aberrations. The black profiles from top to bottom show the first six iterations of correction in the case of (a) the full dark hole and (b) the half dark hole. The 0th iteration in a black curve is similar to the post-AO residuals with static aberrations. |
In the first test, we used the control algorithm to minimize the speckle intensity in a full dark hole of 25 λ/D × 25 λ/D centered on the star. Figure 10c shows the long-exposure image recorded by the camera after five iterations of correction (i.e., six images). The contrast curves for the first five iterations of the SCC correction are presented in Fig 11a in black. The static speckles were corrected and the science image is at the level of the post-AO residuals (Fig. 10a) that no FPWFS can overcome for a given exposure time (see Sect. 3). The only difference between Fig. 10a and c is that they were acquired at different rotation angles of the phase plate.
In the second test, we started again from the image with static aberrations shown in Fig. 10b. We then commanded the algorithm to minimize the speckle intensity in a half dark hole going from −12.5 λ/D to 12.5 λ/D in one direction and 2 λ/D to 12.5 λ/D in the other direction. The coronagraphic image after five iterations is shown in Fig. 10d. The associated contrast curves calculated only inside the half dark hole are plotted in Fig. 11b. The SCC correction in the half dark hole is better than in the full dark hole case (black curves in Fig 11a). This is expected because using a single DM in pupil plane (DM3) for the correction, both amplitude and phase aberrations can be corrected in a half dark hole whereas only phase aberrations can be controlled in a full dark hole. These encouraging results demonstrate that the SCC is capable of actively correcting static aberrations in long exposures reaching the residual limit set by the length of the exposure time and the level of AO residuals.
In Figs. 10c and d, we note that the remaining speckles are spatially modulated by the SCC fringes. We did not use this information in the current paper. However, it can be used to improve the contrast of these images using the post-processing coherence differential imaging mode of the SCC (Baudoz et al. 2012).
7. Conclusion
It is a well known problem that the long-exposure coronagraphic science images usually have an AO halo that adds photon noise to exoplanet detection and speckles that mimic exoplanet images. Static speckles with a temporal evolution longer than a typical angular differential imaging observing sequence can be subtracted in post-processing. However, quasi-static speckles that evolve slowly from one image to the other during the sequence of observations cannot be accurately calibrated post-observation. This paper focused on actively correcting the static and quasi-static speckles in long-exposure science images obtained under ground-based conditions. Given any focal plane wavefront sensor (FPWFS), we first established an expression of the fundamental accuracy on the measurement of static aberrations in a long-exposure in Sect. 2. We then installed an atmospheric residual wheel on the THD2 bench mimicking post-AO residuals seen by the SPHERE/VLT instrument under good observing conditions. We then determined the level of static aberrations that can be measured from a finite long-exposure on THD2 in Sect. 3. By using the self-coherent camera (SCC) as a FPWFS, the electric field was minimized down to the fundamental level set by the post-AO averaged turbulence.
It is shown in the laboratory that the SCC actively suppresses both phase and amplitude static aberrations when applied on AO long exposures. Only a few iterations are required to correct for the aberrations down to the fundamental limit, which means that quasi-static aberrations evolving on the scale of a few exposures could also be addressed with the SCC. A full dark hole with 1σ contrast between 3 × 10−6 and 8 × 10−7 covering the region 5 − 12 λ/D is reached in five iterations with images acquired at 18 s per iteration. In a half dark hole, a contrast of 6 × 10−7 is achieved in the range 12 − 15 λ/D. It is demonstrated that the SCC can actively compensate static and quasi-static aberrations present above the averaged turbulence.
The results presented in this paper are encouraging and provide an opportunity to the current and future HCI instruments to adapt SCC as a FPWFS to actively suppress quasi-static speckles. We also aim to compare the SCC with other FPWFS techniques including the electric field conjugation on the THD2 bench. This study will characterize the performance of different speckle suppression techniques under the same ground-based conditions, thus setting a limit on the highest raw contrast obtainable from the ground.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 798909. This work has also received support of IRIS Origines et Conditions d’Apparition de la Vie of PSL Université under the program “Investissements d’Avenir” launched by the French Government and implemented by ANR with the reference ANR-10-IDEX-0001-02 PSL.
References
- Baudoz, P., Boccaletti, A., Baudrand, J., & Rouan, D. 2006, in IAU Colloq. 200: Direct Imaging of Exoplanets: Science & Techniques, eds. C. Aime, & F. Vakili, 553 [Google Scholar]
- Baudoz, P., Mazoyer, J., Mas, M., Galicher, R., & Rousset, G. 2012, Proc. SPIE, 8446, 84468C [NASA ADS] [CrossRef] [Google Scholar]
- Baudoz, P., Galicher, R., Potier, A., et al. 2018, SPIE Conf. Ser., 10706, 107062O [Google Scholar]
- Belikov, R., Give’on, A., Kern, B., et al. 2007, Proc. SPIE, 6693, 66930Y [CrossRef] [Google Scholar]
- Beuzit, J.-L., Mouillet, D., Lagrange, A.-M., & Paufique, J. 1997, A&AS, 125, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, The Messenger, 125, 29 [NASA ADS] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201935251 [Google Scholar]
- Bloemhof, E. E., Dekany, R. G., Troy, M., & Oppenheimer, B. R. 2001, ApJ, 558, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Boccaletti, A., Chauvin, G., Lagrange, A.-M., & Marchis, F. 2003, A&A, 410, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Riaud, P., Baudoz, P., et al. 2004, PASP, 116, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Bordé, P. J., & Traub, W. A. 2006, ApJ, 638, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Bottom, M., Wallace, J. K., Bartos, R. D., Shelton, J. C., & Serabyn, E. 2017, MNRAS, 464, 2937 [NASA ADS] [CrossRef] [Google Scholar]
- Cavarroc, C., Boccaletti, A., Baudoz, P., Fusco, T., & Rouan, D. 2006, A&A, 447, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delorme, J. R., N’Diaye, M., Galicher, R., et al. 2016, A&A, 592, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Opt. Express, 14, 7515 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco, T., Sauvage, J. F., Mouillet, D., et al. 2016, Proc. SPIE, 9909, 99090U [CrossRef] [Google Scholar]
- Galicher, R., Baudoz, P., Rousset, G., Totems, J., & Mas, M. 2010, A&A, 509, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galicher, R., Baudoz, P., Delorme, J.-R., et al. 2019, A&A, accepted [arXiv:1909.09130] [Google Scholar]
- Give’on, A., Kern, B., Shaklan, S., Moody, D. C., & Pueyo, L. 2007, SPIE Conf. Ser., 6691 [Google Scholar]
- Guyon, O. 2005, ApJ, 629, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Kuchner, M. J., Collins, B., & Ridgway, S. T. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jovanovic, N., Martinache, F., Guyon, O., et al. 2015, PASP, 127, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [Google Scholar]
- Malbet, F., Yu, J. W., & Shao, M. 1995, PASP, 107, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Martinache, F., Guyon, O., Jovanovic, N., et al. 2014, PASP, 126, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Loose, C., Aller Carpentier, E., & Kasper, M. 2012, A&A, 541, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, P., Kasper, M., Costille, A., et al. 2013, A&A, 554, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, C. T., Crepp, J. R., Vasisht, G., & Cady, E. 2017, J. Astron. Telesc. Instrum. Syst., 3, 045001 [NASA ADS] [CrossRef] [Google Scholar]
- Mazoyer, J., Baudoz, P., Galicher, R., Mas, M., & Rousset, G. 2013, A&A, 557, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazoyer, J., Baudoz, P., Galicher, R., & Rousset, G. 2014, A&A, 564, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milli, J., Banas, T., Mouillet, D., et al. 2016, Proc. SPIE, 9909, 99094Z [Google Scholar]
- Oppenheimer, B. R., Golimowski, D. A., Kulkarni, S. R., et al. 2001, AJ, 121, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- Poyneer, L. A., Palmer, D. W., Macintosh, B., et al. 2016, Appl. Opt., 55, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R., Walker, G. A. H., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F. 2004, Adaptive Optics in Astronomy (Cambridge: Cambridge University Press), 419 [Google Scholar]
- Rouan, D., Riaud, P., Boccaletti, A., Clénet, Y., & Labeyrie, A. 2000, PASP, 112, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Sauvage, J.-F., Mugnier, L., Paul, B., & Villecroze, R. 2012, Opt. Lett., 37,4808 [NASA ADS] [CrossRef] [Google Scholar]
- Savransky, D., Macintosh, B. A., Thomas, S. J., et al. 2012, Proc. SPIE, 8447, 84476S [CrossRef] [Google Scholar]
- Singh, G., Lozi, J., Jovanovic, N., et al. 2017, PASP, 129, 095002 [NASA ADS] [CrossRef] [Google Scholar]
- Trauger, J., Moody, D., Gordon, B., Krist, J., & Mawet, D. 2011, Proc. SPIE, 8151, 81510G [Google Scholar]
- Trauger, J., Moody, D., Gordon, B., Krist, J., & Mawet, D. 2012, Proc. SPIE, 8442, 84424Q [CrossRef] [Google Scholar]
- Vigan, A., N’Diaye, M., Dohlen, K., et al. 2019, A&A, 629, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilby, M. J., Keller, C. U., Snik, F., Korkiakoski, V., & Pietrow, A. G. M. 2017, A&A, 597, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Variance of the averaged electric field in long exposure
Here we describe in detail how the equations presented in Sect. 2 are derived. At a position ξ and at a time t, the instantaneous electric field Ψ(ξ, t) at the entrance pupil in the presence of static aberrations ϕ0 and evolving aberrations ϕ1(t) with a lifetime t1 can be represented as
Equations (1) and (A.1) are the same. The terms ϕ0 and ϕ1(t) can be described by Gaussian distributions with zero mean. The perfect coronagraph removes the coherent light (Cavarroc et al. 2006) and the field ΨS(ξ, t) in a pupil after the coronagraph can be written as
Because there is a large number of different values of ϕ0 + ϕ1 inside the pupil, the integral equals to the mathematical expectation. In this case, the expectation of ei ϕ is e−σ2/2 with σ2 the statistical spatial variance of ϕ. Since ϕ0 and ϕ1 are statistically independent, we can write
where  is the spatial variance of ϕi. Here, we assume that
is the spatial variance of ϕi. Here, we assume that  is constant over time. We note that Eq. (2) is a peculiar case of (A.3) (equivalent of Eq. (3)) if ϕ1 is null.
is constant over time. We note that Eq. (2) is a peculiar case of (A.3) (equivalent of Eq. (3)) if ϕ1 is null.
For an infinite exposure, the field ΨS averages over time and the resulting field is
where E[a] is the mathematical expectation of a over time. We then obtain
with  the time variance of ϕ1(ξ, t) that is assumed to be the same at each position ξ in the pupil. If ϕ1 is ergodic, then Σ1 is equal to σ1 and we obtain
the time variance of ϕ1(ξ, t) that is assumed to be the same at each position ξ in the pupil. If ϕ1 is ergodic, then Σ1 is equal to σ1 and we obtain
(A.4) is equivalent to Eq. (4). For a finite exposure, the resulting field  is the average over
is the average over  independent ϕ1(t) and can be written as
independent ϕ1(t) and can be written as
We note here that the lifetime t1 of ϕ1 can be different for each spatial frequency. For example, considering a single layer of frozen turbulent aberration moving at a speed v in front of the telescope of diameter D, the lifetime t1, f of the aberration with a spatial frequency f is proportional to D/(f v). As a result, the expression of  should be written in the Fourier space for a complete description. The resulting equations would be more complicated and will be presented in a future paper. This paper focuses on residual AO aberrations that are dominated by aberrations at low spatial frequencies (≲2 cycles per pupil diameter) and at the cut-off of the AO system (20 cycles per pupil diameter). We can then use the assumption that leads to the derived equation of
should be written in the Fourier space for a complete description. The resulting equations would be more complicated and will be presented in a future paper. This paper focuses on residual AO aberrations that are dominated by aberrations at low spatial frequencies (≲2 cycles per pupil diameter) and at the cut-off of the AO system (20 cycles per pupil diameter). We can then use the assumption that leads to the derived equation of  for these two spatial frequencies neglecting the other frequencies.
for these two spatial frequencies neglecting the other frequencies.
The function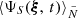 tends towards E[ΨS(ξ, t)] if
tends towards E[ΨS(ξ, t)] if  increases. For a given
increases. For a given  , the variance of
, the variance of  over time gives how much the finite average deviates from mathematical expectation. As all ΨS(ξ, p t1) are independent, we can write
over time gives how much the finite average deviates from mathematical expectation. As all ΨS(ξ, p t1) are independent, we can write
where Var is the variance over time. We then use
The last term in the above equation can be written as
For E[|ΨS(ξ, t)|2], we first write |ΨS(ξ, t)|2 as
with  . Then, we write the cosine as
. Then, we write the cosine as
and as E[ϕ1] is null, the mathematical expectation over time gives
We can then write
We derive the variance of ΨS(ξ, t) from Eqs. (A.5), (A.6), and (A.7):
Finally, the variance of  is
is
All Figures
 |
Fig. 1. Optical layout of a typical coronagraphic system. |
| In the text | |
 |
Fig. 2. Simulated map of the phase function that is induced by the phase plate. The entrance pupil of the THD2 bench is represented by a white circle. The phase plate is rotated around its center to mimic post-AO residual turbulence. |
| In the text | |
 |
Fig. 3. (a) snapshot of one individual phase screen seen through the THD2 pupil. (b) cube of 12 000 phase screens used in the simulation. |
| In the text | |
 |
Fig. 4. Simulated standard deviation within the pupil of the phase aberration averaged over |
| In the text | |
 |
Fig. 5. Focal plane coronagraphic images simulated with the FQPM coronagraph under the post-AO wavefront errors representing the residual level seen by SPHERE when atmospheric conditions are favorable. No additional static aberrations are added. (a) short exposure freezing the AO wavefront ( |
| In the text | |
 |
Fig. 6. Simulated profiles showing azimuthal standard deviation as a function of angular separation for focal plane images presented in Fig. 5. The red profile shows the contrast curve of a short-exposure image depicting what is obtained by SPHERE under good observing conditions. The contrast in the range 5 − 18 λ/D mostly stays around 10−5. For a realistic long exposure, the blue profile is mostly below 3 × 10−6 in the range 5 − 18 λ/D. |
| In the text | |
 |
Fig. 7. Optical diagram of the THD2 bench. The post-AO residual subsystem containing a rotating phase plate is situated immediately after the entrance pupil. |
| In the text | |
 |
Fig. 8. Optical layout of the SCC as used on the THD2 bench. The Lyot stop has a classical on-axis diaphragm and a reference pupil for the SCC. The aberrated starlight that goes through the on-axis diaphragm combines with the reference starlight to spatially modulate the speckle intensity in the science image. |
| In the text | |
 |
Fig. 9. Theoritical (black profile) and measured (red dashed line) PSD of the phase plate shown in Fig. 3. The images of theoretical and measured phase maps are extracted within the area of 3.49 mm × 2.62 mm on the phase plate. |
| In the text | |
 |
Fig. 10. Laboratory SCC science images obtained at an exposure of 18 s on the THD2 bench: (a) under the effect of post-AO aberrations only and (b, c, d) under the effect of both post-AO aberrations and static aberrations. b: 0th iteration of the SCC correction loop (starting point). (c) and (d) obtained after five iterations of the SCC correction loop when controlling speckles inside a full dark hole within a 25 λ/D × 25 λ/D region and a half dark hole going from −12.5 λ/D to 12.5 λ/D in one direction and from 2 λ/D to 12.5 λ/D in the other direction. |
| In the text | |
 |
Fig. 11. Azimuthal standard deviations (i.e., 1 σ contrast detection) of the 18 s exposure images of Fig. 10. The blue dashed curves represent the post-AO aberrations if no static aberrations are added. The red dot-dash ones show the post-AO aberrations after adding static aberrations. The black profiles from top to bottom show the first six iterations of correction in the case of (a) the full dark hole and (b) the half dark hole. The 0th iteration in a black curve is similar to the post-AO residuals with static aberrations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \Psi ({\boldsymbol{\xi }},\,t) = P_0({\boldsymbol{\xi }})\,\mathrm{e}^{i\,\left[ \phi _0({\boldsymbol{\xi }}) +\phi _1({\boldsymbol{\xi }},\,t)\right]} , \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq1.gif)

![$$ \begin{aligned} \Psi _S({\boldsymbol{\xi }},\,t) = P_0({\boldsymbol{\xi }})\,\left(\mathrm{e}^{i\,\left[ \phi _0({\boldsymbol{\xi }}) +\phi _1({\boldsymbol{\xi }},\,t)\right]}-\mathrm{e}^{-(\sigma _0^2+\sigma _1^2)/2}\right), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq4.gif)
![$$ \begin{aligned} E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = P_0({\boldsymbol{\xi }})\,\left(\mathrm{e}^{i\,\phi _0({\boldsymbol{\xi }})}-\mathrm{e}^{-\sigma _0^2/2}\right)\,\mathrm{e}^{-\sigma _1^2/2}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq6.gif)

![$$ \begin{aligned} \mathrm{Var} \left[\langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}}\right]= P_0({\boldsymbol{\xi }})\,\frac{1-\mathrm{e}^{-\sigma _1^2}}{\tilde{N}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq15.gif)
![$$ \begin{aligned} \left\{ \begin{array}{l} E\left[\langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}}\right]\quad \, \simeq \,\,\, i\,P_0({\boldsymbol{\xi }})\,\phi _0({\boldsymbol{\xi }})\\ \mathrm{Var} \left[\langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}}\right] \,\,\, \simeq \,\,\, P_0({\boldsymbol{\xi }})\,\frac{\sigma _1^2}{\tilde{N}}. \end{array} \right. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq16.gif)
![$$ \begin{aligned} \langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}} = i\,P_0({\boldsymbol{\xi }})\,\left[\phi _0({\boldsymbol{\xi }})\pm \epsilon _{\tilde{N}}~({\boldsymbol{\xi }})\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq17.gif)








![$$ \begin{aligned} \Psi ({\boldsymbol{\xi }},\,t) = P_0({\boldsymbol{\xi }})\,\mathrm{e}^{i\,\left[ \phi _0({\boldsymbol{\xi }}) +\phi _1({\boldsymbol{\xi }},\,t)\right]} . \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq57.gif)

![$$ \begin{aligned} \Psi _S({\boldsymbol{\xi }},\,t) = P_0({\boldsymbol{\xi }})\,\left(\mathrm{e}^{i\,\left[ \phi _0({\boldsymbol{\xi }}) +\phi _1({\boldsymbol{\xi }},\,t)\right]}-\mathrm{e}^{-(\sigma _0^2+\sigma _1^2)/2}\right), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq59.gif)
![$$ \begin{aligned} E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = P_0({\boldsymbol{\xi }})\,\left(E\left[\mathrm{e}^{ i\,\left[ \phi _0({\boldsymbol{\xi }}) +\phi _1({\boldsymbol{\xi }},\,t)\right]}\right]-\mathrm{e}^{-(\sigma _0^2+\sigma _1^2)/2}\right), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq62.gif)
![$$ \begin{aligned} E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = P_0({\boldsymbol{\xi }})\,\left(\mathrm{e}^{ i\,\phi _0({\boldsymbol{\xi }}) }\,\mathrm{e}^{-\Sigma _1^2/2}-\mathrm{e}^{-(\sigma _0^2+\sigma _1^2)/2}\right), \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq63.gif)
![$$ \begin{aligned} E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = P_0({\boldsymbol{\xi }})\,\left(\mathrm{e}^{i\,\phi _0({\boldsymbol{\xi }})}-\mathrm{e}^{-\sigma _0^2/2}\right)\,\mathrm{e}^{-\sigma _1^2/2}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq65.gif)

![$$ \begin{aligned} \mathrm{Var} \left[\langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}}\right] = \frac{1}{\tilde{N}}\,\mathrm{Var} \left[\Psi _S({\boldsymbol{\xi }},\,t)\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq75.gif)
![$$ \begin{aligned} \mathrm{Var} \left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = E\left[\left|\Psi _S({\boldsymbol{\xi }},\,t)\right|^2\right] - \left|E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right]\right|^2. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq76.gif)
![$$ \begin{aligned} \left|E\left[\Psi _S({\boldsymbol{\xi }},\,t)\right]\right|^2 = P_0({\boldsymbol{\xi }})\,\mathrm{e}^{-\sigma _1^2}\,\left[1+\mathrm{e}^{-\sigma _0^2}-2\,\mathrm{e}^{-\sigma _0^2/2}\cos {\left(\phi _0({\boldsymbol{\xi }})\right)}\right]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq77.gif)
![$$ \begin{aligned} \left|\Psi _S({\boldsymbol{\xi }},\,t)\right|^2 = P_0({\boldsymbol{\xi }})\,\left[1+\mathrm{e}^{-\sigma ^2}-2\,\mathrm{e}^{-\sigma ^2/2}\,\cos {\left(\phi _0({\boldsymbol{\xi }})+\phi _1({\boldsymbol{\xi }},\,t)\right)}\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq78.gif)

![$$ \begin{aligned} E\left[\cos {\left(\phi _0({\boldsymbol{\xi }})+\phi _1({\boldsymbol{\xi }},\,t)\right)}\right]&= \cos {\left(\phi _0({\boldsymbol{\xi }})\right)}\, E\left[\cos {\left(\phi _1({\boldsymbol{\xi }},\,t)\right)}\right]\\ E\left[\cos {\left(\phi _0({\boldsymbol{\xi }})+\phi _1({\boldsymbol{\xi }},\,t)\right)}\right]&= \cos {\left(\phi _0({\boldsymbol{\xi }})\right)}\,\mathrm{e}^{-\sigma _1^2/2}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq81.gif)
![$$ \begin{aligned} E\left[\left|\Psi _S({\boldsymbol{\xi }},\,t)\right|^2\right] = P_0({\boldsymbol{\xi }})\,\left[1+\mathrm{e}^{-\left(\sigma _0^2+\sigma _1^2\right)}-2\,\mathrm{e}^{-\left(\sigma _0^2/2+\sigma _1^2\right)}\, \cos {\left(\phi _0({\boldsymbol{\xi }})\right)}\right]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq82.gif)
![$$ \begin{aligned} \mathrm{Var} \left[\Psi _S({\boldsymbol{\xi }},\,t)\right] = P_0({\boldsymbol{\xi }})\,\left(1-\mathrm{e}^{-\sigma _1^2}\right). \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq83.gif)
![$$ \begin{aligned} \mathrm{Var} \left[\langle \Psi _S({\boldsymbol{\xi }},\,t)\rangle _{\tilde{N}}\right] = P_0({\boldsymbol{\xi }})\,\frac{1-\mathrm{e}^{-\sigma _1^2}}{\tilde{N}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/11/aa36206-19/aa36206-19-eq85.gif)