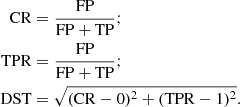| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 23 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935518 | |
| Published online | 21 October 2019 | |
IC 4665 DANCe
I. Members, empirical isochrones, magnitude distributions, present-day system mass function, and spatial distribution⋆
1
Laboratoire d’astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
e-mail: nuria.miret-roig@u-bordeaux.fr
2
Depto. de Inteligencia Artificial, UNED, Juan del Rosal, 16, 28040 Madrid, Spain
3
Department of Astronomy, The University of Tokyo, 7-3-1, Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
4
National Astronomical Observatory of Japan, 2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan
5
Astrobiology Center, 2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan
6
National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson, AZ 85719, USA
7
Institut d’Astrophysique de Paris, CNRS UMR 7095 and UPMC, 98bis bd Arago, 75014 Paris, France
8
Depto. Statistics and Operations Research, University of Cádiz, Campus Universitario Río San Pedro s/n, 11510 Puerto Real, Cádiz, Spain
9
Las Campanas Observatory, Carnegie Institution of Washington, Colina el Pino, 601 Casilla, La Serena, Chile
10
Centro de Astrobiología (CSIC-INTA), ESAC Campus, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
11
AIM Paris Saclay, CNRS/INSU, CEA/Irfu, Université Paris Diderot, Orme des Merisiers, France
12
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
Received:
22
March
2019
Accepted:
23
July
2019
Context. The study of star formation is extremely challenging, due to the lack of complete and clean samples of young nearby clusters and star-forming regions. The recent Gaia DR2 catalogue complemented with the deep ground-based COSMIC DANCe catalogue offers a new database of unprecedented accuracy to revisit the membership of clusters and star-forming regions. The 30 Myr open cluster IC 4665 is one of the few well-known clusters of this age and it is an excellent target where evolutionary models can be tested and planetary formation studied.
Aims. We provide a comprehensive membership analysis of IC 4665 and study the following properties: empirical isochrones, distance, magnitude distribution, present-day system mass function, and spatial distribution.
Methods. We used the Gaia DR2 catalogue together with the DANCe catalogue to look for members via a probabilistic model of the distribution of the observable quantities in both the cluster and background populations.
Results. We obtained a final list of 819 candidate members that cover a 12.4 magnitude range (7 < J < 19.4). We find that 50% are new candidates, and we estimate a conservative contamination rate of 20%. This unique sample of members allows us to obtain a present-day system mass function in the range of 0.02–6 M⊙, which reveals a number of details not seen in previous studies. In addition, we find that a spherically symmetric spatial distribution is favoured by our final list of members for this young open cluster.
Conclusions. Our membership analysis represents a significant increase in the quantity and quality (low contamination) with respect to previous studies. It offers an excellent opportunity to revisit other fundamental parameters such as age.
Key words: proper motions / stars: luminosity function / mass function / open clusters and associations: individual: IC 4665 / stars: low-mass / brown dwarfs
Full Tables 4 and 5 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A57
© N. Miret-Roig et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The initial mass function (IMF), the frequency distribution of stellar masses at birth, is a fundamental parameter in the study of stellar formation and evolution. It was first introduced by Salpeter (1955) in the form of ξ(log10m) = dn/dlog10m, and in this study we adopt the same formalism. Since then, strong efforts have been put into trying to constrain its shape in various environments. While it is fairly well known for intermediate masses, the extremes of the IMF remain uncertain. For the high-mass domain the main difficulty is the low number of stars and their fast evolution, while for the low-mass domain the main difficulty is the high level of contamination and incompleteness, even with the best photometric and astrometric surveys.
The study of the IMF requires an accurate and comprehensive census of the cluster members. In this study, we propose deriving such a census of one nearby young cluster, IC 4665. For this purpose, we use wide-field deep catalogues encompassing a large area around the cluster, and analyse them using a powerful classification algorithm capable of identifying the few hundreds of cluster members within the millions of interlopers. Hereafter, we refer to the candidate members resulting from the membership analysis as “members”.
There are few well-known, nearby (< 500 pc), pre-main sequence open clusters in the age interval 10–50 Myr. One of them is IC 4665, located in the Ophiuchus constellation and first reported by Philippe Loys de Chéseaux in 1745. Its age was estimated using the lithium depletion boundary at 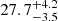 Myr by Manzi et al. (2008). From pre-main sequence isochrone fitting and upper-main sequence turn-off fitting, Cargile & James (2010) derived an age and a distance of 36 ± 9 Myr and 360 ± 12 pc and 42 ± 12 Myr and 357 ± 12 pc, respectively.
Myr by Manzi et al. (2008). From pre-main sequence isochrone fitting and upper-main sequence turn-off fitting, Cargile & James (2010) derived an age and a distance of 36 ± 9 Myr and 360 ± 12 pc and 42 ± 12 Myr and 357 ± 12 pc, respectively.
The first study of the IMF of IC 4665 was carried out by de Wit et al. (2006). They selected their members from photometric observations in the optical obtained at the Canada-France-Hawaii Telescope (CFHT). They estimated a contamination by foreground and background stars of up to 85% using control fields, which can be explained by its low galactic latitude. They reported a mass function best described by a power law with an exponent of –0.6 for the low-mass objects down to ∼0.1 M⊙. Later, Lodieu et al. (2011) performed a similar analysis adding near-infrared photometry from the UKIRT Infrared Deep Sky Survey (UKIDSS; Lawrence et al. 2007) to the previous observations of de Wit et al. (2006). They revised the members of previous studies, and proposed new candidate members as well. They reported a mass function best represented by a log-normal function with a peak at 0.25–0.16 M⊙. The differences between the mass functions obtained with these two studies can be mainly attributed to the high contamination rate of field stars, as we shall see later.
Recently, the second Gaia data release (Gaia Collaboration 2018a; hereafter Gaia DR2) publicly provided the five-parameter astrometric solution (positions on the sky, parallaxes, and proper motions) and G, GBP, and GRP magnitudes for more than 1.3 billion sources, with a limiting magnitude of G ≈ 21 mag at the faint end and G ∼ 3 mag at the bright end. The average astrometric precision is of the order of milliarcsecond per year in proper motion and below the milliarcsecond level in parallax, and the average photometric precision is at the millimagnitude level. This constitutes an astrometric+photometric dataset of unprecedented accuracy ideally suited to studying the census of nearby open clusters. A first demonstration of the power of the Gaia data is presented in Gaia Collaboration (2018b). They studied the fine structures of the Hertzsprung-Russell diagram (HRD) in the field and in open and globular clusters. IC 4665 was among their targets and they provided a list of 174 high-probability members up to magnitude G < 18. Soon after, Cantat-Gaudin et al. (2018) presented another study of open clusters using Gaia DR2 data. They derived another membership list (with the same magnitude limit) made of 175 high-probability members, 146 of which are in common with Gaia Collaboration (2018b). Both studies used only the Gaia data, applied a strict filtering, and discarded sources fainter than G = 18 mag, thus delivering a clean yet highly incomplete sample.
Over the past few years, Bouy et al. (2013) started a survey program, the DANCe project (standing for Dynamical Analysis of Nearby ClustErs), with the aim of deriving a comprehensive and homogeneous census of stellar and substellar sources in the nearby (< 1 kpc) young (< 500 Myr) clusters. This survey combines deep, wide-field, multi-epoch images obtained at various observatories to build a catalogue of accurate proper motions and multi-wavelength photometry with a sensitivity up to 5 mag deeper than Gaia and including near-infrared data. Here we present the DANCe catalogue for the region of IC 4665. After identifying candidate members, we present the cluster properties and in particular the empirical isochrones, distance, magnitude distribution, present-day system mass function (PDSMF), and spatial distribution. The assumptions in this work are based on the properties of the dataset and the cluster. We highly recommend that the reader look at Sect. 2 of Olivares et al. (2019) for more details.
This paper is structured as follows. We introduce the two datasets used in this study in Sect. 2. We present the algorithm that we used for the membership analysis in Sect. 3, and discuss the results obtained including a comparison with previous studies in Sect. 4. Then we provide the empirical iscohrones of this young cluster and compare them with evolutionary models in Sect. 5. In addition, we computes the apparent magnitude distribution and the PDSMF, which we present in Sect. 6. Finally, we present the spatial distribution of the cluster in Sect. 7, and draw our conclusions in Sect. 8.
2. Data
In this work we used two different datasets with different origins and properties to look for members in the IC 4665 open cluster. In this section we describe how we obtained each of them.
2.1. Gaia DR2 dataset
We queried a circular area of 3° radius around the centre of the cluster (RA = 266.6°, Dec = 5.7°), from the Gaia DR2 catalogue (see Appendix A.1). We kept only those sources with a full five-parameter solution available. Some quality checks have been suggested in the literature. We did not apply any filtering techniques because we wanted to be as complete as possible. The filtering recommended by the Gaia team is based on the renormalised unit weighted error (RUWE) and is described in detail in a publicly available technical note1. The RUWE criterion is a quality indicator which can be used when the aim is to have only the most precise, reliable, and consistent astrometric solutions. However, it also leads to a higher degree of incompleteness. For instance, since the Gaia DR2 catalogue does not deal with binaries, their solution is likely to be “inconsistent”, and thus the RUWE filter will remove most of the binaries, already a low number, included in Gaia DR2. We therefore have no strong scientific argument for cutting our sample by this or any other kind of filtering. In addition, the sources with problematic astrometric solutions can be rejected later on based on complementary observations and/or subsequent Gaia DRs.
This sample contains positions, proper motions, parallaxes, and G, GBP, GRP photometry for 1 217 725 sources; hereafter we refer to it as the GDR2 catalogue2. The mean errors of this catalogue are ∼0.5 mas for parallaxes, ∼1 mas yr−1 for proper motions, and < 0.1 mag for the photometry. According to Gaia Collaboration (2018a), the catalogue is mostly complete down to G = 7 mag. On the faint side, Lindegren et al. (2018) reported that the five-parameter solution is 94.5% complete up to G = 19 mag (see their Table B.1). In the following we therefore assume that the GDR2 catalogue is complete between 7 < G < 19 mag.
2.2. DANCe dataset
We searched the European Southern Observatory (ESO) archive, the National Optical Astronomy Observatory (NOAO) archive, the Palomar Transient Factory (PTF) archive hosted at the NASA/IPAC Infrared Science Archive (IRSA), the Canadian Astronomy Data Centre (CADC) archive, the Isaac Newton Group (ING) archive, the WFCAM Science (WSA) archive, and the SMOKA science archive for wide-field images within a circular region of 3° radius, centred on IC 4665. The data found in these public archives was complemented with our own observations using the Las Campanas Swope telescope and its Direct CCD camera, the Dark Energy Camera (DECam) mounted on the Blanco telescope at the Cerro Tololo Inter-American Observatory (CTIO), the NEWFIRM camera mounted on the 4 m telescope at the Kitt Peak National Observatory (KPNO), the Hyper Suprime-Cam (HSC) mounted on the Subaru telescope at the National Astronomical Observatory of Japan, and the Wide Field Camera (WFC) mounted on the Isaac Newton Telescope (INT). A number of observations found in the archives were discarded after a visual inspection because of their poor quality, limited sensitivity, or acquisition problems. Table 1 gives an overview of the various cameras used for this study.
Instruments used in this study.
The airmass and the full width at half maximum (FWHM) measured in the images using point-like sources are two important parameters influencing the achievable astrometric accuracy. About 90% of the observations were obtained at airmass ≤1.5 (see Fig. 1, top). IC 4665 is located at a declination of δ ∼ 5° and we gathered data from both hemispheres. About 82% of the images have FWHM ≤ 1″, and 90% have 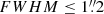 (see Fig. 1, bottom).
(see Fig. 1, bottom).
 |
Fig. 1. Top: cumulative distribution of airmass for the observations. Bottom: cumulative distribution of average FWHM for the images. |
In all cases except for MegaCam, WIRCam, PTF, DECam, UKIRT, and HSC images, the raw data and associated calibration frames were downloaded and processed using standard procedures using an updated version of Alambic (Vandame et al. 2002), a software suite developed and optimised for the processing of large multi-CCD images. In the case of CFHT/MegaCam, the images processed and calibrated with the Elixir pipeline were retrieved from the CADC archive (Magnier & Cuillandre 2004). The WIRCam images processed with the official ‘I‘iwi pipeline were retrieved from the CADC archive. In the case of DECam, the images processed with the community pipeline (Valdes et al. 2014) were retrieved from the NOAO public archive. The pipeline-processed PTF images were downloaded from the IPAC archive. UKIRT images from the UKIDSS and UHS surveys (Dye et al. 2018) processed by the Cambridge Astronomical Survey Unit were retrieved from the WFCAM Science Archive. Finally, the HSC raw images were processed using the official HSC pipeline (Bosch et al. 2018).
2.2.1. Astrometric analysis
After a visual rejection of problematic images (mostly due to loss of guiding, tracking, or electronics problems), the dataset included 6774 individual images originating from 13 instruments. The total amount of data (scientific images, associated calibrations, and intermediate products) was almost 20TB.
The astrometric calibration was performed as described in Bouy et al. (2013). The recently released Gaia DR2 catalogue was used as external astrometric reference instead of the 2MASS catalogue, leading to a much improved astrometric solution.
The final average internal and external 3σ residuals amounted to ∼25 mas for high signal-to-noise (photon noise limited) sources. As explained in Bouy et al. (2013), the proper motions computed are relative and display an offset with respect to the ICRS. We estimated the offset by computing the median offset between our values and the Gaia DR2 proper motion measurements after rejecting outliers using the modified Z-score (Iglewicz & Hoaglin 1993). We find offsets of (Δμαcosδ, Δμδ) = (1.70, 4.48) mas yr−1. The uncertainty on this offset is estimated using bootstrapping and is found to be negligible (< 0.003 mas yr−1).
Given the superiority and robustness of Gaia measurements compared to our ground-based measurements, the Gaia DR2 proper motion measurements are always preferred when available. Therefore, we cross-matched our catalogue with the Gaia DR2 using a 1″ radius and we kept all the Gaia proper motions when available. The median uncertainties in proper motions are ∼2 mas yr−1.
We found that about 1.3% of the sources (∼60 000) were duplicated in the final catalogue. A visual inspection showed that they were almost all very low signal-to-noise and that the SEXTRACTOR deblending algorithm resolved them as two sources instead of one, in one (or a few) images. These resolved sources later fooled the cross-identification algorithm and ultimately resulted in two independent sources instead of one. There is no straightforward solution to this problem for now, but given their very small number we treated them as regular sources in the rest of the analysis and simply looked for duplicated entries in the final list of members.
2.2.2. Photometric analysis
The photometric calibration was performed only for the g, r, i, z, y and J, H, Ks images. It was not attempted for the INT images obtained in any other filter, the ESO2.2 m WFI images, the PTF images (because the camera has a significantly coarser pixel scale and the images reach a depth shallower than Pan-STARRS), and the CPAPIR I-band images.
The photometric zeropoint of all individual images was computed by direct comparison of the instrumental SEXTRACTOR MAGAUTO magnitudes with an external catalogue:
-
J, H, Ks images were tied to the 2MASS catalogue,
-
g, r, i, z, y images were tied to the Pan-STARRS PS1 first release.
The procedure followed to derive the individual zeropoints is described in Olivares et al. (2019). Briefly, the zeropoints are computed as the median of the difference between the instrumental magnitude and the measurements of the closest match within 1″ in the reference catalogue after rejecting outliers using the modified Z-score criterion. We find typical 1σ dispersions of the order of 0.03–0.08 mag depending on the filter.
We median-combined all the images obtained with the same camera and in the same filter to build a deep stack and extracted the corresponding photometry. This allowed us to significantly improve the sensitivity in all filters and to recover or improve the photometry of faint sources obtained in the individual images.
As in Bouy et al. (2013), we complemented the photometry extracted from the images with that of external catalogues: Gaia DR2 (G, GBP, GRP), Pan-STARRS (grizy), 2MASS (JHKs), and ALLWISE (all four bands) to improve the spatial and wavelength coverage of the final dataset (see Appendices A.1–A.4 for the queries used). Either the corresponding photometric measurements were added to our catalogue when no measurement was available in our data, or the weighted average of all measurements (our values and from external catalogues) was computed after rejecting outliers using the modified Z-score criterion.
The differences between the transmission of the various instruments contribute to the photometric dispersion (see e.g. Fig. 2). Moreover recent variability studies of young clusters found typical amplitudes of 0.03 mag (e.g. Rebull et al. 2016, 2018). As explained in Olivares et al. (2019) we add quadratically 0.05 mag to all the photometric measurement uncertainties in our catalogue to take into account these sources of uncertainties in our membership analysis. The final mean uncertainties in photometry depend on the photometric band, and are of the order of 0.07 mag.
 |
Fig. 2. Transmission curves of the i filters used in this study. |
Given the low extinction in that area of the sky, the maximum of the magnitude distributions (Fig. 3) gives an estimate of the completeness limit of the survey. It is nevertheless important to remember that the spatial coverage of the various instruments is not homogeneous and the depth of the survey varies spatially. The limits of sensitivity of the external catalogues merged with our data (2MASS and Pan-STARRS) are sometimes visible as secondary maxima. In Table 2 we give, for each photometric band, the number and percentage of measurements as well as the completeness limits we use in this study. This final catalogue (hereafter the DANCe catalogue) includes 2 358 937 sources.
 |
Fig. 3. Density of sources as a function of magnitude for members of the DANCe catalogue. |
Number of measurements and percentage for each photometric band in the DANCe catalogue.
3. Membership analysis
To select candidate members we used the methodology originally developed by Sarro et al. (2014) and updated by Olivares et al. (2019). Briefly, this algorithm separates all the sources within two populations, namely the cluster and the field. The field model is computed once at the beginning and fixed thereafter, based on the assumption that the few hundred cluster members do not significantly affect the field population model. The cluster model is built iteratively and, at each iteration, both models are used to reclassify the sources until convergence. This algorithm takes into account the covariance matrix of the astrometric parameters when available. To model the cluster and field populations, the algorithm only uses the complete sources (i.e. the sources with measurements available for all the observables). The coverage and sensitivity of the different photometric bands is therefore a key issue in our analysis. The final model allows us to compute a membership probability to incomplete sources after marginalisation over the missing values. To start the analysis and build the first model we need a catalogue of sources for the region of interest and an initial list of members. The latter can be slightly contaminated and incomplete, and serves only to define the cluster locus in the multi-dimensional space in the first iteration.
Because the field and cluster models are built from sources with complete photometric and astrometric measurements, a simultaneous analysis of the GDR2 and DANCe catalogues would not be optimal. Many faint DANCe sources would have missing parallaxes and Gaia photometry, while bright GDR2 sources (saturated in our images) would have missing DANCe photometry, making it difficult (or even impossible) to define a proper representation space in which a sufficient number of sources have complete measurements. As described in Olivares et al. (2019) we therefore decided to analyse the two catalogues independently.
3.1. Initial members
Recently, two studies have published members of IC 4665 using the Gaia DR2 data. The work of Gaia Collaboration (2018b) published a list of 174 members, and the work of Cantat-Gaudin et al. (2018) published a list of 175 members. Both studies have a magnitude limit of G = 18, and most of the sources in common. We combined their results and obtained a list of 203 members, which we used as the initial list for our membership analysis of the GDR2 catalogue.
To start the membership algorithm for the DANCe catalogue, we used the members we obtained with the GDR2 catalogue that have a counterpart in DANCe. In this case, the initial list does not cover the full magnitude range of the catalogue because DANCe goes fainter than the initial list of GDR2 members. However, our algorithm extends the initial principal curve (see the cluster model for the photometry in Sect. 3.4) by progressively and iteratively extrapolating the photometric sequence to fainter regions. These fainter regions of extrapolation are small and the new candidate members found with them are added and used in subsequent iterations to better define (or correct if necessary) the extrapolation. The extrapolation of the photometric curve is guided by the astrometry, which does not change with magnitude. This extrapolation of the principal curve is further explained in Sarro et al. (2014), where we presented for the first time the membership algorithm.
3.2. Representation space
The representation space is the set of astrometric and photometric variables we use for the membership analysis. We always use proper motions, and parallaxes in the case of the GDR2 catalogue. The photometric variables are chosen according to their importance calculated from a random forest algorithm, as in Olivares et al. (2019). The greater the number of features, the more information there is to classify the sources between members and non-members. At the same time, the bands with a large number of missing observations are avoided.
With the representation space established, the whole dataset is split between complete and incomplete sources. A source is said to be complete when it has a measurement for all the variables of the chosen representation space. In consequence, different representation spaces lead to different complete/incomplete ratios.
For the analysis with the GDR2 catalogue, the representation space we used is pmra, pmdec, parallax, GRP, GBP − G, G − GRP. With this representation space 1 184 922 sources (97%) have complete data. For the analysis with the DANCe catalogue, the representation space we used is pmra, pmdec, J, i − z, i − y, i − J. With this representation space, 1 627 593 sources have observations in all the photometric bands, which represents a 69% of the catalogue. We decided not to include the g, r, H, and Ks bands in the representation space because of the large number of sources with missing photometry (see Table 2).
3.3. Field model
The field population is modelled with a Gaussian mixture model (hereafter GMM) in the whole representation space. The field model is computed once at the beginning and fixed thereafter. We explored GMMs with different numbers of components (60, 80, 100, 120, 140, 160, and 180). As the optimum model we chose the simplest one, which minimises the Bayesian information criterion (BIC). This results in 100 components for the analysis with the GDR2 and the DANCe catalogue.
We ran the full model considering several pin thresholds (0.5, 0.6, 0.7, 0.8, and 0.9), and for each we computed the optimum threshold, popt, using synthetic data. In Table 3 we show pin, popt, and the number of complete and incomplete members for each independent analysis (GDR2 and DANCe).
Internal probability threshold (pin), optimum probability threshold (popt), and number of complete and incomplete members (CM, IM) for each of the membership analyses, namely GDR2 and DANCe.
3.4. Cluster model
The cluster model is a product of two independent models: a GMM for the astrometry and a principal curve in photometry. The astrometric model is a GMM and we chose the number of components that optimises the BIC between 1 and 4.
The cluster model is computed iteratively, starting from the initial list of members. At each iteration we independently compute a model for the astrometry and a model for the photometry. Then we assign Bayesian probabilities of membership to all the complete sources. These probabilities, together with a probability threshold, pin, are used to reclassify the complete sources between members and non-members. The pin is a free parameter of the model that defines the degrees of completeness and contamination that we desire for the training set (and as a consequence, for the final list of members). We refer the interested reader to Sarro et al. (2014) and Olivares et al. (2019) for a more detailed description of this parameter. Then the cluster model is recomputed based on the new members list, and we repeat this process until convergence.
When the model has converged, we generate a synthetic dataset from the model learnt with observed data. Therefore, it has similar properties to the observed (e.g. missing values, frequency of members). As a consequence, the results derived from the synthetic dataset are restricted to the used representation space and learnt model.
We use this synthetic dataset to analyse the goodness of our classification and to compute the optimum probability threshold, popt, used for the final classification. The optimum threshold will of course depend on the scientific goal behind the membership analysis. In our case, in order to study the mass function, we are interested in reaching a compromise between the contamination and the true positive rate. To this end, we chose as popt the value that minimises the distance to the perfect classifier (DST). This distance is defined in terms of the contamination rate (CR) and the true positive rate (TPR), which in turn depend on the confusion matrix: true positives (TPs), false positives (FPs), false negatives (FNs), and true negatives (TNs). These indices are defined as follows:
As we have mentioned, the estimations that can be obtained with this synthetic dataset are restricted to the same conditions as the observations and to the assumption that the model correctly represents the observed data. Thus, the measured CR and TPR can be underestimated and overestimated, respectively, with respect to those obtained with better quality data and more realistic models. As we show in Sect. 3.6, this is observed in the CR of DANCe. The value estimated using synthetic data appears to be underestimated with respect to that obtained using the GDR2 members as reference. For more details we refer to Olivares et al. (2019).
3.5. Classification of incomplete sources
We used the field and cluster models described in the previous subsections to compute membership probabilities for the incomplete sources (i.e. the sources that lack one or more magnitudes of the representation space). Then we used the optimum threshold to classify all the sources between members and non-members.
For the GDR2 catalogue there are very few incomplete sources and none of them is classified as a member. For the DANCe catalogue, the number of incomplete sources classified as members is 4–8 depending on the pin. In general, they lack z and/or y photometry, and the brightest ones are also classified as members by the analysis with GDR2.
3.6. Final members lists
Tables 4 and 5 (available at CDS) give the GDR2 and DANCe catalogues used in this work, respectively. For the GDR2 catalogue we provide the Gaia DR2 source ID and the sky positions, and for the DANCe catalogue we compiled all the astrometry and photometry presented in Sect. 2. In addition, for each catalogue we provide the posterior membership probabilities obtained with the different pin discussed in this section. Here we describe the strategy we used to choose the most convenient member list for our requirements. However, we encourage the interested readers to choose the member lists most convenient to their goals.
GDR2 catalogue of IC 4665.
DANCe catalogue of IC 4665.
The membership probabilities obtained with different pin values have to be compared with care. The relation between different membership probabilities (obtained with different pin) is not linear, and lower pin tends to provide higher membership probabilities. In general, the models computed with lower pin permit a greater inclusion of sources initially classified as “field” into the cluster class during the training of the model. This results in lists of members that can include a significant number of contaminants. On the contrary, models computed with higher pin are more restrictive, include fewer additional sources into the cluster model, and thus tend to have lower contamination, but at the same time can be incomplete.
The membership probabilities we compute are not absolute, but are closely related to the model used, which at the same time depends on the representation space and on the pin (desired degree of completeness and contamination). In consequence, the comparison between GDR2 and DANCe membership probabilities is not straightforward, especially due to the different representation spaces of each catalogue (DANCe does not have parallaxes).
To study cluster properties such as the mass function, we needed a unique list of members, the cleanest and most complete list possible. This meant first choosing a pin for each study (GDR2 and DANCe), and then combining the two catalogues. We began with the analysis of GDR2, which was expected to be more robust since it includes a very discriminating variable: the parallax. We used a Kolmogorov–Smirnov (KS) test in different variables of the representation space (proper motions, parallax, and photometry) to see if the distributions of these variables obtained with different pin were compatible with each other. The goal was to see if we could find signs of a strong contamination or a strong incompleteness in one or several of the lists with respect to the others. We started by taking the sources classified as members (i.e. those with p > popt) obtained with the model trained with pin = 0.9 as a reference. This is the most conservative and the least contaminated, but also probably the most incomplete list of members. Then, we compared this list of members with all the rest (pin = 0.5, 0.6, 0.7, and 0.8, one at each time). The KS test showed that for the lists of pin = 0.5 and 0.6, there is evidence that the distribution of their proper motions and parallax values do not come from the same distribution as that obtained with the list of pin = 0.9 with a p-value lower than the significance level 0.01. On the contrary, for the distribution of the astrometric variables coming from the lists of pin = 0.7 and 0.8, the KS test shows no evidence to reject the conclusion that they come from the same distribution as the one obtained with pin = 0.9 with p-values of 0.4–0.5. Then, we investigated the reason for the incompatibility of the lists of pin = 0.5 and 0.6 with respect to the rest. We found that the parallax and proper motions distributions obtained with the lists of pin = 0.5 and 0.6 have significantly more extended wings than the distributions obtained with the lists of higher pin. We interpreted this as contamination, and therefore we discarded these two lists. The remaining lists are compatible according to the KS test so we chose the list of pin = 0.7, which has the largest number of members.
To select the optimum pin for the DANCe analysis we also applied a KS test to find which distributions were compatible with the one obtained with pin = 0.9. In this case there was no evidence to reject the conclusion that the distributions of all the variables analysed for the lists from all pin come from the same distribution as those of pin = 0.9 since all the p-values were > 0.3. Then, to check the consistency between the GDR2 and DANCe lists, we took the members of GDR2 pin = 0.7 as a reference and compared them with the members recovered in the different DANCe lists, in the region where both studies are complete (14.5 ≲ G ≲ 19). We found that all the DANCe lists recovered roughly the same number of GDR2 members (250–266 from 285, ∼90%). On the contrary, the number of members in DANCe that were not in GDR2 decreased with increasing pin. These sources have parallaxes that are in general incompatible with the GDR2 members (beyond 3σ), and thus we believe that most of them are contaminants (representing 30–35% of the DANCe members). In short, for the DANCe analysis we do not find any strong argument for discarding any list. Therefore, we decided to keep the one with largest number of members, the one with pin = 0.5, keeping in mind that it includes a contamination of the order of 30–35% estimated from the comparison with the GDR2 members.
In the rest of this work, we use the GDR2 list with a pin = 0.7 and the DANCe list of pin = 0.5. These two lists amount to a final list of 819 members, which is analysed in more detail in the next section.
4. Members comparison
In this section we analyse and discuss our final members list. We compare the results obtained with the GDR2 and DANCe catalogues, and we also compare our final list with the members already reported in the literature.
4.1. Comparison of GDR2 and DANCe members
Here we compare the two membership analyses obtained with the GDR2 and the DANCe catalogues. We cross-matched the two catalogues (which contain members and field stars) and found 1 211 272 sources in common. In Fig. 4 we compare the membership probabilities obtained with the two catalogues. The diagonal line represents the one-to-one relation, and the vertical and horizontal dashed lines represent the optimum thresholds. We see that most of the sources are clustered in the bottom left (field) and top right (cluster) regions of the diagram. Nonetheless, there are sources that are classified as members by one study and not by the other.
 |
Fig. 4. Comparison between the membership probabilities recovered by the GDR2 and DANCe classifiers, for objects in both catalogues. The diagonal line represents the one-to-one relation, and the horizontal and vertical dashed lines show the optimum probability thresholds. |
To understand the differences between the two classifiers we represented the number of members as a function of the magnitude (Fig. 5). We distinguish between the members obtained with both classifiers (red), the members only from the GDR2 analysis (blue), and the members only from the DANCe analysis (green). Here we discuss the four possible cases regarding the results of the two membership analyses.
 |
Fig. 5. G and i (top and bottom) magnitude distributions of the sources classified as members in the GDR2 and DANCe studies (red), classified as members by GDR2 but not by DANCe (blue), and classified as members by DANCe but not by GDR2 (green). |
4.1.1. Members in GDR2 and DANCe
There are 331 sources that appear as members in both analyses (red in Fig. 5). In the magnitude range where both catalogues are complete, the majority of members are classified as such by the two analyses.
4.1.2. Members in GDR2 only
There are 103 sources that appear as members in the GDR2 analysis, but not in DANCe (blue in Fig. 5). The majority of these are the brightest sources that are saturated in the DANCe catalogue. Most of them have J, H, and Ks photometry, but lack i, z, and y which are essential bands for the representation space we use in DANCe.
In the magnitude range where both analyses are complete, we see that the members obtained only with GDR2 have a low and flat distribution. This can be interpreted as the GDR2 members list having very low contamination, which does not depend on the magnitude. The reason is that the parallax is the most discriminating variable for classifying these members. Although the uncertainties on the parallax depend on the magnitude, they are at the level required to distinguish the cluster from the field along the whole magnitude range. At magnitudes > 18 we see a slight increase, but it is not significant.
4.1.3. Members in DANCe only
There are 385 sources that appear as members in DANCe, but not in GDR2 (green in Fig. 5). Of these sources, 120 objects (31%) do not have the five-parameter solution in Gaia and 186 (48%) have parallax uncertainties > 10%. We discussed in the previous section that we find a ∼30% of contamination in the region where both studies are complete. This is significantly higher than the value we found in other clusters (i.e. the Pleiades and Ruprecht 147; (see Sarro et al. 2014; Olivares et al. 2019, respectively), but this is expected given the lower galactic latitude and significantly low proper motions of IC 4665.
In addition, we see that the amount of members only recovered by DANCe increases as a function of magnitude in the region where both analyses are complete. We interpret this as a dependence of the contamination on the magnitude. The DANCe analysis does not use the parallax and thus it is expected that photometry plays a major role, especially in this cluster with low proper motions.
4.1.4. Non-members in GDR2 and in DANCe
All the remaining sources are classified as field stars by both studies. Most of them have extremely low membership probabilities, which clearly identifies them as field population. There are several sources that have rather high probabilities, but fall below the threshold. This means that we cannot definitely discard them as members, and that we could consider them as candidate members depending on the scientific case. The sources that are spread along the rest of the diagram may suffer from the problems already discussed, or simply the observables in the two catalogues are too different. To clarify the membership of the uncertain cases we would need either a longer temporal base-line to improve the proper motions or spectroscopy to study their properties (i.e. low gravity due to youth).
In short, we see that in general the two independent analyses agree rather well, especially in the magnitude range were both are expected to perform well. The members obtained with both catalogues occupy the same space in the vector point diagram (see Fig. 6, left). The members coming from the DANCe catalogue typically have a larger dispersion and larger uncertainties, expected by the different precision of both catalogues. In the space of parallaxes (Fig. 6, right) we see that the members from the GDR2 analysis are very highly concentrated around the median value (2.84 mas with a standard deviation of 0.36 mas). Some members from the DANCe analysis, which does not use this parameter for the classification, also have parallaxes compatible with the cluster distribution. Others have parallaxes incompatible with the cluster (at 3σ level) and they are either problematic measurements (because they are very faint) or contaminants. Future releases of the Gaia catalogue will help to clarify these cases.
 |
Fig. 6. Vector point diagram (left) and parallax–proper motion diagram (right) of the IC 4665 open cluster. The members are shape- and colour-coded according their origin: GDR2 and DANCe analysis (red circles), only GDR2 analysis (blue left-pointing triangle), and only DANCe analysis (green right-pointing triangle). |
When we introduced the GDR2 catalogue in Sect. 2.1, we mentioned that we have not filtered the data in any manner in order to be the most complete possible. Here, we discuss the RUWE goodness of fit indicator of the members found in this study. Our sample contains sources with a RUWE in the range 0.8–16.3, and only 9% of them have a RUWE larger than the recommended threshold (1.40). However, we insist that all the sources with a RUWE larger than the recommended value do not always have an incorrect solution, and future releases of Gaia or complementary observations will determine this.
4.2. Comparison with other studies
In this section we compared our list of 819 members with other studies in the literature and found that 409 (50%) are new members. We cross-matched each of the members lists reported in the literature with ours using a maximum separation of 1″.
In Fig. 7 we compare the members we found with two of the most representative membership studies of IC 4665: Lodieu et al. (2011), based mainly on photometry, and Cantat-Gaudin et al. (2018), which uses the Gaia DR2 astrometry. As a general trend, purely photometric studies tend to have more contamination than spectroscopic ones or ones based on Gaia DR2 astrometry.
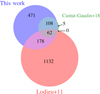 |
Fig. 7. Venn diagram comparing the members in this work to previous studies in the literature (i.e. Lodieu et al. 2011; Cantat-Gaudin et al. 2018). |
4.2.1. de Wit et al. (2006)
These authors photometrically selected 691 low-mass stellar and 94 brown dwarf candidate members over an area of 3.82 square degrees centred on the cluster. In addition, they applied a filter for bright stars based on the proper motions from Tycho-2 and UCAC2 public catalogues.
We detected some astrometric offsets between their positions and ours and consequently extended the cross-match search radius to 2″. We confirmed 195 of their members and rejected the rest of their candidates which have very low membership probabilities in our study. Therefore, we estimate a contamination up to 75% in their study compatible with their own estimate. We believe that one of the reasons of their high amount of contamination is a problematic photometric calibration (their i- and z-band photometry display an offset of ∼1 mag compared to values from Pan-STARRS).
4.2.2. Manzi et al. (2008)
These authors did not attempt to do a comprehensive census of the cluster. Instead, they photometrically selected candidates from the literature and then spectroscopically confirmed 37 of them. Their aim was to determine the age of IC 4665 using the lithium depletion boundary method. We confirmed 29 of their members (78%) and discarded the remaining 8 (two of which were classified as not fully secure members by the authors). These eight members were discarded because their Gaia DR2 parallaxes and/or proper motions are far from the cluster distribution, although their photometry falls on the cluster sequence. Therefore, these sources are either interlopers or have a problematic astrometric solution in Gaia DR2.
4.2.3. Jeffries et al. (2009)
These authors aimed to study the pre-main sequence lithium depletion for low-mass stars in IC 4665. For this purpose, they selected 40 members according to several spectroscopic criteria. We confirmed 30 of their members (75%) and rejected the remaining 10. This study has 12 members in common with Manzi et al. (2008), and only one of these sources was rejected by our study. Again, the ten members were excluded from our list of members because their Gaia DR2 astrometry is incompatible with that of the cluster, but the same reasoning of Manzi et al. (2008) applies.
4.2.4. Cargile & James (2010)
These authors used a photometrically selected sample of members in the central region of the cluster (1 deg−1) to study the age and distance of IC 4665. Their sample contained 382 candidates members, 49 of which were confirmed by our study. From this, we estimated their contamination to be 87%.
4.2.5. Lodieu et al. (2011)
These authors used photometry from UKIDSS and CFHT to identify members in IC 4665. They presented a sample of 1372 members in the magnitude range 15 < i < 20.4, which they used to study the luminosity and mass functions.
Only 240 of their candidates (17%) are classified as members in our work (see Fig. 7). The majority of the rejected candidates have extremely low membership probabilities in our analysis (both in GDR2 and DANCe). We believe the reason for their high amount of contamination (∼80%) is the same photometric offset as for de Wit et al. (2006) since they used the same data.
These works constituted the most exhaustive study, especially regarding the low-mass regime, previous to the results we present here. Given the high levels of contamination found by the present analysis, we hereafter do not attempt any comparison of their luminosity and mass function.
4.2.6. Bravi et al. (2018)
These authors used the Gaia ESO Survey to study the IC 4665 open cluster. They carried out spectrosopic observations of 567 sources in the region of the cluster. They used spectroscopic criteria to exclude obvious contaminants, and then they computed membership probabilities using the radial velocity distribution of the cluster and the field. They ended up with 29 sources with membership probability values higher than 0.5. Of these sources, 24 have probability values higher than > 0.8. From these 29 candidates, 20 were confirmed by our study (15 have probabilities > 0.8 according to their study), and the remaining 9 were definitely rejected from our study. As for the previous spectroscopic surveys, we discarded these nine members because of the Gaia DR2 astrometry, which is incompatible with that of the cluster.
4.2.7. Gaia Collaboration (2018b)
With the purpose of demonstrating the power of Gaia DR2 in highlighting the fine structures of the Hertzsprung-Russell diagram, these authors selected members for a number of open clusters. Their ambitious goal required selecting only the sources with the highest precision in astrometry and photometry, and among other filters, they restricted the selection to sources brighter than G = 18. One of the clusters of their study is IC 4665, for which they provided a list of 174 members based only on the astrometric solution of Gaia DR2. They claimed that their list was not complete, but that it contained potential members, i.e. that it had an extremely low contamination rate.
To make a fair comparison with this study, we only considered the members from our sample that are in the same magnitude and spatial range (brighter than G = 18 and 2.4° radii around the centre of the cluster). This results in 267 members, 215 of which are classified as members by our analysis with the GDR2 catalogue and the rest come from the analysis via the DANCe catalogue alone.
The study of Gaia Collaboration (2018b) and ours have 162 members in common, which is 93% of their list. From the 12 objects classified as members by these authors and not by our study, there are 4 that have probabilities > 0.5 but fall below the optimum threshold we adopted, and 8 that have lower probabilities. Of these eight members, only one was also classified as a member by a similar study (Cantat-Gaudin et al. 2018). These small differences are part of the Poissonian noise of the membership analysis. In addition, we find 53 members not detected by these authors that are spread along all the parameter spaces (proper motions, parallax, and magnitude), following the cluster distribution. Some of these 53 members could have been discarded by the authors in their data filtering.
4.2.8. Cantat-Gaudin et al. (2018)
These authors provided a membership analysis for a large number of clusters making use of the recent Gaia DR2 data. In order to avoid large uncertainties, they restricted the selection to the sources brighter than G = 18. They used an unsupervised membership algorithm to derive membership probabilities using only the astrometry of Gaia DR2, and they found 175 members of IC 4665.
To make a fair comparison with this study, we only considered the members of our sample that are brighter than G = 18 and occupy the same spatial region of the sky (∼2° radius around the centre of the cluster). This results in 244 potential members, 205 of which come from the analysis of the GDR2 catalogue and the rest only from the analysis of the DANCe catalogue.
The study of Cantat-Gaudin et al. (2018) and our study have 170 members in common, which is 97% of their list. From the five objects classified as members by these authors and not by our study, there are four that have probabilities > 0.5 but fall below the optimum threshold we adopted, and one that has a probability of 0.2. Again, these small differences are part of the uncertainties of the membership analysis. In addition, we find 35 members not detected by Cantat-Gaudin et al. (2018), 17 of which are also classified as members by Gaia Collaboration (2018b). These members are randomly distributed within the proper motions and parallax distributions. We found three very bright members with G magnitudes 7.5, 9.5, and 10.5, and the rest fainter than G = 14.5. The DANCe members not classified by GDR2 in this magnitude range (39 sources with 14.5 < G < 18) are likely to be contaminants, as discussed in Sect. 3.
5. Empirical and theoretical isochrones
In this section we provide the empirical isochrones obtained with our members of IC 4665. Then we compare them with theoretical evolutionary models in several apparent colour–magnitude diagrams. Finally, we convert the apparent colour–magnitude diagrams to absolute colour–magnitude diagrams and discuss them.
5.1. Empirical isochrones
The empirical isochrones provide key information for comparing and constraining the theoretical evolutionary models. In this study, we use the membership analysis of IC 4665 to report the empirical isochrone of a 30 Myr old open cluster (see Fig. 8).
 |
Fig. 8. (G, G − GRP) and (i, i − Ks) colour–magnitude diagrams (left and right, respectively) of the IC 4665 open cluster. The members are colour-coded according to their membership probability, and the empirical isochrone is overplotted (black line). |
To obtain the empirical isochrones, we fitted a principal curve to the members in several apparent colour–magnitude diagrams. Then we manually shifted the principal curve to reach the lower edge of the distribution, which is supposed to correspond to the single-star zero age main sequence (ZAMS). In addition, we applied manual offsets where needed to better fit the lower edge of the cluster sequence. The empirical isochrones we provide are thus the lower envelope sequence of the members. This does not correspond to the principal curve, which indicates the mean position of the sequence.
In Tables B.1 and B.2 we give the apparent magnitudes for the IC 4665 empirical sequence in the G, GBP, GRP, i, Y, J, H, Ks over the dynamic range of our dataset. We reiterate that they are just an estimation of the ZAMS locus at the age of IC 4665, which could be used for comparison with other clusters. For more quantitative analysis, we provide the full list of members and let the interested user decide the most convenient way to use them.
5.2. Evolutionary models
In Fig. 9 we compare the observed sequence of IC 4665 and the empirical isochrones described in Sect. 5.1 to the 30 Myr models of PARSEC-COLIBRI3 (Marigo et al. 2017) and BT-Settl4 (Allard 2014) in several colour–magnitude diagrams. The distance modulus applied to the models uses the median parallax of the GDR2 members (2.81 mas). We did not include the effect of any systematic because here we only intend to make a qualitative comparison. We also corrected the models for the median extinction measured with Gaia (AG = 0.62 mag which corresponds to AV = 0.72 mag using the AG/AV = 0.85926 from the PARSEC website, see Footnote 3).
 |
Fig. 9. Comparison of the observations of the IC 4665 sequence (black dots) and the empirical sequence (red lines) to the models of PARSEC+COLIBRI (blue line) and the BT-Settl (green line) for an age of 30 Myr in several colour–magnitude diagrams. |
As a general result, we see that the models show a major improvement with respect to previous versions, especially in the y, J, H, Ks bands (see e.g. the comparison of the Pleiades by Bouy et al. 2015) even at such a young age. The brightest stars are only covered by the PARSEC isochrones, while the faintest are only covered by the BT-Settl models. Between i = 11 − 15 mag, both models agree fairly well with each other and with the observations. However, the PARSEC models start to differ from the observations at i > 15 mag, and in this magnitude range the BT-Settl models are believed to be more accurate. Despite the global improvement of the models in all the photometric bands, we still find a space for improvement in some of them, especially the ones involving the redder bands (see middle left and bottom left panels of Fig. 9). For this, low-contamination samples combined with accurate photometric measurements along a wide magnitude range are essential.
Regarding the Gaia DR2 photometry, it is noticeable that the GBP band shows a larger spread for magnitudes > 18 mag. In the near-infrared our measurements come mostly from 2MASS, which has relatively large errors beyond 14 mag, which in turn explains the larger dispersion between 14 < J < 17. Beyond this value the measurements come from our own deeper images, and both the uncertainties and the dispersion of the isochrone are significantly smaller.
5.3. Absolute colour–magnitude diagram
To build the absolute colour–magnitude diagram, we first converted individual apparent magnitudes to absolute magnitudes. This transformation requires the distance and extinction of each source. Given the different origin of our two catalogues (Gaia provides individual parallaxes and DANCe does not) we decided to follow two different approaches.
For the members obtained with the GDR2 membership analysis we used individual parallaxes to compute distances. We used the Kalkayotl5 code as in Olivares et al. (2019), which performs a Bayesian probabilistic inference to compute posterior probability distributions for the distance of each member. We chose a Cauchy prior, which is the recommended by the manual for clusters. The location of the prior was set to 350 pc (the approximate distance of the cluster), and the scale to 100 pc (in order to have a loose prior). In Fig. 10 we show the individual posterior distance distribution of each of the GDR2 members. The median distance is 351 pc and the standard deviation is 55 pc.
 |
Fig. 10. Individual posterior distance distributions of the members of the GDR2 analysis computed with the Kalkayotl code. |
We estimated the extinction in two independent ways. First, we used the Gaia extinction estimate (a_g_val) for the 88 members that have it available. Andrae et al. (2018) recommend not to use individual values of a_g_val but a statistic of them. Thus, we compute the median AV = 0.72 mag and the standard deviation 0.38 mag. In addition, we inferred the individual absorption of each source using a Bayesian model as in Olivares et al. 2019 (see Sect. 6.2). In this case, we also compute the median of all the individual maximum a posteriori probabilities (MAP) which is AV = 0.66 mag, compatible with the extinctions from Gaia.
To compute the absolute magnitude we sampled the apparent magnitude with a Gaussian centred at the observed magnitude and a standard deviation equal to the uncertainty. Then each sample was converted to absolute magnitude by sampling the posterior distance distribution obtained with Kalkayotl. We added the median absorption of the cluster to each member.
To compute absolute magnitudes for the DANCe members we followed a similar approach. The only difference is that instead of sampling the distance from the individual posterior distributions, we sampled the distance from the cluster distribution obtained with all the GDR2 members.
In Fig. 11 we show the absolute colour–magnitude diagram of IC 4665 where we overplotted the PARSEC and the BT-Settl models. Thanks to the precision of the Gaia DR2 parallaxes, we find that the isochrone has broadened little with respect the one observed in the apparent colour–magnitude diagrams. In addition, we included a mass scale. We have candidate members down to masses of ∼0.02 M⊙, well within the substellar regime. We see that the PARSEC models start to differ for masses < 0.7 M⊙, and in this low-mass regime the BT-Settl models reporduce the observations more closely. For this reason, to convert magnitudes to masses, we use the PARSEC models for the high-mass stars and the BT-Settl models for low-mass stars (see Sect. 6.2).
 |
Fig. 11. Colour–magnitude diagrams of the IC 4665 open cluster: (absolute G, G − GRP, left) and (absolute i, i − Ks, right). The PARSEC+COLIBRI (solid line) and the BT-Settl (dashed line) isochrones of 30 Myr are overplotted. The members are shape- and colour-coded according to their membership classification: red circles for members in GDR2 and DANCe analysis, blue left-pointing triangles for members only in GDR2, and green right-pointing triangles for members only in DANCe. |
6. From the apparent magnitude distribution to the present-day system mass function
In this section we describe the procedure to obtain the magnitude distribution and the PDSMF from the final list of members obtained in Sect. 3.6. In addition, we compare our results with a recent study on the Pleiades (Bouy et al. 2015) and with theoretical models.
6.1. Apparent magnitude distribution
The apparent magnitude distribution is a direct measurement of the number of sources observed at different brightnesses. This function is important because it does not depend on evolutionary models or on distance estimates, and thus its validity does not expire (unless selection problems are present). The magnitude distribution of IC 4665 was obtained applying a Gaussian kernel density estimation (KDE) independently to the GDR2 and the DANCe members. The two samples were treated independently because of the different validity range of each catalogue. To estimate the optimal bandwidth of the KDE we considered Scott’s rule (Scott 1992) and Silverman’s rule (Silverman 1986), which gave similar results. The optimal bandwidth of the KDE was 0.3 mag (both in the GDR2 and DANCe members), and the uncertainties were estimated by means of a bootstrap with 100 repetitions. We estimated the effect of contamination and completeness as a function of the magnitude using synthetic data, as in Olivares et al. (2019). Given that the contamination rate estimated this way is less than 15%, we realised that when we correct for these two effects the magnitude distribution we obtain is compatible with the original distribution within the uncertainties. For this reason we decided to work with the magnitude distribution we obtained directly from the observations. In Fig. 12 we show the magnitude distribution of IC 4665 in the G band for the GDR2 members and in the i band for the DANCe members. These functions are available in Tables B.3 and B.4, respectively.
 |
Fig. 12. Top: G magnitude distribution of IC 4665 with the members found with the GDR2 catalogue. Bottom: i magnitude distribution of IC 4665 with the members found with the DANCe catalogue. In both cases the shaded regions indicate the 1σ and 3σ uncertainties estimated from bootstrap (1σ dark and 3σ faint). The dashed lines indicate the region of incompleteness in each catalogue. |
At G ∼ 14.5 mag there is a flattening of the apparent magnitude distribution that corresponds to the Wielen dip (Wielen et al. 1983). This feature has been reported in other open clusters such as the Pleiades (Lee & Sung 1995; Belikov et al. 1998), Praesepe and Hyades (Lee et al. 1997), NGC 2516 (Jeffries et al. 2001), NGC 2547 (Naylor et al. 2002), and Ruprecht 147 (Olivares et al. 2019). Kroupa et al. (1990) explained this dip as the result of a change in the opacities in the corresponding mass range.
The apparent magnitude distribution peaks at G = 18.2 mag for the GDR2 members and at i = 17.6 mag for the DANCe members in both cases correspond to 0.2 M⊙, according to the PARSEC and BT-Settl models and assuming an age of 30 Myr. This result is in agreement with what Bouy et al. (2015) found in the Pleiades.
A change in slope seems to happen around i ∼ 21 mag, which could indicate that different formation mechanisms are at work for ultracool objects in this mass range. This change in slope is nevertheless very close to our estimated limit of completeness and is not statistically significant yet.
6.2. Present-day system mass function
We estimated the mass of each source using the Sakam6 code (Olivares et al. 2019). This algorithm infers the posterior distribution of the mass together with the AV extinction, given the absolute photometry of each source (computed in Sect. 5.3) and a theoretical evolutionary model. The model does not include effects on the variability of the source due to binarity, activity, or other factors. These effects are eventually included in the extinction estimate, enlarging its uncertainties. We used the PARSEC model to infer masses for the GDR2 members and the BT-Settl model for the DANCe members.
To compute the PDSMF, we took samples of the a posteriori distribution inferred with Sakam and applied a Gaussian KDE with a bandwith of 0.3 (in log10m, where m is the mass, and the bandwidth of the KDE was estimated from the Scott and Silverman rules). We estimated the uncertainties from 100 bootstrap repetitions and reported the 1σ and 3σ confidence levels. The completeness limits were propagated from the catalogue completeness in apparent magnitude (see Table 2). The mass function obtained with the DANCe analysis was renormalised so that the mass distribution functions had the same area in the region where both studies are complete (i.e. 0.15–0.8 M⊙).
Figure 13 shows the PDSMF of IC 4665 for the GDR2 (blue) and DANCe (green) members. We see that the two functions overlap reasonably well. There are some deviations (even inside the complete range), but they are smaller than 3σ. The robustness of our methodology, especially in the error propagation, results in a mass function with an accuracy significantly better than in the past (i.e. de Wit et al. 2006; Lodieu et al. 2011).
 |
Fig. 13. PDSMF of IC 4665 obtained from the GDR2 (blue) and DANCe (green) members. The shaded regions indicate the uncertainty estimated from bootstrap (1σ dark and 3σ faint) and the dashed lines the regions of incompleteness. |
A number of noticeable details are present in the mass function. At 3 M⊙ we observe a feature that has not been reported in the literature before. It is not clear whether this is a real feature of the mass function or an artefact. Several sources of error could be responsible, in particular the following:
-
the uncertainties or errors of the transformation from apparent magnitudes to masses since it is not observed in the magnitude distribution (Fig. 12);
-
multiplicity: the Gaia DR2 catalogue excluded a number of binary stars. Since massive stars are more often in multiple systems than their lower mass counterparts (e.g. Lada 2006) we might be missing a larger fraction of massive members because of multiplicity;
-
variability: massive stars can also display photometric variability, which is not included in our algorithm to determine individual masses. Slowly pulsating variable stars appear at three solar masses and beyond. However, they are small amplitude variables (0.1 in V) and should not have a major impact on our selection.
Additionally, and as mentioned in Sect. 2.1, we assumed that the GDR2 catalogue is complete for G > 7 mag (∼5 M⊙), but a few sources in the range 7 < G < 12 mag (5 ≲ m ≲ 1.6 M⊙) could be missing (Gaia Collaboration 2018a). Nevertheless, this would only increase the number of members in this range.
The Wielen dip reported in the magnitude distribution (Fig. 12) is expected around 0.75 M⊙ in the mass distribution, but is not observed. If confirmed, this result would support the hypothesis of Kroupa et al. (1990) explaining this feature as a change in opacity rather than a change in the mass function. We nevertheless note that the Wielen dip may have been masked by the KDE bandwidth. Olivares et al. (2019) indeed reported a Wielen dip in their mass function in the range 0.6–0.8 M⊙ with a typical scale of Δ log10m ∼ 0.13, smaller than our bandwidth of 0.3 (in log10m).
The function is rather flat between 0.1 and 1 M⊙ having a maximum at 0.28 M⊙. For masses < 0.1 M⊙ the distribution drops. The change in slope at the very low-mass end mentioned above is not visible in the mass function.
The highest mass object has an MAP estimate of 6.2 M⊙ and the lowest mass object has an MAP estimate of 13 MJ according to the PARSEC and BT-Settl models respectively, and assuming an age of 30 Myr. To compute the brown dwarf-to-star ratio we sampled the posterior mass distribution of each member. Then we used these samples to compute the ratio of brown dwarfs to stars within the completeness region of our sample (6–0.05 M⊙) and using a mass threshold of 0.08 M⊙. We did a bootstrap over all the members with 100 repetitions, and we obtained a median ratio of 0.067 ± 0.005. This value is lower than has been seen in other nearby young clusters, such as IC 348 and Taurus (Scholz et al. 2012, and references therein). However, these studies are complete down to lower masses (∼0.02 M⊙).
6.3. Comparison to other clusters and theoretical models
In Fig. 14, we compare the PDSMF we obtained for the 30 Myr open cluster IC 4665 and for the Pleiades (120 Myr; Bouy et al. 2015). To facilitate the comparison, we normalised the mass function of IC 4665 over the whole mass range where it is complete. Then we normalised the Pleiades mass function so that it had the same area of 0.05–0.6 M⊙, a range where both functions are complete. We see that in general the two functions match fairly well within the uncertainties and the main differences are observed at the extremes of the distributions. For the high-mass domain, IC 4665 has more massive stars than the Pleiades. In this range the number of members is quite small (only 12 objects have masses > 3 M⊙ in IC 4665) leading to rather large statistical uncertainties. In addition, multiplicity (more frequent among high-mass stars) and variability affect the luminosities and might contribute to the differences observed. Regarding the low-mass regime, we see that both functions are compatible (within 3σ uncertainties) down to the IC 4665 completeness limit (∼0.05 M⊙). Nonetheless, we observe that between 0.046 and 0.16 M⊙ the mass function of IC 4665 might display a slight overdensity with respect to the Pleiades, but only at the 1σ level. For masses lower than 0.05 M⊙, the Pleiades mass function exhibits a change in slope, which the authors related to a different mechanism of star formation for this regime of masses. In the case of IC 4665 we do not detect this change in slope, perhaps because it is beyond the completeness limit of the catalogue.
 |
Fig. 14. PDSMF of IC 4665 (black) and the Pleiades (red). The shaded regions indicate the uncertainties estimated from bootstrap (1σ dark and 3σ faint). Overplotted are the models from Chabrier (2005) (green) and Thies et al. (2015) (blue). |
In Fig. 14 we overplot the sytem IMF of two models, namely Chabrier (2005) and Thies et al. (2015), normalised in the same mass range as the mass function of IC 4665. In the high-mass regime (> 1 M⊙), both models assume a power law IMF with Salpeter slope that is compatible within the uncertainties with the empirical mass function of IC 4665.
For intermediate and low masses, we see that the mass function of IC 4665 is compatible with the model of Chabrier (2005) between 0.1–1 M⊙. For lower masses, the model predicts too many stars compared to our results. The model of Thies et al. (2015) is compatible with the empirical mass function between 0.2–1 M⊙, but between 0.05–0.2 M⊙ it also predicts too many stars. Below 0.05 M⊙ the model approaches the empirical mass function and beyond this limit our survey is not complete.
7. Projected spatial distribution
The spatial distribution of open clusters provides relevant information on the formation and early evolution of these systems. In Fig. 15 we show the spatial distribution of the members of IC 4665 in galactic coordinates. At first glance we can intuit some structures that depart from a pure spherical symmetry (e.g. the cluster seems elongated towards the Galactic south). In this section, we apply a statistical treatment to quantitatively asses the probability that the structures we might see are significant.
 |
Fig. 15. Spatial distribution of the members of IC 4665. The members are colour-coded according to their magnitude in J band. Background image credit: Pan-STARRS. |
We follow the same approach as in Olivares et al. (2018), and we fit a series of parametric models to the projected spatial distribution of the cluster (i.e. in the plane of the sky). We used the same algorithm as these authors, PyAspidistra7, which computes the Bayesian evidence of each model, the posterior distribution of the parameters which characterise the model, and the Bayes Factor for each pair of models. Here, we consider the same set of models as Olivares et al. (2018): the Elson et al. (1987) model (hereafter EFF); the Generalized Density Profile (hereafter GDP, also known as Nukker; Küpper et al. 2010); the King 1962 model (hereafter King), the Generalised King model (hereafter GKing; Olivares et al. 2018), the Optimum Generalized King model (herafter OGKing; Olivares et al. 2018), and the Restricted Generalized Density Profile (herafter RGDP; Olivares et al. 2018). For each model, the PyAspidistra code has the option that allows the user to infer the coordinates of the cluster centre, its ellipticity, and mass segregation.
Using the equatorial coordinates (J2000), the median distance of the cluster (350 pc), and the J band we ran the PyAspidistra code and obtained the Bayesian evidence for each model and the Bayes Factor for each pair of models. The RGDP model is the one that shows the most evidence in all the family models considered (spherical, elliptical and segregated). The family of models with the most evidence are the spherical models, as is expected for such a young open cluster. However, the strength of this evidence is weak according to the criterion from Jeffreys (1961) so these results should be taken with care, and we cannot definitely discard the possibility of ellipticity or mass segregation. In addition, our results could be biased due to the contamination in the members and the size and shape of our initial catalogues, as we discuss below.
The median parameters of each spherical model are reported in Table 6. The parameters αc and δc correspond to the central coordinates of the cluster in RA and Dec, respectively. The core radius (rc) is the unit scale of the density profile, therefore it differs for each model. The α, δ, and γ parameters correspond to the exponents of the different models. The tidal radius (rt) is only defined for the family of King’s models. We refer the interested reader to Olivares et al. (2018) for a detailed discussion of these parameters. We see that the centre of the cluster is well determined by all the models at RA = 266.6°, Dec = 5.4°. All the models also agree to a core radius of ∼2 pc and the small dispersion is expected since this parameter has a different interpretation in each model. Only the family of King models are defined in terms of a tidal radius. The median values of the tidal radius reported in Table 6 vary from one model to another and have extremely large uncertainties. The King model with more evidence is the OGKing model which predicts a rt = 55 pc, three times larger than the radius analysed in this study (18 pc). This is probably the main reason why we failed to closely constrain this parameter (see also the discussion on the main caveats at the end of the section). However, we note that to date, this study of IC 4665 is the one with largest radius. Our estimate of the tidal radius is much larger than previous values (e.g. de Wit et al. 2006 reported a tidal radius of 1° corresponding to ∼6 pc at the distance of the cluster; however, this value results from a highly contaminated sample).
Median parameters for the spherically symmetric distributed models.
Here we list some of the caveats and limitations of our study of the spatial distribution.
– Our members come from a catalogue that was circularly selected, and the ends of the catalogue can clearly be seen in Fig. 15. This can bias our results to favour a circular over an elliptic model.
– The spatial coverage of the DANCe catalogue (see Sect. 2.2 and Bouy et al. 2013) implies that the faintest members are more likely found in the centre. This region is where we have the highest number of images, and also the deepest ones and the ones with the longest time baseline. As a consequence, the proper motions are in general more precise in this area, which in turn has an influence on the membership probabilities. This can have an impact both on the study of the shape (circular or elliptical) and on the study of the segregation.
– The tidal radius and the contamination rate are degenerate: a high contamination rate increases the density of members and the models need a larger tidal radius to explain the observations. This is especially critical at the outskirts, where we believe we might have a higher contamination. As we discuss in Sects. 3.6 and 4, the majority of our contaminants come from the DANCe catalogue.
– Our members come from a catalogue that was truncated to a radius of ∼18 pc, similar to the expected tidal radius. It is highly difficult to estimate the tidal radius without having information beyond it. All these difficulties are reflected in the Bayesian evidence of each model: the family of King’s models have less evidence. The truncation in radius could also bias the study on the elipticity and segregation of the cluster.
8. Conclusions
We presented an exhaustive study of the properties of the IC 4665 open cluster. We combined the recent Gaia DR2 data with the deep, ground-based observations of the COSMIC DANCe project to search for members. We used the same methodology as Olivares et al. (2019) to derive Bayesian posterior probabilities for all the sources and found 819 members, 50% of which are new members. Our members have magnitudes in the range 7 < J < 19.4, which corresponds to masses of 6.2 M⊙–13 MJ, according to the PARSEC and BT-Settl evolutionary models and assuming an age of 30 Myr. Using this sample we provided the empirical isochrones of the cluster, an estimate for the distance, the magnitude distribution, the PDSMF with unprecedented accuracy for this cluster, and a study of the spatial distribution.
Comparing our members with previous studies in the literature, we found that most of the previous studies were based on highly contaminated (up to 80%) or incomplete samples. The low motion of this cluster with respect to the field (< 10 mas yr−1) complicates the membership analysis. For this reason we found a higher contamination rate in this study compared to others which use the same methodology applied to clusters with larger proper motions (Sarro et al. 2014; Olivares et al. 2019). Using synthetic data, we estimated a CR of 10% for GDR2 and a 13% for DANCe. Comparing the two studies, we estimate that the DANCe contamination reaches up to 30% in the region of completeness. The main reason of this underestimated CR in the DANCe study is the lack of parallaxes. To date, this study provides the most accurate membership analysis by far, and thus offers the possibility to revisit other fundamental parameters such as age.
We find that the PDSMF of IC 4665 in the intermediate mass range (0.1–1 M⊙) is comparable to that of the Pleiades (Bouy et al. 2015) and to models of the IMF (Chabrier 2005; Thies et al. 2015). For higher masses, the observations have a steeper slope than the models (Salpeter slope). In addition, for the case of IC 4665, we find a plateau at 3 M⊙, which if further confirmed would represent a new feature of the mass function. In the mass range 0.05–0.2 M⊙ the models predict too many low-mass stars. For masses lower than 0.05 M⊙ the Pleiades have more members than in IC 4665, but at this mass regime our study is not complete so we might be missing members.
Combining our comprehensive census of the cluster with the Gaia DR2 parallaxes we estimated the distance of the cluster to be of 350 pc, this value being similar to what other studies recently derived (Gaia Collaboration 2018b). We found that the best surface density profile for IC 4665 is the RGDP model with a core radius of 2 pc and spherical symmetry. However, we cannot definitely discard the possibility of ellipticity or of mass segregation. In the future, we aim to include a study on the velocity distribution that would allow us to characterise the kinematic and dynamic state of the cluster in the 6D space phase.
Acknowledgments
We thank the referee for the thorough review and highly appreciate the comments and suggestions that significantly contributed to improving the quality of the publication. We are grateful to Ingo Thies for sharing with us his models of the Initial Mass Function, to France Allard and Isabelle Barraffe for providing us with the latest version of the BT-Settl models, and to Paul Price for his help with the LSST/HSC pipeline. This research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 682903, P.I. H. Bouy), and from the French State in the framework of the “Investments for the future” Program, IdEx Bordeaux, reference ANR-10-IDEX-03-02. This project has been funded by the Spanish State Research Agency (AEI) Project No. ESP2017-87676-C5-1-R and No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu” Centro de Astrobiología (INTA-CSIC). M.T. is supported by MEXT/JSPS KAKENHI grant Nos. 18H05442, 15H02063, and 22000005. Based on observations collected at the European Southern Observatory under ESO programmes 60.A-9120(A), 60.A-9121(A), 60.A-9122(A), 68.C-0311(A), 69.A-9014(A), 69.C-0034(A), 69.C-0260(A), 69.C-0398(B), 69.C-0426(C), 69.D-0582(A), 60.A-9038(A). This research draws upon data distributed by the NOAO Science Archive. NOAO is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the VizieR and Aladin images and catalogue access tools and of the SIMBAD database, operated at the CDS, Strasbourg, France. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of GNU Parallel (Tange 2011), Astropy (Astropy Collaboration 2013), Topcat (Taylor 2005), STILTS (Taylor 2006).
References
- Allard, F. 2014, in Exploring the Formation and Evolution of Planetary Systems, eds. M. Booth, B. C. Matthews, & J. R. Graham, IAU Symp., 299, 271 [Google Scholar]
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Autry, R. G., Probst, R. G., Starr, B. M., et al. 2003, in SPIE Conf. Ser., eds. M. Iye, & A. F. M. Moorwood, 4841, 525 [Google Scholar]
- Baade, D., Meisenheimer, K., Iwert, O., et al. 1999, The Messenger, 95, 15 [NASA ADS] [Google Scholar]
- Belikov, A. N., Hirte, S., Meusinger, H., Piskunov, A. E., & Schilbach, E. 1998, A&A, 332, 575 [NASA ADS] [Google Scholar]
- Bosch, J., Armstrong, R., Bickerton, S., et al. 2018, PASJ, 70, S5 [NASA ADS] [CrossRef] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in SPIE Conf. Ser., eds. M. Iye, & A. F. M. Moorwood, 4841, 72 [Google Scholar]
- Bouy, H., Bertin, E., Moraux, E., et al. 2013, A&A, 554, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouy, H., Bertin, E., Sarro, L. M., et al. 2015, A&A, 577, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bravi, L., Zari, E., Sacco, G. G., et al. 2018, A&A, 615, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cargile, P. A., & James, D. J. 2010, AJ, 140, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Casali, M., Adamson, A., Alves de Oliveira, C., et al. 2007, A&A, 467, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Cuillandre, J. C., Luppino, G. A., Starr, B. M., & Isani, S. 2000, in SPIE Conf. Ser., eds. M. Iye, & A. F. Moorwood, 4008, 1010 [Google Scholar]
- de Wit, W. J., Bouvier, J., Palla, F., et al. 2006, A&A, 448, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dye, S., Lawrence, A., Read, M. A., et al. 2018, MNRAS, 473, 5113 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, R. A. W., Fall, S. M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Flaugher, B. L., Abbott, T. M. C., Annis, J., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77350D [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018b, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglewicz, B., & Hoaglin, D. 1993, How to Detect and Handle Outliers, ASQC Basic References in Quality Control (Milwaukee: ASQC Quality Press) [Google Scholar]
- Ives, D. 1998, IEEE Spectr., 16, 20 [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, 3rd edn. (Oxford, England: Oxford) [Google Scholar]
- Jeffries, R. D., Thurston, M. R., & Hambly, N. C. 2001, A&A, 375, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., James, D. J., & Cargile, P. A. 2009, MNRAS, 400, 317 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1990, MNRAS, 244, 76 [NASA ADS] [Google Scholar]
- Küpper, A. H. W., Kroupa, P., Baumgardt, H., & Heggie, D. C. 2010, MNRAS, 407, 2241 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J. 2006, ApJ, 640, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lee, S.-W., & Sung, H. 1995, J. Korean Astron. Soc., 28, 45 [Google Scholar]
- Lee, S.-W., Sung, H., & Cho, D.-H. 1997, J. Korean Astron. Soc., 30, 181 [NASA ADS] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodieu, N., de Wit, W.-J., Carraro, G., et al. 2011, A&A, 532, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Manzi, S., Randich, S., de Wit, W. J., & Palla, F. 2008, A&A, 479, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Kawanomoto, S., et al. 2018, PASJ, 70, S1 [NASA ADS] [Google Scholar]
- Naylor, T., Totten, E. J., Jeffries, R. D., et al. 2002, MNRAS, 335, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, J., Moraux, E., Sarro, L. M., et al. 2018, A&A, 612, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olivares, J., Bouy, H., Sarro, L. M., et al. 2019, A&A, 625, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahmer, G., Smith, R., Velur, V., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 70144Y [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Bouvier, J., et al. 2016, AJ, 152, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Cody, A. M., et al. 2018, AJ, 155, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Rheault, J. P., Mondrik, N. P., DePoy, D. L., Marshall, J. L., & Suntzeff, N. B. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91475L [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sarro, L. M., Bouy, H., Berihuete, A., et al. 2014, A&A, 563, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, A., Muzic, K., Geers, V., et al. 2012, ApJ, 744, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, D. W. 1992, Multivariate Density Estimation. Theory, Practice, and Visualization (New York: Wiley) [CrossRef] [Google Scholar]
- Silverman, B. W. 1986, Density Estimation (London: Chapman and Hall) [Google Scholar]
- Tange, O. 2011, The USENIX Magazine, 36, 42 [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, M. B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [Google Scholar]
- Thibault, S., Cui, Q., Poirier, M., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 932 [CrossRef] [Google Scholar]
- Thibault, S., Lacoursiere, J., Artigau, E., Vallee, P., & Doyon, R. 2002, in International Optical Design Conference 2002, 4832 [Google Scholar]
- Thies, I., Pflamm-Altenburg, J., Kroupa, P., & Marks, M. 2015, ApJ, 800, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gruendl, & R. DES Project 2014, in Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, ASP Conf. Ser., 485, 379 [Google Scholar]
- Vandame, B. 2002, in Astronomical Data Analysis II, eds. J. L. Starck, & F. D. Murtagh, SPIE Conf. Ser., 4847, 123 [Google Scholar]
- Wielen, R., Jahreiß, H., & Krüger, R. 1983, in IAU Colloq. 76: Nearby Stars and the Stellar Luminosity Function, eds. A. G. D. Philip, & A. R. Upgren, 163 [Google Scholar]
Appendix A: Queries
A.1. Gaia DR2
SELECT
"I/345/gaia2".ra\_epoch2000,
"I/345/gaia2".dec_epoch2000,
"I/345/gaia2".ra_epoch2000\_error,
"I/345/gaia2".dec\_epoch2000_error,
"I/345/gaia2".parallax,
"I/345/gaia2".parallax_error,
"I/345/gaia2".pmra,
"I/345/gaia2".pmra\_error,
"I/345/gaia2".pmdec,
"I/345/gaia2".pmdec\_error,
"I/345/gaia2".phot\_g\_mean\_mag,
"I/345/gaia2".phot_g_mean_mag_error,
"I/345/gaia2".phot_bp_mean_mag,
"I/345/gaia2".phot_bp_mean_mag_error,
"I/345/gaia2".phot_rp_mean_mag,
"I/345/gaia2".phot_rp_mean_mag_error,
"I/345/gaia2".radial_velocity,
"I/345/gaia2".radial_velocity_error,
"I/345/gaia2".teff_val,
"I/345/gaia2".a_g_val,
"I/345/gaia2".lum_val,
"I/345/gaia2".a_g_percentile_lower,
"I/345/gaia2".a_g_percentile_upper,
"I/345/gaia2".dec_parallax_corr,
"I/345/gaia2".dec_pmdec_corr,
"I/345/gaia2".dec_pmra_corr,
"I/345/gaia2".lum_percentile_lower,
"I/345/gaia2".lum_percentile_upper,
"I/345/gaia2".parallax_pmdec_corr,
"I/345/gaia2".parallax_pmra_corr,
"I/345/gaia2".pmra_pmdec_corr,
"I/345/gaia2".ra_parallax_corr,
"I/345/gaia2".ra_pmdec_corr,
"I/345/gaia2".ra_pmra_corr,
"I/345/gaia2".teff_percentile_lower,
"I/345/gaia2".teff_percentile_upper
FROM "I/345/gaia2"
WHERE 1=CONTAINS(POINT('ICRS',
"I/345/gaia2".ra,"I/345/gaia2".dec),
CIRCLE('ICRS', 266.6, 5.7, 3.))
A.2. Pan-STARRS
SELECT
"II/349/ps1".RAJ2000,
"II/349/ps1".DEJ2000,
"II/349/ps1".Qual,
"II/349/ps1".e_RAJ2000,
"II/349/ps1".e_DEJ2000,
"II/349/ps1".Epoch,
"II/349/ps1".Ns,
"II/349/ps1".Nd,
"II/349/ps1".gmag,
"II/349/ps1".e_gmag,
"II/349/ps1".gKmag,
"II/349/ps1".e_gKmag,
"II/349/ps1".gFlags,
"II/349/ps1".rmag,
"II/349/ps1".e_rmag,
"II/349/ps1".rKmag,
"II/349/ps1".e_rKmag,
"II/349/ps1".rFlags,
"II/349/ps1".imag,
"II/349/ps1".e_imag,
"II/349/ps1".iKmag,
"II/349/ps1".e_iKmag,
"II/349/ps1".iFlags,
"II/349/ps1".zmag,
"II/349/ps1".e_zmag,
"II/349/ps1".zKmag,
"II/349/ps1".e_zKmag,
"II/349/ps1".zFlags,
"II/349/ps1".ymag,
"II/349/ps1".e_ymag,
"II/349/ps1".yKmag,
"II/349/ps1".e_yKmag,
"II/349/ps1".yFlags
FROM "II/349/ps1"
WHERE (("II/349/ps1".RAJ2000>=264.8)
AND ("II/349/ps1".RAJ2000 <= 269.8)
AND ("II/349/ps1".DEJ2000>=3.14)
AND ("II/349/ps1".DEJ2000<=7.4))
A.3. 2MASS
SELECT
"II/246/out".RAJ2000,
"II/246/out".DEJ2000,
"II/246/out"."2MASS",
"II/246/out".Jmag,
"II/246/out".e_Jmag,
"II/246/out".Hmag,
"II/246/out".e_Hmag,
"II/246/out".Kmag,
"II/246/out".e_Kmag,
"II/246/out".Qflg
FROM "II/246/out"
WHERE 1=CONTAINS(POINT('ICRS',
"II/246/out".RAJ2000,"II/246/out".DEJ2000),
CIRCLE('ICRS', 266.6, 5.7, 3.))
A.4. WISE
SELECT
"II/328/allwise".RAJ2000,
"II/328/allwise".DEJ2000,
"II/328/allwise".W1mag,
"II/328/allwise".e_W1mag,
"II/328/allwise".W2mag,
"II/328/allwise".e_W2mag,
"II/328/allwise".W3mag,
"II/328/allwise".e_W3mag,
"II/328/allwise".W4mag,
"II/328/allwise".e_W4mag,
"II/328/allwise".ccf,
"II/328/allwise".ex,
"II/328/allwise".var,
"II/328/allwise".pmRA,
"II/328/allwise".e_pmRA,
"II/328/allwise".pmDE,
"II/328/allwise".e_pmDE,
"II/328/allwise".qph
FROM "II/328/allwise"
WHERE (("II/328/allwise".RAJ2000>=264.8)
AND ("II/328/allwise".RAJ2000 <= 269.8)
AND ("II/328/allwise".DEJ2000>=3.14)
AND ("II/328/allwise".DEJ2000<=7.4))
Appendix B: Tables
B.1. Empirical isochrones
Empirical isochrones of IC 4665 for the photometric bands of the Gaia DR2 catalogue.
Empirical isochrones of IC 4665 for the photometric bands of DANCe (Pan-STARRS and 2MASS).
B.2. Magnitude distribution and mass function
Apparent G magnitude distribution of IC 4665 (normalised).
Apparent i magnitude distribution of IC 4665 (normalised).
PDSMF of IC 4665 (normalised).
All Tables
Number of measurements and percentage for each photometric band in the DANCe catalogue.
Internal probability threshold (pin), optimum probability threshold (popt), and number of complete and incomplete members (CM, IM) for each of the membership analyses, namely GDR2 and DANCe.
Empirical isochrones of IC 4665 for the photometric bands of the Gaia DR2 catalogue.
Empirical isochrones of IC 4665 for the photometric bands of DANCe (Pan-STARRS and 2MASS).
All Figures
 |
Fig. 1. Top: cumulative distribution of airmass for the observations. Bottom: cumulative distribution of average FWHM for the images. |
| In the text | |
 |
Fig. 2. Transmission curves of the i filters used in this study. |
| In the text | |
 |
Fig. 3. Density of sources as a function of magnitude for members of the DANCe catalogue. |
| In the text | |
 |
Fig. 4. Comparison between the membership probabilities recovered by the GDR2 and DANCe classifiers, for objects in both catalogues. The diagonal line represents the one-to-one relation, and the horizontal and vertical dashed lines show the optimum probability thresholds. |
| In the text | |
 |
Fig. 5. G and i (top and bottom) magnitude distributions of the sources classified as members in the GDR2 and DANCe studies (red), classified as members by GDR2 but not by DANCe (blue), and classified as members by DANCe but not by GDR2 (green). |
| In the text | |
 |
Fig. 6. Vector point diagram (left) and parallax–proper motion diagram (right) of the IC 4665 open cluster. The members are shape- and colour-coded according their origin: GDR2 and DANCe analysis (red circles), only GDR2 analysis (blue left-pointing triangle), and only DANCe analysis (green right-pointing triangle). |
| In the text | |
 |
Fig. 7. Venn diagram comparing the members in this work to previous studies in the literature (i.e. Lodieu et al. 2011; Cantat-Gaudin et al. 2018). |
| In the text | |
 |
Fig. 8. (G, G − GRP) and (i, i − Ks) colour–magnitude diagrams (left and right, respectively) of the IC 4665 open cluster. The members are colour-coded according to their membership probability, and the empirical isochrone is overplotted (black line). |
| In the text | |
 |
Fig. 9. Comparison of the observations of the IC 4665 sequence (black dots) and the empirical sequence (red lines) to the models of PARSEC+COLIBRI (blue line) and the BT-Settl (green line) for an age of 30 Myr in several colour–magnitude diagrams. |
| In the text | |
 |
Fig. 10. Individual posterior distance distributions of the members of the GDR2 analysis computed with the Kalkayotl code. |
| In the text | |
 |
Fig. 11. Colour–magnitude diagrams of the IC 4665 open cluster: (absolute G, G − GRP, left) and (absolute i, i − Ks, right). The PARSEC+COLIBRI (solid line) and the BT-Settl (dashed line) isochrones of 30 Myr are overplotted. The members are shape- and colour-coded according to their membership classification: red circles for members in GDR2 and DANCe analysis, blue left-pointing triangles for members only in GDR2, and green right-pointing triangles for members only in DANCe. |
| In the text | |
 |
Fig. 12. Top: G magnitude distribution of IC 4665 with the members found with the GDR2 catalogue. Bottom: i magnitude distribution of IC 4665 with the members found with the DANCe catalogue. In both cases the shaded regions indicate the 1σ and 3σ uncertainties estimated from bootstrap (1σ dark and 3σ faint). The dashed lines indicate the region of incompleteness in each catalogue. |
| In the text | |
 |
Fig. 13. PDSMF of IC 4665 obtained from the GDR2 (blue) and DANCe (green) members. The shaded regions indicate the uncertainty estimated from bootstrap (1σ dark and 3σ faint) and the dashed lines the regions of incompleteness. |
| In the text | |
 |
Fig. 14. PDSMF of IC 4665 (black) and the Pleiades (red). The shaded regions indicate the uncertainties estimated from bootstrap (1σ dark and 3σ faint). Overplotted are the models from Chabrier (2005) (green) and Thies et al. (2015) (blue). |
| In the text | |
 |
Fig. 15. Spatial distribution of the members of IC 4665. The members are colour-coded according to their magnitude in J band. Background image credit: Pan-STARRS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.