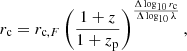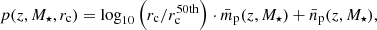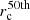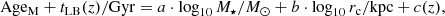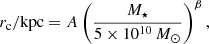| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A158 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935257 | |
| Published online | 13 November 2019 | |
Stellar populations of galaxies in the ALHAMBRA survey up to z ∼ 1
IV. Properties of quiescent galaxies on the stellar mass–size plane⋆
1
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan 1, Floor 2, 44001 Teruel, Spain
2
Academia Sinica Institute of Astronomy & Astrophysics (ASIAA), 11F of Astronomy-Mathematics Building, AS/NTU, No. 1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
e-mail: ladiaz@asiaa.sinica.edu.tw
3
Centro de Estudios de Física del Cosmos de Aragón (CEFCA) – Unidad Asociada al CSIC, Plaza San Juan 1, Floor 2, 44001 Teruel, Spain
4
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
5
Mullard Space Science Laboratory, University College London, Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
6
IAA-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
7
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
8
Depto. Astrofísica, Centro de Astrobiología (INTA-CSIC), ESAC Campus, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Spain
Received:
12
February
2019
Accepted:
6
September
2019
Aims. We perform a comprehensive study of the stellar population properties (formation epoch, age, metallicity, and extinction) of quiescent galaxies as a function of size and stellar mass to constrain the physical mechanism governing the stellar mass assembly and the likely evolutive scenarios that explain their growth in size.
Methods. After selecting all the quiescent galaxies from the ALHAMBRA survey by the dust-corrected stellar mass–colour diagram, we built a shared sample of ∼850 quiescent galaxies with reliable measurements of sizes from the HST. This sample is complete in stellar mass and luminosity, I ≤ 23. The stellar population properties were retrieved using the fitting code for spectral energy distributions called MUlti-Filter FITting for stellar population diagnostics (MUFFIT) with various sets of composite stellar population models. Age, formation epoch, metallicity, and extinction were studied on the stellar mass–size plane as function of size through a Monte Carlo approach. This accounted for uncertainties and degeneracy effects amongst stellar population properties.
Results. The stellar population properties of quiescent galaxies and their stellar mass and size since z ∼ 1 are correlated. At fixed stellar mass, the more compact the quiescent galaxy, the older and richer in metals it is (1 Gyr and 0.1 dex, respectively). In addition, more compact galaxies may present slight lower extinctions than their more extended counterparts at the same stellar mass (< 0.1 mag). By means of studying constant regions of stellar population properties across the stellar mass–size plane, we obtained empirical relations to constrain the physical mechanism that governs the stellar mass assembly of the form M⋆ ∝ rcα, where α amounts to 0.50–0.55 ± 0.09. There are indications that support the idea that the velocity dispersion is tightly correlated with the stellar content of galaxies. The mechanisms driving the evolution of stellar populations can therefore be partly linked to the dynamical properties of galaxies, along with their gravitational potential.
Key words: galaxies: stellar content / galaxies: evolution / galaxies: formation / galaxies: photometry
© ESO 2019
1. Introduction
During the past decades, tight correlations between the stellar mass of a galaxy and its stellar population properties since moderate redshifts have frequently been found (e.g. Ferreras & Silk 2000; Kauffmann et al. 2003; Gallazzi et al. 2005; Thomas et al. 2005; Sánchez-Blázquez et al. 2006; Jimenez et al. 2007; Kaviraj et al. 2007; Panter et al. 2008; Vergani et al. 2008; Ferreras et al. 2009; de La Rosa et al. 2011; Jørgensen & Chiboucas 2013; Jørgensen et al. 2014, 2017; Peng et al. 2015; Díaz-García et al. 2019a,b), where the environment can also be involved in its assembly (e.g. Thomas et al. 2005; Ferreras et al. 2006; Sánchez-Blázquez et al. 2006; Rogers et al. 2010; La Barbera et al. 2014; McDermid et al. 2015). However, some authors concluded that other galaxy properties, such as the stellar surface density (Kauffmann et al. 2003; Franx et al. 2008) or the velocity dispersion (Trager et al. 2000; Gallazzi et al. 2006; Graves & Faber 2010; Cappellari et al. 2013a), strongly correlate with the formation and evolution of the stellar content in galaxies, even more than the proper stellar mass.
On the other hand, the sizes of local galaxies clearly correlate with their stellar masses and luminosities (see e.g. Kormendy 1977; Blanton et al. 2003; Shen et al. 2003), with a tight dependence on morphological aspects and colours (early-type and red galaxies are typically more compact or denser than the late-type and blue galaxies at fixed stellar mass or luminosity). More recently, many studies unveiled striking evidence in favour of a continuous and generalised increase in size of both spheroid-like and quiescent and late-type and star-forming galaxies across cosmic time (e.g. Trujillo et al. 2004, 2006, 2007; Daddi et al. 2005; McIntosh et al. 2005; Toft et al. 2007; Zirm et al. 2007; Buitrago et al. 2008; van Dokkum et al. 2008; Damjanov et al. 2011; Newman et al. 2012; van der Wel et al. 2014). In particular, since z ∼ 2 (z ∼ 1) massive spheroid-like and quiescent galaxies have rapidly increased in size by a factor of ∼4 (1.5–2) up to the present. However, the main mechanism that causes this fast growth in size is not yet completely clear.
First attempts to distinguish why galaxies currently exhibit larger sizes have proposed that the influence of active galactic nuceli (AGNs) might play a role. This scenario, commonly referred to as the “puffing-up” scenario (Fan et al. 2008, 2010; Damjanov et al. 2009), suggested that feedback from AGNs or quasars would remove cold gas from the inner regions of the galaxy and in this way redistribute the stellar content of the inner regions on a timescale of ∼2 Gyr. As a result of this mechanism, more extended galaxies would present older ages in the local Universe and the dispersion of the stellar mass–size relation would increase across cosmic time (Fan et al. 2010). Nevertheless, many observational studies have described the opposite case because they found no significant increase in the dispersion of this relation, and more compact galaxies show features that are expected for older stellar populations (e.g. Cenarro & Trujillo 2009; Shankar & Bernardi 2009; Trujillo et al. 2009, 2011; McDermid et al. 2015; Peralta de Arriba et al. 2015; Gargiulo et al. 2017). For these reasons, this mechanism has mostly been discarded as an explanation of the extended growth in size of galaxies.
Alternatively, mergers were proposed as an efficient mechanism to produce a generalised growth in size (Naab et al. 2009). Under this scenario, galaxies firstly formed their compact and dense cores, which could be the result of mergers between gas-rich discs (which yields compact starbursts of small radii, Hopkins et al. 2008) or of the accretion of cold streams (which forms compact massive bulges and suppresses star formation, Kereš et al. 2005; Dekel et al. 2009). These cores would be the so-called red nuggets observed at z > 2 (Damjanov et al. 2009; de la Rosa et al. 2016). When the core is assembled, galaxies would continue their assembly by a continuous fall of pieces at lower redshifts through mergers (with ex situ stellar populations). In this way, the surroundings of dense cores would be populated in an “inside-out” formation scenario (e.g. de la Rosa et al. 2016). This scenario would be mainly driven by minor mergers on parabolic orbits (Khochfar & Burkert 2006; Khochfar & Silk 2006; Bezanson et al. 2009; Hopkins et al. 2009; Naab et al. 2009; Trujillo et al. 2011) because there are not enough major mergers to reproduce the evolution in size observed since z ∼ 1 (Bundy et al. 2009; de Ravel et al. 2009; López-Sanjuan et al. 2010, 2012). Because merger histories do not preferentially involve compact galaxies (Díaz-García et al. 2013), the growth in size through mergers would be generalised for all the galaxies in the stellar mass–size plane. Under these assumptions, the number of compact galaxies would be reduced at longer cosmic times (Cassata et al. 2013; Quilis & Trujillo 2013; Trujillo et al. 2014; van der Wel et al. 2014). However, the variation with redshift of the number of massive galaxies, with a prominent growth in size, is still a matter of debate. Contradictory studies point out that the number of compact galaxies has remained almost constant since intermediate redshifts (Saracco et al. 2010; Damjanov et al. 2014, 2015; Gargiulo et al. 2017) or experienced only a slight decrease in number (Valentinuzzi et al. 2010; Poggianti et al. 2013). A reliable estimation of the evolution in number of compact and massive galaxies across cosmic time may help to discern whether mergers should be considered as an important mechanism for the growth in size of quiescent or spheroid-like galaxies.
In the past years, the progenitor bias (van Dokkum & Franx 2001) has received more attention. According to this, samples of galaxies at high redshift are biased sub-sets of the nearby counterparts because the samples only include the oldest members of the current distributions. Under this assumption, the first galaxies that formed in the earliest epochs of the Universe were also the densest because they resided in denser halos. At the same time, they would evolve and quench their star-formation processes earlier. Any galaxy formed at later epochs will therefore be larger and evolve later until it reached enough stellar mass for no more star-forming processes to be supported. This would imply that less dense quiescent galaxies (less compact or extended) are also younger because they reach a state of quenching in later epochs (Valentinuzzi et al. 2010; Carollo et al. 2013; Belli et al. 2015). For the quiescent case, after these galaxies quenched their main star formation processes, they would lie on the upper parts of the stellar mass–size plane, yielding a growth of the median size according to the observations of the mass–size relation of star-forming and quiescent galaxies (e.g. Trujillo et al. 2007; Zirm et al. 2007; Buitrago et al. 2008; Newman et al. 2012; van der Wel et al. 2014). At the same time, this would imply that the number density of compact galaxies would be constant, or at least this would suffer mild and increasing modifications across cosmic time. Owing to the progenitor bias, we would expect a correlation between the size of a galaxy and their stellar content age, where denser galaxies exhibit older ages (Shankar & Bernardi 2009; Poggianti et al. 2013; Fagioli et al. 2016; Gargiulo et al. 2017; Williams et al. 2017; Wu et al. 2018; Damjanov et al. 2019) or large quiescent galaxies will reach the red sequence later than their compact counterparts (Belli et al. 2015).
A detailed analysis of stellar populations of compact and extended quiescent galaxies will allow us to shed light on the scenarios or mechanisms related to the prominent growth in size that these galaxies have undergone since high redshift. If extended galaxies would be found to be older than their compact counterparts, it would favour an inside-out formation, whereas the opposite case could be consistent with mergers and progenitor bias. Probing the stellar content of these galaxies in a long period of cosmic time will also provide valuable information with which more complex scenarios could be tested that include not one unique mechanism acting in favour of a growth in size. For instance, Belli et al. (2015) showed that the progenitor bias contribution at 1 < z < 1.6 can only explain half of the average size evolution that quiescent galaxies exhibit during 1.25 < z < 2. In addition, for the generalised evolution of the median metallicity of massive quiescent galaxies reported by Díaz-García et al. (2019b), mergers would be necessary, as would the progenitor bias to interpret the results properly.
This work is part of a series of papers in which our goal is to improve our understanding of quiescent galaxies since z ∼ 1, with the ultimate goal of providing a general picture of the formation and evolution of quiescent galaxies, for which we make use of multiple observables (e.g. number densities, stellar population properties, and sizes). In this work, we present a comprehensive study of the stellar populations of a set of quiescent galaxies as a function of their size, mass, and redshift, in pursuit of finding the most plausible evolution scenarios that can explain their growth in size.
Overall, the structure of this work is as follows. We define the quiescent sample with reliable sizes and stellar population properties in Sect. 2. In Sect. 3 we explore the correlations between the sizes and age, formation epoch, metallicity, and extinction of quiescent galaxies. An empirical expression for the driver of the stellar content of galaxies is obtained in Sect. 4. Our results are discussed and compared with previous work in Sects. 5 and 6, respectively. A brief summary of this research is presented in Sect. 7.
We adopt a lambda cold dark matter (ΛCDM) cosmology with H0 = 71 km s−1, ΩM = 0.27, and ΩΛ = 0.73 throughout. Stellar masses are quoted in solar mass units [M⊙] and magnitudes in the AB-system (Oke & Gunn 1983). We assume Chabrier (2003) and Kroupa universal (Kroupa 2001) initial stellar mass functions (IMF, more details in Sect. 2.1).
2. Sample of quiescent galaxies with reliable sizes
The reference catalogue for this work is the catalogue of quiescent galaxies published by Díaz-García et al. (2019a). This catalogue includes ∼8500 quiescent galaxies from the Advanced Large Homogeneous Area Medium Band Redshift Astronomical survey1 (ALHAMBRA, Moles et al. 2008) at 0.1 ≤ z ≤ 1.1, whose stellar population properties were constrained through spectral energy distribution (SED) fitting techniques. These stellar population properties were studied in detail by Díaz-García et al. (2019b). This sample of galaxies was defined to be complete in stellar mass (95% complete at any redshift bin) and luminosity (I ≤ 23), where a dust-corrected stellar mass-colour diagram (or MCDE) was used to minimise the contamination of dusty star-forming galaxies. In order to assess likely systematics on the stellar population properties owing to the use of population synthesis models, two sets of simple stellar populations (SSP) models were used: the set described by Bruzual & Charlot (2003, hereafter BC03) and that of Vazdekis et al. (2016, EMILES). The method for determining stellar population properties is briefly presented in Sect. 2.1. As our goal is to shed light on potential correlations between the stellar populations of galaxies and their sizes, we complement this catalogue with reliable size measurements of galaxies. Further details are provided in Sect. 2.2.
2.1. Stellar population properties of quiescent galaxies from the ALHAMBRA survey
The ALHAMBRA survey provides flux in 23 photometric bands2, 20 in the optical range (λλ 3500−9700 Å, with a full width at half-maximum of ∼300 Å, see details in Aparicio Villegas et al. 2010) and the near-infrared bands J, H, and Ks (Cristóbal-Hornillos et al. 2009). This survey was acquired with the 3.5 m telescope of the Calar Alto Observatory3 (CAHA), covering a current effective area of ∼2.8 deg2 in 7 non-contiguous fields in the northern hemisphere. The reference catalogue of photometry for this work was the ALHAMBRA Gold catalogue4 (Molino et al. 2014), which contains ∼95 000 galaxies down to I = 23 with accurate photo-redshifts (hereafter photo-z) constraints (σz ∼ 0.012, further details in Molino et al. 2014). This catalogue provides point spread function (PSF) corrected (Coe et al. 2006) and non-fixed aperture photometry, which is ideally suited for stellar population studies, including the total flux emitted by galaxies without biasing their outer parts.
The stellar population properties of quiescent galaxies (age, metallicity, extinction, stellar mass, photo z, and rest-frame luminosities; see Díaz-García et al. 2019a) were determined by the use of the SED-fitting code called MUlti-Filter FITting for stellar population diagnostics (MUFFIT, Díaz-García et al. 2015). To assess potential systematics caused by the varying model prescriptions in these sets, MUFFIT was fed with two independent sets of SSP models to construct a set of composite models of stellar populations for each of them. These composite models consist of a mixture of two individual SSP models, also referred to as two burst formation models. Consequently, the star formation history of quiescent galaxies is approached by one old and one young component, which has proven to reproduce the colour of an underlying red population plus less massive and later events of star formation (e.g. Ferreras & Silk 2000; Kaviraj et al. 2007; Rogers et al. 2010). For this work, we took the SSP models of BC03 and EMILES to build our composite models of stellar population and to subsequently constrain the stellar population properties of quiescent galaxies thorugh SED-fitting. For BC03, 19 ages from 0.06 to 14 Gyr, metallicity values of [M/H] = −1.65, −0.64, −0.33, 0.09, 0.55 dex (Padova1994 stellar tracks), and the Chabrier (2003) IMF were used to constrain stellar population properties. Regarding EMILES, the two sets of theoretical isochrones were taken into account: the scaled-solar isochrones of Girardi et al. (2000, hereafter Padova00), and those of Pietrinferni et al. (2004, BaSTI in the following). Twenty-two ages in the range 0.05–14 Gyr and metallicities of [M/H] = −1.31, −0.71, −0.40, 0.00, 0.22 for Padova00 and [M/H] = −1.26, −0.96, −0.66, −0.35, 0.06, 0.26, 0.40 for BaSTI were selected to perform the SED-fitting analysis, both with a Kroupa universal IMF (Kroupa 2001). For both BC03 and EMILES, the extinction law of Fitzpatrick (1999) was assumed for dust reddening with values in the range AV = 0.0–3.1 and taking a fixed ratio of RV = 3.1. We note that Díaz-García et al. (2019a) stated that stellar masses computed using EMILES SSP models are ∼0.10 dex more massive than those obtained with the BC03 models. For this reason, stellar mass completeness limits of EMILES and BC03 differ at any redshift in all the sections of this work.
Throughout this work, the mass-weighted age and metallicity (AgeM and [M/H]M, respectively) are preferred to the luminosity age and metallicity. The mass-weighted parameters are more representative of the total stellar content of the galaxy, and they are not linked to a defined luminosity weight, which may differ in different works. Look-back times, tLB, were established following the recipes of Hogg (1999). Hereafter, we define the formation epoch as the addition of mass-weighted ages and look-back times, meaning AgeM + tLB.
2.2. Retrieval of sizes of quiescent galaxies
The measurement of galaxy sizes from ground-based surveys, for instance ALHAMBRA, is biased to galaxies with sizes larger than the spatial resolution of the survey. In addition, the evolution of the stellar mass–size relation with redshift complicates a reliable and non-biased measurement of galaxy sizes. To overcome this drawback, we took advantage of the ALHAMBRA fields that overlap with fields of the Hubble Space Telescope (HST), where these limitations do not exist at the ALHAMBRA redshifts.
From the ALHAMBRA galaxy sample presented in Díaz-García et al. (2019a), we constructed a sub-set of shared quiescent galaxies with accurate effective radius measurements derived from HST data. Size measurements were retrieved from the Advanced Camera for Surveys (ACS) general catalogue of structural parameters (hereafter ACS catalogue, Griffith et al. 2012). The ACS catalogue was constructed using the GALAPAGOS5 code (Häußler et al. 2011), which includes both SExtractor (Bertin & Arnouts 1996) and GALFIT6 (Peng et al. 2002), to model and measure structural parameters of each source in the ACS catalogue assuming a Sérsic (1968) profile. In particular, sizes were computed using as initial values to iterate the FLUX_RADIUS, Rf, and MAG_BEST provided by SExtractor and the formula 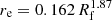 , which was derived through simulations (further details in Griffith et al. 2012). In the following, our reference measurement for size is the circularised effective radius, rc, instead of the provided effective radius, re, which encloses half of the total flux. It is formally expressed as
, which was derived through simulations (further details in Griffith et al. 2012). In the following, our reference measurement for size is the circularised effective radius, rc, instead of the provided effective radius, re, which encloses half of the total flux. It is formally expressed as 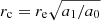 , where a1 and a0 are the semi-major and semi-minor axes, respectively. The projected sizes from Griffith et al. (2012) were converted into physical units and circularised using the axis ratio provided by the ACS catalogue (a1/a0, column BA_GALFIT_HI).
, where a1 and a0 are the semi-major and semi-minor axes, respectively. The projected sizes from Griffith et al. (2012) were converted into physical units and circularised using the axis ratio provided by the ACS catalogue (a1/a0, column BA_GALFIT_HI).
After cross-correlating all the quiescent galaxies from the ALHAMBRA survey (fields 4, 5, and 6) at a stellar mass completeness level of 95% with the ACS catalogue, we finally obtained a common sample of 870, 830, and 828 quiescent galaxies for BC03, EMILES+BaSTI, and EMILES+Padova00, respectively. There is a 90% fraction of galaxies in common in the two EMILES and BC03 samples. Owing to a larger overlapping area with ALHAMBRA, most of structural parameters of quiescent galaxies in this study come from the Cosmological Evolution Survey field (COSMOS, Scoville et al. 2007). In the following, our reference bands for morphological parameters (including apparent size) in the ACS catalogue are F814W, for COSMOS and the All-wavelength Extended Groth Strip International Survey (AEGIS Davis et al. 2007), and F775W for the Hubble Deep Field North (HDF-N Dickinson et al. 2003; Giavalisco et al. 2004). In Table 1 we show a brief summary of the characteristics of this sub-sample. We stated the redshift upper limit of this work at z = 0.9 because the sample at z > 0.9 is constrained to quiescent galaxies with log10 M⋆ ≳ 11.2 and only a few sources have ACS size measurements.
Number of quiescent galaxies with reliable sizes obtained from ACS/HST fields in common with ALHAMBRA for a stellar mass completeness level of 95%.
2.3. Correction for colour gradients
The presence and evolution of colour gradients in galaxies has been extensively studied since moderate redshifts (e.g. Ferreras et al. 2005; Szomoru et al. 2011; van der Wel et al. 2014). Colour gradients affect the measurement of structural parameters such as half-light radius, which decreases at increasing wavelength (see e.g. Kelvin et al. 2012; Wuyts et al. 2012). This is especially relevant in studies involving galaxies at different redshift with a few bands to determine structural parameters. According to this, the effective radius obtained by the F814W band at z = 0.63 and by F775W at z = 0.55 corresponds to the effective radii at a rest-frame wavelength of 5000 Å.
As our sub-sample extends from z = 0.1 to z = 0.9, we mitigated this passband-shifting effect by converting the size measurements obtained from the ACS F814W and F775W images into a common rest-frame wavelength of 5000 Å. Following van der Wel et al. (2014), rc at a rest-frame wavelength of 5000 Å for a galaxy at redshift z is obtained through the expression
where F denotes the bands F814W (COSMOS and AEGIS) and F775W (HDF-N), zp is the pivot wavelength (0.63 and 0.55 for F814W and F775W bands, respectively), and 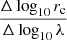 is the size gradient as a function of wavelength. For the size gradient, we assumed the value reported by van der Wel et al. (2014) for quiescent galaxies, Δlog10 rc/Δlog10 λ = −0.25, which is also in agreement with Guo et al. (2011) and Kelvin et al. (2012). Negative values for
is the size gradient as a function of wavelength. For the size gradient, we assumed the value reported by van der Wel et al. (2014) for quiescent galaxies, Δlog10 rc/Δlog10 λ = −0.25, which is also in agreement with Guo et al. (2011) and Kelvin et al. (2012). Negative values for 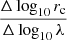 imply that quiescent galaxies are more compact at longer wavelengths. The size corrections introduced by Eq. (1) are mild and do not exceed a 10% fraction with respect the observed values, meaning 0.95 < rc/rc, F < 1.1.
imply that quiescent galaxies are more compact at longer wavelengths. The size corrections introduced by Eq. (1) are mild and do not exceed a 10% fraction with respect the observed values, meaning 0.95 < rc/rc, F < 1.1.
3. Correlations between size and stellar population parameters of quiescent galaxies
In this section, we unveil the correlations that exist between sizes of galaxies and their stellar contents. These results might be explored to shed light on the growth in size mechanisms of quiescent galaxies since z = 1.
To study the distribution of the stellar population parameters on the stellar mass–size plane, we took advantage of the bidimensional and locally weighted regression method, or LOESS (Cleveland 1979; Cleveland & Devlin 1988). This method finds a non-parametric plane to reveal trends on the stellar mass–size plane through the distribution of points (stellar population parameters for this study), which minimises the uncertainty effects in the diagrams by a regression technique. In particular, we used the Python implementation of the LOESS method published by Cappellari et al. (2013b). During the LOESS process, we set a regularisation factor or smoothness of f = 0.6 for all the solutions retrieved during the Monte Carlo approach. In this way, we included correlations and degeneracies between parameters. This is necessary because both sizes and stellar masses also depend on the photo-z determination, as do the remaining stellar population parameters explored here. We report mass-weighted age and formation epoch (Sect. 3.1), metallicity (Sect. 3.2), and extinction (Sect. 3.3). The results of the smoothed distributions of the stellar population properties within the stellar mass–size plane obtained with the LOESS method are shown in Figs. 1–3. Moreover, in Fig. 4 we illustrate the variation in individual stellar population properties and uncertainties provided by MUFFIT as a function of the size, as well as the values retrieved for the same quiescent galaxies after the LOESS smoothing.
 |
Fig. 1. From top to bottom: mass-weighted age, formation epoch, metallicity, and extinction of quiescent galaxies using EMILES+Padova00 models plotted on the circularised radius vs. stellar mass plane down to z = 0.9. All values are colour-coded as indicated by each colour bar and averaged with the LOESS method (for more details, see Sect. 3). The dashed line illustrates the median circularised radius. The number of galaxies in each panel is pointed out in the first row. |
In addition, we are able to quantify the variation in different stellar population parameters with size. This relation is expressed as a function of the median circularised radius, 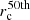 , observed at each redshift and stellar mass. We assumed a linear dependence on size of the form
, observed at each redshift and stellar mass. We assumed a linear dependence on size of the form
where p represents the stellar population parameter (mass-weighted age, formation epoch, metallicity, and extinction), 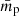 the slope or the correlation with size, and
the slope or the correlation with size, and 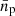 the intercept. The linear fitting was performed with the original values provided by MUFFIT (see Fig. 4) at different redshift and stellar mass bins. The latter to diminish mass dependence effects and differences in median sizes amongst stellar mass ranges.
the intercept. The linear fitting was performed with the original values provided by MUFFIT (see Fig. 4) at different redshift and stellar mass bins. The latter to diminish mass dependence effects and differences in median sizes amongst stellar mass ranges.
 |
Fig. 4. Individual values of stellar population parameters of quiescent galaxies as a function of their size and median circularised radius (rc and |
3.1. Age and formation epoch in the stellar mass–size plane
The results in Figs. 1–3 (see first row panels) show a tight correlation between the size of a quiescent galaxy and its mass-weighted age. This result is confirmed independently of the three sets of SSP models (BC03 and EMILES with isochrones BaSTI and Padova00) we used for the stellar population predictions. We find out a clear trend in which more compact galaxies are systematically older at log10 M⋆ ∼ 9.6, whereas younger quiescent galaxies lie on the upper parts of the stellar mass–size relation. This correlation is extended beyond the nearby Universe up to z = 0.9. Furthermore, there is no strong evidence for a dependence of the size–age correlation on stellar mass, 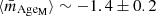 at log10 M⋆ ≳ 9.6. In addition, there is no evidence for an evolution of the size–age relation through cosmic time, meaning that the redshift dependence in Eq. (2) for ages resides in
at log10 M⋆ ≳ 9.6. In addition, there is no evidence for an evolution of the size–age relation through cosmic time, meaning that the redshift dependence in Eq. (2) for ages resides in 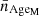 . Consequently, the common age difference between the most compact and most extended galaxies7 is ∼1 Gyr. Even though the stellar mass–size relation is less prominent for quiescent galaxies below log10 M⋆ ≲ 10–10.5 (e.g. Shen et al. 2003; Ferrarese et al. 2012; van der Wel et al. 2014; Guérou et al. 2015; Lange et al. 2015), the size–age correlation is also remarkable below this stellar mass limit.
. Consequently, the common age difference between the most compact and most extended galaxies7 is ∼1 Gyr. Even though the stellar mass–size relation is less prominent for quiescent galaxies below log10 M⋆ ≲ 10–10.5 (e.g. Shen et al. 2003; Ferrarese et al. 2012; van der Wel et al. 2014; Guérou et al. 2015; Lange et al. 2015), the size–age correlation is also remarkable below this stellar mass limit.
Similar results were obtained for the mass-weighted formation epoch (see second row panels in Figs. 1–3). The more compact the quiescent galaxy, the older its stellar population, that is, more compact quiescent galaxies were formed at earlier epochs than the extended ones at same stellar mass.
Interestingly, quiescent galaxies that populate the upper part of the stellar mass–size plane exhibit higher dust-corrected luminosities at 2800 Å (also provided by Díaz-García et al. 2019a). This result is supported by the SSP model sets of BC03 and EMILES and for all the stellar mass ranges explored in this work since z = 0.9. This luminosity reflects a more massive young component or a later event of star formation activity in extended quiescent galaxies (e.g. Ferreras & Silk 2000; Rogers et al. 2010; Vazdekis et al. 2016), which is reflected in the correlation reported above between size and age and formation epoch.
3.2. Metallicity as a function of size and stellar mass
In the stellar population predictions of BC03 and EMILES, we also found indications for a correlation between the size of a quiescent galaxy and its metal content (see third row panels in Figs. 1–3). The more compact the quiescent galaxy, the higher its metallicity. For EMILES SSP models, the size–metallicity correlation is clearer than for the BC03 models. In addition, this correlation is observed at least since z = 0.9. Independently of the stellar mass range, more compact quiescent galaxies are also more metal rich than the extended galaxies of the same stellar mass with a correlation of ![$ \langle \bar{m}_{\mathrm{[M/H]_M}} \rangle \sim -0.11 \pm 0.02 $](/articles/aa/full_html/2019/11/aa35257-19/aa35257-19-eq17.gif) . Because of the uncertainties and differences amongst the three SSP model predictions, and the limitation in the number of quiescent galaxies with reliable size measurements in ALHAMBRA, we cannot confirm that the correlation size–metallicity varies strongly in the redshift range, nor can we report systematic differences amongst different stellar mass ranges at the same redshift. Our results show that on average and using our previous definition, most compact quiescent galaxies at a fixed stellar mass are ∼0.07 dex more metal rich than their extended counterparts.
. Because of the uncertainties and differences amongst the three SSP model predictions, and the limitation in the number of quiescent galaxies with reliable size measurements in ALHAMBRA, we cannot confirm that the correlation size–metallicity varies strongly in the redshift range, nor can we report systematic differences amongst different stellar mass ranges at the same redshift. Our results show that on average and using our previous definition, most compact quiescent galaxies at a fixed stellar mass are ∼0.07 dex more metal rich than their extended counterparts.
As revealed by Díaz-García et al. (2019b), this sample may be affected by cosmic variance at 0.5 ≤ z < 0.7. In addition, when the BC03 SSP models are used for the analysis, Díaz-García et al. (2019b) showed that the lack of quiescent galaxies at this redshift range was more remarkable in ALHAMBRA. The authors also reported a peak or maximum in metallicity that they did not find with EMILES. This means that the metallicity for BC03 SSP models can be affected by this effect, which may mask the real trend of the size–metallicity at 0.5 ≤ z < 0.7.
3.3. Extinction of quiescent galaxies
As highlighted by Díaz-García et al. (2019b), there is no large discrepancies among the extinctions of quiescent galaxies (fairly constrained AV ≲ 0.6) without significant variations with redshift. This a priori limits a remarkable correlation between size and extinction. Despite this, there might be a slight indication that more compact galaxies are compatible with lower levels of extinction in their stellar continuum than the extended quiescent galaxies (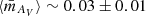 , see fourth row panels in Figs. 1–3). Owing to the narrow range of extinction values in these galaxies, the extinction differences between compact and extended quiescent galaxies are below 0.1 at all the redshift and stellar mass bins we explored. On average, this difference does not exceed a value of 0.05. There is no evidence for a dependence of the size–extinction on either redshift or stellar mass.
, see fourth row panels in Figs. 1–3). Owing to the narrow range of extinction values in these galaxies, the extinction differences between compact and extended quiescent galaxies are below 0.1 at all the redshift and stellar mass bins we explored. On average, this difference does not exceed a value of 0.05. There is no evidence for a dependence of the size–extinction on either redshift or stellar mass.
4. Main driver of the galaxy stellar content
Many efforts have been made in the past decades to track the evolution of stellar population properties, as well as to determine the main physical mechanism or driver that governs the stellar mass assembly. The tight correlation between the stellar content of a galaxy and its stellar mass has often been reported. This is usually interpreted as evidence that mass drives the stellar population of galaxies. Nevertheless, many authors reported that the stellar content of galaxies may be driven by other physical mechanisms such as dynamical and/or morphological properties. Our results agree with this fact (see Sect. 3), pointing out that properties of stellar populations in galaxies are not only related to the mass, but also to size. By means of studying the correlations between the different stellar population properties across the stellar mass–size plane (Sect. 3), we can retrieve empirical relations to set constraints on the mechanisms that govern the stellar mass assembly (Sect. 4.1). In addition, we are able to explore whether other properties of quiescent galaxies such as the stellar mass–size relation (Sect. 4.2), mass, and luminosity surface densities (Sect. 4.3), morphology (Sect. 4.4), and velocity dispersions (Sect. 4.5) exhibit correlations across the stellar mass–size plane similar to those obtained for the stellar population properties explored in this work.
4.1. Empirical constraints on the stellar population driver
For this aim, we empirically distinguished the regions of the stellar mass–size plane that show similar stellar population parameters. A visual inspection of Figs. 1–3 shows that constant formation epochs of quiescent galaxies lie at well-defined positions within the stellar mass–size plane. The formation epoch of a galaxy has been proposed in previous studies as one of the stellar population properties that better correlates with stellar mass (e.g. Thomas et al. 2005; Ferreras et al. 2009). Nevertheless, we find that at fixed stellar mass the formation epoch also correlates with size. On the other hand, previous studies have shown evidence for a non-passive evolution of the stellar populations of quiescent galaxies (e.g. Schiavon et al. 2006; Gallazzi et al. 2014; Siudek et al. 2017; Díaz-García et al. 2019b), which modifies their formation epochs at the same time that galaxies grow in size (Shen et al. 2003; Trujillo et al. 2007; van Dokkum et al. 2008; van der Wel et al. 2014). For these reasons and to unveil correlations with this parameter, we fit the original formation epoch values obtained from MUFFIT to a redshift-dependent plane of the form
where a and b are constants and c(z) is a redshift-dependent function that we assume linear hereafter. As a sanity check, we fit Eq. (3) in each redshift bin in Figs. 1–3 and obtained that our formation epochs are properly fitted by a plane (typical differences below 0.5 Gyr) and that a and b are compatible with no redshift evolution up to a 1σ uncertainty level. From Eq. (3), the regions of the plane of constant formation epoch at a given redshift are those in which 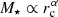 , where α = −b/a. As the stellar population properties of this work are model dependent, we repeated this process for the sets of BC03 and EMILES SSP models. As a result, the regions of constant formation epoch are expressed by α = 0.54 ± 0.09, 0.50 ± 0.07, and 0.55 ± 0.10 for BC03, EMILES+BaSTI, and EMILES+Padova00, respectively. The values of α are compatible within a 1σ confidence level, even though the stellar population predictions from the different SSP models reveal quantitative discrepancies (see e.g. Díaz-García et al. 2019a,b).
, where α = −b/a. As the stellar population properties of this work are model dependent, we repeated this process for the sets of BC03 and EMILES SSP models. As a result, the regions of constant formation epoch are expressed by α = 0.54 ± 0.09, 0.50 ± 0.07, and 0.55 ± 0.10 for BC03, EMILES+BaSTI, and EMILES+Padova00, respectively. The values of α are compatible within a 1σ confidence level, even though the stellar population predictions from the different SSP models reveal quantitative discrepancies (see e.g. Díaz-García et al. 2019a,b).
We checked whether other stellar population properties are also connected to the lines of constant formation epoch, that is, 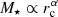 . We repeated the fitting process of Eq. (3), but taking the values of mass-weighted age and metallicity instead of the formation epoch values. In Table 2 we list the α coefficients for age and metallicity that we retrieved during this fitting. Figure 5 and Table 2 illustrate that mass-weighted age and metallicity (panels b and c in Fig. 5, respectively) agree with the α values obtained for the formation epochs. Owing to the large uncertainties for extinction, we constrained the line slope of constant extinction to a range of α = 0–2. We reached the same conclusions independently of the SSP model set we used for the stellar population analysis.
. We repeated the fitting process of Eq. (3), but taking the values of mass-weighted age and metallicity instead of the formation epoch values. In Table 2 we list the α coefficients for age and metallicity that we retrieved during this fitting. Figure 5 and Table 2 illustrate that mass-weighted age and metallicity (panels b and c in Fig. 5, respectively) agree with the α values obtained for the formation epochs. Owing to the large uncertainties for extinction, we constrained the line slope of constant extinction to a range of α = 0–2. We reached the same conclusions independently of the SSP model set we used for the stellar population analysis.
 |
Fig. 5. Smoothed stellar population properties of quiescent galaxies for EMILES SSP models and Padova00 isochrones at 0.3 ≤ z < 0.5 as a function of their positions in the stellar mass–size plane (coloured dots, see colour bar in each panel). Top panels, from left to right: mass-weighted formation epoch, age, and metallicity, and bottom panels: extinction, luminosity surface brightness in the I band, and Sérsic index, respectively. To guide the eye, we illustrate the curve of constant formation epoch (black solid line) and its uncertainty (shaded area), as well as the stellar mass–size relation at this redshift bin (dotted black line). |
4.2. Stellar mass–size relation of quiescent galaxies
It is well known that red galaxies exhibit a correlation between stellar mass and size, which also evolves across cosmic time (e.g. Shen et al. 2003; Trujillo et al. 2007; Buitrago et al. 2008; van Dokkum et al. 2008; van der Wel et al. 2014). As an additional sanity check of the reliability of our sizes and stellar masses, we determined the correlation stellar mass–size and the size evolution of quiescent galaxies since z ∼ 1. This also allowed us to verify whether the lines of constant stellar population properties (age, formation epoch and metallicity) match the stellar mass–size relation of quiescent galaxies.
To parametrise the stellar mass–size relation, we used a power-law function of the form
where A is the intercept of the stellar mass–size relation and β its slope. Throughout this work, we assumed that β is redshift independent, which has often been studied previously (e.g. Damjanov et al. 2011; McLure et al. 2013; van der Wel et al. 2014). However, the intercept A evolves with redshift owing to the increase in size of quiescent galaxies. For simplicity, we assumed that the intercept is a linear function of redshift in the log-space, that is, log10 A(z)=γ ⋅ z + δ. Making use of all the quiescent galaxies in our sample with stellar mass M⋆ ≥ 1010.5 M⊙ to avoid the flattening of the stellar mass–size relation at lower masses, we constrained the set of parameters β, γ, and δ that better fits Eq. (4). As there are discrepancies amongst the sample of quiescent galaxies depending on the SSP model (see also Díaz-García et al. 2019a), we retrieved the β, γ, and δ parameters for each SSP model set.
In Table 3 we summarise the parameters β, γ, and δ that best fit Eq. (4) for our sample. Although the sample of quiescent galaxies is not exactly the same for the three different sets of quiescent galaxies (see Table 1), the parameters β and γ do not present a strong dependence on the SSP model set and they are compatible given the uncertainties. However, δ is more tightly related to the SSP model set, as expected owing to the quantitative differences between stellar content predictions from BC03 and EMILES (see e.g. Díaz-García et al. 2019a). The stellar mass–size correlation, β, is set around 0.72 with an average error of 0.02. The parameter γ reflects the evolution in size of quiescent galaxies since z ∼ 1, for which we obtained a value of γ = −0.43 ± 0.02. A negative value of γ means that quiescent galaxies grow in size at lower redshifts, in agreement with previous studies. Extrapolating these values, we obtained that the growth in size of quiescent galaxies from z ∼ 1 to z = 0 is a factor of 2.5 ± 0.1. Regarding δ, it presents a stronger dependence on the SSP model set used and values in the range δ = 0.6–0.8 for EMILES and BC03 (see Table 3 for further details). In Fig. 5 we illustrate the stellar mass–size relation obtained for EMILES and Padova00 isochrones at z ∼ 0.4 with a dotted line.
Our results show that the lines of constant stellar population properties differ from the stellar mass–size relation (see dashed line in panels a to c in Fig. 5). For extinction (panel d in Fig. 5), we cannot confirm it given the uncertainties in our parameters. If they were equivalent, we would obtain that β ∼ 1/α. Nevertheless, the stellar content of quiescent galaxies is more tightly related to their position with respect to the stellar mass–size than to the stellar mass alone. This may be an indication that the assembly of the structures of galaxies (in this case represented by the effective radius) are related to their stellar content, but there are other mechanisms that also contribute to building it (e.g. mergers, Naab et al. 2009). It is worth mentioning that numerous studies mainly focus on the stellar mass–size relation separated red and blue galaxies based on morphology. Nevertheless, our sample is based on the intrinsic colours of galaxies, that is, on their stellar content. This implies that intrinsically red galaxies with late-type morphologies (Sérsic indices lower than 2.5) can be included in our sample (see Sect. 4.4), which may explain discrepancies with other studies.
On the other hand, van der Wel et al. (2014) studied the stellar mass–size relation of quiescent galaxies from the Cosmic Assembly Near-infrared Deep Extragalactic Legacy survey (CANDELS, Grogin et al. 2011; Koekemoer et al. 2011). These galaxies were selected using a UVJ colour-colour diagram and the stellar masses were obtained using BC03 composite models. The authors found a slope of β = 0.71–0.76 since z = 1.25, which is compatible with our results. In addition, after fitting the intercept obtained by van der Wel et al. (2014) at 0.25 < z < 1.25 to a lineal function with redshift, as in our work, we obtained that γ = −0.46 and δ = 0.75, which shows good agreement with our results when the BC03 SSP models were used.
4.3. Luminosity and mass surface densities in the stellar mass–size plane
Previous studies showed that the stellar content of red galaxies is more correlated with their luminosity or mass surface density (ΣI and ΣM, respectively) than with stellar mass (e.g. Kauffmann et al. 2003; Franx et al. 2008; Gargiulo et al. 2017). To explore this topic, we studied the distribution of the surface brightness computed by Griffith et al. (2012) for the ACS camera (defined as 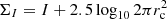 ) across the stellar mass–size plane. As for the stellar population properties derived from the ALHAMBRA photometry, we fit a plane to the original values of surface brightness for the I band, which is the same band as we used to compute the effective radius (see panel e in Fig. 5). We found that constant values of ΣI are properly expressed as
) across the stellar mass–size plane. As for the stellar population properties derived from the ALHAMBRA photometry, we fit a plane to the original values of surface brightness for the I band, which is the same band as we used to compute the effective radius (see panel e in Fig. 5). We found that constant values of ΣI are properly expressed as 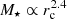 . This means that the regions of constant ΣI differ from the linear relation obtained in this work for constant formation epoch, age, and metallicity. The lines of constant ΣI better correlate with the stellar mass–size relation (see panel e in Fig. 5). Interestingly, the stellar content of quiescent galaxies is more strongly correlated with ΣI than with the stellar mass.
. This means that the regions of constant ΣI differ from the linear relation obtained in this work for constant formation epoch, age, and metallicity. The lines of constant ΣI better correlate with the stellar mass–size relation (see panel e in Fig. 5). Interestingly, the stellar content of quiescent galaxies is more strongly correlated with ΣI than with the stellar mass.
The mass surface density is defined as 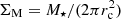 , therefore constant values of ΣM are along
, therefore constant values of ΣM are along 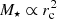 . This trend is similar to the trend obtained for ΣI, but this differs from the trend obtained for constant stellar population properties in Sect. 4.1, which shows a slope of α = 0.50–0.55.
. This trend is similar to the trend obtained for ΣI, but this differs from the trend obtained for constant stellar population properties in Sect. 4.1, which shows a slope of α = 0.50–0.55.
4.4. Sérsic indices of quiescent galaxies in the stellar mass–size plane
Using Sérsic indices as a proxy of morphology, we explored the correlation between morphology and stellar mass and size. We find that more than 80% of the quiescent galaxies in our sample show a Sérsic index, n, higher than 2.5, which is the limit that is typically used in the literature to distinguish between early- and late-type galaxies. Quiescent galaxies with n < 2.5 typically populate the lower parts of the stellar mass–size plane, mainly in the low-mass regimes of our sample. This also illustrates a connection between quiescent and early-type morphologies.
For the case of the surface density, Sect. 4.3, constant lines of the Sérsic index for quiescent galaxies do not reflect the same correlations as are exhibited by constant stellar population parameters (see panel f in Fig. 5). Nevertheless, this correlation follows similar trends as the surface density and the stellar mass–size relation.
4.5. Velocity dispersions and the driver of the stellar populations of quiescent galaxies
In the past decades, the tight correlation between stellar populations and velocity dispersion (usually quoted at one effective radius, σe) obtained in several spectroscopic studies has increasingly be considered evidence that the velocity dispersion drives the evolution of galaxies (σ; e.g. Trager et al. 2000; Gallazzi et al. 2006; Graves & Faber 2010; Cappellari et al. 2013a). Because our sample of quiescent galaxies was obtained through photometric data (resolving power R ∼ 20 for ALHAMBRA), we cannot provide an estimate of σe for each of our galaxies. Instead, we built distributions of σe in the stellar mass–size plane from spectroscopic quiescent galaxies at the same redshift range as our sample.
Making use of the NYU Value Added Galaxy Catalogue DR7 (NYU catalogue hereafter) of the Sloan Digital Sky Survey (SDSS, Blanton et al. 2005; Blanton & Roweis 2007; Adelman-McCarthy et al. 2008; Padmanabhan et al. 2008), we built a sample of quiescent galaxies with spectroscopic measurements of σ, stellar mass, and photometric effective radius for the r and i bands. Adopting the rest-frame colour limits proposed by Schawinski et al. (2014), we selected quiescent galaxies at 0.02 ≤ z ≤ 0.08 from the NYU catalogue using the k-corrected u, g, and J magnitudes (ugJ colour–colour diagram, see Fig. 4 in Schawinski et al. 2014). The stellar mass was scaled to a Chabrier (2003) IMF, and the sample of quiescent galaxies was constrained to log10 M⋆ ≥ 10.8 for the following reasons: (i) to be complete in stellar mass; (ii) to avoid the flattening of the stellar mass–size relation at log10 M⋆ ∼ 10.6; and (iii) to match the stellar mass range in which our sample is complete since z ∼ 1. As in Peralta de Arriba et al. (2014), we applied additional restrictions to the NYU catalogue to avoid unreliable data: 70 ≤ σ ≤ 320 km s−1, 0.3 ≤ re ≤ 30 kpc, and re ≥ 1″. The NYU catalogue contains sizes for r and i bands, we therefore built two final samples of ∼11 600 quiescent galaxies after applying the above restrictions. Owing to the aperture effects of SDSS, the velocity dispersions of quiescent galaxies from the NYU catalogue are out to one re. We therefore corrected them for aperture effects using Eq. (1) of Cappellari et al. (2006). In Fig. 6 we illustrate the mean σe of the final SDSS sample at different regions across the stellar mass–size plane. At fixed stellar mass, more compact quiescent galaxies from the SDSS exhibit larger σe than their more extended counterparts. As in Sect. 4.1, we fit the distribution of individual spectroscopic galaxies to a plane (see Eq. (3)) and obtained an analytic expression of constant σe. As a result of the fitting, constant values of σe are properly described by 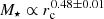 (see the green line in Fig. 6) with typical differences with respect to the plane below 26 km s−1. The parameter σe is not linked to a SED-fitting analysis based on colours, meaning that it is independent of our predictions of stellar population properties. We did not estimate dynamical masses (usually based on the virial theorem and homology), but stellar masses derived from colours and luminosities. This result reflects that at least in the nearby Universe, constant values of formation epoch, age, and metallicity across the stellar mass–size plane occupy regions of constant velocity dispersion within the uncertainties (see the black lines in Fig. 6). This result is consistent independently of the band that is used to determine projected sizes, that is, for r and i bands.
(see the green line in Fig. 6) with typical differences with respect to the plane below 26 km s−1. The parameter σe is not linked to a SED-fitting analysis based on colours, meaning that it is independent of our predictions of stellar population properties. We did not estimate dynamical masses (usually based on the virial theorem and homology), but stellar masses derived from colours and luminosities. This result reflects that at least in the nearby Universe, constant values of formation epoch, age, and metallicity across the stellar mass–size plane occupy regions of constant velocity dispersion within the uncertainties (see the black lines in Fig. 6). This result is consistent independently of the band that is used to determine projected sizes, that is, for r and i bands.
 |
Fig. 6. Average values of the velocity dispersion in the stellar mass–size plane for quiescent galaxies from the SDSS at 0.02 ≤ z ≤ 0.08 for the r band. The size of the marker illustrates the number of galaxies in each bin, and its colour illustrates the average velocity dispersion at one effective radius (see colour bar). Black lines show the empirical relation of constant formation epochs (Eq. (3)) obtained for BC03, EMILES+BaSTI, and EMILES+Padova00 SSP models (solid, dashed, and dotted black lines, respectively). Curves of constant velocity dispersions for one effective radius using SDSS data and the results from Peralta de Arriba et al. (2015) are illustrated with green and red lines, respectively. For each case, the shaded areas show the uncertainties in the fits of constant galaxy properties. |
At intermediate redshifts, z ∼ 1, fewer spectroscopic studies across the stellar mass–size plane that include reliable σe measurements are available. However, Peralta de Arriba et al. (2014, 2015) built samples of massive spheroid-like galaxies (log10 M⋆ ≳ 10.8 for an IMF of Chabrier 2003, n ≥ 4) at z ∼ 1. In particular, Peralta de Arriba et al. (2015) built a sample to cover a broad range on the stellar mass–size plane, which fits the range in stellar mass and redshift that we explore with the quiescent galaxies of ALHAMBRA. Peralta de Arriba et al. (2015) reported a breakdown in the homology assumption (also confirmed in Peralta de Arriba et al. 2014), yielding that constant σe values satisfies 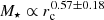 (see the dashed red line in Fig. 6), which is compatible with no redshift evolution since z ∼ 1. This result is in agreement with those obtained from the SDSS for the nearby Universe, but also with the constant regions of stellar population properties of quiescent galaxies since z ∼ 1 (see Fig. 6).
(see the dashed red line in Fig. 6), which is compatible with no redshift evolution since z ∼ 1. This result is in agreement with those obtained from the SDSS for the nearby Universe, but also with the constant regions of stellar population properties of quiescent galaxies since z ∼ 1 (see Fig. 6).
4.6. Main driver of the stellar content of galaxies
Some indications support that velocity dispersions within one effective radius are a good candidate to be tightly correlated with the stellar content of quiescent galaxies, even more than the stellar mass or the other parameters we explored. Nevertheless, this correlation between observables does not confirm that the velocity dispersion drives the evolution of stellar populations. There might be an underlying mechanism favouring the creation of stars that also increases the velocity dispersion. However, this would reflect that the driver of the stellar populations of galaxies would be partly linked to the dynamical properties of galaxies, as well as to their gravitational potential.
In a similar way, Barone et al. (2018) explored plausible drivers of the stellar content of 625 early-type galaxies using Integral Field Spectroscopy (IFS) from the Sydney-Australian-Astronomical-Observatory Multi-object Integral-Field Spectrograph galaxy survey (SAMI, Bryant et al. 2015). The authors compared the correlations between dynamic masses (MD), gravitational potential (Φ), surface density (Σ) and ages, metallicities, and α abundances. Under the assumption of homology in virial equilibrium, we would obtain that 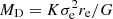 , Φ ∝ MD/re ∝ σ2 and
, Φ ∝ MD/re ∝ σ2 and 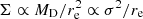 . Based on the correlation between the stellar population parameters and MD, Φ, and Σ, Barone et al. (2018) reported that the metallicity presents a stronger correlation with Φ and the age with Σ. Using the stellar population parameters of quiescent galaxies from ALHAMBRA (Sect. 3 and Figs. 1–3), we explored whether stellar populations are more strongly correlated with gravitational potential (ΦM) or surface density (ΣM). In our case, we used their non-dynamical definitions, that is, ΦM ∝ M⋆/rc and
. Based on the correlation between the stellar population parameters and MD, Φ, and Σ, Barone et al. (2018) reported that the metallicity presents a stronger correlation with Φ and the age with Σ. Using the stellar population parameters of quiescent galaxies from ALHAMBRA (Sect. 3 and Figs. 1–3), we explored whether stellar populations are more strongly correlated with gravitational potential (ΦM) or surface density (ΣM). In our case, we used their non-dynamical definitions, that is, ΦM ∝ M⋆/rc and 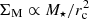 . Similarly to Barone et al. (2018), we quantified the correlation between stellar population parameters and ΦM and ΣM through a Spearman correlation coefficient, and we quantified their scatter assuming a linear relation. As a result, all the stellar population parameters explored in this research exhibit larger correlation coefficients for ΦM than for ΣM at any stellar mass and redshift. It is also remarkable that the scatter with ΦM is lower than for ΣM. This is expected because we observationally constrained that constant values of formation epoch, age, and metallicity lie along linear relations of the form
. Similarly to Barone et al. (2018), we quantified the correlation between stellar population parameters and ΦM and ΣM through a Spearman correlation coefficient, and we quantified their scatter assuming a linear relation. As a result, all the stellar population parameters explored in this research exhibit larger correlation coefficients for ΦM than for ΣM at any stellar mass and redshift. It is also remarkable that the scatter with ΦM is lower than for ΣM. This is expected because we observationally constrained that constant values of formation epoch, age, and metallicity lie along linear relations of the form 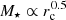 , which is more similar to the gravitational potential (i.e. M⋆ ∝ rc) than to the surface density (i.e.
, which is more similar to the gravitational potential (i.e. M⋆ ∝ rc) than to the surface density (i.e. 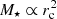 ). The observational discrepancies with respect Φ and Σ can be an indication that other key physical factors may also drive the stellar assembly (e.g. internal kinematics or the primordial angular momentum of gas clouds), external mechanisms such as mergers (e.g. Khochfar & Silk 2006; Naab et al. 2006; Perea & Solanes 2016; Solanes et al. 2016), or the masses of dark matter haloes (e.g. Huang et al. 2018), which should be studied in detail in future works.
). The observational discrepancies with respect Φ and Σ can be an indication that other key physical factors may also drive the stellar assembly (e.g. internal kinematics or the primordial angular momentum of gas clouds), external mechanisms such as mergers (e.g. Khochfar & Silk 2006; Naab et al. 2006; Perea & Solanes 2016; Solanes et al. 2016), or the masses of dark matter haloes (e.g. Huang et al. 2018), which should be studied in detail in future works.
Interestingly, McDermid et al. (2015) and Li et al. (2018) retrieved similar results from spectroscopic studies using the dynamical mass instead of the stellar mass. The authors also found that curves of constant velocity dispersion across the dynamical mass–size plane showed the same trend as constant age, metallicity, and [α/Fe]. This would support other recent studies claiming that dynamical and stellar mass are proportional to a factor that does not significantly change at different stellar mass range (Gavazzi et al. 2007; Taylor et al. 2010; Zahid & Geller 2017).
5. Growth in size of quiescent galaxies
The analysis conducted in this work reveals that more compact quiescent galaxies are older, more metal rich, and less reddened by dust than their more extended counterparts at fixed stellar mass. These results allow us to shed light on the different mechanism acting in the growth in size of these galaxies since z ∼ 1. The correlation between size and age for quiescent galaxies is additional evidence to discard the puffing-up scenario as causing the growth in size of galaxies because this mechanism would imply that compact galaxies were younger than their more extended counterparts.
Mergers and the progenitor bias agree with the results obtained in this topic. Both mechanisms have been extensively studied to explain the growth in size of quiescent galaxies (Hopkins et al. 2009; Naab et al. 2009; Valentinuzzi et al. 2010; Trujillo et al. 2011; Carollo et al. 2013; Belli et al. 2015). The latter because late-types or star-forming galaxies are typically more extended than early-type or quiescent galaxies, and they therefore lie on the upper parts of the quiescent stellar mass–size relation after their star formation has shut down. Recent studies revealed evidence for remnants of low star formation activity in quiescent galaxies (e.g. Vazdekis et al. 2016), which is usually referred to as “frosting”. Nevertheless, it is not clear how this may affect the galaxy size. If the remnants of star formation lie in the inner parts of the galaxy, frosting would reduce the apparent size of the galaxy. Conversely, new stars created in the surroundings of the inner parts (such as a disc or shell around the bulge or galactic nucleus) would probably produce an apparent growth in size for the host galaxy. Therefore frosting should not be discarded as another feasible mechanism to produce the increase in size of galaxies. However, the importance of this mechanism is also related to the star formation activity, which is usually low and should be explored as a function of cosmic time. Overall, the growth in size of quiescent galaxies may not be driven by a unique mechanism.
As revealed by Díaz-García et al. (2013), since z ∼ 1 the merger history of galaxies does not depend on the galaxy size and the growth in size through mergers seems to similarly affect the whole quiescent population. Under this scenario, mergers would contribute to eliminate compact quiescent galaxies throughout cosmic time. A detailed study of the evolution of the number density of compact quiescent galaxies would help to shed light on the importance (or lack thereof) of mergers in terms of the size evolution of quiescent galaxies. Unfortunately, there is no clear consensus about the evolution of the number density of compact quiescent galaxies because some previous studies reported that this number is roughly constant (Saracco et al. 2010; Damjanov et al. 2014, 2015; Gargiulo et al. 2017), whereas other work stated that it exhibits a significant or mild decrement (Valentinuzzi et al. 2010; Cassata et al. 2013; Poggianti et al. 2013; Quilis & Trujillo 2013; Trujillo et al. 2014; van der Wel et al. 2014). For instance, if the co-moving number density of compact quiescent galaxies were lower at more recent epochs, this would reflect that mergers occur, although their importance would be hard to determine. On the other hand, an increasing number of compact galaxies would reflect an arrival of new compact quiescent galaxies, that is, the progenitor bias (van Dokkum & Franx 2001) would also alter the stellar mass–size relation. The sample of quiescent galaxies with reliable size measurements we presented here is not large enough for a reliable and direct study of the evolution in number density of compact quiescent galaxies.
From the results obtained by Díaz-García et al. (2013); Díaz-García et al. (2019b), it is possible to draw the following general picture on the growth in size of the quiescent population. Firstly, instead of a unique mechanism to explain the growth in size of quiescent galaxies, there seems to be a combination of various mechanisms acting in parallel to produce the increase in size observed in quiescent galaxies: mergers, the progenitor bias and possibly frosting. In a downsizing scenario, the first galaxies that quenched their star formation were the galaxies that experienced the most efficient star formation episodes, with very short formation timescales. These are in turn the most massive galaxies. The formation and evolution of the stellar populations of quiescent galaxies also relate to the size of the galaxy, that is, to the stellar mass density of the galaxy, where the most compact galaxies at fixed stellar mass would be formed earlier and more efficiently. After their star formation ceases, they were incorporated into the quiescent population, and under this hypothesis, all the galaxies that were formed later will present more extended sizes and younger stellar populations, which produces the size–age correlation. In addition, there is evidence that star-forming galaxies typically contain stellar populations with lower metallicities than the quiescent ones (e.g. Gallazzi et al. 2014; Peng et al. 2015). Consequently, the star-forming galaxies quenching their star formation activity would populate the upper parts of the stellar mass–size plane and they would be able to exhibit lower metallicity than the already quenched galaxies. However, some authors argued that the metallicity changes during the quenching phase (see e.g. Peng et al. 2015), and depending on the mechanism that shuts the star formation activity down, the progenitor bias may not contribute to the size–metallicity correlation. A further study is necessary to confirm this, however. When these galaxies belong to the quiescent sample, some of them would continue to grow in size through mergers and (maybe) frosting. This means that the continuous arrival of new quiescent galaxies with larger sizes may be an important mechanism that would contribute to modify the stellar mass–size relation (e.g. Belli et al. 2015, reported that the progenitor bias can only be responsible for about half of the growth in size at 1 < z < 1.6).
Secondly, although the growth in size is likely produced by a combination of various mechanisms, their role would depend on cosmic time. For instance, massive quiescent galaxies (log10 M⋆ ≥ 11.2) suffer a rapid increase in number at 1 < z < 3 (e.g. Arnouts et al. 2007; Domínguez Sánchez et al. 2011; Ilbert et al. 2010, 2013), which implies a more striking contribution of the progenitor bias than at z < 1, provided that the majority of massive galaxies are already red at this redshift range (e.g. Davidzon et al. 2013; Ilbert et al. 2013; Moustakas et al. 2013; Tomczak et al. 2014). In addition, major mergers were more frequent at higher redshifts (e.g. Lin et al. 2008; de Ravel et al. 2009; López-Sanjuan et al. 2012, 2013; Xu et al. 2012), and therefore the contribution of mergers to the increase in size might be more relevant. These facts would contribute to explain that the increase in size of quiescent galaxies were more efficient at 1 < z < 2 rather than at 0 < z < 1 (e.g. Trujillo et al. 2007; van Dokkum et al. 2008; Newman et al. 2012; van der Wel et al. 2014).
Thirdly, at fixed redshift, the role of the different mechanisms to produce the growth in size of quiescent galaxies may vary with stellar mass. As discussed above, at z < 1 there is a generalised increase in the number density of quiescent galaxies that at decreasing stellar mass is systematically more prominent (see e.g. Díaz-García et al. 2019b; Damjanov et al. 2019), which means that the importance of the progenitor bias is different at different stellar mass ranges.
6. Comparison with previous studies
Since the discovery of the stellar mass–size relation, several previous works have studied the stellar content of compact galaxies at different ranges of redshift and stellar mass (Shankar & Bernardi 2009; Trujillo et al. 2011; Belli et al. 2015; McDermid et al. 2015; Fagioli et al. 2016; Gargiulo et al. 2017; Scott et al. 2017; Williams et al. 2017; Li et al. 2018; Wu et al. 2018; Damjanov et al. 2019). We here extended this type of studies up to z ∼ 1 to also explore correlations with metallicity and extinction. We devote this section to comparing our results, obtained using photometric data, with the spectroscopic work in the literature (see Table 4 for a brief summary).
Brief description of samples used in previous work to determine stellar population parameters of galaxies as a function of size.
6.1. Stellar populations of compact and extended galaxies in the nearby Universe
Early attempts to unveil the discrepancies between the stellar populations of compact and extended galaxies were carried out using spectroscopic data from the SDSS. Shankar & Bernardi (2009) explored the relation between half-light radii re and the ages of early-type galaxies from the SDSS at 0.013 < z < 0.3. The authors revealed that early-type galaxies of ages older than 9 Gyr systematically present lower effective radii of Δlog10 re ∼ 0.1 dex than those younger than 6 Gyr. This agrees qualitatively with our results.
The pioneering work by Trujillo et al. (2011) determined systematic discrepancies between the extreme age quartiles of early-type galaxies at fixed dynamical mass, where the young galaxies exhibited larger effective radii and a correlation with velocity dispersion. Trujillo et al. (2011) extended this result at z ∼ 1 where little variation in the segregation of the age within the stellar mass–size relation was found, which implies that the evolution of this relation is independent of the galaxy age. This strongly constrained the puffing-up mechanism in explaining the growth in size of galaxies and agrees with our results: the puffing-up model is inconsistent with the observed distribution of ages across the stellar mass–size. However, Trujillo et al. (2011) found smaller age differences between the extreme quartiles than we did. This may be a consequence of the differences in the sample selection because Trujillo et al. (2011) analysed early-type galaxies instead of colour-based quiescent galaxies.
By means of integral field spectroscopy, McDermid et al. (2015) obtained similar correlations across the stellar mass–size plane for index-based ages and metallicities and the mass-weighted ones: more compact galaxies present both older ages and higher metallicities. This result agrees with our predictions of quiescent galaxies at 0.1 < z < 0.3 and log10 M⋆ > 10. Whilst our sample was built using the intrinsic colours of galaxies as spectral discriminator, the sample of McDermid et al. (2015) was morphologically selected and preserves the same correlations with size that we obtained, in part because early-type galaxies frequently present red colours. From the combined flux of spatially resolved galaxies within one effective radius, Scott et al. (2017) and Li et al. (2018) also confirmed the segregation of the stellar population properties with size, that is, more compact galaxies are older and more metal rich. As we also obtain in Sect. 4.5, Li et al. (2018) showed that the distribution of velocity dispersion changes according to the stellar population parameters of galaxies for stellar masses of log10 M⋆ ≳ 10.4. Li et al. (2018) revealed a correlation between the size and the gradients of metallicity and age, which we cannot compare with our results because our study involves integrated stellar populations. Interestingly, McDermid et al. (2015) and Scott et al. (2017) reported more alpha-enhanced stellar populations for compact early-type galaxies, although we are not able to compare this correlation.
6.2. Correlation between age and size at moderate redshift
At moderate redshift, previous spectroscopic studies have mainly focused on the ages as a function of size, but metallicity remains not strongly determined. Belli et al. (2015) explored the stellar populations of quiescent galaxies at 1 < z < 1.6 and obtained that older quiescent galaxies populate the lower parts of the stellar mass–size diagram, which is in agreement with our results at intermediate redshift. By use of the star formation history, Belli et al. (2015) estimated that extended quiescent galaxies arrived later in the quiescent sample than the compact galaxies, which were mainly formed in later formation epochs than the compact counterpart. In addition, Belli et al. (2015) constrained the importance of the progenitor bias in the assembling of the stellar mass–size of quiescent galaxies, which would partly explain the age–size correlation that we observe at lower redshifts.
At a similar redshift range as we explored here, Fagioli et al. (2016) and Gargiulo et al. (2017) also found a general size–age correlation at intermediate redshift. However, Fagioli et al. (2016) did not find evidence of a correlation between age and size for quiescent galaxies more massive than log10 M⋆ = 11. Gargiulo et al. (2017) complemented their study by including the co-moving number densities of compact and extended quiescent galaxies. As a result, extended quiescent galaxies are younger than their compact counterparts since z = 0.8 according to a non-passive evolution (see also Díaz-García et al. 2019b).
At 0.1 < z < 0.6, Damjanov et al. (2019) analysed the distributions of the age-sensitive estimator Dn4000 by segregating a sample of quiescent galaxies according to stellar mass and redshift. For quiescent galaxies at log10 M⋆ < 1011, the Dn4000 distributions of younger quiescent galaxies (defined as 1.5 < Dn4000 < 1.75) showed larger sizes than their older counterpart (Dn4000 > 1.75), meaning a correlation between age and size in which compact galaxies are younger. However, as in Fagioli et al. (2016), galaxies more massive than log10 M⋆ = 11 do not show a trend in the distributions of Dn4000 with size. In a similar way and since z ∼ 1.2, Williams et al. (2017) also measured the Dn4000 index for different size bins, but the authors also complemented their results by including age predictions from the Hδ index. For Hδ, Williams et al. (2017) estimated age differences of ∼2.5 Gyr between compact and extended sources, but for Dn4000 this difference decreases to ∼0.3 Gyr. This supports our difference in age of ∼1 Gyr between compact and extended quiescent galaxies. Also interpreting age-sensitive index variations, Dn4000 and Hδ, Wu et al. (2018) discerned younger stellar populations in quiescent galaxies at larger sizes and fixed stellar mass. More precisely, larger quiescent galaxies are ∼500 Myr younger than the compact ones, which is a smaller difference in age than our results (∼1 Gyr). Nevertheless, we used mass-weighted stellar population properties. This may introduce discrepancies with respect to the outcomes obtained using luminosity-weighted properties because composite stellar population models can be more affected by recent bursts of star formation (Ferreras & Yi 2004; Serra & Trager 2007; Ferreras et al. 2009; Rogers et al. 2010). It is of note that Wu et al. (2018) obtained consistent results using three independent methods to define their quiescent galaxy sample.
The results from different studies were obtained by different techniques based on other sensitive features, SSP models, star formation histories, and even with different criteria to separate quiescent galaxies, which may yield quantitative discrepancies and/or biased samples. Despite these potential discrepancies, there is an overall agreement and our work converges to a common qualitative outcome with the results obtained from other spectroscopic studies.
7. Summary and conclusions
After selecting all the quiescent galaxies from ALHAMBRA with reliable sizes (circularised effective radius) in HST fields, we obtained a sub-sample of more than 800 galaxies with stellar population parameters. We used this sub-sample to discern any correlations between the stellar content of quiescent galaxies and their sizes at fixed stellar mass.
Our results show evidence for strong correlations between the size and the age, formation epoch, and metallicity of quiescent galaxies, although there are indications for a slight correlation with extinction as well. This outcome does not depend on the SSP model used, and it was obtained for three SSP model predictions: BC03, EMILES with BaSTI isochrones, and EMILES with Padova00 isochrones.
These correlations were studied in detail and revealed remarkable insights. Firstly, the size of a quiescent galaxy and its age are tightly correlated. A generalised trend is that more compact quiescent galaxies are older than their more extended counterparts. The difference in age is established around 1 Gyr for stellar masses log10 M⋆ > 9.6 and up to z ∼ 0.9, where the average size–age correlation is 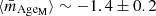 (see Eq. (2)). This trend is reflected in the dust-corrected luminosity at 2800 Å, where less compact quiescent galaxies exhibit higher ultraviolet luminosities, possibly as a result of a more recent or longer star formation activity. Secondly, compact quiescent galaxies are systematically more metal rich than the less dense galaxies at the same stellar mass. Differences between metallicity of compact and extended quiescent galaxies amount to ∼0.07 dex, at least since z = 0.9, where the correlation size–metallicity is
(see Eq. (2)). This trend is reflected in the dust-corrected luminosity at 2800 Å, where less compact quiescent galaxies exhibit higher ultraviolet luminosities, possibly as a result of a more recent or longer star formation activity. Secondly, compact quiescent galaxies are systematically more metal rich than the less dense galaxies at the same stellar mass. Differences between metallicity of compact and extended quiescent galaxies amount to ∼0.07 dex, at least since z = 0.9, where the correlation size–metallicity is ![$ \langle \bar{m}_{\mathrm{[M/H]_M}} \rangle \sim -0.11 \pm 0.02 $](/articles/aa/full_html/2019/11/aa35257-19/aa35257-19-eq36.gif) on average. Finally, extended quiescent galaxies may present slight higher extinctions of < 0.1 independently of their stellar mass range and redshift,
on average. Finally, extended quiescent galaxies may present slight higher extinctions of < 0.1 independently of their stellar mass range and redshift, 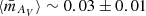 .
.
We determined the regions of constant formation epoch across the stellar mass–size plane to empirically set constraints on the physical mechanism that govern the evolution of stellar populations in galaxies. Our results indicate that this relation is properly expressed by 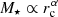 , for which we obtained values of α = 0.54 ± 0.09, 0.50 ± 0.07, and 0.55 ± 0.10 for BC03 and EMILES SSP models, respectively (the latter including BaSTI and Padova00 isochrones). This is also supported by other stellar population parameters such as mass-weighted age and metallicity. After studying several stellar population properties, some indications support the idea that constant velocity dispersions within one effective radius lie in constant regions of stellar population properties across the stellar mass–size plane, that is, they are tightly correlated with the stellar content of quiescent galaxies. This may reflect that the driver of the stellar populations of galaxies might be partly linked to the dynamical properties of galaxies, as well as to their gravitational potential.
, for which we obtained values of α = 0.54 ± 0.09, 0.50 ± 0.07, and 0.55 ± 0.10 for BC03 and EMILES SSP models, respectively (the latter including BaSTI and Padova00 isochrones). This is also supported by other stellar population parameters such as mass-weighted age and metallicity. After studying several stellar population properties, some indications support the idea that constant velocity dispersions within one effective radius lie in constant regions of stellar population properties across the stellar mass–size plane, that is, they are tightly correlated with the stellar content of quiescent galaxies. This may reflect that the driver of the stellar populations of galaxies might be partly linked to the dynamical properties of galaxies, as well as to their gravitational potential.
In view of these results, the puffing-up scenario can be discarded as a responsible mechanism of the growth in size of galaxies (in good agreement with the pioneering work by Trujillo et al. 2011, which gave strong evidence against the puffing-up mechanism of gas expulsion) because this scenario would imply that compact galaxies were younger than their more extended counterparts. However, the progenitor bias agrees with the results obtained in this research, as well as mergers. The progenitor bias and mergers homogeneously act across the stellar mass–size plane, which may contribute to explain the growth in size of quiescent galaxies since z ∼ 1, where the importance of these mechanisms may vary depending on the redshift and stellar mass range explored.
Finally, we compared our results with previous spectroscopic work on this topic, mostly focused on probing potential age differences between compact and extended galaxies. Overall, there is a very good agreement regarding these age effects. Interestingly, our results greatly extend some of the conclusions obtained in the nearby Universe: more compact quiescent galaxies are more metal rich than their extended counterparts, but this is also observed for the first time since z ∼ 1 through data from the large-scale multi-filter ALHAMBRA survey. A correlation between size and extinction was also explored, which constitutes a complement for future studies.
Acknowledgments
This work has been supported by the Programa Nacional de Astronomía y Astrofísica of the Spanish Ministry of Economy and Competitiveness (MINECO, grants AYA2012-30789 and AYA2015-66211-C2-1-P), by the Government of Aragón (Research Group E103), by the Ministry of Science and Technology of Taiwan (grant MOST 106-2628-M-001-003-MY3), and by the Academia Sinica (grant AS-IA-107-M01). The authors also acknowledge support from the Spanish Ministry for Economy and Competitiveness and FEDER funds through grants AYA2010-15081, AYA2010-15169, AYA2010-22111-C03-01, AYA2010-22111-C03-02, AYA2011-29517-C03-01, AYA2012-39620, AYA2013-40611-P, AYA2013-42227-P, AYA2013-43188-P, AYA2013-48623-C2-1, AYA2013-48623-C2-2, ESP2013-48274, AYA2014-57490-P, AYA2014-58861-C3-1, AYA2016-76682-C3-1-P, AYA2016-76682-C3-3-P, AYA2016-77846-P Generalitat Valenciana projects Prometeo 2009/064 and PROMETEOII/2014/060, Junta de Andalucía grants TIC114, JA2828, P10-FQM-6444, and Generalitat de Catalunya project SGR-1398. In this work we made use of the NYU Value Added Galaxy Catalogue DR7, which includes data from the Sloan Digital Sky Survey (SDSS) and the Two Micron All Sky Survey (2MASS). Funding for the SDSS has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, Princeton University, the United States Naval Observatory, and the University of Washington. This publication makes use of data products from the 2MASS, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The authors thank the constructive and fruitful comments provided by the anonymous referee that surely helped to improve this paper. Throughout this research, we made use of the Matplotlib package (Hunter 2007), a 2D graphics package used for Python that is designed for interactive scripting and quality image generation. This paper is dedicated to Marian León Canalejo for being there when L.A.D.G. needed her most and for her patience and continuous encouragement while finishing his PhD.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Aparicio Villegas, T., Alfaro, E. J., Cabrera-Caño, J., et al. 2010, AJ, 139, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barone, T. M., D”Eugenio, F., Colless, M., et al. 2018, ApJ, 856, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Newman, A. B., & Ellis, R. S. 2015, ApJ, 799, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., van Dokkum, P. G., Tal, T., et al. 2009, ApJ, 697, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 594, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Schlegel, D. J., Strauss, M. A., et al. 2005, AJ, 129, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bryant, J. J., Owers, M. S., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2857 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Conselice, C. J., et al. 2008, ApJ, 687, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Fukugita, M., Ellis, R. S., et al. 2009, ApJ, 697, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013a, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013b, MNRAS, 432, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., Bschorr, T. J., Renzini, A., et al. 2013, ApJ, 773, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Giavalisco, M., Williams, C. C., et al. 2013, ApJ, 775, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., & Trujillo, I. 2009, ApJ, 696, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cleveland, W. S. 1979, J. Am. Stat. Assoc., 74, 829 [Google Scholar]
- Cleveland, W., & Devlin, S. 1988, J. Am. Stat. Assoc., 83, 596 [CrossRef] [Google Scholar]
- Coe, D., Benítez, N., Sánchez, S. F., et al. 2006, AJ, 132, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Cristóbal-Hornillos, D., Aguerri, J. A. L., Moles, M., et al. 2009, ApJ, 696, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., McCarthy, P. J., Abraham, R. G., et al. 2009, ApJ, 695, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Abraham, R. G., Glazebrook, K., et al. 2011, ApJ, 739, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Hwang, H. S., Geller, M. J., & Chilingarian, I. 2014, ApJ, 793, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Geller, M. J., Zahid, H. J., & Hwang, H. S. 2015, ApJ, 806, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Zahid, H. J., Geller, M. J., et al. 2019, ApJ, 872, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, 558, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- de La Rosa, I. G., La Barbera, F., Ferreras, I., & de Carvalho, R. R. 2011, MNRAS, 418, L74 [NASA ADS] [CrossRef] [Google Scholar]
- de la Rosa, I. G., La Barbera, F., Ferreras, I., et al. 2016, MNRAS, 457, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-García, L. A., Mármol-Queraltó, E., Trujillo, I., et al. 2013, MNRAS, 433, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2015, A&A, 582, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2019a, A&A, 631, A156 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2019b, A&A, 631, A157 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickinson, M., Giavalisco, M., & GOODS Team 2003, in The Mass of Galaxies at Low and High Redshift, eds. R. Bender, & A. Renzini, 324 [Google Scholar]
- Domínguez Sánchez, H., Pozzi, F., Gruppioni, C., et al. 2011, MNRAS, 417, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Fagioli, M., Carollo, C. M., Renzini, A., et al. 2016, ApJ, 831, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, L., Lapi, A., De Zotti, G., & Danese, L. 2008, ApJ, 689, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, L., Lapi, A., Bressan, A., et al. 2010, ApJ, 718, 1460 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., Côté, P., Cuillandre, J.-C., et al. 2012, ApJS, 200, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., & Silk, J. 2000, ApJ, 541, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., & Yi, S. K. 2004, MNRAS, 350, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Lisker, T., Carollo, C. M., Lilly, S. J., & Mobasher, B. 2005, ApJ, 635, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Pasquali, A., de Carvalho, R. R., de la Rosa, I. G., & Lahav, O. 2006, MNRAS, 370, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Pasquali, A., Malhotra, S., et al. 2009, ApJ, 706, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., van Dokkum, P. G., Förster Schreiber, N. M., et al. 2008, ApJ, 688, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., & White, S. D. M. 2006, MNRAS, 370, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Zibetti, S., Brinchmann, J., & Kelson, D. D. 2014, ApJ, 788, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Gargiulo, A., Bolzonella, M., Scodeggio, M., et al. 2017, A&A, 606, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graves, G. J., & Faber, S. M. 2010, ApJ, 717, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Griffith, R. L., Cooper, M. C., Newman, J. A., et al. 2012, ApJS, 200, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guérou, A., Emsellem, E., McDermid, R. M., et al. 2015, ApJ, 804, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Giavalisco, M., Cassata, P., et al. 2011, ApJ, 735, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Häußler, B., Barden, M., Bamford, S. P., & Rojas, A. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 155 [NASA ADS] [Google Scholar]
- Hogg, D. W. 1999, ArXiv e-prints [arXiv:astro-ph/9905116] [Google Scholar]
- Hopkins, P. F., Cox, T. J., & Hernquist, L. 2008, ApJ, 689, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Keres, D., & Wuyts, S. 2009, ApJ, 691, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Leauthaud, A., Greene, J., et al. 2018, MNRAS, 480, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jimenez, R., Bernardi, M., Haiman, Z., Panter, B., & Heavens, A. F. 2007, ApJ, 669, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., & Chiboucas, K. 2013, AJ, 145, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Chiboucas, K., Toft, S., et al. 2014, AJ, 148, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Chiboucas, K., Berkson, E., et al. 2017, AJ, 154, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kaviraj, S., Schawinski, K., Devriendt, J. E. G., et al. 2007, ApJS, 173, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2012, MNRAS, 421, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., & Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khochfar, S., & Silk, J. 2006, ApJ, 648, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1977, ApJ, 217, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Pasquali, A., Ferreras, I., et al. 2014, MNRAS, 445, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, R., Driver, S. P., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Mao, S., Cappellari, M., et al. 2018, MNRAS, 476, 1765 [NASA ADS] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2010, ApJ, 710, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Tasca, L. A. M., et al. 2013, A&A, 553, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDermid, R. M., Alatalo, K., Blitz, L., et al. 2015, MNRAS, 448, 3484 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, D. H., Bell, E. F., Rix, H.-W., et al. 2005, ApJ, 632, 191 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Moles, M., Benítez, N., Aguerri, J. A. L., et al. 2008, AJ, 136, 1325 [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2014, MNRAS, 441, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Coil, A. L., Aird, J., et al. 2013, ApJ, 767, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., Bundy, K., & Treu, T. 2012, ApJ, 746, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, N., Schlegel, D. J., Finkbeiner, D. P., et al. 2008, ApJ, 674, 1217 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Panter, B., Jimenez, R., Heavens, A. F., & Charlot, S. 2008, MNRAS, 391, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Maiolino, R., & Cochrane, R. 2015, Nature, 521, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Peralta de Arriba, L., Balcells, M., Falcón-Barroso, J., & Trujillo, I. 2014, MNRAS, 440, 1634 [NASA ADS] [CrossRef] [Google Scholar]
- Peralta de Arriba, L., Balcells, M., Trujillo, I., et al. 2015, MNRAS, 453, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Perea, J. D., & Solanes, J. M. 2016, MNRAS, 461, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Calvi, R., Bindoni, D., et al. 2013, ApJ, 762, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Quilis, V., & Trujillo, I. 2013, ApJ, 773, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, B., Ferreras, I., Peletier, R., & Silk, J. 2010, MNRAS, 402, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Gorgas, J., Cardiel, N., & González, J. J. 2006, A&A, 457, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saracco, P., Longhetti, M., & Gargiulo, A. 2010, MNRAS, 408, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Urry, C. M., Simmons, B. D., et al. 2014, MNRAS, 440, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Schiavon, R. P., Faber, S. M., Konidaris, N., et al. 2006, ApJ, 651, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, N., Brough, S., Croom, S. M., et al. 2017, MNRAS, 472, 2833 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., & Trager, S. C. 2007, MNRAS, 374, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de Galaxias Australes (Cordoba: Observatorio Astronomico) [Google Scholar]
- Shankar, F., & Bernardi, M. 2009, MNRAS, 396, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Siudek, M., Małek, K., Scodeggio, M., et al. 2017, A&A, 597, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanes, J. M., Perea, J. D., Darriba, L., et al. 2016, MNRAS, 461, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Szomoru, D., Franx, M., Bouwens, R. J., et al. 2011, ApJ, 735, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, E. N., Franx, M., Brinchmann, J., van der Wel, A., & van Dokkum, P. G. 2010, ApJ, 722, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Toft, S., van Dokkum, P., Franx, M., et al. 2007, ApJ, 671, 285 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2014, ApJ, 783, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Rudnick, G., Rix, H.-W., et al. 2004, ApJ, 604, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Feulner, G., Goranova, Y., et al. 2006, MNRAS, 373, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Cenarro, A. J., de Lorenzo-Cáceres, A., et al. 2009, ApJ, 692, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Ferreras, I., & de La Rosa, I. G. 2011, MNRAS, 415, 3903 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Ferré-Mateu, A., Balcells, M., Vazdekis, A., & Sánchez-Blázquez, P. 2014, ApJ, 780, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Valentinuzzi, T., Poggianti, B. M., Saglia, R. P., et al. 2010, ApJ, 721, L19 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Franx, M. 2001, ApJ, 553, 90 [Google Scholar]
- van Dokkum, P. G., Franx, M., Kriek, M., et al. 2008, ApJ, 677, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Vergani, D., Scodeggio, M., Pozzetti, L., et al. 2008, A&A, 487, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, C. C., Giavalisco, M., Bezanson, R., et al. 2017, ApJ, 838, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.-F., van der Wel, A., Bezanson, R., et al. 2018, ApJ, 868, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Genzel, R., et al. 2012, ApJ, 753, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Zhao, Y., Scoville, N., et al. 2012, ApJ, 747, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., & Geller, M. J. 2017, ApJ, 841, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Zirm, A. W., van der Wel, A., Franx, M., et al. 2007, ApJ, 656, 66 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Number of quiescent galaxies with reliable sizes obtained from ACS/HST fields in common with ALHAMBRA for a stellar mass completeness level of 95%.
Brief description of samples used in previous work to determine stellar population parameters of galaxies as a function of size.
All Figures
 |
Fig. 1. From top to bottom: mass-weighted age, formation epoch, metallicity, and extinction of quiescent galaxies using EMILES+Padova00 models plotted on the circularised radius vs. stellar mass plane down to z = 0.9. All values are colour-coded as indicated by each colour bar and averaged with the LOESS method (for more details, see Sect. 3). The dashed line illustrates the median circularised radius. The number of galaxies in each panel is pointed out in the first row. |
| In the text | |
 |
Fig. 2. Same as Fig. 1, but for EMILES+BaSTI SSP models. |
| In the text | |
 |
Fig. 3. Same as Fig. 1, but for BC03 SSP models. |
| In the text | |
 |
Fig. 4. Individual values of stellar population parameters of quiescent galaxies as a function of their size and median circularised radius (rc and |
| In the text | |
 |
Fig. 5. Smoothed stellar population properties of quiescent galaxies for EMILES SSP models and Padova00 isochrones at 0.3 ≤ z < 0.5 as a function of their positions in the stellar mass–size plane (coloured dots, see colour bar in each panel). Top panels, from left to right: mass-weighted formation epoch, age, and metallicity, and bottom panels: extinction, luminosity surface brightness in the I band, and Sérsic index, respectively. To guide the eye, we illustrate the curve of constant formation epoch (black solid line) and its uncertainty (shaded area), as well as the stellar mass–size relation at this redshift bin (dotted black line). |
| In the text | |
 |
Fig. 6. Average values of the velocity dispersion in the stellar mass–size plane for quiescent galaxies from the SDSS at 0.02 ≤ z ≤ 0.08 for the r band. The size of the marker illustrates the number of galaxies in each bin, and its colour illustrates the average velocity dispersion at one effective radius (see colour bar). Black lines show the empirical relation of constant formation epochs (Eq. (3)) obtained for BC03, EMILES+BaSTI, and EMILES+Padova00 SSP models (solid, dashed, and dotted black lines, respectively). Curves of constant velocity dispersions for one effective radius using SDSS data and the results from Peralta de Arriba et al. (2015) are illustrated with green and red lines, respectively. For each case, the shaded areas show the uncertainties in the fits of constant galaxy properties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.