| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201936478 | |
| Published online | 23 September 2019 | |
Letter to the Editor
1:1 orbital resonance of circumbinary planets
Institut für Astronomie und Astrophysik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
e-mail: anna.penzlin@uni-tuebingen.de, sareh.ataiee@uni-tuebingen.de, wilhelm.kley@uni-tuebingen.de
Received:
7
August
2019
Accepted:
22
August
2019
The recent detection of the third planet in Kepler-47 has shown that binary stars can host several planets in circumbinary orbits. To understand the evolution of these systems we have performed two-dimensional hydrodynamic simulations of the circumbinary disc with two embedded planets for several Kepler systems. In two cases, Kepler-47 and -413, the planets are captured in a 1:1 mean-motion resonance at the planet “parking position” near the inner edge of the disc. The orbits are fully aligned and have mean eccentricities of about 0.25 to 0.30; the planets are entangled in a horseshoe-type motion. Subsequent n-body simulations without the disc show that the configurations are stable. Our results point to the existence of a new class of stable resonant orbits around binary stars. It remains to be seen if such orbits exist in reality.
Key words: hydrodynamics / planet-disk interactions / binaries: general / planets and satellites: formation
© ESO 2019
1. Introduction
To date, about a dozen planets orbiting around binary star systems have been detected by the Kepler space mission. All of them are single-planet systems, except Kepler-47 whose third planet was recently detected (Orosz et al. 2019), demonstrating that circumbinary systems can host multiple planets. This raises the question about their formation, evolution, and stability.
Following previous approaches we assume that the planets formed further away from the central binary in more quiet disc regions and then migrated inwards where they remained, “parked” at the cavity edge. Using hydrodynamical disc simulations, we modelled the migration of multiple planets in six of the known Kepler circumbinary systems and discovered stable coorbital resonant configurations in Kepler-47 and -413.
Thus far, 1:1 resonances have not yet been observed in exoplanet systems, but only for minor solar system objects. Well known are the population of Trojans of Jupiter and Saturn, and the moons Janus and Epimetheus that orbit Saturn, which have similar mass and are on mutual horseshoe orbits (Yoder et al. 1983). For the latter, Rodríguez et al. (2019) have recently presented a formation mechanism involving migration in a circumplanetary disc. Relating to exoplanets, the formation of 1:1 resonance objects can proceed for example in situ (Beaugé et al. 2007) or through a convergent migration process (Cresswell & Nelson 2006). In the first scenario the planets begin on tadpole orbits, in the second case they start out with a horseshoe motion that later turns into a tadpole as well (Cresswell & Nelson 2006).
However, continued migration of the resonant pair in a gas disc will lead to an increase in the libration amplitude, which can destabilise the system (Cresswell & Nelson 2009), in particular for more massive planets (Pierens & Raymond 2014). Stabilisation of a system can be achieved if the pair is in resonance with a third planet (Cresswell & Nelson 2009; Leleu et al. 2019a), whose presence may also assist in forming the 1:1 resonance in the first place, by providing additional perturbations. Around a binary star, planets reach a stable parking position near the disc’s inner cavity, as determined by the binary and the disc parameters. In the case of a successful capture near this position one might expect long-term stability for such coorbital configurations as they do not migrate any further.
For the pure n-body case, the dynamics and stability of eccentric coplanar coorbitals around single stars has been studied for the equal planet mass case in Leleu et al. (2018). They show that for low mass planets around 10−5 of the stellar mass, stable horseshoe and tadpole orbits exist up to an orbital eccentricity of about 0.5. The stability of 1:1 resonances between low mass planets has been studied in the special case of an equal mass binary star on a circular orbit by Michalodimitrakis & Grigorelis (1989), who found stability only in the zero mass limit of the planets.
Here we present the disc-driven migration of two small and equal mass planets in the Kepler-47 and Kepler-413 systems. We show that in both cases stable 1:1 resonant configurations are possible. In Sect. 2 we describe our model set-up, in Sect. 3 we focus on the resulting 1:1 resonances, and in Sect. 4 we discuss out results.
2. Models
To model discs around binary stars, we performed viscous hydrodynamic simulations of thin discs in two dimensions (2D) using a modified version of the PLUTO-code (Mignone et al. 2007) that allows for computation on graphics processing units (Thun et al. 2017). We used a locally isothermal disc because the final equilibrium structure of circumbinary discs with full radiative cooling and viscous heating is similar to a locally isothermal model using the equilibrium temperature (see Kley et al. 2019). They find the disc aspect ratios, h, to be between 0.04 and 0.05, depending on the binary system and disc parameters. Here, we chose h = 0.04, for the viscosity parameter α = 0.001, and a disc mass of 1% of the binary mass. The orbital parameter of the two modelled systems, Kepler-413 and -47, are listed in the upper block of Table 1.
Parameters for Kepler-413 and -47, as used in the simulations.
The simulations presented here were performed using the same approach and method as described in Thun & Kley (2018) and Kley et al. (2019). We used cylindrical coordinates centred on the barycentre of the binary and a radially logarithmic grid with 684 × 584 cells, which stretches from 1 to 40 binary separations, abin. This domain size and resolution has shown to be sufficient for this type of study (Thun & Kley 2018). For the n-body integrator we used a fouth-order Runge-Kutta scheme, which is of sufficient accuracy, given an average time-step size of 2 × 10−3 Tbin.
First, we simulated the discs without planets to their convergent states, which are reached after about 20 000 binary orbits, Tbin, and then embedded the planets. The simulations of the circumbinary discs converged to a disc with a large, eccentric, and precessing inner cavity. The mean orbital parameters of the cavities, calculated by fitting the inner disc edge (see Thun et al. 2017 for details), are given in the lower block of Table 1. The cavity size and eccentricity are determined by the binary eccentricity and mass ratio, and the disc height and viscosity. In agreement with Thun & Kley (2018), systems with low ebin show very high cavity eccentricities. In our case we obtained ecav ∼ 0.45 (see Table 1).
Then we added the planets into the disc at different initial locations on circular orbits, and let them migrate. The planets did not accrete mass. In the case of Kepler-47, we added three planets, initially at 7.5, 14, and 20 abin. The two inner planets each have a mass of 25 M⊕, while the outer planet has 5 M⊕. The masses of the planets lie within the error bars of the newly discovered three-planet system in Kepler-47 (Orosz et al. 2019). As the additional outer planet has a much lower mass, and remains further out in the disc, it has little effect on dynamical evolution of the two inner planets, and is not discussed here any further. Even though in Kepler-413 only one planet is observed, we embedded two planets at 9 and 11.5 abin each with 0.21 MJup which is identical to the observed planet mass in Kepler-413 (Kostov et al. 2014).
3. Forming a stable 1:1 resonance
In both cases the planets migrate toward the stable parking position near the inner cavity of the disc, which is first reached by the inner planet (blue curves in Fig. 1). Such low mass planets do not open a complete gap, hence their orbits align with the cavity and gain in eccentricity (Kley et al. 2019). The second planet, starting further out, takes more time to reach the cavity and acquire eccentricity. This process takes longer for Kepler-47, as lower mass planets migrate more slowly, and the outer planet is initialised further away.
 |
Fig. 1. Time evolution of the orbital elements of the inserted planets in the Kepler-413 and -47 systems while embedded in a disc, simulated for 20 000 Tbin prior to insertion. |
As the parking position of planets around binaries is determined by the disc’s cavity edge, the incoming second planet reaches the same orbit as the first. In our case this leads to capture in 1:1 orbital resonant configurations. As shown in Fig. 1, this happens after ∼5000 Tbin for Kepler-413 and ∼13 000 Tbin for Kepler-47. During the capture process the two planets show initially larger excursions in semi-major axis and eccentricity. During this process the planets do not collide with each other, as the minimum distance between them is ∼10−2 abin. The excursions are damped by the action of the disc, but the orbits remain eccentric. After the capture, we continued the hydrodynamical simulations for more than 10 000 Tbin and the final orbital configuration of the planets remained stable.
The shape of the orbits in relation to the disc’s structure in this phase of the simulations is displayed in Fig. 2, where snapshots of the configurations are plotted at around the capture time (left panels) and in equilibrium at 20 000 Tbin after planet insertion (right panels). The orbits lie near the disc’s inner edge, are more circular than the cavity, but still have an eccentricity of ∼0.25−0.30. They begin to align just before capture, and their precession rate and that of the cavity match exactly as soon as the planets arrive in their stable parking positions. In the subsequent evolution, the orbits remain fully aligned with a maximum libration angle of 6°. For Kepler-413 the precession rate of the cavity is lowered to 1900 Tbin after introducing the planets. In Kepler-47, whose planets are less massive than those of Kepler-413, the cavity almost maintains its previous precession rate of 2600 Tbin. The presence of these small planets does not significantly change the cavity size and eccentricity for either system.
 |
Fig. 2. Density distribution at the time right before the capture (left) and in the coorbital configuration (right) for Kepler-47 (top) and Kepler-413 (bottom). The white ellipse indicates the location of the cavity in the disc and the light blue ellipses show the orbits of the two planets, where the yellow dots mark their positions. The orbital parameters of the outer planet are quoted in the top left corner. |
The orbital dynamics of the two planets engaged in the 1:1 resonance while still embedded in the disc is displayed in Fig. 3. It shows that the difference in mean longitude between the two planets never drops below 20°. So they never have a close encounter and do not collide, but are rather engulfed in a periodic motion of a 1:1 resonance. In both cases the planets move on horseshoe orbits around the Lagrange points L4 and L5. In the case of Kepler-413 the motion is quite regular with a libration period of about 1330 Tbin. In the case of Kepler-47 the motion is more irregular and a planet moves multiple times around one Lagrange point before switching over to the other. We suspect that the reason for this irregular behaviour is the lower mass of the planets and stronger perturbed disc compared to Kepler-413. In such a condition, the disc perturbation can give higher random acceleration to the planets and send them back and forth to the horseshoe and Lagrange points.
 |
Fig. 3. Dynamical structure of the 1:1 resonances while the planets are still embedded in the disc, on the left Kepler-413 and on the right Kepler-47. Top: semi-major axis difference of the planets vs. the difference in mean longitude. The colour changes linearly from blue to yellow over the time span displayed in the lower panels. The red dots indicate the location of the Lagrange points L4 and L5 in the case of circular motion. Bottom: angular distance between the planets vs. time. |
To check the long-term stability of these orbits in the absence of the disc, we extracted the final positions and velocities of the planets and stars, and used them as the initial condition for a pure n-body simulation containing the two stars with the planets (n = 4). In Fig. 4, we show the evolution of semi-major axis and eccentricity over a time span 22 000 Tbin. In both systems, the orbits are stable and the planets remain in the 1:1 resonance. The orbits retain their previous eccentricity (with disc) and change periodically their positions upon close approach, where the planet in the inner position switches to the outer and vice versa, as is typical for horseshoe orbits.
 |
Fig. 4. Evolution of semi-major axes and eccentricities of the two planets orbiting Kepler-413 and -47 for the pure n-body case without disc. |
In the pure n-body case, the orbits are much more regular than in the case with the disc, and in both systems the planets are on regular, smooth horseshoe orbits (see Fig. 5). Without the disc, the radial excursions of the planets are similar to the case with the disc present. The libration period is 1920 Tbin for Kepler-47 and 1055 Tbin for Kepler-413. With the disc present, these periods are longer, for example by 300 Tbin in the case of Kepler-413, because interaction with the disc influences the orbital properties of the embedded planets. During one libration period in the n-body simulation, the planets approach each other only up to a mean longitude difference between the planets of about 25°, ensuring stability (see Fig. 5).
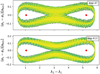 |
Fig. 5. Difference in mean longitude of the two planets for the pure n-body case without a disc. The colour changes linearly with time over 1600 years or 57 900 Tbin for Kepler-413 and 78 500 Tbin for Kepler-47. |
Without the disc, the aligned planetary orbits precess around the binary at a slower rate than with a disc present. This is expected as the precession of the planets in the disc was aligned with the inner cavity. In the n-body simulation we find precession periods of 4245 Tbin for Kepler-47 and 2275 Tbin for Kepler-413. These periods correspond to that of a single planet with the mean orbital elements of the planet pair.
4. Discussion and conclusion
Using a migration scenario for two planets in a circumbinary disc we have shown that low eccentricity binary systems like Kepler-47 and -413 are able to host two small, equal-mass planets in a stable coorbital resonance where the planets are on horseshoe-type orbits with an average eccentricity of about 0.25 to 0.30. The orbits are aligned and precess slowly around the binary.
These properties are different from the coorbital resonances observed to date. In the Saturnian system, Janus and Epimetheus are on nearly circular orbits and in the case of Trojans, very small objects are in resonance with a much larger planet whose orbit is nearly circular. However, for Trojans the small asteroid can be on an eccentric and inclined orbit that changes the resonant structure (Namouni et al. 1999). In our case, the resonant planet pair orbits a binary star on quite eccentric orbits.
Having found possible resonant states for only two cases of the Kepler sample, it is presently not known for which orbital parameters of a binary star system stable coorbital configurations can exist. Our investigated systems both have very low ebin, 0.02 and 0.04, which appears to be an important factor for the stability of such systems. Using a comparable set-up for Kepler-35 (ebin = 0.14), we did not find any coorbital resonant orbits, but one of the planets was ejected after an interaction between the two planets. In the case of the highly eccentric binary Kepler-34 with ebin = 0.52, both planets were ejected after a close encounter.
In addition to our equal planet mass studies, we ran a model with a different planet-planet mass ratio for the Kepler-47 case. In this simulation, the mass of the inner planet was about 20% greater than the outer one with otherwise identical initial conditions. The system evolved again into a stable coorbital configuration. However, in this case the planets ended up in a tadpole type orbit around each other with a mean eccentricity of about 0.28. Further exploration of the parameter space using different binary eccentricities and planet masses will be the topic of future work.
The disc surrounding appears to be essential for the trapping mechanism of the planets. We also tested the Kepler-47 system with a less viscous disc α = 10−4. In such a low viscosity disc, the planets are able to open a gap, which leads to joint inward migration where the outer planet pushes the inner planet inward, while exciting the eccentricity of the inner planet. As a result the inner planet gets ejected as soon as the outer planet migrates closer than two binary separations to the inner planet. In the case of massive planets (masses 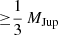 ) both planets reach stable orbits at different semi-major axes. Therefore, massive planets and inviscid environments may inhibit formation of coorbital resonances.
) both planets reach stable orbits at different semi-major axes. Therefore, massive planets and inviscid environments may inhibit formation of coorbital resonances.
Compared to the observations, our planets are located further away from the stars, which is the consequence of their being trapped at the parking position away from the cavity edge. The more massive the planets are, the closer they migrate towards the edge of the cavity. Lower disc viscosities and aspect ratios also bring the cavity edge closer to the stars1. However, in such cases, the planets are more vulnerable to the gap-opening which, as explained, can prevent them from getting into 1:1 resonance. Hence, we do not expect the coorbitals to form sufficiently close to the stars such that the stars’ perturbation can affect them. To analyse the general stability of these coorbitals closer to the stars and to check whether they are similar to single planet orbits will require extensive future parameter studies, for example thorough n-body simulations.
After showing that stable coorbital resonances with moderate orbital eccentricities around binary stars are a natural outcome of a convergent migration process, it will be worthwhile to search for such systems in the Kepler data. A recent study suggests that the single star TOI-178 is orbited by a coorbital planet pair, and an additional planet (Leleu et al. 2019b).
Acknowledgments
We thank Zsolt Sandor for fruitful discussions. Anna Penzlin was funded by grant KL 650/26-1 of the German Research Foundation (DFG). The authors acknowledge support from the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC, and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG. All plots in this paper were made with the Python library matplotlib (Hunter 2007).
References
- Beaugé, C., Sándor, Z., Érdi, B., & Süli, Á. 2007, A&A, 463, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2009, A&A, 493, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., Thun, D., & Penzlin, A. B. T. 2019, A&A, 627, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostov, V. B., McCullough, P. R., Carter, J. A., et al. 2014, ApJ, 784, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Leleu, A., Robutel, P., & Correia, A. C. M. 2018, Celest. Mech. Dyn. Astron., 130, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Leleu, A., Coleman, G., & Ataiee, S. 2019a, ArXiv e-prints [arXiv:1901.07640] [Google Scholar]
- Leleu, A., Lillo-Box, J., Sestovic, M., et al. 2019b, A&A, 624, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalodimitrakis, M., & Grigorelis, F. 1989, JApA, 10, 347 [NASA ADS] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Namouni, F., Christou, A. A., & Murray, C. D. 1999, Phys. Rev. Lett., 83, 2506 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., Welsh, W. F., Haghighipour, N., et al. 2019, AJ, 157, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., & Raymond, S. N. 2014, MNRAS, 442, 2296 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, A., Correa-Otto, J. A., & Michtchenko, T. A. 2019, MNRAS, 487, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Thun, D., & Kley, W. 2018, A&A, 616, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thun, D., Kley, W., & Picogna, G. 2017, A&A, 604, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoder, C. F., Colombo, G., Synnott, S. P., & Yoder, K. A. 1983, Icarus, 53, 431 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Time evolution of the orbital elements of the inserted planets in the Kepler-413 and -47 systems while embedded in a disc, simulated for 20 000 Tbin prior to insertion. |
| In the text | |
 |
Fig. 2. Density distribution at the time right before the capture (left) and in the coorbital configuration (right) for Kepler-47 (top) and Kepler-413 (bottom). The white ellipse indicates the location of the cavity in the disc and the light blue ellipses show the orbits of the two planets, where the yellow dots mark their positions. The orbital parameters of the outer planet are quoted in the top left corner. |
| In the text | |
 |
Fig. 3. Dynamical structure of the 1:1 resonances while the planets are still embedded in the disc, on the left Kepler-413 and on the right Kepler-47. Top: semi-major axis difference of the planets vs. the difference in mean longitude. The colour changes linearly from blue to yellow over the time span displayed in the lower panels. The red dots indicate the location of the Lagrange points L4 and L5 in the case of circular motion. Bottom: angular distance between the planets vs. time. |
| In the text | |
 |
Fig. 4. Evolution of semi-major axes and eccentricities of the two planets orbiting Kepler-413 and -47 for the pure n-body case without disc. |
| In the text | |
 |
Fig. 5. Difference in mean longitude of the two planets for the pure n-body case without a disc. The colour changes linearly with time over 1600 years or 57 900 Tbin for Kepler-413 and 78 500 Tbin for Kepler-47. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


