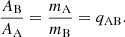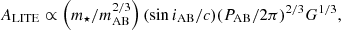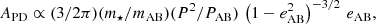| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 14 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201936328 | |
| Published online | 04 October 2019 | |
Doubly eclipsing systems
1
Astronomical Institute, Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2
Private Observatory, Pohoří 71, 254 01 Jílové u Prahy, Czech Republic
3
Institute of Physics, Czech Academy of Sciences, Na Slovance 1999/2, 182 21 Praha 8, Czech Republic
4
Variable Star and Exoplanet Section, Czech Astronomical Society, Czech Republic
5
BSObservatory, Modrá 587, 760 01 Zlín, Czech Republic
Received:
17
July
2019
Accepted:
22
August
2019
Context. Only several doubly eclipsing quadruple stellar systems are known to date, and no dedicated effort to characterize population properties of these interesting objects has yet been made.
Aims. Our first goal was to increase number of known doubly eclipsing systems such that the resulting dataset would allow us to study this category of objects via statistical means. In order to minimize biases, we used long-lasting, homogeneous, and well-documented photometric surveys. Second, a common problem of basically all known doubly eclipsing systems is the lack of proof that they constitute gravitationally bound quadruple system in the 2+2 architecture (as opposed to two unrelated binaries that are projected onto the same location in the sky by chance). When possible, we thus sought evidence for the relative motion of the two binaries. In that case, we tried to determine the relevant orbital periods and other parameters.
Methods. We analysed photometric data for eclipsing binaries provided by the OGLE survey and we focused on the LMC fields. We found a large number of new doubly eclipsing systems (our discoveries are three times more numerous than the previously known cases in this dataset). In order to prove relative motion of the binaries about a common centre of mass, we made use of the fact that OGLE photometry covers several years. With a typical orbital period of days for the observed binaries, we sought eclipse time variations (ETVs) on the timescale comparable to a decade (this is the same method used for an archetype of the doubly eclipsing system, namely V994 Her). In the cases where we were able to detect the ETV period, the difference between the inner and outer periods in the quadruple system is large enough. This allows us to interpret ETVs primarily as the light-time effect, thus providing an interesting constraint on masses of the binaries.
Results. In addition to significantly enlarging the database of known doubly eclipsing systems, we performed a thorough analysis of 72 cases. ETVs for 28 of them (39% of the studied cases) showed evidence of relative motion. Among these individual systems, we note OGLE BLG-ECL-145467, by far the most interesting case; it is bright (12.6 mag in I filter), consists of two detached binaries with periods of ≃3.3 d and ≃4.9 d (making it a candidate for a 3:2 resonant system) revolving about each other in only ≃1538 d. Distribution of the orbital period ratio PA/PB of binaries in 2+2 quadruples shows statistically significant excess at ≃1 and ≃1.5. The former is likely a natural statistical preference in weakly interacting systems with periods within the same range. The latter is thought to be evidence of a capture in the 3:2 mean motion resonance of the two binaries. This sets important constraints on evolutionary channels in these systems.
Conclusions. The total number of doubly eclipsing systems increased to 146, more than 90% of which are at low declinations on the southern sky. This motivates us to use southern hemisphere facilities to further characterize these systems, and to seek possibilities to complement this dataset with northern sky systems.
Key words: binaries: eclipsing / stars: fundamental parameters / stars: early-type / Magellanic Clouds
© ESO 2019
1. Introduction
Some stars in the solar neighbourhood, in our Galaxy, or in neighbouring galaxies live in solitude; the majority, however, have companions. They can form binaries, triples, or even higher multiples, bound gravitationally together and exhibiting motion about their common centre of mass. Because of their increasing complexity, higher multiples are less frequent (e.g. Tokovinin 2018a). Still, analysis of their architecture can bring interesting results. For instance, the first multiples that arise in various non-trivial architectures are stellar quadruple systems. Long-term stability dictates that they may exist as a triple system accompanied by an additional and distant component (3+1 variant). However, there is also another possibility. Quadruples may also exist as a pair of binaries, whose centres of mass revolve about each other on a nearly elliptic orbit. This is known as the 2+2 variant of quadruples. The census of known quadruple stellar systems is still quite low, but they can bring interesting insights to our knowledge of stellar formation, evolution, and the processes acting during the life of the star (see e.g. Tokovinin 2018b; Bataille et al. 2018). As pointed out by Tokovinin (2018b), the origin of the quadruple systems is still an intriguing question, with even a possibility that their two architecture variants (3+1 and 2+2) form via different mechanisms and channels. For that reason, further analysis of quadruples is desirable.
Here we focus on systems in 2+2 architecture, which potentially offer an interesting possibility when both binaries are eclipsing. This is a very fortuitous situation because the analysis of classical eclipsing binaries still generally provides the most precise method of deriving stellar parameters, such as masses or radii (e.g. Southworth 2012). Several dozens of candidates for such systems were discovered during the last decade mainly due to the long-lasting photometric surveys such as the Optical Gravitational Lensing Experiment (OGLE; Udalski et al. 2008, 2015). They were dubbed “doubly eclipsing systems”, or sometimes “double-eclipsing” systems1. Characteristic to them are two sets of eclipses belonging to the time series of photometry of a single source on the sky. The very first of these systems, V994 Her, was discovered more then ten years ago by Lee et al. (2008), and it is also the first that was proven to constitute a real, gravitationally bound quadruple system, due to determination of mutual motion of the two binaries about a common centre of mass (see Zasche & Uhlař 2016). V994 Her was soon followed with OGLE LMC-ECL-10429 by Ofir (2008), which was the first suggested to have the orbital periods of the binaries in mutual 3:2 resonance.
For the sake of completeness, we also note optically resolved, separate pairs of eclipsing binaries very close to each other on the sky (see Table 1). Because of the large separation, their mutual motion is not determined, but it is conceivable that they form gravitationally bound quadruples. An archetype for this category is the system consisting of BV Dra and BW Dra. The system CoRoT 211659387, often classified as doubly eclipsing, was actually resolved thanks to the PDR (Zejda et al. 2019) and the ZTF survey (Masci et al. 2019; Bellm et al. 2019). The CRTS survey (Drake et al. 2009) helped to resolve the other systems listed in Table 1. Using a small telescope, these systems can be seen to behave like doubly eclipsing systems, but because of the recognized separation we do not include them in our analysis.
Optically resolved pairs of eclipsing binaries.
Once some level of understanding of the doubly eclipsing system is reached, especially if the parameters of the mutual motion of the binaries are determined, the quadruple may become a valuable laboratory for testing important astrophysical tasks. First, in a traditional fashion, data for individual binaries in the system can be used to track their evolutionary status, derive their age, determine their chemical composition, and so on. The added value of these data is that the two binaries should share most of these same parameters (age, chemical composition, distance, etc.). Having thus two independent ways to derive the same parameters should in principle help to increase their accuracy. Second, the dynamics of 2+2 quadruples is sufficiently rich and, if compact enough, even the secular evolution may be on interestingly short timescales (see e.g. Vokrouhlický 2016; Hamers & Portegies 2016; Hamers & Lai 2017). In addition to the plethora of short-term effects exhibited by eclipse time variations (ETVs; e.g. Borkovits et al. 2003, 2011), secular effects such as apsidal precession of inner binaries or inclination change can also be detected (e.g. Zasche & Uhlař 2016; Rappaport et al. 2013; Juryšek et al. 2018). Finally, as for any class of stellar systems, if data are gathered for a large enough ensemble of cases, we can start studying statistical trends related to different parameters. Those typically hide valuable hints about formation mechanisms and/or evolutionary tracks of the binary orbits driven by mutual gravitational interaction and tides (e.g. Tokovinin 2008). The 2+2 quadruples seem to have a special status in this endeavour as also argued in a recent review by Tokovinin (2018b). All these arguments motivated their study, especially in the situation when not many doubly eclipsing systems are still not known today.
2. Data source and analysis strategy
Observations provided by the OGLE survey (Udalski et al. 1992) are very suitable for our task of finding new quadruple systems thanks to their completeness, availability, well-documented and easily downloadable catalogue, long-term stable and uniform photometry of the observed targets, and data covering more than a decade for most of the fields. All these qualities facilitate our task. We focused on the LMC fields for several reasons: (i) OGLE III data were available for a total of eight seasons, OGLE IV for four seasons, sometimes also complemented by data from OGLE II from four seasons, (ii) MACHO data are also available for some of the systems, and (iii) southern declinations are suitable for the Danish 1.54 m telescope at La Silla, available to our group, which allows dedicated extensions of the survey data. We note that OGLE LMC fields contain 26121 documented eclipsing binaries2. This is both large enough to hope for a meaningful search for doubly eclipsing systems and small enough to be treatable in a semi-manual way by a single person.
A simple code was written to scan the entire OGLE III LMC dataset, and each source (eclipsing binary) was considered keeping in mind several criteria: (i) a sufficient number of observations, (ii) magnitude <19 mag in the I filter, (iii) period of eclipse in the range3 0.7 < PA < 15 d, and (iv) the amplitude of variation larger than its scatter. Using this strategy, we browsed the OGLE binaries one by one, and we judged by eye whether the source should be considered as a potential candidate for a doubly eclipsing system or not. The human eye is a good instrument for this strategy because a normal eclipsing binary should have all its data points located tightly around a well-defined light curve (LC) profile when phase-folded. Doubly eclipsing systems, on the other hand, should have many deviating data points outlying from the standard shape of the binary light curve (corresponding to dimming of the second binary in the system when it occurs in eclipse).
It took us about a month to search through the whole catalogue with this procedure, and this resulted in a list of suspected (candidate) systems. These potential doubly eclipsing binaries (156 in total) were further analysed in detail and many false positives were found. For some of these systems the second period was detectable even in the complete raw data; for others the second period could only be derived on the residuals after subtraction of the main curve of pair A. Most often the prominent period belongs to pair A, and it also has larger amplitude of photometric variations. This period of pair A (PA) was taken from the original OGLE catalogue by Soszyński et al. (2016). After completing this scrutiny, we were left with 72 confirmed doubly eclipsing systems for which we were able to determine both eclipsing periods. Among them, 17 cases had previously been found to be doubly eclipsing and were flagged this way in the original OGLE III catalogue4 by Graczyk et al. (2011). This is encouraging and tells us that our procedure is quite efficient, in fact more successful than the previous automated analysis of the OGLE team (Graczyk & Eyer 2010). Obviously, some limitations come from our initial criteria constraining periods and magnitudes of targets. Our final list of presently known doubly eclipsing systems is given in Table 2. We note that it also contains systems from other sources than analysed in this paper.
Currently known doubly eclipsing systems.
3. Determination of quadruple nature for candidate systems
A double-period source on the sky may not necessarily imply that it represents a quadruple system in the 2+2 architecture. In some cases, it may perhaps represent a binary with one or both components eclipsing. Therefore, our final step towards proving we deal with the quadruple systems represents the detection of mutual motions of the two binaries about a common centre of mass. As mentioned in the Introduction, this has been already achieved for a few systems, but this sample remains very small.
There are several possibilities for achieving the task. For instance, one could rely on a high-quality spectroscopic measurements of the candidate systems. If things go right, one could disentangle spectral lines from the system into two binaries, determine their radial velocities, and thus detect and characterize their relative motion. Obviously, this assumes spectroscopy available at least over the whole cycle of the relative orbit. As a rule of thumb, stability of the 2+2 systems requires at the zero approximation PAB ≳ 5 max (PA, PB), with more detailed criteria involving masses of the binaries and eccentricity of the relative orbit (e.g. Mardling & Aarseth 2001). However, for most systems, PAB is significantly longer and may extend to years, decades, or even centuries (e.g. Duquennoy & Mayor 1991; Tokovinin 2008; Raghavan et al. 2010). Moreover, many of the candidate systems are rather faint, so middle- or large-scale telescopes would be needed for a sufficiently good spectroscopic observation. Therefore, we believe spectroscopy is important and needed for further characterization of already recognized quadruples, but it is not primarily suitable for their detection.
Because the primary recognition of the system as doubly eclipsing relies entirely on its photometry, it would have been profitable to use the photometric series to also determine parameters of their relative orbit. Here again, there are several possibilities. For instance, if the system is not entirely coplanar (i.e. if the orbital plane of the binaries does not coincide exactly with the orbital plane of the relative orbit), mutual interaction triggers a precession about a conserved total angular momentum (typically dominated by the contribution from the relative orbit; e.g. Vokrouhlický 2016). This makes the binary orbital planes change their geometry with respect to the observer and thus affects their light curve. An obvious consequence is a change in depth of the eclipses. However, the characteristic secular precession period is typically long:  (Söderhjelm 1975). Unless the system is quite compact, the timescale needed to reveal some changes in the depth of eclipses is long and, additionally, not very suitable for determining parameters of the mutual orbit. For that reason, so far we have only one example of a doubly eclipsing system where changes in the binary inclination have been detected (Hong et al. 2018).
(Söderhjelm 1975). Unless the system is quite compact, the timescale needed to reveal some changes in the depth of eclipses is long and, additionally, not very suitable for determining parameters of the mutual orbit. For that reason, so far we have only one example of a doubly eclipsing system where changes in the binary inclination have been detected (Hong et al. 2018).
Narrowing the strategy, we see that the minimum approach (and at the same time the optimum approach) will be to detect a phenomenon having a period equal to the period PAB of the relative orbit. The most straightforward approach consists of detecting ETVs, if possible simultaneously for both binaries A and B. ETVs arise from period changes in both binaries apparent to the observer, and may have various origins. The most readable is simply due to near-elliptic motion of the two binaries about the centre of mass. Assuming that the inclination iAB of the relative orbit is not zero, the systems move periodically towards and away from the observer. The finite velocity of light then simply affects the periodicity of eclipse series, a phenomenon called the LIght Time Effect (LITE; e.g. Irwin 1959; Mayer 1990). An important aspect of LITE in quadruples is that the ETVs for both binaries are strictly anticorrelated in time, a property which can be readily checked. The LITE approach has been successfully used to determine the quadruple nature of the first doubly eclipsing system V994 Her (e.g. Zasche & Uhlař 2016), a study which may be taken as a proof of concept of our method. We note that ETVs may also have a different, or additional, origin than simply LITE. We discuss this topic in more detail in Sect. 5.
Our model thus assumes motion of all stars in the quadruple composed of three elliptic orbits, both binaries and the relative orbit. Ephemerides of the eclipsing binaries depend on a minimum of two parameters5: (i) the epoch JD0 of a reference primary eclipse and (ii) the orbital period P. If the orbit is eccentric, additional parameters are (iii) the eccentricity e, (iv) the argument of pericentre ω, and (v) in some cases also the apsidal motion6
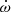 . This represents altogether ten solved-for parameters of the binary orbits. Additionally, we consider six parameters of the relative orbit fitted by the ETV time series of both binaries: (i) the period PAB, (ii) the epoch of pericentre T0, (iii) the amplitudes AA and AB of the ETV series of binary A and B, (iv) the eccentricity eAB, and (v) the argument of pericentre ωAB. Each of these parameter sets is fitted using standard chi-square methods independently. As a result, we obtain full correlation analysis, including parameter uncertainties, for the individual sets of the parameters, but we do not solve correlations across them.
. This represents altogether ten solved-for parameters of the binary orbits. Additionally, we consider six parameters of the relative orbit fitted by the ETV time series of both binaries: (i) the period PAB, (ii) the epoch of pericentre T0, (iii) the amplitudes AA and AB of the ETV series of binary A and B, (iv) the eccentricity eAB, and (v) the argument of pericentre ωAB. Each of these parameter sets is fitted using standard chi-square methods independently. As a result, we obtain full correlation analysis, including parameter uncertainties, for the individual sets of the parameters, but we do not solve correlations across them.
Independently, the light curves of both eclipsing binaries were analysed using the program PHOEBE (Prša et al. 2016). The output provides individual inclination values iA and iB for the orbital planes of the two binaries, relative radii of the components, and their luminosity ratios, among other values. The light curve templates were also used to derive the epochs of the eclipses using the Automatic Fitting Procedure AFP method introduced earlier (see Zasche et al. 2014), and those used to construct the ETV series. This approach also provides an estimate of uncertainty of the ETV values.
As above, our primary source of the photometric data are the catalogues of different phases of the OGLE survey. The most interesting systems were also observed by us using the Danish 1.54 m telescope at La Silla during the 2018 and 2019 seasons. Because the OGLE III data terminated in 2015, our observations often suitably extended the database to solve for typically long PAB periods. Additionally, the MACHO photometry (Faccioli et al. 2007) was also used for particular systems when available, and in some rare cases we also added data from the ASAS-SN database (e.g. Shappee et al. 2014; Kochanek et al. 2017).
4. Landscape of our main results
We analysed 72 systems selected and described in Sect. 2, a subset of all doubly eclipsing sources listed in Table 2. In 28 cases (39% of the analysed sample) we were able to find evidence of the relative motion of the binaries. According to the quality of the solution, the results can be divided into three separate groups:
-
Group 1 comprises the systems where our analysis was positively conclusive (the ETV series for both binaries A and B are well covered with sufficiently high signal-to-noise ratio; the LITE assumption is well justified, which implies a good anticorrelation of the ETVs; and the period PAB is well determined, typically shorter than the data time span);
-
Group 2 comprises the systems where some indication of period variation for both pairs was found, but the results are still not very conclusive (the PAB is too long, the signal-to-noise ratio of the ETVs is low, or there is some other disturbance of a good solution of parameters of the relative orbit);
-
Group 3 comprises the systems where only weak or indirect evidence of mutual motion of binaries A and B was found (the ETVs were reliable for one of the binaries only or some other effects of a more complicated nature that cannot be explained by our simple model were present in the data).
The relative fraction of systems in these groups is as follows: Group 1 contains 46% of the cases, Group 2 contains 36% of the cases, and Group 3 contains 18% of the cases. The overall level of our success rate in proving the doubly eclipsing systems to be true quadruples is further discussed and interpreted in Sect. 8.
What is the main limitation of our method that causes our effort to sometimes fail? Apart from the obvious case of a too long period PAB, a very important role is played by the amplitudes AA and AB of the ETV series. We recall that our procedure requires fitting both series of ETVs for binary A and B: if one of them is not detectable in the photometric noise, for instance due to unbalanced masses in the two binaries, our method fails. Additionally, we note that ETVs are not directly observed quantities, but instead are constructed. For that reason their amplitude should be compared with the orbital period of the eclipsing binary itself. As an example, we assume an ETV amplitude of ≃0.01 d (typical to our systems). For a system with an orbital period of ≃1 d, such an ETV amplitude represents about 1%. This is still acceptable because we are often able to determine the eclipse epoch at this level of precision. However, if the binary period were 10 d or longer, the ETV amplitude would become ≲0.1%, and it would be problematic to resolve them. So there is also a selection bias in our approach towards systems with binaries having periods that are not too long (see Table 4 below).
Once successful, though, the analysis of the two ETV series brings an interesting result. Assuming that LITE dominates ETVs (see further discussion in Sect. 5) the factor expressing their anticorrelation directly provides the ratio of masses mA and mB of the two binaries. In particular, the ratio of their amplitudes is directly related to the mass ratio qAB:
We note that this relation holds independently of iAB, provided that its value is not too low to still assure dominance of LITE in ETVs. The possibility to derive this mass ratio from photometry only, without spectroscopic observations, is unique. As mentioned above, many of our systems are faint (distant or even located in other galaxies), and obtaining good-quality spectroscopy would require time on medium- to large-scale telescopes.
Remaining ambitious, we note that under favourable circumstances we could do even more. Analysis of the phase-folded light curves of the two binaries may serve to derive their photometric mass ratios. This may be problematic for well-detached systems, but for those with significant out-of-eclipse variations and obvious ellipsoidal variations this method can provide us with a good estimate of the inner mass ratios qA and qB. Having now both the outer and inner mass ratios of the component in the quadruple system, the only missing piece of information for deriving all individual masses is the total mass of the system.
Unfortunately, this last step is tricky. The fit of ETVs of the binaries itself helps to calculate the mass function: for instance, for binary A we obtain 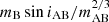 , and similarly for system B. This allows us to determine the minimum masses in the two systems unless some additional information is known about iAB. On the other hand, the maximum masses can be inferred from the general astrophysical knowledge for stars of a given luminosity. If the gap between the minimum and maximum values is narrow, the information may be interesting. In general, however, we need additional information about the nature of the stars (e.g. from spectroscopy), of the orbit, and thus of iAB (e.g. from interferometry).
, and similarly for system B. This allows us to determine the minimum masses in the two systems unless some additional information is known about iAB. On the other hand, the maximum masses can be inferred from the general astrophysical knowledge for stars of a given luminosity. If the gap between the minimum and maximum values is narrow, the information may be interesting. In general, however, we need additional information about the nature of the stars (e.g. from spectroscopy), of the orbit, and thus of iAB (e.g. from interferometry).
5. Individual systems
Because of the heterogeneous sample of systems found as quadruples, we will focus in more detail only on those with conclusive solutions (stars from Group 1). The remaining systems will be briefly mentioned later. The quadruples from Group 1 have the final solutions of their light curves and LITEs given in Tables 3 and 4. Some of the remaining systems are listed in Table 5, where we provide comments on their LITE fits.
Parameters derived from the light curve fits of the two inner binaries.
Some other analysed systems.
In passing we also justify our assumption about LITE dominance in the ETV signal for systems in Group 1. A competing effect, with the same orbital period PAB of binaries A and B about their common centre of mass, is named physical delay (PD) by Rappaport et al. (2013). PD originates from a direct mutual perturbation between systems A and B, namely system B changing the instantaneous mean motion of components in A and vice versa. This change depends on the instantaneous distance of the two systems, and thus it is modulated during the outer orbital cycle provided the relative orbit of A and B is eccentric. Because of their different physical natures, LITE and PD have different dependences on the parameters of the quadruple system, and this allows us to distinguish between them. In brief, assuming that the values of eccentricity and inclination for the outer orbit are not extreme and that all masses of the stars are comparable, LITE typically dominates for wide systems with high enough values of PAB, therefore low values of PA/PAB and PB/PAB. This is true because the LITE amplitude scales as
where m⋆ is the mass of the companion binary, mAB is the total mass of all stars, iAB is the inclination of the outer orbit, and c is the light velocity, while the PD amplitude scales as
where P is the orbital period of the system whose ETVs are computed – A or B – and eAB is the eccentricity of the outer orbit, the estimate being valid to the linear order in eAB and for near-coplanar systems, otherwise see Sect. 4.1.2 in Rappaport et al. (2013).
Assuming coplanar configuration iAB ≃ 90°, we can use the above given formulas to estimate the ratio ALITE/APD for our best systems listed in Tables 3 and 4. The result is shown in Fig. 1. For most cases PAB is long enough compared to PA or PB, and the ratio ALITE/APD is safely higher then unity. However, there are a few exceptions: the system OGLE LMC-ECL-04623 due to its orbital period PB ≃ 10.6 d of the system B, the longest in our sample, while the outer orbit has a sufficiently short orbital period (PAB ≃ 4.55 yr) and high eccentricity (eAB ≃ 0.5). Some other systems have a ratio of about 8, while for the rest the LITE contribution significantly dominates the ETV. All systems having ALITE/APD ≲ 10 for one or both components are flagged with a star in Table 4. We note that the Kepler systems analysed by Rappaport et al. (2013) often have PD dominating LITE mainly because of their small PAB values (on average about five times smaller than ours). Our dataset and methods do not allow us to detect such small values of outer periods.
 |
Fig. 1. Ratio ALITE/APD of estimated amplitudes for the light-time and physical delay contributions to ETVs for the best-characterized systems in Tables 3 and 4: blue symbols for binary A, red symbols for binary B (those ones having the ratio below 10 are denoted with their names). For sake of simplicity we assumed iAB ≃ 90°, while the other parameters were taken from Table 4. The horizontal uncertainty reflects directly uncertainty of PAB, the vertical uncertainty is a statistical composition of other parameters’ uncertainties. |
5.1. OGLE BLG-ECL-145467
By far the most interesting target from our sample is OGLE BLG-ECL-145467 thanks to a conjunction of several reasons: (i) it is rather bright (12.65 mag in I filter out of eclipses), (ii) the two binaries have conveniently short orbital periods of (PA ≃ 3.30 d and PB ≃ 4.91 d) and a relatively short period of their mutual motion (PAB ≃ 1538 d), and (iii) there is a well-detached configuration for both binaries with slightly eccentric orbits. Additionally, the inferred inner orbital periods imply that this system may be representative of an interesting category of systems captured in the 3:2 mean motion resonance (see Sect. 7). The spectral types are probably B9 for pair A, while about B9−A0 for pair B. Assuming iAB ≃ 90° and a total mass of ≃10 M⊙, we estimate the amplitude of the physical delay should amount to about 12% of light time effect. So, at the zero approximation the latter dominates, but a fine analysis would profit from a combination of the two effects in an interpretation of ETVs. All these factors make this object an ideal target of future detailed study. More photometric data will help to refine the analysis of ETVs, but it is mainly spectroscopy that is needed to help determine the mass of all the individual components in this system. With that information available, we could also further constrain the overall architecture of the system, such as the mutual inclination of all participating orbits. This is a prerequisite for a more detailed dynamical study. For instance, the low eccentricity of binary B (≃0.07) would, in a standard view, be understood as a formation relic, not yet damped by tidal circularization. However, as we argue in Sect. 7, it might also have been excited recently by capture in the 3:2 resonant state.
Figure 2 summarizes our modelling of both phase-folded LCs of the inner binaries (left) and the ETVs revealing their mutual motion about a common centre of mass (right). For clarity, we subtracted a slow apsidal motion in the right panels; pair A shows a more prominent motion with a period of about 125 yr. The principal fitted parameters, together with their uncertainties, are listed in Tables 3 and 4. We note that our own observations include data over seven nights during the 2018 and 2019 seasons resulting in seven new eclipse epochs, and suitably complement data from the OGLE surveys. These data match very closely the ETV trend and obviously help to better constrain the parameters of the mutual orbit. Under the assumption that all components are located on the main sequence, the results of our modelling imply that the composite mass of binary A is at least 5 M⊙, while that of binary B is about 4 M⊙. Fractional contributions to the luminosity are 55% for pair A and 45% for pair B. Given its apparent magnitude, the system should be at least 2 kpc from the Sun. With this solution we can roughly estimate an angular separation of ≃2.2 mas of the two binaries for a prospective interferometric detection.
 |
Fig. 2. Results of fitting observations of the system OGLE BLG-ECL-145467. Left: phase-folded light curves of both inner binaries. Right: period variation (ETVs) as the two binaries move on their respective orbits; the primary eclipses are denoted as full dots, secondary eclipses as open circles. Shown are our new measurements using the Danish 1.54 m telescope (red symbols; the size represents their relative precision). The typical uncertainty is plotted as an error bar in the right panels. The red curves are our model. |
5.2. OGLE BLG-ECL-018877
Another system on our list, OGLE BLG-ECL-018877, is fainter and has a maximum brightness of about 17.7 mag in I filter. The inferred surface temperatures (Table 3) make us think that all components are G-type stars. According to our modelling (Fig. 3 and Tables 3 and 4), the system comprises two compact binaries, one of which is detached and the other a contact binary. Their orbits have undetectable eccentricities with our data. What we call pair A (shorter period of ≃0.6 d) seems to be less massive than pair B (longer period of ≃1.56 d), and their luminosity ratio is about 30%:70%. The eccentricity of the mutual orbit, only about 0.14, is the lowest in our sample, and its period, only about 1400 d, also belongs to the shortest. Both are somewhat uncertain because of the source faintness, and because the smaller amplitude of the ETVs results in a lower signal-to-noise ratio. New accurate observations will help to constrain these values better.
5.3. OGLE BLG-ECL-061232
Similar to OGLE BLG-ECL-018877 is the system OGLE BLG-ECL-061232: it is made up of a contact binary A, having a short orbital period of ≃0.38 d, and a detached binary B with longer period of ≃1.47 d, and again the inner eccentricities are not detectable. Additionally, the mutual motion, unambiguously revealed by the ETVs (see Fig. 4), has the shortest period in our sample of ≃1250 d, though the eccentricity is slightly higher. We note that because of very short periods PA and PB, this and the previous systems should have their observed ETVs safely dominated by the light time effect (see also Fig. 1). Assuming normal main sequence components, both binaries consist of F-G spectral type stars, while binary A slightly dominates; the luminosity ratio is approximately 65%:35%.
5.4. OGLE BLG-ECL-088871
Another system with a pair of well-detached binaries is OGLE BLG-ECL-088871, an alter-ego of OGLE BLG-ECL-145467. It is bright enough to have a good prospect in follow-up observations, including spectroscopy. It consists of wide systems with PA ≃ 3.88 d and PB ≃ 5.65 d, apparently very close to the 3:2 resonance. Binary B, with longer period, has a low eccentricity eB ≃ 0.03, but no apsidal motion has been detected in our data. This is likely because the mutual orbit has a longer period of ≃4116 d, implying the period of the apsidal motion for system B is long and the stars distant enough from each other such that tidal interaction is weak. The large value of PAB also implies that the physical delay contributes ETVs almost negligibly (see Fig. 1). The light curve analysis in Fig. 5 reveals that the eclipses of binary A are about five times deeper than those of binary B, likely an expression of a slight non-coplanarity. Stars in binary B contribute only about 35% of the total luminosity of the system. All the components seem to be A-type stars.
5.5. OGLE BLG-ECL-103591
The analysis of yet another well-detached system OGLE BLG-ECL-103591 is shown in Fig. 6. With orbital periods of the inner binaries of ≃2.23 d and ≃2.28 d, it is representative of the PA ≃ PB configurations, though unlikely to be located in the corresponding resonance (see discussion in Sect. 7). All the components are probably F type, while the individual relative luminosities of binaries A and B contribute 60% and 40% of the total luminosity of the system, in agreement with their ETV amplitudes AA and AB.
5.6. OGLE LMC-ECL-02903
Our next example, system OGLE LMC-ECL-02903, is located in the Large Magellanic Cloud. While consisting of two detached binaries, like several others mentioned earlier, this system is an exception because of the high eccentricity of binary B: eB ≃ 0.26 (see Fig. 7). Because the system is not overly compact, the period of mutual revolution of the A and B binaries is ≃1808 d, the apsidal motion of binary B has quite a long period of ≃500 yr and is barely detectable in our dataset. Binary B seems to be slightly more massive than binary A; the corresponding fraction of the whole luminosity is 47% and 53%, respectively. The spectral classification of all components in this quadruple seems to be of B type.
5.7. OGLE LMC-ECL-04236
The second system located in the LMC fields is called OGLE LMC-ECL-04236. It is composed of two pairs of binaries with their respective orbital periods of 2.41 d and 2.46 d. However, both binaries are rather different from each other. Pair A dominates the system (it produces about 80% of the total luminosity) and probably consists of two B3 stars. The second pair’s components are of a significantly later spectral type (about B8−B9). Their mutual orbit has a period of about 2016 d, but new observations are still needed to better constrain its orbital parameters because the ETV amplitude is rather small, ≲0.01 d, and thanks to the faintness of the system the signal-to-noise ratio is rather poor (see Fig. 8).
5.8. OGLE LMC-ECL-21569
OGLE LMC-ECL-21569 is another very interesting system in our portfolio. Photometric analysis reveals short orbital periods for binaries A and B: PA ≃ 1.98 d and PB ≃ 2.93 d. These values are again suspiciously close to the 3:2 ratio, perhaps evidence of residence in the corresponding mean motion resonance. Binary B is notable for its low eccentricity (eB ≃ 0.08), and its rather short period of apsidal motion, only ≃100 yr. Interestingly, the amplitude of the ETVs is the largest in our sample, and its mutual orbital period PAB is the longest, nearly ≃5046 d (luckily, we secured observations of this interesting target in the 2018−2019 season and this helped to constrain better this long PAB period; Fig. 9). This implies that the light time effect dominates the physical delay (see also Fig. 1) and the masses of the two binaries should thus be the same.
OGLE LMC-ECL-21569 is unique among our Group 1 systems because some spectral observations were published (Sana et al. 2013; Almeida et al. 2017) and the star is classified as an O8V object. Unfortunately, only the lines of the most dominant component of pair A were detected with no signature of the four components, hence we are still dealing with a single-lined SB1 spectroscopic binary. From the amplitudes of the LITEs of both pairs we would expect to also have similar luminosity contributions from both pairs, but this is not true here. For the analysis we used an assumption of standard mass-luminosity-bolometric magnitude relations for stars on the main sequence (see tables in e.g. Pecaut & Mamajek 2013 with recent updates online7, and a method of estimating the photometric mass ratio by Graczyk 2003). From the radial velocities we obtain a = 20.3 R⊙ and qA = 0.26 for pair A, hence the secondary of A is about B2−3. For pair B the situation is as follows: qB = 0.73 and both B components are of about B0−1 spectral type. From this it follows that the luminosity fraction of the A and B pairs is about 75%:25%. In addition, both components of pair B are less luminous than the primary of A, which should be the reason why only the lines of the O8V star were detected in the spectra. This result of our fitting is plotted in Fig. 9 and is also given in Tables 3 and 4.
5.9. Other systems from Group 1
Here we only briefly mention the remaining systems in Group 1, which all have adequately good coverage of their light curves and also ETVs detectable for both binaries A and B, yet their analysis should be still considered as preliminary (see Fig. 10). Often the problem has to do with less than optimum coverage of the relative orbit by ETVs, their low signal-to-noise ratio, and so on. We consider the case of OGLE BLG-ECL-190427, which has the smallest amplitude of ETVs among our studied quadruples (the amplitude of ≃0.003 d is just 0.1% of the orbital period of binary B). Binary A in the system OGLE LMC-ECL-17182 exhibits a fast apsidal motion, an estimated period of only ≃70 yr. Similarly, binary B in the system OGLE GD-ECL-07157 shows an apsidal motion with a slightly longer period of ≃130 yr. Both of these periods are rather uncertain due to fairly incomplete coverage by data. Their uncertain fit may affect our derived ETV series. Interestingly, both systems also have the highest eccentricity eAB of the relative orbit.
 |
Fig. 10. Results of fitting of four other systems from Group 1 (using the same scheme as in Fig. 2): (A) OGLE BLG-ECL-190427 (top left), (B) OGLE GD-ECL-07157 (top right), (C) OGLE LMC-ECL-04623 (bottom left), and (D) OGLE LMC-ECL-17182 (bottom right). |
5.10. 1SWASP J093010.78+533859.5
Let us finally point out another doubly eclipsing system that does not belong to Group 1 with well-derived orbit, but still adequately interesting. We paid attention to system 1SWASP J093010.78+533859.5 for several reasons: (i) it is one of only a few systems on the northern sky (see Sect. 6); (ii) it is quite bright, and can be observed by even small-scale telescopes; and (iii) it has already been the target of several publications (see Lohr et al. 2013, 2015; Koo et al. 2014; Haroon et al. 2018). In spite of this effort, none of the previous studies revealed evidence of the relative motion of the two binaries having rather short orbital periods PA ≃ 1.31 d and PB ≃ 0.23 d.
We applied the same approach as above to the observations of the 1SWASP J093010.78+533859.5 system; in particular, we constructed and analysed the ETV series for the two binaries. The result, shown in Fig. 11, indeed suggests a regular signal of the LITE due to relative motion. However, due to a long period PAB, likely longer than 15 yr, the coverage of the full cycle of mutual motion is still incomplete. As a result, all the parameters, such as eAB ≃ 0.2, AA ≃ 0.006 d, or AB ≃ 0.004 d, are still quite uncertain. Long-term follow-up photometric observations during the next decade are thus strongly encouraged.
 |
Fig. 11. System 1SWASP J093010.78+533859.5 showing the ETV series of the eclipsing binaries: A (top) and B (bottom). |
Previous studies of this system by Koo et al. (2014) and Lohr et al. (2015) allowed us to determine a distance to 1SWASP J093010.78+533859.5 of 66−78 pc. This is an interestingly small value. Assuming our solution of PAB is correct, we can estimate the maximum predicted angular separation of the two binaries on the sky. We obtained a range ≃(90−110) mas. This value is comfortably within the detection limit of modern optical interferometers, and given its rather high brightness (about 10 mag in V filter), it should be a viable task to resolve the double and derive the relative orbit of the two binaries using interferometry. This data will provide independent constraints on the physical parameters of all participating stars in this interesting quadruple, and will allow us to derive the mutual inclination of the orbits.
5.11. Other systems from Group 2 and Group 3
Finally, we make a few comments on several Group 2 and Group 3 systems, namely those for which the dataset is insufficient for reliable confirmation of LITE variation in their ETVs. Often there are too few observations to construct meaningful series of ETVs, the noise is too high or the amplitude is too small, the period PAB of relative orbit is too long, or some other issue. Still, some ETVs were detected and many of the systems warrant further observations. Specific comments on these systems are given in Table 5.
A peculiar behaviour has been observed in the system OGLE LMC-ECL-22891, for which the ETVs of both binary A and B are in phase and behave similarly. This contradicts our simple model based on LITE and their motion about a common centre of mass. Unless there is a more complicated explanation, there is always the possibility of a fifth star in the system accompanying as a distant component of the quadruple consisting of the two eclipsing binaries. Certainly more observations are needed to clarify the situation.
6. Population-scale statistics
The current sky-distribution of identified doubly eclipsing systems is very uneven (see Fig. 12), implying that we have information about a small sample of a potentially much vaster population. The majority of known systems comes from the analysis of data collected by the OGLE surveys targeting the Magellanic clouds (note the prominent peak at ≃−70° declination in Fig. 12) and the Galactic bulge (note the broader peak between ≃−20° and ≃−40° declination in Fig. 12). Long-lasting and sufficiently homogeneous OGLE data are very fortuitous, thus provided a great opportunity to search for doubly eclipsing systems. Only 14 out of a total of 146 of the systems (less than 10%) are located on the northern sky with the largest contribution from the Kepler fields (see Table 2). Only a handful of the known systems come from coincidental discoveries. The sky-distribution skewness has a second aspect related to the already identified systems. Once discovered by photometric observations, many of the systems would require a better characterization by means of spectroscopic or interferometric observations. Oversubscription of the limited number of telescopes in the southern hemisphere works against this possibility, leaving these interesting systems poorly understood so far.
 |
Fig. 12. Distribution of currently identified doubly eclipsing systems on the sky expressed as a function of their declination. Analysis of data provided by OGLE surveys resulted in more than 90% of the cases, making them located on the southern sky. |
Perhaps our most interesting population-scale result is shown in Fig. 13, where we plot the distribution of the orbital period ratio PA/PB for binaries constituting the 2+2 quadruple systems: (i) for doubly eclipsing systems only (bottom panel), and (ii) for all systems (upper panel), where the data of doubly eclipsing systems were also incremented by information of non-eclipsing systems from the MSC catalogue (Tokovinin 2018a). In the case of eclipsing systems, we use also data for those systems where the relative motion has not been proven yet. By definition, we consider PA/PB ≥ 1, otherwise we re-index the binaries. Some systems have PA/PB > 4, limiting the value shown in Fig. 13, but these data become increasingly sparse. We believe they basically express a growing bias against the identification of these systems, and thus we disregard this data from our analysis.
 |
Fig. 13. Distribution of period ratio PA/PB for binaries in quadruple systems (the limiting maximum value of 4 was chosen because information beyond this threshold is very sparse and certainly heavily biased). Top panel: all quadruples in the 2+2 architecture. Blue histograms for previously known doubly eclipsing systems, orange histograms for our new discoveries (see Table 2). The data include the cases where the relative motion of the binaries A and B was proven, and those where we lack this information. Green histograms are other quadruple systems in the 2+2 architecture from the MSC catalogue (Tokovinin 2018a). Bottom panel: same as above, but only for the doubly eclipsing systems (sum of blue and orange above). Declining curves at the bottom panel are predictions in a simple model where periods PA and PB are entirely independent variables and have identical probability density distribution: uniform (black) or linearly increasing towards longer orbital periods (red; see discussion in Sect. 7). Both are able to explain the preferential PA ≃ PB configuration. While still noisy, there are two major deviations from their prediction: (i) dearth of systems with period ratio between ≃1.2 and ≃1.5, and (ii) excess of systems with PA/PB ≃ 3/2. On the contrary, the dip at PA/PB ≃ 2 may still reflect data fluctuations. |
Although it is affected by the still small amount of data, we feel the distribution of PA/PB reveals several interesting features. Before performing a more involved analysis, and disregarding bin-to-bin statistical fluctuations, there are two possible major features: (i) excess of systems with PA/PB ≃ 1, and (ii) excess of systems with PA/PB ≃ 1.5. There is a hint of a similar feature at PA/PB ≃ 2.5, and a dip in the distribution at PA/PB ≃ 2, but they are not statistically robust enough, which leaves us with the two major features. We believe the interpretation is actually different and we discuss it briefly in Sect. 7.
Keeping in mind the underlying dynamical processes, it is interesting to first compare the period ratio in the 2+2 quadruples (Fig. 13) with the orbital period ratio of neighbouring planets. For instance, Quinn et al. (2019) in their Fig. 10 show this information for Kepler candidates in multiplanet systems (see also Fabrycky et al. 2014; Pichierri et al. 2019). There are interesting similarities and dissimilarities. Starting with the latter, we note that only a few exoplanet configurations are found with a period ratio below ≃1.2. This is understood, since the formation of co-orbiting exoplanets is possible (e.g. Cresswell & Nelson 2006; Lyra et al. 2009; Giuppone et al. 2012), but it is rather rare. Mutual perturbations tend to destabilize such configurations (e.g. Cresswell & Nelson 2009; Rodriguez et al. 2013). On the contrary, the formation of 2+2 binaries with near-to-equal orbital periods is easily possible and, as we argue below, perhaps even preferential. So the major difference in the period-ratio distributions for exoplanets and binaries in the 2+2 stellar quadruples readily follows from the orbital architecture.
Focusing now on period ratio values ≳1.3, we note that the distributions for exoplanets and binaries in quadruples are strikingly similar. Both show a slight decline towards a higher value of PA/PB, punctuated with an excess at resonant value PA/PB ≃ 1.5. The exoplanet data, which are numerous enough, also indicate a dip at PA/PB ≃ 2 (followed by an excess at values just wide of this value). There is a hint of such a dip in the binary data in Fig. 13, but the statistics is still rather poor. More data are needed to explore this feature. The excess of planetary orbits at (or near) the 3:2 resonant orbital periods is clearly understood by convergent migration followed by resonant capture (e.g. Lithwick & Wu 2012; Batygin & Morbidelli 2013a; Pichierri et al. 2019). In the next section, we argue that the same also applies to the stellar binary systems in quadruples.
7. Resonant 2+2 configurations?
As mentioned above, the statistical distribution of the period ratio PA/PB for our sample of binaries in the 2+2 quadruples suggests an overabundance of systems with (i) PA/PB ≃ 1 and (ii) PA/PB ≃ 3/2, apparently the lowest-order mean motion resonances 1 : 1 and 3:2 between the A and B systems. Interestingly, a careful analysis of these dynamical configurations has not been carried out yet. This is primarily because the available observational evidence is poor and has not motivated their study (as also mentioned by Breiter & Vokrouhlický 2018, these interesting resonances in 2+2 quadruples do not have equivalent configurations in the planetary systems and therefore have been overlooked in the mainstream orbital mechanics). Only recently have Breiter & Vokrouhlický (2018) given a closer look to the case of PA/PB ≃ 1 resonant configurations, planning to extend their efforts to the first-order resonances, such as PA/PB ≃ 2/1 or PA/PB ≃ 3/2, in their forthcoming work. While still limited, the results from their work helped us to draw some preliminary conclusions. The point is that the occurrence of systems in these resonances is only interesting if investigated together with the question of how they become resonant in the first place. These resonances are very weak and occupy a tiny portion of a vast space of parameters that characterize quadruple systems (e.g. stellar masses, orbital parameters of their relative orbits). So the most straightforward explanation of their origin is capture, a process which itself imposes constraints on orbital evolution of the participating binaries (of tidal or mass-exchange origin).
With regard to the PA/PB ≃ 1 configuration, Breiter & Vokrouhlický (2018) described in detail the structure of the resonance for planar configuration. They found a parametric dependence of the resonance width and studied the possibility of capture. Interestingly, Breiter & Vokrouhlický (2018) determined that capture is very unlikely (at least for the planar systems). Without the option of capture, the number of systems piling up near the first two bins in the distribution shown in Fig. 13 requires a different explanation. A straightforward possibility is as follows. We assume a simple model in which the periods of binaries A and B are entirely uncorrelated quantities. Those which contributed to the construction of data shown in the bottom panel of Fig. 13 have a value in a limited interval, for example 0.5 d to 15 d. We assume that both PA and PB have the same probability distribution in this interval. For a uniform distribution, we can easily show that the ratio PA/PB should have a probability distribution function ∝(PA/PB)−2. Likewise, if the probability distribution of PA and PB linearly increases towards higher values, the ratio PA/PB should have a probability distribution function ∝(PA/PB)−3 (and more complex variants could be easily tested). Each of these predictions (see the declining curves in the bottom panel of Fig. 13) have a maximum for the equal period situation (i.e. PA/PB = 1). This is logical, because there are many more possibilities within the considered interval of value of PA and PB of this configuration when compared to non-equal values. Nevertheless, we note that neither of these possibilities matches the observed distribution of PA/PB exactly. Applying the Kolmogorov–Smirnov test to its cumulative variants, we obtain that there is only a ≃10−5 (resp. ≃10−4) probability of a statistical match between the data and these simple models (preferring slightly the case with linearly increasing probability of systems with longer periods, as might be visually guessed from Fig. 13). One of the problems with the predictions is their inability to describe a dearth of systems with PA/PB in the interval ≃1.2 to ≃1.5, prior the significant excess of the PA/PB ≃ 1.5 configurations. One possibility to fix this problem would be to assume a small number of truly 1 : 1 dynamically resonant configurations (perhaps helped by non-coplanar configurations, for which the resonance was not studied yet). More likely, though, the problem is that the ratio PA/PB is not static (as implicitly assumed in the previously mentioned, naive model), but time-dependent due to the tidal interaction between stars in the binaries. We assume, for instance, that the 2+2 systems preferentially form near the equal-period configuration. If so, their tidal evolution may be similar and therefore they would remain in the state near the PA/PB ≃ 1 ratio for a long time. This would help to increase the excess of this configuration. Modelling the statistical distribution of PA/PB in such a dynamical model is beyond the scope of this paper. Nevertheless, its value in describing the population parameters of quadruple systems should be a motivation to increase number of known systems with the goal of a less noisy description of the PA/PB distribution.
None of the above-mentioned simple models also allows us to explain the excess of PA/PB ≃ 3/2 configurations. Here the situation is quite different and we believe the principally false assumption was the independence of PA and PB. This is broken if the corresponding 3:2 resonant situation exists. Breiter & Vokrouhlický (in prep.) studied the first-order mean-motion resonance in 2+2 quadruples, again restricting the analysis to the planar configurations. First, in this case, the resonance strength and width are even smaller than in the PA/PB ≃ 1 resonance. This is primarily because it requires non-zero orbital eccentricity eA of the system with longer period PA (for the 3:2 case), and the resonance strength/width is multiplied by this factor. As an example, the ratio PA/PB must be within a factor of about ≲10−5 near a specific resonant value. This reference state is not universal, but depends on tidal interaction of stars in system A (nevertheless, the scatter of the reference values is definitely smaller than the width of the bins shown in Fig. 13). Second, the 3:2 resonance allows capture since it is adequately described by the second fundamental model of a resonance introduced by Henrard & Lemaître (1983). This model has been extensively studied in context of planetary dynamics, including details of capture conditions (e.g. Henrard & Lemaître 1983; Engels & Henrard 1994). For instance, if the pre-capture eccentricity of the A system is very low (eA ≃ 0), the capture occurs with a 100% probability and necessarily leads to an increase in eA. The capture may be driven by different effects. Perhaps the most obvious channel relates to decrease in PA and PB by tidal phenomena. Intriguingly, the theory then requires that PA decreases faster than PB, thus PA/PB approaches ≃1.5 from an initially higher value. There are other possible channels of capture, driven for instance by mass exchange or variations in non-coplanarity of the system, but they have not been studied yet. Finally, the capture in the 3:2 is only temporary and its duration depends on various factors, such as tidal interaction of stars in the A and B systems. Generally, as the eccentricity eA increases, the libration amplitude of the critical angle increases as well. Approaching its maximum value of 180°, the non-resonant dynamical degrees of freedom lead to a break in the resonant lock and the system keeps evolving away from the resonance. We note that there are close analogues (but not exact in details) of behaviour of the first-order resonances in 2+2 quadruples to several problems in planetary astronomy: (i) capture of dust particles evolving due to the Poynting-Robertston drag in the exterior resonances with planets (e.g. Weidenschilling & Jackson 1993), (ii) capture of planetesimals evolving due to the gas drag in the exterior resonances with planetary embryos (e.g. Weidenschilling & Davis 1985), or (iii) tidally or gas-drag driven dynamics of exoplanets converging towards their mutual resonances (e.g. Lithwick & Wu 2012; Batygin & Morbidelli 2013b,a; Pichierri et al. 2019).
Finally, we make a brief comment about the suggested residence of the systems in the resonant state (especially for the 3:2 case): Could we prove that those which contribute to the peak in the PA/PB near 1.5 value are truly in resonance? Unfortunately, the answer is no. From the orbital point of view the resonant state is characterized by the libration of the critical angle about the value specified by the stationary point characteristic to the resonance. For instance, in the case of the 3:2 resonance the angle 3λA − 2λB − ϖA must librate about the value 180° with a small-enough amplitude (here λA and λB denote longitude in orbit of systems A and B, and ϖA is the longitude of pericentre of system A). Similarly, in the case of 1 : 1 resonance, the critical angle λA − λB must librate either about 90° or 270° (e.g. Breiter & Vokrouhlický 2018). In order to check these properties, we would need to know accurately enough (i) the whole orbital architecture of the quadruple system, and (ii) the other physical parameters that define tidal interaction of the stars in the A and B systems. This is not available at the level needed for any of the systems so far. At this moment we can only suggest that the systems are either in, or very close to, the resonant state from the known PA/PB ratio. Interestingly, several of the best characterized systems suggested to be in the 3:2 resonance, for which the relative motion of binaries A and B was proven (e.g. OGLE BLG-ECL-145467, OGLE BLG-ECL-088871, and OGLE LMC-ECL-21569; see Table 4), exhibit consistent non-zero eccentricity values of the longer-period binary as required. Further, constraints on the orbital and physical parameters will help in understanding the dynamical state more accurately.
In conclusion, we note that a detailed census and analysis of resonant 2+2 configurations, in the first place the 3:2 case, has a very interesting potential to put constraints on the orbital evolution of these systems. To achieve this goal, however, the systems must be very carefully characterized.
8. Conclusions
We have demonstrated that uniform photometric datasets of long-lasting surveys, such as OGLE in our case, are very suitable for the analysis of ETV signals in doubly eclipsing quadruple systems. We succeeded in proving that 28 of 72 analysed systems indeed provide evidence of mutual motion of the two binaries about their common centre of mass, thus constituting gravitationally bound quadruples. This is the first time that such a large fraction of new quadruples has been detected. In most of our cases, we also can interpret the observed ETVs as light-time effect, rather than physical delay, and this sets a direct estimate of a mass ratio of binaries A and B. Such a situation is rather unusual in stellar physics, given that only photometric series are available.
Furthermore, we may try to draw additional conclusions from the analysis of this limited dataset in which slightly less than ≃40% of systems were positively proven to be gravitationally bound in this discovery. What about the remaining ≃60%? To that end we recall that we analysed a category of eclipsing binaries with periods of a few days, and the inferred outer periods were between ≃3 yr and ≃14 yr (see Table 4). The architecture of known triple and quadruple systems, however, easily accommodates outer periods that are shorter and especially longer than our restricted interval. Consulting the statistical distribution of long periods in triples and quadruples by Tokovinin (2008); Tokovinin (2018b), for instance, we estimate that the range of our PAB may represent ≃(10−20)% of typical quadruples. This allows us to believe that 44 of the systems we analysed and did not conclusively determine PAB may well have those values larger, or smaller, than detectable by our method. This is because our ≃40% success rate is actually quite high. It is therefore conceivable that basically all detected doubly eclipsing systems, namely the 146 cases listed in Table 2, are truly members in gravitationally bound quadruples. With that conclusion we can also justify that in Sect. 6 we might have used all these systems for analysis of the period ratio PA/PB.
The sky location of presently known doubly eclipsing systems in skewed to the southern declinations for reasons explained in Sect. 6 (see Fig. 12). Interestingly, though, the VSX database (Watson et al. 2006) contains information about eclipsing binaries whose number on northern sky (≃60 000) basically equals that on the southern sky (≃80 000). Obviously, the northern systems were compiled from much less uniform sources if compared to the southern systems. Nevertheless, we could expect that information about a number of northern doubly eclipsing systems is already partly available, but they have not been recognized and properly analysed yet. Still, a dedicated quest for these systems with innovative means of how to use the existing data could result in further significant increase in the number of known doubly eclipsing systems.
The doubly eclipsing systems, in our concept, should not be confused with the rare situation of triples exhibiting exceptional coplanarity, where both the inner binary system is eclipsing and the third star also shows mutual eclipses with components in the binary (e.g. Borkovits et al. 2019, and references therein).
There are even more detected eclipsing binaries (40204) in the OGLE IV data (Pawlak et al. 2016), but we use them only in conjunction with the OGLE III observations because our primary strategy relied on the long time span of the data.
Conceptually, the apsidal motion is revealed as a part of ETVs of the respective binary (e.g. Borkovits et al. 2015). For reasons of tradition, we treat this part independently from other ETVs and together with determination of the orbital parameters of the binaries.
Acknowledgments
We would like to thank Andrei Tokovinin for sending us the MSC data for 2+2 systems, and for his valuable comments about the topic. The research was supported by the grant MSMT INGO II LG 15010. We would also like to thank the Pierre Auger Collaboration for the use of its facilities. The operation of the robotic telescope FRAM is supported by the grant of the Ministry of Education of the Czech Republic LM2015038. The data calibration and analysis related to the FRAM telescope is supported by the Ministry of Education of the Czech Republic MSMT-CR LTT18004 and MSMT/EU funds CZ.02.1.01/0.0/0.0/16_013/0001402. We also thank the OGLE team for making all of the observations easily available. We are also grateful to the ESO team at the La Silla Observatory for their help in maintaining and operating the Danish telescope. This paper makes use of data from the DR1 of the WASP data (Butters et al. 2010) provided by the WASP consortium, and the computing and storage facilities at the CERIT Scientific Cloud, reg. no. CZ.1.05/3.2.00/08.0144, which is operated by Masaryk University, Czech Republic. This paper utilizes public domain data obtained by the MACHO Project, jointly funded by the US Department of Energy through the University of California, Lawrence Livermore National Laboratory under contract No. W-7405-Eng-48, by the National Science Foundation through the Center for Particle Astrophysics of the University of California under cooperative agreement AST−8809616, and by the Mount Stromlo and Siding Spring Observatory, part of the Australian National University. The CSS survey is funded by the National Aeronautics and Space Administration under Grant No. NNG05GF22G issued through the Science Mission Directorate Near-Earth Objects Observations Program. The CRTS survey is supported by the US National Science Foundation under grants AST−0909182 and AST−1313422. This research has made use of the SIMBAD and VIZIER databases, operated at CDS, Strasbourg, France, and the NASA Astrophysics Data System Bibliographic Services.
References
- Almeida, L. A., Sana, H., Taylor, W., et al. 2017, A&A, 598, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bataille, M., Libert, A.-S., & Correia, A. C. M. 2018, MNRAS, 479, 4749 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2013a, AJ, 145, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2013b, A&A, 556, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Érdi, B., Forgács-Dajka, E., & Kovács, T. 2003, A&A, 398, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Csizmadia, S., Forgács-Dajka, E., & Hegedus, T. 2011, A&A, 528, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Rappaport, S., Hajdu, T., et al. 2015, MNRAS, 448, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Albrecht, S., Rappaport, S., et al. 2018, MNRAS, 478, 5135 [NASA ADS] [Google Scholar]
- Borkovits, T., Rappaport, S., Kaye, T., et al. 2019, MNRAS, 483, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Breiter, S., & Vokrouhlický, D. 2018, MNRAS, 475, 5215 [NASA ADS] [CrossRef] [Google Scholar]
- Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, A&A, 520, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cagaš, P. 2019, Res. Notes Am. Astron. Soc., 3, 80 [NASA ADS] [Google Scholar]
- Cagaš, P., & Pejcha, O. 2012, A&A, 544, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2009, A&A, 493, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2009, ApJ, 696, 870 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Drake, A. J., Graham, M. J., Djorgovski, S. G., et al. 2014, ApJS, 213, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Engels, J. R., & Henrard, J. 1994, Cel. Mech., 58, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Erikson, A., Santerne, A., Renner, S., et al. 2012, A&A, 539, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Faccioli, L., Alcock, C., Cook, K., et al. 2007, AJ, 134, 1963 [NASA ADS] [CrossRef] [Google Scholar]
- Fedurco, M., & Parimucha, Š. 2018, Ap&SS, 363, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández Fernández, J., & Chou, D.-Y. 2015, PASP, 127, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Geyer, E. H., Hoffmann, M., & Karimie, M. T. 1982, A&AS, 48, 85 [NASA ADS] [Google Scholar]
- Giuppone, C. A., Benitez-Llambay, P., & Beaugé, C. 2012, MNRAS, 421, 356 [NASA ADS] [Google Scholar]
- Graczyk, D. 2003, MNRAS, 342, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., & Eyer, L. 2010, Acta Astron., 60, 109 [NASA ADS] [Google Scholar]
- Graczyk, D., Soszyński, I., Poleski, R., et al. 2011, Acta Astron., 61, 103 [Google Scholar]
- Hajdu, T., Borkovits, T., Forgács-Dajka, E., et al. 2017, MNRAS, 471, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Hamers, A. S., & Lai, D. 2017, MNRAS, 470, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Hamers, A. S., & Portegies Zwart, S. F. 2016, MNRAS, 459, 2827 [NASA ADS] [CrossRef] [Google Scholar]
- Haroon, A. A., Essam, A., & Basurah, H. 2018, Astrophysics, 61, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Hełminiak, K. G., Ukita, N., Kambe, E., et al. 2017, A&A, 602, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henrard, J., & Lemaître, A. 1983, Cel. Mech., 30, 197 [Google Scholar]
- Hong, K., Koo, J.-R., Lee, J. W., et al. 2018, PASP, 130, 54204 [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Juryšek, J., Zasche, P., Wolf, M., et al. 2018, A&A, 609, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khruslov, A. V. 2018, Peremennye Zvezdy, 38 [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, J.-R., Lee, J. W., Lee, B.-C., et al. 2014, AJ, 147, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-U., Kim, S.-L., Lee, J. W., et al. 2008, MNRAS, 389, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, H., Zechmeister, M., Dreizler, S., Schuh, S., & Kanzler, R. 2012, A&A, 541, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lithwick, Y., & Wu, Y. 2012, ApJ, 756, 11 [Google Scholar]
- Lohr, M. E., Norton, A. J., Kolb, U. C., et al. 2013, A&A, 549, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lohr, M. E., Norton, A. J., Gillen, E., et al. 2015, A&A, 578, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mardling, R. A., & Aarseth, S. J. 2001, MNRAS, 321, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P. 1990, Astron. Inst. Czechoslov. Bull., 41, 231 [NASA ADS] [Google Scholar]
- Ofir, A. 2008, Inf. Bull. Var. Stars, 5868, 1 [NASA ADS] [Google Scholar]
- Pawlak, M., Graczyk, D., Soszyński, I., et al. 2013, Acta Astron., 63, 323 [NASA ADS] [Google Scholar]
- Pawlak, M., Soszyński, I., Udalski, A., et al. 2016, Acta Astron., 66, 421 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pichierri, G., Batygin, K., & Morbidelli, A. 2019, A&A, 625, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrukowicz, P., Mróz, P., Soszyński, I., et al. 2013, Acta Astron., 63, 115 [NASA ADS] [Google Scholar]
- Prša, A., Conroy, K. E., Horvat, M., et al. 2016, ApJS, 227, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, S. N., Becker, J. C., Rodriguez, J. E., et al. 2019, AAS J., submitted [arXiv:1901.09092] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S., Deck, K., Levine, A., et al. 2013, ApJ, 768, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Lehmann, H., Kalomeni, B., et al. 2016, MNRAS, 462, 1812 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Vanderburg, A., Borkovits, T., et al. 2017, MNRAS, 467, 2160 [NASA ADS] [Google Scholar]
- Rodriguez, A., Giuppone, C. A., & Beaugé, C. 2013, Cel. Mech. Dyn. Astron., 117, 59 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Söderhjelm, S. 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
- Soszyński, I., Pawlak, M., Pietrukowicz, P., et al. 2016, Acta Astron., 66, 405 [NASA ADS] [Google Scholar]
- Southworth, J. 2012, Orbital Couples: Pas de Deux in the Solar System and the Milky Way, 51 [Google Scholar]
- Tokovinin, A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2018a, ApJS, 235, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2018b, AJ, 155, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Sandberg Lacy, C. H., Fekel, F. C., Wolf, M., & Muterspaugh, M. W. 2017, ApJ, 846, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Udalski, A., Szymanski, M. K., Soszynski, I., & Poleski, R. 2008, Acta Astron., 58, 69 [NASA ADS] [Google Scholar]
- Udalski, A., Szymański, M. K., & Szymański, G. 2015, Acta Astron., 65, 1 [NASA ADS] [Google Scholar]
- Vokrouhlický, D. 2016, MNRAS, 461, 3964 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. L., Henden, A. A., & Price, A. 2006, Soc. Astron. Sci., 25, 47 [Google Scholar]
- Weidenschilling, S. J., & Davis, D. R. 1985, Icarus, 62, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Jackson, A. A. 1993, Icarus, 104, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., & Uhlař, R. 2016, A&A, 588, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., Wolf, M., Vraštil, J., et al. 2014, A&A, 572, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zejda, M., Skýba, O., Krajčovič, M., Gajdoš, P., & Fedurco, M. 2019, Contrib. Astron. Obs. Skal. Pleso, 49, 132 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Ratio ALITE/APD of estimated amplitudes for the light-time and physical delay contributions to ETVs for the best-characterized systems in Tables 3 and 4: blue symbols for binary A, red symbols for binary B (those ones having the ratio below 10 are denoted with their names). For sake of simplicity we assumed iAB ≃ 90°, while the other parameters were taken from Table 4. The horizontal uncertainty reflects directly uncertainty of PAB, the vertical uncertainty is a statistical composition of other parameters’ uncertainties. |
| In the text | |
 |
Fig. 2. Results of fitting observations of the system OGLE BLG-ECL-145467. Left: phase-folded light curves of both inner binaries. Right: period variation (ETVs) as the two binaries move on their respective orbits; the primary eclipses are denoted as full dots, secondary eclipses as open circles. Shown are our new measurements using the Danish 1.54 m telescope (red symbols; the size represents their relative precision). The typical uncertainty is plotted as an error bar in the right panels. The red curves are our model. |
| In the text | |
 |
Fig. 3. As in Fig. 2, but for the system OGLE BLG-ECL-018877. |
| In the text | |
 |
Fig. 4. As in Fig. 2, but for the system OGLE BLG-ECL-061232. |
| In the text | |
 |
Fig. 5. As in Fig. 2, but for the system OGLE BLG-ECL-088871. |
| In the text | |
 |
Fig. 6. As in Fig. 2, but for the system OGLE BLG-ECL-103591. |
| In the text | |
 |
Fig. 7. As in Fig. 2, but for the system OGLE LMC-ECL-02903. |
| In the text | |
 |
Fig. 8. As in Fig. 2, but for the system OGLE LMC-ECL-04236. |
| In the text | |
 |
Fig. 9. As in Fig. 2, but for the system OGLE LMC-ECL-21569. |
| In the text | |
 |
Fig. 10. Results of fitting of four other systems from Group 1 (using the same scheme as in Fig. 2): (A) OGLE BLG-ECL-190427 (top left), (B) OGLE GD-ECL-07157 (top right), (C) OGLE LMC-ECL-04623 (bottom left), and (D) OGLE LMC-ECL-17182 (bottom right). |
| In the text | |
 |
Fig. 11. System 1SWASP J093010.78+533859.5 showing the ETV series of the eclipsing binaries: A (top) and B (bottom). |
| In the text | |
 |
Fig. 12. Distribution of currently identified doubly eclipsing systems on the sky expressed as a function of their declination. Analysis of data provided by OGLE surveys resulted in more than 90% of the cases, making them located on the southern sky. |
| In the text | |
 |
Fig. 13. Distribution of period ratio PA/PB for binaries in quadruple systems (the limiting maximum value of 4 was chosen because information beyond this threshold is very sparse and certainly heavily biased). Top panel: all quadruples in the 2+2 architecture. Blue histograms for previously known doubly eclipsing systems, orange histograms for our new discoveries (see Table 2). The data include the cases where the relative motion of the binaries A and B was proven, and those where we lack this information. Green histograms are other quadruple systems in the 2+2 architecture from the MSC catalogue (Tokovinin 2018a). Bottom panel: same as above, but only for the doubly eclipsing systems (sum of blue and orange above). Declining curves at the bottom panel are predictions in a simple model where periods PA and PB are entirely independent variables and have identical probability density distribution: uniform (black) or linearly increasing towards longer orbital periods (red; see discussion in Sect. 7). Both are able to explain the preferential PA ≃ PB configuration. While still noisy, there are two major deviations from their prediction: (i) dearth of systems with period ratio between ≃1.2 and ≃1.5, and (ii) excess of systems with PA/PB ≃ 3/2. On the contrary, the dip at PA/PB ≃ 2 may still reflect data fluctuations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.