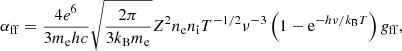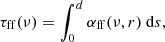| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201935960 | |
| Published online | 16 September 2019 | |
A model for high-mass microquasar jets under the influence of a strong stellar wind
1
Departament de Física Quàntica i Astrofísica, Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: emolina@fqa.ub.edu, vbosch@fqa.ub.edu
2
Instituto Argentino de Radioastronomía (CCT-La Plata, CONICET; CICPBA), C.C.5, 1894 Villa Elisa, Argentina
e-mail: sdelpalacio@iar.unlp.edu.ar
Received:
27
May
2019
Accepted:
21
August
2019
Context. High-mass microquasars (HMMQs) are systems from which relativistic jets are launched. At the scales of several times the binary system size, the jets are expected to follow a helical path caused by the interaction with a strong stellar wind and orbital motion. Such a trajectory has its influence on the non-thermal emission of the jets, which also depends strongly on the observing angle due to Doppler boosting effects.
Aims. We explore how the expected non-thermal emission of HMMQ jets at small scales is affected by the impact of the stellar wind and the orbital motion on the jet propagation.
Methods. We studied the broadband non-thermal emission, from radio to gamma rays, produced in HMMQ jets up to a distance of several orbital separations, taking into account a realistic jet trajectory, different model parameters, and orbital modulation. The jet trajectory is computed by considering momentum transfer with the stellar wind. Electrons are injected at the position where a recollimation shock in the jets is expected due to the wind impact. Their distribution along the jet path is obtained assuming local acceleration at the recollimation shock, and cooling via adiabatic, synchrotron, and inverse Compton processes. The synchrotron and inverse Compton emission is calculated taking into account synchrotron self-absorption within the jet, free-free absorption with the stellar wind, and absorption by stellar photons via pair production.
Results. The spectrum is totally dominated by the jet over the counter-jet due to Doppler boosting. Broadband emission from microwaves to gamma rays is predicted, with radio emission being totally absorbed. This emission is rather concentrated in the regions close to the binary system and features strong orbital modulation at high energies. Asymmetric light curves are obtained owing to the helical trajectory of the jets.
Conclusions. The presence of helical shaped jets could be inferred from asymmetries in the light curves, which become noticeable only for large jet Lorentz factors and low magnetic fields. Model parameters could be constrained if accurate phase-resolved light curves from GeV to TeV energies were available. The predictions for the synchrotron and the inverse Compton radiation are quite sensitive of the parameters determining the wind-jet interaction structure.
Key words: X-rays: binaries / radiation mechanisms: non-thermal / relativistic processes / stars: winds / outflows / stars: massive
© ESO 2019
1. Introduction
Microquasars are binary systems consisting of a compact object (CO), either a black hole or a neutron star, that launches relativistic jets powered by accretion of matter from a companion star. When the companion is a massive star, these systems are called high-mass microquasars (HMMQs) and accretion onto the CO takes place as the latter captures a fraction of the stellar wind. This mechanism is compatible with the presence of an accretion disk around the CO (El Mellah et al. 2019b), which is a necessary condition for jet formation. In HMMQs, interaction between the jets and the stellar wind may play an important role in both the propagation and the radiation produced by the jet, as the combined effect of the wind and orbital motion deviates the jets from a straight trajectory. Several works study the dynamical influence of the stellar wind on the jets of HMMQs, and their expected radiative output, at the scales of the binary system (e.g., Romero & Orellana 2005; Khangulyan et al. 2008, 2018; Perucho & Bosch-Ramon 2008, 2012; Araudo et al. 2009; Owocki et al. 2009; Perucho et al. 2010; Yoon et al. 2016).
At larger scales, the effect of orbital motion becomes important and could make the jets follow a helical trajectory (see, e.g., Bosch-Ramon & Barkov 2016, for a semi-analytical study about this). Current observations allow for a detection of this kind of pattern in microquasars. The most famous case is perhaps SS433, in which the helical structure is likely caused by precession of the accretion disk (Begelman et al. 2006; Monceau-Baroux et al. 2014). Jet precession has also been observed in 1E 1740.7−2942 (Luque-Escamilla et al. 2015), even though it is a low-mass microquasar in which the stellar wind is not expected to have a strong dynamical influence. Cygnus X-3 is another system for which helix-like jets have been found (Mioduszewski et al. 2001; Miller-Jones et al. 2004), although the cause of their shape remains unclear. Finally, one may expect a strong wind-jet interaction in Cygnus X-1, given that it hosts a massive star close to the CO (e.g., Yoon et al. 2016; Bosch-Ramon & Barkov 2016). Nevertheless, observations have not shown evidence of the presence of helical jets in Cygnus X-1 so far (Stirling et al. 2001).
Since the orbital motion could leave a strong imprint on jet radiation in HMMQs, Molina & Bosch-Ramon (2018, hereafter MB18) computed the non-thermal radiative output of helical jets along the orbit using a phenomenological prescription for the jet kinematics. That work focused on a jet region rather far from the binary system, and the jet speed was taken well below the speed of light, due to a braking effect caused by instability growth and subsequent mixing of jet and wind material (Bosch-Ramon & Barkov 2016). However, closer to the launching site, within a few orbital separations from the jet base, the jet is thought to be relativistic (e.g., Fender et al. 2004). In that case, absorption processes and radiation cooling become more important, and Doppler boosting should be considered to compute the observable radiation.
The work presented here complements what was done in MB18 by studying in detail the wind-jet interaction on the scales of the binary system and its peripheral region. For that purpose, the jet trajectory is computed accounting for orbital motion and the momentum transferred by interaction with the stellar wind. The leptonic jet radiation is computed using a semi-analytical code, modeling the jets as one-dimensional emitters that radiate via the synchrotron and inverse Compton (IC) mechanisms. Absorption in radio and gamma rays is also accounted for.
The paper is organized as follows: in Sect. 2, we describe the physical system under study, as well as the the technical aspects of the dynamical and radiative models adopted. In Sect. 3, we present the main results of this work. Finally, a summary and a discussion of the results are given in Sect. 4.
2. Model description
2.1. System properties
The system studied in this work is a generic HMMQ, similar to Cygnus X-1, in which a CO is accreting matter from a massive companion star. The orbit is considered to be circular, with a period of T = 4 days and a separation of a = 3 × 1012 cm ≈ 0.2 AU. A jet and a counter-jet are ejected in opposite directions perpendicularly to the orbital plane, and progressively deviate from their initial direction by the combined effects of the stellar wind and orbital motion. The star is located at the origin of our coordinate system, which co-rotates with the CO counter-clockwise. For simplicity, we assumed that the star rotates synchronously with the coordinate system. The initial direction of the jets is taken as the z-axis. The x-axis is defined by the star-CO direction and the y-axis is perpendicular to it, in the direction of the orbital motion. The orbital phase of the CO is characterized by φ. The system is assumed to be at a distance of d = 3 kpc from an observer that sees the system with an inclination i with respect to the z-axis. Figure 1 illustrates this scenario.
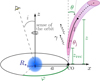 |
Fig. 1. Sketch of considered scenario (not to scale). We show a jet segment at a height z (black dot) and its projection in the xz-plane (grey dot). We also show the recollimation height zrec, the length l along the jet, the jet half-opening angle θj, the jet bending angle with respect to the z-axis (θ), the inclination angle of the orbit i, the orbital separation a, the star radius R⋆, and the orbital phase φ (set to 0 and 0.5 for the inferior and superior conjunctions, respectively). The counter-jet (not shown) is symmetric to the jet with respect to the xy-plane. |
The companion is a typical O-type star in the main sequence, with a temperature of T⋆ = 40 000 K and a luminosity of L⋆ = 1039 erg s−1 (Heap et al. 2006), which correspond to a radius of R⋆ ≈ 7.4 × 1011 cm. The stellar wind is assumed isotropic, with a velocity following the usual β-law form 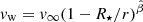 , where v∞ = 2 × 108 cm s−1 is the terminal wind speed, r is the distance to the star, and
, where v∞ = 2 × 108 cm s−1 is the terminal wind speed, r is the distance to the star, and 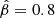 is typical for hot massive stars (e.g., Pauldrach et al. 1986). Although the
is typical for hot massive stars (e.g., Pauldrach et al. 1986). Although the 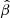 -value is not tightly constrained, our results are almost insensitive to it within its usual range for O-type stars,
-value is not tightly constrained, our results are almost insensitive to it within its usual range for O-type stars, 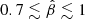 (Puls et al. 1996), and not very sensitive to values of
(Puls et al. 1996), and not very sensitive to values of  up to 3 found for some stars with different spectral types (Crowther et al. 2006). However, if a smaller a was considered, a variation of the
up to 3 found for some stars with different spectral types (Crowther et al. 2006). However, if a smaller a was considered, a variation of the 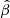 -value would have a higher impact in our results given the proximity of the jets to the star. We also note that the adopted v∞ is typical for O-type stars, but can be significantly lower for those with a later spectral type (∼500 km s−1 for the B-supergiant in Vela X-1; Sander et al. 2018). The combination of a larger
-value would have a higher impact in our results given the proximity of the jets to the star. We also note that the adopted v∞ is typical for O-type stars, but can be significantly lower for those with a later spectral type (∼500 km s−1 for the B-supergiant in Vela X-1; Sander et al. 2018). The combination of a larger 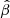 and a smaller v∞ for stars with a later spectral type would likely make their wind influence on the jets negligible. The mass-loss rate of the stellar wind is taken as Ṁw = 10−6 M⊙ yr−1, which is also a characteristic value for O-type stars (Lamers & Cassinelli 1999; Muijres et al. 2012).
and a smaller v∞ for stars with a later spectral type would likely make their wind influence on the jets negligible. The mass-loss rate of the stellar wind is taken as Ṁw = 10−6 M⊙ yr−1, which is also a characteristic value for O-type stars (Lamers & Cassinelli 1999; Muijres et al. 2012).
As shown in Fig. 4 of Yoon et al. (2016), for a case similar to that studied here, the geometry of a jet shocked by the stellar wind departs from that of a conical jet. On the other hand, the shocked material surrounding the jet also takes part in the wind-jet momentum transfer, although this effect is difficult to capture without detailed simulations. Thus, for simplicity, we assume that the jets have a conical shape of half-opening angle θj = 0.1 rad, since they have been shown to be significantly collimated (e.g., Stirling et al. 2001). The jets are assumed to have a constant Lorentz factor γj from their launching to end points, the latter located at several a. Two values of γj are considered in order to assess the impact of this parameter in the results (e.g., due to different Doppler boosting).
Both jet and counter-jet have a kinetic power of Lj = 5 × 1036 erg s−1, a fraction ηNT of which is injected into non-thermal electrons accelerated with a rate Ėacc = ηaccecB, where ηacc is the acceleration efficiency, and e the elementary charge. The fiducial values of ηNT and ηacc are both set to 0.1, but they are not well constrained beyond the fact that they both should be ≤1 (see Sect. 4). We focus here on electrons (and positrons) as hadronic radiation processes are far less efficient than leptonic ones under the conditions assumed in the emitting regions (e.g., Bosch-Ramon & Khangulyan 2009). We characterize the magnetic field at the jet base through a fraction ηB of the total jet energy density (see Sect. 2.3). Table 1 summarizes the different parameters that are used in this work.
Jet, star, and system parameters that are used throughout this work.
2.2. Jet dynamics
The trajectory of the jet is computed starting from a height z0 = 2 × 1010 cm, small enough so that wind effects are negligible. The counter-jet starts at −z0. Initially the jets propagate in the 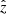 direction. However, the interaction with the stellar wind bends them away from the star in the
direction. However, the interaction with the stellar wind bends them away from the star in the 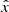 direction within the scales of the binary system. Additionally, at larger scales, the Coriolis force related to the orbital motion makes the jets bend in the
direction within the scales of the binary system. Additionally, at larger scales, the Coriolis force related to the orbital motion makes the jets bend in the 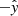 direction, opposite to the sense of the orbit. We obtain the trajectory of the jets by dividing them into segments and computing iteratively how they are reoriented due to the momentum transfer by the stellar wind. In cylindrical coordinates, the first jet segment sets the following initial conditions for the position r and the momentum P:
direction, opposite to the sense of the orbit. We obtain the trajectory of the jets by dividing them into segments and computing iteratively how they are reoriented due to the momentum transfer by the stellar wind. In cylindrical coordinates, the first jet segment sets the following initial conditions for the position r and the momentum P:
where Ṗj = Ljγjβj/c(γj − 1) is the total jet thrust, βj = vj/c is the jet propagation velocity in units of the speed of light c, and dt is the segment advection time. In order to get the initial conditions for the counter-jet trajectory one just needs to change the sign of the z coordinate in both r1 and P1. The Coriolis plus wind forces acting on each segment are:
where ρw is the wind density, θ is the angle between the r and z coordinates of the segment, and S⋆ and Sϕ are the segment surfaces perpendicular to the x and ϕ directions, respectively. As we work under the assumption of an isotropic, spherically symmetric wind, 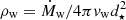 , with d⋆ = ∥r∥ being the distance to the star. Nevertheless, it is worth mentioning that some level of wind beaming towards the accretor is expected, especially for slow winds (Friend & Castor 1982; Gies & Bolton 1986; El Mellah et al. 2019a). This would increase the wind density in the orbital plane with respect to the isotropic case, while decreasing it off the plane, thus reducing the wind influence on the jets farther from the CO. Nonetheless, we neglect wind beaming since we work with a simplified prescription and a fast stellar wind is considered. The first term in the min function is the velocity corresponding to the Coriolis force at each segment position, while the second term is the wind velocity in the ϕ direction as seen from the jet, as the wind-jet relative ϕ-velocity cannot be larger than the wind tangential velocity in the non-inertial frame1. The forces in Eq. (2) are then used to compute the momentum of the subsequent segments as:
, with d⋆ = ∥r∥ being the distance to the star. Nevertheless, it is worth mentioning that some level of wind beaming towards the accretor is expected, especially for slow winds (Friend & Castor 1982; Gies & Bolton 1986; El Mellah et al. 2019a). This would increase the wind density in the orbital plane with respect to the isotropic case, while decreasing it off the plane, thus reducing the wind influence on the jets farther from the CO. Nonetheless, we neglect wind beaming since we work with a simplified prescription and a fast stellar wind is considered. The first term in the min function is the velocity corresponding to the Coriolis force at each segment position, while the second term is the wind velocity in the ϕ direction as seen from the jet, as the wind-jet relative ϕ-velocity cannot be larger than the wind tangential velocity in the non-inertial frame1. The forces in Eq. (2) are then used to compute the momentum of the subsequent segments as:
As we are taking here a constant propagation velocity vj, the additional momentum that this prescription generates is assumed to go into heat of the shocked structure made of interacting jet and wind material. However, we do not consider the back reaction of the accumulated heat, nor instability growth and mixing, on the interacting flows. A more accurate and realistic account of the process would require carrying out costly 3-dimensional, relativistic hydrodynamical simulations. For simplicity, we use a phenomenological approach to compute the jet trajectory, acknowledging that as the jet segments get farther from the binary, our model becomes less realistic. Nevertheless, as the most relevant emitting regions are close to the binary system (see Sect. 3), we consider our approach a reasonable one at this stage. For illustrative purposes, Fig. 2 shows the path followed by the jet for γj = 1.2 and 3.
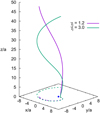 |
Fig. 2. Trajectory followed by the jet for γj = 1.2 (solid purple line) and 3 (solid green line). The projections in the orbital plane are also shown with dashed lines. The jet length is 50a, and the counter-jet is symmetric to it with respect to the xy-plane (not shown). The blue circle at the origin of coordinates represents the star (to scale). The jets are plotted starting from the corresponding recollimation shocks. |
2.3. Particle cooling
In this work, primed quantities refer to quantities in the fluid frame (FF), whereas unprimed quantities refer to the laboratory frame (LF). The jet emission is computed as in MB18, but accounting for relativistic effects and additional absorption mechanisms. The electron distribution and the synchrotron and IC luminosities are calculated first in the FF at each point along the jets. Then, the luminosities are computed as seen by the observer taking into account Doppler (de)boosting. Finally, these luminosities are corrected by different absorption processes.
The point where the non-thermal electrons are injected is located at a height zrec (−zrec for the counter-jet) for which a recollimation shock is formed due to the jet and wind momentum fluxes balancing each other in the y-axis direction (perpendicular to the jet propagation). This condition can be approximately expressed as follows (Bosch-Ramon & Barkov 2016):
where Ṗw = Ṁwvw is the wind thrust. For γj = 1.2 we obtain zrec = 1.4 × 1012 cm ≈ 0.47a, whereas for γj = 3, zrec = 3.1 × 1011 cm ≈ 0.10a. Some combinations of Ṗw, Ṗj and γj yield non-physical (complex) values of zrec in Eq. (4), which means that for those sets of parameters no recollimation shock is formed, as the momentum flux balance is never reached (see Yoon et al. 2016, for a non-relativistic simulation where this effect is studied).
Electrons are injected at 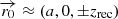 , since the jet displacement in the x and y coordinates is small at z = ±zrec (≲0.005a in the worst case). The particles are assumed to follow a power-law energy distribution with spectral index −2, typical for acceleration in strong shocks via the Fermi I mechanism (e.g Drury 1983), with a minimum energy of
, since the jet displacement in the x and y coordinates is small at z = ±zrec (≲0.005a in the worst case). The particles are assumed to follow a power-law energy distribution with spectral index −2, typical for acceleration in strong shocks via the Fermi I mechanism (e.g Drury 1983), with a minimum energy of 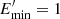 MeV. An exponential cutoff is also assumed:
MeV. An exponential cutoff is also assumed:
where E′ is the electron energy in the FF. The normalization of Q′(E′) is obtained from the condition that the total power available for non-thermal electrons in the FF is 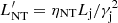 . Electrons are convected from
. Electrons are convected from 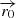 along the jet path while they cool down via adiabatic, synchrotron and IC processes. For simplicity, we neglect particle acceleration beyond
along the jet path while they cool down via adiabatic, synchrotron and IC processes. For simplicity, we neglect particle acceleration beyond 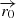 , even though weak shocks and turbulence may (re)accelerate particles further downstream in the jets. Analytical expressions are used for the energy losses in the FF (see Longair 1981; Khangulyan et al. 2014 for synchrotron and IC losses, respectively). The characteristic timescale for adiabatic cooling is
, even though weak shocks and turbulence may (re)accelerate particles further downstream in the jets. Analytical expressions are used for the energy losses in the FF (see Longair 1981; Khangulyan et al. 2014 for synchrotron and IC losses, respectively). The characteristic timescale for adiabatic cooling is 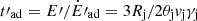 , where Rj(l)∝l is the jet radius.
, where Rj(l)∝l is the jet radius.
The magnetic pressure at the accelerator (located at 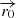 ) is characterized in the FF as a fraction ηB of the total jet energy density:
) is characterized in the FF as a fraction ηB of the total jet energy density:
where 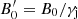 and rj, 0 = Rj(zrec) are the magnetic field and the jet radius at
and rj, 0 = Rj(zrec) are the magnetic field and the jet radius at 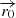 , respectively. For the same
, respectively. For the same 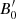 , this fraction relates to the ratio of magnetic pressure to stellar photon energy density in the LF as
, this fraction relates to the ratio of magnetic pressure to stellar photon energy density in the LF as 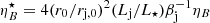 , which is useful to compare the expected radiation outputs of synchrotron and IC processes. This yields
, which is useful to compare the expected radiation outputs of synchrotron and IC processes. This yields 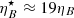 for γj = 1.2, and
for γj = 1.2, and 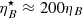 for γj = 3. The jet magnetic field is assumed perpendicular to the flow in the FF, since at the scales considered in this work, far from the jet launching point, a dominant toroidal component for the magnetic field is expected (e.g., Pudritz et al. 2012). Given the adopted assumptions plus frozen in conditions, the magnetic field at each jet point can be computed as:
for γj = 3. The jet magnetic field is assumed perpendicular to the flow in the FF, since at the scales considered in this work, far from the jet launching point, a dominant toroidal component for the magnetic field is expected (e.g., Pudritz et al. 2012). Given the adopted assumptions plus frozen in conditions, the magnetic field at each jet point can be computed as:
The cutoff energy 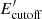 is the maximum energy that the electrons can achieve in the accelerator region in the FF, and it is obtained as follows:
is the maximum energy that the electrons can achieve in the accelerator region in the FF, and it is obtained as follows:
-
We compare the acceleration timescale
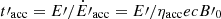 with the cooling timescale
with the cooling timescale 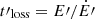 , where Ė′ is the cooling rate accounting for adiabatic, synchrotron and IC losses. In this work we set ηacc = 0.1 as a representative case with efficient particle acceleration. The energy
, where Ė′ is the cooling rate accounting for adiabatic, synchrotron and IC losses. In this work we set ηacc = 0.1 as a representative case with efficient particle acceleration. The energy 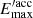 at which the two timescales are equal is the maximum energy that electrons can attain before the energy losses overcome the energy gain by acceleration.
at which the two timescales are equal is the maximum energy that electrons can attain before the energy losses overcome the energy gain by acceleration. -
We compare
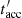 with the diffusion timescale
with the diffusion timescale 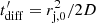 , where
, where 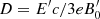 is the diffusion coefficient in the Bohm regime. If diffusion is a dominant process, particles cannot reach
is the diffusion coefficient in the Bohm regime. If diffusion is a dominant process, particles cannot reach 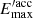 before escaping the accelerating region. We can estimate the maximum energy attainable by the electrons before they diffuse away from the accelerator,
before escaping the accelerating region. We can estimate the maximum energy attainable by the electrons before they diffuse away from the accelerator, 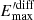 , by equating
, by equating 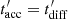 .
. -
We obtain the cutoff energy as
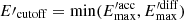 . For the different sets of parameters considered in this work we always obtain a
. For the different sets of parameters considered in this work we always obtain a 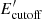 of a few TeV.
of a few TeV.
In order to compute the electron energy distribution N′(E′,l) along the jet, the latter is divided into 1500 segments with size dl = 1011 cm, extending to a total length of lj = 1.5 × 1014 cm =50a. Once the injection function Q′(E′) is determined, the electron energy distribution N′(E′,l) is computed for each segment l in an iterative way as done in MB18, but considering that all quantities must be expressed in the FF. This defines a structured, linear relativistic emitter along the trajectory shown in Fig. 2.
2.4. Radiation
We focus our study in the computation of synchrotron and IC radiation of leptons along the jets. Hadronic processes are likely much less efficient at the scales considered in this work, given the conditions of the emitting regions. Relativistic bremsstrahlung is also expected to be unimportant in comparison to the synchrotron and IC mechanisms (Bosch-Ramon & Khangulyan 2009).
At each segment of the jet, the spectral energy distribution (SED) of the emitted synchrotron radiation for an isotropic population of electrons in the FF is given by (Pacholczyk 1970):
where ε′ is the photon energy, me is the electron mass, h is the Planck constant, 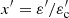 , and
, and 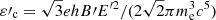 is the critical photon energy assuming an isotropic distribution of the pitch angle
is the critical photon energy assuming an isotropic distribution of the pitch angle 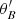 between the electron velocity and the magnetic field, such that
between the electron velocity and the magnetic field, such that 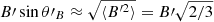 . The function F(x′) can be approximated by F(x′) ≈ 1.85
. The function F(x′) can be approximated by F(x′) ≈ 1.85 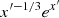 for x′∈[0.1, 10] (Aharonian 2004).
for x′∈[0.1, 10] (Aharonian 2004).
For the calculation of the IC emission we only consider the up-scattering of stellar photons; other radiation fields (such as the one from the accretion disk) are negligible in comparison to the stellar one on the relevant scales. Synchrotron self-Compton also turns out to be negligible. We use the prescription developed by Khangulyan et al. (2014) to compute the interaction rate of an electron with a monodirectional field of target photons with a black body distribution, d2N′/dε′dt′. For simplicity, we do not consider possible deviations from a black-body spectrum owing to absorption of stellar photons by wind material, since this is not expected to have a significant effect on the IC emission (see Reitberger et al. 2014, for an illustrative comparison between a black-body and a monochromatic stellar spectrum in colliding-wind binaries). Assuming an isotropic distribution of electrons in the FF, the IC SED at each jet segment is computed as:
Once the luminosities are obtained in the FF, we transform them into what would be seen by the observer. For a stationary jet such as the one considered in this work, we have 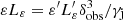 (Sikora et al. 1997), where δobs = [γj(1 − βjcosθobs)]−1 is the Doppler factor between the emitter and the observer, the velocity of the former and the latter making an angle θobs in the LF (e.g., Dermer & Schlickeiser 2002). This transformation is done individually for each jet segment, as θobs, and thus δobs, varies from one to another. Photon energies as seen by the observer are ε = δobsε′.
(Sikora et al. 1997), where δobs = [γj(1 − βjcosθobs)]−1 is the Doppler factor between the emitter and the observer, the velocity of the former and the latter making an angle θobs in the LF (e.g., Dermer & Schlickeiser 2002). This transformation is done individually for each jet segment, as θobs, and thus δobs, varies from one to another. Photon energies as seen by the observer are ε = δobsε′.
2.5. Absorption mechanisms
Two main photon absorption processes are considered in this work: electron-positron pair creation from gamma rays interacting with stellar photons (γγ−absorption, GGA), and the absorption of low-energy photons by the free ions present in the wind (free-free absorption, FFA). Synchrotron self-absorption is also computed and found to be negligible in comparison to FFA in this scenario, regardless of the adopted parameters. The absorption coefficients are calculated directly in the LF, as the emitted luminosities are previously transformed to what would be seen by the observer (see Sect. 2.4).
The optical depth for GGA is computed as follows:
where s parametrizes the gamma-ray photon trajectory along the line-of-sight, d is the distance to the observer, θγγ is the angle between the momentum of this photon and the stellar photons, ε0 is the energy of the latter, which follows a black body distribution n(ε0), and σγγ is the cross-section for GGA, obtained from Eq. (1) of Gould & Schréder (1967). The lower integral limit 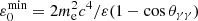 is the energy threshold for the creation of an electron-positron pair.
is the energy threshold for the creation of an electron-positron pair.
Regarding the FFA process, its absorption coefficient is given by (e.g., Rybicki & Lightman 1986):
with ni, e being the number density of ions/electrons in the wind, T its temperature, Z the mean atomic number (taken as 1), ν the photon frequency, and gff the average Gaunt factor, which can be estimated as gff ≈ 9.77[1 + 0.056 ln(T3/2/Zν)] (Leitherer & Robert 1991).
FFA is strongly dependent on the wind density (as 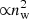 ), and consequently would also be significantly affected by the presence of wind beaming (see Sect. 2.2). Also, for hν ≪ kBT the absorption is ∝ν−2, so its effect is much larger for low radio frequencies. The FFA optical depth can be calculated as
), and consequently would also be significantly affected by the presence of wind beaming (see Sect. 2.2). Also, for hν ≪ kBT the absorption is ∝ν−2, so its effect is much larger for low radio frequencies. The FFA optical depth can be calculated as
where r is the distance to the star. Given that the stellar wind has a density nw ∝ r−2 and that we are modeling a compact system in which the jet inner regions are close to the star, strong absorption is expected in radio.
In addition to the three aforementioned absorption processes, occultation of some parts of the jets by the star is also taken into account (e.g., Khangulyan et al. 2018). Although unimportant for most system configurations, stellar occultation can have a moderate impact on the radiation output for high system inclinations (i ≳ 60°) when the CO is behind the star (see Sect. 3.3).
3. Results
We explore different values for three free parameters of our model: γj, ηB, and i (see Table 1). Moreover, we also study the orbital variability of the results by varying φ between 0 and 1 (see Fig. 1). The energy losses and the particle energy distribution are only affected by γj and ηB, whereas the radiative outputs also depend on i and φ. The observer is assumed to be always in a position such that the CO is closest to the observer for φ = 0 (inferior conjunction), and farthest from the observer for φ = 0.5 (superior conjunction). As we are considering a circular orbit, by studying a whole period we cover all the possible system configurations.
3.1. Particle distribution
In Fig. 3, we show the electron energy distribution of each jet segment for γj = 1.2 and ηB = 10−2 and 1 (which yield 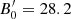 G and 282 G, respectively), as well as the total electron energy distribution up to three different lengths along the jet. The relevant timescales for the first jet segment, where relativistic electrons are injected, are shown in Fig. 4 for γj = 1.2 and ηB = 10−2. Both the electron distribution and the timescales associated to it are the same for the jet and the counter-jet. For ηB = 1, synchrotron is the dominant cooling mechanism for electrons with E′≳50 MeV, and those with E′≳1 GeV cool down already within the first segment. At lower electron energies the cooling is dominated by the adiabatic expansion of the jet, which allows most of the particles below ∼50 MeV to reach distances outside the binary system. For ηB = 10−2, the synchrotron dominance only happens above ∼30 GeV, and there is also a significant contribution of IC losses for 1 GeV ≲ E′≲70 GeV, as seen in Fig. 4. However, this contribution is only relevant for the inner l ∼ 1013 cm of the jet, where the stellar radiation field is strong; farther away adiabatic losses also dominate in this energy range.
G and 282 G, respectively), as well as the total electron energy distribution up to three different lengths along the jet. The relevant timescales for the first jet segment, where relativistic electrons are injected, are shown in Fig. 4 for γj = 1.2 and ηB = 10−2. Both the electron distribution and the timescales associated to it are the same for the jet and the counter-jet. For ηB = 1, synchrotron is the dominant cooling mechanism for electrons with E′≳50 MeV, and those with E′≳1 GeV cool down already within the first segment. At lower electron energies the cooling is dominated by the adiabatic expansion of the jet, which allows most of the particles below ∼50 MeV to reach distances outside the binary system. For ηB = 10−2, the synchrotron dominance only happens above ∼30 GeV, and there is also a significant contribution of IC losses for 1 GeV ≲ E′≲70 GeV, as seen in Fig. 4. However, this contribution is only relevant for the inner l ∼ 1013 cm of the jet, where the stellar radiation field is strong; farther away adiabatic losses also dominate in this energy range.
 |
Fig. 3. Energy distribution of the electrons along the jet up to 0.1a (dotted line), a (dashed line), and the whole jet (solid line), for γj = 1.2, ηB = 10−2 (top panel), and ηB = 1 (bottom panel). The contribution of the individual jet segments is color-coded, with the color scale representing the position of each segment along the jet. Segments have a constant length of dl = 1011 cm ≈ 0.03a. |
 |
Fig. 4. Characteristic timescales for the first jet segment for γj = 1.2 and ηB = 10−2. Cooling (solid lines), acceleration (dashed line), and diffusion (dotted line) processes are shown. |
3.2. Spectral energy distribution
The SEDs in this section are computed using φ = 0.25 as a representative situation. Figure 5 shows the combined SED (as seen by the observer) of the jet and the counter-jet for γj = 1.2, i = 30°, and ηB = 10−2 and 1. The contribution of the regions of the jets further from to the CO is also depicted. The bump at low energies of the synchrotron SED for ηB = 1 is a numerical artifact without physical meaning caused by how the first jet segment is treated when computing the particle distribution for intense energy losses (see MB18, a bump is also hinted in the electron energy distribution in Fig. 3). The ηB-value has a strong influence on the synchrotron and IC luminosities, as expected from its relation to 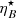 . The SED is totally dominated by the emission at the binary system scales, except for the low-energy end of the synchrotron component, in which the radiation output comes mainly from the more external regions given the high level of FFA close to the star. This same absorption process is the responsible for the lack of radio emission in the spectrum. GGA is significant even for small system inclinations, despite a low i not favouring this absorption process.
. The SED is totally dominated by the emission at the binary system scales, except for the low-energy end of the synchrotron component, in which the radiation output comes mainly from the more external regions given the high level of FFA close to the star. This same absorption process is the responsible for the lack of radio emission in the spectrum. GGA is significant even for small system inclinations, despite a low i not favouring this absorption process.
 |
Fig. 5. Total (jet + counter-jet) synchrotron and IC SEDs for γj = 1.2, i = 30°, φ = 0.25, and ηB = 10−2 (purple lines) and 1 (green lines). Dashed lines show the contribution of the jets beyond a length a, and black dotted lines represent the unabsorbed emission. |
The separate jet and counter-jet SEDs are presented in Fig. 6 for i = 0°, 30° and 60°, ηB = 10−2, and γj = 1.2 and 3. The jet is responsible for most of the emission even for a high inclination, which reduces the effect of Doppler boosting. Figure 7 shows the evolution along the jet of the Doppler boosting factor, 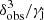 , for γj = 1.2 and 3, and i = 0°, 30° and 60°. Results are only shown up to l = 10a, as the contribution of the jets to the SED beyond this length is negligible. For γj = 1.2,
, for γj = 1.2 and 3, and i = 0°, 30° and 60°. Results are only shown up to l = 10a, as the contribution of the jets to the SED beyond this length is negligible. For γj = 1.2, 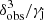 remains almost constant because θobs does so, given the small jet deviation with respect to a straight trajectory at the scales shown in the plot (see Fig. 2). For this γj−value, the emission is boosted with respect to the FF as long as i ≲ 60°. For γj = 3 the variation of the Doppler boosting factor along the jet becomes more important due to its helical shape, and the emission is already deboosted for i ≳ 30°. We note that a higher γj implies more boosting only when i ∼ 0. This can further be seen in Fig. 6, where only for the case of i = 0 the SED for γj = 3 becomes comparable to that for γj = 1.2.
remains almost constant because θobs does so, given the small jet deviation with respect to a straight trajectory at the scales shown in the plot (see Fig. 2). For this γj−value, the emission is boosted with respect to the FF as long as i ≲ 60°. For γj = 3 the variation of the Doppler boosting factor along the jet becomes more important due to its helical shape, and the emission is already deboosted for i ≳ 30°. We note that a higher γj implies more boosting only when i ∼ 0. This can further be seen in Fig. 6, where only for the case of i = 0 the SED for γj = 3 becomes comparable to that for γj = 1.2.
 |
Fig. 6. SEDs of the jet (purple lines) and the counter-jet (green lines) for ηB = 10−2, φ = 0.25, i = 0 (top) 30° (middle) and 60° (bottom), and γj = 1.2 (solid lines) and 3 (dashed lines). |
 |
Fig. 7. Doppler boosting factor as a function of jet position for φ = 0.25, γj = 1.2 and 3, and i = 0 (solid lines), i = 30° (dashed lines), and i = 60° (dotted lines). The black solid line at |
The intrinsic jet emission is also highly influenced by the value of γj as the latter affects the magnetic and photon fields in the FF. In terms of particle cooling, the relative importance of each process varies with γj. Synchrotron losses become less efficient for increasing Lorentz factor, as 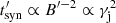 , whereas adiabatic losses become more dominant, as
, whereas adiabatic losses become more dominant, as 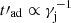 . The dependence of IC cooling with γj is more complex (see Khangulyan et al. 2014), but for the cases considered in this work the variation of
. The dependence of IC cooling with γj is more complex (see Khangulyan et al. 2014), but for the cases considered in this work the variation of 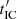 is small compared to that of
is small compared to that of 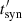 and
and 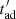 . In general, the combination of the effects of γj on the intrinsic and observed radiative outputs results in a decrease of the detected emission when γj increases, except for small enough values of i.
. In general, the combination of the effects of γj on the intrinsic and observed radiative outputs results in a decrease of the detected emission when γj increases, except for small enough values of i.
3.3. Orbital variability
Figures 8 and 9 show the total SEDs for ηB = 10−2, i = 30° and 60°, and different values of φ ∈ [0, 0.5], γj = 1.2 and 3, respectively. Emission is almost symmetric for the remaining orbit, that is φ ∈ (0.5, 1), despite the helical trajectory of the jets. The difference, thus, being only of a few percent, is not shown in the plot. Synchrotron emission at ε ≳ 10−2 eV remains almost constant over the whole orbit, with slight variations corresponding to small changes in the δobs in the inner jet regions. At lower energies, especially for i = 60°, the difference becomes a bit more noticeable due to FFA becoming stronger as the CO approaches the superior conjunction (φ = 0.5). Both IC emission and GGA are strongly affected by the orbital phase and steadily increase as φ goes from 0 to 0.5. This makes the IC radiation output at most photon energies increase towards the superior conjunction, with the exception of the highest gamma-ray energies (ε ≳ 100 GeV), for which the emission of the phases closer to the inferior conjunction is larger due to less efficient GGA. This effect is more pronounced for high inclinations, as the strength of GGA increases with i close to the superior conjunction.
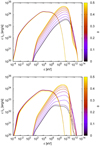 |
Fig. 8. Total synchrotron and IC SEDs for γj = 1.2, ηB = 10−2, i = 30° (top) and 60° (bottom), and different orbital phases between 0 and 0.5. SEDs for 0.5 < φ < 1 are not represented because they almost overlap with those shown. |
Figures 10 and 11 show the light curves at different energy bands for γj = 1.2 and 3, respectively. Two inclinations, i = 30° and 60°, are studied for ηB = 10−2. Light curves for straight (unbent) jets moving perpendicular to the orbital plane are also shown for comparison, although we note that this is not a realistic case given the adopted wind and jet parameters. The bumps seen at φ = 0.5 and ε ≤ 10 GeV are caused by photon occultation by the star. Orbital modulation for ε ≥ 100 MeV becomes more important the higher the system inclination is. As an example, in the case of γj = 3 (Fig. 11) and 10 GeV ≤ ε ≤ 100 GeV, for i = 30° the flux changes only by a factor of ∼3 along the orbit, whereas for i = 60° it changes by a factor of ∼20. This effect is not observed for ε < 100 MeV, as the weakly φ-dependent synchrotron emission dominates at these energies.
 |
Fig. 10. Integrated light curves for γj = 1.2, ηB = 10−2, i = 30° and 60°, and different photon energy ranges. Purple lines represent the values for bent jets such as those in Fig. 2, whereas green lines represent the results for straight jets. Dashed lines show the orbit-averaged flux values. Note the change in the flux normalization for each i. |
The fluxes for bent and straight jets are similar between them, with differences of at most ∼15% for ηB = 10−2. The situation is the same when one considers the orbit-averaged values. This is explained by the strong concentration of the emission at the jet inner regions (≲a; see Fig. 5), where the difference in the shape of straight and helical jets is small. For γj = 1.2, this difference remains small even for l ≫ a. If one considers a lower magnetic field, however, the situation changes. Figure 12 shows the light curves for γj = 3 and ηB = 10−4 (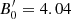 G). As the energy losses close to the CO are less intense, IC emission is more significant for l > a and the light curves have distinct features due to the helical jet trajectory. On the one hand, the difference in the fluxes with respect to straight jets is higher, up to ∼40% for ε > 10 GeV. On the other hand, asymmetries in the light curves with respect to φ = 0.5 arise for i = 60°.
G). As the energy losses close to the CO are less intense, IC emission is more significant for l > a and the light curves have distinct features due to the helical jet trajectory. On the one hand, the difference in the fluxes with respect to straight jets is higher, up to ∼40% for ε > 10 GeV. On the other hand, asymmetries in the light curves with respect to φ = 0.5 arise for i = 60°.
4. Summary and discussion
We have extended the study performed in MB18 to the inner regions of HMMQ jets in order to assess the role of the wind-jet interaction at the binary system scales. On those scales, the jet is likely to be more relativistic than further away from the binary (i.e., MB18, the scales studied in). We have shown that the stellar wind plus orbital motion can have a significant effect on the jet radiative output. As a result of this wind-jet interaction, the jets get a helical shape that affects angle-dependent processes such as IC scattering, GGA, and relativistic Doppler boosting. Most of the jet emission is produced at distances below a few orbital separations. If one compares the present results to those of MB18, one finds that the predicted fluxes are similar, although LNT is here an order of magnitude higher, meaning more efficient acceleration is assumed in the strong, asymmetric jet recollimation shock than in the shock at larger scales considered in MB18. The radio emission is severely absorbed in the stellar wind via FFA. This prevents us to use this emission to trace the helical jet structure, as it was done in MB18. Additionally, the small scales considered in this work would require a very high (μ-arcsecond) angular resolution to address such a study. The high proximity to the star also makes IC emission and GGA more susceptible to change along the orbit, which results in a much stronger orbital modulation than in MB18, especially for high-energy gamma rays with ε ≳ 100 MeV. Evidence of such a modulation has been found for Cygnus X-3 (Zdziarski et al. 2018), and hints of such an effect have also been observed in Cygnus X-1 (Zanin et al. 2016; Zdziarski et al. 2017).
Including the helical shape of the jets has a moderate impact on the predicted light curves with respect to the straight jet case, introducing a variation not higher than ∼40%, with this value depending on the strength of the magnetic field. At the energies at which GGA plays an important role (ε ≳ 10 GeV), the emission from helical jets is consistently more absorbed close to the superior conjunction due to the additional distance that the gamma-rays have to travel embedded in the stellar photon field. Nonetheless, this feature must be taken with caution, as a similar effect could be seen for straight jets with acceleration at z < zrec, not associated with the recollimation shock. Moreover, helical jets may have stronger energy dissipation, and thereby particle acceleration, than straight jets at z > zrec (not considered here), which could counterbalance also this effect. For small magnetic fields, the asymmetry in the light curves of jets with a helical shape could hint at the presence of this kind of jet structure in HMMQs. This asymmetries were also obtained by Dubus et al. (2010) when studying the effect of jet precession in the gamma-ray light curve of Cygnus X-3.
The parameters ηNT and ηacc used in our model are very difficult to constrain both observationally and from first principles, and thus we have only taken representative values for them. In the case of ηNT, the values of the luminosities and fluxes are easily scalable as ∝ηNT. The value of ηacc affects the maximum energy that the electrons can attain, and consequently the peak position of the synchrotron and IC components in the SED. A significantly lower value of ηacc would not allow synchrotron (IC) photons to reach X-rays (gamma rays above 100 GeV), whereas the GeV emission would remain relatively unaffected. As noted, it is also possible that electrons are accelerated in a continuous region extending beyond 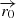 . This would modify the particle distribution in such a way that relativistic electrons could propagate further downstream along the jet without cooling down within the first jet segment. As synchrotron losses would not be so dominant further from the CO, this would result in an increase in the emitted gamma-ray luminosity and a decrease in the X-ray luminosity. In addition, the maximum electron and emitted photon energies could be somewhat higher if not limited by synchrotron cooling but by the accelerator size (e.g., Khangulyan et al. 2008). In the present work, for simplicity, we neglect electron acceleration beyond zrec, but this possibility should be considered in future studies.
. This would modify the particle distribution in such a way that relativistic electrons could propagate further downstream along the jet without cooling down within the first jet segment. As synchrotron losses would not be so dominant further from the CO, this would result in an increase in the emitted gamma-ray luminosity and a decrease in the X-ray luminosity. In addition, the maximum electron and emitted photon energies could be somewhat higher if not limited by synchrotron cooling but by the accelerator size (e.g., Khangulyan et al. 2008). In the present work, for simplicity, we neglect electron acceleration beyond zrec, but this possibility should be considered in future studies.
Another free parameter in our model is related to the magnetic field strength, ηB. As shown in Fig. 5, this parameter has a strong impact on the produced fluxes at all photon energies, and it also affects the degree of concentration of the emission close to the CO: the higher ηB is, the more concentrated the emission is. The position of the synchrotron high-energy cutoff is rather insensitive to ηB, whereas it strongly affects the (unabsorbed) IC high-energy cutoff. Therefore, for a higher ηB (stronger B) the synchrotron and IC cutoffs get closer. It is worth noting as well that, for a matter dominated jet, it is not expected that ηB approaches 1. However, depending on the location of zrec (and thus on the value of γj), even values of ηB well below one could still mean rather high values for 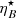 , yielding an IC flux comparable or even higher than the synchrotron one. As an example, a magnetic fraction ηB = 10−2 implies
, yielding an IC flux comparable or even higher than the synchrotron one. As an example, a magnetic fraction ηB = 10−2 implies 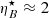 for γj = 3, and
for γj = 3, and 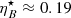 for γj = 1.2. This also means that, regardless of the value of ηB, the strong impact of zrec on the value of
for γj = 1.2. This also means that, regardless of the value of ηB, the strong impact of zrec on the value of 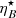 , shows that the synchrotron and the IC predictions are rather sensitive to the parameters determining the wind-jet interaction, which are not well constrained (e.g., Yoon et al. 2016; Bosch-Ramon & Barkov 2016).
, shows that the synchrotron and the IC predictions are rather sensitive to the parameters determining the wind-jet interaction, which are not well constrained (e.g., Yoon et al. 2016; Bosch-Ramon & Barkov 2016).
The wind-jet interaction makes our results valid only for distances up to a few a. The development of instabilities and significant mixing of the jet and wind material are expected to happen already on the binary system scales (Perucho et al. 2010). The former could have an important effect on the jet trajectory at larger scales, while the latter would imply a reduction of γj the more the wind material is mixed with the jets. The assumption of a constant θj-value is also a simplification, as it is likely that the aperture of the jets is modified by the action of the stellar wind (Bosch-Ramon & Barkov 2016). Despite all this, these effects should not have a significant impact on our results as in our model the radiation output tends to be concentrated on a region at z ≲ a (except for zrec ∼ a). In any case, proper 3D relativistic simulations of HMMQ jets on large scales would be needed for a more accurate study of the wind-jet interaction.
Both jet instability growth and wind-jet mixing are expected to become more important for clumpy winds (Perucho & Bosch-Ramon 2012), which are usual in massive stars (Owocki & Cohen 2006; Moffat 2008). Non-homogeneous winds may also change the accretion rate of material onto the CO by a few 10% within timescales of several minutes, with a time-averaged value similar to that of an isotropic wind (El Mellah et al. 2018). This would consequently modify the jet power, introducing also a time variability in Lj. Moreover, a clumpy wind would also affect the intensity of FFA, given the latter’s dependence on the wind density. Considering a simple microclumping model, typical clumping factors ≤100 (e.g., Mokiem et al. 2007; de Koter et al. 2008) would increase the free-free opacity by a factor of f ≲ 10 (Muijres et al. 2011), and the wind would remain opaque up to frequencies f1/2 ≲ 3 times larger than for a homogeneous wind (see Eq. (11)). Therefore, the qualitative results presented in this work regarding the absorption at radio frequencies are independent of the detailed considerations on wind clumping.
Finally, we emphasize that detailed information (e.g., well-sampled light curves) in different energy bands is required in order to significantly constrain the parameter space of the system physical properties. This is the only possible way to disentangle the degeneracy arising from multiple parameter combinations that yield similar results for quantities such as the average flux at a specific energy band. Such studies could be addressed in a future with current and in development observatories, such as NuSTAR (hard X-rays), e-ASTROGAM (MeV gamma-rays), Fermi (high-energy gamma rays), and CTA (very high-energy gamma rays). Devoted observing time with these instruments would help to improve our knowledge on the interplay between the stellar wind and the jets in HMMQs, and the associated non-thermal processes.
Acknowledgments
We want to thank the referee, Ileyk El Mellah, for his extensive and constructive comments that helped to improve this work. EM and VB acknowledge support by the Spanish Ministerio de Economía y Competitividad (MINECO/FEDER, UE) under grant AYA2016-76012-C3-1-P, with partial support by the European Regional Development Fund (ERDF/FEDER) and MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”). EM acknowledges support from MINECO through grant BES-2016-076342. SdP acknowledges support from CONICET. VB acknowledges support from the Catalan DEC grant 2017 SGR 643.
References
- Aharonian, F. A. 2004, Very High Energy Cosmic Gamma Radiation: A Crucial Window on the Extreme Universe (World Scientific Publishing Co) [CrossRef] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2009, A&A, 503, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Barkov, M. V. 2016, A&A, 590, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2009, Int. J. Mod. Phys. D, 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Koter, A., Vink, J. S., & Muijres, L. 2008, in Clumping in Hot-Star Winds, eds. W. R. Hamann, A. Feldmeier, & L. M. Oskinova, 47 [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 2002, ApJ, 575, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., Cerutti, B., & Henri, G. 2010, MNRAS, 404, L55 [NASA ADS] [Google Scholar]
- El Mellah, I., Sundqvist, J. O., & Keppens, R. 2018, MNRAS, 475, 3240 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Sundqvist, J. O., & Keppens, R. 2019a, A&A, 622, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El Mellah, I., Sander, A. A. C., Sundqvist, J. O., & Keppens, R. 2019b, A&A, 622, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Friend, D. B., & Castor, J. I. 1982, ApJ, 261, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., & Bolton, C. T. 1986, ApJ, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, R. J., & Schréder, G. P. 1967, Phys. Rev., 155, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F., & Bosch-Ramon, V. 2008, MNRAS, 383, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F. A., & Kelner, S. R. 2014, ApJ, 783, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Bosch-Ramon, V., & Uchiyama, Y. 2018, MNRAS, 481, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds (Cambridge University Press) [CrossRef] [Google Scholar]
- Leitherer, C., & Robert, C. 1991, ApJ, 377, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 1981, High Energy Astrophysics (Cambridge University Press) [Google Scholar]
- Luque-Escamilla, P. L., Martí, J., & Martínez-Aroza, J. 2015, A&A, 584, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller-Jones, J. C. A., Blundell, K. M., Rupen, M. P., et al. 2004, ApJ, 600, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Mioduszewski, A. J., Rupen, M. P., Hjellming, R. M., Pooley, G. G., & Waltman, E. B. 2001, ApJ, 553, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, A. F. J. 2008, in Clumping in Hot-Star Winds, eds. W. R. Hamann, A. Feldmeier, & L. M. Oskinova, 17 [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molina, E., & Bosch-Ramon, V. 2018, A&A, 618, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monceau-Baroux, R., Porth, O., Meliani, Z., & Keppens, R. 2014, A&A, 561, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muijres, L. E., de Koter, A., Vink, J. S., et al. 2011, A&A, 526, A32 [Google Scholar]
- Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P., & Cohen, D. H. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Romero, G. E., Townsend, R. H. D., & Araudo, A. T. 2009, ApJ, 696, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics. Nonthermal Processes in Galactic and Extragalactic Sources (W. H. Freeman & Company) [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Perucho, M., & Bosch-Ramon, V. 2008, A&A, 482, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., & Bosch-Ramon, V. 2012, A&A, 539, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Bosch-Ramon, V., & Khangulyan, D. 2010, A&A, 512, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pudritz, R. E., Hardcastle, M. J., & Gabuzda, D. C. 2012, Space Sci. Rev., 169, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Kudritzki, R. P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Reitberger, K., Kissmann, R., Reimer, A., & Reimer, O. 2014, ApJ, 789, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., & Orellana, M. 2005, A&A, 439, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Sander, A. A. C., Fürst, F., Kretschmar, P., et al. 2018, A&A, 610, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sikora, M., Madejski, G., Moderski, R., & Poutanen, J. 1997, ApJ, 484, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Stirling, A. M., Spencer, R. E., de la Force, C. J., et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, D., Zdziarski, A. A., & Heinz, S. 2016, MNRAS, 456, 3638 [NASA ADS] [CrossRef] [Google Scholar]
- Zanin, R., Fernández-Barral, A., de Oña Wilhelmi, E., et al. 2016, A&A, 596, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Malyshev, D., Chernyakova, M., & Pooley, G. G. 2017, MNRAS, 471, 3657 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Malyshev, D., Dubus, G., et al. 2018, MNRAS, 479, 4399 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Sketch of considered scenario (not to scale). We show a jet segment at a height z (black dot) and its projection in the xz-plane (grey dot). We also show the recollimation height zrec, the length l along the jet, the jet half-opening angle θj, the jet bending angle with respect to the z-axis (θ), the inclination angle of the orbit i, the orbital separation a, the star radius R⋆, and the orbital phase φ (set to 0 and 0.5 for the inferior and superior conjunctions, respectively). The counter-jet (not shown) is symmetric to the jet with respect to the xy-plane. |
| In the text | |
 |
Fig. 2. Trajectory followed by the jet for γj = 1.2 (solid purple line) and 3 (solid green line). The projections in the orbital plane are also shown with dashed lines. The jet length is 50a, and the counter-jet is symmetric to it with respect to the xy-plane (not shown). The blue circle at the origin of coordinates represents the star (to scale). The jets are plotted starting from the corresponding recollimation shocks. |
| In the text | |
 |
Fig. 3. Energy distribution of the electrons along the jet up to 0.1a (dotted line), a (dashed line), and the whole jet (solid line), for γj = 1.2, ηB = 10−2 (top panel), and ηB = 1 (bottom panel). The contribution of the individual jet segments is color-coded, with the color scale representing the position of each segment along the jet. Segments have a constant length of dl = 1011 cm ≈ 0.03a. |
| In the text | |
 |
Fig. 4. Characteristic timescales for the first jet segment for γj = 1.2 and ηB = 10−2. Cooling (solid lines), acceleration (dashed line), and diffusion (dotted line) processes are shown. |
| In the text | |
 |
Fig. 5. Total (jet + counter-jet) synchrotron and IC SEDs for γj = 1.2, i = 30°, φ = 0.25, and ηB = 10−2 (purple lines) and 1 (green lines). Dashed lines show the contribution of the jets beyond a length a, and black dotted lines represent the unabsorbed emission. |
| In the text | |
 |
Fig. 6. SEDs of the jet (purple lines) and the counter-jet (green lines) for ηB = 10−2, φ = 0.25, i = 0 (top) 30° (middle) and 60° (bottom), and γj = 1.2 (solid lines) and 3 (dashed lines). |
| In the text | |
 |
Fig. 7. Doppler boosting factor as a function of jet position for φ = 0.25, γj = 1.2 and 3, and i = 0 (solid lines), i = 30° (dashed lines), and i = 60° (dotted lines). The black solid line at |
| In the text | |
 |
Fig. 8. Total synchrotron and IC SEDs for γj = 1.2, ηB = 10−2, i = 30° (top) and 60° (bottom), and different orbital phases between 0 and 0.5. SEDs for 0.5 < φ < 1 are not represented because they almost overlap with those shown. |
| In the text | |
 |
Fig. 9. Same as in Fig. 8, but for γj = 3.0. Note the change in the y-axis scale. |
| In the text | |
 |
Fig. 10. Integrated light curves for γj = 1.2, ηB = 10−2, i = 30° and 60°, and different photon energy ranges. Purple lines represent the values for bent jets such as those in Fig. 2, whereas green lines represent the results for straight jets. Dashed lines show the orbit-averaged flux values. Note the change in the flux normalization for each i. |
| In the text | |
 |
Fig. 11. Same as in Fig. 10, but for γj = 3. |
| In the text | |
 |
Fig. 12. Same as in Fig. 10, but for γj = 3 and ηB = 10−4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



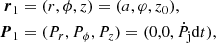
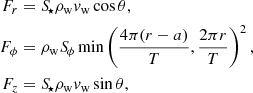
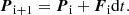
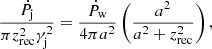
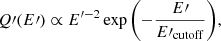
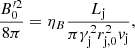
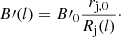
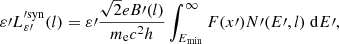
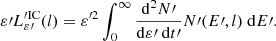
![$$ \begin{aligned} \tau _{\gamma \gamma }(\varepsilon ) = \int _0^d \mathrm{d}s \ [1-\cos {\theta _{\gamma \gamma }(s)}] \int _{\varepsilon _0^\mathrm{min}(\theta _{\gamma \gamma })}^\infty \mathrm{d}\varepsilon _0 \ n(\varepsilon _0) \sigma _{\gamma \gamma }(\varepsilon ,\varepsilon _0,s), \end{aligned} $$](/articles/aa/full_html/2019/09/aa35960-19/aa35960-19-eq53.gif)