| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201935374 | |
| Published online | 09 August 2019 | |
Superflares on AB Doradus observed with TESS
Hamburger Sternwarte,
Gojenbergsweg 112,
21029
Hamburg,
Germany
e-mail: jschmitt@hs.uni-hamburg.de
Received:
27
February
2019
Accepted:
30
April
2019
We present short-cadence data of the ultra-active star AB Dor measured by the Transiting Exoplanet Survey Satellite (TESS). In the TESS light curves of AB Dor, we found numerous flare events in addition to time-variable rotational modulation with an amplitude of up to 7%. We identified eight superflares (releasing more than 1034 erg) and studied their morphologies and energetics. We compared these flares to both the most energetic solar flare seen in total solar irradiance measurements as well as to a very energetic flare on AB Dor observed by XMM-Newton, the superflare nature of which we also demonstrate. The total energy of both the solar flare and the event on AB Dor emitted in the optical exceed their respective X-ray outputs possibly by an order of magnitude, suggesting that the dominant energy loss of such flares actually occurs at optical wavelengths. Superflares are found to take place on AB Dor at a rate of about one per week, and due to the star’s proximity and brightness can be studied in excruciating detail. Thus the TESS data offer a superb possibility to study the frequency and energetics of superflare events for stars in the solar neighborhood and at large.
Key words: stars: activity / stars: flare / stars: solar-type
© ESO 2019
1 Introduction
While flare stars as a class of variable stellar source have been known since the late 1940s (Švestka 1954), up to a few years ago essentially no data on flares from solar-like stars in the optical band were available. On the Sun white light flares have been known for a long time (Neidig 1989), however, these flares are difficult to observe since one usually requires spatially resolved observations of the flare site on the solar disk. In spatially integrated, “stellar-like,” full-disk observations of the Sun, white light flares can only occasionally be observed (Woods et al. 2004; Kopp et al. 2005; Kretzschmar et al. 2010; Kretzschmar 2011).
There is considerable interest in what is the largest flare the Sun is capable of producing. Solar flares and especially the solar energetic particles (SEP) produced in such events can have substantial impact on the Earth if and when they enter the Earth’s magnetosphere, as evidenced, for example, by the famous electric power blackout in Québec on March 13, 1989, a consequence of an X15 flare associated with a coronal mass ejection on March 10, 1989. The damage caused by such geomagnetic storms can be very massive and this particular event has contributed to producing an awareness of the issue of “space weather” on Earth. Clearly protective measures can be taken, but what is the largest possible solar flare one needs protection from?
Using state-of-the-art magnetohydrodynamic (MHD) models, Aulanier et al. (2013) study the energies that can be maximally released in solar flares and conclude that this maximum energy amounts to ≈6 × 1033 erg. On the same issue, Shibata et al. (2013) take a different approach and study the magnetic flux generation and emergence in the Sun using basic dynamo theory since large flares require the build-up of sufficient magnetic flux. Shibata et al. (2013) then argue that the timescale for the magnetic flux storage necessary for a 1034 erg flare is well below the solar cycle period, while that for a 1035 erg flare is about 40 yr, raising the question of whether and how the premature emergence of this large magnetic flux can be inhibited. The largest solar (X-ray) flare so far recorded in modern times appears to be that of November 4, 2003, which saturated the X-ray detectors on the GOES-12 satellite for 12 min and is believed to have been of class X40 (Brodrick et al. 2005). The famous “Carrington event” (Carrington 1859) was definitely a solar flare, causing substantial geomagnetic disturbances, yet we have no way to ascertain its total energy output.
Furthermore, it has been suggested that several historical events were caused by solar flares, which would have had to be almost two magnitudes stronger than the strongest solar flares hitherto observed (Usoskin 2017). One case in question is the so-called “Charlemagne event” in AD 745, which was recorded in tree rings all over the Earth as an increase in the isotopic abundance of 14C produced as a byproduct of atmospheric cascades induced by cosmic-rays (Usoskin 2017). However, one should bear in mind that quite a number of possible interpretations have been proposed for this event, ranging from comet impacts to a nearby supernova explosion (see Stephenson (2015) for an overview). Still to us the interpretation of the “Charlemagne event” as a rather extreme SEP event appears to be the most plausible (and conservative) one. This would be in line with a similar enhancement of 14C detected in tree rings around the year 994 AD, which is associated by Hayakawa et al. (2017) with the occurrence of spectacular aurorae as reported by various sources in Korea, Germany, and Ireland, suggesting indeed very large geomagnetic storms driven by solar activity as the cause of the observed 14C anomaly.
The Kepler mission (Borucki et al. 2010) has fundamentally changed optical monitoring photometry. With the Kepler telescope, more than 150 000 stars were continuously monitored for four years. Following up on earlier work by Schaefer et al. (2000) in studies dedicated specifically to solar-like stars, Maehara et al. (2012) and later Shibayama et al. (2013) report the discovery of powerful flares with energy releases up to 1036 erg and more, that is, much larger than those observed for the Sun, dubbing those events “superflares”. It should be noted that there is no universally agreed upon definition of a superflare; for the purposes of this paper we refer to superflares as flares with a total energy output in excess of 1034 erg.
In a follow-up study, Maehara et al. (2017) examine the Kepler light curves of 64 239 main sequence stars in the effective temperature range 5600 K < Teff < 6300 K to search for those stellar parameters most relevant for the occurrence of superflares. Not unexpectedly, the greatest superflare producers are those stars with the largest rotational variations and the shortest periods. Interestingly Maehara et al. (2017) conclude that their “results suggest that the magnetic activity we observe on solar-type stars with superflares and on the Sun is caused by the same physical processes.” This is in conflict with the expectations of maximally possible flare energies for a sun-like star (cf., Aulanier et al. 2013), but not necessarily with the magnetic flux considerations proposed by Shibata et al. (2013).
A nearby, bright, rapidly rotating, heavily spotted, and chromospherically and coronally very active star is the star AB Dor, which according to the above ought to be a copious producer of superflares. The purpose of this paper is to examine the first two available months of AB Dor TESS data for the occurrence of optical superflares and relate them to the known X-ray properties of AB Dor.
2 AB Doradus and the TESS satellite
2.1 The target star AB Doradus
AB Dor is a very active, nearby star (d = 15.3 pc) with a rotation period of 0.51 days. AB Dor A is a member of a quadruple system discussed in detail by Guirado et al. (2011), however, the other system components are much fainter and ignored in the following. As a consequence of its rapid rotation, AB Dor shows the usual magnetic activity phenomena such as star spots and strong chromospheric and coronal emission.
In the X-ray range, AB Dor has been observed essentially with all satellites ever since its detection as an X-ray source by the Einstein Observatory (Pakull 1981). Extensive X-ray studies of AB Dor were later carried out with ROSAT (Kürster et al. 1997), XMM-Newton (Güdel et al. 2001, Lalitha et al. 2013), and Chandra (Hussain et al. 2007). AB Dor frequently flares at X-ray wavelengths, and a detailed statistical study of these X-ray flares is presented by Lalitha (2016), extending an earlier study based on GINGA data by Vilhu et al. (1993).
Furthermore, extensive ground-based photometry of AB Dor taken over decades is available and has been presented by Järvinen et al. (2005). One of the main results of this study is the conclusion that the “spots on the surface of AB Dor are grouped around two active longitudes which are separated on average by 180° and migrate with a variable rate due to surface differential rotation.”
Due to its photospheric modulations and rapid rotation, AB Dor is a prime target for Doppler imaging. For example, images showing the spatial distribution of star spots have been presented by Kürster et al. (1994); and on the basis of a series of Doppler images, Donati & Collier Cameron (1997) derive a differential rotation law of the form Ω(l) = 12.2423–0.0564 sin(l)2 rad day−1, with Ω(l) denoting the latitudinal dependence of the rotation rate. Furthermore, Doppler imaging allows an estimate of the inclination i of the stellar rotation axis with respect to the observer, and values of i ≈ 60° are found.
2.2 The TESS satellite
The Transiting Exoplanet Survey Satellite (TESS) was launched on April 18, 2018 into a highly elliptical 13.7 day orbit in a 2:1 resonance with the Moon, which provides a very stable environment for its operations; a detailed description of the TESS mission is given by Ricker et al. (2015). The TESS mission is devoted to detecting exoplanets around the brighter stars by using the transit method, and to this end TESS performs differential photometry for many hundreds and thousands of stars. TESS is equipped with four red-band optimized, wide-field cameras that continuously observe a 24° × 96° strip on the sky for 27 days consecutively.
The light curves of pre-selected targets are downloaded with a cadence of two minutes, while the full-frame images are available with a cadence of 30 min. Our study of AB Dor is based upon the short-cadence TESS data, made publicly available with the first two data releases in December 2018 and January 2019. Because of its fortuitous location close to the southern ecliptic pole, AB Dor is essentially monitored by TESS more or less continuously during the satellite’s first year of operation. The TESS light curves were generated with the so-called Science Processing Operations Center (SPOC) pipeline, which was derived from the corresponding pipeline for the Kepler mission (Jenkins et al. 2016)1.
3 Results
3.1 TESS light curves for AB Dor
In Fig. 1 we provide an impression of the quality of the TESS short-cadence data of AB Dor: we show the SAP flux as a function of time for one day, covering almost two rotations of AB Dor; since AB Dor is rather bright, the formal (relative) errors of the TESS flux measurements are on the order 10−4 and entirely negligible. The light curve reveals large peak-to-peak modulations, the light curves near flux maximum (with smallest spot coverage) are very similar, and one recognizes two small flares at T = 1327.55 d and T = 1328.05, and a much larger flare at T = 1327.92 d, which we discuss in detail below. The low data points near T = 1327.845 d are artifacts after a data gap and have been removed from analysis. For all times we use the TESS convention, meaning the quoted times are barycentric dynamical time with the number 2 457 000 removed. In the data covering the first two months there are some gaps and some parts of the data are quite noisy, which are therefore excluded from further analysis.
In Fig. 2 we present the total TESS light curve of AB Dor folded with a period of 0.514275 days. It should be noted that the chosen phasing is arbitrary and the phase ϕ = 0 has been setto that time when the star is consistently encountered at maximum brightness. This light curve is remarkable for its large amplitude of modulation, reaching a peak-to-peak variation of 7% as well as the occurrence of substantially sized flares. This is a little surprising since the TESS band (cf., our discussion in Sect. 3.3) is quite red and centered on the I band, while flares are normally observed in the B or U band.
To show the temporal evolution of the star spots on AB Dor, we plot the same data in a time-brightness diagram in Fig. 3. Both Fig. 2 and Fig. 3 show that the dark feature near phase ϕ ~ 0.25 and the bright feature near phase ϕ ~ 0 are very stable over the two months of TESS data currently available. On the “other” hemisphere of the star near phase ϕ ≈ 0.6, the photometric variability is much larger. At times this hemisphere contains only few spots and reaches levels of brightness near ϕ ≈ 0, while at other times this hemisphere is far more spotted, although never lowers to the brightness observed near phase ϕ ≈ 0.3.
We note that our folding period of 0.514275 days does not agree with AB Dor’s “canonical” rotation period of 0.51479 days as reported by Innis et al. (1988). Since photometry always measures the period of the spots dominantly causing the rotational modulation, finding different periods at different epochs need not be surprising. In the present case, that difference amounts to only 0.1% and could be explained by spots located at different latitudes rotating with different periods. We further note in this context that Pakull (1981) quotes a period of 0.51423 ± 0.00005 days, which is actually very similar to “our” period.
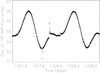 |
Fig. 1 Part of TESS AB Dor light curve with typical features; see text for details. |
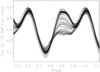 |
Fig. 2 TESSAB Dor light curve folded with a period of 0.514275 days. It should be noted that the data points with phase belowzero and above unity are repeated for better visibility. See text for details. |
3.2 Large flares on AB Dor
In the short-cadence TESS light curve of AB Dor (cf., Fig. 2) one recognizes numerous flare events. Here we want to concentrate on large flares in the superflare regime, which we identify by visual inspection. Such flares need to be detected against the “background” of rotational modulation of the light curve. To subtract this “background”, we consider either the data with the same rotational phase before or after the flare event, or model the “background” with a low order polynomial connecting flare-free data before and after the flare event. Needless to say, there is always some ambiguity. While the start of the flare is very rapid and can be determined quite accurately, the end of the flare is more difficult to determine and depends on the chosen background model. Fortunately, the latter problem is not as severe for the flare energetics, which we are mostly interested in. We are confident that the largest flares with a rapid rise were all identified.
In the following we present the large flares that we identified in the TESS light curves of the first two releases. We provide the photospheric background-subtracted TESS light curves and estimates for the flare start, flare peak, and its decay time. Our results are summarized in Table 1 and our procedures for deriving the flare luminosities and energetics are described in Sect. 3.3.
 |
Fig. 3 TESSAB Dor light curve folded with a period of 0.514275 days as a function of time (from bottom to top); see text for details. |
 |
Fig. 4 TESS light curve of flare 1. Shown are the photospheric background-subtracted flux measurements (diamonds) and an “ad hoc” flare model (solid curve); see text for details. |
3.2.1 Flare 1
In Fig. 4 we show the TESS light curve of flare 1, which occurred at BJD 1327.89. We show the photospheric background-subtracted TESS measurements and an “ad hoc” flare model (solid line), which consists of a linear rise from zero to the largest measured data point, followed by a simple exponential decay. Flare 1 is a like a textbook example of a stellar flare. The rise phase isbarely resolved by short-cadence TESS data so that we can merely say it is greater than two and less than four minutes. Also, the peak flux and hence the peak luminosity are averages of over two minutes, with the true peak values likely to be quite a bit larger. On the contrary, the decay is well resolved and almost perfectly described by an assumed simple exponential decay with a characteristic decay timescale of 480 s. The whole event can be traced for almost 40 min, although it is naturally difficult to determine the precise “end” of the flare, meaning when the flare signal merges with the rotationally modulated stellar signal. During forty minutes the star rotates by almost 20° and normally there is substantial variation on this timescale (cf., Fig. 1).
3.2.2 Flare 2
In Fig. 5 we show the TESS light curve of flare 2, which occurred at BJD 1328.70. Again we show the photospheric, background-subtracted TESS measurements and our “ad hoc” flare model (solid line). Flare 2 shows a more complicated temporal structure. Again, the rise phase is barely resolved, and the second flare data point is already at the maximum. Then, as in flare 1, an exponential decay is observed, yet after about 15 min a second event starts. We estimate the total energy release in this second, smaller event to about 30% as compared to that of the main event. Since we have no further information, this second event could of course be entirely independent from the first one, however, flares with that strength do occur on AB Dor more or less regularly, although the probability for two such events to occur simultaneously is small. The same proportions apply to the total energy output.
 |
Fig. 5 TESS light curve of flare 2. Shown are the photospheric background-subtracted flux measurements (diamonds) and an “ad hoc” flare model as in Fig. 4. |
3.2.3 Flare 3
In Fig. 6 we show the TESS light curve of flare 3, which occurred at BJD 1346.84. Flare 3 holds the record in our sample of TESS flares observed on AB Dor. Due to its long decay timescale of 3000 s, the total energy release of 5 × 1035 erg is the largest one observed so far. Yet the rise time of this flare is again quite short, with the flare reaching its maximum in less than sixminutes. The decay time is extremely well described by an exponential law and the apparent deviations towards the end may well be caused by an incorrect “background” subtraction as is the curvature in the light curve prior to flare start. Since the total energy output is determined by the product of peak amplitude and decay time, the numbers quoted in Table 1 should not be significantly affected.
3.2.4 Flares 4–7
In Figs. 7–10 we show the TESS light curves of the remaining large flares 4–7, which occurred at BJD 1351.87, BJD 1360.10, BJD 1370.82, and BJD 1379.29 respectively. As is immediately apparent, flares 5 and 6 exhibit a simple exponential decay, while flares 4 and 7 have a more complicated structure.
3.2.5 Flare 8
Flare 8, whose light curve is shown in Fig. 11, is a special case. As is clear from Fig. 11, the flare shows, in comparison to the other flares presented in this paper, a somewhat unusual morphology.First of all, the flare rise is not as fast; it takes about 20 min to reach the peak luminosity of 3 × 1031 erg s−1, which is notvery large compared to the other flares (see Table 1). After the peak the light curve decreases exponentially with a decay time of about 1500 s unit about 30 min after peak, when the decay becomes slower. The light curve becomes more irregular with several heating events taking place, and merges after about 4.5 h into the photospheric background. The whole event lasts about 5.5 h, which corresponds to 45% of AB Dor’s rotation period, yet no signs of self eclipses are visible in the light curve. Hence, the flare site was either quite fortuitously placed for us earthlings or located in AB Dor’s northern hemisphere close to or even in its polar regions.
We point out in this context that the above interpretation heavily depends on which photospheric background model is subtracted. The flare did occur at a phase (ϕ ≈ 0.8), where this background shows the largest variations (cf. Fig. 2). The flare light curve shown in Fig. 11 was constructed by subtracting the photospheric background encountered in the subsequent rotation, which agrees well with the photospheric background measured in previous rotation prior to the flare and six hours after the flare. However, there may be the possibility that we are being misled by the data and that the flux elevation seen after about 100 min in Fig. 11 is not related to the flare event but to a photospheric background variation. Inthis case, the total energy reported in Table 1 would have to be reduced by a factor of three.
Measured quantities and derived physical parameters for the observed flares.
3.3 TESS response and flare energetics
The spectral band pass of TESS is relatively broad and comprises the wavelength range between 6000 Å and 10 000 Å centered on the I-band and captures only some part of the overall flux. In Fig. 12 we plot the fraction of the total flux of a blackbody source recorded in the TESS band as a function of temperature. As seen in Fig. 12, the largest fraction of ≈0.35 is observed fortemperatures near 5000 K, and for lower and higher temperatures that fraction decreases since the spectral regions contributingmost of the flux move outside the band pass.
We are aware of the fact that the photospheric spectrum of AB Dor is not that of a blackbody, but a rather complicated superposition of “mini-photospheres” with different effective temperatures, yet a more detailed modeling is not warranted here, given the broadband TESS data. The problem becomes aggravated when the flare sets in. In the early phases of flares one usually sees a zoo of emission lines (Fuhrmeister et al. 2008), and the flare temperature varies essentially all the time. The flare temperatureis known to considerably exceed the photospheric temperature, eventually falling back to photospheric temperatures.
Since the TESS data provide no means diagnose these changes, we assume ad hoc a constant mean temperaturefor the flaring plasma. Since the typical (photospheric) flare temperatures are in the range 8000–15 000 K, it is clear that a substantial fraction of the emission falls outside the TESS band pass. To convert the instrumental TESS fluxes into physical values, we assume a bolometric flux for AB Dor of 1.5 × 1033 erg sec−1 and a distance of 15.3 pc. In the literature one finds a range of possible effective temperatures, yet those differences lead to very small changes in the conversion from SAP rates to energy fluxes. The flares are characterized by a more or less linear increase from zero tothe peak, followed by a more or less exponential decay. Most of the energy is radiated during the decay phase. To convert the flare SAP rates, we assume a (constant) flare temperature of 12 000 K and the curve shown in Fig. 12. Since we have no information on the flares’ cooling history, there is substantial uncertainty in the numbers provided in Table 1. Changing the temperature between 8000 and 15 000 K leads to changes by a factor of two, such that more emission is produced at higher temperatures. Since most of the flux is emitted in the early decay phase when the temperature is larger, the actual numbers might be even larger. A quantitative estimate of the accuracy of our energy output estimates is essentially impossible, but we believe that our numbers are accurate to about 50%.
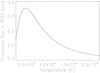 |
Fig. 12 Fraction of total emitted flux registered with the TESS sensitivity as a function of blackbody temperature. |
3.4 Flare-filling factors
With the numbers above we can derive rough estimates for the flare-filling factors. Based on the determined peak luminosity and assumed flare temperature, the emitting area can be computed from Stefan–Boltzmann’s law. For example, for flare 1 with Lpeak = 1032 erg s−1 one finds (assuming a circular area) a radius of ≈50 000 km, and the flare site radii scale with the square root of the observed peak luminosity; given all the uncertainties, these numbers should be considered as estimates of order of magnitude. At any rate, as expected, the involved flaring areas are still small compared to the stellar radius. This finding is in stark contrast to the spot filling factors required to explain the observed modulations of up to 7%. Using the formulae provided by Maehara et al. (2017), we find spot-filling factors of 10–20% for the whole star, depending on the assumed temperature difference between spots and unperturbed photosphere.
3.5 Comparison with X-ray flare observations of AB Dor
As an active star, AB Dor is known to be a copious producer of X-ray emission and X-ray flares. Because of its fortuitous location on the sky, AB Dor is being used by XMM-Newton as a spectral calibration source and has consequently obtained long exposure times. Lalitha (2016) analyzed these observations for flares and managed to identify a total of 45 flares in these data. The total XMM-Newton “on-time” is more than 1000 ksec, corresponding to more than eleven days. However, these data are somewhat heterogeneous with respect to exposure times (some exposures are quite short) and instrumental setups (some exposures were run only with the reflection grating spectrometer), yet we can be certain that the total XMM-Newton exposure was at least one week. As with our TESS data, estimates for the peak X-ray luminosity LX,peak and total released (X-ray) energy Etot,X-ray could be obtained. Inspecting Table 1 in Lalitha (2016), one finds peak X-ray luminosities of a few times 1030 erg s−1 with a spread of a factor of four to five, and total emitted (X-ray) energies in the range of a few 1032 erg to below 1034 erg. None of the 45 flares studied by Lalitha (2016) exceed 1034 erg in terms of total (X-ray) energy release. The largest flare is the one analyzed in detail by Lalitha et al. (2013), which we re-analyze in the following.
A detailed analysis of this flare, which was observed in the context of of a multi-wavelength campaign involving XMM-Newton and VLT UVES, was described by Lalitha et al. (2013). The light curve morphology of this event (see Fig. 1 and Table 2 in that paper), was rather complicated. The observed count rate first increased quite rapidly, followed by a similarly rapid decrease. Afterwards, the count rate stayed more or less constant for an hour, whereupon it decreased again for about two hours reaching preflare levels. Then a third and smaller second event occurred. Two large spikes coincident with the X-ray events were observed in the XMM-Newton optical monitor (OM), operated in fast mode with the UVM2 filter, which has a band pass in the ultraviolet centered at around 2310 Å, with a width of 480 Å. Here we consider only the first event, assuming that the second event was unrelated. Unfortunately, no concurrent ground-based photometry is available for these observations.
In Fig. 13 (lower panel) we show the data taken with the XMM-Newton OM and in Fig. 13 (middle panel) the available reprocessed XMM-Newton data in the X-ray range (XMM-Newton EPIC pn) with a time resolution of 10 s. A quiescent rate of 30 cts s−1 has been subtracted from the pn data, setting the pre-flare level to zero (cf., Fig. 13). In theXMM-Newton X-ray light curve, one recognizes an enhancement of about 5 cts s−1 in the two hours prior to the flare; whether or not this is related to the flare eruption, is unknown. A quiescent rate of 73 cts s−1 has been subtracted from the OM data, and for better visibility the OM data is plotted logarithmically to better demonstrate the decay time behavior.
In its fast mode, the OM cannot be operated continuously and between individual exposures shorter time gaps of a few hundred seconds appear. Unfortunately, the start and rise phases of the large flare were not covered with the OM, but were covered only in the X-ray range (cf., Fig. 13), so that the actual peak emission of the flare may have remained unobserved in the OM data. However, if we assume first, that the start times of the X-ray and UV flare coincide, and second, that the rise time is two minutes, then the solid curve shown in Fig. 13 (lower panel) results, from which we conclude that the observed peak in the OM rate must be very close to the actual peak rate. This conclusion can only be avoided by assuming that the UV flare started considerably earlier than the X-ray flare, and/or, that its rise phase was much shorter than two minutes, and both of these assumptions appear unlikely. Also, concurrent VLT/UVES spectral data (albeit with a lower time resolution) support this conclusion; see Lalitha et al. (2013) for more information on this data set.
As demonstrated by the solid line in Fig. 13 (lower panel), the decay of the OM light curve can be well described by two distinct exponential phases, a first fast decay phase with a decay timescale of 250 s, and a second slow decay phase with a decay timescale of 2000 s. In addition there seems to appear another heating event near 75 min and the gap starting at 95 min is again caused by the start of a new OM exposure. Just like the X-ray light curve, the observed OM rate stays above preflare levels all the time, however, we can obviously not exclude variations in the background level. Only after the second flare (not shown in Fig. 13) are pre-flare levels reached.
From our empirical light curve model it is straightforward to compute the total number of flare counts attributable to the flare. Using the conversion factor from count rate to flux provided in the XMM-Newton Science Analysis System User guide2 we compute the total cumulative energy release, registered in the OM data, as a function of time; this curve is plotted as solid line in Fig. 13 (upper panel), and we find a total OM energy release (for the first flare) of 5.6 × 1033 erg in the OM band. Carrying out the same exercise for the EPIC pn flare, we can directly integrate the registered X-ray light curves, convert to luminosities using a conversion factor of 1.59 10−12 erg cm−2 ct−1, as appropriate for a solar abundance plasma with log (T) = 7.25, and a distance of 15.3 pc, which results in the dashed line in Fig. 13 (upper panel). After 85 min about 4.8 × 1033 erg were released, and overall about 1 × 1034 erg were released in the first flare.
Since the OM calibration has been derived from white dwarfs, the derived fluxes and energies ought to be quite accurate for our flare data. However, substantial parts of the total optical flux appear at out-of-band wavelengths especially at later times when the flaring plasma may be cooler. It is difficult to correct for this out-of-band flux, since we neither know the spectral energy distribution nor the cooling history of the flare. Experimenting with blackbody spectra, we find that for temperatures of 15 000 K the OM UVM2 captures 15% of the total flux, and that ratio is continuously decreasing with lower temperatures, reaching sub-percent levels for temperatures of 6000 K and below. We therefore estimate it to be quite likely that only about 10% (and possibly even less) of the total (optical) flux are actually captured by the OM and that, therefore, the total flare energy in the optical exceeds 3.5 ×1034 erg. As can be seen from Fig. 13, during the first 30 min more energy was released in the OM band alone than in the X-ray band,and correcting for out-of-band losses we are led to the conclusion that the total radiative flare energy loss is dominated by radiation at optical but not at X-ray wavelengths. As far as the rate of such flare events on AB Dor is concerned, both the XMM-Newton and TESS data are consistent with a rate of about one to two per week.
 |
Fig. 13 Light curves of the flare on AB Dor (from November 26, 2009) observed with EPIC pn (diamonds), OM UVM2 (crosses, scaled by a factor 0.2) and solid line denoting our empirical model; see text for details. |
3.6 Comparison with solar flares
It is furthermore instructive to compare our results of AB Dor superflares to the largest solar flares observed in total solar irradiance measurements (TSI), which is the X17 flare from October 25, 2003. Kopp et al. (2005) present a detailed analysis of these data and derive from their TSI data a total flare energy release of 5 × 1032 erg, albeit with substantial uncertainty, as first, solar oscillations provide a time variable background (against which the flare decay needs to be identified), and second, the spacecraft went inopportunely into the Earth’s shadow, so that part of the flare’s TSI light curve remained unobserved. Yet the phenomenology of this solar flare appears to be very similar to the AB Dor flares reported in this paper: It has a short rise time of two to four minutes, and a long decay time with a typical decay timescale of about 900 s (see Fig. 7 and Fig. 8 in the paper by Kopp et al. 2005). Woods et al. (2004) use additional, spectrally resolved irradiance measurements to study the distribution of the released energy over the different wavebands and conclude that only about 20% of the flare’s energy was emitted at XUV and X-ray wavelengths, implying that the bulk part of the flare’s energy was emitted at optical wavelengths. These results are confirmed and expanded by Kretzschmar (2011), who in studying the stacked, butspectrally resolved light curves of solar flares as a function of the total energy released arrives at similar conclusions.Therefore, the solar X17 flare from October 25, 2003 seems to have had very similar properties to the AB Dor flare from November 26, 2009, and by analogy we suggest thatthe same applies to the TESS flares reported in this paper. Finally, we note that what is likely to be the largest solar flare measured in modern times, that is the class X40 flare discussed by Brodrick et al. (2005), occurred right at the solar limb, and was thus, in contrast to the X-ray range, only faintly visible in TSI data (Kopp et al. 2005).
4 Discussion and conclusions
A flare represents a rather complicated, time-dependent phenomenon. Both in the solar case (except for those few flares with TSI measurements) and in the stellar case, it is notoriously difficult to measure the total energy budget of flares, since time-dependent multi-wavelength data are required. There are a few reports of ground-based observations of superflares in the literature. For example, Mathioudakis et al. (1992) present flare observations of the RSCVn star II Peg and report two flares with U-band energies of 1.8 1035 erg, without giving many details of their observations. II Peg is also known to produce powerful X-ray flares, and an analysis of a flare having triggered the Burst Alert Telescope onboard SWIFT by Osten et al. (2007) yielded a total energy loss of about 6 × 1036 erg at energies above 10 eV. Earlier, a very large flare on II Peg had been observed using the GINGA satellite, but the various flare phases were not covered completely in the different wavebands, so that the estimates of the overall energy release remained somewhat uncertain (Doyle et al. 1991).
In pre-Kepler times, reports of energy releases in stellar flares on the order of > 1036 erg were rare, but not unique: For example, Schmitt & Favata (1999) describe a giant flare on Algol with a total X-ray output of ≈1.5 × 1037 erg; Kürster and Schmitt (1996) a flare on the RS CVn star CF Tuc with an output of ≈1.4 × 1037 erg; and Preibisch et al. (1995) a giant flare on the T Tau star P1724 with a total X-ray release of 5 × 1037 erg. As far as optical observations are concerned, Kozhevnikova et al. (2007) report the observation of a large flare on the RS CVn-like variable star WY Cnc, observed in the B, V, and R bands and reaching a magnitude of 0.134 mag in the B band. As with our TESS AB Dor flare, a short rise time of about three minutes was observed, followed by a much longer decay time of 64 min. From their photometry Kozhevnikova et al. (2007) derive total energy losses of 10.2 × 1034 erg, 5.63 × 1034 erg, and 0.96 × 1034 erg in the B, V, and R bands respectively, which put that flare well into the superflare category. There appear to be no dedicated X-ray observations of WY Cnc, yet an inspection of the catalog of ROSAT all-sky survey (RASS) sources by Boller et al. (2016) shows the X-ray source 2RXS J090155.1+264112, which we identify with WY Cnc. Translating the measured RASS rate of 0.49 ± 0.04 cts s−1 into an X-ray luminosity, assuming a distance of 71 pc, we find a value of 2 × 1030 erg s−1, a typical value for an RS CVn system, and, as a matter of fact, also for AB Dor (Lalitha et al. 2013).
Flare observations in the optical range have traditionally been carried out at blue wavelengths using Johnson B or U filters. Since the flaring plasma in the photosphere and chromosphere has temperatures around 10 000 K, these filters are appropriate.Also, for the rather cool M-type stars, the contrast between flaring and non-flaring atmospheres is largest at these wavelengths. What is easily overlooked in this context is that the flaring plasma emits large fractions of its radiation spectrum at out-of-band wavelengths. It is a straightforward exercise to compute that fraction of the total emitted spectrum (assuming blackbody spectra for simplicity) that are captured, for example, in the U, B, and TESS bands, whereupon one finds that for temperatures below 12 000 K the flux fraction in the red TESS band is actually larger than in the bluer bands, and is steadily increasing towards lower temperatures. Along the same vein, computing for a star with a surface temperature of 5000 K (as appropriate for AB Dor) and assuming a flare comprising, say, 1% of the star’s surface, we find a flux increase of around 10% for a flare temperature of Tfl = 10 000 K and 1% for Tfl = 6000 K. Given the superb quality of the TESS photometry for the rather bright star AB Dor (the formal errors of the flux measurements are about 0.015%), it is therefore clear that flares with surface areas considerably smaller than 1% of AB Dor’s surface can be detected, with the proviso that the variations in the photospheric background can be adequately modeled.
Thus in contrast to Kepler, TESS allows the investigation of superflares on nearby, often well-studied stars. Our study of the first two months of TESS data of the active star AB Dor clearly demonstrates that superflares with total energy releases above 1034 erg, can be well studied with TESS photometry despite the quite red sensitivity of TESS CCDs and the large rotational modulation of the light curve. The TESS data suggest an occurrence rate of such flares of about one per week. The optical rise times of these flares are always quite fast with rise times of two to three minutes. On the other hand, the decay times can vary substantially. In about half the cases one observes a more or less simple exponential decay, in the other cases more complicated decay light curves are observed.
Comparing our results to a statistical study of X-ray flares of AB Dor by Lalitha (2016), we find that none of the X-ray flares is comparable in terms of energy output with the TESS superflares, suggesting that flares release more energy in the optical than in the X-ray band. This conclusion is corroborated by a detailed multi-wavelength analysis of a large flare on AB Dor, as well as the largest solar flares observed. Thus, the energy release of at least the larger flares in the optical exceeds the energy release at X-ray wavelengths reaching an order of magnitude in contradiction to some preconceived notions. In the approximately eight weeks of TESS observations of AB Dor, three flares with energy releases above 1035 erg, and five flares with energy releases in the range 1034 –1035 erg were observed. Computing the flare rates and comparing them to the rates derived by Shibayama et al. (2013) yields good agreement (cf., Fig. 8 in that paper), but clearly once the full set of TESS AB Dor is available, a rather accurate flare frequency diagram can be constructed for this star. The flare rate of the star KIC10422252, the most frequent superflarer in the sample of Shibayama et al. (2013) with 57 superflares in about 500 days, agrees well with that observed for AB Dor. However, little is known about KIC10422252. Its Gaia parallax of 1.128 (±0.0018) mas puts it at a rather large distance and a few magnitudes above the main sequence, yet this distance seems inconsistent with the similarly large proper motion. The TESS data offer the possibility to study nearby, well-known stars, which are also capable of producing superflares, and the TESS data already collected and to be collected until its mission end are expected to contain thousands of superflares waiting to be explored.
Acknowledgements
This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). This paper also includes observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. We further acknowledge fruitful discussions with Dr. G. Kopp on the energetics of powerful solar flares.
References
- Aulanier, G., Démoulin, P., Schrijver, C. J., et al. 2013, A&A, 549, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brodrick, D., Tingay, S., & Wieringa, M. 2005, J. Geophys. Res. Space Phys., 110, A09S36 [Google Scholar]
- Carrington, R. C. 1859, MNRAS, 20, 13 [Google Scholar]
- Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, J. G., Kellett, B. J., Byrne, P. B., et al. 1991, MNRAS, 248, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., Liefke, C., Schmitt, J. H. M. M., & Reiners, A. 2008, A&A, 487, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Audard, M., Briggs, K., et al. 2001, A&A, 365, L336 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guirado, J. C., Marcaide, J. M., Martí-Vidal, I., et al. 2011, A&A, 533, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayakawa, H., Tamazawa, H., Uchiyama, Y., et al. 2017, Sol. Phys., 292, 12 [Google Scholar]
- Hussain, G. A. J., Jardine, M., Donati, J.-F., et al. 2007, MNRAS, 377, 1488 [NASA ADS] [CrossRef] [Google Scholar]
- Innis, J. L., Thompson, K., Coates, D. W., & Evans, T. L. 1988, MNRAS, 235, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Järvinen, S. P., Berdyugina, S. V., Tuominen, I., Cutispoto, G., & Bos, M. 2005, A&A, 432, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
- Kopp, G., Lawrence, G., & Rottman, G. 2005, Sol. Phys., 230, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kozhevnikova, A. V., Alekseev, I. Y., Heckert, P. A., & Kozhevnikov, V. P. 2007, Astron. Rep., 51, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Kretzschmar, M. 2011, A&A, 530, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretzschmar, M., de Wit, T. D., Schmutz, W., et al. 2010, Nat. Phys., 6, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Kürster, M., & Schmitt, J.H.M.M. 1996, A&A, 311, 211 [NASA ADS] [Google Scholar]
- Kürster, M., Schmitt, J. H. M. M., & Cutispoto, G. 1994, A&A, 289, 899 [NASA ADS] [Google Scholar]
- Kürster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
- Lalitha, S. 2016, Solar and Stellar Flares and their Effects on Planets, IAU Symp., 320, 155 [NASA ADS] [Google Scholar]
- Lalitha, S., Fuhrmeister, B., Wolter, U., et al. 2013, A&A, 560, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maehara, H., Shibayama, T., Notsu, S., et al. 2012, Nature, 485, 478 [NASA ADS] [Google Scholar]
- Maehara, H., Notsu, Y., Notsu, S., et al. 2017, PASJ, 69, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mathioudakis, M., Doyle, J. G., Avgoloupis, V., Mavridis, L. N., & Seiradakis, J. H. 1992, MNRAS, 255, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Neidig, D. F. 1989, Sol. Phys., 121, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Osten, R. A., Drake, S., Tueller, J., et al. 2007, ApJ, 654, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Pakull, M. W. 1981, A&A, 104, 33 [NASA ADS] [Google Scholar]
- Preibisch, T., Neuhaeuser, R., & Alcala, J. M. 1995, A&A, 304, L13 [NASA ADS] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E., King, J. R., & Deliyannis, C. P. 2000, ApJ, 529, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Isobe, H., Hillier, A., et al. 2013, PASJ, 65, 49 [NASA ADS] [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., & Favata, F. 1999, Nature, 401, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Stephenson, F. R. 2015, Adv. Space Res., 55, 1537 [NASA ADS] [CrossRef] [Google Scholar]
- Švestka, Z. 1954, Bull. Astron. Inst. Czechoslovakia, 5, 4 [NASA ADS] [Google Scholar]
- Usoskin, I. G. 2017, Liv. Rev. Sol. Phys., 14, 3 [Google Scholar]
- Vilhu, O., Tsuru, T., Collier Cameron, A., et al. 1993, A&A, 278, 467 [NASA ADS] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Fontenla, J., et al. 2004, Geophys. Res. Lett., 31, L10802 [NASA ADS] [CrossRef] [Google Scholar]
For further information consult the web site at https://heasarc.gsfc.nasa.gov/docs/tess/pipeline.html
All Tables
All Figures
 |
Fig. 1 Part of TESS AB Dor light curve with typical features; see text for details. |
| In the text | |
 |
Fig. 2 TESSAB Dor light curve folded with a period of 0.514275 days. It should be noted that the data points with phase belowzero and above unity are repeated for better visibility. See text for details. |
| In the text | |
 |
Fig. 3 TESSAB Dor light curve folded with a period of 0.514275 days as a function of time (from bottom to top); see text for details. |
| In the text | |
 |
Fig. 4 TESS light curve of flare 1. Shown are the photospheric background-subtracted flux measurements (diamonds) and an “ad hoc” flare model (solid curve); see text for details. |
| In the text | |
 |
Fig. 5 TESS light curve of flare 2. Shown are the photospheric background-subtracted flux measurements (diamonds) and an “ad hoc” flare model as in Fig. 4. |
| In the text | |
 |
Fig. 6 TESS light curve for flare 3; see caption Fig. 4. |
| In the text | |
 |
Fig. 7 TESS light curve for flare 4; see caption Fig. 4. |
| In the text | |
 |
Fig. 8 TESS light curve for flare 5; see caption Fig. 4. |
| In the text | |
 |
Fig. 9 TESS light curve for flare 6; see caption Fig. 4. |
| In the text | |
 |
Fig. 10 TESS light curve for flare 7; see caption Fig. 4. |
| In the text | |
 |
Fig. 11 TESS light curve for flare 8; see caption Fig. 4. |
| In the text | |
 |
Fig. 12 Fraction of total emitted flux registered with the TESS sensitivity as a function of blackbody temperature. |
| In the text | |
 |
Fig. 13 Light curves of the flare on AB Dor (from November 26, 2009) observed with EPIC pn (diamonds), OM UVM2 (crosses, scaled by a factor 0.2) and solid line denoting our empirical model; see text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


