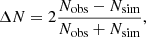| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834267 | |
| Published online | 06 August 2019 | |
Effects of 22Ne sedimentation and metallicity on the local 40 pc white dwarf luminosity function
1
Departament de Física, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
e-mail: santiago.torres@upc.edu
2
Institute for Space Studies of Catalonia, c/Gran Capita 2-4, Edif. Nexus 104, 08034 Barcelona, Spain
3
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
4
Instituto de Astrofísica de La Plata, UNLP-CONICET, Paseo del Bosque s/n, 1900 La Plata, Argentina
Received:
18
September
2018
Accepted:
19
June
2019
Aims. We analyzed the effect of the sedimentation of 22Ne on the local white dwarf luminosity function by studying scenarios under different Galactic metallicity models.
Methods. We use an advanced population synthesis code based on Monte Carlo techniques to derive the synthetic luminosity function. The code incorporates the most recent and reliable cooling sequences and an accurate modeling of the observational biases under different scenarios. We first analyzed the case for a model with constant solar metallicity and compared the models with and without 22Ne sedimentation with the observed luminosity function for a pure thin-disk population. Then we analyzed the possible effects of a thick-disk contribution. We also studied model scenarios with different metallicities, including 22Ne sedimentation. The analysis was quantified from a statistical χ2-test value for the complete and also for the most significant regions of the white dwarf luminosity function. Finally, a best-fit model along with a disk age estimate was derived.
Results. Models with constant solar metallicity cannot simultaneously reproduce the peak and cutoff of the white dwarf luminosity function. The additional release of energy due to 22Ne sedimentation piles up more objects in brighter bins of the faint end of the luminosity function. The contribution of a single-burst thick-disk population increases the number of stars in the magnitude interval centered around Mbol = 15.75. The metallicity model that follows a Twarog profile is disposable. Our best-fit model was obtained when a dispersion in metallicities of about solar metallicity was considered along with a 22Ne sedimentation model, a thick-disk contribution, and an age of the thin disk of 8.8 ± 0.2 Gyr.
Conclusions. Our population synthesis model is able to reproduce the local white dwarf luminosity function with a high degree of precision when a dispersion in metallicities around a model with solar values is adopted. Although the effects of 22Ne sedimentation are only marginal and the contribution of a thick-disk population is minor, both of them help in better fitting the peak and the cutoff regions of the white dwarf luminosity function.
Key words: white dwarfs / stars: luminosity function / mass function
© ESO 2019
1. Introduction
White dwarfs are the most common final stage of stellar evolution. Low- and intermediate-mass stars, that is, those with M ≲ 8 ∼ 11 M⊙ depending on the metallicity and intensity of the core overshooting (e.g., Siess 2007), end their lives as white dwarfs. These stars are very dense objects without relevant nuclear energy sources, where the pressure against gravitational collapse arises essentially from the degenerate electrons. Consequently, white dwarfs undergo a slow and long cooling process. The white dwarf structure is relatively simple, and their evolutionary properties are reasonably well understood; see the review Althaus et al. (2010a) and references therein for an in-depth discussion. The cores of the vast majority of white dwarfs are a mixture of C and O plus some impurities, among which 22Ne is the most abundant. White dwarfs with masses M ≲ 0.45 M⊙ have He cores, and those with masses M ≳ 1.1 M⊙ have O-Ne cores. Independently of their inner composition, white dwarf cores are surrounded by a thin nondegenerate envelope that typically has ∼1% of the total mass of the star. The degenerate core that contains the bulk of the mass of the white dwarf acts as an energy reservoir, and the thin envelope is the responsible for controlling the energy outflow.
In approximately 20% of the white dwarfs, the whole envelope is mainly formed by helium. However, in the remaining ∼80% of the cases, the helium envelope is surrounded by an even thinner layer of hydrogen of mass 10−4–10−15 M⊙. White dwarfs that display hydrogen lines in their spectra are known as DA, and those that are characterized by the absence of this feature are generically referred to as non-DA white dwarfs.
As long-living and well-understood objects from a theoretical point of view, white dwarfs have been used to derive not only important properties of the Galaxy and its components, but also to delimit theoretical cooling models and new physical processes. To cite a few examples, the white dwarf population has been used to study the nature and history of the different components of our Galaxy, that is, the thin and thick disks (Winget et al. 1987; García-Berro et al. 1988, 1999; Torres et al. 2002; Rowell & Hambly 2011; Rowell 2013; Kilic et al. 2017), the Galactic halo (Mochkovitch et al. 1990; Isern et al. 1998; García-Berro et al. 2004; van Oirschot et al. 2014; Kilic et al. 2019), and more recently, the Galactic bulge (Calamida et al. 2014; Torres et al. 2018). Moreover, white dwarfs have also been employed in the study of important characteristics, such as the age, subpopulation identification, white dwarf cooling, and other relevant parameters, of open and globular clusters. To cite some of the most representative studies, we mention the works of Salaris et al. (2001), Calamida et al. (2008), García-Berro et al. (2010), Jeffery et al. (2011), Hansen et al. (2013), and Torres et al. (2015).
A key point in the study of the properties of the white dwarf population is the white dwarf luminosity function. A comprehensive review can be found in García-Berro & Oswalt (2016). Initially derived by Weidemann (1968), the white dwarf luminosity function is defined as the number of white dwarfs per cubic parsec and bolometric magnitude unit. The function represents the scenario where the different ingredients of the white dwarf cooling theory as well as the past history and evolution of the Galaxy manifest themselves. As previously referenced, the white dwarf luminosity function has been used to determine the age of the Galactic disk and its star formation history as well as to constrain the physics of white dwarf cooling, including neutrino emission at high temperatures and crystallization processes at relative low core temperatures. Moreover, the white dwarf luminosity function has also been applied to corroborate or discard nonstandard physical theories such as the testing of the gravitational constant, G (García-Berro et al. 1995, 2011), or as an astroparticle physics laboratory (Isern et al. 1992, 2008; Dreiner et al. 2013; Miller Bertolami et al. 2014).
The advent of modern large-scale automated surveys and more sophisticated observational techniques has provided us with unprecedented white dwarf samples from which we can test the physics of the white dwarf cooling process. These detailed and more complete available samples are not exclusive to the disk population, but also include open and globular clusters. In particular, the analysis of the observed white dwarf luminosity function in clusters has provided useful independent determinations of their ages, sometimes in contrast with those derived from main-sequence turnoff stars. As an illustrative example of this aspect, the theoretical studies have been performed a few decades ago to examine the role of minor chemical species, in particular, the sedimentation of 22Ne, in white dwarf cooling (Isern et al. 1991, 1997, 2000; Bildsten & Hall 2001). Unfortunately, the scarcity of complete and statistically significant white dwarf samples at that time prevented any conclusive result or distinction among different theoretical predictions. It was not until recently that with the aid of Hubble Space Telescope observations, the old metal-rich open cluster NGC 6791 could be tracked deeply enough to allow the identification of a clear and significant sample of white dwarfs from which it was possible to obtain its luminosity function (Bedin et al. 2005, 2008). The initial discrepancy between the age of NGC 6791 determined by the main-sequence turnoff point (∼8 Gyr) and the age derived from the termination of the white dwarf cooling sequence (∼6 Gyr) could only be reconciled when the sedimentation of 22Ne along with detailed models of phase separation during the crystallization of typical CO white dwarfs were taken into account (García-Berro et al. 2010).
The main physical reason for the effects induced by 22Ne in the white dwarf cooling is the neutron excess of this isotope. 22Ne nuclei are formed as a result of helium captures on 14N left from hydrogen burning in the CNO cycle, through the reactions 14N(α, γ)18F(β+)18O(α, γ)22Ne. The excess of neutrons (two relative to the predominant A = 2Z nuclei) of 22Ne causes a downward force on them, which biases its diffusive equilibrium and sinks these nuclei into the deep interior of the white dwarfs (e.g., Bildsten & Hall 2001). This is responsible for the rapid sedimentation of 22Ne in the interior of white dwarfs (Isern et al. 1991; Deloye & Bildsten 2002; Althaus et al. 2010b; Camisassa et al. 2016). This diffusion process releases energy, yielding a marked delay in the cooling times of white dwarfs in solar and super-solar metallicity environments. Particularly in white dwarfs that arise from solar metallicity progenitors, the delays in cooling times reach about 1 Gyr (see, e.g., Camisassa et al. 2016). These delays are expected to alter the local white dwarf luminosity function. The effect of 22Ne diffusion is usually ignored in the evolutionary calculations in the literature, and is thus not considered in the population synthesis studies performed on the local sample of white dwarfs. In this study, we aim to asses the effects of this process on the white dwarf luminosity function of the 40 pc local sample and to estimate the accuracy of the predictions of the usual calculations that ignore this process.
Our paper is organized as follows. In Sect. 2 we describe in detail the set of observations to which we compare our theoretical simulations. A summarized description of our population synthesis code along with its main physical inputs is provided in Sect. 3. In Sect. 4 we describe the different metallicity models we considered in this study, and in Sect. 5 we present the results of our Monte Carlo population synthesis calculations. In particular, in Sect. 5.1 we compare models with and without 22Ne sedimentation. Section 5.3 is devoted to analyzing the effects of 22Ne sedimentation when a metallicity dispersion is considered. In Sect. 5.4 we analyze the observational metallicity models, and in Sect. 5.5 we present our best-fit model. Finally, Sect. 6 summarizes our main results and discusses their significance.
2. Observational sample
As previously stated, the white dwarf luminosity function represents a capital tool in the study of white dwarf evolutionary physical processes and also provides an inexhaustible source of information of the evolutionary history of our Galaxy. A clear key point in these studies is the comparison between the theoretically derived and observed luminosity functions. To that end, a statistically significant and complete luminosity function is essential for analyzing the properties of the white dwarf luminosity function.
Recent samples limited in magnitude and proper motion such as the Sloan Digital Sky Survey (SDSS; Harris et al. 2006) or the SuperCOSMOS Sky Survey (Rowell & Hambly 2011; Rowell 2013), respectively, have substantially increased the number of known white dwarfs over the past decade. This has allowed a deeper search into the Galaxy by up to several hundred parsecs. However, these samples are severely affected by observational biases, completeness problems, and selection procedures, which must necessarily be taken into account in any detailed analysis. Moreover, the detection of faint objects is inherently difficult in magnitude-limited surveys, and as a consequence, these samples suffer from a paucity of white dwarfs at the faintest bins of the luminosity function. This problem is especially important because valuable information is enclosed in those faint bins. Even with the unquestionable improvement in data that Gaia has provided (e.g., Hollands et al. 2018; Jiménez-Esteban et al. 2018), the resulting white dwarf sample is not exempt from such biases. The limiting magnitude, parallax errors, photometric flux excess factors, and other criteria applied in selecting Gaia white dwarf samples can introduce a source of incompleteness for the faintest luminosity bins (e.g., Torres et al. 2005; Barstow et al. 2014; Jiménez-Esteban et al. 2018). In addition, a throughly spectroscopic study is needed in order to obtain accurate luminosity estimates.
On the other hand, volume-limited samples are the best approach to an effectively complete sample. In this sense, Holberg et al. (2008) and Giammichele et al. (2012) studied the white dwarf population within 20 pc of the Sun for an unbiased and nearly complete sample of ∼130 white dwarfs. More recently, Holberg et al. (2016) extended the survey to 25 pc. This last sample included 232 objects, but the global estimate for its completeness was no greater than a 70%.
Nevertheless, our choice for this study was the white dwarf population within 40 pc of the Sun from Limoges et al. (2015). This compilation of white dwarfs, extracted from the SUPERBLINK survey, corresponds to that of a magnitude- and proper-motion-limited sample that contains ∼500 objects in the northern hemisphere. Although the sample is magnitude limited, it is expected to be ∼70% complete. A detailed analysis of selection criteria effects indicates that the average completeness for objects brighter than Mbol = 14 is close to 85%, while there is a strong deficit of objects for magnitudes higher than Mbol > 16 (Torres & García-Berro 2016). In spite of this, it is possible to resolve the observed drop-off of the luminosity function as an unambiguous consequence of the finite age of the Galactic disk. Hence, the 40 pc sample of Limoges et al. (2015) gathers an acceptable degree of completeness and a statistically significant number of objects that exceeds that of current volume-limited surveys. For instance, the 40 pc Limoges et al. (2015) sample contains 492 objects, but the practically complete 20 pc sample of Hollands et al. (2018) includes only 130 stars. This permits resolving many of the main characteristics of the Galactic history through its luminosity function, and at the same time, it is completely suitable for studying the evolutionary cooling of white dwarfs in detail.
3. Population synthesis code
A detailed description of the main ingredients employed in our Monte Carlo population synthesis code can be found in our previous works (García-Berro et al. 1999, 2004; Torres et al. 2001, 2002). Here, we briefly describe the most important characteristics of our simulator in modeling the thin- and thick-disk populations. In addition, we provide details about the evolutionary sequences used in this work.
First of all, we spatially distributed our stars by randomly generating their positions in a spherical region centered on the Sun and adopting a radius of 50 pc. We used a double exponential distribution for the local density of stars. The spatial distribution perpendicular to the Galactic plane followed an exponential profile with an adopted constant Galactic scale height of 250 pc for the thin-disk population and 1.5 kpc for the thick disk. Similarly, the distribution in the Galactic plane was generated according to a constant scale length of 2.6 kpc and 3.5 kpc for the thin and thick disk, respectively. Second, the time at which each synthetic star was born was generated according to a constant star formation rate after an age of the Galactic thin disk, tdisk, was adopted. The burst of star formation that occurred 0.6 Gyr ago was also introduced in order to reproduce the excess of hot objects (Torres & García-Berro 2016). The thick disk was modeled according to a single burst of star formation (e.g., Reid 2005) for which we adopted a duration of 1 Gyr. The age of the thick disk was assumed to be 1.6 Gyr older than the thin disk (see Kilic et al. (2017) and Sect. 5.2 for a further discussion). In parallel, the mass of each star was drawn according to a Salpeter mass function (Salpeter 1955) with an exponent α = −2.35. This prescription for the relevant range of masses studied here is equivalent to the standard initial mass function of Kroupa (2001). When our synthetic thin-disk star was formed, we associated a metallicity according to a certain metallicity law with it (see Sect. 4). In all cases, a metallicity of [Fe/H]≈ − 0.7 dex was adopted for thick disk stars. The evolutionary ages of the progenitors were those of Althaus (priv. comm.), which for the range of masses and metallicities used here are equivalent to those of BaSTI1 models. Knowing the age of the Galactic disk and the age, metallicity, and mass of the progenitor stars, we know which of these stars had time to become white dwarfs. In these cases, we self-consistently derived the white dwarf masses from the evolutionary tracks of Renedo et al. (2010), which are equivalent to using the semi-empirical initial-to-final mass relation of Catalán et al. (2008). We also randomly assigned an atmospheric composition to each artificial white dwarf. In particular, we adopted the canonical fraction of 80% of white dwarfs with pure hydrogen atmospheres, and assumed the remaining objects to have pure helium atmospheres. Finally, velocities for each star were randomly chosen taking into account the differential rotation of the Galaxy and the peculiar velocity of the Sun, (U⊙, V⊙, W⊙) = (7.90, 11.73, 7.39) km s−1 (Bobylev 2017). The mean Galactic velocity values with respect to the local standard of rest (LSR) and their dispersions for the thin- and thick-disk populations are those from Torres et al. (2019), their Table 2.
The set of adopted cooling sequences employed here encompasses the most recent evolutionary calculations for different white dwarf masses. For white dwarfs masses lower than 1.1 M⊙, we adopted the cooling tracks of H-rich atmosphere and carbon-oxygen cores of Camisassa et al. (2016), which are suitable for solar metallicity populations. These recent cooling tracks are the result of the full evolutionary calculations of their progenitor stars, starting at the zero-age main sequence (ZAMS), all the way through central hydrogen and helium burning, thermally pulsing asymptotic giant branch (AGB) and post-AGB phases. For H-deficient white dwarfs with masses lower than 1.1 M⊙, we additionally calculated new cooling sequences for the purpose of this work, which were evolved from the ZAMS through the born-again scenario for solar metallicity progenitors, as described in Camisassa et al. (2017). The subsolar metallicity DA white dwarf cooling tracks were those of Althaus et al. (2015); they consider residual hydrogen shell burning. In all cases, the cooling tracks take the energy released by latent heat into account and include the separation phase of carbon and oxygen due to crystallization, following the phase diagram of Horowitz et al. (2010). Additionally, the solar metallicity cooling tracks (for both H-rich and H-deficient atmospheres) we described above also take into account the sedimentation of 22Ne nuclei, employing the new diffusion coefficients based on molecular dynamics simulations of Hughto et al. (2010). For white dwarf masses higher than 1.1 M⊙, we used the evolutionary sequences for DA oxygen-neon white dwarfs of Althaus et al. (2005) and Althaus et al. (2007). Finally, for each white dwarf we interpolated the luminosity, effective temperature, and the value of log g, together with all the relevant parameters, in the corresponding white dwarf evolutionary track. We also interpolated their UBVRI colors, which we then converted to the ugriz color system in order to apply the selection criteria of the observed sample (Limoges et al. 2015; Torres & García-Berro 2016).
The final synthetic white dwarf population for each of our models is the result of 50 independent Monte Carlo simulations of different initial seeds that were normalized to the exact number (492 objects) of the observed sample (see Sect. 2). Each particular simulation contained a number of synthetic white dwarfs of about that number of objects. This ensured convergence in all the final values of the relevant quantities.
4. Metallicity models
Metallicity is a fundamental parameter that not only rules the evolutionary lifetime of stars, but is also deeply linked to the Galactic evolutionary history. Consequently, it is important to understand the influence of metallicity on the white dwarf luminosity function, and in particular, in the age estimation of the Galactic disk. A recent analysis by Cojocaru et al. (2014) showed that regardless of the choice of the metallicity law, estimating the disk age derived from the white dwarf luminosity function is a robust method because the cutoff remains unchanged. Moreover, this study showed that neither the shape of the bright portion of the white dwarf luminosity function nor the position of its cutoff at low luminosities is affected by the assumed metallicity law or the ratio of DA to non-DA white dwarfs. It is also worth mentioning that Rebassa-Mansergas et al. (2016) recently analyzed a pilot sample of 23 white dwarfs in binary systems with main-sequence companions. From these objects they derived accurate white dwarf ages and main-sequence star metallicities and found that there is not a clear correlation between age and metallicity at young and intermediate ages (0–7 Gyr). This large scatter of metallicity values can also be extended for older ages, as observed when single main-sequence star samples are analyzed (Casagrande et al. 2011, 2016; Haywood et al. 2013; Bergemann et al. 2014). This implies that some physical mechanism underlies the observed scatter of the age-metallicity relation.
Although at first approximation, metallicity seems not to play an important role in the white dwarf luminosity function, the observed scatter of metallicity values may induce some variations in the cooling evolution of individual stars. This is precisely the effect that we aim to study here because detailed white dwarf evolutionary sequences, as previously shown, suggest changes in the cooling rate as a function of the metallicity. It is also important to note that a smaller sample may be more affected by local inhomogeneities (e.g., moving groups, star associations) and thus the effects of a scatter in metallicities could be enhanced. In contrast, metallicity values are averaged in larger magnitude-limited samples (e.g., Cojocaru et al. 2014), but nevertheless, the completeness of these samples is lower. For all these reasons, we consider it important to extend our study of the local sample of white dwarfs to other metallicity models than those used by Cojocaru et al. (2014).
The models we used here are as follows. Our first model assumes a constant solar metallicity of Z⊙ = 0.014 independently of the age of the star. This is our reference model for the rest of the analysis. Our second model considers a dispersion along the solar metallicity value of σ[Fe/H] ≈ 0.4 dex, which implies that the range of Z is expanded from subsolar values of ≈0.003 up to supersolar values of ≈0.05. This dispersion is in agreement with the data collected by the Geneva-Copenhagen survey for isolated main-sequence stars (Casagrande et al. 2011) as well as with more recent seismic ages that were obtained using red giants observed by Kepler (Casagrande et al. 2016). It is also in complete agreement with the age–metallicity relation that was specifically derived for white dwarfs by Rebassa-Mansergas et al. (2016).
The third model is based on the observed age–metallicity relation provided by Casagrande et al. (2011, 2016), Haywood et al. (2013), and Bergemann et al. (2014). In particular, we consider a gradual decrease in [Fe/H] for objects older than 8 Gyr. Consequently, this model considers that the first stars in the Galaxy have [Fe/H] ≈ − 0.3 dex, and that [Fe/H] linearly increases until a solar metallicity value with a dispersion of σ[Fe/H] ≈ 0.35 dex is achieved. For stars with ages younger than 8 Gyr, this third model considers [Fe/H] to remain constant and equal to the solar metallicity with a dispersion of σ[Fe/H] ≈ 0.4 dex. Finally, the fourth and last model assumes the classic Twarog (1980) age–metallicity relation. That is, a law that predicts a monotonous increase in [Fe/H] that begins with a zero value for the oldest stars and that ends with a solar metallicity value for present-day stars. A dispersion of σ[Fe/H] ≈ 0.1 dex is added to the mean value at a given age.
5. Results
5.1. Effects of 22Ne sedimentation in the thin-disk population
First of all, we analyzed the effects of 22Ne sedimentation by comparing the models with and without this feature for a pure thin-disk population. In both cases we fixed the metallicity to the constant standard solar value and adopted a disk age of Tdisk = 9.0 Gyr, in accordance with Torres & García-Berro (2016). It is worth noting that this age value represents an initial guess. A wide spread in ages exists for the 40 pc sample of Limoges et al. (2015) depending on the model assumptions (e.g., the main-sequence lifetime or the initial-to-final mass relation) or the estimate contamination in the cutoff region from the thick-disk population. Lower limits for a thin-disk population can be as short as 6.8 Gyr (Kilic et al. 2017), while upper limits find a disk age of around 11 Gyr (Limoges et al. 2015). For our purpose here it is enough to adopt a reasonable guess, and we postpone a more detailed analysis of the effects of the age and the thick-disk population to the next sections.
The results are shown in Fig. 1, where we plot the observed white dwarf luminosity function (solid squares and red lines) of Limoges et al. (2015) compared with the model that incorporates the 22Ne sedimentation (solid squares and black lines) and the model without the 22Ne sedimentation (open circles and gray lines). Additionally, in the bottom panel of Fig. 1 we display the residuals (e.g., Cojocaru et al. 2014) for both the observed and simulated luminosity functions, which helps to assess the differences between the two simulations better. This is defined as
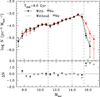 |
Fig. 1. Synthetic white dwarf luminosity functions that result from the models with and without 22Ne sedimentation (black solid squares and gray open circles, respectively) and that assume a constant solar metallicity, compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). In the bottom panel we show the residuals between the simulated and the observed samples. See text for details. |
where Nobs stands for the number of objects per bin of the observed sample and Nsim for the corresponding synthetic simulated sample.
Moreover, in order to determine the best fit in a quantitative way for our models and to help in the subsequent discussion, we performed a multiple χ2 test. We recall that in the white dwarf luminosity function a difference of nearly two orders of magnitude in the number of objects between the peak and the less populated bins exists. Therefore it is clear that a simple statistical test underestimates the physical characteristics of the less populated regions. For this reason, we considered not only the entire aspect of the luminosity function, but also divided it into four regions of relevant physical importance: the hot branch (Mbol ≤ 11.0) related to a possible recent burst of star formation, a middle region with constant slope (11.0 < Mbol ≤ 14.0), the peak region (14.0 < Mbol ≤ 15.5), and the cutoff region (Mbol > 15.5), which contains valuable information on the initial formation of the disk. We call these regions burst, middle, peak, and cutoff. They are delimited by a dashed vertical line and are easily identified from left to right, respectively, in Fig. 1. After we obtained the 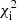 for each of these regions, we derive the reduced value as
for each of these regions, we derive the reduced value as 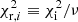 , where ν is the degree of freedom defined as the number of observations minus the number of constraints. In our case, the number of constraints is one because the synthetic samples are normalized to the same number of objects as the observed sample. Thus, we obtain ν = 6, 5, 2, 2, and 18 for the burst, middle, peak, cutoff and entire luminosity function, respectively. Additionally, we used our Monte Carlo simulator to estimate the error deviation per bin. This allowed us to calibrate our
, where ν is the degree of freedom defined as the number of observations minus the number of constraints. In our case, the number of constraints is one because the synthetic samples are normalized to the same number of objects as the observed sample. Thus, we obtain ν = 6, 5, 2, 2, and 18 for the burst, middle, peak, cutoff and entire luminosity function, respectively. Additionally, we used our Monte Carlo simulator to estimate the error deviation per bin. This allowed us to calibrate our 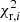 , hence avoiding exceptionally lower values of
, hence avoiding exceptionally lower values of 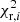 through error overestimation. It is also worth saying that the χ2 test performed here is not interpreted as an absolute measure of the adjustment, but as a tool for comparative purposes among models. For further discussion of the χ2 capabilities and other statistical methods, we refer to Andrae et al. (2010) and Feigelson & Babu (2012).
through error overestimation. It is also worth saying that the χ2 test performed here is not interpreted as an absolute measure of the adjustment, but as a tool for comparative purposes among models. For further discussion of the χ2 capabilities and other statistical methods, we refer to Andrae et al. (2010) and Feigelson & Babu (2012).
At first glance, Fig. 1 highlights a reasonably good global agreement between the simulated and the observed samples, even though some discrepancies arise in the peak region for the model without 22Ne diffusion and in the cutoff region for both models. The slope of the luminosity function for hot and moderate luminosities is suitably reproduced by both synthetic functions as derived by the values close to 1 of the reduced χ2 test in these regions (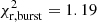 and
and 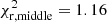 for the model with 22Ne diffusion, and
for the model with 22Ne diffusion, and 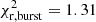 and
and 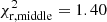 for the model without). This is borne out by the almost zero values of the residual for the 22Ne sedimentation model (solid black squares) and the model without this effect (open black circles), see bottom panel of Fig. 1. Discrepancies arise only in the peak and cutoff region of the luminosity function. In the peak region, the residuals indicate that the sample resulting from the model that incorporates 22Ne sedimentation agrees substantially better with the observed sample. The reduced χ2 test in this region,
for the model without). This is borne out by the almost zero values of the residual for the 22Ne sedimentation model (solid black squares) and the model without this effect (open black circles), see bottom panel of Fig. 1. Discrepancies arise only in the peak and cutoff region of the luminosity function. In the peak region, the residuals indicate that the sample resulting from the model that incorporates 22Ne sedimentation agrees substantially better with the observed sample. The reduced χ2 test in this region, 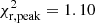 and
and 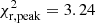 for the models with and without 22Ne diffusion, respectively, also confirms this result. A visual inspection of the peak region in Fig. 1 clearly shows that the model with 22Ne sedimentation resembles the observed shape very well, while the model that ignored 22Ne diffusion continues with an increasing slope, even far beyond the observed maximum. This is a direct consequence of the additional release of energy due to the diffusion of 22Ne, which induces a delay in the cooling times of white dwarfs. Consequently, for a fixed disk age, more objects remain in brighter luminosity bins when diffusion of 22Ne is taken into account, while objects reach lower luminosities when 22Ne diffusion is ignored. In the cutoff region, at least for a disk age of 9.0 Gyr and for a pure thin-disk population, both synthetic models seem far away from reproducing the observed values (
for the models with and without 22Ne diffusion, respectively, also confirms this result. A visual inspection of the peak region in Fig. 1 clearly shows that the model with 22Ne sedimentation resembles the observed shape very well, while the model that ignored 22Ne diffusion continues with an increasing slope, even far beyond the observed maximum. This is a direct consequence of the additional release of energy due to the diffusion of 22Ne, which induces a delay in the cooling times of white dwarfs. Consequently, for a fixed disk age, more objects remain in brighter luminosity bins when diffusion of 22Ne is taken into account, while objects reach lower luminosities when 22Ne diffusion is ignored. In the cutoff region, at least for a disk age of 9.0 Gyr and for a pure thin-disk population, both synthetic models seem far away from reproducing the observed values (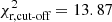 and
and 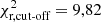 , for the models with and without 22Ne diffusion, respectively). Finally, when the entire luminosity function is considered, the model with 22Ne sedimentation reproduces the observed luminosity function better (
, for the models with and without 22Ne diffusion, respectively). Finally, when the entire luminosity function is considered, the model with 22Ne sedimentation reproduces the observed luminosity function better (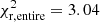 for the model with, and
for the model with, and 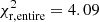 for the model without 22Ne sedimentation). However, both χ2 test values are far from being considered an adequate adjustment.
for the model without 22Ne sedimentation). However, both χ2 test values are far from being considered an adequate adjustment.
Before we studied the contanimation effect of the thick-disk population, we analyzed the age effect of the thin-disk population in our models with and without 22Ne sedimentation. We derived the corresponding luminosity function for the range of ages between 7 and 12 Gyr, while in Fig. 2 we plot the corresponding luminosity functions for ages between 8 and 11 Gyr. The complete set of values for the χ2 test of the different regions, models, and ages is presented in Table 1. For comparative purposes, we also show the observational luminosity function (red lines) of Limoges et al. (2015). The results obtained reinforce our previous idea that neither of the two models is able to simultaneously reproduce the cutoff and the peak. The best fit of the cutoff is achieved for an age of 11 Gyr for the model with 22Ne diffusion and for an age of 10 Gyr for the model without, which is a clear consequence of the additional energy release in the 22Ne sedimentation models. However, at these ages the peak region is inadequately resolved in both models. On the other hand, the peak region is well resolved for an age of 9 Gyr when 22Ne diffusion is taken into account, while models that ignored it require ages < 7 Gyr for a reasonable fitting.
 |
Fig. 2. Synthetic white dwarf luminosity function (black lines) for different disk ages, a constant solar metallicity, and a pure thin-disk model, compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). |
Reduced χ2 test values for the different regions, for the entire luminosity function, and for the different parameters of our models.
To summarize, the effects of the 22Ne sedimentation are negligible in the hot and medium region of the white dwarf luminosity function, while neither of the two models, with or without 22Ne sedimentation, is able to reproduce the observed low-luminosity bins when a pure thin-disk model and constant metallicity are considered. However, we found indications that the model that includes 22Ne sedimentation is in principle more plausible in reproducing the observed peak region.
5.2. Effects of a thick-disk population
An approximately 20% contribution of the thick-disk population to the mass budget of white dwarfs in the solar neighborhood is expected (e.g., Reid 2005). Moreover, in a recent population classification study, Torres et al. (2019) estimated that for the nearly complete Gaia-DR2 white dwarf sample within 100 pc, the contribution of the thick-disk population is 25%, which increases to 35% for the faint magnitude regime. Consequently, the inclusion of the thick-disk population is expected to be relevant for a good modeling of the luminosity function cutoff. As explained in Sect. 3, we introduced a low-metallicity, old, single-burst population and adopted a fraction of 25% in the number of thick disk stars. For the age of the thick-disk population, we followed the result reported by Kilic et al. (2017), that is, the age of the thick disk is 1.6 Gyr older than the thin-disk age. This permits us to use only one free parameter, that is, the thin-disk age, as long as the difference between the two Galactic components remains constant.
The results obtained for the thin- plus thick-disk population with and without 22Ne sedimentation along with their corresponding reduced χ2 test values for the different regions and the entire luminosity function are presented in Fig. 3 and Table 1. Additionally, we plot (blue continuous line, right axis) the fraction of thick-disk white dwarfs, fthick, defined as the number of thick-disk white dwarfs with respect to the total number of objects for the same magnitude bins as the luminosity function. A comparison of Figs. 2 and 3 reveals only marginal changes in the white dwarf luminosity function when the thick-disk population is taken into account. In particular, the burst, middle, and peak regions of the luminosity function are not affected by the thick-disk population. As expected, only in the cutoff region are some slight changes observable, but only for a given interval of bolometric magnitude. For instance, for a disk age of 9 Gyr, the bin around Mbol = 16.0 is dominated by thick-disk white dwarfs (fthick > 60%). However, other bins of the cutoff region remain unaffected. This is a consequence of the adopted single-burst formation model for the thick-disk population. As is well known, single bursts of star formation manifest themselves as peaks in the luminosity function (Noh & Scalo 1990). Consequently, the thick-disk population, modeled as an old single formation burst, produces an increment of these objects only for a certain magnitude interval. Even though we modeled the burst along 1 Gyr of star formation, this is not enough to extend the thick-disk contribution to more than a pair of bins in the luminosity function. On the other hand, the longer the burst duration, the weaker the corresponding peak in the luminosity function, that is, lower values of the fraction fthick.
 |
Fig. 3. Same as Fig. 2, but considering a thin- plus thick-disk population. The fraction of thick-disk white dwarfs is also plotted (blue continuous line, right axis). See text for details. |
Nevertheless, although including the thick-disk population does not adequately reproduce the cutoff of the observed white dwarf luminosity function, it seems to help in the overall fitting. The best fit for the models analyzed so far (see Table 1) corresponds to a model that includes the thick-disk population, takes into account 22Ne diffusion, and has a disk age of 9 Gyr (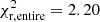 ). Although a thorough analysis of the thick-disk contribution is beyond the scope of the present work, we have checked other possibilities. For instance, Kilic et al. (2017) derived best-fit ages of 6.8 Gyr for the thin disk and 8.7 Gyr for the thick disk. When we adopt these ages, our population synthesis analysis derives a reduced χ2 value for the entire luminosity function of
). Although a thorough analysis of the thick-disk contribution is beyond the scope of the present work, we have checked other possibilities. For instance, Kilic et al. (2017) derived best-fit ages of 6.8 Gyr for the thin disk and 8.7 Gyr for the thick disk. When we adopt these ages, our population synthesis analysis derives a reduced χ2 value for the entire luminosity function of 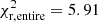 and
and 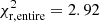 for the cases with and without 22Ne diffusion, respectively. However, for ages of 8.2 and 10.1 Gyr for the thin and thick disk, respectively, the model with 22Ne diffusion achieves a better fit with
for the cases with and without 22Ne diffusion, respectively. However, for ages of 8.2 and 10.1 Gyr for the thin and thick disk, respectively, the model with 22Ne diffusion achieves a better fit with 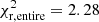 , while the case without is
, while the case without is 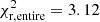 . Other possibilities include fitting the ages of the thin and thick disk separately from the peak and the cutoff, respectively, and leaving the fraction of thick-disk stars as a free parameter. However, for a reasonable range of ages and values of the thick-disk contribution, the final fitting is not substantially improved with respect to our best fit. Consequently, we study below the effect of the metallicity for models that include 22Ne diffusion and a thick-disk population as adopted in the best-fit model.
. Other possibilities include fitting the ages of the thin and thick disk separately from the peak and the cutoff, respectively, and leaving the fraction of thick-disk stars as a free parameter. However, for a reasonable range of ages and values of the thick-disk contribution, the final fitting is not substantially improved with respect to our best fit. Consequently, we study below the effect of the metallicity for models that include 22Ne diffusion and a thick-disk population as adopted in the best-fit model.
5.3. Effects of a metallicity dispersion
We continue by analyzing the effects of adding a constant metallicity dispersion of about solar-metallicity (Model 2). The derived luminosity functions for different disk ages are shown in Fig. 4 (black solid lines), and for comparative purposes, the observational luminosity function (red lines) of Limoges et al. (2015) is also shown.
 |
Fig. 4. Same as Fig. 2, but considering a thin-plus thick-disk population and metallicity model with a dispersion of about solar metallicity (Model 2). See text for details. |
The first evident trend that we observe for Model 2 is that the extended tail of the synthetic luminosity function (Fig. 4) perfectly matches the drop-off region of the observed luminosity function, in particular, for a disk age of 9 Gyr. A series of factors seems to contribute to this fact. First of all, higher metallicity values reduce the lifetimes of white dwarf progenitors, thus promoting more objects to the faint end of the luminosity function, especially those that are more massive. Second, the additional energy release provided by 22Ne sedimentation is more intense for supersolar metallicities. Consequently, more objects are piled up in brighter bins when 22Ne sedimentation is taken into account. This last fact can be visualized in Fig. 4, where in the panel for a disk age of 9 Gyr we superimpose the luminosity function (gray line, open symbols) for the case when 22Ne diffusion is omitted. Even though the change is minor, the inclusion of 22Ne sedimentation in the models permits slightly shifting objects to brighter bins and then perfectly matching the observed distribution.
In Table 2 we provide the values for the different reduced χ2 tests. The goodness of the fitting for Model 2 as described above, in particular, for a disk age of 9 Gyr, is quantified by the almost 1 reduced χ2 test values. A value of 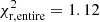 for the overall luminosity function is achieved, while values close to 1 are also obtained for each of its different parts.
for the overall luminosity function is achieved, while values close to 1 are also obtained for each of its different parts.
We therefore conclude that when a realistic distribution of metallicities whose values are spread around the solar value is taken into account, detailed models including the sedimentation of 22Ne as well as thick-disk contribution reproduce the different characteristics of the white dwarf luminosity function fairly well for an age of the thin disk of about 9 Gyr.
5.4. Effects of the age–metallicity relation
In this section we analyze two additional models based on two different observed age–metallicity relations: our Model 3, based on the observed age–metallicity relation presented by Casagrande et al. (2011, 2016), Haywood et al. (2013), and Bergemann et al. (2014), and our Model 4, based on the age-metallicity relation provided by Twarog (1980). As previously stated in Sect. 4, our Model 3 consists of a linearly increasing metallicity for stars older than 8 Gyr, and a constant metallicity (solar with a dispersion of 0.4 dex) for younger stars. Additionally, our Model 4 predicts a monotonous increase in [Fe/H] beginning with a zero value for the oldest stars and ending with solar metallicity for present-day stars.
In Fig. 5 we display the synthetic luminosity function resulting from our Model 3 (black line and dots) compared with the observed luminosity function (red line and dots) of Limoges et al. (2015). Additionally, the corresponding χ2 values are presented in Table 2. Figure 5 shows that the synthetic luminosity function reproduces the observed features with high accuracy. This is indeed shown by the reduced χ2 values of almost 1 that are achieved by the fits for the different regions considered. Specifically, for an age of 9 Gyr, we obtain a 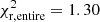 for the entire luminosity function.
for the entire luminosity function.
 |
Fig. 5. Same as Fig. 2, but considering our Model 3, which is based on Casagrande et al. (2011). |
As a final exercise, our Model 4 reproduces the classical Twarog age–metallicity model. The synthetic and observed luminosity functions are shown in Fig. 6, while the corresponding χ2 tests are provided in Table 2. A first look at Fig. 6 reveals that the general good agreement obtained with previous models (Models 2 and 3) is now lost. The best fit of the peak region is achieved for a disk age of 8 Gyr, while the cutoff is better fit for an age of about 10 Gyr. This clearly indicates that it is impossible to find a good fit for any age for this model. Thus, we can conclude that an increasing age–metallicity model hardly seems to explain the observed characteristics of the local white dwarf luminosity function.
5.5. Best-fit models
Of the models studied so far, the best fits to the observational data are obtained for our Models 2 and 3. They take into account a metallicity dispersion of about solar and the metallicity following Casagrande et al. (2011) data, respectively. We recall that both models include 22Ne sedimentation and a thick-disk population. Because both models reproduce the different regions of the white dwarf luminosity function with a high degree of accuracy, we aim to determine the disk age that best fits the entire luminosity function. Thus, we ran our code for a wide range of ages of between 7 and 12 Gyr, and with a polynomial fit, we determined the minimum reduced χ2 test value. The resulting distributions for Models 2 and 3 are presented in Fig. 7 along with their corresponding polynomial fit (red line). By determining the minimum for these polynomials, we derive a disk age of Tdisk = 8.8 ± 0.2 Gyr for Model 2 and slightly higher, Tdisk = 9.2 ± 0.3 Gyr, for Model 3. The best fit from Model 2 moreover achieves a better statistical solution than the equivalent for Model 3: 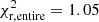 for Model 2, while
for Model 2, while 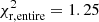 for Model 3.
for Model 3.
 |
Fig. 7. Reduced χ2 test value for the entire luminosity function as function of disk age for Models 3 and 4. A polynomial fit is represented as the red line. |
Figure 8 shows that the overall shapes of both synthetic luminosity functions excellently reproduce the observed data from Limoges et al. (2015) (red line). The different regions of the observed luminosity function are perfectly matched by our models; they are slightly better fit by Model 2, as is shown by the values of their residuals, which are closer to zero. However, from an strictly statistical point of view, these small discrepancies are not enough to discard Model 3. The older disk age derived with Model 3 is attributed to the lack of high-metallicity stars during the first gigayear of formation in Model 3. As previously stated, however, given that both models are consistent with the observed data, is not possible to discern the existence or absence of suprasolar metallicity stars at the beginning of the thin-disk formation.
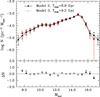 |
Fig. 8. Synthetic white dwarf luminosity functions that result from our best-fit metallicity Model 2 (black solid squares) and Model 3 (gray open circles), compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). In the bottom panel we show the residuals between the simulated and the observed samples. See text for details. |
Finally, in order to summarize the effects of the different assumptions in our models, we analyze in greater detail the faint downturn region of the luminosity function. In Fig. 9 we plot the peak and cutoff regions of the observed luminosity function from Limoges et al. (2015) compared to our Model 2 when 22Ne sedimentation and a thick-disk population are taken into account, when a thick disk population is included but 22Ne sedimentation is ignored, and when 22Ne sedimentation is considered, but only for a pure thin-disk population. It seems clear from Fig. 9 that the best match is achieved when 22Ne sedimentation and a thick-disk population are considered in a dispersion metallicity model. When, for instance, the thick-disk population is ignored, a substantial lack of objects appears in the bin interval centered at Mbol = 15.75. Consequently, this excess of observed objects with respect to a pure thin-disk population is, as previously analyzed in Sect. 5.2, a clear signature of an old burst population. On the other hand, when we include a thick-disk population but disregard the 22Ne sedimentation, the resulting luminosity function does not properly recover the observed distribution. In this situation, an excess of objects appears in the faintest bins and also in the interval centered at Mbol = 15.25. As described in Sect. 5.1, the lack of an additional source of energy, as is provided by the diffusion of 22Ne, entails an increase in the number of objects in the faintest bins. The quantitative analysis of the χ2 test shows a reasonably acceptable value for the entire luminosity function, 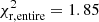 , but a poorer fit in the peak region,
, but a poorer fit in the peak region, 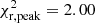 . Although the effects of a thick-disk population and the sedimentation of 22Ne are minor, including them in the modeling clearly permits a better fit of the observed data.
. Although the effects of a thick-disk population and the sedimentation of 22Ne are minor, including them in the modeling clearly permits a better fit of the observed data.
 |
Fig. 9. Faint end of the observed white dwarf luminosity function from Limoges et al. (2015; solid square and continuous red line) compared to our best-fit Model 2 when 22Ne sedimentation and a thick-disk population is taken into account (solid square and continuous black line), when 22Ne sedimentation is disregarded (open circle and continuous gray line), and when only a pure thin-disk population is considered (solid triangles and dashed blue line). |
6. Conclusions
With an advanced Monte Carlo simulator that incorporates the most recently derived white dwarf evolutionary sequences, we have studied possible effects of cooling-time delays induced by 22Ne sedimentation in the local white dwarf luminosity function along with different age–metallicity relation models and the possible contamination of a thick-disk population. First of all, we analyzed a hypothetical scenario in which all stars belonged to a pure thin-disk population and had the same metallicity, fixed to solar. In this case, the synthetic models that result from incorporating and excluding 22Ne sedimentation perfectly match the observational data in the hot and medium region of the luminosity function. In these regions the effects of 22Ne sedimentation are negligible. A small discrepancy arises between models in the peak and cutoff regions. Although neither of the two models is able to adequately recover the drop-off of the observed luminosity function for any of the disk ages studied here, we find indications that the model including 22Ne sedimentation seems to fit the peak region better. This fact is understood as a consequence of the additional energy release through 22Ne sedimentation, which implies that more objects pile up in brighter magnitude intervals.
When a thick-disk population was included in our models, the resulting effect appeared as an increase in the number of stars in the interval centered around Mbol = 15.75. The fact that thick-disk stars are modeled according to a single old burst formation implies that these stars concentrate in a specific magnitude interval, in some cases contributing more than 60% in this interval. Consequently, the inclusion of a thick-disk population does not allow us to fully recover the observed distribution of objects in the entire cutoff region, but it improves the fit in this region.
We considered additional metallicity models that incorporated a dispersion around our fixed solar metallicity value and different age–metallicity relations. We found that models including a metallicity dispersion perfectly match the observations and are in particular able to excellently reproduce the cutoff region. The combined effect of shorter lifetimes for high metallicity progenitors, in addition to the greater efficiency of the 22Ne sedimentation for suprasolar metallicities, are suggested as the main causes for the agreement with the observed data. On the other hand, our Model 4, which assumes Twarog’s law of increasing metallicity with age, may be ruled out because of its poor agreement in particular of the peak and cutoff regions. Consequently, models that include a metallicity dispersion (Models 2 and 3), that incorporate 22Ne sedimentation and a thick-disk population present the better statistical performance and excellently reproduce the faint end along with the rest of the luminosity function. This permits us to robustly constrain the age of the Galactic disk by fitting not only the cutoff, but also the entire luminosity function. In particular, our best-fit model assumes a dispersion of about solar metallicity and an age of 8.8 ± 0.2 Gyr for the thin disk. The derived age for the thick disk in our best-fit model is 10.4 ± 0.2 Gyr for a 1 Gyr single-burst formation. Although the effects of 22Ne sedimentation and a thick-disk population assumption in the best-fit model are only minor, including them permits a better fit of the peak and cutoff regions. Additionally, our Model 3, which is modeled according to Casagrande et al. (2011) data, cannot be disregarded although it obtains a slight poorer performance. The derived disk age for this model is slightly older, 9.2 ± 0.3 Gyr.
The luminosity function arising from our best-fit models reproduces all observed features with high accuracy: the bump at Mbol ≈ 10.5 (assuming a recent enhanced star formation 0.6 Gyr ago, as claimed in Torres & García-Berro 2016 as one plausible hypothesis), as well as the peak and the cutoff regions. For these models, the discrepancies between the cases with and without 22Ne sedimentation are only marginal, although the model that takes 22Ne sedimentation into account obtains better values in the statistical tests. In the same sense, a thick-disk population appears to reproduce the magnitude interval centered around Mbol = 15.75 better, but it is only secondary in the fitting of the entire cutoff region. Metallicity effects that are due to a dispersion of about solar metallicity are clearly the most important factor for a proper reproduction of the faint end along with the peak of the local white dwarf luminosity function.
Acknowledgments
This work was partially supported by the MINECO grant AYA2017-86274-P and the Ramón y Cajal programme RYC-2016-20254, by the AGAUR, by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, and by PIP 112-200801-00940 grant from CONICET. We acknowledge our anonymous referee for the detailed and valuable report.
References
- Althaus, L. G., García-Berro, E., Isern, J., & Córsico, A. H. 2005, A&A, 441, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010a, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010b, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrae, R., Schulze-Hartung, T., & Melchior, P. 2010, ArXiv e-prints [arXiv:1012.3754] [Google Scholar]
- Barstow, M. A., Casewell, S. L., Catalan, S., et al. 2014, ArXiv e-prints [arXiv:1407.6163] [Google Scholar]
- Bedin, L. R., Salaris, M., Piotto, G., et al. 2005, ApJ, 624, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., King, I. R., Anderson, J., et al. 2008, ApJ, 678, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bildsten, L., & Hall, D. M. 2001, ApJ, 549, L219 [NASA ADS] [CrossRef] [Google Scholar]
- Bobylev, V. V. 2017, Astron. Lett., 43, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Corsi, C. E., Bono, G., et al. 2008, ApJ, 673, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Sahu, K. C., Anderson, J., et al. 2014, ApJ, 790, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2016, ApJ, 823, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Rohrmann, R. D., et al. 2017, ApJ, 839, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Silva Aguirre, V., Schlesinger, K. J., et al. 2016, MNRAS, 455, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán, S., Isern, J., García-Berro, E., & Ribas, I. 2008, MNRAS, 387, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cojocaru, R., Torres, S., Isern, J., & García-Berro, E. 2014, A&A, 566, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deloye, C. J., & Bildsten, L. 2002, ApJ, 580, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Dreiner, H. K., Fortin, J.-F., Isern, J., & Ubaldi, L. 2013, Phys. Rev. D, 88, 043517 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Babu, G. J. 2012, Modern Statistical Methods for Astronomy (Cambridge, UK: Cambridge University Press) [Google Scholar]
- García-Berro, E., & Oswalt, T. D. 2016, New Astron. Rev., 72, 1 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1988, Nature, 333, 642 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1995, MNRAS, 277, 801 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 1999, MNRAS, 302, 173 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 2004, A&A, 418, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Torres, S., Althaus, L. G., & Isern, J. 2011, JCAP, 5, 021 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Bergeron, P., & Dufour, P. 2012, ApJS, 199, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, H. C., Munn, J. A., Kilic, M., et al. 2006, AJ, 131, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holberg, J. B., Sion, E. M., Oswalt, T., et al. 2008, AJ, 135, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Holberg, J. B., Oswalt, T. D., Sion, E. M., & McCook, G. P. 2016, MNRAS, 462, 2295 [NASA ADS] [CrossRef] [Google Scholar]
- Hollands, M. A., Tremblay, P.-E., Gänsicke, B. T., Gentile-Fusillo, N. P., & Toonen, S. 2018, MNRAS, 480, 3942 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hughto, J., Schneider, A. S., Horowitz, C. J., & Berry, D. K. 2010, Phys. Rev. E, 82, 066401 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Hernanz, M., Mochkovitch, R., & Garcia-Berro, E. 1991, A&A, 241, L29 [NASA ADS] [Google Scholar]
- Isern, J., Hernanz, M., & Garcia-Berro, E. 1992, ApJ, 392, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Mochkovitch, R., García-Berro, E., & Hernanz, M. 1997, ApJ, 485, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., Mochkovitch, R., & Torres, S. 1998, ApJ, 503, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., & Chabrier, G. 2000, ApJ, 528, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, E. J., von Hippel, T., DeGennaro, S., et al. 2011, ApJ, 730, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Esteban, F. M., Torres, S., Rebassa-Mansergas, A., et al. 2018, MNRAS, 480, 4505 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Munn, J. A., Harris, H. C., et al. 2017, ApJ, 837, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Bergeron, P., Dame, K., et al. 2019, MNRAS, 482, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Limoges, M.-M., Bergeron, P., & Lépine, S. 2015, ApJS, 219, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Melendez, B. E., Althaus, L. G., & Isern, J. 2014, JCAP, 10, 069 [NASA ADS] [CrossRef] [Google Scholar]
- Mochkovitch, R., Garcia-Berro, E., Hernanz, M., Isern, J., & Panis, J. F. 1990, A&A, 233, 456 [NASA ADS] [Google Scholar]
- Noh, H.-R., & Scalo, J. 1990, ApJ, 352, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Anguiano, B., García-Berro, E., et al. 2016, MNRAS, 463, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N. 2005, ARA&A, 43, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rowell, N. 2013, MNRAS, 434, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Rowell, N., & Hambly, N. C. 2011, MNRAS, 417, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., García-Berro, E., Isern, J., & Torres, S. 2001, A&A, 371, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, S., & García-Berro, E. 2016, A&A, 588, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, S., García-Berro, E., Burkert, A., & Isern, J. 2001, MNRAS, 328, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., García-Berro, E., Burkert, A., & Isern, J. 2002, MNRAS, 336, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., García-Berro, E., Isern, J., & Figueras, F. 2005, MNRAS, 360, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., García-Berro, E., Althaus, L. G., & Camisassa, M. E. 2015, A&A, 581, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, S., García-Berro, E., Cojocaru, R., & Calamida, A. 2018, MNRAS, 476, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., Cantero, C., Rebassa-Mansergas, A., et al. 2019, MNRAS, 485, 5573 [NASA ADS] [CrossRef] [Google Scholar]
- Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
- van Oirschot, P., Nelemans, G., Toonen, S., et al. 2014, A&A, 569, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidemann, V. 1968, ARA&A, 6, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Hansen, C. J., Liebert, J., et al. 1987, ApJ, 315, L77 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Reduced χ2 test values for the different regions, for the entire luminosity function, and for the different parameters of our models.
All Figures
 |
Fig. 1. Synthetic white dwarf luminosity functions that result from the models with and without 22Ne sedimentation (black solid squares and gray open circles, respectively) and that assume a constant solar metallicity, compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). In the bottom panel we show the residuals between the simulated and the observed samples. See text for details. |
| In the text | |
 |
Fig. 2. Synthetic white dwarf luminosity function (black lines) for different disk ages, a constant solar metallicity, and a pure thin-disk model, compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). |
| In the text | |
 |
Fig. 3. Same as Fig. 2, but considering a thin- plus thick-disk population. The fraction of thick-disk white dwarfs is also plotted (blue continuous line, right axis). See text for details. |
| In the text | |
 |
Fig. 4. Same as Fig. 2, but considering a thin-plus thick-disk population and metallicity model with a dispersion of about solar metallicity (Model 2). See text for details. |
| In the text | |
 |
Fig. 5. Same as Fig. 2, but considering our Model 3, which is based on Casagrande et al. (2011). |
| In the text | |
 |
Fig. 6. Same as Fig. 2, but considering our Model 4, which is based on Twarog’s law. |
| In the text | |
 |
Fig. 7. Reduced χ2 test value for the entire luminosity function as function of disk age for Models 3 and 4. A polynomial fit is represented as the red line. |
| In the text | |
 |
Fig. 8. Synthetic white dwarf luminosity functions that result from our best-fit metallicity Model 2 (black solid squares) and Model 3 (gray open circles), compared with the observed white dwarf luminosity function (red lines) of Limoges et al. (2015). In the bottom panel we show the residuals between the simulated and the observed samples. See text for details. |
| In the text | |
 |
Fig. 9. Faint end of the observed white dwarf luminosity function from Limoges et al. (2015; solid square and continuous red line) compared to our best-fit Model 2 when 22Ne sedimentation and a thick-disk population is taken into account (solid square and continuous black line), when 22Ne sedimentation is disregarded (open circle and continuous gray line), and when only a pure thin-disk population is considered (solid triangles and dashed blue line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.