| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 16 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201935472 | |
| Published online | 14 June 2019 | |
Precession of the non-rigid Earth: Effect of the mass redistribution
1
Dept. of Sciences and Informatics, University Centre of Defence at the Spanish Air Force Academy, 30720 Santiago de la Ribera, Spain
e-mail: tomas.baenas@cud.upct.es
2
Dept. of Aerospace Engineering, University of León, 24071 León, Spain
3
Dept. of Applied Mathematics, University of Alicante, PO Box 99, 03080 Alicante, Spain
Received:
14
March
2019
Accepted:
25
April
2019
This research is focused on determining the contribution to the precession of the Earth’s equator due to the mass redistribution stemming from the gravitational action of the Moon and the Sun on a rotating solid Earth. In the IAU2006 precession theory, this effect is taken into account through a contribution of −0.960 mas cy−1 for the precession in longitude (with the unspecific name of non-linear effect). In this work, the revised value of that second-order contribution reaches −37.847 mas cy−1 when using the Love numbers values given in IERS Conventions, and −43.945 mas cy−1 if those values are supplemented with the contributions of the oceanic tides. Such variations impose a change of the first-order precession value that induces relative changes of the Earth’s dynamical ellipticity of about 7.3 and 8.5 ppm, respectively. The corresponding values for the obliquity rate are 0.0751 and 0.9341 mas cy−1, respectively, in contrast to 0.340 mas cy−1 considered in IAU2006. The fundamentals of the modeling have been revisited by giving a clear construction of the redistribution potential of the Earth through the corresponding changes in the Earth tensor of inertia. The dynamical problem is tackled within the Hamiltonian framework of a two-layer Earth model, introduced and developed by Getino and Ferrándiz. This approach allows for the achievement of closed-analytical formulae for the precession in longitude and obliquity. It makes it possible to obtain numerical values for different Earth models once a set of associated Love numbers is selected. The research is completed with a discussion on the permanent tide and the related estimation of the variation of the second degree zonal Stokes parameter, J2, and also the indirect effects on nutations arising from the relative change of the Earth’s dynamical ellipticity.
Key words: celestial mechanics / methods: analytical / Earth / reference systems
© ESO 2019
1. Introduction
Most of the theoretical contributions to the precessional rate of the Earth’s equator, included in the current IAU2006 theory (Capitaine et al. 2003, 2005), were taken from previous works by Williams (1994) and Mathews et al. (2002). The effect of the tidal deformations on the precession rates in longitude and obliquity – the main scope of this work – is included in the IAU2006 set of contributions with the unspecific name of non-linear effect, and it is established as −0.960 mas cy−1 for the precession rate in longitude, and 0.340 mas cy−1 in obliquity.
A recent publication by Liu & Capitaine (2017) has evaluated the possibility of upgrading IAU2006 precession theory. In that process, the updated values of the non-linear effect to be considered would be −0.124 and 1.844 mas cy−1, as reported in Lambert & Mathews (2008). Liu & Capitaine (2017) designate those contributions as an effect of the second-order torque on precession rates.
In a previous study by the authors (Baenas et al. 2017), the revision of such components of the secular motion of the equator was initiated, and it was shown that the second-order lunisolar contribution changes significantly when the assumed rigid Earth model is replaced by a two-layer one that incorporates some of the effects of the deformation one (achieving a difference of −8.51 mas cy−1 in the precession in longitude with respect to the IAU2006 reference value).
In this study, the IAU2006 contributions arising from the variations of the Earth’s gravitational potential induced by the deformations resulting from the action of the lunisolar gravitational potential (also known as tidal potential or tide-raising potential) are revisited. The physical phenomenon is referred to as tidal deformation (Love 1906, Sect. 185) or bodily tide (Jeffreys 1976, Chap. 7), and the additional term in the gravitational energy of the system is known as redistribution tidal potential (as it is caused by a mass redistribution). We show that the changes of the precession rates are not negligible when realistic hypotheses about the Earth’s rheology and dynamics are assumed. The resulting contributions are numerically comparable to some of the components of the current precession theory, displayed, for example, in Table 2 of Baenas et al. (2017).
The effects of the redistribution potential on Earth nutation and precession have been partially discussed by Souchay & Folgueira (2000), Escapa et al. (2003, 2004), Ferrándiz et al. (2012), and Baenas (2014), within a Hamiltonian framework. Another approach to the problem, based on an application of modified SOS (Sasao et al. 1980) equations, can be found in Lambert & Capitaine (2004) and Lambert & Mathews (2006, 2008). Krasinsky (1999) and, recently, Williams & Boggs (2016), computed the obliquity rate from the vectorial Euler equations. In the works by Lambert & Capitaine (2004) and Souchay & Folgueira (2000), a simplification of the problem, consisting in considering only the zonal contribution of the redistribution tidal potential, was performed. This hypothesis must be improved since the other harmonic contributions of the potential, the tesseral and sectorial terms, are of the same magnitude. The formalism used in Lambert & Mathews (2006, 2008) does not provide simple analytical formulae that allow for the recomputing of the precession and nutation due to the redistribution of mass when the Love numbers model is changed. That is the case, for example, when considering a Love numbers set that includes, in addition to the ocean load, the ocean tide direct effect on the redistribution (Williams & Boggs 2016 and this work). That inclusion produces significant differences with respect to the values provided in Lambert & Mathews (2006, 2008) as is shown in Sect. 4.
The works by Escapa et al. (2003, 2004), Ferrándiz et al. (2012) and Baenas (2014) constitute a progressive line that leads to the present article, in which the problem of the redistribution of mass in the evolution of the Earth’s rotation will be thoroughly studied by means of the Hamiltonian formalism and the use of canonical perturbation methods, allowing an analytical approach. With these tools, closed-analytical formulae for the precession rates will be obtained, which enables a simple numerical evaluation of the redistribution effects under different elastic responses of the Earth (or rheologies), characterized by means of the Love numbers formalism.
The effects of the mass redistribution are particulary relevant in the Earth’s precession modeling, due to its connection with the Earth’s dynamical ellipticity1Hd = 1 − A/C (expression for an axial symmetric Earth, A and C being the principal moments of inertia, equatorial and polar, respectively). It should be remarked that, in spite of the simplified notation, A is taken in most of the theories (including IAU2000) as the mean (A + B)/2 of the equatorial moments of inertia. This simplification suffices for this paper, although it is pertinent to cite that the triaxial problem has been treated in many different papers; some examples are Chao et al. (1991), Getino et al. (2000), Escapa et al. (2002), Shen et al. (2007), Chen & Shen (2010), Bizouard & Zotov (2013), and Chen et al. (2015).
Independently of the symmetry assumed in the background model, the Hd parameter is inferred from the precession rate in longitude adjusted from astronomical observations at an epoch, pA (general precession in longitude). Hence, it must be readjusted when some of the smaller components of pA, which are treated in the process like known constants, are modified. Besides, corrections to the dynamical ellipticity indirectly affect the nutation amplitudes at the tens of μas level, through a consistency factor (Hd + δHd)/Hd (Escapa et al. 2016).
The structure of the paper is as follows. In Sect. 2, the fundamentals of the Earth redistribution potential theory are described, with special emphasis in the process leading to its analytical formulation and its generalization through Love numbers formalism. In Sect. 3, the analytical formulae for the precession rates are obtained by means of the Hamiltonian approach. Section 4 is composed of the computation of the precession rates for different Earth models, given by the corresponding Love numbers sets. In Sect. 5, the main implications of the numerical results derived formerly are discussed. They refer to the permanent tide, the change in the dynamical ellipticity of the Earth, and its effects on the nutations. We also draw some of the fundamental conclusions of this research. Finally, two appendices have been added for clarifications and additional material.
2. Earth redistribution tidal potential
2.1. Basic hypothesis
The external gravitational potential energy of an extended body can be expanded in a series of spherical harmonics (e.g., MacMillan 1958, Sect. 172). That procedure is especially suitable when both the geometry and the mass density functions of the body are not far from the spherical symmetry, or when the potential energy is evaluated at great distances compared with the dimensions of the body.
From the point of view of continuum mechanics, the spherical harmonics expansion depends only on the volume of the body and its volumic mass distribution2. This fact is neatly appreciated when the expansion is written in terms of the inertial integrals (Ibid, Sect. 204) given by
In this expression, r = (x1,x2,x3)t are the Cartesian coordinates of a material particle of the extended body with volume B and volumic density function ρ(r), and d3r stands for the volume element. Since the effects to be investigated are small, it is enough to consider just the second degree terms in the expansion of the external gravitational potential energy.
The relationships of the Iij matrix elements of the inertia tensor of the body3,
with the second degree inertial integrals (l + m + n = 2) lead to the well-known expression of the second degree terms in the multipolar expansion of the external gravitational potential (MacCullagh’s formula, MacCullagh 1844; Peale 1973)
Here rp = (x1, p,x2, p,x3, p)t and rp = |rp| represent the position vector and the modulus of a material particle of mass m, labeled as p, where the gravitational potential energy is evaluated, and G is the gravitational constant.
Possible temporal dependence has not been made explicit in the previous formulae. The matrix of inertia, I=(Iij), or the inertial integrals, Eq. (1), might depend on time, inducing a similar dependence on the expansion of the external gravitational potential. In turn, they can also depend on time due to an explicit temporal variation of rp. Whereas the second situation does not present special difficulties, it is not the case for the first one, so it will be analyzed with some detail.
In such a case, time dependence in I can be due to two facts. First, the reference system employed in the computation of the matrix of inertia can be animated with a motion independent of that of the extended body. Second, the extended body can experience changes of shape and volume (redistribution of mass). Both situations would make the volume and volumic density of the extended body time dependent, B = B(t) and ρ = ρ(r,t), however, they have a quite different nature. The first one has a kinematical origin, while the second one is due to the deformable character of the extended body. A convenient way to separate, to some extent, those two facts is to attach in some prescribed way a reference system to the extended body.
The procedure is best appreciated if the case in which a rigid extended body is first considered. Since by definition the distances between its material particles must keep constant (invariable form and shape), all the time dependence in B(t) and ρ(r,t) emerges as a consequence of the motion of the reference system used in their description. Alternatively, the extended body temporal evolution is a rigid motion given by a combination of a translation of the barycenter of the body O, and a rotation around it.
It entails that there exist reference systems, or body figure axes, where I is independent of time. Among them, it is especially convenient to employ the principal axes system, Oxyz, because I is a diagonal matrix in it (for specific problems, another choice of the reference system might be more suitable in order to simplify the formulation of the rotational dynamics problem.).
In this way, the motion of the extended body can be completely identified with the motion of the reference system Oxyz and vice versa, that motion referred to another reference system, OXYZ, not necessarily inertial but with known time evolution. In the study of the rotation of the Earth, those other reference systems are also assumed to be geocentric like, for example, the one defined by the ecliptic of date.
The question is more complex for deformable bodies as was early recognized in Tisserand (1891, Tome II, Sect. 213). Following a similar procedure to that used in the case of the rigid body, first a reference system Oxyz can be linked to the extended body. It will induce a rigid motion common for all its material particles.
However, since the body is deformable, in general there will exist other part of the motion not described by that of Oxyz, and depending on each material particle. This will be referred to as deformation. In this way, the motion of the extended body is split into two components: a rotation around O (rigid motion) plus a deformation.
It allows the unambiguous definition of the rotation of a deformable body through the rotation of Oxyz relative to OXYZ (see, e.g., Escapa 2011). In contrast to the rigid case situation, however, the tensor of inertia I will depend on time due to the deformation component of the motion, even when it is described from Oxyz (which entails a variation of the relative distance among the material particles of the body).
The main problem with this approach is that the decomposition of the motion is not unique. Different criteria can be employed in order to define the rigid and deformable components (Munk & MacDonald 1960, Chap. 3, Sect. 2).
From the point of view of establishing the dynamics of the extended body, the prescription of the well-defined direct orthonormal Oxyz reference system called the Tisserand system is especially suitable (Ibid., Moritz & Mueller 1986; Kinoshita & Sasao 1977; see Escapa 2011 for clarifications on the equivalence of the different definitions).
In the Tisserand system4, the position r′ of every material particle in the deformed body (or deformed state of the body), with integration domain B′, will be obtained by means of a transformation defined by a Lagrangian particle displacement vector field, u(r), given by
The modulus of u(r) vectors will be assumed to be small enough to admit a first-order deformation theory, where any related magnitude is linear in the components of the displacement vector or its spatial derivatives. The Jacobian of the change of variable r′(r) related to the previous transformation, in the linear elasticity limit, is given by (Landau & Lifshitz 1959, Chap. 1)
being the divergence of u known as volume dilatation, as it stands for the relative volume change in the deformation between volume elements, d3r′ = [1 + ∇u(r)]d3r. Besides, by means of the displacement field, the volumic density function ρ′(r′) in the deformed state can be also linked to its counterpart distribution in the undeformed domain (Moritz & Mueller 1986, Chap. 4),
The last result is not only a consequence of the definition of u(r), but of the continuity equation in the case of an Eulerian change of density due to an instantaneous deformation, δρ(r′) ≡ ρ′ (r′) − ρ(r′) = −∇[ρ(r)u(r)] (Backus 1967).
Equations (4)–(6) can be used to perform the calculation of the inertial integrals over the deformed state B′, 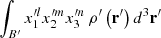 , and consequently the matrix elements of the inertia tensor of the deformed body, through an integration over the undeformed volume B. This is achieved by means of a first-order Taylor expansion of the product
, and consequently the matrix elements of the inertia tensor of the deformed body, through an integration over the undeformed volume B. This is achieved by means of a first-order Taylor expansion of the product 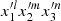 induced by the transformations
induced by the transformations 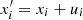 and the smallness of ui in the linear elasticity limit, so that the following expression is obtained:
and the smallness of ui in the linear elasticity limit, so that the following expression is obtained:
The application of this result to the integrals of 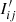 elements (given by Eq. (2)), with primed variables in the case of a deformed extended body, allows us to decompose them into two parts: the matrix elements of the undeformed state, Iij, and the perturbation due to the deformed one, ΔIij, performed over the undeformed B volume, namely,
elements (given by Eq. (2)), with primed variables in the case of a deformed extended body, allows us to decompose them into two parts: the matrix elements of the undeformed state, Iij, and the perturbation due to the deformed one, ΔIij, performed over the undeformed B volume, namely,
where (see, e.g., Chandrasekhar 1969, Sect. 15, or Wahr 1981)
In matrix form, Eq. (8) will be written as I′ = I + ΔI.
The substitution of Eq. (9) into Eq. (3) leads to a similar decomposition for the external gravitational potential of the extended body
with
The additional term 𝒱t (rp) in the potential energy is the redistribution potential, since it arises from the redistribution of mass associated with the deformation field u(r). As it is derived from Eqs. (9) and (12), the form of 𝒱t (rp) is determined once u(r) is known. For example, in the case of the bodily tide of the Earth, it would be necessary to find the displacement vector field produced on its body by the attraction of the Moon and the Sun. The way of constructing the redistribution potential shown here is a generalization of the method proposed in Getino & Ferrándiz (1990, see also Escapa 2011).
Another widespread procedure to obtain 𝒱t (rp) is by solving directly the elastic problem, since the dynamical equations of motion of the displacement vector field must be supplemented with the Poisson equation for the redistribution potential. This is the approach followed by classical works on the bodily tide like, for example, those of Love (1906), Takeuchi (1950), and Alterman et al. (1959), leading to the introduction of Love numbers. This method allows the use of Eq. (3) in reverse: from the known form of the redistribution potential it is possible to obtain the variation of the inertia matrix due to deformation (e.g., Jeffreys 1976, Chap. 7, Peale 1973; Sasao et al. 1980).
2.2. Earth redistribution tidal potential for SNREI models
The SNREI (seismology acronym, Dahlen 1968) model refers to an (oceanless) Earth assuming a Spherical, Non-Rotating, Elastic and Isotropic body, in the undeformed state. SNREI Earth models have also been considered when determining the bodily tide (e.g., Love 1906; Takeuchi 1950). Although the real Earth departs from the SNREI model, those theories provide reasonable results for the tidal deformations (Wahr 1982), which makes them suitable to study the effects that the bodily tides have on other motions of the Earth.
It is the case when determining the effects of the tidal deformations on the Earth rotation (e.g., Jeffreys & Vicente 1957; Sasao et al. 1980; Getino & Ferrándiz 1995, or Escapa 2011). Since the variations of the Earth rotation, the displacement vector field associated with the tide, and the deviations of the SNREI Earth model with respect to the real Earth are small, ignoring rotational and elliptical effects on the bodily tide leads to a very good first approximation when studying Earth rotation5. This fact has been explicitly confirmed by theories of the Earth rotation that include first-order rotational and elliptical effects in the deformations, as it is stated in the very elucidating notes by Wahr (1982).
The features of a SNREI model imply the following assumptions. Firstly, the deformation is purely elastic, which implies instantaneity and reversibility6, both properties consistent with the discussion made in the previous section. Moreover, rotational and elliptical effects are not considered on the Earth’s deformation. In order to perform the ΔIij integrals given by Eq. (9), the density function in a SNREI model is assumed to be isotropic or spherical, ρ(r) = ρ(r).
In this situation, the case of a deformation induced by an external (gravitational) potential, proportional to solid spherical harmonics (of second degree), 𝒰2, was studied by Love (1911) and Takeuchi (1950). In fact, let (rq,θq,ϕq) be the spherical coordinates of a perturber q, the tidal (or tide-raising) degree-2 potential due to the gravitational action of the perturber q on a point (r,θ,ϕ) of the Earth is given by the well-known expression
where γ is the angular separation between vectors rq and r, and P2 is the second degree Legendre polynomial. Then, the acceleration derives from the potential in the form −∇𝒰2. The solution for the displacement field is given by (Love 1911, Sect. 109),
with F2 and G2 being some functions of r only7. We note that the toroidal component (proportional to r × ∇𝒰2) is null in this model. Therefore, using the addition theorem for the un-normalized degree-2 spherical harmonic (Whittaker & Watson 1950, Sect. 15.7) in Eq. (12),
is obtained, 𝒞2m and 𝒮2m functions being real surface spherical harmonics of second degree, 𝒞2m (θ,ϕ) = P2m (cos θ) cos (mθ), 𝒮2m (θ,ϕ) = P2m (cos θ)sin(mθ), and P2m the associate Legendre function. In Eq. (14) the arguments of the spherical harmonics have been omitted, for the sake of simplifying the notation. We note that those with q subscript are related to the spherical coordinates of the perturber.
Taking into account the previous considerations, the integral of the perturbation ΔIij to the inertia matrix elements (Eq. (9)) can be performed. This requires a rewriting of the Cartesian coordinates ui of the displacement vector in spherical ones, given by
where the relation ∂𝒰2/∂r = 2𝒰2/r has been used, in addition to the spherical expression of ∇𝒰2. Then, performing the integral in the angular variables (θ,ϕ), the following expression of the perturbation of the matrix of inertia due to the perturber q is obtained:
with κt, q being a parameter describing the elastic response of the SNREI Earth to the perturbation caused by the perturber, whose integral form is
In Eqs. (16) and (17), the mean distance between the geocenter and the perturber, aq, has been introduced by normalization convenience; aE is the Earth’s mean equatorial radius, used to define the integral in the radial coordinate. Equation (16) is equivalent to those of Peale (1973), Kubo (1991), Getino & Ferrándiz (1990, 1995), or Lambert & Mathews (2006), but the parameters describing the elastic behavior are different up to proportionality factors.
However, the process that we have followed in their computation is different. In those works Eq. (16) is obtained from MacCullagh’s formula (3), since the redistribution tidal potential is known from the solution of the elastic problem. Here, we construct the increment of the matrix of inertia through the displacement vector. This approach provides an alternative derivation to that presented in Getino & Ferrándiz (1990). It should be recalled that the trace(ΔI) is null, due to a general result of linear elasticity (Rochester & Smylie 1974, generalizing Darwin’s theorem, Darwin 1910, for a solenoidal deformation).
2.3. Expression of the redistribution tidal potential
MacCullagh’s formula, Eq. (3), allows the linking of the perturbation of the inertia tensor to the additional gravitational potential energy related to the mass redistribution. Therefore, from Eq. (11), the redistribution tidal potential energy, 𝒱t; p, q, due to a couple of perturbed (p) and perturbing (q) bodies is written as
Here rp = (x1, p,x2, p,x3, p) are the Cartesian coordinates of the point where the gravitational potential is evaluated; in our application, it will be the position of the perturbed body p. After some algebra, introducing the ΔIij, q elements given by Eq. (16), and taking into account that the solid spherical harmonics of the second degree can be expressed as linear combinations of products xi, pxj, p, namely,
the 𝒱t; p, q potential becomes
It will be useful for the purpose of this study to link the κt, q parameter with the Love number k2 (Love 1911, Sect. 59), due to the widespread use of such formalism in the study of the Earth’s deformability, as will be shown in the next sections. By definition, k2 Love number is given by the proportionality between the additional redistribution potential at the (displaced) surface, arising solely from the redistribution of mass (Munk & MacDonald 1960, Chap. 5).
Therefore, in order to use Eqs. (14) and (20), the following relation will be fulfilled, 𝒱t; p, q(rp = aE)/mp = k2𝒰2(r = aE), which simplifies to
Obviously, k2 is independent from the perturber q, and characterizes the elastic response of Earth in a SNREI model. The well-known form of the redistribution potential is then recovered,
with 𝒰2 given by Eq. (14). This general expression is used, for instance, in Munk & MacDonald (1960), Peale (1973) or, in recent works, by Efroimsky (2012a,b) or Williams & Boggs (2016).
The tide-raising potential is commonly referred to the Earth surface (e.g., Kaula 1964; Efroimsky 2012a,b, or Williams & Boggs 2016). By writing rp = rpep and with the aid of Eq. (14), we derive that
where we have introduced the abridged notation 𝒰2(aEep,rq) = 𝒰2(rq). In this way, we can write Eq. (22) in the form
At the Earth surface rp = aE; the former equation provides the Love number k2 as the constant of proportionality between the redistribution potential and the tide-raising potential on the spherical Earth surface. In what follows, the criterion given by Eq. (24) will be adopted, due to its wider use.
From Eq. (17), an integral form for the k2 Love number in the SNREI Earth model can be provided,
This expression allows a numerical integration in order to obtain the k2 value for different Earth rheologies (within the SNREI modeling). The Takeuchi (1950) computational procedure to obtain F2 and G2 functions was followed, as an example of a similar procedure, by Getino & Ferrándiz (1991) 8 – with Takeuchi’s Earth model – or Getino (1993) – with 1066A and 1066B Gilbert & Dziewonski (1975) models. However, this is not the purpose of this research, and the numerical values of k2 (and those of its generalizations for more realistic Earth models) will be considered instead, as inputs of the theory, as occurs with the ephemeris describing the motion of the perturbers.
The time dependence of the redistribution tidal potential (Eq. (20)) is due to that of the Love number and the relative motion of the perturber q. It is better described in the frequency domain. The dependence of k2 with the tidal forcing frequencies, due to the relative motion of the perturber q in a SNREI Earth model, is very weak at least when they are smaller than the free elastic oscillations of the Earth model as is the case (e.g., Wahr 1982 or Moritz & Mueller 1986, Chap. 4). It means that when deriving the expression of the displacement vector, it is possible to assume that the tide-raising potential is a constant function, that is, its forcing frequency equals zero. In other words, the elastic response of the SNREI Earth model is an equilibrium response giving rise to what is usually referred to as the static, or quasi-static, approximation (Moritz & Mueller 1986, Chap. 4). In entails that with those provisos the Love number k2 is constant.
With respect to the part related to the perturber q, its resulting frequency set arises from a combination of the orbital evolution features of q with the Earth rotational motion. This kind of Fourier decomposition is common in tidal studies, leading to tide generating potential (TGP) expansions, and can be accomplished from multiple approaches (e.g., Doodson 1922; Kaula 1964, or Kudryavtsev 2004).
For the purposes of this study, however, it is more convenient to obtain the Fourier decomposition with the same method as that introduced by Kinoshita (1977) when developing the disturbing function in his theory of the Hamiltonian rotation of the rigid Earth. In this way, all the considered perturbations on the Earth rotation coming from the Moon and the Sun are developed from an identical baseline expansion, which enhances the consistency of the canonical approaches.
2.4. Generalization to the Earth redistribution potential
For the consideration of a more general elastic response of the Earth, mainly two kinds of effects can be introduced within the scope of the elastic-viscoelastic analogy9: the anelastic behavior intrinsic to the rheological model, and the contributions of the ellipticity and rotation to the deformation, both involving the transition from the stationary Love number k2 to its dynamic version (time dependent).
2.4.1. Anelastic response (rheological model)
The anelastic behavior implies that 𝒱t; p, q and 𝒰2 in Eq. (24) are not determined at the same time, but with delay (without loss of reversibility). This fact can be written, with explicit arguments, as (Efroimsky 2012b)
with k2(t − t′) being the kernel of an integral representation of the dynamic counterpart of the Love number (the dot represents the time derivative), which acts as an operator mapping 𝒰2 onto 𝒱t; p, q. This formalism generalizes the classic idea of the constant time lag for the description of the delayed response relative to the perturbing potential, which is inconsistent in certain aspects as discussed in Efroimsky & Makarov (2013). We note that if k2 (t − t′) = k2Θ(t − t′) (Θ being the Heaviside step-function), Eq. (24) is recovered, describing an instantaneous reaction or, in other words, a perfectly elastic response.
In such an approach, the frequency-dependent complex Love functions, k̄2(ω), are defined as Fourier transforms of 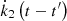 by means of
by means of
where, in the second equality, the module-argument expression of the Love function, 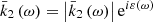 , has been used.
, has been used.
2.4.2. Rotation and ellipticity (dynamical model)
The influence of rotation and ellipticity on the bodily tides has been long studied, for instance, within the rheological theories where the undeformed state is assumed to be ellipsoidal (or oblate) and rotating. This implies forgetting the simplifying hypotheses of the SNREI model. This is the case for Smith (1974); Shen & Mansinha (1976), and Wahr (1981) among others. Other approaches to the problem are those of Mathews et al. (1995), Dehant et al. (1999), or its generalization in the IERS Conventions (2010), both of them on the basis of the Sasao et al. (1980) dynamical theory (known as SOS formalism).
As these works show, such type of behavior can be built with a frequency (or mode) dependence of the Love numbers or, more precisely, Love functions (Efroimsky 2012b), which are introduced in Eq. (26). Strictly speaking, this equation involves any mass redistribution effect that can be formally described with a 2-degree 𝒰2-like potential, which can be incorporated into the external tide-generating potential. This is the case, for instance, for oceanic loads and tides (see, e.g., the Love number model for an Earth with oceans in Williams & Boggs 2016, which will be considered in Sect. 4.3).
In the presence of rotation and ellipticity there appear normal modes related to the Earth rotation (e.g., Escapa et al. 2001). Those modes depend on the unperturbed rotation state and the internal structure of the Earth. For example, for a two-layer Earth model with a solid mantle and a fluid core, the most important ones are the Chandler wobble (CW) and the retrograde free core nutation (RFCN, or simply FCN). If we consider that the core contains a solid part, the solid inner core, we have two additional modes: the inner core wobble (ICW) and the prograde free core nutation (PFCN).
Among all those modes the FCN has a particularly notable effect on the Earth rotation. The reason is that its associated frequency relative to the Earth system, also referred to as nearly-diurnal free wobble (NDFW), is in the diurnal band10, as a consequence of the value of the ellipticity in the core-mantle boundary. Since there are also some frequencies of the tide-generating potential in the same band, a resonance phenomenon appears. Its presence has been modeled in different Earth rotation models (e.g., Poincaré 1910; Wahr 1981, or Getino & Ferrándiz 2001) and its effects on the nutations observed (e.g., IERS Conventions 2010, Chap. 5).
The excitation of the FCN mode by the forcing frequencies, related to the perturber q, couples with the Earth tidal deformation. It makes the Love number k2 resonant at the FCN frequency (e.g., Jeffreys 1976, Chap. 7, Wahr 1982; Moritz & Mueller 1986, Chap. 4). That resonance of k2 in the diurnal band has emerged in many studies using quite different approaches (e.g., Jeffreys & Vicente 1957; Sasao et al. 1980, or Wahr 1981).
The mechanisms entering into this process are complex and lead to a resonance expansion of the Love number k2, as it is explained in the comprehensive work by Mathews et al. (1995). Recently, this problem has been revisited within the Hamiltonian formalism by Baenas et al. (2017), achieving closed-analytical formulae compatible with the previous works. That expansion can be written in the general form (e.g., Mathews et al. 1995) in the frequency domain as
where the sum runs over the rotation normal modes of the Earth model. The numbers L0 and Li are constant and ωi is the frequency of the i normal mode relative to the Earth system. In the context of this research, the most relevant contribution to that resonance formula comes from the FCN mode.
The effects of rotation and ellipticity, by themselves, are conservative, so the numbers in Eq. (28) are real. However, if some dissipative torque is incorporated into the Earth rotation model, those constant numbers become complex. That induces a small imaginary part in 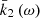 or, equivalently, a phase ε(ω) as in the anelastic situation. That is the case, for example, when considering a viscous-electromagnetic torque at the core-mantle boundary (e.g., Getino & Ferrándiz 2001).
or, equivalently, a phase ε(ω) as in the anelastic situation. That is the case, for example, when considering a viscous-electromagnetic torque at the core-mantle boundary (e.g., Getino & Ferrándiz 2001).
There are different resonance expansions generalizing Eq. (28) according to the features of the Earth rotation model under consideration. Typical examples are those provided in Mathews et al. (1995) or in IERS Conventions (2010, Chap. 6).
2.4.3. Earth redistribution potential
Both effects described in Sects. 2.4.1 and 2.4.2 can be incorporated into a sole formalism for the Love functions by using complex Love functions (similar to the complex compliances in SOS formalism), within the language of complex Fourier expansion of the involved potentials used by the IERS Conventions (2010). Therefore, Eq. (24) can be written in terms of the Fourier complex components of 𝒱t; p, q and 𝒰2 in the frequency domain as
Equation (27) and (29) come from a standard Fourier expansion and details can be consulted in Efroimsky (2012b). In our formalism, the concise notation ω for the excitation frequency will be substituted by mωE ± nj, m being the frequency band (spherical harmonics order), ωE the mean value of the Earth’s angular velocity, and nj the j-th orbital frequency. These frequencies are obtained from a Fourier-like expansion of the orbital motion of the perturbing bodies, referred to the terrestial reference system (Kinoshita 1977, see Appendix A). Complex Love functions, usually named as complex Love numbers, will be denoted as
It should be remembered that the frequency dependencies 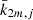 must be given by the addition of a rheological and a dynamical model. Within a first-order theory, the solution offered by both models is a known function of time. In other words,
must be given by the addition of a rheological and a dynamical model. Within a first-order theory, the solution offered by both models is a known function of time. In other words, 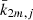 values and the related frequencies are not affected by their own corrections on the Earth’s rotational motion, as happens with the orbital motion of the perturbers.
values and the related frequencies are not affected by their own corrections on the Earth’s rotational motion, as happens with the orbital motion of the perturbers.
It should be recalled that, by relying on Eq. (29), the redistribution potential energy is therefore generalized by extracting the real part of the complex 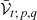 function in Eq. (29). Then, the following expression including arguments of the trigonometric functions within the spherical harmonics holds:
function in Eq. (29). Then, the following expression including arguments of the trigonometric functions within the spherical harmonics holds:
We note that the complete expressions of the real spherical harmonics also depend on the orbital frequencies, once they are provided by some calculation of ephemeris (for perturbed and perturbing bodies). This fact is implicit in Eq. (31). The total redistribution potential energy, 𝒱t, is the sum over p and q – both representing either Moon or Sun – of terms 𝒱t; p, q. Each portion can be also partitioned in the sum of zonal (long-period, m = 0), tesseral (diurnal, m = 1), and sectorial (semidiurnal, m = 2) harmonic components of the tide-raising potential.
3. Precession formulae
Once the expression of the redistribution potential energy has been derived in a quite general form (Eq. (31)), it is necessary to quantify its contribution to the Earth precession rates in longitude and obliquity. Although other approaches are possible, the formulation of this problem in the Hamiltonian formalism of the rotation of the non-rigid Earth (e.g., Getino & Ferrándiz 1995, 2001; Escapa et al. 2001, or Escapa 2011) presents some advantages (e.g., Baenas et al. 2017).
Two of the most relevant are the achievement of a consistent theory because all the effects are derived from a sole function, the Hamiltonian of the system, and the suitability of this framework to obtain analytical expressions even for the second-order terms, that is, terms that are quadratic in the small parameters. This is specially useful from our perspective, since the contributions of the redistribution of mass to the precession can be easily recomputed for different rheologies and dynamical Earth models. Next, the main elements necessary for this construction will be sketched. Further details can be found in two recent works by the authors, Baenas et al. (2017) and Escapa et al. (2017), and references therein.
3.1. Canonical formulation of the rotational problem of a non-rigid two-layer Earth
An Andoyer-like set of canonical variables (Getino 1995) {λ,μ,ν,λc,μc,νc;Λ,M,N,Λc,Mc,Nc} is used to describe the rotation that transforms the non-rotating (OXYZ) system into the (Oxyz) system linked – in Tisserand’s sense – to the Earth, which is referred to as a terrestrial system. The coordinates {λ,μ,ν} and their conjugated moments {Λ,M,N} stand for the Andoyer variables of the whole Earth, and the rest, with subscript c, for the fluid outer core (FOC). The auxiliary angles σ (between the angular momentum and the figure axis) and I (between the angular momentum vector and the Z axis of the non-rotating or quasi-inertial system) are defined through Λ = Mcos I and N = Mcos σ. The order of magnitude of σ is about 10−6 rad (Kinoshita 1977). More details on these variables within the precession context can be found in Ferrándiz et al. (2004) or Baenas et al. (2017).
The Hamiltonian of the problem is given by
where 𝒯0 is the kinetic energy corresponding to the rigid mantle case (Poincaré model, Getino & Ferrándiz 2001); 𝒱0 is the degree-2 gravitational perturbation exerted by Moon (M) and Sun (S) (𝒱0 = 𝒰2; M + 𝒰2; S);ℰ is the non-inertial complementary term (due to ecliptic motion, Kinoshita 1977); 𝒯t is the redistribution kinetic energy (Getino & Ferrándiz 2001), and 𝒱t is the redistribution potential energy, given in Sect. 2.4.3.
The precessional motion is caused by the secular part of the Hamiltonian. This is obtained from Expression (32) by means of the elimination of the periodic terms through a Lie-Hori canonical transformation (Hori 1966; Ferraz-Mello 2007), which leads to the averaged Hamiltonian, responsible for the secular motion of the equatorial plane.
The contribution of each term can be studied separately, obtaining the final values of the precession rates from summing up all the effects. The precession rate in longitude corresponding to 𝒯0 + 𝒱0 + ℰ (Poincaré model) was computed up to the second-order of perturbation by Ferrándiz et al. (2004). The effect of the mantle elasticity, introduced through the 𝒯t term, was performed by Baenas et al. (2017), which is a second-order effect11 in the scope of the perturbation methods, and updates the value of the general precession in longitude given by the previous work.
Therefore, this work’s aims are restricted to the secular Hamiltonian
whose order of magnitude, O(𝒱t/𝒯0) ∼ 1.7 × 10−12, allows the use of a first-order perturbation method12.
The contribution of 𝒱t, sec to the precessional motion is determined through the variation of the derivatives nλ = dλ/dt, for the precession in longitude, and nI = dI/dt, in obliquity. We will denote by δnλ and δnI the new additive contributions, stemming from the application of the dynamical equations to the secular Hamiltonian.
These equations are given by δ(df/dt) = {f,ℋsec}, f being a smooth function of the canonical set, while {−,−} stands for the Poisson bracket written down in the Andoyer-like canonical variables. In this case,
is obtained.
It should be noted that the contributions δnλ and δnI are strictly related to the angular momentum axis motion. Within our order of approximation, those rates are the same as those of the longitude and obliquity of the figure axis (Kinoshita 1977). Besides, the commonly used astronomical longitude and obliquity angles, ψ = −λf and ε = −If, will be henceforth employed in this work to express the precessional rates, δnψ = −δnλ and δnε = −δnI.
3.2. Canonical expression of the secular redistribution potential
Considering Eq. (31), the real spherical harmonics must be expressed in the Andoyer-like canonical set of variables of the Earth, as a combination of spherical harmonics defined in the OXYZ system. In this work, the Moon and the Sun are considered as the sole perturbing bodies. Although some planets have an appreciable direct effect on Earth precession, as first demonstrated by Vondrák (1982), their direct influence on the Earth’s mass redistribution precession can be neglected within the current accuracy threshold13.
In this way, when the orbital motions of the Moon and the Sun are provided by some ephemeris (Kinoshita 1977), the redistribution tidal potential energy can be re-expressed in terms of Andoyer-like canonical variables. This process, at first order in σ, is given in Eq. (A.1). The related expressions are applicable to both perturbing and perturbed bodies, then a different notation will be used in order to distinguish them: dummy indexes i, τ for perturbed bodies, and j, ϵ for perturbing ones.
As the orbital motion of the perturbing bodies is considered to be decoupled from the Earth’s rotational motion, the related Andoyer coordinates, 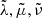 , and the fundamental argument,
, and the fundamental argument, 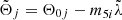 (defined in Appendix A), are not canonical variables, but explicit time-dependent functions. The tilde symbol (∼) will be used from now on to denote time-dependent functions or, in other words, magnitudes depending on the variables or coordinates of the perturbers q.
(defined in Appendix A), are not canonical variables, but explicit time-dependent functions. The tilde symbol (∼) will be used from now on to denote time-dependent functions or, in other words, magnitudes depending on the variables or coordinates of the perturbers q.
The forcing orbital frequencies are given by 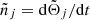 . The spherical harmonics expansion in such case (with the tilde symbol) can be truncated at the zero order in
. The spherical harmonics expansion in such case (with the tilde symbol) can be truncated at the zero order in 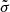 because of the small magnitude of this angle as a function of time, and the fact that it does not participate in the construction of the equations of motion (e.g., Kubo 1991, appendix).
because of the small magnitude of this angle as a function of time, and the fact that it does not participate in the construction of the equations of motion (e.g., Kubo 1991, appendix).
The secular part of the redistribution potential energy, 𝒱t, sec, is computed in order to be free from short-period terms, following a similar procedure to that of Kinoshita (1977). This will be achieved by making explicit the canonical variables in Eq. (31) through Eq. (A.1), and then retaining only the terms whose frequency vanishes. In this procedure, some canonical variables can be substituted by their values in the steady rotation state. These are (see, e.g., Escapa 2011)
where the subscript 0 stands for integration constants, N0 ≃ M0 = CωE, and consequently, I = I0, σ = σ0 ≃ 0 (note that the remaining unperturbed solutions are not needed because they do not participate at the first order in σ, inasmuch as no derivatives with respect to σ are present in the dynamical equations for the precession).
Finally, the application of this technique results in
where the (0), (1), and (2) superscripts stand for the zonal, tesseral, and sectorial contributions of the redistribution potential, respectively, and are given by
Here, ℐ set has been defined for the summation conditions
equivalent to the aforesaid cancelation of the frequency of the trigonometric arguments of 𝒱t. In the previous expression and hereinafter, j subscript of Love and Kinoshita’s functions refers to an abridged notation for ϵ = ±1 and jth orbital frequency, which in fact should be denoted with a different subindex. However, this abuse of notation is kept due to the absence of likelihood of confusion.
The kp parameter is the one defined by Kinoshita (1977), and the dimensionless fq parameter has been introduced for notational convenience, namely,
3.3. Resulting precession formulae
Once Lie derivatives of Eqs. (34) have been computed, it is possible to identify the (μ,ν,λ) canonical variables with the 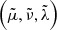 time functions, given the coincidence between perturbed and perturbing bodies. This fact involves identifying the arguments Θi and
time functions, given the coincidence between perturbed and perturbing bodies. This fact involves identifying the arguments Θi and 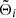 likewise. The Kinoshita’s orbital functions, Bi, Ci, and Di, can be evaluated at some epoch wherein I = Ĩ ≡ I0, keeping Eq. (35) as a good approximation for this purpose (see, e.g., Escapa 2011). Finally, the precession rates read as
likewise. The Kinoshita’s orbital functions, Bi, Ci, and Di, can be evaluated at some epoch wherein I = Ĩ ≡ I0, keeping Eq. (35) as a good approximation for this purpose (see, e.g., Escapa 2011). Finally, the precession rates read as
where the following functions have been defined
In these expressions, the ∼ symbol has been kept, although now it is strictly redundant.
Equations (40) and (41) are one of the main achievements of this work. They allow the numerical computation of the precessional rates due to the redistribution of mass once given the corresponding Love numbers of the model. In this way there is no need to recompute the redistribution potential energy itself.
4. Redistribution precession for different Earth Love numbers sets
In order to obtain numerical values for the precessional rates, the dependence of the Love numbers on the forcing frequencies is needed. In this research, some different models of Earth’s rheology have been considered.
The main parameters used to perform the calculations are included in Table 1. In turn, Table 2 separately displays the contributions coming from the different harmonic terms of the tidal potential – zonal, tesseral, and sectorial – for each Earth model.
Numerical parameters used in this work.
Redistribution potential contributions to precession rates (unit: mas cy−1).
In the different models under consideration, the contribution of the time-independent part of the redistribution potential will be discounted (further details will be discussed in Sect. 5.1). From Eq. (16) –the form of ΔIq– and Eq. (A.1), the time-independent part in the Earth’s inertia tensor comes from the zonal contribution and is given by
when 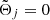 (zero frequency), or equivalently, with index j = (0, 0, 0, 0, 0). The portion of the deformation coming from this time-independent zonal contribution of the Earth’s inertia tensor is named permanent tide.
(zero frequency), or equivalently, with index j = (0, 0, 0, 0, 0). The portion of the deformation coming from this time-independent zonal contribution of the Earth’s inertia tensor is named permanent tide.
The permanent tide contribution to precession in Table 2 has been computed using the fluid (limit) Love number, k2f = 0.94 (Burša & KarelPěč 1993, Sect. 4.9; Lambeck 1980, Sect. 2.4) and k2f = 0.30 = k2 for comparative purposes.
The fluid Love number arises from considering the Earth response to forces that stay constant over very long periods of the order of billions of years, not to tidal periodic ones. It entails considering a completely fluid Earth model instead of a typical SNREI Earth model, hence the difference in the values of tidal-effective k2 and fluid14kf Love numbers (e.g., Munk & MacDonald 1960, Chap. 5; Lambeck 1980, Chap. 2; or Moritz & Mueller 1986, Chap. 3).
When making comparisons between different studies involving Earth parameters like its inertia moments, ellipticity, J2 Stokes coefficient, and others, it is very important to take into account in what way the effects of the permanent tide have been considered. It leads to the denominations zero-tide (including the permanent tide) or tide-free (excluding the permanent tide) systems, recommended in IERS Conventions (2010, Chap. 1). The zero-tide system is also known as the zero-frequency one (e.g., Burša & KarelPěč 1993, Chap. 4). Its use is recommended by the Resolutions of the International Association of Geodesy, as noted in the IERS Conventions (2010, Chap. 6).
In this regard, since tide-free values are unobservable and the value of kf is uncertain, some authors prefer to consider the parameters in the zero-frequency system (Burša 1995). In our case, it would imply that the permanent tide contributions would be contained in the values of the moments of inertia of the undeformed state. In Eq. (42) and Kinoshita’s constant, Eq. (39), the dynamical ellipticity Hd is a zero-tide magnitude. The corresponding parameter of IAU2000 also includes the permanent tide (Groten 2004).
4.1. SNREI Earth
The tidal response of a SNREI model constitutes a topic of the literature that addresses the definition of Love numbers (e.g., Jeffreys 1976; Moritz & Mueller 1986, among many others). For the purposes of this study, its features can be characterized by taking a single constant value for the Love number set, 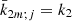 , and it can be analytically proved (Krasinsky 1999; Escapa et al. 2003, 2004; Lambert & Mathews 2006; Baenas 2014) that the contributions given by Eq. (40) to the precessional motion are cancelled out, δnψ = δnε = 0. A succinct demonstration of this fact can also be found in Appendix B. The first column in Table 2 shows numerically the cancelation of the harmonic contributions of the secular rates, on the last row of the table. It should be remarked that the cancelation is only achieved by adding the contribution of the permanent tide, assuming the same Love number as for the remaining tides, k2f = k2 = 0.30.
, and it can be analytically proved (Krasinsky 1999; Escapa et al. 2003, 2004; Lambert & Mathews 2006; Baenas 2014) that the contributions given by Eq. (40) to the precessional motion are cancelled out, δnψ = δnε = 0. A succinct demonstration of this fact can also be found in Appendix B. The first column in Table 2 shows numerically the cancelation of the harmonic contributions of the secular rates, on the last row of the table. It should be remarked that the cancelation is only achieved by adding the contribution of the permanent tide, assuming the same Love number as for the remaining tides, k2f = k2 = 0.30.
As displayed in Table 2, the obliquity rate for this model is zero. This result comes from Eq. (40), which show that this effect is only present when the Love numbers are complex, with any ε2m, j ≠ 0. This is not the case for a perfect elastic, oceanless Earth model.
4.2. IERS Conventions (2010) models for solid Earth tides
4.2.1. Constant Love numbers per frequency band
In order to progressively show the influence on the precessional rates of the frequency dependence in the Earth’s anelastic response, a model with a nominal, reference value of the Love numbers for each harmonic order (or frequency band, long-period, diurnal, and semidiurnal) m, will be considered, that is, 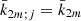 (Col. 2 in Table 2). Basically, the band structure reflects the influence of rotation and ellipticity, whereas the imaginary part is related to the anelastic Earth response. This model is taken from Table 6.3 of IERS Conventions (2010) with
(Col. 2 in Table 2). Basically, the band structure reflects the influence of rotation and ellipticity, whereas the imaginary part is related to the anelastic Earth response. This model is taken from Table 6.3 of IERS Conventions (2010) with 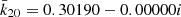 ,
, 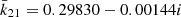 , and
, and 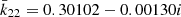 .
.
4.2.2. IERS Conventions frequency-dependent Love numbers
In the IERS Conventions (2010), the frequency dependence in the Love numbers set (related to the rotation and ellipticity and the anelastic response of the mantle, Sect. 2.4) is introduced via the resonance formulae (Ibid, Eq. (6.9)), which update and summarize previous works by Wahr (1981), Mathews et al. (1995), and Dehant et al. (1999), among others. The modeling takes into account the retrograde free core nutation (FCN), the Chandler wobble (CW), and the free inner core nutation resonance processes in the diurnal band of frequencies for the solid Earth tides. In a second step, an effective ocean tide contribution (OT), 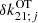 related to
related to 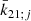 , following Wahr & Sasao (1981), is considered. This contribution incorporates the ocean load on the solid Earth tides. The
, following Wahr & Sasao (1981), is considered. This contribution incorporates the ocean load on the solid Earth tides. The 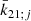 value is directly calculated from the nominal
value is directly calculated from the nominal 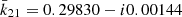 (Ibid., Table 6.3) and the tabulated δkf; j values (Ibid., Table 6.5a), which are defined as
(Ibid., Table 6.3) and the tabulated δkf; j values (Ibid., Table 6.5a), which are defined as
with Lk being the complex constants of the resonance formula for solid tides (Ibid., Eq. (69) and Table 6.4). In the zonal band, the IERS Conventions (2010) provide the following model, due to the mantle anelasticity (based in Wahr & Bergen 1986),
where σj is the excitation frequency (mωE − ϵñj), σk and σr are reference frequencies, and α = 0.15 (Ibid., Table 6.4). The 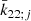 complex Love number can be accurately approximated by its nominal value 0.30102 − i0.00130 (Ibid., Table 6.3). The related values of the precession rates components are shown in the third column (resonance formula) and fourth column (including the ocean load correction) of Table 2.
complex Love number can be accurately approximated by its nominal value 0.30102 − i0.00130 (Ibid., Table 6.3). The related values of the precession rates components are shown in the third column (resonance formula) and fourth column (including the ocean load correction) of Table 2.
4.3. Williams & Boggs (2016) frequency-dependent Love numbers for the Earth with oceans
Finally, the last column in Table 2 shows the secular rates values obtained by using the Love numbers model of the Earth with oceans from Williams & Boggs (2016). This model is built over the IERS Conventions (2010) one for solid Earth tides (previous section), and the ocean model FES2004 (Lyard et al. 2006), giving a very complete description of the anelastic behavior of the tide effect. The Love numbers set can be consulted in Williams & Boggs (2016), Table 6, and the algorithm described on page 105.
This model allows us to compare the results obtained for the precessional rate in obliquity. Specifically, Williams & Boggs (2016) got the value for the precessional rate in obliquity (Ibid., Eq. (29)). They used a quite different approach from that followed here. In particular, they employed the Euler equations of vectorial mechanics, and constructed the Fourier expansion of the tide-generating potential with the same orbital ephemeris as us, but without introducing canonical variables in their derivations. By means of that procedure, Williams & Boggs (2016) derived a total tidal obliquity rate of 0.92 mas cy−1 (which is split into −0.07 mas cy−1, 0.1 mas cy−1, and 0.89 mas cy−1 for zonal, diurnal, and semidiurnal terms, respectively), while in this work an obliquity rate of 0.9341 mas cy−1 (which is split into −0.0636 mas cy−1, 0.0948 mas cy−1, and 0.9030 mas cy−1 for zonal, tesseral, and sectorial contributions, respectively) is obtained, showing an excellent agreement between both studies.
These equivalent results for the obliquity rate suppose a mutual validation of the procedures, due to them having been achieved through quite different approaches. In particular, it supports the correctness of Eqs. (40) and (41). Williams & Boggs (2016) do not provide a value for the longitude rate, as it is out of the scope of their work.
Lambert & Mathews (2006, 2008) also computed precession rates for a model close to that of Williams & Boggs (2016), but using the ocean tide model CSR4. The discrepancies with their numerical values are quite significant (see next section).
5. Discussion and conclusions
5.1. Contribution of the permanent tide
For the sake of convenience, the precession rate in longitude given by Eq. (40) will be decomposed in two parts, δnψ = pP + pP̄, pP being the contribution of the permanent tide (zonal zero-frequency terms, i.e., those associated with B0; p function), and pP̄, the remaining non-permanent part (the “p” standardized notation is used for precession contributions). Therefore, from Eqs. (40) and (41), pP can be written as
Here, the 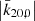 parameter has been simplified by k2f fluid Love number, corresponding to permanent deformation. The first bracket of the decomposition coincides with the first-order lunisolar precession term, denoted as
parameter has been simplified by k2f fluid Love number, corresponding to permanent deformation. The first bracket of the decomposition coincides with the first-order lunisolar precession term, denoted as 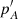 in Souchay & Kinoshita (1996) (an expanded form can be found in Kinoshita & Souchay 1990, Eq. (8.7)). The second one is related to the variation of the Earth dynamic ellipticity due to the permanent tide.
in Souchay & Kinoshita (1996) (an expanded form can be found in Kinoshita & Souchay 1990, Eq. (8.7)). The second one is related to the variation of the Earth dynamic ellipticity due to the permanent tide.
In fact, considering the tide-free dynamic ellipticity of a symmetric Earth (previous to tidal deformation), Hd, 0 = (C−A)/C, and its zero-tide counterpart, due to the permanent variation of the inertia moments,
a first-order expansion in the small magnitude ΔC/C leads to the relation
Therefore, the δHd, p following variation of the dynamic ellipticity holds
where, in the last equality, the relation ΔC + 2ΔA = 0 has been applied (Sect. 2.2). Recovering Eq. (42), with ΔC = ∑qΔCq,
which matches with the second bracket in Eq. (45). Hence, within a first-order precession theory (i.e., proportional to Hd, p), pP can be written as
It should be recalled that Hd, P is a primary parameter (Hd, P = Hd, 0 + δHd, P decomposition is not observationally distinguishable), while the tide-free Hd, 0 is a derived one. Accordingly, the pP contribution should not be considered in the zero-tide system, since its effects are included within the Hd, P Earth dynamic ellipticity.
However, the precession rate due to the non-permanent tides, pP̄, must be taken into account in correcting the reference value of Hd, P, as will be shown in the next section. In order to have a numerical estimate, pP = 136.5964 mas cy−1 (Table 2), and 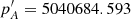 mas cy−1 (obtained by subtraction in Capitaine et al. 2005) can be considered, thus
mas cy−1 (obtained by subtraction in Capitaine et al. 2005) can be considered, thus
We note that the approximately equal sign has been used as a reminder that the Hd, p value has been taken (Table 1) instead of the unobservable tide-free Hd, 0. Due to factor 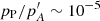 and the smallness of δHd, P, this is an admissible approximation.
and the smallness of δHd, P, this is an admissible approximation.
The second zonal Stokes parameter for a symmetric Earth, 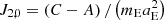 , is also consequently sensitive to the permanent tide. This effect has been previously studied, for instance, in Burša (1995), solving a boundary-value problem and leading to a numerical estimate of δJ2, P = (3.08 × 10−8)k2f (notation of this work).
, is also consequently sensitive to the permanent tide. This effect has been previously studied, for instance, in Burša (1995), solving a boundary-value problem and leading to a numerical estimate of δJ2, P = (3.08 × 10−8)k2f (notation of this work).
In our case, by means of Eq. (50) it is only necessary to link the δJ2, P variation with δHd, P, which can be performed in a similar way to Escapa et al. (2017) (Eq. (16)) or combining Eqs. (48) and (50) with the definition of J2, 0, Hd, 0, and 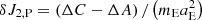 . This relationship reads as
. This relationship reads as
Here, the zero-tide values for Hd, p and J2, P = 1082635.9 × 10−9 (Groten 2004) have been used. This value can be considered in good agreement (a relative error of 1.5%) with that of Burša (1995), taking into account the modeling differences and the updating of physical parameters. In this sense, this fact also confirms the suitability of Eqs. (40) and (41) to treat the effects of the permanent tide.
5.2. Dynamical ellipticity variations due to non-permanent tides
In the general precession in longitude, pA, the main component is the first-order lunisolar precession 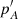 (see, for instance, Table 2 in Baenas et al. 2017). It is obtained by substraction of a set of higher order contributions, denoted as pS, to the observed value of the precession, that is,
(see, for instance, Table 2 in Baenas et al. 2017). It is obtained by substraction of a set of higher order contributions, denoted as pS, to the observed value of the precession, that is, 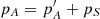 . The
. The 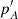 derived value allows the determination of the Hd, P dynamic ellipticity, through
derived value allows the determination of the Hd, P dynamic ellipticity, through 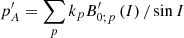 , recalling Eq. (39) for the linear relationship between kp and Hd, P (see Kinoshita & Souchay 1990; Fukushima 2003 or Escapa et al. 2016, for more details on this procedure). The last expression will be formally and briefly written as
, recalling Eq. (39) for the linear relationship between kp and Hd, P (see Kinoshita & Souchay 1990; Fukushima 2003 or Escapa et al. 2016, for more details on this procedure). The last expression will be formally and briefly written as 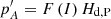 .
.
If any change in the higher order part pS is performed with respect to the reference value (in practice relative to IAU2006 precession one), the 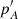 must be compensated by an equal and opposite change, and thus the Hd, P has to be recalculated. This is the case, for instance, for the recomputation of previously considered effects, like the second-order lunisolar precession (Baenas et al. 2017), the geodesic precession (Fukushima 2003), or the non-permanent pP̄ component due to the redistribution of mass performed in this work, among others.
must be compensated by an equal and opposite change, and thus the Hd, P has to be recalculated. This is the case, for instance, for the recomputation of previously considered effects, like the second-order lunisolar precession (Baenas et al. 2017), the geodesic precession (Fukushima 2003), or the non-permanent pP̄ component due to the redistribution of mass performed in this work, among others.
Let δpS be a correction of pS, the new value for the first-order lunisolar precession will be 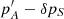 , and the variation the dynamical ellipticity, δHd, δpS will be obtained from the equation
, and the variation the dynamical ellipticity, δHd, δpS will be obtained from the equation 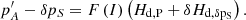 Using that
Using that 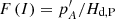 , this equation yields the general expression
, this equation yields the general expression
pointed out, for instance, in Ferrándiz et al. (2012) or Baenas et al. (2017).
Considering δpS = pP̄ = −37.8472 mas cy−1 (Table 2), the deviation from the IAU2006 reference value (−0.960 mas cy−1, Ibid.) has an associate δHd, δpS = 2.396 × 10−8, which implies a relative Hd, P change of +7.3 ppm. Therefore, 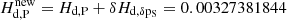 is obtained. This value is somewhat higher if the Love numbers set for an Earth with oceans according to Williams & Boggs (2016) is considered. In particular, we have
is obtained. This value is somewhat higher if the Love numbers set for an Earth with oceans according to Williams & Boggs (2016) is considered. In particular, we have 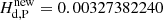 , with δHd, δpS = 2.792 × 10−8 and a relative change of +8.5 ppm.
, with δHd, δpS = 2.792 × 10−8 and a relative change of +8.5 ppm.
5.3. Indirect effects on nutation
Given a δpS correction of pS, the indirect effects on nutational motion emerge from the changes in the value of the dynamical ellipticity, δHd, δpS (Escapa et al. 2016). Computed in the linear approximation, these effects are obtained by multiplying the nutation amplitudes by the factor (Hd, P+δHd, δpS)/Hd, P.
The main terms arising from factor δHd, δpS/Hd, P have been displayed in Table 3, considering the corrections to the dynamical ellipticity due to the second-order lunisolar precession (Baenas et al. 2017), and the redistribution potential (this work). The original nutation terms have been taken from Getino & Ferrándiz (2001).
Precession corrections and indirect effects on nutation.
The relative Hd, P change used in IERS2010 and WB2016 columns are those of the previous section. Some of the corrections are in the tens of μas level, and so they are relevant within the pursued accuracy of the current Earth rotation theories. Strictly speaking, these effects must be considered in the reconstruction of the Earth rotation theory, refitting the basic Earth parameters. However, the magnitudes provided in Table 3 are a clear indication that the effects of the redistribution tidal potential must be taken into account.
5.4. Conclusions
In this research the contributions to the IAU2006 precession of the mass redistribution processes induced on Earth by the gravitational action of the Moon and the Sun have been revisited. Closed analytical formulae for the precession rates in longitude and obliquity have been obtained, by means of the Hamiltonian formalism of the Earth rotation, through the consideration of the redistribution of tidal potential energy, whose derivation has been addressed in a comprehensive way from the changes in the Earth’s matrix of inertia. The analytical formulation enables the numerical computation of the precession rates in longitude and obliquity through Eqs. (40) and (41), under diverse Earth models or rheologies, characterized by different Love numbers that run from a SNREI model to those of an anelastic, elliptic and rotating Earth with oceans models.
The validation of Eqs. (40) and (41) has been shown in different contexts. For example, the precession rates formulae show the analytical cancelation in the SNREI model when the Love number is assumed to be constant regardless of the forcing frequency (including the long period through the permanent tide contribution). This result is consistent with other research (Krasinsky 1999; Lambert & Mathews 2006) that employed quite different methods. In addition, an excellent numerical agreement with Williams & Boggs (2016) in terms of the precession rate in obliquity for an Earth with oceans (with agreement in every frequency band) and Burša (1995) in relation to the permanent tide contribution to the zonal Stokes parameter, has been found.
The values displayed in Col. 4 of Table 2 are quite different from those computed Lambert & Mathews (2006, erratum Lambert & Mathews 2008). Although the authors do not specify which sets of Love numbers they used, it may be inferred that the basic elements used in their approach are similar to those employed in Williams & Boggs (2016). They got the value 1.84 mas cy−1 (Lambert & Mathews 2008) replacing the former estimation of 0.13 mas cy−1 (Lambert & Mathews 2006) for the obliquity rate. The value of 1.84 mas cy−1 is quite close to 2.44 mas cy−1 determined by Williams (1994). However, Williams & Boggs (2016) stated that the value 2.44 mas cy−1 (Williams 1994) was derived under incorrect assumptions, because tidal forces have some components out of the ecliptic. Their new value of 0.92 mas cy−1 is also consistent with similar results by Krasinsky (1999) and that obtained in this work.
In addition to the obliquity rate, our approach has allowed us to obtain the precession rate for the same model. Its numeric value also differs from that of Lambert & Mathews (2006, 2008). Since in those works explicit analytical formulae are not provided to compute the precession rates, it has not been possible to determine the source of those discrepancies. As we have pointed out, our Eqs. (40) and (41) are consistent with the results provided by other authors.
In conclusion, significant differences (−43.945 mas cy−1 in longitude, 0.934 mas cy−1 in obliquity) with respect to the values considered in IAU2006 precession (−0.960 mas cy−1 in longitude, 0.340 mas cy−1 in obliquity) have been found. This circumstance should be carefully considered when assessing a possible update of the IAU precession model (Liu & Capitaine 2017).
On the other hand, the indirect effects on nutations, due to the change of the dynamical ellipticity of some parts per million, must be taken into account for full consistency between the precession and nutation theories, required by the IAU Resolutions and also a main goal of the Global Geodetic Observing System (GGOS) of the International Association of Geodesy (IAG) and the IAU/IAG Joint Working Group on theory of Earth rotation and validation (Ferrándiz & Gross 2015; Transactions IAU 2015; IAG Travaux Reports 2017).
In turn, the obtained numerical results mean that much attention must be paid to the ocean tide models because of their relevant influence in precession and nutation. Our computation relies on the developments by to Williams & Boggs (2016) based on the ocean tide model FES2004 (IERS Conventions 2010, Sect. 6.3.2). Other models might be explored and their results given in a clear form adapted to the Love number formalism, in a similar way to Williams & Boggs (2016). The usefulness of that approach has been proven in this work.
In a general situation, other mechanisms can also contribute to the gravitational potential of an extended body like surface mass distributions, and loads. However, their inclusion does not change the fundamentals of the present exposition, so, for the sake of simplicity, they will not be considered here.
Basically, in those works the effects of the rotation and the deformation are separated, the deformation ones being considered for a spherically symmetric non-rotating Earth (e.g., Wahr 1982; Moritz & Mueller 1986, Chap 4, or Kinoshita & Sasao 1977).
We refer the reader to the illuminating material “Continuum mechanics. A celestial-mechanician’s survival kit”, provided in the extended version of Efroimsky (2012a).
This approach is analogous to the classical separation of variables technique of a scalar field. In this case, the displacement vector is separated as products of the unknown functions F2 and G2, and functions derived from 𝒰2 that depend on r, θ and ϕ (see, e.g., Wahr 1982 or Moritz & Mueller 1986, Chap. 4). The substitution of Eq. (13) in the original partial differential equations of the vibratory motion of an SNREI model, and its boundary conditions, leads to a system of ordinary differential equations in F2 and G2. It can be solved when supplemented with the Poisson equation (Takeuchi 1950; Getino 1993).
The parameter κt, q is similar to that named D, or Dt, in Getino & Ferrándiz (1990); Getino & Ferrándiz (1995). However, in those works the formulae defining D should appear without the term proportional to the radial derivative of the density.
Efroimsky (2012a) and references therein provide a comprehensive discussion on the correspondence principle.
The PFCN mode is also in the diurnal band. However, since the inner core moments of inertia are small when compared with those of the fluid core and the mantle, its effects are quite limited. This explains why, when considering second-order effects on the Earth rotation like in this study, or Lambert & Mathews (2006), it is enough to work with a two-layer Earth model.
From Eq. (31), the order of magnitude of the redistribution caused by a planet of mass mpl and geocentric distance rpl when compared with that of the Sun can be characterized by the ratio (mpl/mS) × (rS/rpl)3. This factor is less than 10−5 (Kinoshita & Souchay 1990, Table XIII). So, its contribution to the precession is smaller than 0.01 μas cy−1 (see Table 2 in Sect. 4 for typical values of the redistribution precession).
Munk & MacDonald (1960) also introduce the secular Love number ks, discussing its relationship with kf.
Acknowledgments
The authors thank the anonymous referee and the Editor for their valuable comments and suggestions that helped to improve the manuscript. This work has been partially supported by the Spanish project AYA2016-79775-P (AEI/FEDER, UE).
References
- Alterman, Z., Jarosch, H., & Pekeris, C. 1959, Proc. R. Soc. London Ser. A, 252, 80 [Google Scholar]
- Backus, G. E. 1967, Geophys. J. R. Astron. Soc., 13, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Baenas, T. 2014, PhD Thesis, University of Alicante, Alicante (in Spanish) [Google Scholar]
- Baenas, T., Ferrándiz, J. M., Escapa, A., Getino, J., & Navarro, J. F. 2017, AJ, 153, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bizouard, C., & Zotov, L. 2013, Celest. Mech. Dyn. Astron., 116, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Burša, M. 1995, Earth Moon Planets, 69, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Burša, M., & KarelPěč, P. 1993, Gravity Field and Dynamics of the Earth (Berlin: Springer-Verlag) [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2003, A&A, 412, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2004, A&A, 421, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2005, A&A, 432, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1969, Ellipsoidal Figures of Equilibrium (New Haven, London: Yale University Press) [Google Scholar]
- Chao, B. F., Dong, D. N., Liu, H. S., & Herring, T. A. 1991, Geophys. Res. Lett., 18, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., & Shen, W. 2010, J. Geophys. Res. Solid Earth, 115, B12419 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., Li, J. C., Shen, W. B., & Huang, C. L. 2015, J. Geodesy, 89, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, F. A. 1968, Geophys. J. R. Astron. Soc., 16, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Darwin, G. H. 1910, Scientific Papers (London: Cambridge University Press), 3 [Google Scholar]
- Dehant, V., Defraigne, P., & Wahr, J. M. 1999, J. Geophys. Res., 104, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Doodson, A. T. 1922, Proc. R. Soc. London Ser. A, 100, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M. 2012a, Celest. Mech. Dyn. Astron., 112, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M. 2012b, A&A, 544, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efroimsky, M., & Makarov, V. V. 2013, Astr. J., 764, 26 [Google Scholar]
- Escapa, A. 2011, Celest. Mech. Dyn. Astron., 110, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2001, J. Geophys. Res., 106, 11387 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2002, A&A, 389, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2003, in Book of Abstracts of the Journés 2003 “Astrometry, Geodynamics and Solar System Dynamics: From Milliarcseconds to Microarcseconds”, ed. A. Finkelstein (St. Petersburg, Russia: Institute of Applied Astronomy of Russian Academy of Science (IAA RAS)), 17 [Google Scholar]
- Escapa, A., Getino, J., & Ferrándiz, J. M. 2004, in Proceedings Journeés, ed. N. Nicole (Paris: Observatoire de Paris) [Google Scholar]
- Escapa, A., Ferrándiz, J. M., Baenas, T., et al. 2016, Pure Appl. Geophys., 173, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Escapa, A., Getino, J., Ferrándiz, J. M., & Baenas, T. 2017, A&A, 604, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrándiz, J. M., Navarro, J. F., & Escapa, A. 2004, Astron. J., 128, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrándiz, J. M., Baenas, T., & Escapa, A. 2012, Geophysical Research Abstracts 14, EGU2012-6175, EGU General Assembly 2012 [Google Scholar]
- Ferrándiz, J. M., & Gross, R. S. 2015, in IAG 150 Years, International Association of Geodesy Symposia 143, eds. C. Rizos, & P. Willis [Google Scholar]
- Ferraz-Mello, S. 2007, Canonical Perturbation Theories: Degenerate Systems and Resonance (New York: Springer) [Google Scholar]
- Fukushima, T. 2003, AJ, 126, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J. 1993, Z. Angew. Math. Phys., 44, 998 [CrossRef] [Google Scholar]
- Getino, J. 1995, Geophys. J. Int., 122, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1990, Celest. Mech. Dyn. Astron., 49, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1991, Celest. Mech. Dyn. Astron., 51, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 1995, Celest. Mech. Dyn. Astron., 61, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., & Ferrándiz, J. M. 2001, MNRAS, 322, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., González, A. B., & Escapa, A. 2000, Celest. Mech. Dyn. Astron., 76, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Getino, J., Escapa, A., & Miguel, D. 2010, AJ, 139, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, F., & Dziewonski, A. M. 1975, Phil. Trans. R. Soc., 278, A187 [NASA ADS] [CrossRef] [Google Scholar]
- Groten, E. 2004, J. Geodesy, 77, 724 [Google Scholar]
- Hori, G. I. 1966, Publ. Astron. Soc. Jpn., 18, 287 [Google Scholar]
- IAG Travaux Reports 2017, in IAG Travaux Volume 40 Reports 2015–2017, eds. H. Drewes, & F. Kuglitsch [Google Scholar]
- IERS Conventions 2010, in IERS Technical Note 36, eds. G. Petit, & B. Luzum, 179 [Google Scholar]
- Jeffreys, H. 1976, The Earth, 6th edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Jeffreys, H., & Vicente, R. O. 1957, MNRAS, 117, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Kaula, W. M. 1964, Rev. Geophys., 2, 661 [Google Scholar]
- Kinoshita, H. 1972, Publ. Astron. Soc. Jpn., 24, 423 [NASA ADS] [Google Scholar]
- Kinoshita, H. 1975, Smithsonian Astrophys. Obs. Special Report, No. 364 [Google Scholar]
- Kinoshita, H. 1977, Celest. Mech. Dyn. Astron., 15, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Kinoshita, H., & Sasao, T. in Theoretical Aspects of the Earth Rotation, eds. J. Kovalevsky, I. I. Mueller, & B. Kolaczek, Astrophys. Space Sci. Lib., 154, 173 [Google Scholar]
- Krasinsky, G. A. 1999, Celest. Mech. Dyn. Astron., 75, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Kinoshita, H., & Souchay, J. 1990, Celest. Mech. Dyn. Astron., 48, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, Y. 1991, Celest. Mech. Dyn. Astron., 50, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Kudryavtsev, S. M. 2004, J. Geodesy, 77, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Lambeck, K. 1980, The Earth’s variable rotation: geophysical causes and consequences (Cambridge: Cambridge University Press) [Google Scholar]
- Lambert, S. B., & Capitaine, N. 2004, A&A, 428, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, S. B., & Mathews, P. M. 2006, A&A, 453, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, S. B., & Mathews, P. M. 2008, A&A, 481, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1959, Theory of Elasticity (Oxford: Pergamon Press) [Google Scholar]
- Liu, J. C., & Capitaine, N. 2017, A&A, 597, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyard, F., Lefevre, F., Letellier, T., & Francis, O. 2006, Ocean Dyn., 56, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Love, A. E. H. 1906, A treatise on the Mathematical Theory of Elasticity (Cambridge: Cambridge University Press) [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Luzum, B., Capitaine, N., Fienga, et al. 2011, Mech. Dyn. Astron., 110, 293 [NASA ADS] [CrossRef] [Google Scholar]
- MacCullagh, J. 1844, Proc. Royal Irish Acad., 520, 542 [Google Scholar]
- MacMillan, W. D. 1958, The Theory of the Potential (New York: Dover) [Google Scholar]
- Mathews, P. M., Buffet, B. A., & Shapiro, I. I. 1995, Res. Lett., 22, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, P. M., Herring, T. A., & Buffet, B. A. 2002, J. Geophys. Res., 107, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Moritz, H., & Mueller, I. 1986, Earth Rotation (New York: Frederic Ungar) [Google Scholar]
- Munk, W. K., & MacDonald, G. J. F. 1960, The Rotation of the Earth: A Geophysical Discussion (Cambridge: Cambridge University Press) [Google Scholar]
- Peale, S. J. 1973, Rev. Geophys. Space. Phys., 11, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Poincaré, H. 1910, Bull. Astron., 27, 321 [Google Scholar]
- Rochester, M. G., & Smylie, D. E. 1974, J. Geophys. Res., 79, 4948 [NASA ADS] [CrossRef] [Google Scholar]
- Sasao, T., Okubo, S., & Saito, M. 1980, in Proceedings of IAU Symposium, eds. E. P. Federvo, M. L. Smith, & P. L. Bender, 78, 165 [NASA ADS] [Google Scholar]
- Shen, P.-Y., & Mansinha, L. 1976, Geophys. J. R. Astron. Soc., 46, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, W., Chen, W., Wang, S., & Liang, Y. 2007, Geo-Spatial Inf. Sci., 10, 85 [CrossRef] [Google Scholar]
- Smith, M. L. 1974, Geophys. J. R. Astron. Soc., 37, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Souchay, J., & Folgueira, M. 2000, Earth Moon Planets, 81, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Souchay, J., & Kinoshita, H. 1996, A&A, 312, 1017 [NASA ADS] [Google Scholar]
- Takeuchi, H. 1950, Trans. Am. Geophys. Union, 31, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Tisserand, F. 1891, Traité de Mécanique Cé leste (Paris: Gauthier-Villars et Fils) (Tome II) [Google Scholar]
- Transactions IAU 2015, in Proc. IAU Symp., ed. T. Montmerle, XXIXA, 60 [Google Scholar]
- Vondrák, J. 1982, Bull. Astron. Inst. Czechosl., 33, 26 [NASA ADS] [Google Scholar]
- Wahr, J. M. 1981, Geophys. J. R. Astron. Soc., 64, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Wahr, J. M. 1982, in Proc. 3rd Int. Summer School in the mountain, Geodesy and Global Geodynamics, Admont, Austria, eds. H. Moritz, & H. Sünkel, 327 [Google Scholar]
- Wahr, J. M., & Bergen, Z. 1986, Geophys. J. R. Astron. Soc., 87, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Wahr, J. M., & Sasao, T. 1981, Geophys. J. R. Astron. Soc., 64, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Whittaker, E. T., & Watson, G. N. 1950, A Course of Modern Analysis (Cambridge: Cambridge University) [Google Scholar]
- Williams, J. G. 1994, AJ, 108, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. G., & Boggs, D. H. 2016, Celest. Mech. Dyn. Astron., 126, 89 [Google Scholar]
Appendix A: Expansion of the spherical harmonics
The real spherical harmonics appearing in the potential energy and inertia tensor expressions, referred to the rotating system, can be developed to the first order in σ in the following form (Kinoshita 1977; Getino & Ferrándiz 1995):
These expansions depend on the i subscript, which is a 5-tuple of integers mki (k = 1, 2, …, 5), and the fundamental argument Θi given by
where l, g, and h are the Delaunay variables of the Moon, l′, g′ y h′ for the Sun, F = l + g, D = l + g + h − l′ − g′ − h′, and Ω = h − λ. The functions Bi(I), Ci(I, τ), and Di(I, τ) are the ones defined by Kinoshita (1977) and depend on the orbital coefficients  provided in Kinoshita & Souchay (1990), with an update in Escapa et al. (2017):
provided in Kinoshita & Souchay (1990), with an update in Escapa et al. (2017):
In this work, Eqs. (A.1)–(A.3) are used both for perturbed and perturbing bodies. Due to the fact that i and τ play as dummy indices in the expressions of the redistribution potential and precession formulae, they are renamed as j and ϵ in the case of perturbing bodies, keeping the original notation for the perturbed ones.
Appendix B: Analytical cancelation of precession formulae in the SNREI model with k2f = k2
The quantities  (Eq. (41)) are specific combinations of the Kinoshita Bi, Ci, and Di functions, defined by Eq. (A.3), which in turn depend on the
(Eq. (41)) are specific combinations of the Kinoshita Bi, Ci, and Di functions, defined by Eq. (A.3), which in turn depend on the 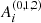 orbital coefficients (of perturbing and perturbed bodies) provided originally by Kinoshita (1977). Then, any mathematical property derived from the definition of these coefficients will be transferred to the mathematical features of the precession formulae.
orbital coefficients (of perturbing and perturbed bodies) provided originally by Kinoshita (1977). Then, any mathematical property derived from the definition of these coefficients will be transferred to the mathematical features of the precession formulae.
This is the case of the following conditions, namely,
indicated by Kinoshita (1977) and Kinoshita & Souchay (1990). These conditions are implicitly included in the expression of the redistribution potential, and also within the precession formulae, through the expansions (A.1) of the spherical harmonics. Due to the second-order expansion of the tide-raising potential, the integer m5i just takes the values 0, 1, and 2, for the listed components of the fundamental arguments Θi, thus the conditions (B.1) hold in all the cases, and can be used to simplify the Bi, Ci, and Di functions.
The conditions (B.1) are a consequence of the 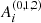 definition. By way of example, the coefficient
definition. By way of example, the coefficient 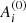 is related to the spherical harmonic C20 of a perturbing body with spherical angular coordinates
is related to the spherical harmonic C20 of a perturbing body with spherical angular coordinates 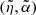 by means of Kinoshita (1977)
by means of Kinoshita (1977)
Here the longitude 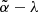 excludes the Z-axis rotation of angle λ in the definition of the Andoyer-like set of canonical variables, and causes the implicit dependence with λ of the fundamental arguments, through Ω = h − λ. Since
excludes the Z-axis rotation of angle λ in the definition of the Andoyer-like set of canonical variables, and causes the implicit dependence with λ of the fundamental arguments, through Ω = h − λ. Since 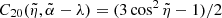 does not depend on λ, but Θi does,
does not depend on λ, but Θi does, 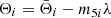 , necessarily
, necessarily  if m5i ≠ 0 (m5i = 1, 2), which is the first of the conditions (B.1). The remaining conditions can be analogously proven by making the form of the related spherical harmonics explicit.
if m5i ≠ 0 (m5i = 1, 2), which is the first of the conditions (B.1). The remaining conditions can be analogously proven by making the form of the related spherical harmonics explicit.
It should be noted that the precession rate in obliquity, δnε, is directly canceled out due to ε2m, j = 0 in Eq. (40). In order to show the cancelation of the longitude rate, δnψ, the 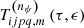 function will be written down using Eq. (B.1) as
function will be written down using Eq. (B.1) as
with fm5i being functions of the obliquity I, defined by
We note that m subscript has been omitted due to the existence of a sole value k2 in the Love number set in the SNREI model with k2f = k2. Considering that i, j, τ, and ϵ subscripts are related by 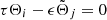 within the sum, and the highlighted equivalence between perturbing and perturbed bodies,
within the sum, and the highlighted equivalence between perturbing and perturbed bodies,  , Eq. (B.3) must be rewritten with i = j and τ = ϵ, regardless of the value of the p, q subscripts. Under these conditions, fm5i(I, τ, ϵ) functions verify the property
, Eq. (B.3) must be rewritten with i = j and τ = ϵ, regardless of the value of the p, q subscripts. Under these conditions, fm5i(I, τ, ϵ) functions verify the property 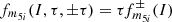 , where
, where 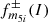 denotes the remaining functions after taking τ as common factor. Thus, Eq. (B.3) looks like
denotes the remaining functions after taking τ as common factor. Thus, Eq. (B.3) looks like
Replacing Eq. (B.5) in the first formula (Eq. 40), and the equivalent summation conditions, the following expression for the precessional rate in longitude is obtained:
which demonstrates its exact cancelation due to the sum over τ index, that is, δnψ = 0. This result can also be derived from certain relationships satisfied by the Kinoshita orbital functions B, C, and D (Escapa et al. 2003, 2004).
From a physical point of view, the analytical cancelation of the precession formulae is a consequence of that of the torque components associated with the redistribution potential. This fact was directly shown via vectorial mechanics, for instance, in Krasinsky (1999) or Lambert & Mathews (2006). The demonstration is somewhat more costly in the Hamiltonian framework, although it follows the same mechanism as the previous case. A complete proof of the exact cancelation of the torque induced by redistribution potential in a SNREI model with k2f = k2 can be found in Baenas (2014).
All Tables
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



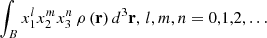
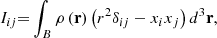
![$$ \begin{aligned} \mathcal{V} \left( \mathbf r _p\right) =-\frac{Gm_p}{2r_p^{5}} \sum \limits _{i,j=1(j\ge i)}^{3}I_{ij}\left[ r_p^{2}\delta _{ij}-\left( 3-2\delta _{ij}\right) x_{i,p}x_{j,p}\right] \mathrm{.} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq3.gif)
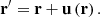
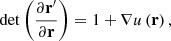
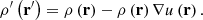
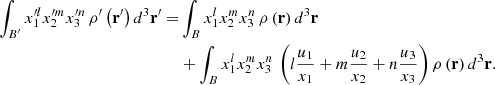
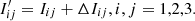
![$$ \begin{aligned}&I_{ij}^{\prime } =\int _{B^{\prime }}\rho ^{\prime }\left( \mathbf r ^{\prime }\right) \left( r^{\prime 2}\delta _{ij}-x_{i}^{\prime }x_{j}^{\prime }\right) d^{3}\mathbf r ^{\prime }\mathrm{,} \nonumber \\&I_{ij} =\int _{B}\rho \left( \mathbf r \right) \left( r^{2}\delta _{ij}-x_{i}x_{j}\right) d^{3}\mathbf r \mathrm{,} \nonumber \\&\Delta I_{ij} =\int _{B}\rho \left( \mathbf r \right) \left[ 2\left( \mathbf u\cdot r \right) \delta _{ij}-\left( u_{i}x_{j}+u_{j}x_{i}\right) \right] d^{3}\mathbf r \mathrm{.} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq13.gif)
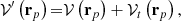
![$$ \begin{aligned} \mathcal{V} \left( \mathbf r _p\right)&= -\frac{Gm_p}{2r_p^{5}} \sum \limits _{i,j=1(j\ge i)}^{3}I_{ij}\left[ r_p^{2}\delta _{ij}-\left( 3-2\delta _{ij}\right) x_{i,p}x_{j,p}\right] , \nonumber \\ \mathcal{V} _{t}\left( \mathbf r _p\right)&= -\frac{Gm_p}{2r_p^{5}} \sum \limits _{i,j=1(j\ge i)}^{3}\Delta I_{ij}\left[ r_p^{2}\delta _{ij}-\left( 3-2\delta _{ij}\right) x_{i,p}x_{j,p}\right]. \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq15.gif)
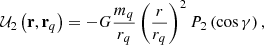
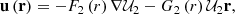
![$$ \begin{aligned} {\begin{array}{l} \displaystyle \mathcal{U} _{2}\left( \mathbf r ,\mathbf r _{q}\right) =-G \frac{m_{q}}{r_{q}}\left( \frac{r}{r_{q}}\right) ^{2}\times \Bigg [ \mathcal{C } _{20}\mathcal{C} _{20,q} \\ \qquad \qquad \quad \left. + \displaystyle \frac{1}{3}\left( \mathcal{C} _{21}\mathcal{C} _{21,q}+\mathcal{S} _{21} \mathcal{S} _{21,q}\right) +\frac{1}{12}\left( \mathcal{C} _{22}\mathcal{C} _{22,q}+\mathcal{S} _{22}\mathcal{S} _{22,q}\right) \right]\mathrm{,} \end{array}} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq18.gif)
![$$ \begin{aligned} u_{r}&= -\left[ 2\frac{F_{2}\left( r\right) }{r}+G_{2}\left( r\right) r \right] \mathcal{U} _{2}\mathrm{,} \mathrm \ \nonumber \\ u_{\theta }&=-\frac{F_{2}\left( r\right) }{r}\frac{\partial \mathcal{U} _{2} }{\partial \theta }\mathrm{,} \\ u_{\phi }&=-\frac{F_{2}\left( r\right) }{r\sin \theta }\frac{\partial \mathcal{U} _{2}}{\partial \phi }\mathrm{,} \nonumber \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq19.gif)
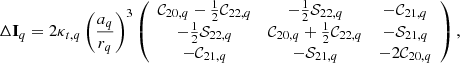
![$$ \begin{aligned} \kappa _{t,q}=\frac{4\pi }{15}\frac{Gm_{q}}{a_{q}^{3}}\int _{0}^{a_{\rm E}}r^{4} \rho \left( r\right) \left[ 5F_{2}\left( r\right) +r^{2}G_{2}\left( r\right) \right] dr\mathrm{.} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq21.gif)
![$$ \begin{aligned} \mathcal{V} _{t;p,q}=-G\frac{m_p}{2r_p^{5}}\sum \limits _{i,j=1(j\ge i)}^{3}\Delta I_{ij,q}\left[ r_p^{2}\delta _{ij}-3\left( 2-\delta _{ij}\right) x_{i,p}x_{j,p}\right] . \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq22.gif)
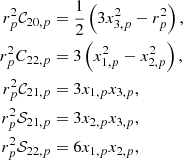
![$$ \begin{aligned} \begin{array}{l} \mathcal{V} _{t;p,q}=-G \displaystyle \frac{m_p}{a_p^{3}}\left( \frac{a_p}{r_p}\right) ^{3}\left( \frac{ a_{q}}{r_{q}}\right) ^{3}\kappa _{t,q}\times \Bigg [ 6\mathcal{C} _{20,p} \mathcal{C} _{20,q} \\ \left. + \displaystyle 2\left( \mathcal{C} _{21,p}\mathcal{C} _{21,q}+\mathcal{S} _{21,p}\mathcal{S} _{21,q}\right) +\frac{1}{2}\left( \mathcal{C} _{22,p}\mathcal{C} _{22,q}+ \mathcal{S} _{22,p}\mathcal{S} _{22,q}\right) \right]. \end{array} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq24.gif)
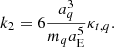
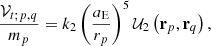
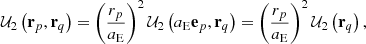
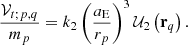
![$$ \begin{aligned} k_{2}=\frac{8\pi }{5}\frac{G}{a_{\rm E}^{{5}}}\int _{0}^{a_{\rm E}}r^{4}\rho \left( r\right) \left[ 5F_{2}\left( r\right) +r^{2}G_{2}\left( r\right) \right] \mathrm{d}r \mathrm{.} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq29.gif)
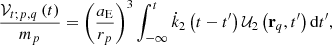
![$$ \begin{aligned} \dot{k}_{2}\left( t-t^{\prime }\right) =\int _{-\infty }^{\infty }\bar{k} _{2}\left( \omega \right) \mathrm{e}^{i\omega \left( t-t^{\prime }\right) }\,\mathrm{d}\omega =\int _{-\infty }^{\infty }\left|\bar{k}_{2}\left( \omega \right) \right|\mathrm{e}^{i\left[ \omega \left( t-t^{\prime }\right) +\varepsilon \left( \omega \right) \right] }\,\mathrm{d}\omega \mathrm{,} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq32.gif)
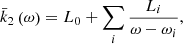
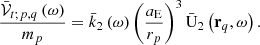
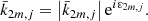
![$$ \begin{aligned} \mathcal{V} _{t;p,q}&= -Gm_pm_{q}\sum \limits _{j}\frac{a_{\rm E}^{5}}{ r_{q}^{3}r_p^{3}} \\&\quad \times \left\{ \left|\bar{k}_{20,j}\right|\cos \varepsilon _{20} \mathcal{C} _{20,p}\left( \theta _p,\phi _p\right) \mathcal{C} _{20,q}\left( \theta _{q},\phi _{q}\right)\right. \nonumber \\&\quad \left. +\frac{1}{3}\left|\bar{k}_{21,j}\right|\left[ \begin{array}{c} \mathcal{C} _{21,p}\left( \theta _p,\phi _p\right) \mathcal{C} _{21,q}\left( \theta _{q},\phi _{q}-\varepsilon _{21,j}\right) \\ +\mathcal{S} _{21,p}\left( \theta _p,\phi _p\right) \mathcal{S} _{21,q}\left( \theta _{q},\phi _{q}-\varepsilon _{21,j}\right) \end{array} \right] \right. \nonumber \\&\quad \left. +\frac{1}{12}\left|\bar{k}_{22,j}\right|\left[ \begin{array}{c} \mathcal{C} _{22,p}\left( \theta _p,\phi _p\right) \mathcal{C} _{22,q}\left( \theta _{q},\phi _{q}-\frac{\varepsilon _{22,j}}{2}\right) \\ +\mathcal{S} _{22,p}\left( \theta _p,\phi _p\right) \mathcal{S} _{22,q}\left( \theta _{q},\phi _{q}-\frac{\varepsilon _{22,j}}{2}\right) \end{array} \right] \right\} . \nonumber \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq41.gif)
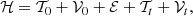
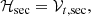
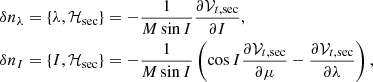
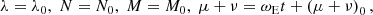
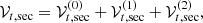
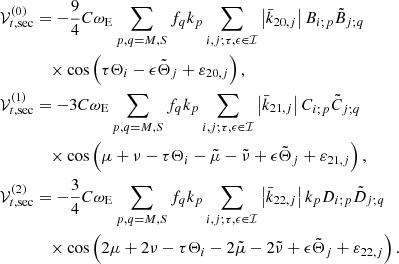
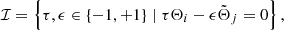
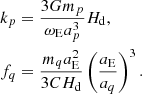
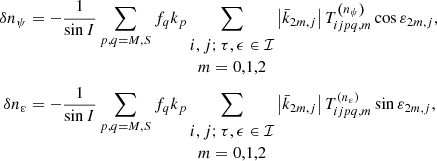
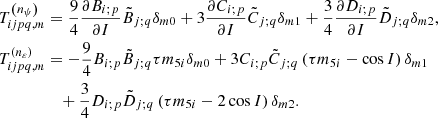
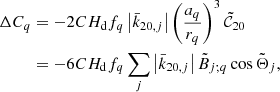

![$$ \begin{aligned} \bar{k}_{20;j}=0.29525-5.795\times 10^{-4}\left\{ \cot \frac{\alpha \pi }{2} \left[ 1-\left( \frac{\sigma _{r}}{\sigma _{j}}\right) ^{\alpha }\right] +i\left( \frac{\sigma _{r}}{\sigma _{j}}\right) ^{\alpha }\right\} \mathrm{,} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq70.gif)
![$$ \begin{aligned} p_{\rm P}&= -\frac{1}{\sin I}\sum _{p,q=M,S}k_{2f}f_{q}k_p\sum _{\tau ,\epsilon =\pm 1}\frac{9}{4}\frac{\partial B_{0;p}}{\partial I}\tilde{B}_{0;q} \nonumber \\&=\left[ \frac{1}{\sin I}\sum _{p=M,S}k_p\frac{\partial B_{0;p}}{\partial I }\right] \left[ -9k_{2f}\sum _{q=M,S}f_{q}\tilde{B}_{0;q}\right] \mathrm{.} \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq72.gif)
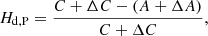
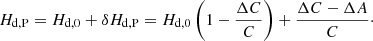
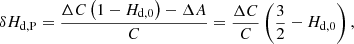
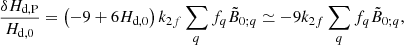
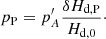
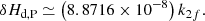
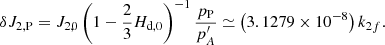
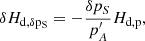
![$$ \begin{aligned} \left( \frac{a}{r}\right) ^{3}\mathcal{C} _{20}\left( \eta ,\alpha \right)&=3\sum \limits _{i}B_{i}(I)\cos \Theta _{i} \nonumber \\&\quad -3\sigma \sum \limits _{i,\tau =\pm 1}C_{i}(I,\tau )\cos \left( \mu -\tau \Theta _{i}\right) \mathrm{,} \nonumber \\ \left( \frac{a}{r}\right) ^{3}\mathcal{C} _{21}\left( \eta ,\alpha \right)&= 3\sum \limits _{i,\tau =\pm 1}C_{i}(I,\tau )\sin \left( \mu +\nu -\tau \Theta _{i}\right) \nonumber \\&\quad +\sigma \sum \limits _{i,\tau =\pm 1}\left[ \frac{9}{2}B_{i}(I)\sin \left( \nu -\tau \Theta _{i}\right) \right. \nonumber \\&\quad \left. -\frac{3}{2}D_{i}(I,\tau )\sin \left( 2\mu +\nu -\tau \Theta _{i}\right) \right] \mathrm{,} \nonumber \\ \left( \frac{a}{r}\right) ^{3}\mathcal{S} _{21}\left( \eta ,\alpha \right)&=3\sum \limits _{i,\tau =\pm 1}C_{i}(I,\tau )\cos \left( \mu +\nu -\tau \Theta _{i}\right) \nonumber \\&\quad +\sigma \sum \limits _{i,\tau =\pm 1}\left[ \frac{9}{2}B_{i}(I)\cos \left( \nu -\tau \Theta _{i}\right) \right. \\&\quad \left. -\frac{3}{2}D_{i}(I,\tau )\cos \left( 2\mu +\nu -\tau \Theta _{i}\right) \right] \mathrm{,} \nonumber \\ \left( \frac{a}{r}\right) ^{3}\mathcal{C} _{22}\left( \eta ,\alpha \right)&=-3\sum \limits _{i,\tau =\pm 1}D_{i}(I,\tau )\cos \left( 2\mu +2\nu -\tau \Theta _{i}\right) \nonumber \\&\quad -6\sigma \sum \limits _{i,\tau =\pm 1}C_{i}(I,\tau )\cos \left( \mu +2\nu -\tau \Theta _{i}\right) \mathrm{,} \nonumber \\ \left( \frac{a}{r}\right) ^{3}\mathcal{S} _{22}\left( \eta ,\alpha \right)&=3\sum \limits _{i,\tau =\pm 1}D_{i}(I,\tau )\sin \left( 2\mu +2\nu -\tau \Theta _{i}\right) \nonumber \\&\quad +6\sigma \sum \limits _{i,\tau =\pm 1}C_{i}(I,\tau )\sin \left( \mu +2\nu -\tau \Theta _{i}\right) \mathrm{.} \nonumber \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq99.gif)
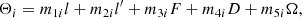
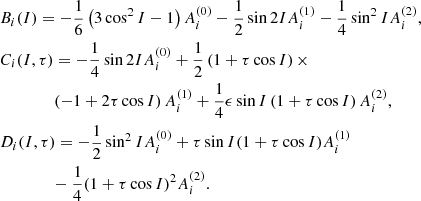
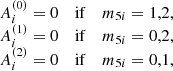
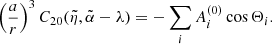
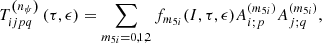
![$$ \begin{aligned} f_{0}(I,\tau ,\epsilon )&=0\mathrm{,} \nonumber \\ f_{1}(I,\tau ,\epsilon )&=-\frac{3}{4}\sin I\left[ \epsilon -\tau +\cos ^{2}I\left( \tau +2\epsilon \right) \right] \mathrm{,} \\ f_{2}(I,\tau ,\epsilon )&=-\frac{3}{32}\sin ^{3}I\left( 2\epsilon +\tau \right) \mathrm{.} \nonumber \end{aligned} $$](/articles/aa/full_html/2019/06/aa35472-19/aa35472-19-eq116.gif)