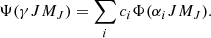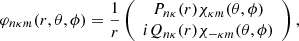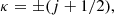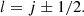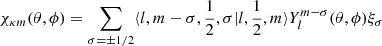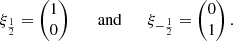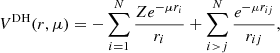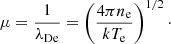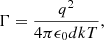| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935444 | |
| Published online | 18 June 2019 | |
Plasma environment effects on K lines of astrophysical interest
II. Ionization potentials, K thresholds, radiative rates, and Auger widths in Ne- through He-like iron ions (Fe XVII – Fe XXV)⋆
1
Physique Atomique et Astrophysique, Université de Mons – UMONS, 7000 Mons, Belgium
e-mail: patrick.palmeri@umons.ac.be
2
Department of Physics, Western Michigan University, Kalamazoo, MI 49008, USA
3
Helmholtz Institut Jena, 07743 Jena, Germany
4
Theoretisch Physikalisches Institut, Friedrich Schiller Universität Jena, 07743 Jena, Germany
5
Cahill Center for Astronomy and Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA
6
Dr. Karl Remeis-Observatory and Erlangen Centre for Astroparticle Physics, Sternwartstr. 7, 96049 Bamberg, Germany
7
NASA Goddard Space Flight Center, Code 662, Greenbelt, MD, USA
8
IPNAS, Université de Liège, Sart Tilman 4000 Liège, Belgium
e-mail: Pascal.Quinet@umons.ac.be
Received:
11
March
2019
Accepted:
4
May
2019
Aims. In the context of accretion disks around black holes, we estimate plasma-environment effects on the atomic parameters associated with the decay of K-vacancy states in highly charged iron ions, namely Fe XVII – Fe XXV.
Methods. Within the relativistic multiconfiguration Dirac–Fock (MCDF) framework, the electron–nucleus and electron–electron plasma screenings were approximated with a time-averaged Debye–Hückel potential.
Results. Modified ionization potentials, K thresholds, wavelengths, radiative emission rates, and Auger widths are reported for astrophysical plasmas characterized by electron temperatures and densities in the ranges 105 − 107 K and 1018 − 1022 cm−3, respectively.
Conclusions. We conclude that the high-resolution microcalorimeters on board future X-ray missions such as XRISM and ATHENA are expected to be sensitive to the lowering of the iron K edge due to the extreme plasma conditions occurring in accretion disks around compact objects.
Key words: black hole physics / plasmas / atomic data / X-rays: general
Full Tables 5 and 6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/626/A83.
© ESO 2019
1. Introduction
Accurate descriptions of K-shell atomic processes are essential in the analysis of the X-ray spectra from space telescopes such as Chandra, XMM-Newton, Suzaku, and NuSTAR. In this respect, we have been involved for the past two decades in extensive computations of the relevant atomic data for cosmic abundant elements with atomic number Z ≤ 30; we focused on iron in particular but trace elements with odd Z were also considered (see, for example, Palmeri et al. 2002, 2003a,b, 2008, 2011, 2012, 2016; Bautista et al. 2003, 2004; Kallman et al. 2004; García et al. 2005, 2009, 2011; Mendoza et al. 2004, 2017, 2018; Witthoeft et al. 2009, 2011; Gorczyka et al. 2013; Hasoglu et al. 2014).
This data collection has become a reference source in several atomic databases for astrophysical applications, for example, Bautista & Kallman (2001), AtomDB1, CHIANTI (Landi et al. 2012), and uaDB2 as well as in spectral modeling codes such as XSTAR (Kallman & Bautista 2001), CLOUDY (Ferland et al. 2013), SPEX (Kaastra et al. 1996), and ION (Netzer 1996). However, these atomic parameters have been computed neglecting plasma-embedding effects, and consequently, they are not expected to be applicable at relatively high electron densities, say ne > 1018 cm−3 (Smith & Brickhouse 2014).
Absorption and emission of high-energy photons in dense plasmas occur in a wide range of astrophysical phenomena; among the most exciting perhaps are the X-rays produced and reprocessed in the regions close to compact objects such as black holes and neutron stars. In these systems the gas inflow caused by the strong gravitational potential forms an accretion disk from which copious X-ray radiation is emitted (e.g., Krolik 1999; Done et al. 2007). Observed spectra are usually imprinted with atomic features, both in emission and absorption, from a wide variety of ionic species, the modeling of which provides reliable insights of the composition, temperature, and degree of ionization of the plasma (Ross & Fabian 2005; García & Kallman 2010). In the case of a black hole, its angular momentum can be inferred by modeling the distortion of the Fe K emission complex caused by the strong relativistic effects (e.g., Reynolds 2013; García et al. 2014).
X-ray emission lines from accreting sources, in particular the Kα and Kβ lines from Fe ions, are characterized by observed widths and shifts mostly implying an origin close to the compact object (Reynolds & Nowak 2003); that is, the innermost stable circular orbit in the case of a black hole or the stellar surface in the case of a neutron star. Line intensities may thus provide estimates of key properties of these exotic dense-plasma environments, including the effects of both special and general relativity in the emitting region that are not attainable through other observational windows. In order to analyze the Kα and Kβ emission lines to derive, for instance, the Fe ionic fractions and abundance, it is of paramount importance to rely on accurate radiative and Auger data to infer the emission and absorption rates under various extreme conditions.
Dynamical models of black-hole accretion flows appear to support densities as high as 1021 − 1022 cm−3 (Reis & Miller 2013; Schnittman et al. 2013; Tomsick et al. 2018; Jiang et al. 2019), but thus far their effect on line emission has not been studied in detail. It is worth noting that iron-ion survival near a black hole requires such high densities to counteract the strong ionization. Therefore, plasma embedding effects on the ionic structure, K photoexcitation, and photoionization, and both radiative and Auger decay become unavoidable issues.
Following previous work on the oxygen isonuclear sequence by Deprince et al. (2019a), we estimated density effects on the atomic parameters associated with the K-vacancy states of highly charged iron ions. Multiconfiguration Dirac–Fock computations have been carried out for these species representing the plasma electron–nucleus and electron–electron shieldings with a time-averaged Debye–Hückel potential. Deprince et al. (2019a) have shown that both of these plasma interactions must be taken into account. We use a combination of the GRASP92 code (Parpia et al. 1996) to obtain the wave functions and RATIP (Fritzsche 2012) to calculate the atomic parameters. We report a first set of results on the ionization potentials (IPs), K thresholds, transition wavelengths, radiative emission rates, and Auger widths for nine ions: from Fe XVII (Ne-like) to Fe XXV (He-like).
2. Theoretical model
2.1. Relativistic multiconfiguration Dirac–Fock method
Wave functions for the ionic species Fe XVII–Fe XXV are obtained using the fully relativistic multiconfiguration Dirac–Fock (MCDF) method, implemented in the GRASP92 version (Parpia et al. 1996) of the General-purpose Relativistic Atomic Structure Program (GRASP) initially developed by Grant et al. (1980), McKenzie et al. (1980), and Grant (1988). In this approach the atomic state functions (ASF) Ψ(γJMJ) are expanded in linear combinations of the configuration state functions (CSF) Φ(αiJMJ)
The CSF are in turn taken as linear combinations of Slater determinants constructed from monoelectronic spin-orbitals of the form
where Pnκ(r) and Qnκ(r) are the large and small components of the radial wave function, respectively, and the angular functions χκm(θ, ϕ) are spinor spherical harmonics. The αi coefficients represent all the one-electron and intermediate quantum numbers needed to completely define the CSF, and γ is usually chosen as the αi corresponding to the CSF with the largest weight |ci|2. The κ quantum number is given by
j being the electron total angular momentum. The sign before the parenthesis in Eq. (3) corresponds to the coupling relation between the electron orbital momentum l and its spin
The angular functions χκm(θ, ϕ) are spinor spherical harmonics in the lsj coupling scheme. Following Grant (2007) their expression is given by
with the two spinors
The radial functions Pnκ(r) and Qnκ(r) are numerically represented on a logarithmic grid and are required to be orthonormal within each κ symmetry. In the MCDF variational procedure, the radial functions and expansion coefficients ci are optimized self-consistently.
In the present work the restricted active space (RAS) method is used to obtain the MCDF expansions for each ionic system. In this method electrons are excited from prescribed reference configurations to a given active set of orbitals; that is, the RAS is built up by considering all the single and double excitations from the spectroscopic configurations, i.e., the configurations for which it is desirable to compute their properties, to the n = 3 configuration space. The list of reference configurations (i.e., the spectroscopic configurations) for each ionic system is specified as follows:
-
Fe XVII:
1s22s22p6, 1s22s22p53s, 1s22s22p53p, 1s2s22p63s, 1s2s22p63p
-
Fe XVIII:
1s22s22p5, 1s2s22p6
-
Fe XIX:
1s22s22p4, 1s22s2p5, 1s22p6, 1s2s22p5, 1s2s2p6
-
Fe XX:
1s22s22p3, 1s22s2p4, 1s22p5, 1s2s22p4, 1s2s2p5, 1s2p6
-
Fe XXI:
1s22s22p2, 1s22s2p3, 1s22p4, 1s2s22p3, 1s2s2p4, 1s2p5
-
Fe XXII:
1s22s22p, 1s22s2p2, 1s22p3, 1s2s22p2, 1s2s2p3, 1s2p4
-
Fe XXIII:
1s22s2, 1s22s2p, 1s22p2, 1s2s22p, 1s2s2p2, 1s2p3
-
Fe XXIV:
(1s+2s+2p)3
-
Fe XXV:
1s2, 1s2s, 1s2p.
Computations are carried out with the extended average level (EAL) option optimizing a weighted trace of the Hamiltonian using level weights proportional to (2J + 1), and they are completed with the inclusion of the relativistic two-body Breit interaction and the quantum electrodynamic corrections (QED) due to the self-energy and vacuum polarization. The MCDF ionic bound states generated by GRASP92 are then used in RATIP (Fritzsche 2012) to compute the atomic structure and the radiative and Auger parameters associated with K-vacancy states.
2.2. Plasma screening effects
We use a Debye–Hückel (DH) potential to model the plasma screening effects on the atomic properties, which in atomic units (a.u.) is given by
where N is the number of bound electrons, ri is the distance of the ith electron from the nucleus, and rij is the distance between the i and j electrons. The plasma screening parameter μ is the inverse of the Debye shielding length λDe, and can be expressed in terms of the plasma electron density ne and temperature Te as
A given value of μ is then associated with a certain type of plasma environment. For example, according to the magnetohydrodynamic simulations reported by Schnittman et al. (2013) for accreting black holes with ten solar masses and an accretion rate of 10%, the plasma conditions were estimated at Te = 105 − 107 K and ne = 1018 − 1022 cm−3. As shown in Table 1, this range corresponds to values of μ ≲ 0.25 a.u. for which the plasma-coupling parameter (Piel 2010)
Screening parameter μ (a.u.) for different electron temperatures and densities.
denoting the ratio of the electrostatic energy of neighboring particles to the thermal energy in the astrophysical plasma (predominantly protons and electrons), is always smaller (much smaller in most cases) than unity. This is in fact the validity condition for the statistically shielded DH potential to describe appropriately the screened Coulomb electrostatic interaction (see, for example, Saha & Fritzsche 2006; Belkhiri et al. 2015; Das et al. 2016). In Eq. (9) q is the charge of the neighboring particles separated by a typical distance d = (3/4πne)1/3.
Therefore, when computing the atomic data with the RATIP code, we replace the electron–nucleus and electron–electron Coulomb interactions of the ionic system with the corresponding DH potential terms of Eq. (7) assuming values of the plasma screening parameter in the range 0 ≤ μ ≤ 0.25 a.u. The applicability of this approach was recently discussed for the oxygen isonuclear sequence by Deprince et al. (2019a).
3. Results and discussion
3.1. Ionization potentials and K thresholds
The IP and K thresholds we computed with screening parameters in the range 0 ≤ μ ≤ 0.25 a.u. are summarized in Tables 2–3. For the isolated ions (μ = 0) we reproduce the IPs listed in the spectroscopic database of the National Institute of Standards and Technology (NIST; Kramida et al. 2019) to an accuracy better than 0.2%. The inclusion of the DH potential leads to reductions of the IP and K-threshold energy positions that increase with μ; namely 3% and 8% for μ = 0.10 and μ = 0.25, respectively, except for Fe XXV for which the reduction is less than 2% as a consequence of its large IP > 8600 eV. For the same reason, the K-threshold reductions are only marginal (< 2%).
Computed IPs (eV) for Fe XVII–Fe XXV as a function of the plasma screening parameter μ (a.u.).
Computed K thresholds (eV) for Fe XVII–Fe XXV as a function of the plasma screening parameter μ (a.u.).
This threshold lowering is a well-known phenomenon in dense-plasma physics, whose behavior is further illustrated in Figs. 1–2. For each of the ionic species considered, the DH potential predicts a linear decrease of the IP downshift with μ at a gradient that grows with ionic charge (see Fig. 1); however, as shown in Fig. 2, the IP-shift variation with effective ionic charge Zeff = Z − N + 1 for a particular μ is only moderate, i.e., ∼30%. On the other hand, we find that, for any specific ionic species, the IP and K-threshold energy shifts are practically the same (see Fig. 2).
 |
Fig. 1. Ionization potential shifts in Fe XVII–Fe XXV as a function of the plasma screening parameter μ. |
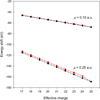 |
Fig. 2. Ionization potentials (black points) and K-threshold (red points) energy shifts in Fe ions as a function of effective charge Zeff for μ = 0.1 a.u. and μ = 0.25 a.u. |
It is interesting to highlight the fact that the inclusion of the electron–electron Debye screening effect in our calculations, in addition to that of the electron–nucleus, leads as shown in Table 4 to a substantially less pronounced IP lowering, i.e., 4% in Fe XXV to 50% in Fe XVII. This was also underlined in our previous study on the oxygen isonuclear sequence (Deprince et al. 2019a). As expected, this discrepancy grows inversely with Zeff as the number of interacting electron–electron pairs is larger for the low-charge states.
Ionization potentials (eV) for Fe XVII–Fe XXV computed with the DH nucleus–electron screening and with and without the electron–electron screening.
The importance of the screening effects by the electron–electron pair interactions has also been recently brought to the fore by Das et al. (2016), who found significant influence of such effects on the IP lowering and excitation energies in Al ions, in particular in the neutral and lowly ionized species. They also found that more stable atomic systems are predicted when the electron–electron screening is taken into account, i.e., giving rise to larger IPs than those computed using a DH potential excluding the screening of the electron–electron interaction. The Debye electron–nucleus and electron–electron screening effects have been amply discussed by, for instance, Winkler (1996), Kar & Ho (2004, 2005), Saha & Fritzsche (2006), Xie et al. (2012), Certik & Winkler (2013), Jiao & Ho (2014), and Deprince et al. (2019a).
3.2. Radiative transitions
Computed wavelengths and transition probabilities for the stronger K lines (A > 1013 s−1) of Fe XVII–Fe XXV with the three plasma screening parameters μ = 0.0, 0.1, and 0.25 a.u. are listed in Table 5. If our data for the isolated ion (μ = 0) are compared with Palmeri et al. (2003a) and Mendoza et al. (2004), who used the pseudo-relativistic Hartree–Fock (HFR) method, good agreement is generally found. For the transitions listed in Table 5, the wavelengths agree to better than 0.1% while the transition probabilities can show differences at the 25% level. Since we took into account similar configuration-interaction effects in our atomic models as Palmeri et al. (2003a) and Mendoza et al. (2004), the main discrepancy source must be attributed to relativistic effects, which are formally treated in the MCDF method. Furthermore, we find excellent agreement (within 5%) among our A-values computed in the Babushkin and Coulomb gauges, although only transition probabilities obtained in the Babushkin gauge are reported in Table 5.
Comparison of wavelengths and transition probabilities for the K lines of Fe XVII – Fe XXV (17 ≤ Zeff ≤ 25) computed with plasma screening parameters μ = 0.0, 0.1, and 0.25 a.u.
A close inspection of Table 5 brings out the meager effects of the plasma environment on the K-line radiative parameters. For screening parameters μ = 0.10 and μ = 0.25, wavelengths appear redshifted relative to those of the isolated ion by less than 0.1 mÅ and 1 mÅ, respectively, while the variations of the radiative decay rates do not exceed more than a few percent. To illustrate this point we show in Fig. 3 the reddening of the [1s]3p 1P1–2p6 1S0 Kβ line in Fe XVII, which for μ = 0.25 amounts to ∼2 mÅ. Similarly, for the [1s]2p42D3/2–2p3 2D3/2 and [1s]2p42S1/2–2p3 2P3/2 Kα lines in Fe XX in Fig. 4, the reddening is less than 1 mÅ.
 |
Fig. 3. Wavelength reddening as a function of the plasma screening parameter μ for the [1s]3p 1P1–2p6 1S0 Kβ line in Fe XVII. |
 |
Fig. 4. Wavelength reddening as a function of the plasma screening parameter μ for the [1s]2p4 2D3/2–2p3 2D3/2 and [1s]2p4 2S1/2–2p3 2P3/2 Kα lines in Fe XX. |
It is shown in Fig. 5 for the [1s]3p 3P0–[2p]3p 3S1 and [1s]3p 1P1–2p61S0 lines in Fe XVII that the plasma effects on the radiative transition probabilities (A-values) are less than 1%, although they can increase or decrease their nominal values (μ = 0). In Fe XXII the changes are somewhat larger (3%) as illustrated in Fig. 6 with the 1s2s2p34S3/2–[2s]2p2 2D3/2 and 1s2s2p32D5/2– [2s]2p2 2D5/2 lines.
 |
Fig. 5. Variation of the radiative transition probability (A-value) with the plasma screening parameter μ for the [1s]3p 3P0–[2p]3p 3S1 and [1s]3p 1P1–2p6 1S0 lines in Fe XVII. |
 |
Fig. 6. Variation of the transition probability (A-value) with the plasma screening parameter μ for the 1s2s2p3 4S3/2–[2s]2p2 2D3/2 and 1s2s2p3 2D5/2–[2s]2p2 2D5/2 lines in Fe XXII. |
3.3. Auger widths
Computed Auger widths for the K-vacancy levels with screening parameters μ = 0, 0.1, and 0.25 a.u. are tabulated in Table 6. Present widths for the isolated ion case (μ = 0 a.u.) are found to be in good agreement (within 5%) with those computed previously with HFR by Palmeri et al. (2003a). The DH potential leads to more noticeable decrements of the Auger widths, namely by up to 3% and 10% for μ = 0.1 and 0.25 a.u., respectively. This variation is exemplified in Fig. 7 with the 1s2s2p3 2D3/2 and 1s2s22p2 4P5/2 K-vacancy levels in Fe XXII. We also find that the Auger widths for the higher iron ionization stages seem to be more affected by the plasma environment. As previously shown for Fe XVII, Fe XVIII, and Fe XIX by Deprince et al. (2019b) because of the weak variations of both the radiative rates and Auger widths with μ, the K-line fluorescence yields in the iron ions considered herein are hardly affected (3% at most).
Plasma environment effects on the Auger widths of K-vacancy states in Fe XVII –Fe XXV (17 ≤ Zeff ≤ 25) computed with plasma screening parameters μ = 0.0, 0.1, and 0.25 a.u.
 |
Fig. 7. Variation of the Auger width with the plasma screening parameter μ for two K-vacancy levels in Fe XXII. |
4. Astrophysical implications
The atomic calculations hereby presented are expected to influence plasma modeling predictions in environments in which the density and temperature of the gas are such that the screening parameter μ becomes important; i.e., as shown in Table 1, for relatively low temperatures (Te < 105 K) and high densities (nee > 1018 cm−3). These conditions are encountered in astrophysical environments such as the solar interior (near the convective zone) or in the inner-most regions of accretion disks around compact objects (white dwarfs, neutron stars, and black holes).
Regarding plasma embedding effects in the solar interior, Krief et al. (2018) have used the ion–ion correlation model of Rozsnyai (1991, 1992) to re-evaluate the Fe Rosseland mean opacity in conditions similar to the base of the convection zone and have found a 15% increase. However, a more recent calculation (Ovechkin et al. 2019) based on the Starrett–Saumon average-atom model has questioned this result as an overestimate due to a limited treatment of the ion–ion repulsion, which is one of the points we have emphasized in the present work.
While the inclusion of the DH potential has a very small effect on the energy levels, radiative probabilities, and Auger widths, it does shift the IP and K threshold of each ion to lower energies. This effect would modify the part of the ionizing radiation field sampled by the photoionization cross section and, thus, the ionization rates in a photoionized plasma. For simplicity, if we assume a canonical radiation field in the form of an energy power law, the spectrum can be crudely represented by a power law (hν)−α. Therefore, for a flat spectrum in energy (α = 1), the rates grow proportionally with the reduction of the K-threshold energy leading to a higher ionization rate; moreover, the steeper spectra the larger the change.
The emissivity of the fluorescent lines also displays the same dependence increasing the intensity of the observed lines. The heating of the gas due to direct photoionization has the weaker dependence (hν)1 − α. However, it also couples the atomic parameters to the photoionized plasma equilibrium temperature resulting from the heating–cooling balance (which directly depends on DH screened scattering atomic data not treated in the present work) through the plasma screening parameter. Therefore, at this stage it is hard to make simple assumptions about the resulting spectra and deduced plasma parameters without carrying out careful simulations incorporating all the atomic data with a grid of plasma screening parameters in a photoionized plasma modeling code.
The shifts in the K thresholds are of ∼110 − 170 eV for Fe XVII–Fe XXV at the largest screening parameter considered in this work. These shifts are marginally too small to be detected with the available X-ray observatories. Nevertheless, changes in the Fe K-edge position will be resolved with new instruments such as the microcalorimeters aboard the future missions, namely, the X-ray Imaging and Spectroscopy Mission (XRISM; Tashiro et al. 2018; Guainazzi & Tashiro 2018) and the Advanced Telescope for High ENergy Astrophysics (ATHENA; Nandra et al. 2013; Guainazzi & Tashiro 2018), which will have a resolution of a few electronvolts. It is worth mentioning that, unlike the energies of the K thresholds, the energies of the Kα and Kβ lines are almost unaffected by high density plasma effects. Hence, high spectral resolution observations should yield information on the ionization structure of the plasma and plasma effect simultaneously. This is by constraining the presence of different ionic stages on the position and structure of the K lines, while diagnosing plasma screening effects on the position and structure of the respective K thresholds. Moreover, we emphasize that the effects mentioned in this work only concern changes in the ionic radiative properties. Other plasma effects at high densities, such as the continuum lowering and increase of the collisional rates, are expected to introduce additional modifications to the observed spectra. These effects will be a matter of further study in our ongoing projects.
5. Summary and conclusions
The influence of the plasma environment on the atomic structure and the radiative and Auger properties of K lines in highly charged iron ions (from He-like Fe XXV to Ne-like Fe XVII) has been studied by means of a time-averaged Debye–Hückel screened potential in the context of the relativistic multiconfiguration Dirac–Fock framework. The explored plasma screening-parameter space of the problem spans 0 ≤ μ ≤ 0.25 a.u. corresponding to conditions expected in compact-object accretion disks. The results can be summarized as follows:
-
The IPs and K-threshold energies are both lowered by the plasma environment. The lowering is found to be linearly dependent on both the plasma screening parameter μ and the ionic effective charge Zeff. They vary from ∼110 eV to ∼170 eV for μ = 0.25 a.u. corresponding to extreme plasma conditions.
-
The importance of the electron–electron plasma screening has been reconfirmed.
-
Plasma environment effects are negligibly small on the wavelengths (redshifted by less than ∼0.1 Å), the transition probabilities, and the Auger widths; the transition probabilities decrease or increase, depending on transitions, by a few percent and the Auger widths decrease by at most ∼10%.
In conclusion, the high-resolution X-ray spectrometers aboard future missions such as XRISM and ATHENA are expected to be sensitive to the lowering of the iron K edge due to the extreme plasma conditions occurring in accretion disks around compact objects.
Acknowledgments
J.D. is Research Fellow of the Belgian Fund for Research Training in Industry and Agriculture (FRIA) while P.P. and P.Q. are, respectively, Research Associate and Research Director of the Belgian Fund for Scientific Research (F.R.S.-FNRS). Financial supports from these organizations, as well as from the NASA Astrophysics Research and Analysis Program (grant 80NSSC17K0345) are gratefully acknowledged. J.A.G. acknowledges support from the Alexander von Humboldt Foundation.
References
- Bautista, M. A., & Kallman, T. R. 2001, ApJS, 134, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2003, A&A, 403, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2004, A&A, 418, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkhiri, M., Fontes, C. J., & Poirier, M. 2015, Phys. Rev. A, 92, 032501 [NASA ADS] [CrossRef] [Google Scholar]
- Certik, O., & Winkler, P. 2013, Int. J. Quant. Chem., 113, 2012 [CrossRef] [Google Scholar]
- Das, M., Sahoo, B. K., & Pal, S. 2016, Phys. Rev. A, 93, 052513 [NASA ADS] [CrossRef] [Google Scholar]
- Deprince, J., Bautista, M. A., Fritzsche, S., et al. 2019a, A&A, submitted [Google Scholar]
- Deprince, J., Bautista, M. A., Fritzsche, S., et al. 2019b, X-Ray Spectrom, submitted [Google Scholar]
- Done, C., Gierlinski, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrophys., 49, 137 [Google Scholar]
- Fritzsche, S. 2012, Comput. Phys. Commun., 183, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Mendoza, C., Bautista, M. A., et al. 2005, ApJS, 158, 68 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Kallman, T. R., Witthoeft, M. C., et al. 2009, ApJS, 185, 477 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Kallman, T. R., & Mushotzky, R. F. 2011, ApJ, 731, 131 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Gorczyka, T. W., Bautista, M. A., & Hasoglu, M. F. 2013, ApJ, 779, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, I. P. 1988, Meth. Comput. Chem., 2, 1 [Google Scholar]
- Grant, I. P. 2007, Relativistic Quantum Theory of Atoms and Molecules (New York: Springer-Verlag) [CrossRef] [Google Scholar]
- Grant, I. P., McKenzie, B. J., Norrington, P. H., Mayers, D. F., & Pyper, N. C. 1980, Comput. Phys. Commun., 21, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Guainazzi, M., & Tashiro, M. S. 2018, ArXiv e-prints [arXiv:1807.06903] [Google Scholar]
- Hasoglu, M. F., Abdel-Naby, S. A., Gatuzz, E., et al. 2014, ApJS, 214, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Fabian, A. C., Wang, J., et al. 2019, MNRAS, 484, 1972 [NASA ADS] [CrossRef] [Google Scholar]
- Jiao, L. G., & Ho, Y. K. 2014, J. Quant. Spectr. Rad. Transf., 144, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, eds. K. Yamashita, & T. Watanabe, 411 [Google Scholar]
- Kallman, T. R., & Bautista, M. A. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T. R., Palmeri, P., Bautista, M. A., Mendoza, C., & Krolik, J. H. 2004, ApJS, 155, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Kar, S., & Ho, Y. K. 2004, Phys. Rev. E, 70, 066411 [NASA ADS] [CrossRef] [Google Scholar]
- Kar, S., & Ho, Y. K. 2005, New. J. Phys., 7, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kramida, A., Ralchenko, Yu, Reader, J., & NIST ASD Team. 2018, NIST Atomic Spectra Database (version 5.6.1). Available: http://physics.nist.gov/asd [2019, February 1] (Gaithersburg, MD: National Institute of Standards and Technology) [Google Scholar]
- Krief, M., Kurzweil, Y., Feigel, A., & Gazit, D. 2018, ApJ, 856, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H. 1999, Active Galactic Nuclei from the Central Black Hole to the Galactic Environment (Princeton: Princeton Univ. Press) [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, B. J., Grant, I. P., & Norrington, P. H. 1980, Comput. Phys. Commun., 21, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, C., Kallman, T. R., Bautista, M. A., & Palmeri, P. 2004, A&A, 414, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendoza, C., Bautista, M. A., Palmeri, P., et al. 2017, A&A, 604, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendoza, C., Bautista, M. A., Palmeri, P., et al. 2018, A&A, 616, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Netzer, H. 1996, ApJ, 473, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Ovechkin, A. A., Loboda, P. A., & Falkov, A. L. 2019, High Energy Density Phys., 30, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., & Bautista, M. A. 2002, ApJ, 577, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., & Bautista, M. A. 2003a, A&A, 403, 1175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003b, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2008, ApJS, 177, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2011, A&A, 525, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2012, A&A, 543, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2016, A&A, 589, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parpia, F. A., Fischer, C. F., & Grant, I. P. 1996, Comput. Phys. Commun., 94, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Piel, A. 2010, Plasma Physics: An Introduction to Laboratory: Space and Fusion Plasmas (Berlin-Heidelberg: Springer Verlag) [Google Scholar]
- Reis, R. C., & Miller, J. M. 2013, ApJ, 769, L7 [Google Scholar]
- Reynolds, C. S. 2013, Class. Quant. Grav., 30, 244004 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., & Nowak, M. A. 2003, Phys. Rep., 377, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Rozsnyai, B. F. 1991, Phys. Rev. A, 43, 3035 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rozsnyai, B. F. 1992, ApJ, 393, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, B., & Fritzsche, S. 2006, Phys. Rev. E, 73, 036405 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., Krolik, J. H., & Noble, S. C. 2013, ApJ, 769, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., & Brickhouse, N. S. 2014, Adv. At. Mol. Opt. Phys., 63, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Tashiro, M., Maejima, H., Toda, K., et al. 2018, SPIE Conf. Ser., 10699, 1069922 [Google Scholar]
- Tomsick, J. A., Parker, M. L., García, J. A., et al. 2018, ApJ, 855, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, P. 1996, Phys. Rev. E, 53, 5517 [NASA ADS] [CrossRef] [Google Scholar]
- Witthoeft, M. C., Bautista, M. A., Mendoza, C., et al. 2009, ApJS, 182, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Witthoeft, M. C., García, J., Kallman, T. R., et al. 2011, ApJS, 192, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, L. Y., Wang, J. G., Janev, R. K., Qu, Y. Z., & Dong, C. Z. 2012, Eur. Phys. J. D, 66, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Computed IPs (eV) for Fe XVII–Fe XXV as a function of the plasma screening parameter μ (a.u.).
Computed K thresholds (eV) for Fe XVII–Fe XXV as a function of the plasma screening parameter μ (a.u.).
Ionization potentials (eV) for Fe XVII–Fe XXV computed with the DH nucleus–electron screening and with and without the electron–electron screening.
Comparison of wavelengths and transition probabilities for the K lines of Fe XVII – Fe XXV (17 ≤ Zeff ≤ 25) computed with plasma screening parameters μ = 0.0, 0.1, and 0.25 a.u.
Plasma environment effects on the Auger widths of K-vacancy states in Fe XVII –Fe XXV (17 ≤ Zeff ≤ 25) computed with plasma screening parameters μ = 0.0, 0.1, and 0.25 a.u.
All Figures
 |
Fig. 1. Ionization potential shifts in Fe XVII–Fe XXV as a function of the plasma screening parameter μ. |
| In the text | |
 |
Fig. 2. Ionization potentials (black points) and K-threshold (red points) energy shifts in Fe ions as a function of effective charge Zeff for μ = 0.1 a.u. and μ = 0.25 a.u. |
| In the text | |
 |
Fig. 3. Wavelength reddening as a function of the plasma screening parameter μ for the [1s]3p 1P1–2p6 1S0 Kβ line in Fe XVII. |
| In the text | |
 |
Fig. 4. Wavelength reddening as a function of the plasma screening parameter μ for the [1s]2p4 2D3/2–2p3 2D3/2 and [1s]2p4 2S1/2–2p3 2P3/2 Kα lines in Fe XX. |
| In the text | |
 |
Fig. 5. Variation of the radiative transition probability (A-value) with the plasma screening parameter μ for the [1s]3p 3P0–[2p]3p 3S1 and [1s]3p 1P1–2p6 1S0 lines in Fe XVII. |
| In the text | |
 |
Fig. 6. Variation of the transition probability (A-value) with the plasma screening parameter μ for the 1s2s2p3 4S3/2–[2s]2p2 2D3/2 and 1s2s2p3 2D5/2–[2s]2p2 2D5/2 lines in Fe XXII. |
| In the text | |
 |
Fig. 7. Variation of the Auger width with the plasma screening parameter μ for two K-vacancy levels in Fe XXII. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.