| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935360 | |
| Published online | 24 June 2019 | |
Fornax 3D project: a two-dimensional view of the stellar initial mass function in the massive lenticular galaxy FCC 167
1
University of California Santa Cruz, 1156 High Street, Santa Cruz, CA 95064, USA
e-mail: imartinn@ucsc.edu
2
Max-Planck Institut für Astronomie, Konigstuhl 17, 69117 Heidelberg, Germany
3
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching b. München, Germany
4
University of Vienna, Department of Astrophysics, Türkenschanzstrasse 17, 1180 Vienna, Austria
5
Instituto de Astrofísica de Canarias, c/ Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
6
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
7
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, vicolo dell’Osservatorio 3, 35122 Padova, Italy
8
INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
9
INAF–Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
10
Department of Physics and Astronomy, Macquarie University, Sydney NSW 2109, Australia
11
Australian Astronomical Observatory, PO Box 915, Sydney NSW 1670, Australia
12
Armagh Observatory and Planetarium, College Hill, Armagh BT61 9DG, UK
13
Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
14
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281, 9000 Gent, Belgium
15
Sterrewacht Leiden, Leiden University, Postbus 9513, 2300 RA Leiden, The Netherlands
16
Max-Planck-Institut fuer extraterrestrische Physik, Giessenbachstrasse, 85741 Garching bei München, Germany
Received:
25
February
2019
Accepted:
22
March
2019
The stellar initial mass function (IMF) regulates the baryonic cycle within galaxies, and is a key ingredient for translating observations into physical quantities. Although it was assumed to be universal for decades, there is now growing observational evidence showing that the center of massive early-type galaxies hosts a larger population of low-mass stars than is expected based on observations from the Milky Way. Moreover, these variations in the IMF have been found to be related to radial metallicity variations in massive galaxies. We present here a two-dimensional stellar population analysis of the massive lenticular galaxy FCC 167 (NGC 1380) as part of the Fornax3D project. Using a newly developed stellar population fitting scheme, we derive a full two-dimensional IMF map of an early-type galaxy. This two-dimensional analysis allows us go further than a radial analysis, showing how the metallicity changes along a disk-like structure while the IMF follows a distinct, less disky distribution. Thus, our findings indicate that metallicity cannot be the sole driver of the observed radial IMF variations. In addition, a comparison with the orbital decomposition shows suggestive evidence of a coupling between stellar population properties and the internal dynamical structure of FCC 167, where metallicity and IMF maps seem to track the distribution of cold and warm orbits, respectively.
Key words: galaxies: formation / galaxies: evolution / galaxies: elliptical and lenticular, cD / galaxies: stellar content / Galaxy: abundances / Galaxy: fundamental parameters
© ESO 2019
1. Introduction
The stellar initial mass function (IMF) describes the mass spectrum of stars at birth and plays a fundamental role in our understanding of galaxies. From stellar feedback (e.g., Gutcke & Springel 2019; Barber et al. 2018) to chemical enrichment (e.g., Ferreras et al. 2015; Martín-Navarro 2016; Philcox et al. 2018; Barber et al. 2019), baryonic processes in the Universe ultimately depend on the IMF. Moreover, observationally, our interpretation of the electromagnetic spectrum of unresolved stellar populations is heavily sensitive to the IMF. Beyond a few megaparsec, where the properties of resolved individual stars cannot still be measured, translating spectrophotometric measurements into physical quantities requires strong assumptions on the shape of the IMF. From star formation rate (e.g., Kennicutt 1998; Madau & Dickinson 2014) and stellar mass measurements (e.g., Mitchell et al. 2013; Courteau et al. 2014; Bernardi et al. 2018) to chemical enrichment predictions (e.g., McGee et al. 2014; Clauwens et al. 2016), the shape of the IMF has to be either fixed or modeled.
The pioneering work of Salpeter (1955) showed that the IMF in the Milky Way can be described by a power law,
with a slope Γ = 1.35 for stellar masses above 1 M⊙. These initial measurements were later extended to lower-mass stars (M ≲ 0.5 M⊙), where the slope of the IMF was found to be flatter (Γ ∼ 0) than for massive stars (e.g., Miller & Scalo 1979). The seminal works of Kroupa (2001, 2002) and Chabrier (2003) consolidated the idea of a universal, Milky Way-like IMF, independent of the local star formation conditions (e.g., Bastian et al. 2010).
Measurements of the IMF are not limited to the relatively small local volume around the Milky Way, however. In unresolved stellar populations, two main approaches have been developed to constrain the IMF shape. The first approach makes use of the effect of the IMF on the mass-to-light (M/L) ratio. Low-mass stars constitute the bulk of stellar mass in galaxies, but high-mass stars dominate the light budget. Hence, a change in IMF slope (i.e., in the relative number of low-mass to massive stars) will have a measurable effect on the expected M/L, and the shape of the IMF can be estimated by independently measuring the total mass (through dynamics or gravitational lensing) and luminosity of a stellar population (see, e.g., Treu et al. 2010; Thomas et al. 2011). This technique suffers from a strong degeneracy between dark matter halo mass and IMF slope, however (e.g., Auger et al. 2010). Alternatively, the shape of the IMF can also be measured in unresolved stellar populations by analyzing their integrated absorption spectra. In particular, IMF-sensitive features vary subtly, at a fixed effective temperature, with the surface gravity of stars, and therefore can be used to measure the dwarf-to-giant ratio, i.e., the slope of the IMF (e.g., van Dokkum & Conroy 2010). Although it is more direct than the dynamical or lensing approach, measuring the IMF from integrated spectra is observationally challenging because the contribution of low-mass stars to the observed spectrum is usually outshone by the flux emitted by more massive stars.
The relative simplicity of the stellar populations (i.e., roughly coeval) in massive early-type galaxies (ETGs) has made them benchmark test cases to study IMF variations beyond the Local Group. In addition, massive ETGs are more metal rich, denser, and have experienced more intense star formation events than the Milky Way. The universality of the IMF shape can therefore be tested under much more extreme conditions. Over the past decade, IMF studies in ETGs have consistently indicated a non-universal IMF shape in massive ETGs: the IMF becomes increasingly steeper with increasing galaxy mass. It is important to note that ETGs host very old stellar populations and that IMF measurements in these objects are therefore restricted to long-lived stars, with masses m ≲ 1 M⊙, which makes these measurements insensitive to variations in the high-mass end of the IMF. In general, the agreement between dynamics-based (Auger et al. 2010; Cappellari et al. 2012; Dutton et al. 2012; Wegner et al. 2012; Tortora et al. 2013, 2014; Läsker et al. 2013; Corsini et al. 2017) and stellar population-based studies (van Dokkum & Conroy 2010; Spiniello et al. 2012, 2014, 2015; Conroy & van Dokkum 2012a; Smith et al. 2012; Ferreras et al. 2013; La Barbera et al. 2013; Tang & Worthey 2017) supports a systematic variation in the IMF of massive ETGs. However, dynamical and stellar population studies do not necessarily agree on the details (see, e.g., Smith 2014; Smith & Lucey 2013; Newman et al. 2017). This seems to suggest that both approaches might effectively be probing different mass-scales of the IMF, although differences between dynamical and stellar population-bases studies are not as striking after a proper systematics modeling (Lyubenova et al. 2016).
Variations in IMF with galaxy mass, however, provide limited information about the process(es) shaping the IMF because in general, galaxy properties tend to scale with galaxy mass. Therefore, galaxy-wide IMF variations may be equally attributed to a number of different mechanisms (e.g., Conroy & van Dokkum 2012a; La Barbera et al. 2013, 2015). This observational degeneracy can be partially broken by analyzing how the IMF shape changes as a function of radius because different parameters such as velocity dispersion, stellar density, metallicity, or abundance pattern vary differently with galactocentric distance. Since they were first measured in the massive galaxy NGC 4552 (Martín-Navarro et al. 2015a), radial IMF gradients have been widely found in very many massive ETGs (Martín-Navarro et al. 2015b; La Barbera et al. 2016; Davis & McDermid 2017; van Dokkum et al. 2017; Oldham & Auger 2018; Parikh et al. 2018; Sarzi et al. 2018a; Vaughan et al. 2018a). These spatially resolved IMF studies have shown that IMF variations occur in the inner regions of massive ETGs, and that metallicity seems to be the local property that better tracks the observed IMF variations (Martín-Navarro et al. 2015c). However, it is not clear whether the observed correlation with metallicity is sufficient to explain all IMF variations (e.g., Villaume et al. 2017), or even if there are massive ETGs with Milky Way-like IMF slopes (McConnell et al. 2016; Zieleniewski et al. 2017; Alton et al. 2018; Vaughan et al. 2018b).
The aim of this work is to take a step further in the observational characterization of the IMF by analyzing its two-dimensional (2D) variation in the massive (MB = −20.3), fast-rotating ETG FCC 167 (NGC 1380), as part of the Fornax 3D project (F3D). Taking advantage of the unparalleled capabilities of the Multi Unit Spectroscopic Explorer (MUSE) integral-field spectrograph (Bacon et al. 2010), we present here a 2D analysis of the stellar population properties of FCC 167, showing for the first time the IMF map of a massive ETG. The paper is organized as follows: in Sect. 2 we briefly present the data. Stellar population model ingredients are described in Sect. 3. Section 4 contains a detailed explanation of the stellar population modeling and fitting method 9, and in Sect. 5 the results of the stellar population analysis of FCC 167 are presented. In Sect. 6 we discuss our findings. Finally, in Sect. 7 we summarize the main conclusions of this work, briefly describing future IMF efforts within the Fornax 3D project.
2. Data
We based our stellar population analysis on MUSE data from F3D that are described in Sarzi et al. (2018b). In short, F3D is an IFU survey of 33 bright (mB < 15) galaxies selected from the Fornax Cluster Catalog (FCC, Ferguson 1989) within the virial radius of the Fornax cluster (Drinkwater et al. 2001). The survey was carried out using the Wide Field Mode of the MUSE IFU (Bacon et al. 2010), which provides a 1 × 1 arcmin2 field of view at a 0.2 arcsec pixel−1 spatial scale. The wavelength range covers from 4650 Å to 9300 Å, with a spectral sampling of 1.25 Å pixel−1 and a nominal resolution with an FWHM = 2.5 Å at λ = 7000 Å.
This work is focused on the ETG (S0/a) galaxy FCC 167, located at a distance of 21.2 Mpc (Blakeslee et al. 2009) and at 222 kpc from NGC 1399, the brightest galaxy in the cluster. The total stellar mass of FCC 167 is 9.85 × 1010 M⊙, with an effective radius of Re = 6.17 kpc (60 arcsec) in the i band (Iodice et al. 2019). Sarzi et al. (2018b) found that FCC 167 has two embedded (thin and thick) disks based on its orbital decomposition. The thin disk is clearly seen in the photometric structure, along with some other interesting features. Nebular gas emission is present in the central regions (Viaene et al. 2019), and the exquisite spatial resolution of the MUSE data allows us to systematically detect and characterize planetary nebulae within the MUSE field of view (Sarzi et al. 2018b).
The final F3D data cube of FCC 167 combines three different pointings that cover from the center of the galaxy out to ∼4 Re, with a total exposure time per pointing of ∼1.2 h. The data were reduced using the MUSE pipeline (Weilbacher et al. 2016) running under the ESO Reflex environment (Freudling et al. 2013). The initial sky subtraction was made using either dedicated sky exposures or IFU spaxels that were free from galactic flux at the edge of the MUSE field of view. In a later step, the sky subtraction process was further improved by using the Zurich Atmospheric Purge (ZAP) algorithm (Soto et al. 2016). More details on the observational strategy and data reduction process are given in the F3D presentation paper (Sarzi et al. 2018b).
In order to measure IMF variation in the absorption spectra of galaxies, it is necessary to accurately model variations of a few percent in the depth of gravity-sensitive features. We achieved the required precision level by spatially binning the MUSE data into Voronoi bins with a signal-to-noise ratio (S/N) of at least ∼100 per bin (Cappellari & Copin 2003). This S/N threshold is similar to that used in previous IMF studies, but the exquisite spatial resolution and sensitivity of MUSE combined with the 2D information provides an unprecedented number of spatial bins: while IMF gradients have usually been measured using ∼10 data points (e.g., Martín-Navarro et al. 2015a; van Dokkum et al. 2017), our S/N = 100 binned cube of FCC 167 consists of more than 6000 independent Voronoi bins.
3. Ingredients of the stellar population model
Our stellar population analysis relies on the most recent version of the MILES evolutionary stellar population synthesis models (Vazdekis et al. 2015). These models are fed with the MILES stellar library of Sánchez-Blázquez et al. (2006), which has a constant spectral resolution of 2.51 Å (FWHM, Falcón-Barroso et al. 2011).
The main difference of the single stellar population models (SSP) of Vazdekis et al. (2015) with respect to previous MILES models (e.g., Vazdekis et al. 2010) is the treatment of the α-element abundance ratio. In this new set of models, MILES stars are used to populate BaSTI isochrones (Pietrinferni et al. 2004, 2006) that were explicitly calculated at [α/Fe] = 0.4 and at the solar scale ([α/Fe] = 0.0). To compute [α/Fe] = 0.0 models at low metallicities, which is a regime where MILES stars are α-enhanced (Milone et al. 2011), a theoretical differential correction was applied to the fully empirical SSP. The same procedure was followed to generate [α/Fe] = 0.4 SSP models at high metallicities. Therefore this new version of the MILES models allows for a self-consistent treatment of the abundance pattern.
In addition to variable [α/Fe] (0.0 and +0.4), the Vazdekis et al. (2015) MILES models fed with BaSTI isochrones cover a range in metallicities ([M/H]) from −2.27 to +0.261 that expands from 0.03 Gyr to 14 Gyr. The wavelength range in the [α/Fe]-variable models is relatively short (Vazdekis et al. 2016), from λ = 3540 Å to λ = 7410 Å, but it contains enough gravity-sensitive features to safely measure the IMF effect.
For the IMF functional form, we assumed the so-called bimodal shape (Vazdekis et al. 1996). In this parameterization, the IMF is varied through the (logarithmic) high-mass end slope ΓB. The main difference between this IMF shape and a single power-law parameterization is that the bimodal IMF flattens for masses below ∼0.5 M⊙. This feature allows for a better agreement with dynamical IMF measurements (Lyubenova et al. 2016) while recovering a Milky Way-like behavior for ΓB = 1.3. Although ΓB controls the high-mass end slope, the number of low-mass stars is effectively varied at the same time as the integral of the IMF is normalized to 1 M⊙. We note that a variation in the high-mass end of the IMF as presented here would be in tension with the observed chemical composition of massive ETGs unless the slope of the IMF also changes with time (Weidner et al. 2013; Ferreras et al. 2015; Martín-Navarro 2016). However, our stellar population analysis of FCC 167 is completely insensitive to this potential problem (see details below).
Understanding IMF variations in unresolved, old stellar populations from optical and near-IR spectra requires acknowledging two empirical limitations. First, only stars less massive than ∼1 M⊙ contribute to the light budget, and IMF measurements from integrated spectra are therefore insensitive to variations of the high-mass end slope. Second, the contribution from very low-mass stars close to the hydrogen-burning limit (m ∼ 0.1 M⊙) is virtually unconstrained unless very specific near-IR spectral features are targeted (Conroy & van Dokkum 2012a; Conroy et al. 2017). The lack of constraints on the number of very low-mass stars explains why a single power-law IMF parameterization fits the observed spectra of massive ETGs equally well (La Barbera et al. 2013; Spiniello et al. 2014), but dramatically overestimates the expected M/L ratios (Ferreras et al. 2013; Lyubenova et al. 2016). In practice, these two limitations imply that stellar population-based IMF measurements are mostly sensitive to the IMF slope for stars with masses 0.2 ≲ m ≲ 1 M⊙ regardless of the adopted IMF parameterization.
Given the rising number of stellar population-based IMF measurements and the need for an unbiased comparison among them, we introduce here a new quantity, ξ, which is virtually independent of the IMF parametrization. The ξ parameter quantifies the mass fraction locked in low-mass stars, and it is defined as follows:
where in the second equality the IMF, X(m), is expressed in linear mass units. This is similar to the definition of F0.5 in La Barbera et al. (2013), but ξ is normalized only to the mass contained in stars below 1 M⊙, while La Barbera et al. (2013) normalized to the mass in stars below 100 M⊙. Hence, ξ does not depend on the number of massive stars, which in fact cannot be measured from the absorption spectra of ETGs. Moreover, because the denominator in Eq. (2) is roughly equivalent to the total stellar mass for old stellar populations, ξ offers a quick conversion factor to transform the observed stellar mass of a galaxy into the total mass in low-mass stars. This definition of ξ explicitly takes into account the fact that very low-mass stars (M ≲ 0.2 M⊙) are not strongly constrained by most optical or near-IR spectroscopic data. We also note that ξ does not account for the amount of mass locked in stellar remnants. This dark stellar mass is only measurable through dynamical studies, and it heavily depends on the shape and slope of the high-mass end of the IMF.
The ξ parameter as defined by Eq. (2) is therefore a useful quantity to compare different IMF measurements, as shown in Sect. 4, and it can even be applied to IMF functional forms without a well-defined low-mass end IMF slope (e.g., Chabrier et al. 2014; Conroy et al. 2017). Table 1 shows how commonly used IMF functional forms can be translated into ξ mass ratios.
Conversion coefficients between commonly used IMF shapes and ξ mass ratios.
4. Full-index fitting: a novel approach
Measuring detailed stellar population properties, and in particular IMF variations, from the absorption spectra of unresolved stellar populations requires a precise and reliable comparison between stellar population models and data. Two main approaches are usually followed. The standard line-strength analysis makes use of the equivalent width of well-defined spectral features to derive the stellar population properties of a given spectrum (e.g., Burstein et al. 1984). The main advantage of this method is that it focuses on relatively narrow spectral regions where the bulk of the information about the stellar population properties is encoded. Moreover, these narrow spectral features have been thoroughly studied and their dependence on the different stellar population parameters has been extremely well characterized (e.g., Worthey 1994; Cenarro et al. 2001; Thomas et al. 2003; Schiavon 2007; Johansson et al. 2012). However, only a handful of these indices can usually be analysed simultaneously, which may lead to degeneracies in the recovered stellar population properties (Sánchez-Blázquez et al. 2011).
Additionally, and thanks to the development of intermediate resolution stellar population models, full spectral fitting techniques are now widely adopted (e.g., Cid Fernandes et al. 2005; Ocvirk et al. 2006; Conroy et al. 2009; Cappellari 2017; Wilkinson et al. 2017). Instead of focusing on specific absorption features, this second approach aims to fit every pixel across a relatively wide wavelength range (∼1000 Å). Since every pixel is treated as an independent measurement, S/N requirements are lower than for a line-strength analysis, and with a given S/N ratio, degeneracies in the recovered stellar population parameters tend to be weaker using full spectral fitting algorithms (Sánchez-Blázquez et al. 2011). Although this has clear advantages over the use of line-strength indices, the number of free parameters is also higher with full spectral stellar population fitting (e.g., Conroy et al. 2018), which increases the computational cost. Moreover, since every pixel in the spectrum is treated equally, the information about the stellar population properties that is concentrated in narrow features might become diluted (La Barbera et al. 2013).
A hybrid approach, in between line-strength analysis and full spectral fitting, is also possible. The idea consists of selecting key absorption features in which the information about the stellar population properties is concentrated. Then, instead of calculating the equivalent widths, every pixel within the feature is fit after normalizing the continuum using the index definition (Martín-Navarro et al. 2015d). In practice, this is a generalization of the line-strength analysis: while in the standard approach the equivalent width is measured with respect to a well-defined continuum, the hybrid method quantifies the depth of each pixel with respect to the same continuum definition. Figure 1 exemplifies normalized Mgb 5177 and TiO2 spectral features.
 |
Fig. 1. Full-index-fitting (FIF) approach. Top panels: Mgb 5177 (left) and the TiO2 (right) spectral features, normalized using the index pseudo-continua (blue shaded regions). In the FIF approach, every pixel within the central bandpass (gray area) is fit to measure the stellar population parameters. The black line corresponds to a model of solar metallicity [M/H] = 0, [Mg/Fe] = 0, [Ti/Fe] = 0, and Kroupa-like IMF, at a resolution of 200 km s−1. The FIF approach breaks the degeneracies more efficiently than the standard line-strength analysis because every pixel responds differently to changes in the stellar population properties. Colors in the bottom panels show the relative change in the spectrum after different stellar population parameters were varied. For reference, the IMF slope was varied by ΔΓB = 1, the metallicity and abundance ratios by 0.2 dex, and the age by 2 Gyr. |
This hybrid approach, or FIF, presents significant advantages. First, only specific spectral features are fit, in which the information is concentrated and the behavior of the stellar population properties is well determined. This allows for a low number of free parameters, as in the standard line-strength analysis; this reduces the computational time. This is a key feature given the large number of spatial bins provided by the MUSE spectrograph. Moreover, because the continuum is fit by a straight line using the index definition, the FIF approach is insensitive to large-scale flux calibration problems in the data. Compared with the line-strength analysis, the main advantage of the FIF method is that the number of independent observables is significantly increased. For example, in a standard index-index diagram (e.g., Hβ versus Mgb 5177), only two measurements are compared to the model predictions. However, using FIF, the same two indices lead to more than ∼100 measurements (at the MILES resolution). In practice, adjacent pixels in the observed spectrum of a galaxy are correlated so that the effective improvement of the S/N does not necessarily scale as 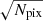 . In addition to these practical advantages, the use of FIF has a crucial characteristic: each pixel in a given spectral feature depends differently on the stellar populations parameters, as shown in Fig. 1. This implies that not only the S/N requirements are lower, but also that degeneracies among stellar population properties become weaker (see Fig. 2).
. In addition to these practical advantages, the use of FIF has a crucial characteristic: each pixel in a given spectral feature depends differently on the stellar populations parameters, as shown in Fig. 1. This implies that not only the S/N requirements are lower, but also that degeneracies among stellar population properties become weaker (see Fig. 2).
 |
Fig. 2. Best-fitting stellar population properties. Posterior distributions for one of the spatial bins of FCC 167 showing that our FIF approach is able to recover the stellar population properties with high precision, breaking the degeneracies among them. Vertical red lines indicate the best-fitting value (solid line) and the 1σ uncertainty (dashed lines). These values are quoted on top of the posterior distributions. The luminosity-weighted age of this bin is 12.7 Gyr. |
4.1. Application to F3D data
In order to apply the FIF method to the F3D data of FCC 167, we first measured the stellar kinematics (mean velocity and velocity dispersion) of each individual spatial bin (see Sect. 2) using the pPXF code presented in Cappellari & Emsellem (2004). For consistency, we fed pPXF with the same set of MILES models as we used for the stellar population analysis. Spectral regions potentially contaminated by ionized gas emission were masked in this first step of the fitting process. For consistency, we did not use the kinematics described in the survey presentation paper (Sarzi et al. 2018b) because we made different assumptions in the modeling process.
An important limitation of the MUSE spectrograph is the relatively red wavelength coverage, which starts at λ = 4650 Å. Consequently, the only reliable age sensitive feature in the observed wavelength range is the Hβ line. However, Hβ is known to depend not only on the age, but also on some other stellar population properties. In particular, Hβ shows a significant sensitivity to the [C/Fe] abundance ratio (Conroy & van Dokkum 2012b; La Barbera et al. 2016). Unfortunately, there are no prominent C-sensitive features in the MUSE data, making the use of Hβ unreliable. We overcame this problem by measuring the luminosity-weighted age of FCC 167 using the pPXF regularization scheme (Cappellari 2017), which can provide reliable stellar population measurements (McDermid et al. 2015). Given the sensitivity of recovered star formation histories on the assumed IMF slope (Ferré-Mateu et al. 2013), we regularized over the age–metallicity–IMF slope parameter space, and then we fixed the pPXF best-fitting age throughout the rest of the stellar population analysis.
Given the wavelength coverage of the [α/Fe]-variable MILES models (λλ = 3540−7410 Å), we based our stellar population analysis of FCC 167 on features blueward of λ ∼ 7000. This wavelength range shows a wide variety of stellar population-sensitive features and is much less affected by telluric absorption than the near-IR regime. To constrain the metallicity and [α/Fe] ratio, we focused on the Fe 5270, Fe 5335, and Mgb 5177 indices (Trager et al. 1998). Although all α elements are varied in lockstep in the MILES models, our only [α/Fe]-sensitive feature is the Mgb 5177 absorption feature. Hence, only the [Mg/Fe] abundance ratio is constrained by our analysis. In the MUSE wavelength range, the most important IMF sensitive features are the aTiO (Jorgensen 1994), the TiO1, and the TiO2 absorptions (Serven et al. 2005). We therefore also included the effect of [Ti/Fe] as an additional free parameter using the response functions of Conroy & van Dokkum (2012b). The [Ti/Fe] is not treated in the same way as the [Mg/Fe] ratio because the same response function is assumed regardless of the value of the other stellar population parameters (see Spiniello et al. 2015). Effectively, [Ti/Fe] has a relatively mild effect on the selected features. Finally, because the effect of [C/Fe] in our set of features balances that of the [α/Fe] out (La Barbera et al. 2016), and both ratios are expected to track each other (Johansson et al. 2012), we neglected the [α/Fe] sensitivity of the MILES models beyond λ = 5400 Å.
In short, we followed the FIF stellar population fitting approach described in Sect. 4 and focused on six spectral features (Fe 5270, Fe 5335, Mgb 5177, aTiO, TiO1, and TiO2). We fit for four stellar population parameters, namely, metallicity, [Mg/Fe], [Ti/Fe], and IMF slope (ΓB). The age was fixed to that measured using pPXF, and the effect of the [Mg/Fe] was only considered for wavelengths λ ≦ 5400 Å. The implications of these assumptions on the recovered stellar population parameters are shown and discussed in Sect. 4.2.
In order to compare models and data, we implemented the same scheme as in Martín-Navarro et al. (2018). We used the emcee Bayesian Markov chain Monte Carlo sampler (Foreman-Mackey et al. 2013), powered by the Astropy project (Astropy Collaboration 2013, 2018), to maximize the following objective function:
where S = {ΓB, [M/H],[Mg/Fe],[Ti/Fe]}. The summation extends over all the pixels within the bandpasses of the selected spectral features. On and Mn are the observed and the model flux2 of the nth-pixel, and σn the measured uncertainty. Equation (3) is therefore just a Gaussian likelihood function, where the distance (scaled by the expected uncertainity) between data and models is minimized. For FCC 167, model predictions Mn were calculated at a common resolution of 250 km s−1 so they had to be calculated only once and not for every spatial bin. This resolution corresponds to the lowest measured in FCC 167. Before comparing models and data, every MUSE spectrum was smoothed to match the 250 km s−1 resolution of the models using the velocity dispersion measurements from pPXF. Figure 2 shows that our approach is able to break the degeneracies among the different stellar population parameters when it is applied to FCC 167 F3D data.
With the Bayesian fitting scheme described above, we could further improve the reliability of our results by imposing informative priors. In particular, we used the best-fitting metallicity and IMF values from the regularized pPXF fit as Gaussian priors on the final solution. This final improvement does not bias the solution, but increases the stability of the recovered stellar population parameters, as shown in Fig. 3. We assumed flat priors for the other free parameters (e.g., [Mg/Fe] and [Ti/Fe]).
 |
Fig. 3. From top to bottom: metallicity, [Mg/Fe], and IMF (ξ) scaling relations with galaxy velocity dispersion. The recovered trends agree with expectations from previous studies. In particular, the measured IMF-σ relation is remarkably close to the results of La Barbera et al. (2013) and Spiniello et al. (2014) (gray and orange shaded regions in the bottom panel, respectively), even though they relied on different model assumptions. |
4.2. ETG scaling relations
The stellar population properties of ETGs follow tight scaling relations with galaxy mass (e.g., Worthey et al. 1992; Thomas et al. 2005; Kuntschner et al. 2010). Before attempting the stellar population analysis of FCC 167, we therefore tested whether our FIF approach was able to recover these well-known trends. We made use of the ETG stacked spectra of La Barbera et al. (2013), based on the public Sloan Digital Sky Survey DR6 (Adelman-McCarthy et al. 2008), and we fit them with our reference setup described above. In addition, to understand the effect of the different model assumptions on the recovered stellar population properties, we also performed a series of tests where we varied our fitting scheme. The first variation consisted of removing the informative priors. Second, we also tested the effect of allowing for the [Mg/Fe] variations to affect wavelengths beyond λ = 5400 Å. Third, the reliability of the FIF approach and its dependence on the set of indices was put to the test by removing all IMF sensitive features except for TiO2 from the analysis. The results of these tests are shown in Fig. 3.
The top panel of Fig. 3 shows the metallicity–stellar velocity dispersion using our FIF approach. The expected trend, that is, that galaxies with higher velocity dispersion (more massive) are more metal rich, is recovered (e.g., Thomas et al. 2010). Only when the TiO2 is our only IMF-sensitive feature does this depart from the rest, proving that metallicity is well constrained by our approach.
The middle panel in Fig. 3 shows the change in [Mg/Fe] abundance ratio as a function of galaxy velocity dispersion. Again, as for the metallicity, all the different variations agree, and they show that more massive galaxies are more [Mg/Fe] enhanced. An important point should be noted: the [Mg/Fe] – velocity dispersion relation is flatter than expected (e.g., Thomas et al. 2010; de La Rosa et al. 2011; La Barbera et al. 2014; Conroy et al. 2014). We verified that this flattening is not due to the FIF approach by repeating the analysis with the standard line-strength indices and found the same result. The weak [Mg/Fe] trend with galaxy velocity dispersion results from the combination of two processes that have not been explored in previous studies. First, the new MILES models consistently capture the effect of the [Mg/Fe], whose effect becomes weaker at sub-solar metallicities (Vazdekis et al. 2015). This implies that for low-σ galaxies, where metallicities are also low, a higher [Mg/Fe] is needed to match the data than other stellar population models. In consequence, low-σ galaxies are found to have higher [Mg/Fe] than previously reported (Sybilska et al. 2017). The second effect that flattens the [Mg/Fe]–σ relation has to do with the sensitivity of the Mgb 5177 feature to the IMF, as shown for example in the left panels of Fig. 1. A variation in the IMF slope of δΓ ∼ 1 as typically observed in massive ETGs leads to a change in the Mgb 5177 index, which is equivalent to an increment of δ[Mg/Fe] ∼ 0.1. Hence, the depth of the Mgb 5177 absorption feature, traditionally interpreted as a change in the [Mg/Fe] (Thomas et al. 2005), is also driven by a steepening in the IMF slope of massive ETGs (Conroy & van Dokkum 2012b).
Finally, the bottom panel of Fig. 3 shows the recovered trend between IMF slope (ξ) and galaxy mass, in very good agreement with previous works. Shaded regions indicate the trends found by La Barbera et al. (2013) and Spiniello et al. (2014) with the typical 1σ uncertainty. It is clear from this panel that with our FIF approach, we do not only recover the expected trends, but also recover them with a smaller uncertainty. This is ultimately due to the larger number of pixels used in the analysis and to the effect of model systematics3. Even using a single IMF indicator, in this case the TiO2 feature, we are able to reliably measure the IMF in ETGs. Moreover, Fig. 3 also shows that our ξ definition is able to unify IMF measurements based on different IMF parameterizations. It is also worth mentioning that our FIF approach and the works of La Barbera et al. (2013) and Spiniello et al. (2014) are based on different sets of indices and even different stellar population model ingredients. This makes the agreement among the three approaches even more remarkable.
5. Results
After validating the FIF approach with the stacked spectra of La Barbera et al. (2013), we applied our stellar population fitting scheme to the F3D data cube of FCC 167. As mentioned in Sect. 2, after spatially binning the three MUSE pointings of FCC 167, we measured the stellar population properties in ∼6000 independent Voronoi bins, mapping the 2D structure of the galaxy. The main results of our analysis are shown in Fig. 4.
 |
Fig. 4. Stellar population maps of FCC 167. Top left panel: age map, as measured from pPXF, where a relatively older central component is clearly visible. The metallicity (top right) and the [Mg/Fe] (bottom left) maps show the clear signature of a chemically evolved disk, confined within a vertical height of ∼10 arcsec, which coincides with the kinematically cold component observed in this galaxy (Sarzi et al. 2018b). The IMF map on the bottom right exhibits a different 2D structure, however, that does not follow the metallicity variations, but closely follows the hot+warm orbits of this galaxy (Sarzi et al. 2018b). |
In the top left panel of Fig. 4, the age map of FCC 167 shows that this galaxy hosts old stellar populations at all radii, although they are slightly older in the center. These relatively older stars seem to track the bulge-like structure of FCC 167 (as shown in Fig. 10 of Sarzi et al. 2018b). The ages shown in Fig. 4 are luminosity-weighted values derived using pPXF (where IMF and metallicity were also left as free parameters in a 20 (age) × 10 ([M/H]) × 10 (IMF) model grid, covering the same parameter space as described in Sect. 3).
The metallicity (top right) and [Mg/Fe] (bottom left) maps show clear evidence of the presence of a chemically evolved thin disk. Interestingly, the age map appears partially decoupled from the chemical properties of FCC 167. It is particularly striking that some of the oldest regions, where star formation ceased very early in the evolution of FCC 167, show at the same time chemically evolved (e.g., metal-rich and [Mg/Fe]-poor) stellar populations.
Finally, the bottom right panel in Fig. 4 shows for the first time the IMF map of an ETG. The overall behavior of the IMF is similar to what has previously been found in massive ETGs: the fraction of low-mass stars in the central region appears larger than would be expected based on observations made in the Milky Way (e.g., Martín-Navarro et al. 2015b; La Barbera et al. 2016; van Dokkum et al. 2017). At a distance of ∼100 arcsec from the center of FCC 167, a Milky Way-like IMF slope is found. However, an important difference with respect to previous studies should be noted. The 2D structure of the IMF in this galaxy is clearly decoupled from the chemical structure, in particular, from the metallicity map (Martín-Navarro et al. 2015c). Instead of following a disky structure, the IMF map of FCC 167 appears much less elongated.
6. Discussion
The ground-breaking potential of the F3D project to help understanding the formation and evolution of ETGs through their stellar population properties is clear from the 2D maps shown in Fig. 4. In spatially unresolved studies, the global properties of ETGs appear highly coupled because more massive galaxies are also denser, more metal rich, more [Mg/Fe] enhanced, older, and have steeper (low-mass end) IMF slopes (e.g., Thomas et al. 2010; La Barbera et al. 2013). In the same way, by collapsing the information of a galaxy into a 1D radial gradient, valuable information about the stellar population parameters is lost. For example, in FCC 167, both IMF slope and metallicity decrease smoothly with radius, but only when we study its full 2D structure does their different behavior become evident.
6.1. Age – [Mg/Fe] discrepancy
The [Mg/Fe] map in FCC 167 is clearly anticorrelated with the age map (Fig. 4), which transitions from old and low [Mg/Fe] populations in the center toward relatively younger and more Mg-enhanced outskirts. Under the standard interpretation, age and [Mg/Fe] should tightly track each other because lower [Mg/Fe] is reached by longer star formation histories (e.g., Thomas et al. 1999). In FCC 167, the age map and its chemical properties seem to describe two different formation histories. The [Mg/Fe] map, in agreement with the metallicity distribution, suggests that the outer parts of the galaxy formed rapidly, which led to chemically immature stellar populations (high [Mg/Fe] and low metallicities). This picture for the formation of the outskirts of FCC 167 is in agreement with the properties of the Milky Way halo (e.g., Venn et al. 2004; Hayes et al. 2018; Fernández-Alvar et al. 2019) and other spiral galaxies (e.g., Vargas et al. 2014; Molaeinezhad et al. 2017). The inner metal-rich, low [Mg/Fe] regions would have formed during a longer period of time, leaving enough time to recycle stellar ejecta into new generations of stars. However, this scenario would imply a relatively younger inner disk, which is not evident from the age map. This apparent contradiction suggests that in order to truly understand the stellar population properties of ETGs, SSP-glasses are not enough, and a more complex chemical evolution modeling is needed that takes the time evolution of the different stellar population parameters and our limitations on the stellar population modeling side into account, in particular, the coarse time-resolution inherent to old stellar populations. This apparent tension between age and chemical composition properties is not unique to FCC 167 and has been reported in previous IFU-based studies (e.g., Martín-Navarro et al. 2018).
6.2. IMF – metallicity relation
The difficulty of understanding the stellar population properties of ETGs with the advent of IFU spectroscopy is further increased by the observed IMF variations. In Fig. 5 we show how IMF and metallicity measurements compare in FCC 167, where the dashed line shows the relation found by Martín-Navarro et al. (2015c). The agreement between the FCC 167 measurements and the empirical IMF–metallicity is remarkable given all the differences in the stellar population modeling between the two studies, further supporting the reliability of our approach. However, it is clear that the IMF–metallicity relation of Martín-Navarro et al. (2015c) is not enough to explain the 2D stellar population structure of FCC 167. The core of FCC 167 agrees with the expectations, but it clearly departs in the outer (lower metallicity and ξ) regions. This is expected because the measurements of Martín-Navarro et al. (2015c) are biased toward the central regions of their sample of ETGs from the CALIFA survey (Sánchez et al. 2012). It is worth mentioning that Sarzi et al. (2018a) found a good agreement between the metallicity and the IMF gradients in M 87, tightly following the IMF–metallicity found by Martín-Navarro et al. (2015c). The decoupling in FCC 167 likely arises because its internal structure has been preserved over cosmic time as a result of the lack of major disruptive merger events, which would have washed out the observed differences. Hence, massive lenticular galaxies appear to be ideal laboratories for studying the origin of the observed IMF variations.
 |
Fig. 5. IMF–metallicity relation. The individual bins of FCC 167 are shown color-coded by their distance to the center of the galaxy, compared with the empirical relation of Martín-Navarro et al. (2015c), shown as an blue dashed line. This relation agrees with the FCC 167 measurements in the central regions of the galaxy (top right corner), but it does not hold for the outskirts, where an additional parameter is needed to explain the observed variations in the IMF. The ξ ratio of the Milky Way (Kroupa 2001) is shown as a gray dashed line. |
The different behavior of the stellar population properties in FCC 167 can also be seen by comparing the iso-metallicity and the iso-IMF contours. Figure 6 shows the r-band surface brightness map of FCC 167 as measured from the MUSE F3D datacubes. In addition to the surface brightness map, the iso-metallicity and the iso-IMF contours are also shown. To generate the contours in Fig. 6, we fit the stellar population maps with a multi-Gaussian expansion model (Emsellem et al. 1994; Cappellari 2002), as is generally done with photometric data. This allows a smooth modeling of the large-scale behavior of the stellar population maps, which can then be easily transformed into iso-contours.
 |
Fig. 6. Iso-metallicity vs. iso-IMF contours. The surface brightness map of FCC 167 is shown as measured from the F3D data cube, with the iso-metallicity (solid lines) and iso-IMF contours (dashed lines) overplotted. As in Fig. 4, this figure shows that the 2D IMF map does not exactly follow the metallicity variations. IMF variations appear more closely related to the surface brightness distribution, in particular, around the central bulge. The metallicity distribution, in contrast, is structured in a more disk-like configuration. |
The decoupling in the 2D structure of the IMF and metallicity maps appears clearly in Fig. 6. As described above, the metallicity distribution follows a diskier structure, which is consistent with a long-lasting chemical recycling within the cold kinematic component of FCC 167. The IMF, on the other hand, follows a rounder, more symmetric distribution.
6.3. Stellar populations properties versus orbital decomposition
In order to further investigate the connection between the internal structure of FCC 167 and its stellar population properties, we fit the synthetic r-band image with a bulge plus exponential disk model using Imfit (Erwin 2015). The top panels of Fig. 7 compare the metallicity and IMF maps of FCC 167 with its photometric decomposition. It is clear that the disk component does not capture the observed structure of the metallicity map. The agreement between IMF variations and bulge light distribution is slightly better, although the latter is much rounder. Thus, a simple bulge plus disk analysis is unable to capture the variation observed in the stellar population properties.
 |
Fig. 7. Internal structure vs. stellar population maps. The top panels show the comparison between metallicity and photometric disk (top left) and IMF and bulge (top right). Neither the disk nor the bulge seem to follow the structure of the stellar population maps. The three bottom panels compare the orbital decomposition of FCC 167 with the stellar population properties. On the left, the agreement between the metallicity structure (white solid lines) and the spatial distribution of the cold orbits indicates that the chemically evolved (metal-rich and [Mg/Fe]-poor) structure observed in the stellar population maps corresponds to a cold stellar disk with an extended star formation history. IMF contours (white dashed lines), on the other hand, closely follow the distribution of warm orbits (right). Hot orbits, in contrast, are decoupled from the stellar population properties. |
Sarzi et al. (2018b) presented a Schwarzschild orbit-based decomposition (van den Bosch et al. 2008; Zhu et al. 2018a) of FCC 167, where they roughly distinguished between three types of orbits: cold (λz > 0.7), warm (0.2 < λz < 0.7), and hot (λz < 0.2). The bottom three panels in Fig. 7 present the comparison between light distributions of these three types of orbits and the metallicity and IMF maps of FCC 167. The coupling between the metallicity (and therefore the [Mg/Fe] ratio) maps and the spatial distribution of cold orbits is remarkable. This further supports the idea that the elongated structure shown by the chemical properties of FCC 167 indeed tracks a dynamically cold disk. A relatively more extended star formation history in this disk would naturally explain the high metallicities and low [Mg/Fe] ratios.
The IMF variations, in contrast, seem to closely track the distribution of warm orbits, particularly in the central regions of FCC 167. This result is rather unexpected, as it has been extensively argued that IMF variations are associated with the extreme star formation conditions within the cores of massive ETGs (e.g., Martín-Navarro et al. 2015a,b; van Dokkum et al. 2017). The comparison shown in Fig. 7 suggests, however, that the IMF was set during the early formation of the warm (thick-disk) component of FCC 167, where the pressure and density conditions may have had an effect on the shape of the IMF (Chabrier et al. 2014; Jerabkova et al. 2019). The weak correlation between stellar population properties and hot orbits might have strong implications for our understanding of bulge formation because it suggests that most of the stars belonging to this dynamically hot structure were not born hot, but must have been heated up at a later stage (e.g., Grand et al. 2016; Garrison-Kimmel et al. 2018).
From Fig. 7 it becomes clear that the orbital decomposition offers a more meaningful and physically motivated framework than a standard photometric analysis (Zhu et al. 2018b). The connection with the metallicity and IMF distribution opens an alternative approach for understanding the origin of the stellar population radial variations, in particular, in lenticular galaxies such as FCC 167 with a rich internal structure. We note, however, than while the stellar population maps are integrated quantities, the orbital analysis shown in Fig. 7 is a decomposition into different orbit types, and this has to be taken into account before any further interpretation. For example, the iso-IMF contours are more elongated than the isophotes of the warm orbits in the outskirts of FCC 167 because at large radii the flux starts to be dominated by cold orbits. A more quantitative comparison between stellar population properties and orbital distributions will be presented in an upcoming F3D paper.
7. Summary and conclusions
We have shown that the spatially resolved stellar population properties of ETGs can be reliably measured through the high-quality MUSE-IFU data from the Fornax 3D project, combined with a novel approach that benefits from the advantages of both line-strength analysis and full-spectral fitting techniques. The analysis tools described in this work have allowed us to measure the 2D stellar population property maps of the massive S0/a galaxy FCC 167.
The chemical properties (i.e., metallicity and [Mg/Fe]) show a clear disk-like structure, associated with the cold orbital component of FCC 167. IMF variations roughly follow the radial metallicity variation, in agreement with previous studies, but with a clearly distinct spatial distribution. Iso-IMF contours are much rounder than iso-metallicity contours, and seem to follow the distribution of hot and warm orbits in this galaxy. These results suggest that metallicity cannot be the only driver of the observed IMF variations in ETGs.
The comparison between the orbital decomposition and the stellar population properties provides a physically meaningful framework that captures the underlying IMF and metallicity variations in FCC 167 better than a standard photometric decomposition. Our analysis describes a scenario where the IMF was set during the early formation of the stars with relatively warm orbits. The formation of the cold orbital component took place during a more extended period of time, leading to metal-rich and [Mg/Fe]-poor stellar populations. We argue that the time difference between the assembly of these two components is too short to be measured in old stellar populations. The chemical properties of ETGs, regulated by the ejecta of massive stars, would therefore be a finer timer than SSP-equivalent ages. Finally, the hot orbital component of FCC 167 appears to be decoupled from the stellar population properties, suggesting that the bulge probably formed through a stellar heating process. The orbit-based analysis therefore appears as a probe that provides insight into the relation between galaxy structure and the emergence of the stellar population properties, and it will be explored in a upcoming work (Martín-Navarro et al., in prep.).
With the complex IMF variations shown by this object, understanding the stellar population properties of ETGs in the IFU era requires a deep change in both our modeling and our analysis of this type of galaxies. Well-known scaling relations supporting our picture of galaxy formation and evolution might be partially biased by the lack of spatial resolution. Moreover, the stellar population properties and the IMF in these objects have likely evolved over time (e.g., Weidner et al. 2013; De Masi et al. 2019; Fontanot et al. 2018), and at z ∼ 0, we only see an integrated snapshot of their lives. The assumption of SSP-like stellar populations in ETGs is starting to break down under the pressure of wider and deeper spectroscopic data, and the ongoing projects within the F3D project will contribute to this change of paradigm (e.g., Pinna et al. 2019). In an upcoming paper, we will present and discuss the IMF variations for the whole sample of F3D galaxies, covering a wide range in masses and star formation conditions.
La Barbera et al. (2013) also included in their error budget uncertainties on the treatment of abundance patterns and the emission correction on Balmer lines.
Acknowledgments
We would like to thank Bronwyn Reichardt Chu for her useful comments and for the fruitful discussions, and also the referee for a careful and efficient revision of the manuscript. IMN, JFB, and FP acknowledge support from the AYA2016-77237-C3-1-P grant from the Spanish Ministry of Economy and Competitiveness (MINECO). IMN acknowledges support from the Marie Skłodowska-Curie Individual SPanD Fellowship 702607. GvdV acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 724857 (Consolidator Grant ArcheoDyn). E.M.C. acknowledges financial support from Padua University through grants DOR1699945/16, DOR1715817/17, DOR1885254/18, and BIRD164402/16. FP acknowledges Fundación La Caixa for the financial support received in the form of a post-doc contract.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Alton, P. D., Smith, R. J., & Lucey, J. R. 2018, MNRAS, 478, 4464 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Auger, M. W., Treu, T., Gavazzi, R., et al. 2010, ApJ, 721, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 773508 [CrossRef] [Google Scholar]
- Barber, C., Crain, R. A., & Schaye, J. 2018, MNRAS, 479, 5448 [NASA ADS] [Google Scholar]
- Barber, C., Schaye, J., & Crain, R. A. 2019, MNRAS, 483, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Sheth, R. K., Fischer, J.-L., et al. 2018, MNRAS, 475, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, ApJ, 694, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D., Faber, S. M., Gaskell, C. M., & Krumm, N. 1984, ApJ, 287, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2012, Nature, 484, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Cardiel, N., Gorgas, J., et al. 2001, MNRAS, 326, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Hennebelle, P., & Charlot, S. 2014, ApJ, 796, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Clauwens, B., Schaye, J., & Franx, M. 2016, MNRAS, 462, 2832 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & van Dokkum, P. G. 2012a, ApJ, 760, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & van Dokkum, P. 2012b, ApJ, 747, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Gunn, J. E., & White, M. 2009, ApJ, 699, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Graves, G. J., & van Dokkum, P. G. 2014, ApJ, 780, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., van Dokkum, P. G., & Villaume, A. 2017, ApJ, 837, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Villaume, A., van Dokkum, P. G., & Lind, K. 2018, ApJ, 854, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Corsini, E. M., Wegner, G. A., Thomas, J., Saglia, R. P., & Bender, R. 2017, MNRAS, 466, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R. S., et al. 2014, Rev. Mod. Phys., 86, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., & McDermid, R. M. 2017, MNRAS, 464, 453 [NASA ADS] [CrossRef] [Google Scholar]
- de La Rosa, I. G., La Barbera, F., Ferreras, I., & de Carvalho, R. R. 2011, MNRAS, 418, L74 [NASA ADS] [CrossRef] [Google Scholar]
- De Masi, C., Vincenzo, F., Matteucci, F., et al. 2019, MNRAS, 483, 2217 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Gregg, M. D., & Colless, M. 2001, ApJ, 548, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., Mendel, J. T., & Simard, L. 2012, MNRAS, 422, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Monnet, G., & Bacon, R. 1994, A&A, 285, 723 [NASA ADS] [Google Scholar]
- Erwin, P. 2015, ApJ, 799, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, H. C. 1989, AJ, 98, 367 [Google Scholar]
- Fernández-Alvar, E., Tissera, P. B., Carigi, L., et al. 2019, MNRAS, 485, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Ferré-Mateu, A., Vazdekis, A., & de la Rosa, I. G. 2013, MNRAS, 431, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., La Barbera, F., de la Rosa, I. G., et al. 2013, MNRAS, 429, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Weidner, C., Vazdekis, A., & La Barbera, F. 2015, MNRAS, 448, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., La Barbera, F., De Lucia, G., Pasquali, A., & Vazdekis, A. 2018, MNRAS, 479, 5678 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrison-Kimmel, S., Hopkins, P. F., Wetzel, A., et al. 2018, MNRAS, 481, 4133 [NASA ADS] [CrossRef] [Google Scholar]
- Grand, R. J. J., Springel, V., Gómez, F. A., et al. 2016, MNRAS, 459, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Gutcke, T. A., & Springel, V. 2019, MNRAS, 482, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, C. R., Majewski, S. R., Shetrone, M., et al. 2018, ApJ, 852, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Iodice, E., Spavone, M., Capaccioli, M., et al. 2019, A&A, 623, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jerabkova, T., Zonoozi, A. H., Kroupa, P., et al. 2019, A&A, 620, A39 [Google Scholar]
- Johansson, J., Thomas, D., & Maraston, C. 2012, MNRAS, 421, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgensen, U. G. 1994, A&A, 284, 179 [NASA ADS] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuntschner, H., Emsellem, E., Bacon, R., et al. 2010, MNRAS, 408, 97 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Ferreras, I., Vazdekis, A., et al. 2013, MNRAS, 433, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Pasquali, A., Ferreras, I., et al. 2014, MNRAS, 445, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Ferreras, I., & Vazdekis, A. 2015, MNRAS, 449, L137 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Vazdekis, A., Ferreras, I., et al. 2016, MNRAS, 457, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Läsker, R., van den Bosch, R. C. E., van de Ven, G., et al. 2013, MNRAS, 434, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubenova, M., Martín-Navarro, I., van de Ven, G., et al. 2016, MNRAS, 463, 3220 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I. 2016, MNRAS, 456, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., La Barbera, F., Vazdekis, A., Falcón-Barroso, J., & Ferreras, I. 2015a, MNRAS, 447, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., La Barbera, F., Vazdekis, A., et al. 2015b, MNRAS, 451, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., Vazdekis, A., La Barbera, F., et al. 2015c, ApJ, 806, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., Pérez-González, P. G., Trujillo, I., et al. 2015d, ApJ, 798, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., Vazdekis, A., Falcón-Barroso, J., et al. 2018, MNRAS, 475, 3700 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, N. J., Lu, J. R., & Mann, A. W. 2016, ApJ, 821, 39 [NASA ADS] [CrossRef] [Google Scholar]
- McDermid, R. M., Alatalo, K., Blitz, L., et al. 2015, MNRAS, 448, 3484 [NASA ADS] [CrossRef] [Google Scholar]
- McGee, S. L., Goto, R., & Balogh, M. L. 2014, MNRAS, 438, 3188 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. D. C., Sansom, A. E., & Sánchez-Blázquez, P. 2011, MNRAS, 414, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, P. D., Lacey, C. G., Baugh, C. M., & Cole, S. 2013, MNRAS, 435, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Molaeinezhad, A., Falcón-Barroso, J., Martínez-Valpuesta, I., et al. 2017, MNRAS, 467, 353 [NASA ADS] [Google Scholar]
- Newman, A. B., Smith, R. J., Conroy, C., Villaume, A., & van Dokkum, P. 2017, ApJ, 845, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., Lançon, A., & Thiébaut, E. 2006, MNRAS, 365, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Oldham, L., & Auger, M. 2018, MNRAS, 474, 4169 [NASA ADS] [CrossRef] [Google Scholar]
- Parikh, T., Thomas, D., Maraston, C., et al. 2018, MNRAS, 477, 3954 [NASA ADS] [CrossRef] [Google Scholar]
- Philcox, O., Rybizki, J., & Gutcke, T. A. 2018, ApJ, 861, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Pinna, F., Falcón-Barroso, J., Martig, M., et al. 2019, A&A, 623, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Ocvirk, P., Gibson, B. K., Pérez, I., & Peletier, R. F. 2011, MNRAS, 415, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Spiniello, C., La Barbera, F., Krajnović, D., & van den Bosch, R. 2018a, MNRAS, 478, 4084 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Iodice, E., Coccato, L., et al. 2018b, A&A, 616, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schiavon, R. P. 2007, ApJS, 171, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Serven, J., Worthey, G., & Briley, M. M. 2005, ApJ, 627, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J. 2014, MNRAS, 443, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., & Lucey, J. R. 2013, MNRAS, 434, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., & Carter, D. 2012, MNRAS, 426, 2994 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Trager, S. C., Koopmans, L. V. E., & Chen, Y. P. 2012, ApJ, 753, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Trager, S., Koopmans, L. V. E., & Conroy, C. 2014, MNRAS, 438, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Trager, S. C., & Koopmans, L. V. E. 2015, ApJ, 803, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Sybilska, A., Lisker, T., Kuntschner, H., et al. 2017, MNRAS, 470, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, B., & Worthey, G. 2017, MNRAS, 467, 674 [NASA ADS] [Google Scholar]
- Thomas, D., Greggio, L., & Bender, R. 1999, MNRAS, 302, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., & Bender, R. 2003, MNRAS, 339, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2011, MNRAS, 415, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Romanowsky, A. J., & Napolitano, N. R. 2013, ApJ, 765, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., La Barbera, F., Napolitano, N. R., et al. 2014, MNRAS, 445, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Treu, T., Auger, M. W., Koopmans, L. V. E., et al. 2010, ApJ, 709, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E., van de Ven, G., Verolme, E. K., Cappellari, M., & de Zeeuw, P. T. 2008, MNRAS, 385, 647 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2010, Nature, 468, 940 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P., Conroy, C., Villaume, A., Brodie, J., & Romanowsky, A. J. 2017, ApJ, 841, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Vargas, L. C., Gilbert, K. M., Geha, M., et al. 2014, ApJ, 797, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S. P., Davies, R. L., Zieleniewski, S., & Houghton, R. C. W. 2018a, MNRAS, 479, 2443 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S. P., Davies, R. L., Zieleniewski, S., & Houghton, R. C. W. 2018b, MNRAS, 475, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Vazdekis, A., Coelho, P., Cassisi, S., et al. 2015, MNRAS, 449, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Viaene, S., Sarzi, M., Zabel, N., et al. 2019, A&A, 622, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villaume, A., Brodie, J., Conroy, C., Romanowsky, A. J., & van Dokkum, P. 2017, ApJ, 850, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Wegner, G. A., Corsini, E. M., Thomas, J., et al. 2012, AJ, 144, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Ferreras, I., Vazdekis, A., & La Barbera, F. 2013, MNRAS, 435, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Weilbacher, P. M., Streicher, O., & Palsa, R. 2016, Astrophysics Source Code Library [record ascl:1610.004] [Google Scholar]
- Wilkinson, D. M., Maraston, C., Goddard, D., Thomas, D., & Parikh, T. 2017, MNRAS, 472, 4297 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., & Gonzalez, J. J. 1992, ApJ, 398, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., van den Bosch, R., van de Ven, G., et al. 2018a, MNRAS, 473, 3000 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., van de Ven, G., Méndez-Abreu, J., & Obreja, A. 2018b, MNRAS, 479, 945 [Google Scholar]
- Zieleniewski, S., Houghton, R. C. W., Thatte, N., Davies, R. L., & Vaughan, S. P. 2017, MNRAS, 465, 192 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Full-index-fitting (FIF) approach. Top panels: Mgb 5177 (left) and the TiO2 (right) spectral features, normalized using the index pseudo-continua (blue shaded regions). In the FIF approach, every pixel within the central bandpass (gray area) is fit to measure the stellar population parameters. The black line corresponds to a model of solar metallicity [M/H] = 0, [Mg/Fe] = 0, [Ti/Fe] = 0, and Kroupa-like IMF, at a resolution of 200 km s−1. The FIF approach breaks the degeneracies more efficiently than the standard line-strength analysis because every pixel responds differently to changes in the stellar population properties. Colors in the bottom panels show the relative change in the spectrum after different stellar population parameters were varied. For reference, the IMF slope was varied by ΔΓB = 1, the metallicity and abundance ratios by 0.2 dex, and the age by 2 Gyr. |
| In the text | |
 |
Fig. 2. Best-fitting stellar population properties. Posterior distributions for one of the spatial bins of FCC 167 showing that our FIF approach is able to recover the stellar population properties with high precision, breaking the degeneracies among them. Vertical red lines indicate the best-fitting value (solid line) and the 1σ uncertainty (dashed lines). These values are quoted on top of the posterior distributions. The luminosity-weighted age of this bin is 12.7 Gyr. |
| In the text | |
 |
Fig. 3. From top to bottom: metallicity, [Mg/Fe], and IMF (ξ) scaling relations with galaxy velocity dispersion. The recovered trends agree with expectations from previous studies. In particular, the measured IMF-σ relation is remarkably close to the results of La Barbera et al. (2013) and Spiniello et al. (2014) (gray and orange shaded regions in the bottom panel, respectively), even though they relied on different model assumptions. |
| In the text | |
 |
Fig. 4. Stellar population maps of FCC 167. Top left panel: age map, as measured from pPXF, where a relatively older central component is clearly visible. The metallicity (top right) and the [Mg/Fe] (bottom left) maps show the clear signature of a chemically evolved disk, confined within a vertical height of ∼10 arcsec, which coincides with the kinematically cold component observed in this galaxy (Sarzi et al. 2018b). The IMF map on the bottom right exhibits a different 2D structure, however, that does not follow the metallicity variations, but closely follows the hot+warm orbits of this galaxy (Sarzi et al. 2018b). |
| In the text | |
 |
Fig. 5. IMF–metallicity relation. The individual bins of FCC 167 are shown color-coded by their distance to the center of the galaxy, compared with the empirical relation of Martín-Navarro et al. (2015c), shown as an blue dashed line. This relation agrees with the FCC 167 measurements in the central regions of the galaxy (top right corner), but it does not hold for the outskirts, where an additional parameter is needed to explain the observed variations in the IMF. The ξ ratio of the Milky Way (Kroupa 2001) is shown as a gray dashed line. |
| In the text | |
 |
Fig. 6. Iso-metallicity vs. iso-IMF contours. The surface brightness map of FCC 167 is shown as measured from the F3D data cube, with the iso-metallicity (solid lines) and iso-IMF contours (dashed lines) overplotted. As in Fig. 4, this figure shows that the 2D IMF map does not exactly follow the metallicity variations. IMF variations appear more closely related to the surface brightness distribution, in particular, around the central bulge. The metallicity distribution, in contrast, is structured in a more disk-like configuration. |
| In the text | |
 |
Fig. 7. Internal structure vs. stellar population maps. The top panels show the comparison between metallicity and photometric disk (top left) and IMF and bulge (top right). Neither the disk nor the bulge seem to follow the structure of the stellar population maps. The three bottom panels compare the orbital decomposition of FCC 167 with the stellar population properties. On the left, the agreement between the metallicity structure (white solid lines) and the spatial distribution of the cold orbits indicates that the chemically evolved (metal-rich and [Mg/Fe]-poor) structure observed in the stellar population maps corresponds to a cold stellar disk with an extended star formation history. IMF contours (white dashed lines), on the other hand, closely follow the distribution of warm orbits (right). Hot orbits, in contrast, are decoupled from the stellar population properties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



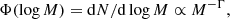
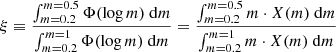
![$$ \begin{aligned} \ln (\mathbf{O} \, | \, \mathbf{S} ) = -\frac{1}{2} \mathop {\sum }_n \bigg [ \frac{({O}_n - {M}_n)^2}{\sigma _n^2}-\ln \frac{1}{\sigma _n^2}\bigg ] , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35360-19/aa35360-19-eq4.gif)