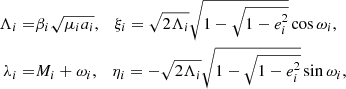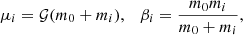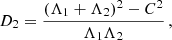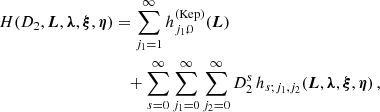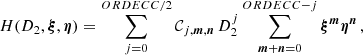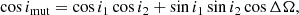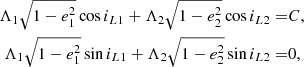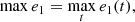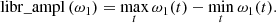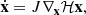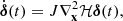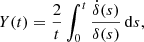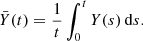| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201834896 | |
| Published online | 14 June 2019 | |
The 3D secular dynamics of radial-velocity-detected planetary systems
NaXys, Department of Mathematics, University of Namur, Rempart de la Vierge 8, 5000 Namur, Belgium
e-mail: mara.volpi@unamur.be
Received:
17
December
2018
Accepted:
26
April
2019
Aims. To date, more than 600 multi-planetary systems have been discovered. Due to the limitations of the detection methods, our knowledge of the systems is usually far from complete. In particular, for planetary systems discovered with the radial velocity (RV) technique, the inclinations of the orbital planes, and thus the mutual inclinations and planetary masses, are unknown. Our work aims to constrain the spatial configuration of several RV-detected extrasolar systems that are not in a mean-motion resonance.
Methods. Through an analytical study based on a first-order secular Hamiltonian expansion and numerical explorations performed with a chaos detector, we identified ranges of values for the orbital inclinations and the mutual inclinations, which ensure the long-term stability of the system. Our results were validated by comparison with n-body simulations, showing the accuracy of our analytical approach up to high mutual inclinations (∼70 ° −80°).
Results. We find that, given the current estimations for the parameters of the selected systems, long-term regular evolution of the spatial configurations is observed, for all the systems, (i) at low mutual inclinations (typically less than 35°) and (ii) at higher mutual inclinations, preferentially if the system is in a Lidov-Kozai resonance. Indeed, a rapid destabilisation of highly mutually inclined orbits is commonly observed, due to the significant chaos that develops around the stability islands of the Lidov-Kozai resonance. The extent of the Lidov-Kozai resonant region is discussed for ten planetary systems (HD 11506, HD 12661, HD 134987, HD 142, HD 154857, HD 164922, HD 169830, HD 207832, HD 4732, and HD 74156).
Key words: celestial mechanics / planets and satellites: dynamical evolution and stability / methods: analytical / planetary systems
© ESO 2019
1. Introduction
The number of detected multi-planetary systems continually increases. Despite the rising number of discoveries, our knowledge of the physical and orbital parameters of the systems is still partial due to the limitations of the observational techniques. Nevertheless, it is important to acquire a deeper knowledge of the detected extrasolar systems, in particular a more accurate understanding of the architecture of the systems. Regarding the two-planet systems detected via the radial velocity (RV) method, we have fairly precise data about the planetary mass ratio, the semi-major axes, and the eccentricities. However, we have no information either on the orbital inclinations i (i.e. the angles the planetary orbits form with the plane of the sky) – which means that only minimal planetary masses can be inferred – or on the mutual inclination between the planetary orbital planes imut. This raises questions about possible three-dimensional (3D) configurations of the detected planetary systems. Let us note that a relevant clue to the possible existence of 3D systems has been provided for υ Andromedae c and d, whose mutual inclination between the orbital planes is estimated to be 30° (Deitrick et al. 2015).
A few studies on the dynamics of extrasolar systems have been devoted to the 3D problem. Analytical works by Michtchenko et al. (2006); Libert & Henrard (2007), and Libert & Henrard (2008) investigated the secular evolution of 3D exosystems that are not in a mean-motion resonance. They showed that mutually inclined planetary systems can be long-term stable. In particular, these works focused on the analysis of the equilibria of the 3D planetary three-body problem, showing the generation of stable Lidov-Kozai (LK) equilibria (Lidov 1962; Kozai 1962) through bifurcation from a central equilibrium, which itself becomes unstable at high mutual inclination. Thus, around the stability islands of the LK resonance, which offers a secular phase-protection mechanism and ensures the stability of the system, chaotic motion of the planets occurs, limiting the possible 3D configurations of planetary systems.
Using n-body simulations, Libert & Tsiganis (2009) investigated the possibility that five extrasolar two-planet systems, namely υ Andromedae, HD 12661, HD 169830, HD 74156, and HD 155358, are actually in a LK-resonant state for mutual inclinations in the range [40°, 60°]. They showed that the physical and orbital parameters of four of the systems are consistent with a LK-type orbital motion, at some specific values of the mutual inclination, while around 30%−50% of the simulations generally lead to chaotic motion. The work also suggests that the extent of the LK-resonant region varies significantly for each planetary system considered.
Extensive long-term n-body integrations of five hierarchical multi-planetary systems (HD 11964, HD 38529, HD 108874, HD 168443, and HD 190360) were performed by Veras & Ford (2010). They showed a wide variety of dynamical behaviour when assuming different inclinations of the orbital plane with respect to the line of sight and mutual inclinations between the orbital planes. They often reported LK oscillations for stable highly inclined systems.
In Dawson & Chiang (2014), the authors presented evidence that several eccentric warm Jupiters discovered with eccentric giant companions are highly mutually inclined (i.e. with a mutual inclination in the range [35 ° ,65 ° ]). For instance, this is the case of the HD 169830 and HD 74156 systems, which will also be discussed in the present work.
Recently, Volpi et al. (2018) used a reverse KAM method (Kolmogorov 1954; Arnol’d 1963; Moser 1962) to estimate the mutual inclinations of several low-eccentric RV-detected extrasolar systems (HD 141399, HD 143761, and HD 40307). This analytical work addressed the long-term stability of planetary systems in a KAM sense, requiring that the algorithm constructing KAM invariant tori is convergent. This demanding condition leads to upper values of the mutual inclinations of the systems close to ∼15°.
In the spirit of Libert & Tsiganis (2009), the aim of the present work is to determine the possible 3D architectures of RV-detected systems by identifying ranges of values for the mutual inclinations that ensure the long-term stability of the systems. Particular attention will be given to the possibility of the detected extrasolar systems being in a LK-resonant state, since it offers a secular phase-protection mechanism for mutually inclined systems, even though the two orbits may suffer large variations both in eccentricity and inclination. Indeed, the variations occur in a coherent way, such that close approaches do not occur and the system remains stable.
To reduce the number of unknown parameters to take into account, we use an analytical approach, expanding the Hamiltonian of the three-body problem in power series of the eccentricities and inclinations. Being interested in the long-term stability of the system, we consider its secular evolution, averaging the Hamiltonian over the fast angles. Thanks to the adoption of the Laplace plane, we can further reduce the expansion to two degrees of freedom. It was shown in previous works (see for example Libert & Henrard 2007; Libert & Sansottera 2013) that if the planetary system is far from a mean-motion resonance, the secular approximation at the first order in the masses is accurate enough to describe the evolution of the system. Such an analytical approach is of interest for the present purpose, since, being faster than pure n-body simulations which also consider small-period effects, it allows us to perform an extensive parametric exploration at a reasonable computational cost. Moreover, in the present work we will show that the analytical expansion is highly reliable, fulfilling its task up to high values of the mutual inclination.
The goal of the present work is twofold. On the one hand, we study the 3D secular dynamics of ten RV-detected extrasolar systems, identifying for each one the values in the parameter space (imut, i) that induce a LK-resonant behaviour of the system. On the other hand, through numerical explorations performed with a chaos detector, we identify the ranges of values for which a long-term stability of the orbits is observed, unveiling for each system the extent of the chaotic region around the LK stability islands.
The paper is organised as follows. In Sect. 2, we describe the analytical secular approximation and discuss its accuracy to study the 3D dynamics of planetary systems in Sect. 3, as well as the methodology of our parametric study. The question of possible 3D configurations of RV-detected planetary systems is addressed in Sect. 4. Our results are finally summarised in Sect. 5.
2. Analytical secular approximation
We focus on the three-body problem of two exoplanets revolving around a central star. The indexes 0, 1, and 2 refer to the star, the inner planet, and the outer planet, respectively. Since the total angular momentum vector C is an integral of motion of the problem, we adopt as a reference plane the constant plane orthogonal to C, the so-called Laplace plane. In this plane, the Hamiltonian formulation of the problem no longer depends on the two angles Ω1 and Ω2, but only on their constant difference Ω1 − Ω2 = π. Thus, thanks to the reduction of the nodes, the problem is reduced to four degrees of freedom. We adopt the Poincaré variables,
where a, e, ω, and M refer to the semi-major axis, eccentricity, argument of the pericenter, and mean anomaly, respectively, and with
for i = 1, 2 . Moreover, we consider the parameter D2 (as defined in Robutel 1995)
which measures the difference between the actual norm of the total angular momentum vector C and the one the system would have if the orbits were circular and coplanar (by definition, D2 is quadratic in eccentricities and inclinations).
We introduce the translation 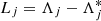 , where
, where 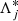 is the value of Λj for the observed semi-major axis aj, for j = 1, 2. We then expand the Hamiltonian in power series of the variables L, ξ, η, and the parameter D2 and in Fourier series of λ, as in Volpi et al. (2018),
is the value of Λj for the observed semi-major axis aj, for j = 1, 2. We then expand the Hamiltonian in power series of the variables L, ξ, η, and the parameter D2 and in Fourier series of λ, as in Volpi et al. (2018),
where
-
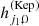 is a homogeneous polynomial function of degree j1 in L;
is a homogeneous polynomial function of degree j1 in L; -
hs; j1, j2 is a homogeneous polynomial function of degree j1 in L, degree j2 in ξ and η, and with coefficients that are trigonometric polynomials in λ.
As we are interested in the secular evolution of the system, the Hamiltonian can be averaged over the fast angles,
where ORDECC indicates the maximal order in eccentricities considered, here fixed to 12. When the system is far from a mean-motion resonance, such an analytical approach at first order in the masses is accurate enough to describe the secular evolution of extrasolar systems (see for example Libert & Sansottera 2013). The Hamiltonian formulation Eq. (5) has only two degrees of freedom, with the semi-major axes being constant in the secular approach.
3. Parametric study
In the following, we describe the parametric study carried out in the present work. The selection of the systems considered here is described in Sect. 3.1, and the accuracy of the analytical expansion for the secular evolution of the selected systems is discussed in Sect. 3.2.
3.1. Methodology
The present work aims to identify the possible 3D architectures of RV-detected extrasolar systems. From the online database exoplanets.eu, we selected all the two-planet systems that fulfil the following criteria: (a) the period of the inner planet is longer than 45 days (no tidal effects induced by the star); (b) the semi-major axis of the outer planet is smaller than 10 AU (systems with significant planet–planet interactions); (c) the system is not close to a mean-motion resonance; (d) the planetary eccentricities are lower than 0.65; (e) the masses of the planets are smaller than 10 MJ. The orbital parameters of the ten selected systems are listed in Table 1, as well as the reference from which they have been derived.
Orbital parameters of the selected systems.
In this work, the secular evolutions of the systems are considered when varying the mutual inclination imut and the orbital plane inclination i with respect to the plane of the sky. It is important to note that, although the inclinations i1 and i2 of the two orbital planes may differ, we decided here to set the same value i for both planes. Thus both masses are varied using the same scaling factor sini.
In the general reference frame, the following relation holds:
being ΔΩ = Ω1 − Ω2. It should be noted that Eq. (6) can be solved if imut ≤ 2i, thus for a given value of i it determines boundaries for the compatible values of imut. Since i1 = i2 = i, having fixed the values of imut, we can determine the value of the longitudes of the nodes by setting Ω1 = ΔΩ and Ω2 = 0, thus obtaining the complete set of initial conditions. A consequent change of coordinates to the Laplace plane is finally performed by using the following relations valid in the Laplace plane:
where iL1 and iL2 denote the orbital inclinations in the Laplace-plane reference frame.
For our parametric study, we varied the value of the mutual inclination imut from 0° to 80° with an increasing step of 0.5°, while the common orbital plane inclination i runs from 5° to 90° with an increasing step of 5°. As the coefficients 𝒞j, m, n in Eq. (5) depend on L, and therefore on the masses of the planets, we recomputed them for each value of i. Regarding the integration of the secular approach, we fixed the integration time to 106 yr with an integration step of 1 yr, and the energy preservation was monitored along the integration.
3.2. Accuracy of the analytical approach
Before discussing the results of our parametric study, we need to ensure that the Hamiltonian formulation, Eq. (5), provides an accurate description of the planetary dynamics for all sets of parameters considered in the study, in particular for high values of the mutual inclination imut. As already shown in previous papers (e.g. Libert & Henrard 2005 for the coplanar problem, Libert & Henrard 2007 for the 3D problem), the series of the secular terms converge better than the full perturbation. However, the higher the value of D2, the weaker the convergence, as expected. In the following, we discuss the numerical convergence of the expansion for the selected extrasolar systems, also called convergence au sens des astronomes, as opposed to the mathematical convergence (Poincaré 1893).
Table 2 lists, for the ten systems, the contributions to the Hamiltonian value of the terms from order 2 to order 12 in eccentricities and inclinations (i.e. j + m + n in Eq. (5)). The entries are the sums of the terms appearing at a given order, computed at the orbital parameters given in Table 1 and at i = 50° and imut = 50°, in order to evaluate the convergence au sens des astronomes at high mutual inclination. The numerical convergence of the expansion at high mutual inclination is obvious for most of the systems. However, when the decrease of the terms is less marked, we should keep in mind that results at higher mutual inclinations should be analysed with caution. Moreover, the last column of Table 1 gives an estimation of the remainder of the truncated expansion. It shows the relative error between the secular Hamiltonian computed by numerical quadrature and our polynomial formulation Eq. (5), confirming the previous observations.
Convergence au sens des astronomes for the ten systems.
To further illustrate the accuracy of our analytical approach, we show in Fig. 1 the evolutions of HD 12661 given by the analytical expansion Eq. (5) (red curves) for the mutual inclinations imut = 20°, 40°, 50°, and 80° (i is fixed to 50°), and compare them to the evolutions obtained by the numerical integration of the three-body problem with the SWIFT package (Levison & Duncan 1994, blue curves). Although the numerical convergence observed in Table 2 is not excellent for HD 12661, the agreement of the analytical approach with the numerical integration of the full problem is very good. The dynamical evolutions are well reproduced up to high values of the mutual inclination (imut = 20°, 40°, 50°). Only small differences in the periods are observed and can be attributed to the short-period terms not considered in our secular formulation. For very high values (imut = 80°), the dynamical evolutions given by the two methods no longer coincide, but follow the same trend. As will be shown in Sect. 4.3, the orbits are generally chaotic at such high mutual inclinations.
 |
Fig. 1. Dynamical evolutions of HD 12661 system given by the analytical expansion (in red) and by n-body simulations (in blue), for imut = 20° (top left), 40° (top right), 50° (bottom left), and 80° (bottom right). The inclination of the orbital plane is fixed to i = 50°. |
4. Results
The question of the 3D secular dynamics of RV-detected planetary systems is addressed here in two directions. Firstly, we focus on identifying the inclination values for which a LK-resonant regime is observed in our parametric study. Secondly, the long-term stability of the mutually inclined systems is unveiled by means of a chaos detector.
4.1. Extent of the Lidov-Kozai regions
Regarding the possible 3D configurations of extrasolar systems, we are particularly interested in the LK resonance. This protective mechanism ensures that the system remains stable, despite large eccentricity and inclination variations. It is characterised, in the Laplace-plane reference frame, by the coupled variation of the eccentricity and the inclination of the inner planet, and the libration of the argument of the pericenter of the same planet around ±90° (Lidov 1962; Kozai 1962).
As a first example, we investigate the dynamics of the HD 12661 extrasolar system. In the left panel of Fig. 2, we show, for varying (imut, i) values, the maximal eccentricity of the inner planet reached during the dynamical evolution of the system,
 |
Fig. 2. Long-term evolution of HD 12661 system when varying the mutual inclination imut (x-axis) and the inclination of the orbital plane i (y-axis), both expressed in degrees. Left panel: maximal eccentricity of the inner planet, as defined by Eq. (8). Right panel: libration amplitude of the argument of the pericenter ω1 (in degrees), as defined by Eq. (9). The three highlighted points are related to the representative planes shown in Fig. 3. |
being e1(t) the eccentricity of the inner planet at time t. Let us note that this quantity is often used to determine the regularity of planetary orbits, since for low (e < 0.2) and high (e > 0.8) eccentricity values it is generally found to be in good agreement with chaos indicators (see for instance Funk et al. 2011). On the right panel, we report, for all the considered (imut, i) values, the libration amplitude of the angle ω1, defined as
This value will serve as a guide for the detection of the LK-resonant behaviour characterised by the libration of ω1, and thus by a small value of libr_ampl (ω1).
When following an horizontal line in Fig. 2, the mutual inclination imut varies while the orbital inclination i, and thus the planetary masses, are kept fixed. On the other hand, the inclination of the common orbital plane decreases when moving down along a vertical line, while the planetary masses increase accordingly. As previously stated, this implies the recomputation of the coefficients 𝒞j, m, n of Eq. (5). Let us recall that all (imut, i) pairs cannot be considered here since, for fixed i1 = i2 = i values, Eq. (6) cannot be solved for all the mutual inclinations.
We see that the eccentricity variations of 3D configurations of HD 12661 are small1 for low mutual inclinations (blue in the left panel of Fig. 2) and become large for high mutual inclinations (red). Additionally, the argument of the pericenter ω1 circulates for low imut values (light blue in the right panel of Fig. 2) and librates for high imut values (dark blue). Thus, for high mutual inclinations, the system is in a LK-resonant state.
To visualise the different dynamics, we draw, for a given D2 value, the level curves of the Hamiltonian Eq. (5) in the representative plane (e1sinω1, e2sinω2) where both pericenter arguments are fixed to ±90° (see Libert & Henrard 2007 for more details on the representative plane). This plane is neither a phase portrait nor a surface of section, since the problem is four dimensional. However, nearly all the orbits will cross the representative plane at several points of intersection on the same energy curve. Figure 3 shows the representative planes of HD 12661 for imut = 20° (i.e. D2 = 0.35, left panel), 40° (i.e. D2 = 0.67, middle panel), and 50° (i.e. D2 = 0.90, right panel), the inclination of the orbital plane being fixed to 50°. These three system configurations are also indicated with white crosses in Fig. 2 and their dynamical evolutions are those presented in Fig. 1.
 |
Fig. 3. Representative plane for HD 12661 system, having fixed the inclination of the orbital plane to i = 50°, for imut = 20° (left panel), imut = 40° (middle panel), and imut = 50° (right panel). The level curve of Hamiltonian relative to the orbital parameters of HD 12661 is highlighted in red. The crosses indicate the intersections of the orbit with the representative plane. |
For low values of imut, circular orbits (e1 = e2 = 0) constitute a point of stable equilibrium (left panel of Fig. 3). As we increase the mutual inclination (central and right panels of Fig. 3), the central equilibrium becomes unstable and bifurcates into the two stable LK equilibria. The red crosses represent the intersections of the evolution of the mutually inclined HD 12661 system with the representative plane. For low mutual inclinations, the crosses are located on both sides of the representative plane, so the argument of the inner pericenter circulates. For imut = 50° (right panel of Fig. 3), the crosses are inside the LK island in the left side of the representative plane, associated with the libration of ω1 around 270° (as can also be observed in the bottom left dynamical evolution shown in Fig. 1). We see that the corresponding white cross on the right side of Fig. 2 is likewise located inside the dark blue region of the LK resonance.
The critical value of the mutual inclination, which corresponds to the change of stability of the central equilibrium, depends on the mass and semi-major axis ratios (see e.g. Libert & Henrard 2007) and is typically around 40 ° −45° for mass ratios between 0.5 and 2. For increasing mutual inclinations, the stable LK equilibria reach higher inner eccentricity values and the orbit of the considered system possibly crosses the representative plane inside a LK island. Therefore, the dark blue LK region in Fig. 2 starts around 40 ° −55°, the exact value for the change of dynamics depending on the inclination of the orbital plane since the expansion (Eq. 5) depends on the inclination i via the planetary mass.
Let us note that, even if the numerical convergence of the analytical expansion of the HD 12661 system is not excellent (see Table 2), the LK-resonant region perfectly matches the one obtained with n-body simulations additionally performed for validation, except at very high mutual inclinations (imut ≥ 70°). Indeed, for the HD 12661 and HD 74156 systems, a destabilisation of the orbits is observed at very high mutual inclinations and slightly reduces the stable LK region.
A second example is shown in Fig. 4 for the HD 11506 system. The LK region is now located at smaller mutual inclinations, making visible the right border of the LK region. For each i value, the interval of mutual inclinations associated with the libration of the angle ω1 begins at ∼40°, whereas its amplitude depends on i. No spatial configuration of HD 11506 can be found in a LK-resonant state for a mutual inclination higher than 65°.
Let us note that some additional dark blue points can be observed for low values of the inclinations of the orbital plane i. These systems are close to the separatrix of the LK resonance and will be destabilised on a longer timescale, as will be shown in the next section.
In Fig. 5 we display the libration amplitude of the argument of the pericenter of the inner planet for the ten systems considered here. All the graphs do show a LK region. In other words, all the selected RV-detected systems, when considered with a significant mutual inclination, have physical and orbital parameters compatible with a LK-resonant state. Table 3 summarises information on the extent of the LK region for each system. The second and third columns display the minimum values of the mutual inclination imut (with an accuracy of 1°) and the orbital inclination i, respectively, for which a libration of the argument of the pericenter ω1 is observed. The percentage of initial conditions inside the (dark blue) LK region is given in the fourth column. The last column reports the percentage of chaos in the whole set of initial conditions and will be discussed in Sect. 4.3.
 |
Fig. 5. Libration amplitude of ω1 for the ten systems considered here, when varying the mutual inclination imut (x-axis) and the inclination of the orbital plane i (y-axis). |
Extent of the LK region for the ten systems.
4.2. Sensitivity to observational uncertainties
So far, we have considered the nominal values of the orbital parameters given by the observations. However, due to the limitations of the detection techniques, observational data come with relevant uncertainties, and to explore the influence of such uncertainties on the previous results is relevant. As typical examples, we show in Fig. 6 the extent of the LK region for the HD 12661 and HD 142 systems, when considering extremal orbital parameters within the confidence regions given by the observations, instead of the best-fit parameter values. The errors on each orbital parameter are listed in Table 1 for both planetary systems. Two extremal cases are examined in the following, where the minimal/maximal values are adopted for all the parameters simultaneously.
 |
Fig. 6. Libration amplitude of ω1, as in Fig. 5, for the HD 12661 (top) and HD 142 (bottom) systems, when considering the minimal values (left), the nominal values (middle), and the maximal values (right) of the orbital parameters. |
In the case of the HD 12661 system, the location and extent of the LK region are very similar when adopting the minimal values (top left panel of Fig. 6), the nominal values (top middle), and the maximal values (top right) of the orbital parameters. Concerning HD 142, the situation is quite different. We observe, in the bottom panels of Fig. 6, a significant variation of the LK region in its extent and shape, probably due to the greater size of the observational errors on the different orbital elements.
As a result, the location and extent of the LK resonance regions are sensitive to observational uncertainties in the orbital elements, especially when they are significant, and this should be taken into account in detailed studies of the selected systems. Nevertheless, we stress that, when considering extremal values within the confidence regions, the dynamics remains qualitatively the same, with the existence of stable LK islands at high mutual inclinations for both systems.
4.3. Stability of planetary systems
In this section, we aim to determine if the LK-resonant state of a 3D planetary system is essential to ensure its long-term stability. To do so, we have used the Mean Exponential Growth factor of Nearby Orbits (MEGNO) chaos indicator, briefly described in the following (for an extensive discussion on the properties of the MEGNO, see Cincotta & Simo 2000; Maffione et al. 2011).
Let H(p, q) with p, q ∈ ℝN be an autonomous Hamiltonian of N degrees of freedom. The Hamiltonian vector field can be expressed as
where 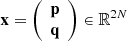 and J =
and J = 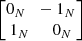 , being 1N and 0N the unitary and null N × N matrices, respectively. In order to apply the MEGNO chaos indicator, we need to compute the evolution of deviation vectors δ(t). These vectors satisfy the variational equations
, being 1N and 0N the unitary and null N × N matrices, respectively. In order to apply the MEGNO chaos indicator, we need to compute the evolution of deviation vectors δ(t). These vectors satisfy the variational equations
being 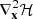 the Hessian matrix of the Hamiltonian. As in Cincotta & Simo (2000), the Mean Exponential Growth Factor is defined as
the Hessian matrix of the Hamiltonian. As in Cincotta & Simo (2000), the Mean Exponential Growth Factor is defined as
where δ(s) is the Euclidean norm of δ(s). We consider here the mean MEGNO, that is, the time-averaged MEGNO,
The limit for t → ∞ provides a good characterisation of the orbits. The MEGNO chaos indicator is particularly convenient since we have:
-
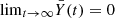 for stable periodic orbits,
for stable periodic orbits, -
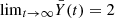 for quasi-periodic orbits and for orbits close to stable periodic ones,
for quasi-periodic orbits and for orbits close to stable periodic ones, -
for irregular orbits,
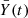 diverges with time.
diverges with time.
For each set of initial conditions we choose the initial deviation vector δ(0) as a random unitary vector. We then study its evolution along the orbit and compute the corresponding evolution of the mean MEGNO. Two main factors have motivated the choice of this chaos indicator. First, it requires the study of the evolution of only one deviation vector, saving valuable computational time. Second, it returns an absolute value, as it classifies each orbit independently.
As previously noted, the LK-resonant state is surrounded by a chaotic zone associated with the bifurcation of the central equilibrium at null eccentricities. Therefore, a chaos indicator can be useful to highlight the extent of the chaotic zone and identify with precision the (imut, i) values ensuring the regularity of the orbits for a long time.
On the left panel of Fig. 7, we show the values of the mean MEGNO for HD 11506 computed with our analytical approach. We can appreciate how the region at high inclinations characterised as regular by the mean MEGNO (purple) clearly superimposes with the LK-resonant region identified in Fig 4. The surrounding chaotic region displayed in yellow extends up to high mutual inclinations, showing that highly mutually inclined configurations of the HD 11506 system can only be expected in a LK-resonant state. Regarding low mutual inclinations, nearly all spatial configurations present regular motion up to a mutual inclination of ∼35°, where the LK resonance comes into play.
 |
Fig. 7. Mean MEGNO values for the HD 11506 system given by our analytical approach (left panel) and n-body simulations (right panel). |
A comparison with n-body simulations (short-period effects included) is given in the right panel of Fig. 7, where numerical integrations have been carried out with SWIFT (for every 1° instead of 0.5° to reduce the computational cost). The two panels look very similar, showing that our secular approach is reliable for systems that are far from a mean-motion resonance.
Similar observations can be made for the ten extrasolar systems considered here. In Fig. 8, the chaotic region associated to a mean MEGNO value greater than eight with our analytical approach, is indicated in white on the plot showing the libration amplitude of ω1 (Fig. 5). Also, more information on the extent of the chaotic zone for each system can be found in the last column of Table 3. The chaotic region around the stable LK islands is broad for half of the systems (HD 11506, HD 12661, HD 169830, HD 207832, and HD 4732), moderate for the HD 142, HD 15487, and HD 74156 systems, and not significant for the HD 134987 and HD 164922 systems, given the integration timescale and the grid of initial conditions considered. For the first category of systems, long-term regular evolutions of the orbits are only possible for low mutual inclinations and, for higher mutual inclinations, in the LK region, while in the two other cases regular evolutions are also observed at high mutual inclinations outside the LK regions.
 |
Fig. 8. Same as Fig. 5, where the initial system parameters leading to chaotic motion (defined by the mean MEGNO value greater than 8) are coloured in white (above the black curve). |
5. Conclusions
In this work, we studied the possibility for ten RV-detected exoplanetary systems to be in a 3D configuration. Using a secular Hamiltonian approximation (expansion in eccentricities and inclinations), we studied the secular dynamics of possible 3D planetary configurations of the systems. In particular, we determined ranges of orbital and mutual inclinations for which the system is in a LK-resonant state. Our results were compared with n-body simulations, showing the accuracy of the analytical approach up to very high inclinations (∼70 ° −80°). We showed that all the systems considered here might be in a LK-resonant state for a sufficiently mutually inclined orbit. By means of the MEGNO chaos indicator, we revealed the extent of the chaotic zone surrounding the stability islands of the LK resonance. Long-term regular evolutions of the orbits are possible (i) at low mutual inclinations and (ii) at high mutual inclinations, preferentially in the LK region, due to the significant extent of the chaotic zone in many systems.
It should be stressed that the present work excludes systems whose inner planet is close to the star. For those systems, relativistic effects have to be considered and we leave for future work how their inclusion will influence the extent of the LK region.
Acknowledgments
The authors thank the anonymous referee for her or his critical review of the first version of the manuscript and useful suggestions. M.V. acknowledges financial support from the FRIA fellowship (F.R.S.-FNRS). The work of A.R. is supported by a F.R.S.-FNRS research fellowship. Computational resources have been provided by the PTCI (Consortium des Équipements de Calcul Intensif CECI), funded by the FNRS-FRFC, the Walloon Region, and the University of Namur (Conventions No. 2.5020.11, GEQ U.G006.15, 1610468 et RW/GEQ2016).
References
- Arnol’d, V. I. 1963, Russ. Math. Surv., 18, 9 [Google Scholar]
- Cincotta, P. M., & Simo, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Chiang, E. 2014, Science, 346, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Deitrick, R., Barnes, R., McArthur, B., et al. 2015, ApJ, 798, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, Y. K., Wright, J. T., Nelson, B., et al. 2015, ApJ, 800, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Howard, A. W., Weiss, L. M., et al. 2016, ApJ, 830, 46 [NASA ADS] [Google Scholar]
- Funk, B., Libert, A.-S., Süli, Á., & Pilat-Lohinger, E. 2011, A&A, 526, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haghighipour, N., Butler, R. P., Rivera, E. J., Henry, G. W., & Vogt, S. S. 2012, ApJ, 756, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, H. R. A., Butler, R. P., Tinney, C. G., et al. 2010, MNRAS, 403, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. N. 1954, Dokl. Akad. Nauk SSSR, 98, 527 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2005, Celest. Mech. Dyn. Astron., 93, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2007, Icarus, 191, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2008, Celest. Mech. Dyn. Astron., 100, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Sansottera, M. 2013, Celest. Mech. Dyn. Astron., 117, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Tsiganis, K. 2009, A&A, 493, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Maffione, N. P., Giordano, C. M., & Cincotta, P. M. 2011, Int. J. Non-Linear Mech., 46, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Naef, D., et al. 2004, A&A, 415, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michtchenko, T. A., Ferraz-Mello, S., & Beaugé, C. 2006, Icarus, 181, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Moser, J. 1962, Matematika, 6, 51 [Google Scholar]
- Poincaré, H. 1893, Les méthodes nouvelles de la mécanique céleste: Méthodes de MM. Newcomb, Glydén, Lindstedt et Bohlin (Gauthier-Villars et fils) [Google Scholar]
- Robutel, P. 1995, Celest. Mech. Dyn. Astron., 62, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Omiya, M., Wittenmyer, R. A., et al. 2013, ApJ, 762, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., & Kotiranta, S. 2009, A&A, 496, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veras, D., & Ford, E. B. 2010, ApJ, 715, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Volpi, M., Locatelli, U., & Sansottera, M. 2018, Celest. Mech. Dyn. Astron., 130, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Horner, J., Tuomi, M., et al. 2012, ApJ, 753, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Horner, J., Tinney, C. G., et al. 2014, ApJ, 783, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Upadhyay, S., Marcy, G. W., et al. 2009, ApJ, 693, 1084 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Dynamical evolutions of HD 12661 system given by the analytical expansion (in red) and by n-body simulations (in blue), for imut = 20° (top left), 40° (top right), 50° (bottom left), and 80° (bottom right). The inclination of the orbital plane is fixed to i = 50°. |
| In the text | |
 |
Fig. 2. Long-term evolution of HD 12661 system when varying the mutual inclination imut (x-axis) and the inclination of the orbital plane i (y-axis), both expressed in degrees. Left panel: maximal eccentricity of the inner planet, as defined by Eq. (8). Right panel: libration amplitude of the argument of the pericenter ω1 (in degrees), as defined by Eq. (9). The three highlighted points are related to the representative planes shown in Fig. 3. |
| In the text | |
 |
Fig. 3. Representative plane for HD 12661 system, having fixed the inclination of the orbital plane to i = 50°, for imut = 20° (left panel), imut = 40° (middle panel), and imut = 50° (right panel). The level curve of Hamiltonian relative to the orbital parameters of HD 12661 is highlighted in red. The crosses indicate the intersections of the orbit with the representative plane. |
| In the text | |
 |
Fig. 4. Same as Fig. 2 for HD 11506 system. |
| In the text | |
 |
Fig. 5. Libration amplitude of ω1 for the ten systems considered here, when varying the mutual inclination imut (x-axis) and the inclination of the orbital plane i (y-axis). |
| In the text | |
 |
Fig. 6. Libration amplitude of ω1, as in Fig. 5, for the HD 12661 (top) and HD 142 (bottom) systems, when considering the minimal values (left), the nominal values (middle), and the maximal values (right) of the orbital parameters. |
| In the text | |
 |
Fig. 7. Mean MEGNO values for the HD 11506 system given by our analytical approach (left panel) and n-body simulations (right panel). |
| In the text | |
 |
Fig. 8. Same as Fig. 5, where the initial system parameters leading to chaotic motion (defined by the mean MEGNO value greater than 8) are coloured in white (above the black curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.