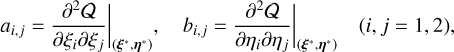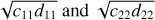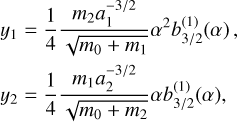| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A193 | |
| Number of page(s) | 12 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202346727 | |
| Published online | 20 March 2024 | |
The effects of general relativity on close-in radial-velocity-detected exosystems
1
Department of Mathematics of the University of Rome “Tor Vergata”,
00133
Rome,
Italy
e-mail: dr.maravolpi@gmail.com
2
naXys, Department of Mathematics, University of Namur,
Rue de Bruxelles 61,
5000
Namur,
Belgium
Received:
21
April
2023
Accepted:
8
January
2024
Aims. The detection of the first exoplanet around a solar-type star revealed the existence of close-in planets. Several of these close-in planets are part of multi-planet systems. For systems detected via the radial velocity (RV) method, we lack information on the mutual inclination of the orbital planes. The aim of this work is to study the long-term stability of RV-detected two-planet systems with close-in planets and identify possible three-dimensional configurations for these systems that are compatible with observations. To do so, we focused on the protective mechanism of the Lidov-Kozai (LK) secular resonance and studied the effects of general relativity (GR) on long-term evolution.
Methods. By means of an analytical study based on a high-order secular Hamiltonian expansion in the eccentricities and inclinations, we first identified ranges of values for the orbital and mutual inclinations that are compatible with the presence of the LK resonance in the purely gravitational case. Then, adding the secular contribution of the relativistic corrections exerted by the central star on the inner planet, namely the advance of its pericenter precession, we analysed the outcomes of the two sets of simulations. We compared our results to analytical estimates to determine the importance of GR effects.
Results. We find that for the majority of the systems considered, GR strongly affects the dynamics of the system and, most of the time, voids the LK resonance, as observed for GJ 649, GJ 832, HD 187123, HD 190360, HD 217107, and HD 47186. The long-term stability of these systems is then possible whatever the mutual inclination of the orbits. On the contrary, for GJ 682, HD 11964, HD 147018, and HD 9446, the LK resonant region in the parameter space of the orbital and mutual inclinations is left (almost) unchanged when GR effects are considered, and consequently their long-term stability is only possible if the mutual inclination of the orbits is low or if the systems are in the LK regime with a high mutual inclination.
Key words: celestial mechanics / planets and satellites: dynamical evolution and stability / planet-star interactions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
More than 5000 extrasolar planets have been observed so far, with hundreds of multi-planet systems listed in the catalogues. However, these discoveries alone do not provide us with a deeper knowledge of planetary systems. The current limitations of the detection techniques in particular hinder our complete understanding of the formation and evolution of planetary systems, as some of the orbital parameters are still unknown in the vast majority of cases. We have focused our study on systems detected via the radial velocity (RV) method. This detection method does not provide any information on the inclinations of a multi-planet system, since neither the orbital inclinations, i, of the planets (i.e. the inclination with respect to the line of sight) nor the mutual inclination, imut, between their orbital planes are determined. These unknowns entail uncertainties for the actual masses of the planets (for which only a minimal value can be inferred) and the potentially three-dimensional (3D) structure of the systems. There are a few rare cases in which inclinations were determined by combining different detection methods, and there is proof that exoplanetary systems can show a highly mutually inclined architecture. The most famous example is υ Andromedae, with a mutual inclination between the orbital planes of planets c and d of ~30º (McArthur et al. 2010). There are also Kepler-108, with its two giants that are mutually inclined by 24º (Mills & Fabrycky 2017), and K2 – 266b, with two different pairs, at imut = 12º and 15º (Rodriguez et al. 2018).
The dynamics of mutually inclined systems is strongly affected by the Lidov–Kozai (LK) resonance (von Zeipel 1909; Lidov 1962; Kozai 1962). This secular resonance can serve as a phase-protection mechanism for such systems, even though the eccentricity and inclination of both planetary orbits vary strongly. The LK resonance has been investigated for a wide variety of problems involving different mass ratios among the bodies (for instance, see the review by Libert 2022 on the LK resonance at different scales) and in the contexts of multi-planet systems (e.g. Michtchenko et al. 2006; Libert & Henrard 2007; Migaszewski & Goździewski 2009) and multi-star systems (e.g. Innanen et al. 1997; Naoz et al. 2013). In addition to being a phase-protection mechanism, its relevance for the formation of extrasolar systems has also been highlighted. In particular, the migration through LK cycles, combined with the tidal friction, has been widely invoked to explain the formation of hot Jupiters in binary star systems (e.g. Wu & Murray 2003; Fabrycky & Tremaine 2007; Naoz et al. 2012; Petrovich 2015; Anderson et al. 2016; Ngo et al. 2016; Vick et al. 2019), while alternative scenarios based on secular planet-planet interactions have also been put forward (e.g. Petrovich & Tremaine 2016).
In this work we focus on the long-term stability of RV-detected two-planet exosystems, in particular the stability of possible 3D configurations of these systems; we do not address the question of their formation. Following the preliminary investigations of Libert & Tsiganis (2009), Volpi et al. (2019) recently studied the dynamics of RV-detected two-planet systems by focusing on their long-term stability for different values in the parameter space (i, imut), in order to identify 3D system parametrisations compatible with the observations and thereby constrain the unknown system parameters. The stability of the systems was studied not only by means of a chaos indicator to identify the regular regions of the parameter space, but also by using an analytical model to identify the subsets of the parameter space that are influenced by the LK resonance. They find that all ten of the RV-detected exosystems considered in their work have orbital parameters compatible with the LK resonance (in particular the eccentricity values) when considering highly inclined system configurations. In particular, long-term regular evolutions were identified either at a low mutual inclination of the two planetary orbits or at high mutual inclination, preferentially for LK-resonant evolutions, due to the significant extent of chaos along the separatrix of the resonance for many systems.
However, the Volpi et al. (2019) study was limited to systems whose planets are distant enough from the central star that the action of general relativity (GR) could be disregarded without affecting the reliability of the results. In the present work, we aim to extend this previous study to RV-detected two-planet systems with close-in planets and place constraints on the orbital inclinations, i, and mutual inclination, imut, that would guarantee the long-term stability of these systems. A correct description of the evolution of the system must then include GR, whose major effect on the motion of the planet is the advance of the precession of its pericenter. Given that the LK resonance acts on the pericenter as well, it is relevant to study how these two phenomena compete over the long-term evolution of the two-planet systems. As in Volpi et al. (2019), we reduced the dimensions of the problem using an analytical approach. We considered a high-order Hamiltonian power series expansion in the eccentricities and inclinations, which is reduced to four degrees by adopting the Laplace invariant plane and accurately describes the secular dynamics of two-planet systems (Libert & Henrard 2007; Libert & Sansottera 2013; Volpi et al. 2019).
Several previous works have studied the effects of GR on extrasolar systems using different approaches and for different contexts. Veras & Ford (2010) carried out extensive long-term N-body integrations to explore the dynamics of five hierarchical two-planet systems (i.e. with small semi-major axis ratios) with close-in planets, studying the full range of possible line-of-sight and relative inclinations. They concluded that GR affects the dynamics of systems with high relative inclinations. However, unlike in analytical works, providing a general picture of the dynamics for the whole phase space is particularly tricky. By analytically expanding the perturbing Hamiltonian in the ratio of the semi-major axes, Migaszewski & Goździewski (2011) investigated the dynamics of hierarchical systems, such as cir-cumbinary planets, and showed that the dynamics is qualitatively different when considering GR. By using the same approximation but limited to the octupole level, Naoz et al. (2013) discussed how GR can suppress or excite the eccentricities in triple-star systems. More recently, employing linear secular theory, Marzari & Nagasawa (2020) showed that, for coplanar two-planet systems with a close-in planet, a significant damping of the eccentricities of the inner and outer planets occurs when GR is included, which implies that systems with a chaotic behaviour caused by mutual interactions between the planets could actually have a stable evolution thanks to GR effects.
We should remark that we do not consider here the tidal effects from the host star, which act on planets extremely close to the star (a ≲ 0.08 AU typically), for several reasons. Firstly, the computation of the tidal effects relies on parameters (such as the radius of the planet and the tidal Love number) that are currently not known for most of the RV-detected exoplanets. Secondly, with these parameters fixed to arbitrary values, previous works (e.g. Migaszewski & Goździewski 2009; Veras & Ford 2010) found that the tidal effects are generally negligible with respect to the relativistic corrections. Thirdly, the perturbation due to the dynamical flattening of the star and/or of the inner planet depends on the orbital inclination of the equatorial plane of the star (see e.g. Migaszewski & Goździewski 2009), which implies that the Laplace plane is no longer a constant reference plane and a new analytical approach to reduce the number of degrees of freedom is required.
The paper is organised as follows: in Sect. 2 we briefly describe the analytical secular model used here, as well as the properties of the LK resonance. In Sect. 3, we set the parametric study and the criteria for the selection of the RV-detected systems analysed here. An in-depth study of our results regarding the extent of the LK region for the selected systems is given in Sect. 4. We draw our conclusions in Sect. 5.
2 Analytical secular approximation
The analytical expansion used in this study is an extension of the secular approximation from Volpi et al. (2019), which is briefly described in Sect. 2.1. The inclusion of GR terms is detailed in Sect. 2.2. Finally, the LK resonance is presented in Sect. 2.3.
2.1 Secular expansion of the three-body problem
We studied the dynamics of a system formed by a central star (referred to by the index 0) and two planets (indexes 1 and 2 for the inner and outer planet, respectively) that are not close to a mean-motion resonance. As a reference plane, we chose the invariant Laplace plane, which is perpendicular to the constant total angular momentum of the system. This allowed us to perform the Jacobi reduction of the nodes (Jacobi 1842). In this plane, the Hamiltonian formulation of the problem no longer depends on the longitudes of the nodes Ω1 and Ω2, only on their constant difference: ΔΩ = Ω1 - Ω2 = π. The problem is then reduced to four degrees of freedom, and for a fixed total angular momentum, the inclinations can be expressed as functions of the eccentricities. We considered the four Poincaré variables,
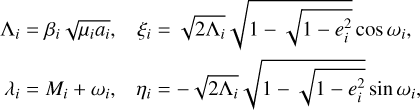 (1)
(1)
where a, e, ω, and M are the semi-major axis, eccentricity, argument of the pericenter, and mean anomaly, respectively, and having set
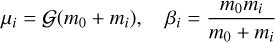 (2)
(2)
for i = 1,2. The parameter D2, defined in Robutel (1995) as
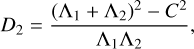 (3)
(3)
with C the norm of the total angular momentum of the system, is a variation of the angular momentum deficit (e.g. Laskar 1997) and is by definition quadratic in terms of eccentricities and inclinations.
We expanded the Hamiltonian of the three-body problem into power series of the variables L, ξ, and η and the parameter D2, and into Fourier series of λ, at first order in the masses. As our goal is to study the secular dynamics of the system, we averaged the Hamiltonian over the fast angles, λ, and obtained the following expression:
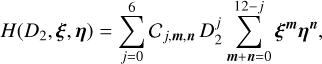 (4)
(4)
where we have fixed the maximal order in the eccentricities considered here to 12. We highlight that the Hamiltonian, Eq. (4), is expanded with respect to the eccentricities and inclinations, and not with respect to the semi-major axis ratio, α, as is the case for the quadrupole and octupole expressions1. As a result, this analytical approach is valid for a wide range of orbital separations between the two planets, not just for hierarchical planetary systems. Moreover, it has been shown that the secular evolution of extrasolar systems that are far from a mean-motion resonance is accurately described by this Hamiltonian approach (e.g. Libert & Henrard 2007; Libert & Sansottera 2013). A further validation for highly inclined system configurations is performed in Sect. 3. Within the two-degrees-of-freedom secular Hamiltonian formulation, Eq. (4), the semi-major axes of the two planets are constant throughout the evolution. We refer to Volpi et al. (2018, 2019) for more details.
2.2 GR correction
The main effect induced by GR on the planetary motion is an advance of the pericenter. It is common practice in the secular approximation framework to consider the effects of GR on the inner planet only (e.g. Naoz 2016) when studying the LK resonance, since the argument of the pericenter of the inner planet, ω1, is a critical angle for the LK resonance (see Sect. 2.3). As we focused on the long-term evolution of the system, we added to the purely gravitational three-body problem described by the Hamiltonian formulation, Eq. (4), the well-known expression of secular perturbation caused by GR on the pericenter of the inner planet after an averaging over the fast angles (e.g. Migaszewski & Goździewski 2009):
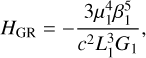 (5)
(5)
where c is the speed of light, and L1 = Λ1 and 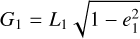 are the Delaunay variables. Since the coordinate relative to the conjugate momentum, G1, is the argument of the pericenter of the inner planet, ω2, it results in the following precession induced by GR on the inner planet:
are the Delaunay variables. Since the coordinate relative to the conjugate momentum, G1, is the argument of the pericenter of the inner planet, ω2, it results in the following precession induced by GR on the inner planet:
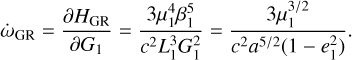 (6)
(6)
The secular Hamiltonian that includes the GR correction can be rewritten in the heliocentric Poincaré variables as:
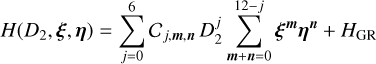 (7)
(7)
2.3 LK resonance
The LK resonance has been widely discussed since the discovery of exoplanets in eccentric orbits. This secular resonance acting on 3D configurations of planetary systems is a highly effective phase-protection mechanism that ensures their stability in the long term, even though both orbits can vary widely in terms of both eccentricity and inclination. As previously said, in the invariant Laplace plane reference frame, the planetary three-body problem averaged over the short periods can be reduced to two degrees of freedom. The main dynamical features depend on the location and stability of the equilibria of the problem. As shown by Libert & Henrard (2007), there exists an equilibrium at which both eccentricities are zero, which is stable for small mutual inclinations between the two orbital planes. However, for larger mutual inclinations, the equilibrium becomes unstable and induces a large chaotic zone around it, but also generates via bifurcation two new stable equilibria around which two regular regions exist, the so-called LK resonance regions. The LK resonance is identified by the coupled variation in the eccentricity and the inclination of the inner planet as well as the libration of the argument of the pericenter of the same planet around 90° or 270° (in the Laplace plane reference frame; see e.g. Libert & Tsiganis 2009). Additional details on the LK resonance can be found in the reviews by Naoz (2016) and Libert (2021).
The critical mutual inclination corresponding to the change in stability of the equilibrium at zero eccentricities (and thus the apparition of the LK equilibria) depends on the mass and semi-major axis ratios and is typically around 40°–45° for mass ratios between 0.5 and 2 (Libert & Henrard 2007). The linear stability of the central equilibrium can be studied by following the approach adopted in, for example, Henrard & Lemaître (2005) and Libert & Henrard (2007). Around an equilibrium point (ξ*, η*), the quadratic approximation of the Hamiltonian, Eqs. (4) or (7), can be written as
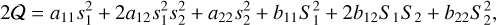 (9)
(9)
and (si, Si) are the increments relative to the variables (ξi, ηi). Applying the untangling transformation described in detail in Henrard & Lemaître (2005), we obtain a new formulation of the Hamiltonian, which can now be written as a linear combination of squares:
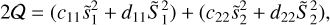 (11)
(11)
where 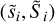 for i, j = 1,2 are the new variables. By studying the sign of the products ciidii, we can determine the linear stability: when it is positive, the corresponding degree of freedom is linearly stable; otherwise, it is linearly unstable. The linear frequencies can be easily computed when ciidii > 0 by introducing a new set of action-angle variables:
for i, j = 1,2 are the new variables. By studying the sign of the products ciidii, we can determine the linear stability: when it is positive, the corresponding degree of freedom is linearly stable; otherwise, it is linearly unstable. The linear frequencies can be easily computed when ciidii > 0 by introducing a new set of action-angle variables:
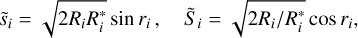 (12)
(12)
where 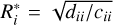 . We finally obtain the following simplified form of the Hamiltonian:
. We finally obtain the following simplified form of the Hamiltonian:
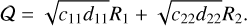 (13)
(13)
Thus, the evolution of the ratio between the two linear frequencies, 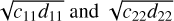 , associated with the equilibrium at zero eccentricities (also called central equilibrium), when increasing the value of the mutual inclination, provides the information needed about the change in stability of the central equilibrium.
, associated with the equilibrium at zero eccentricities (also called central equilibrium), when increasing the value of the mutual inclination, provides the information needed about the change in stability of the central equilibrium.
Orbital parameters of the selected systems.
3 Parametric study
In this section, we first present the criteria used to select the systems analysed in this work as well as the parametric study we carried out. A validation of the analytical approach is then performed.
3.1 Methodology
In order to select two-planet systems with close-in planets around a single star (no binary companion) investigated here, we used the following criteria: (a) the orbital period of the inner planet is shorter than 45 days (close-in inner planet), (b) the semi-major axis of the outer planet is smaller than 10 AU (systems with significant planet-planet interactions), (c) the system is not close to a mean-motion resonance, (d) the planetary eccentricities are less than 0.65, and (e) the masses of the planets are lower than 10 MJ. The first condition comes from the observation that, for the systems considered in Volpi et al. (2019; i.e. with inner orbital periods longer than 45 days), the GR effects do not influence the dynamics. All the two-planet systems referenced on exoplanet.eu that meet these criteria are listed in Table 1 along with their orbital parameters and references. As of today, 11 extrasolar systems fulfilling all the criteria have been reported.
For the parametric study, we used the same approach as in Volpi et al. (2019). We assumed that the two orbital planes are inclined by the same angle to the line of sight; therefore, i1 = i2 = i. We varied both the inclination, i, of the orbital planes and the mutual inclination between the orbital planes, imut, since these two quantities are unknown. We set the grid for the mutual inclination, imut, to range from 0° to 80° in steps of 0.5° and for the orbital inclination, i, from 5° to 90° in steps of 5°. These variations affect other quantities. Firstly, as the observed planetary mass is m sin i, for each value of i considered, we had to change the mass accordingly by multiplying it by a factor of 1 / sin i. Secondly, in the general reference frame, the following relation holds,
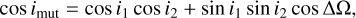 (14)
(14)
and it determines boundaries for the compatible values of imut for a given value of i, namely imut ≤ 2i. Having fixed the values of i and imut, we used Eq. (14) to determine the values of the longitudes of the nodes by setting Ω1 = ΔΩ and Ω2 = 0. By doing so, we obtained the complete set of initial conditions, all the other parameters being fixed to their observational values. We finally performed a change of coordinates to the Laplace plane by using the following relations:
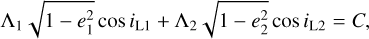 (15)
(15)
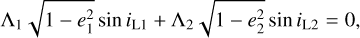 (16)
(16)
where iL1 and iL2 denote the orbital inclinations in the Laplace plane reference frame.
Concerning the parameters relative to the numerical integration, the fact that some of the selected systems have planets whose orbital periods are only a few days has to be taken into account. The time step must therefore be chosen such that we can perform integrations that correctly reproduce the dynamics. In order to achieve an optimal balance between precision and computational cost, we set the time step as either 20 times the orbital period of the inner planet or 1 yr, whichever was shorter. We fixed the integration time to 106 yr. On one hand, said integration time is long enough to evaluate the preservation of the energy and, if any, the libration of the angle ω1. On the other, it does not demand a high computational cost: this is a crucial factor, considering the extent of the parametric study we propose. We chose a fourth-order Runge-Kutta integrator to integrate the Hamiltonian equations associated with Eq. (7).
Convergence au sens des astronomes for the 11 systems when considering (imut, i) = (50º, 50º).
3.2 Validation of the approach
To validate our analytical approach, we studied the convergence of the Hamiltonian, Eq. (4), for the selected systems. The goal was to ensure the accuracy of the analytical approximation, in particular for high mutual inclinations, imut. In Table 2, we show the convergence au sens des astronomes (i.e. the numerical convergence of the expansion, instead of the mathematical one) computed for i = imut = 50º (see Poincaré 1893; Libert & Henrard 2005). Having set the values for both inclinations, the parameter D2 can be evaluated and therefore the Hamiltonian takes the form
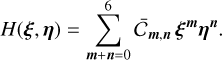 (17)
(17)
The quantities shown in Table 2 are defined as the contributions to the Hamiltonian value of the terms (in absolute values) from order 2-12 in eccentricities and inclinations. More precisely,
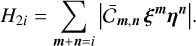 (18)
(18)
From the last column of Table 2, which shows the ratio between H12 and H2, we see that the numerical convergence of the expansion at high mutual inclinations is obvious for the majority of the systems. For cases that show a less clear decrease in the value of H2i, the results concerning higher mutual inclinations should be considered with caution.
4 Results
The goal of the present work is to study how GR affects the long-term evolution of systems that harbour close-in planets, in particular when considering 3D configurations of the systems. The influence of GR on the extent of the LK region is discussed in Sect. 4.1 for the 11 selected RV-detected systems with close-in planets, while analytical estimates for the importance of the GR effects in these systems are presented in Sect. 4.2.
4.1 Influence of GR on the extent of the LK region
First, we focus here on the evolution of two specific systems we chose as examples, as they depict the two main behaviours we have encountered. In Fig. 1, we show the results obtained for the HD 147018 system, whose orbital parameters are listed in Table 1. The top panels show the long-term evolution of the system for i = 50º and imut = 30º given by our analytical approach without and with relativistic corrections (left and right panels, respectively). Similarly, the bottom panels refer to the evolutions when i = 50º and imut = 50º. At low mutual inclination, namely imut = 30º, the argument of the pericenter of the inner planet, ω1, circulates (red curve); thus, the system, as expected, is not in a LK resonance. On the contrary, when imut = 50º, we observe the libration of ω1, as the system is in a LK-resonant state. When the relativistic corrections are considered (right panels), we do not observe any significant difference for HD 147018, neither concerning the LK resonance nor the general behaviour.
In the top panels of Fig. 2, we show, for the whole (imut, i) parameter space for which Eq. (14) can be solved, the maximal eccentricity of the inner planet, defined as
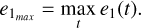 (19)
(19)
The bottom panels show instead the libration amplitude of the angle ω1, which we computed as
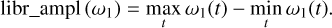 (20)
(20)
We note that the planetary masses are fixed along a horizontal line in Fig. 2 and increase when moving down along a vertical line, which means that the coefficients Cj,m,n of Eq. (7) have to be recomputed for each horizontal line. In the left panels, we show the results obtained with the purely gravitational formulation, Eq. (4). We remark the presence of a LK resonance region where the argument of pericenter, ω1, librates, appearing from imut ≃ 40° (dark blue in the bottom panel). On the right, we present the plots for which relativistic corrections are included in the Hamiltonian formulation, Eq. (7). It is straightforward to note that there is no significant difference between the two cases; in particular, the LK resonance region is unperturbed by the additional effect.
The negligible effect of GR for HD 147018 can also be observed when studying the linear stability of the central equilibrium point, as previously detailed in Sect. 2.3. In Fig. 3 (top panels), we show the evolution of the ratio of the linear frequencies 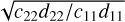 relative to the central equilibrium point, having fixed i = 50°. In the left panel, we display the results when taking only gravitational forces into account, and in the right panel when also including the relativistic corrections. This shows that the critical value of the mutual inclination (i.e. when the ratio changes sign, namely imut ≃ 40°) is not affected by the introduction of the relativistic effects.
relative to the central equilibrium point, having fixed i = 50°. In the left panel, we display the results when taking only gravitational forces into account, and in the right panel when also including the relativistic corrections. This shows that the critical value of the mutual inclination (i.e. when the ratio changes sign, namely imut ≃ 40°) is not affected by the introduction of the relativistic effects.
We now focus on the GJ 649 system, whose orbital parameters are listed in Table 1. In Fig. 4 we show the long-term evolution of the system for i = 50° and imut = 30° (top panels) and i = 50° and imut = 50° (bottom panels). Again, in the left panels, we show the results obtained considering only gravitational interactions, and in the right panels those related to the model that also includes the relativistic corrections. Unlike the previous case, the differences between the left and right plots are obvious. For imut = 30° (top panels), we observe a drastic change in the secular period of the evolution: for example, the secular period of the eccentricity of the inner planet decreases from ~1.1 × 105 yr down to ~1.5 × 104 yr. Moreover, we see that the eccentricity excitation of the inner planet is reduced with the GR contribution (see e.g. Migaszewski & Goździewski 2009; Sansottera et al. 2014; Marzari & Nagasawa 2020). For imut = 50° (bottom panels), we note an additional consequence: the libration of the angle ω1 (bottom left) vanishes when considering relativistic corrections (bottom right). The introduction of GR has therefore inhibited the LK resonance. Moreover, we observe effects of GR on the eccentricity of the outer planet as well. In Fig. 5, we focus on the evolution of e2 when considering the purely gravitational model (red line) and when including GR (blue line), for imut = 30° (left panel) and imut = 50° (rightpanel). An important variation decrease is observed when introducing the GR corrections (as previously observed in e.g. Marzari & Nagasawa 2020).
The effects of GR are even clearer when we plot the maximal eccentricity of the inner planet and the libration amplitude of ω1 for the whole (imut, i) parameter space (Fig. 6). In the top-right panel, we see a stabilising effect for high mutual inclinations: the maximal eccentricity of the inner planet is much closer to the initial value (e1 = 0.2) since the excitation is damped by GR. The LK resonance region vanishes when GR effects are included: all the initial conditions show the circulation of the angle ω1 (bottom-right panel).
This can also be observed when studying the linear stability of the central equilibrium point. In Fig. 3 (bottom panels), we show the evolution of the ratio of the linear frequencies 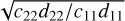 , associated with i = 50°, without considering the GR effects (left panel) and when including the relativistic corrections (right panel). In the last case, we observe no change in the linear stability of the central equilibrium around imut = 40°, but the destabilisation, if any, would take place at a very high mutual inclination. This explains why no LK resonance region is observed in the bottom-right panel of Fig. 6.
, associated with i = 50°, without considering the GR effects (left panel) and when including the relativistic corrections (right panel). In the last case, we observe no change in the linear stability of the central equilibrium around imut = 40°, but the destabilisation, if any, would take place at a very high mutual inclination. This explains why no LK resonance region is observed in the bottom-right panel of Fig. 6.
In Figs. 7 and 8, we present the results for the 11 systems with close-in planets considered here, namely the maximal eccentricity and the libration amplitude of the argument of the pericenter for the inner planet, respectively, in the purely gravitational case. In Figs. 9 and 10, we display the corresponding results when taking the relativistic corrections into account. We observe that many systems experience a damping of the excitation of the inner eccentricity at high mutual inclinations, similar to the one observed for GJ 649. This is in line with the results obtained by Veras & Ford (2010), who show that the inclusion of GR in the simulations flattens the evolution of the eccentricities. Our results show that this flattening corresponds to the disappearance of the LK resonance region. As can be observed from Fig. 10, the LK region remains in place for only four systems when the relativistic effects are considered. It should be noted that the systems HD 187123, HD 217107, and HD 47186 present, in the purely gravitational case, extremely long secular periods (see Sect. 4.2). This explains the strange shape of their LK resonance region in Fig. 8, whose actual extent could be revealed by integrations over a longer time span.
 |
Fig. 1 Dynamical evolution of the HD 147018 system. In the left panels, the evolution is given by the secular Hamiltonian, Eq. (4), and in the right panels by the Hamiltonian that includes relativistic corrections, Eq. (7). The inclination of the orbital plane is fixed to i = 50° and the mutual inclination between the planets to imut = 30° (top panels) and 50° (bottom panels). |
 |
Fig. 2 Long-term evolution of the HD 147018 system when varying the mutual inclination, imut (x-axis) and the inclination of the orbital plane, i (y-axis), both expressed in degrees. Top panels: maximal eccentricity of the inner planet, as defined by Eq. (19), without (left) and with (right) relativistic corrections. Bottom panels: libration amplitude of the argument of the pericenter, ω1 (in degrees), as defined by Eq. (20), without (left) and with (right) relativistic corrections. |
 |
Fig. 3 Evolution of the ratio of the linear frequencies |
 |
Fig. 5 Evolution of the eccentricity of the outer planet of GJ 649 for ί = 50°, with and without relativistic effects. Left panel: imut = 30°. Right panel: imut = 50°. |
4.2 Analytical estimates for the importance of the GR effects
As highlighted in the previous section, the relevance of GR in the dynamics of the selected systems varies from case to case. We were therefore interested in evaluating the relative contributions of the different effects acting on the pericenter of the inner planet. To investigate the importance of the GR effects on the inner planet, we computed two different ratios of the precession rates, following Veras & Ford (2010), namely 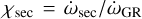 and
and 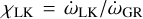 , with
, with 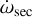 the pericenter precession induced by the outer planet and
the pericenter precession induced by the outer planet and 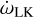 the one corresponding to the LK oscillations.
the one corresponding to the LK oscillations.
The expression of the pericenter precession due to GR was previously derived in Eq. (5). The precession caused by the secular interaction of the inner planet with the outer planet can be derived using the Laplace-Lagrange secular theory (approximation to the second order in the eccentricities) and can be written as (e.g. Zhou & Sun 2003)
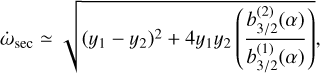 (21)
(21)
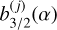 are the Laplace coefficients, and α = a1/a2 is the semi-major axis ratio.
are the Laplace coefficients, and α = a1/a2 is the semi-major axis ratio.
The ratio of these two precession rates,
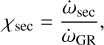 (23)
(23)
gives us an estimation of the importance of GR for the long-term evolution of the system. The smaller the value of χsec, the more relevant the GR effects. In Table 3 (third column), we list the values of χsec for the 11 exosystems considered with i=90○.The result shown in Figs. 7–10, are perfectly coherent with the values of χsec. All the systems for which χsec ≪ 1 are clearly affected by the introduction of the relativistic corrections, namely GJ 649, GJ 832, HD 187123, HD 190360, HD 217107, and HD 47186. This is particularly visible in Fig. 9, where the maximal eccentricity of the inner planet in these systems stays almost constant at a low level for all imut values. The importance of the GR corrections for the GJ 649 system is also apparent in Fig. 4. For all the other systems, the influence of the relativistic effects are more limited. No variation in the long-term evolution is reported when χsec ≫ 1, as previously shown in Fig. 1 for the HD 147018 system.
Regarding the highly mutually inclined systems, we can also estimate the influence of the relativistic effects on the LK resonance. The period of the LK oscillations is given by (Kiseleva etal. 1998)
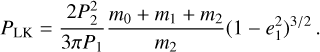 (24)
(24)
Consequently, the ratio of the two precession rates can be written as
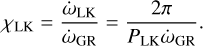 (25)
(25)
The smaller the value of χLK, the more relevant the effects of GR on the long-term evolution. Table 3 (fourth column) reports the values of χLK for the different systems. The systems for which the LK region is clearly maintained in Fig. 10, namely GJ 682, HD 11964, HD 147018, and HD 9446, correspond well to the higher values of χLK in Table 3.
It should be noted that both χsec and χLK depend on the masses of the three bodies. Therefore, they should be computed for each value of the orbital plane inclination, i, as its variation determines a change in the masses of the planets as well. In Table 3, we list the precession ratios corresponding to different i values for GJ 649, which is highly influenced by GR, and HD 147018, which is not significantly affected by GR. We see that the change in the precession ratios is small, and for the two systems considered here, we observe that the balance between the effects is independent of the value of the inclination of the orbital plane.
 |
Fig. 7 Maximal eccentricity of the inner planet of the 11 systems listed in Table 1 when no relativistic corrections are taken into account. |
 |
Fig. 8 Libration amplitude of ω1 for the 11 systems listed in Table 1 when no relativistic corrections are taken into account. |
Values of χsec,χLK, and PLĸ for the 11 selected systems.
5 Conclusions
We have studied the possibility that 11 RV-detected exoplanetary systems with close-in planets have a stable evolution in a 3D configuration. Given the proximity to the host star, we considered the relativistic corrections for the innermost planet and determined how the GR effects influence the purely gravitational evolution. To do so, we adopted an analytical approach in a Hamiltonian formalism, where a term for the GR effects on the pericenter was added to the classical expansion in the eccentricities and inclinations. We find that most of the considered systems show LK resonance regions when we only take the gravitational interactions between the bodies into account, in line with the results obtained in previous studies (see Libert & Tsiganis 2009; Volpi et al. 2019). However, in the majority of the cases, since the LK resonance and GR both act on the evolution of the argument of the pericenter of the inner planet, the LK resonance region disappears as we introduce the relativistic corrections. These observations are in agreement with analytical estimates for the pericenter precession ratios, highlighting the validity of our secular Hamiltonian approach.
Thanks to this study, we can now address the question of the possible architectures of RV-detected exosystems with close-in planets. Our study indicates that there are two categories of systems. On the one hand, the long-term stability of the GJ 649, GJ 832, HD 187123, HD 190360, HD 217107, and HD 47186 systems is possible whatever the mutual inclination of the two planetary orbits, since GR strongly affects the dynamical evolution of the planets and dominates over the LK resonance. On the other hand, the GJ 682, HD 11964, HD 147018, and HD 9446 exosystems are not compatible with all the mutual inclinations between the two orbital planes, only either at a low mutual inclination of the orbits or in the LK regime at high mutual inclination. This is due to the rapid destabilisation of highly mutually inclined orbits resulting from the significant chaos that develops around the stability islands of the LK resonance (see Volpi et al. 2019, for more details). The analytical estimates described in this work can easily be used to determine which category a given system belongs to.
This work is open to future developments. Firstly, a careful study of the stability of the systems by means of a chaos indicator would be complementary to the present study. It would provide a more complete panoramic view of the stability of the systems and precisely identify all the initial conditions that guarantee long-term stability. Secondly, taking tidal effects into account, which we have not done here, would provide a more precise description of the dynamics of the systems. However, as previously noted, this is not straightforward and is beyond the scope of this work.
Acknowledgements
M.V. acknowledges financial support from the FRIA fellowship (F.R.S.-FNRS). The work of A.-S.L. is supported by the Fonds de la Recherche Scientifique – FNRS under Grant No. F.4523.20 (DYNAMITE MIS-project). Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under Grant No. 2.5020.11.
References
- Anderson, K. R., Storch, N. I., & Lai, D. 2016, MNRAS, 456, 3671 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Mayor, M., Lovis, C., et al. 2009, A&A, 496, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Henrard, J., & Lemaître, A. 2005, AJ, 130, 2415 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, M. L., Mocnik, T., Kane, S. R., et al. 2020, AJ, 159, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Innanen, K. A., Zheng, J. Q., Mikkola, S., & Valtonen, M. J. 1997, AJ, 113, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobi, M. 1842, Astron. Nachr., 20, 81 [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Laskar, J. 1997, A&A, 317, L75 [NASA ADS] [Google Scholar]
- Libert, A.-S. 2021, Proc. Int. Astron. Union, 15, 52 [Google Scholar]
- Libert, A.-S. 2022, IAU Symp., 364, 52 [NASA ADS] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2005, Celest. Mech. Dyn. Astron., 93, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2007, Icarus, 191, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Sansottera, M. 2013, Celest. Mech. Dyn. Astron., 117, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Tsiganis, K. 2009, A&A, 493, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
- Marzari, F., & Nagasawa, M. 2020, MNRAS, 493, 427 [NASA ADS] [CrossRef] [Google Scholar]
- McArthur, B. E., Benedict, G. F., Barnes, R., et al. 2010, ApJ, 715, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Ferraz-Mello, S., & Beaugé, C. 2006, Icarus, 181, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Migaszewski, C., & Gozdziewski, K. 2009, MNRAS, 392, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Migaszewski, C., & Gozdziewski, K. 2011, MNRAS, 411, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, S. M., & Fabrycky, D. C. 2017, AJ, 153, 45 [Google Scholar]
- Moutou, C., Hébrard, G., Bouchy, F., et al. 2014, A&A, 563, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
- Naoz, S., Farr, W. M., & Rasio, F. A. 2012, ApJ, 754, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2013, MNRAS, 431, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- Ngo, H., Knutson, H. A., Hinkley, S., et al. 2016, ApJ, 827, 8 [Google Scholar]
- Petrovich, C. 2015, ApJ, 799, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovich, C., & Tremaine, S. 2016, ApJ, 829, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Poincaré, H. 1893, Les méthodes nouvelles de la mécanique céleste: Méthodes de MM. Newcomb, Glydén, Lindstedt et Bohlin (Gauthier-Villars et fils) [Google Scholar]
- Robutel, P. 1995, Celest. Mech. Dyn. Astron., 62, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J. E., Becker, J. C., Eastman, J. D., et al. 2018, AJ, 156, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Sansottera, M., Grassi, L., & Giorgilli, A. 2014, in Complex Planetary Systems, Proceedings of the International Astronomical Union, IAU Symp., 310, 74 [CrossRef] [Google Scholar]
- Ségransan, D., Udry, S., Mayor, M., et al. 2010, A&A, 511, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Jones, H. R. A., Barnes, J. R., Anglada-Escudé, G., & Jenkins, J. S. 2014, MNRAS, 441, 1545 [Google Scholar]
- Veras, D., & Ford, E. B. 2010, ApJ, 715, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vick, M., Lai, D., & Anderson, K. R. 2019, MNRAS, 484, 5645 [NASA ADS] [Google Scholar]
- Volpi, M., Locatelli, U., & Sansottera, M. 2018, Celest. Mech. Dyn. Astron., 130, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Volpi, M., Roisin, A., & Libert, A.-S. 2019, A&A, 626, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1909, Astron. Nachr., 183, 345 [Google Scholar]
- Wittenmyer, R. A., Wang, S., Horner, J., et al. 2013, ApJ, 208, 2 [NASA ADS] [Google Scholar]
- Wittenmyer, R. A., Tuomi, M., Butler, R. P., et al. 2014, ApJ, 791, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Upadhyay, S., Marcy, G. W., et al. 2009, ApJ, 693, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [Google Scholar]
- Zhou, J.-L., & Sun, Y.-S. 2003, ApJ, 598, 1290 [NASA ADS] [CrossRef] [Google Scholar]
The dependence on α in the Hamiltonian equation, Eq. (4), lies in the Laplace coefficients, which converge when α < 0.687.
All Tables
Convergence au sens des astronomes for the 11 systems when considering (imut, i) = (50º, 50º).
All Figures
 |
Fig. 1 Dynamical evolution of the HD 147018 system. In the left panels, the evolution is given by the secular Hamiltonian, Eq. (4), and in the right panels by the Hamiltonian that includes relativistic corrections, Eq. (7). The inclination of the orbital plane is fixed to i = 50° and the mutual inclination between the planets to imut = 30° (top panels) and 50° (bottom panels). |
| In the text | |
 |
Fig. 2 Long-term evolution of the HD 147018 system when varying the mutual inclination, imut (x-axis) and the inclination of the orbital plane, i (y-axis), both expressed in degrees. Top panels: maximal eccentricity of the inner planet, as defined by Eq. (19), without (left) and with (right) relativistic corrections. Bottom panels: libration amplitude of the argument of the pericenter, ω1 (in degrees), as defined by Eq. (20), without (left) and with (right) relativistic corrections. |
| In the text | |
 |
Fig. 3 Evolution of the ratio of the linear frequencies |
| In the text | |
 |
Fig. 4 Same as Fig. 1 but for the GJ 649 system. |
| In the text | |
 |
Fig. 5 Evolution of the eccentricity of the outer planet of GJ 649 for ί = 50°, with and without relativistic effects. Left panel: imut = 30°. Right panel: imut = 50°. |
| In the text | |
 |
Fig. 6 Same as Fig. 2 but for the GJ 649 system. |
| In the text | |
 |
Fig. 7 Maximal eccentricity of the inner planet of the 11 systems listed in Table 1 when no relativistic corrections are taken into account. |
| In the text | |
 |
Fig. 8 Libration amplitude of ω1 for the 11 systems listed in Table 1 when no relativistic corrections are taken into account. |
| In the text | |
 |
Fig. 9 Same as Fig. 7, but with relativistic corrections included. |
| In the text | |
 |
Fig. 10 Same as Fig. 8, but with relativistic corrections included. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${H_{{\rm{GR}}}} = - 3\mu _1^4\beta _1^5{\left[ {{c^2}\Lambda _1^3\left( {{\Lambda _1} - {{\xi _1^2 + \eta _1^2} \over 2}} \right)} \right]^{ - 1}}.$](/articles/aa/full_html/2024/03/aa46727-23/aa46727-23-eq9.png)