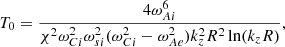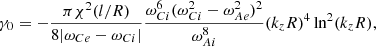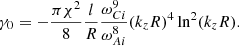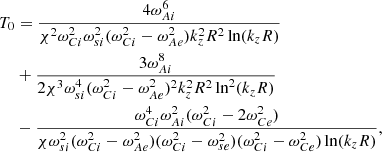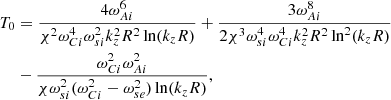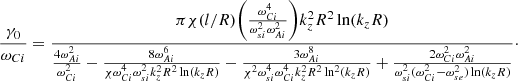| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | C2 | |
| Number of page(s) | 1 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201630355e | |
| Published online | 12 June 2019 | |
Resonant absorption of the slow sausage wave in the slow continuum (Corrigendum)
Centre for mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B bus 2400, 3001 Leuven, Belgium
Key words: magnetohydrodynamics (MHD) / Sun: photosphere / Sun: oscillations / errata, addenda
The derivation of the damping rate in the long wavelength limit by Yu et al. (2017) is incorrect. This was already noted independently by Sadeghi and Karami (2019) and by Roberts (2019, priv. comm.). What follows is the correct derivation. The sign of P0 (A.7) in Appendix A was incorrect. Equation (41) should read
and for Eq. (43)
where we have only retained the first term (see Eq. (C.1) below). Equations (44) and (45) should then read
These expressions for γ0 are the same as those obtained by Roberts (2019) by using a different approach.
Equations (C.1), (C.3), and (C.4) in Appendix C should read
and
 |
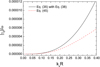Fig. 5. Damping rate |γ0|/ω versus kzR for slow sausage surface mode (ss) where l/R = 0.1. The other parameters are the same as in the previous figures. For the linear cusp velocity, we compared the analytical formula, Eq. (35), with the simplified formula in the long wavelength limit, Eq. (45). |
| Open with DEXTER | |
It should be noted that the values of the quantity |γ 0|/ω in Fig. 5 are small as can be understood from the equation for |γ 0|/ω for the values of k z R ≤ 0.4 used in Fig. 5.
We note also that eight in the second paragraph after Eq. (10) and 8 in the caption of Fig. 1 should read four.
Acknowledgments
We are grateful to B. Roberts for pointing out the error in our manuscript. Equations (41), (43)–(45), (A.7), (C.1), (C.3), and (C.4) were wrong in our paper.
References
- Yu, D. J., Van Doorsselaere, T., & Goossens, M. 2017, A&A 602, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadeghi, M. & Karami, K. 2019, ArXiv e-prints [arXiv:1903.04171] [Google Scholar]
© ESO 2019
All Figures
|
Fig. 5. Damping rate |γ0|/ω versus kzR for slow sausage surface mode (ss) where l/R = 0.1. The other parameters are the same as in the previous figures. For the linear cusp velocity, we compared the analytical formula, Eq. (35), with the simplified formula in the long wavelength limit, Eq. (45). |
| Open with DEXTER | |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.