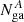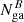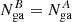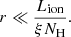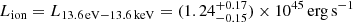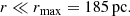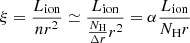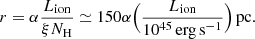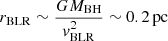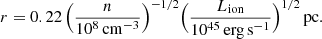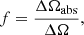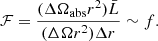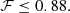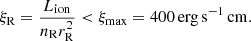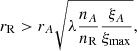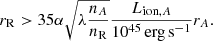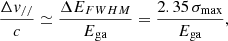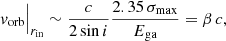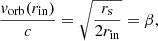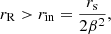| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935176 | |
| Published online | 03 May 2019 | |
X-ray analysis of the accreting supermassive black hole in the radio galaxy PKS 2251+11
1
Gran Sasso Science Institute (GSSI), Viale Francesco Crispi, 7, 67100 L’Aquila, AQ, Italy
e-mail: samuele.ronchini@gssi.it
2
Department of Physics, University of Rome “Tor Vergata”, Via della Ricerca Scientifica 1, 00133 Rome, Italy
3
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
4
NASA/Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA
5
INAF-Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monteporzio Catone, Italy
6
INAF-Istituto di Astrofisica e Planetologia Spaziali, via Fosso del Cavaliere 100, 00133 Roma, Italy
Received:
31
January
2019
Accepted:
13
March
2019
Context. We have investigated the dichotomy between jetted and non-jetted active galactic nuclei (AGNs), focusing on the fundamental differences of these two classes in the accretion physics onto the central supermassive black hole (SMBH). We tested the validity of the unification model of AGNs through the characterization of the mutual interaction between accreting and outflowing matter in radio galaxies.
Aims. Our aim is to study and constrain the structure, kinematics and physical state of the nuclear environment in the broad line radio galaxy (BLRG) PKS 2251+11. The high X-ray luminosity and the relative proximity make such AGN an ideal candidate for a detailed analysis of the accretion regions in radio galaxies. The investigation will help to shed light on the analogies and differences between the BLRGs and the larger class of radio-quiet Seyfert galaxies and hence on the processes that trigger the launch of a relativistic jet.
Methods. We performed a spectral and timing analysis of a ∼64 ks observation of PKS 2251+11 in the X-ray band with XMM-Newton. We modeled the spectrum considering an absorbed power law superimposed to a reflection component. We performed a time-resolved spectral analysis to search for variability of the X-ray flux and of the individual spectral components.
Results. We find that the power law has a photon index Γ = 1.8 ± 0.1, absorbed by an ionized partial covering medium with a column density NH = (10.1 ± 0.8) × 1023 cm−2, a ionization parameter log ξ = 1.3 ± 0.1 erg s−1 cm and a covering factor f ≃ 90%. Considering a density of the absorber typical of the broad line region (BLR), its distance from the central SMBH is of the order of r ∼ 0.1 pc. An Fe Kα emission line is found at 6.4 keV, whose intensity shows variability on timescales of hours. We derive that the reflecting material is located at a distance r ≳ 600rs, where rs is the Schwarzschild radius.
Conclusions. Concerning the X-ray properties, we found that PKS 2251+11 does not differ significantly from the non-jetted AGNs, confirming the validity of the unified model in describing the inner regions around the central SMBH, but the lack of information regarding the state of the very innermost disk and SMBH spin still leaves unconstrained the origin of the jet.
Key words: galaxies: active / galaxies: nuclei / accretion, accretion disks
© ESO 2019
1. Introduction
Accretion onto supermassive black holes (SMBHs) is the physical mechanism powering active galactic nuclei (AGNs). As such, these sources are very efficient at converting the gravitational energy of the accreting mass in other forms of energy, as radiation or powerful outflows. The primary radiation emitted by the accreting material is reprocessed by the surrounding nuclear environment, so that the AGN is observable at all wavelengths, from radio to γ-rays. While there is consensus about what powers AGN, the structure of the nuclear environment is still a matter of debate. The unified model of AGNs (e.g. Antonucci 1993) posits that all active galaxies share a common structure, which can be summarized with a few fundamental components: i) a central SMBH; ii) an accretion disk; iii) a dusty obscuring torus, typically on the same plane of the accretion disk; and iv) outflows, in the form of highly collimated relativistic jets, or wide-angle nuclear winds (Padovani et al. 2017). According to the unified model, the distinction between unobscured (Type 1) and obscured (Type 2) AGNs is related to the inclination of the line of sight with respect to the plane of the accretion disk (Urry & Padovani 1995). Radio-loud quasars and less-luminous radio galaxies are capable of launching powerful, relativistic jets, while radio-quiet QSOs and Seyfert galaxies have jets that are much less powerful (the role of jet production in the AGN classification is reviewed by Padovani 2017). The mechanism responsible for the launching and the collimation of the relativistic jet is an open issue, and is likely related to the interaction between the magnetic field and the accretion disk (e.g. Romero et al. 2017, Keppens & Meliani 2010).
In this regard, X-ray observations provide a powerful tool for the investigation of the accretion-ejection physics in the neighborhood of the SMBH (e.g. Matt et al. 2007; Turner & Miller 2009; Reynolds 2016). While non-jetted AGNs are relatively well studied in the X-rays, we have a limited sample of radio galaxies whose X-ray properties are well constrained. For this reason we cannot yet confidently affirm that the underlying structure of the nuclear environment is the same for both non-jetted and jetted AGNs (e.g. Gliozzi et al. 2007). Since the fraction of absorbed AGN is comparable among non-radio galaxies and radio galaxies (Panessa et al. 2016), they could share a common obscuring structure, as predicted by the unified model. The presence or not of systematic differences in the X-ray properties between these two populations would help to clarify the role of the accretion processes in the triggering of the jet. AGNs show similarities with stellar BH binaries (Merloni et al. 2003), where the X-ray luminosity and the hardness of the X-ray spectrum are related with the production of jets and winds (Ponti et al. 2012; Fender & Muñoz-Darias 2016).
In this regard, the broad line radio galaxies (BLRGs) are especially suitable for high quality X-ray studies, given that they have the highest X-ray fluxes in the radio-loud population. The inclination angle between the line of sight (l.o.s.) and the perpendicular to the accretion disk in BLRGs has an intermediate value, meaning that the radiation coming out from the nuclear region is neither suppressed by the obscuring torus, nor overwhelmed by the relativistically boosted emission of the jet, as in blazars. Thanks to this characteristic, we are able to observe directly the optical emission of the broad line region (BLR) and we can also investigate the structure, the geometry, and the physics of the nuclear environment down to sub-pc scales.
Since the early observations with X-ray telescopes, radio loud (RL) AGNs appear slightly more luminous in the X-ray band, compared to the radio quiet (RQ) counterpart with comparable optical luminosity (Worrall et al. 1987; Chiaraluce et al. 2018). RL AGNs have also slightly flatter power law continuum, with ⟨ΓRL⟩ ∼ ⟨ΓRQ⟩ − 0.5 (e.g. Lawson & Turner 1997). However, these early results were affected by the low sensitivity of the instruments. For instance, Sambruna et al. (1999) found only a weak indication that the 2–10 keV spectra of BLRGs are flatter than those of Seyferts 1 galaxies. Wozniak et al. (1998) found in a sample of five BLRGs an average Fe Kα equivalent width (EW) of ∼100 eV and a Compton hump significantly weaker compared to those observed in RQ AGNs. The weakness of reflection components in BLRGs was confirmed by Eracleous et al. (2000), who proposed that this effect may be due to a small solid angle subtended by the disk to the primary continuum. This scenario is compatible with two-temperature disks, optically thick in the outer part and truncated in the inner part. The truncation may be induced by an advection-dominated accretion flow (ADAF) or ion-supported tori.
On the other hand, Ballantyne et al. (2002) suggest that the weakness of reflection features is not necessarily due to geometrical factors. Instead, they propose that the reprocessing by an ionized accretion disk could produce a similar effect, discarding the hypothesis that the RL–RQ dichotomy, and hence the production of the jet, is due to an intrinsic difference in the disk accretion state. In fact, other fundamental parameters could play a significant role in the production of the jet, such as high accretion rates and/or high values of mass and spin of the SMBH. Nonetheless, it is still not clear which combination of these parameters is the most favorable to trigger the jet emission (Chiaberge et al. 2015; Chiaberge & Marconi 2011). Ballantyne (2007) claims that the accretion geometry of RL AGNs could be related to the accretion efficiency, in turn linked to the AGN luminosity. In particular, for bolometric luminosities Lbol < 0.01LEdd the accretion transits to ADAFs, explaining the absence of reflection by the inner part of the disk (LEdd is the Eddington luminosity). For Lbol > 0.01LEdd, the disk is not truncated and the reflection can extend down to the innermost stable circular orbit (ISCO). The presence of reflecting material close to the SMBH is responsible for the emission of a relativistically broadened Fe Kα line, whose evidence is mixed in the case of BLRGs. The Fe Kα line can be originated by several components, such as the accretion disk, the BLR, or the inner part of the obscuring torus. In BLRGs each component can contribute differently, producing a final Fe Kα line width that varies case by case (e.g. Tombesi et al. 2010a; Ogle et al. 2005; Lohfink et al. 2013; Sambruna et al. 2009; Lohfink et al. 2015).
In the discussion of Sambruna et al. (2009), the authors infer that there is also a dichotomy in the outflow typology between BLRGs and Seyfert galaxies. In this scenario, accretion disk winds would be produced only by Seyferts, while the jet is a prerogative of radio galaxies. If we suppose that the bulk of accretion energy is used for winds acceleration, the jet formation is prevented, thus explaining the lack of jets in Seyferts. Nevertheless, the subsequent work of Tombesi et al. (2014) controverts this scenario, demonstrating that the production of mildly-relativistic disk winds is not a prerogative of RQ AGNs. In fact ultra fast outflows (UFOs) are found in both RQ and BLRGs (Tombesi et al. 2010b, 2014; Gofford et al. 2013; Reeves et al. 2010; Longinotti et al. 2015), indicating that their origin is somewhat independent of the formation of the relativistic jet. On the other hand, the presence of this latter remains a prerogative of RL galaxies.
Recent X-ray observations with XMM-Newton, Suzaku and NuSTAR (Sambruna et al. 2011; Ballantyne et al. 2014; Reynolds et al. 2015; Ursini et al. 2018) suggest that the accretion structure in BLRGs and in Seyfert galaxies is similar, therefore indicating that the separation in different classes is subtle. Instead, on the basis of these last results, the first ones can be considered as a sub-class of the second ones.
2. PKS 2251+11
PKS 2251+11 is a BLRG with a redshift z = 0.3255, derived from optical emission lines. Mor et al. (2009), modeling the infrared spectrum emitted by the dusty torus, derived the angle i between the direction of the jet and the l.o.s., obtaining i = 67°. This result indicates that PKS 2251+11 may be at the border between Type 1s and Type 2s, possibly intercepting part of the obscuring torus. Since the authors do not indicate the uncertainty associated with the estimation of i, in our analysis we will assume an inclination angle contained in the range 50° < i < 70°. Besides, the authors estimated an opening angle of the torus equal to σ = 15°, whose value is one of the smallest among the other sources in the sample.
Wandel (1991) used two independent methods for estimating the mass of the central SMBH MBH in this object, obtaining MBH ≃ 1.4 × 109 M⊙ and MBH ≃ 1.7 × 109 M⊙, with a fractional difference of ∼17%. In the same article the authors also derived log [ηṀc2/LEdd] = −1.52 and Ṁ ≃ 1 M⊙ yr−1 (Ṁ is the mass accretion rate and η is the accretion efficiency).
Davis & Laor (2011), using a dynamical approach, estimated MBH ≃ 7.2 × 108 M⊙. Assuming the optical emission dominated by the accretion disk, the authors derive also a mass accretion rate of Ṁ = 4.6 M⊙ yr−1, which is not far from the value obtained by Wandel (1991). Other derived quantities are Lbol = (1.35 ± 0.03) × 1046 erg s−1 and an accretion efficiency η = 0.066. Vestergaard (2002), through single-epoch spectroscopic measurements, obtained 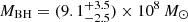 , comparable both with the estimates given by Davis & Laor (2011) and Wandel (1991). In the following we will consider only the value given by Vestergaard (2002), as it is likely the most accurate estimate.
, comparable both with the estimates given by Davis & Laor (2011) and Wandel (1991). In the following we will consider only the value given by Vestergaard (2002), as it is likely the most accurate estimate.
Laor & Behar (2008), studying the correlation between the radio and X-ray luminosities in a sample of both RL and RQ AGNs, report for PKS 2251+11 these quantities: LR = νLν|ν=6 cm = 1.15 × 1043 erg s−1, where LR is the total radio luminosity at 6 cm (taken from Kellermann et al. 1989, which also found that the contribution of the core to the radio luminosity is less than 1%); LX = 1.15 × 1044 erg s−1, with LX is the X-ray luminosity in the energy range E = 0.2−20 keV; αox = 0.372 log [Fν = 2 keV/Fν = 3000 Å] = −1.86; log R = 2.56, where R is the radio loudness, equivalent to R = 1.36 × 105L5/LB, with L5 = Lν|ν = 5 GHz and LB = Lν|ν = 4400 Å. Sambruna et al. (1999), performing an X-ray spectral analysis of RL AGNs observed with ASCA, reported radio archival data of PKS 2251+11. They derived the parameter logℛ = [radiocorepower/lobesradiopower] = −1.51, which indicates that the core contributes only to 3% of the total radio luminosity. In the same article the X-ray spectrum of PKS 2251+11 is analyzed and the adopted model is an absorbed power law. The derived best fit parameters are 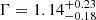 and
and 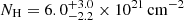 . Especially for E < 2 keV, absorption and emission features appear rather complex. The authors tried to add a Gaussian line in correspondence of the Fe Kα line, keeping fixed during the fit the energy at 6.4 keV and the width at σga = 50 eV. They derive an upper limit of the equivalent width of EW < 315 eV.
. Especially for E < 2 keV, absorption and emission features appear rather complex. The authors tried to add a Gaussian line in correspondence of the Fe Kα line, keeping fixed during the fit the energy at 6.4 keV and the width at σga = 50 eV. They derive an upper limit of the equivalent width of EW < 315 eV.
3. Data reduction
PKS 2251+11 was observed with XMM-Newton on 2011 December 18, for a total exposure of 63.8 ks. In this work we consider the EPIC-pn data. The detector operated in full window imaging mode. Data reduction and analysis were performed following the SAS standard procedure1. In order to check the presence of particle flaring background, we considered the entire field of view and we selected only the photons with energy in the range E = 10−12 keV. Then we plotted a light curve of the selected photons, excluding from the initial observation all the intervals of time in which the count rate is higher than 0.6. Subsequently, we extracted a circular region centered on the source, with a radius of 35″. The background region is of the same shape and dimension but centered in an area free of emission from point sources, located in the same CCD. The test for the presence of pile-up gave a negative response. After the filtering procedure, the net exposure of the observation was reduced to 57.3 ks. Along with the cleaned spectrum, a redistribution matrix file (RMF) and an ancillary response function (ARF) were created with standard SAS tools. The spectral data were grouped choosing a minimal threshold of 25 photons per bin and a χ2 statistic is adopted. Only in the case of time resolved spectroscopy (see below) the minimal threshold is lowered to five or ten photons per bin and a C-statistic is adopted. Unless otherwise specified, the errors are reported with at 1σ level of confidence, while the upper and lower limits are reported with a 90% level of confidence.
4. Spectral analysis
Our analysis is performed using the Heasarc v. 6.21 and XSPEC v. 12.9.1. We began trying to fit the data with an absorbed power law, following the standard assumption that a hot corona comptonizes the soft seed photons emitted by the accretion disk (e.g. Haardt & Maraschi 1991).
4.1. Neutral total covering absorber
First we included only the absorption due to the interstellar medium (ISM) in our Galaxy, for which Dickey & Lockman (1990) estimate a column density 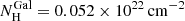 . For the estimate of the absorption cross section, we refer to the Tuebingen-Boulder model (Wilms et al. 2000), which in XSPEC is indicated as tbabs. The fit gives a χ2/d.o.f. = 917.5/369. Therefore the Galactic absorption is not sufficient to fit the spectrum and we added an absorption component due to neutral gas in the AGN host galaxy, but this does not improve the fit (χ2/d.o.f. = 917.5/368).
. For the estimate of the absorption cross section, we refer to the Tuebingen-Boulder model (Wilms et al. 2000), which in XSPEC is indicated as tbabs. The fit gives a χ2/d.o.f. = 917.5/369. Therefore the Galactic absorption is not sufficient to fit the spectrum and we added an absorption component due to neutral gas in the AGN host galaxy, but this does not improve the fit (χ2/d.o.f. = 917.5/368).
4.2. Neutral partial covering absorber
Then we tested the hypothesis of a neutral partial covering absorption, modeled in XSPEC as pcfabs. The resulting model is written in XSPEC language as zpcfabs*tbabs*zpo. Adding just one parameter, the fit improves to a value χ2/d.o.f. = 448.3/367. The validity of this improvement is also confirmed by the ftest, which gives a confidence larger than 5σ. The derived best fit parameters are  , f = 0.85 ± 0.01 and Γ = 1.76 ± 0.04, where NH is the column density of the gas in the source host galaxy, f is the covering factor, in other words, the fraction of the solid angle subtended by the absorbing medium, and Γ the photon index of the power law. The comparison between this model and the EPIC-pn spectrum is showed in Fig. 1.
, f = 0.85 ± 0.01 and Γ = 1.76 ± 0.04, where NH is the column density of the gas in the source host galaxy, f is the covering factor, in other words, the fraction of the solid angle subtended by the absorbing medium, and Γ the photon index of the power law. The comparison between this model and the EPIC-pn spectrum is showed in Fig. 1.
 |
Fig. 1. Comparison between the EPIC-pn spectrum and the model zpcfabs*tbabs*zpo. The data to model ratio is showed in the bottom panel. |
4.3. The Fe Kα line
As can be seen in Fig. 2, there is an excess of counts between 6 and 7 keV, which we identify with the Fe Kα fluorescence line. This last is modeled with a Gaussian profile, with a centroid Ega and a width σga. The model is written as zpcfabs*tbabs*(zpo+zga). Letting both the parameters Ega and σga vary freely during the fit, we find that the line is unresolved, since we obtain only an upper limit for σga ≤ 120 eV. The inclusion of this component improves the fit to χ2/d.o.f. = 424.8/364. The best fit value for the energy is Ega = 6.41 ± 0.03 keV. The significance for the addition of this line is > 3.7σ. In the following, since the line is unresolved, we fixed the width σga at 10 eV.
 |
Fig. 2. Zoom of the data to model ratio in the Fe K band at energies E = 6−7 keV for zpcfabs model. The bump around 6.4 keV suggests a possible neutral Fe Kα emission line. |
4.4. Ionized partial covering absorber
A further improvement of the fit occurs if we relax the hypothesis of neutral absorbing gas, which is no more valid if the primary continuum is particularly intense and/or if the absorber is located close to the X-ray source. In this case we substituted in XSPEC the model pcfabs with the model zxipcf (Reeves et al. 2008), which introduces the ionization parameter ξ = Lion/(nr2), where Lion is ionizing luminosity in the energy range E = 13.6 eV–13.6 keV, while n and r are the density and the distance form the SMHB of the absorber, respectively. The fit gives a high improvement to χ2/d.o.f. = 382.9/364. The best fit values are 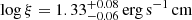 ,
, 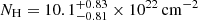 , f = 0.88 ± 0.01 and Γ = 1.78 ± 0.05. The comparison between this model and the spectrum is showed in Fig. 3. Until now we have assumed that the redshift z of the source and that of the absorber zabs are the same, namely that this last is at rest in the source reference frame. Then, if we let free zabs during the fit, we can explore the possibility that the absorber has a motion along the line of sight in the rest frame of the source. However, given the low energy resolution of the EPIC-pn and relatively low soft X-ray flux of the source, we are not able to statistically constrain the kinematics of the absorber.
, f = 0.88 ± 0.01 and Γ = 1.78 ± 0.05. The comparison between this model and the spectrum is showed in Fig. 3. Until now we have assumed that the redshift z of the source and that of the absorber zabs are the same, namely that this last is at rest in the source reference frame. Then, if we let free zabs during the fit, we can explore the possibility that the absorber has a motion along the line of sight in the rest frame of the source. However, given the low energy resolution of the EPIC-pn and relatively low soft X-ray flux of the source, we are not able to statistically constrain the kinematics of the absorber.
 |
Fig. 3. Comparison between the EPIC-pn spectrum and the model zxipcf*tbabs*(zpo+zga). With respect to the Fig. 1 the agreement improves especially in the band E = 0.5−1 keV, where the presence of ionization lines and edges most influences the overall shape of the spectrum. The data to model ratio is showed in the bottom panel. |
From the final best-fit model including zxipcf we derive an absorbed flux in the energy range E = 0.5−10 keV equal to 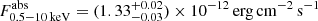 . The unabsorbed flux is
. The unabsorbed flux is  , which is the flux emitted by the primary continuum without considering the the suppression due to absorption. The corresponding intrinsic X-ray luminosity in the energy range E = 0.5−10 keV is
, which is the flux emitted by the primary continuum without considering the the suppression due to absorption. The corresponding intrinsic X-ray luminosity in the energy range E = 0.5−10 keV is 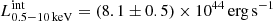 . Therefore the absorption causes a significant decrease of the intrinsic flux equal to [Funabs − Fabs]/Funabs ≃ 47%.
. Therefore the absorption causes a significant decrease of the intrinsic flux equal to [Funabs − Fabs]/Funabs ≃ 47%.
4.5. The pexmon model
Finally we tried to investigate the nature of the Fe Kα emission line using the reflection model pexmon (Nandra et al. 2007) which introduces the parameter R = Ω/2π, namely the fraction of the solid angle covered by the reflecting medium, seen by the primary X-ray source. We assume a solar abundance, a high-energy cutoff at 150 keV, an inclination angle i = 60° (in the middle of our confidence range 50° < i < 70°), while we let free Γ, R and the parameters of the absorber. We derive 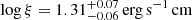 ,
, 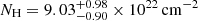 , f = 0.87 ± 0.01, Γ = 1.79 ± 0.05 and
, f = 0.87 ± 0.01, Γ = 1.79 ± 0.05 and 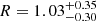 . Even assuming an inclination angle in the range between 50° and 70°, the reflection factor does not change significantly, being in any case compatible with 1. The results from zxipcf and pexmon models are summarized in Table 1.
. Even assuming an inclination angle in the range between 50° and 70°, the reflection factor does not change significantly, being in any case compatible with 1. The results from zxipcf and pexmon models are summarized in Table 1.
Values of the best-fit model including a Gaussian emission line for the Fe Kα or pexmon.
5. Timing analysis
5.1. X-ray variability
In order to check for X-ray variability, we created a light curve of the count rate in the energy band E = 0.3−10 keV. For different bin times (100 s, 500 s, 1000 s, 5000 s and 10 000 s) we have calculated: i) the average value ⟨C⟩ of the count rate; ii) the χ2 probability p, which indicates the probability that the observed variability is due to chance. As a threshold, we consider significant the variability only when 1 − p > 99.7% (3σ level of confidence); iii) the ![$ \sigma_{\mathrm{var}}=[C_{\mathrm{max}}-C_{\mathrm{min}}]/\sqrt{\sigma_{\mathrm{max}}^2+\sigma_{\mathrm{min}}^2} $](/articles/aa/full_html/2019/05/aa35176-19/aa35176-19-eq22.gif) , with Cmax and Cmin the highest and lowest points in the light curve, while σmax and σmin the respective errors of Cmax and Cmin; iv) the normalized excess variance
, with Cmax and Cmin the highest and lowest points in the light curve, while σmax and σmin the respective errors of Cmax and Cmin; iv) the normalized excess variance ![$ \sigma _{{\rm{NXS}}}^2 = [{S^2} - \left\langle {{\sigma ^2}} \right\rangle ]/\left\langle {{C^2}} \right\rangle $](/articles/aa/full_html/2019/05/aa35176-19/aa35176-19-eq23.gif) , where S2 is the variance of the light curve, that is
, where S2 is the variance of the light curve, that is ![$ {S^2} = [\sum\nolimits_i {C_i^2} - \left\langle {{C^2}} \right\rangle ]/N $](/articles/aa/full_html/2019/05/aa35176-19/aa35176-19-eq24.gif) , where the sum is extended over all the N points and ⟨C⟩ is the average value of the count rate; ⟨σ2⟩ is the average value of the errors associated to each point.
, where the sum is extended over all the N points and ⟨C⟩ is the average value of the count rate; ⟨σ2⟩ is the average value of the errors associated to each point.
For a bin time of 500 s we report the light curve of the count rate in Fig. 4. From Table 2 we can see that the variability is not significant for any choice of bin time.
 |
Fig. 4. Light curve of the photon count rate in the energy range E = 0.3−10 keV, from the EPIC-pn observation. The horizontal blue line indicates the average value of the count rate. A, B, and C indicate the time intervals defined in Sect. 5.2. |
Variability estimator values for different choices of bin time.
5.2. Time resolved spectral analysis
At this point, we tested the variability of the individual spectral components through a time resolved spectral analysis. First, we have produced two light curves, one in the soft X-ray band E = 0.5−2 keV and the other in the hard X-ray band E = 5−10 keV (the energies are referred to the source reference frame). Then we computed the hardness ratio as HR(t) = C5−10 keV(t)/C0.5−2 keV(t), where C5−10 keV(t) and C0.5−2 keV(t) are the hard and soft light curves, respectively. From the Fig. 5, the HR is almost constant apart in some time intervals where it increases during a time scale of 104 s. We divided the whole exposure in three sub-intervals, namely the interval A → [0 ks < t < 10 ks]+[16 ks < t < 52 ks]+[56 ks < t < 62 ks]; the interval B → 10 ks < t < 16 ks; the interval C → 52 ks < t < 56 ks. For each of these intervals we have extracted the spectrum. Since the intervals B and C have a very short exposure, the collected photons are ∼1/10 of those of the total observation, with subsequent poor statistic for spectral parameters determination. So we first tried to merge B and C, gaining in S/N, but loosing information on the individual intervals. The new interval BC has [10 ks < t < 16 ks] + [52 ks < t < 56 ks]. We analyzed at the same time the spectra from A and BC, with the model zxipcf*tbabs*(zpo+zga). Apart from 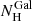 , σga and the redshift of the components, all the other parameters are left free during the fit. No parameter changes significantly from A to BC, apart for the normalization of the Fe Kα line, which increases in BC, when the hardness ratio is higher.
, σga and the redshift of the components, all the other parameters are left free during the fit. No parameter changes significantly from A to BC, apart for the normalization of the Fe Kα line, which increases in BC, when the hardness ratio is higher.
 |
Fig. 5. Hardness ratio HR as a function of time, for a bin time choice of 2000 s. The horizontal solid line is the average value of HR. Around 16 ks and 55 ks the HR differentiates from its average value. A, B, and C indicate the time intervals defined in Sect. 5.2. |
Then we analyzed A, B, and C separately. Since the counts in B and C are few, if we let the spectral parameters for A, B, and C vary freely, the fit does not converge, or the errors are large. So we assumed that, apart the normalization of the Fe Kα, all the parameters do not change during the observation, obtaining 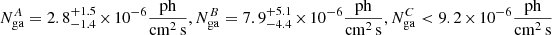 , where the superscript refers to the line normalization in A, B and C, respectively.
, where the superscript refers to the line normalization in A, B and C, respectively.
Apparently, within the errors, in A, B, and C the Nga is compatible with a constant. Although, since the exposure of C is too short, we cannot have a precise constraint on Nga, while the variability from A to B is more remarkable. In order to test the variability of Nga between A and B, we considered the contour plot of 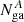 and
and 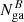 in Fig. 6, where we drew the line
in Fig. 6, where we drew the line 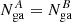 . The green region shows the area in the parameter space where
. The green region shows the area in the parameter space where 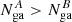 with a 90% level of confidence. As evident, it is considerably more probable that
with a 90% level of confidence. As evident, it is considerably more probable that 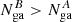 . As a further check, we tried to use the model zxipcf*tbabs*pexmon, following the same procedure described above, fixing all the parameters equal for A, B and C and letting free only the reflection parameter R. In A, B and C the reflection parameter assumes the values
. As a further check, we tried to use the model zxipcf*tbabs*pexmon, following the same procedure described above, fixing all the parameters equal for A, B and C and letting free only the reflection parameter R. In A, B and C the reflection parameter assumes the values 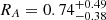 ,
, 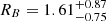 and
and 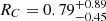 , respectively. They are all compatible within the errors, but looking at the contour plot of RA and RB we notice that the intersection between the 90% area and the region where RA > RB is extremely small. Therefore we can affirm that also the reflection parameter varies sensibly from A to B. Such result is in agreement with the increasing of Nga in the interval B. In fact, the greater is the solid angle covered by the reflector, the higher is the intensity of the reflection component. Finally we tried to vary the inclination angle i between 50° and 70°, always finding that RB ∼ 2 × RA, while RC ∼ RA.
, respectively. They are all compatible within the errors, but looking at the contour plot of RA and RB we notice that the intersection between the 90% area and the region where RA > RB is extremely small. Therefore we can affirm that also the reflection parameter varies sensibly from A to B. Such result is in agreement with the increasing of Nga in the interval B. In fact, the greater is the solid angle covered by the reflector, the higher is the intensity of the reflection component. Finally we tried to vary the inclination angle i between 50° and 70°, always finding that RB ∼ 2 × RA, while RC ∼ RA.
 |
Fig. 6. Confidence contours for |
6. Results and discussion
In our spectral analysis of the X-ray spectrum of PKS 2251+11, the best-fit is obtained considering an absorbed power law, where the absorbing medium is ionized and partially covers the primary X-ray source. We also detect the presence of an unresolved Fe Kα emission line at 6.4 keV.
6.1. Location of the absorber
The ionization parameter 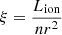 , used in the photoionization models, contains information about the physical state of the absorber, which is likely to be stratified along the line of sight. The stratification implies that the gas has a value of ξ that changes with r. In this case r and n are defined as the inner radius of the absorber and the corresponding density, respectively. Usually the ionizing luminosity is well constrained by the spectral analysis, while the highest uncertainty is associated with r and n. An upper limit for r can be obtained writing NH ≃ nΔr, with Δr as the thickness of the absorber along the line of sight. Then, assuming that Δr < r we can write
, used in the photoionization models, contains information about the physical state of the absorber, which is likely to be stratified along the line of sight. The stratification implies that the gas has a value of ξ that changes with r. In this case r and n are defined as the inner radius of the absorber and the corresponding density, respectively. Usually the ionizing luminosity is well constrained by the spectral analysis, while the highest uncertainty is associated with r and n. An upper limit for r can be obtained writing NH ≃ nΔr, with Δr as the thickness of the absorber along the line of sight. Then, assuming that Δr < r we can write 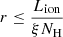 .
.
From the spectral analysis we see that the assumption of a single partial covering ionized medium is sufficient to give a good agreement with data. Therefore we can exclude that the absorption is due to a medium with a large range of ionization parameter and/or distributed along a broad range of distances from the center. If this were the case, the fit with a single absorbing component would not give the agreement that we obtain. Consequently, we can assume, as a first order approximation, that the absorber is composed by a single medium, whose thickness is much smaller than its distance from the center, namely Δr ≪ r, and whose ionization parameter is contained in a small range ξ0 − Δξ < ξ < ξ0 + Δξ, with Δξ ≪ ξ0. In this case we can write
In order to estimate Lion, we assumed that the ionizing continuum between 13.6 eV and 13.6 keV follows a power law, with the same photon index found in the X-ray band. In XSPEC we used the task clumin to obtain
which gives
Alternatively, we can also parametrize Δr = αr, with α an unknown constant. The photoionization model that we considered in our spectral analysis assumes a thin shell of absorbing material and therefore we can assume α ≪ 1. Thus we can write
and hence, for NH = 10.1 × 1022 cm−2 and log ξ = 1.33 erg s−1 cm
For comparison, we can consider the location of the BLR, which can be deduced using the HβFWHM = 4160 km s−1 = vBLR (Vestergaard 2002). Assuming a Keplerian orbit around the SMBH, we have
Therefore, for α ∼ 10−3 the ionized partial covering absorber can be identified with the BLR, while for 10−3 ≲ α ≪ 1 the absorber is more likely identified with the obscuring torus. Furthermore, we can use the definition of the ionization parameter ξ to write the distance r as a function of the density n of the absorber, obtaining:
If we consider a density n = 109 cm−3, typical of the BLR clouds (e.g. Snedden & Gaskell 1999), and using Lion = 1.24 × 1045 erg s−1, the distance of the absorber is r ∼ 0.1 pc. We notice that this distance is comparable with the previous estimate of the location of the BLR.
 |
Fig. 7. Confidence contours for RA and RB. The straight black line is drawn in correspondence of RA = RB. The green area is the intersection between the half-plane below the black line and the region contained inside the 90% contour. |
6.2. Covering factor and filling factor of the absorber
Adopting the zxipcf model, we obtained a covering factor f = 0.88, meaning that the absorber is not homogeneous, but rather has a clumpy structure. In the following, we show how we can relate the covering factor f with the filling factor ℱ. Assuming that the absorber is composed by several distinct clouds, we can define N0 the number of clouds per unit volume and V̄ the average volume of a single cloud. Thus we can write
The covering factor, instead, is defined as
with ΔΩ the solid angle subtended by the primary X-ray source, while ΔΩabs is the portion of this solid angle covered by the absorber. If we call 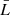 the typical dimension of a single cloud, then
the typical dimension of a single cloud, then ![$ \bar{L}=\sqrt[3]{\bar{V}} $](/articles/aa/full_html/2019/05/aa35176-19/aa35176-19-eq51.gif) and we can distinguish two cases: 1) the thickness of the absorber
and we can distinguish two cases: 1) the thickness of the absorber 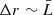 and 2)
and 2) 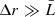 . In the first case, since the linear dimension of the clouds
. In the first case, since the linear dimension of the clouds 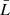 is of the same order of magnitude of the thickness of the absorber, we can assume that the clouds do not overlap along the l.o.s. Thus the filling factor can be rewritten as
is of the same order of magnitude of the thickness of the absorber, we can assume that the clouds do not overlap along the l.o.s. Thus the filling factor can be rewritten as
We find an interesting consequence: given a thin absorbing shell with a certain covering factor, we have ℱ ∼ f, independently on the distance from the primary source. This reasoning is no more valid for a thick shell, namely when 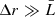 . We can consider, for instance, a thin shell with a certain filling factor ℱ = N0V̄ ∼ f. Then, if we imagine a thick shell with the same value of ℱ, several clouds would overlap along the l.o.s. and a greater fraction of ΔΩ would be covered, implying ℱ < f. Thus we can conclude that, even if
. We can consider, for instance, a thin shell with a certain filling factor ℱ = N0V̄ ∼ f. Then, if we imagine a thick shell with the same value of ℱ, several clouds would overlap along the l.o.s. and a greater fraction of ΔΩ would be covered, implying ℱ < f. Thus we can conclude that, even if 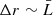 or
or 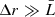 , the covering factor f represents always an upper limit for the filling factor ℱ. In our case we have
, the covering factor f represents always an upper limit for the filling factor ℱ. In our case we have
We note that, even if in the thin shell limit we could assume ℱ ∼ f, N0 and V̄ would still remain degenerate.
6.3. Location and geometry of the reflector
Furthermore, analyzing the Fe Kα line, we can infer useful information about the location of the reflecting material. Firstly, we note that the best fit value of the line centroid is 6.41 keV, which already indicates qualitatively that the bulk of the reflector is lowly ionized. In order to quantify the level of ionization we refer to Matt et al. (1993), who studied the physical properties of an accretion disk illuminated by an ionizing continuum. In particular, in Fig. 1 of Matt et al. (1993) the centroid of the Fe Kα line is plotted as a function of the ionization parameter ξ. Combining this figure and the results of our spectral analysis, we can affirm that, at 90% level of confidence, Ega < 6.5 keV, which implies ξ < 400 erg s−1 cm. Thus, calling ξR, nR and rR the ionization parameter, the density and the distance of the reflector, respectively, we can write:
Analogously we can define ξA, nA and rA the ionization parameter, the density and the distance of the absorber, respectively. In general, the reflector and the absorber do not receive the same ionizing luminosity, due to the complexity of the nuclear geometry. In particular, if the reflector is much farther from the SMBH compared to the absorber, there is a time lag in the propagation of the ionizing continuum. Therefore we can parametrize 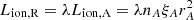 , where the subscript “A” refers to the absorber, while “R” to the reflector. Using Eq. (7), we can write
, where the subscript “A” refers to the absorber, while “R” to the reflector. Using Eq. (7), we can write
which can be rewritten using the Eq. (3) as
Such relation imposes a lower limit for the location of the reflector, but it contains unknowns that cannot be directly derived from our analysis, such as λ, nA and nR. We can qualitatively deduce that the density of the reflector is likely much higher than that of the absorber, since the reflection component is not strong and the reflecting gas is less ionized than the absorbing gas. Nevertheless, this is not sufficient to derive a numerical constraint for a lower limit of rR.
Another interesting information about the location of the reflector comes from the width of the Fe Kα line, which appears not resolved. Indeed, if we let free the parameters Ega and σga during the fit, we find σga < 120 eV. This result is in accordance with what has been found in the literature for other BLRGs, which rarely show a relativistic broadened iron line. If we suppose that the broadening is due mostly to a Doppler kinematic effect, we can infer another constraint on the location of the reflector. Let us suppose that the reflector follows almost circular Keplerian orbits. In this configuration, part of the reflector moves toward the observer, part moves away, causing the Doppler broadening of the line. Since the orbital velocity increases at lower distances, we may say that an upper limit of σga implies a lower limit rin for the distance of the reflector. In order to find rin, we make the rough approximation
where σmax = 120 eV, Δv// = Δvsini and Δv = 2 vorb|rin. Therefore
For 50° < i < 70°, we have that 0.024 < β < 0.030. Then, knowing that
with 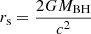 , we obtain
, we obtain
where 600 rs ≲ rin ≲ 900 rs. Although, we stress that this lower limit for rR is related to the reflecting material that produces the observed narrow Fe Kα line. In principle, a fainter and broader iron line can be present in the spectrum, but not detectable with the S/N of our data. It could be also possible that the inner part of the disk (rR ≲ 600rs) does not contribute considerably to the emission of Fe fluorescence because its level of ionization is too high and most of the outer electrons are ripped off the atoms.
The pexmon model does not modify sensibly the best fit values of NH, log ξ, f and Γ. The reflection parameter R is constrained in the range 0.64 < R < 1.85, having assumed an inclination angle in the range 50° < i < 70°. Such result is compatible with a scenario where the reflector covers most of the solid angle illuminated by the primary source. If also the dusty torus contributes to the reflection, a value of R ∼ 1 implies that the torus has a flattened geometry, meaning that almost all the radiation emitted by the primary source is reflected toward the observer. The scenario of a flattened torus is also supported by Mor et al. (2009), who found an opening angle of only 15°. Anyway, the data quality is not good enough to infer further information about the geometry of the reflector.
6.4. Variability of the reflection component
The timing analysis of the source light curve does not show any significant evidence of variability of the total flux during the entire exposure. Then we investigated the variability of the hardness ratio. Two intervals, that we called B and C, of the duration of 6 ks and 4 ks respectively, show an HR significantly higher than the average value. We analyzed the spectrum in these intervals, in order to test the variability of the individual spectral components.
Neither the fit parameters associated with the absorber nor the properties of the power law change significantly when the HR is higher. Instead, the reflection component shows evidence of variability, especially in the interval B. If the Fe Kα line is modeled with a Gaussian, its normalization increases at least of a factor of two in B. As a consistency check, also using the pexmon model the reflection factor has an average value of ⟨R⟩ ≲ 1 in A, while R > 1 in B.
In order to explain the variability of the reflection component, we notice that the intensity of this last is directly proportional to the incoming primary flux. In the case of the Fe Kα line, since the fluorescence is due to the absorption of X-ray photons with E ≥ 7 keV, a variability of the incoming flux above 7 keV (F>7 keV) causes the variability of the line intensity. Therefore, we propose two different scenarios: i) We interpret the reflection variability as an effect of Compton thick clouds rapidly moving in the immediate vicinity of the X-ray primary source. If such clouds intercept the flux directed to the reflector, the flux F>7 keV is partly suppressed, otherwise it increases. In such scenario the variability timescales of the reflection component are related to the dynamical time scales of the obscuring clouds. Alternatively we could suppose that the obscuring clouds are not located between the primary source and the reflector, but rather between the reflector and the observer. Though, in this case, two drawbacks arise. First, if the obscuring clouds are on the line of sight, we should observe at the same time a variability of both the reflection component and the column density NH, which is not our case. Second, since we have derived a lower limit for the distance of the material that produces the Fe Kα line, the dynamical time scales of the obscuring clouds would be too long to explain the variability of the reflection on time scales of ∼104 s. ii) The reflection variability is directly caused by an intrinsic variability of the primary source luminosity, but since the narrow Fe Kα line is produced at a distance RR ≳ 600 rs, there is a net time lag between the arrival time of the primary continuum and the reflected component. The time lag would be at least of 60 days, which could explain why in a single exposure of ∼17 h, we do not observe an increase of the primary flux followed by the increase of the reflection component.
7. Conclusions
Through the X-ray analysis of an observation performed with the XMM-Newton observatory, we have obtained novel information about the geometry, kinematics, and physical state of the regions surrounding the accreting SMBH at the center of the BLRG PKS 2251+11. The X-ray spectrum is consistent with a primary component described by a power law, which is absorbed by an ionized partial covering medium. Considering a density of the absorber typical of the BLR, its distance from the SMBH is of the order of R = 0.1 pc. This estimate is comparable with the location of the BLR, estimated through the virial theorem and knowing the FWHM of the Hβ. Alternatively, if we assume lower values of density, it is not excluded that the absorber is located farther from the SMBH, in the zone of the dusty torus. The absorber is likely clumpy, in other words, composed by distinct clouds with a covering factor f ≃ 90% and a filling factor ℱ ≲ f. The spectral analysis confirms the presence of an unresolved Fe Kα line and the bulk of the emission occurs at a distance rR > 600rs.
Besides the intensity of the Fe Kα line, no other spectral parameters show significant variability during the observation. Due to the considerable distance between the reflector and the SMBH, the variability of the Fe Kα intensity is likely due to past variations of the primary flux. Nonetheless, a rearrangement of the absorber geometry may also be a valid alternative.
An interesting follow up investigation could be an observation with the NuSTAR observatory of the high-energy part (E > 10 keV) of X-ray spectrum. With such analysis we could see if the power law has the same photon index also at higher energies, understanding in this way whether other components, such as the radio jet, can contribute to the X-ray emission of this AGN. Furthermore the energy of the power law cut-off (typically around 100 keV) is directly connected with the temperature of the electrons of the hot corona.
It would be also interesting to extend this work to a multi-epoch X-ray observation of PKS 2251+11, exploring the variability on timescales of days or months. For instance the scenario of a delayed response of the reflection component after a variation of the primary flux could be further tested. The light curves of the primary continuum and the reflection component could be cross-correlated, similarly to the method adopted in reverberation mapping of the BLR in the optical/UV band. Possible evidence of delay could further constrain the location of the reflector. With an X-ray multi-epoch study we could also test the way in which the geometry of the absorber influences the variability of the spectrum at energies E < 2 keV.
Described by the threads on the web page https://www.cosmos.esa.int/web/xmm-newton/sas-threads
Acknowledgments
S. Ronchini, who carried out this work during his master thesis at the University of Rome “Tor Vergata”, thanks the other authors for the valuable support. F. Tombesi acknowledges support by the Programma per Giovani Ricercatori - anno 2014 “Rita Levi Montalcini”. G.Bruni acknowledges financial support under the INTEGRAL ASI-INAF agreement 2013-025. R01. The authors thank the anonymous referee for the constructive comments.
References
- Antonucci, R. 1993, Annu. Rev. Astron. Astrophys., 31, 473 [Google Scholar]
- Ballantyne, D. R. 2007, Mod. Phys. Lett. A, 22, 2397 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Ross, R. R., & Fabian, A. C. 2002, MNRAS, 332, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Bollenbacher, J. M., Brenneman, L. W., et al. 2014, ApJ, 794, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., & Marconi, A. 2011, MNRAS, 416, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Gilli, R., Lotz, J. M., & Norman, C. 2015, ApJ, 806, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaraluce, E., Vagnetti, F., Tombesi, F., & Paolillo, M. 2018, A&A, 619, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, S. W., & Laor, A. 2011, ApJ, 728, 98 [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, Annu. Rev. Astron. Astrophys., 28, 215 [Google Scholar]
- Eracleous, M., Sambruna, R., & Mushotzky, R. F. 2000, ApJ, 537, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R., & Muñoz-Darias, T. 2016, in The Balance of Power: Accretion and Feedback in Stellar Mass Black Holes, eds. F. Haardt, V. Gorini, U. Moschella, A. Treves, & M. Colpi, 65 [Google Scholar]
- Gliozzi, M., Sambruna, R. M., Eracleous, M., & Yaqoob, T. 2007, ApJ, 664, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Gofford, J., Reeves, J. N., Tombesi, F., et al. 2013, MNRAS, 430, 60 [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., & Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Meliani, Z. 2010, in Numerical Modeling of Space Plasma Flows, Astronum-2009, eds. N. V. Pogorelov, E. Audit, & G. P. Zank, ASP Conf. Ser., 429, 91 [NASA ADS] [Google Scholar]
- Laor, A., & Behar, E. 2008, MNRAS, 390, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Lawson, A. J., & Turner, M. J. L. 1997, MNRAS, 288, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Lohfink, A. M., Reynolds, C. S., Jorstad, S. G., et al. 2013, ApJ, 772, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Lohfink, A. M., Ogle, P., Tombesi, F., et al. 2015, ApJ, 814, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Longinotti, A. L., Krongold, Y., Guainazzi, M., et al. 2015, ApJ, 813, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G. 2007, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J. W. Wang, ASP Conf. Ser., 373, 125 [NASA ADS] [Google Scholar]
- Matt, G., Fabian, A. C., & Ross, R. R. 1993, MNRAS, 262, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Heinz, S., & di Matteo, T. 2003, MNRAS, 345, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ogle, P. M., Davis, S. W., Antonucci, R. R. J., et al. 2005, in X-Ray and Radio Connections, eds. L. O. Sjouwerman, & K. K. Dyer, 7.20 [Google Scholar]
- Padovani, P. 2017, Nat. Astron., 1, 0194 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv, 25, 2 [Google Scholar]
- Panessa, F., Bassani, L., Landi, R., et al. 2016, MNRAS, 461, 3153 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Fender, R. P., Begelman, M. C., et al. 2012, MNRAS, 422, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J., Done, C., Pounds, K., et al. 2008, MNRAS, 385, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Gofford, J., Braito, V., & Sambruna, R. 2010, ApJ, 725, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 2016, Astron. Nachr., 337, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., Lohfink, A. M., Ogle, P. M., et al. 2015, ApJ, 808, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Boettcher, M., Markoff, S., & Tavecchio, F. 2017, Space Sci. Rev., 207, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Eracleous, M., & Mushotzky, R. F. 1999, ApJ, 526, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Reeves, J. N., Braito, V., et al. 2009, ApJ, 700, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Tombesi, F., Reeves, J. N., et al. 2011, ApJ, 734, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Snedden, S. A., & Gaskell, C. M. 1999, ApJ, 521, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Sambruna, R. M., Reeves, J. N., et al. 2010a, ApJ, 719, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010b, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tombesi, F., Tazaki, F., Mushotzky, R. F., et al. 2014, MNRAS, 443, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., & Miller, L. 2009, A&ARv, 17, 47 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Ursini, F., Petrucci, P. O., Matt, G., et al. 2018, MNRAS, 478, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M. 2002, ApJ, 571, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Wandel, A. 1991, A&A, 241, 5 [NASA ADS] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Worrall, D. M., Giommi, P., Tananbaum, H., & Zamorani, G. 1987, ApJ, 313, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, P. R., Zdziarski, A. A., Smith, D., Madejski, G. M., & Johnson, W. N. 1998, MNRAS, 299, 449 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Values of the best-fit model including a Gaussian emission line for the Fe Kα or pexmon.
All Figures
 |
Fig. 1. Comparison between the EPIC-pn spectrum and the model zpcfabs*tbabs*zpo. The data to model ratio is showed in the bottom panel. |
| In the text | |
 |
Fig. 2. Zoom of the data to model ratio in the Fe K band at energies E = 6−7 keV for zpcfabs model. The bump around 6.4 keV suggests a possible neutral Fe Kα emission line. |
| In the text | |
 |
Fig. 3. Comparison between the EPIC-pn spectrum and the model zxipcf*tbabs*(zpo+zga). With respect to the Fig. 1 the agreement improves especially in the band E = 0.5−1 keV, where the presence of ionization lines and edges most influences the overall shape of the spectrum. The data to model ratio is showed in the bottom panel. |
| In the text | |
 |
Fig. 4. Light curve of the photon count rate in the energy range E = 0.3−10 keV, from the EPIC-pn observation. The horizontal blue line indicates the average value of the count rate. A, B, and C indicate the time intervals defined in Sect. 5.2. |
| In the text | |
 |
Fig. 5. Hardness ratio HR as a function of time, for a bin time choice of 2000 s. The horizontal solid line is the average value of HR. Around 16 ks and 55 ks the HR differentiates from its average value. A, B, and C indicate the time intervals defined in Sect. 5.2. |
| In the text | |
 |
Fig. 6. Confidence contours for |
| In the text | |
 |
Fig. 7. Confidence contours for RA and RB. The straight black line is drawn in correspondence of RA = RB. The green area is the intersection between the half-plane below the black line and the region contained inside the 90% contour. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.