| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834658 | |
| Published online | 30 April 2019 | |
The habitability of stagnant-lid Earths around dwarf stars
1
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
10623
Berlin, Germany
e-mail: godolt@astro.physik.tu-berlin.de
2
Institut für Planetenforschung, Deutsches Zentrum für Luft- und Raumfahrt,
Rutherfordstraße 2,
12489
Berlin, Germany
3
Leibniz-Institut für Evolutions- und Biodiversitätsforschung, Museum für Naturkunde,
Invalidenstr. 43,
10115
Berlin, Germany
4
Institut für Geologische Wissenschaften, Freie Universität Berlin,
Malteserstr. 74–100,
12249
Berlin, Germany
Received:
15
November
2018
Accepted:
28
February
2019
Context. The habitability of a planet depends on various factors, such as the delivery of water during its formation, the co-evolution of the interior and the atmosphere, and the stellar irradiation which changes in time.
Aims. Since an unknown number of rocky extrasolar planets may operate in a one-plate convective regime, i.e. without plate tectonics, our aim is to understand the conditions under which planets in such a stagnant-lid regime may support habitable surface conditions. Understanding the interaction of the planetary interior and outgassing of volatiles in combination with the evolution of the host star is crucial to determining the potential habitability. M-dwarf stars in particular possess a high-luminosity pre-main sequence phase that endangers the habitability of planets around them via water loss. We therefore explore the potential of secondary outgassing from the planetary interior to rebuild a water reservoir allowing for habitability at a later stage.
Methods. We compute the boundaries of the habitable zone around M-, K-, G-, and F-dwarf stars using a 1D cloud-free radiative-convective climate model accounting for the outgassing history of CO2 and H2O from an interior evolution and outgassing model for different interior compositions and stellar luminosity evolutions.
Results. The outer edge of the habitable zone strongly depends on the amount of CO2 outgassed from the interior, while the inner edge is mainly determined via the stellar irradiation, as soon as a sufficiently large water reservoir has been outgassed. A build-up of a secondary surface and atmospheric water reservoir for planets around M-dwarf stars is possible even after severe water loss during the high-luminosity pre-main sequence phase as long as some water has been retained within the mantle. For small mantle water reservoirs, between 62 and 125 ppm, a time delay in outgassing from the interior permits such a secondary water reservoir build-up especially for early and mid-M dwarfs because their pre-main sequence lifetimes are shorter than the outgassing timescale.
Conclusions. We show that Earth-like stagnant-lid planets allow for habitable surface conditions within a continuous habitable zone that is dependent on interior composition. Secondary outgassing from the interior may allow for habitability of planets around M-dwarf stars after severe water loss during the high-luminosity pre-main sequence phase by rebuilding a surface water reservoir.
Key words: planets and satellites: atmospheres / planets and satellites: interiors / planets and satellites: terrestrial planets / astrobiology / stars: evolution / planets and satellites: physical evolution
© ESO 2019
1 Introduction
Nearly 4000 extrasolar planets have been found since their first detections in the 1990s. A major goal of exoplanetary research is to find and characterize potentially habitable planets. This requires a good understanding of the factors affecting their potential habitability. In an exoplanet context, habitability is usually defined by the presence of liquid water on the surface of the planet. This criterion puts constraints on the surface temperature and pressure, and is used for the definition of the circumstellar habitable zone (HZ), which defines the range of orbital distances around a star where liquid water may be present on the surface (see e.g. Hart 1979; Kasting et al. 1993). Whether or not water is really present critically depends on various factors, such as the atmospheric composition and mass, the water reservoir, and the evolution of these quantities.
The most commonly used HZ boundaries computed by Kasting et al. (1993) and updated by Kopparapu et al. (2013) assume an Earth-like planet with an atmosphere composed of molecular nitrogen (N2), carbon dioxide (CO2), and water (H2O) around M-, K-, G-, and F-dwarf stars. The inner edge of the habitable zone (IHZ) is determined by evaluating the distance at which the entire water reservoir of 270 bar (one Earth ocean) would reside within the atmosphere (runaway greenhouse limit) or the distance at which the upper atmosphere becomes wet enough so that atmospheric escape would lead to the loss of one Earth ocean within the lifetime of the Earth, i.e. in 4.5 Gyr. The outer edge of the HZ (OHZ) is placed at the distance at which an Earth-like planet with an atmosphere providing a maximum greenhouse effect of CO2 would have a surface temperature at the freezing point of water (273.15 K). This maximum greenhouse effect occurs due to the competing processes of an increased absorption of thermal radiation and increased Rayleigh scattering of the stellar irradiation upon increasing the amount of CO2 residing in the atmosphere. This approach is based on the assumption that a planet with an operating carbonate–silicate cycle, which is responsible for a stable climate on the Earth over long time spans (see e.g. Walker et al. 1981), will regulate the amount of CO2 in the atmosphere to obtain habitable conditions. However, the long-term carbonate–silicate cycle on the Earth involves plate tectonics, a tectonic regime which has been securely observed only for the Earth. Since the other terrestrial planets in the solar system operate in a one-plate tectonic regime with a stagnant lid, one may assume that some of the rocky extrasolar planets may also possess a stagnant lid.
The habitability of planets without plate tectonics has been studied previously by Noack et al. (2014, 2017), Tosi et al. (2017), Dorn et al. (2018), Valencia et al. (2018), and Foley & Smye (2018), among others. The last two studies propose alternative mechanisms for carbonate cycling on stagnant-lid planets, whereas the others mainly focus on the outgassing of volatiles from the interior. While most studies focus on the impact of outgassing (and cycling) of CO2 from the planetary interior, in a previous paper (Tosi et al. 2017) we investigated the habitability of stagnant-lid planets around the Sun accounting for the build-upof CO2 and H2O in the atmosphere via secondary outgassing from the interior. The study showed that stagnant-lid planets can in principle be habitable, though the HZ may be less extended due to limited outgassing for certain interior compositions. In addition, we found that an Earth-like ocean, i.e. with 270 bar, cannot result from secondary outgassing from the interior. Because of the pressure-dependent solubility of water in basaltic melts, outgassing of H2O strongly decreases as the pressure of the atmosphere increases over time. Nevertheless, depending on the assumed composition, a water reservoir of up to a few tens of bars can be outgassed from the interior (Tosi et al. 2017).
Building up a water reservoir via secondary outgassing may be especially important for the habitability of planets that experienced water loss during their early evolutionary stages, as proposed for planets around M-dwarf stars. Stellar evolution models, for example by Baraffe et al. (2015), clearly indicate that planets within the HZ around main sequence M-dwarf stars have experienced a much higher stellar irradiation (up to 2–3 orders of magnitude) during the pre-main sequence phase of the star, which lasts longer for M-dwarf stars than for Sun-like stars. Consequences of this high-luminosity pre-main sequence phase have been discussed by Luger & Barnes (2015), Ramirez & Kaltenegger (2014), Tian & Ida (2015), and Owen & Mohanty (2016), among others. This higher irradiation probably leads to much higher surface temperatures during the early evolution, leading to the evaporation of a potential surface water reservoir, photolysis of water molecules, and subsequent loss of hydrogen. Hence, rocky planets with a limited water reservoir may have lost their surface and atmospheric water during this early evolutionary stage.
We investigate here whether secondary outgassing from the interior may rebuild a surface water reservoir after the high-luminosity pre-main sequence phase. This will require that some water has been retained in the mantle despite an early phase of high stellar irradiation that probably led to severe atmospheric escape. Furthermore, higher irradiation during the early stages could lead to a long-term magma ocean, as found for Earth-like planets around the Sun at distances smaller than 0.7 au by Hamano et al. (2013). Determining the duration of such a magma ocean phase and its consequences for the interior and atmospheric water reservoir would require a different modelling approach than the one used here and is beyond the scope of this paper. However, in order to account for different outcomes from such a magma ocean phase, we perform a parameter study using a variety of interior mantle water reservoirs. We base this study on the interior evolution and outgassing described in Tosi et al. (2017). In the current paper we study the evolution of the HZ boundaries of Earth-sized planets due to outgassing of CO2 and H2O, and the luminosity evolution of their M-, K-, G-, and F-dwarf host stars.
The paper is structured as follows. Section 2 describes the interior evolution and outgassing model, and the 1D radiative-convective climate model that have been used to calculate the HZ boundaries. Furthermore, it motivates the modelled scenarios. Section 3 shows and discusses the results. Here, we first show the interior and outgassing evolution in Sect. 3.1 and then focus on the HZ evolution around the different dwarf stars (F, G, K, M) in Sect. 3.2 for relatively large water reservoirs. In Sect. 3.3 we then investigate the impact of the initial mantle water concentrations on the fate of the water reservoir of stagnant-lid planets around early to late M dwarfs. After putting our results into a broader context in the discussions section (Sect. 4), we briefly summarize and conclude our study in Sect. 5.
2 Computational details
2.1 Model description
Figure 1 shows a sketch of the modelling approach applied. For the interior we used a one-dimensional (1D) parameterized model of stagnant-lid mantle convection. Partial melt generated in the convective mantle beneath the lithosphere buoyantly percolates upwards and builds the crust. Carbon dioxide and water are outgassed from the melt that ultimately reaches the surface. The outgassed amount of these volatiles is then used in a 1D cloud-free radiative-convective climate model to calculate the boundaries of the HZ around different dwarf stars.
We follow the same approach as Tosi et al. (2017) to model the thermal evolution of the interior and the accompanying outgassing of a planet with the same mass, radius, and core size as the Earth, but operating in the stagnant-lid mode of convection (i.e. without plate tectonics) over 4.5 Gyr. Here we only present the main features of the model and refer the reader to the above study for a detailed description.
We use a classic 1D approach to parameterized mantle convection based on boundary layer theory (e.g. Turcotte & Schubert 2002). For an assumed initial temperature distribution, amount of long-lived radioactive elements, mantle water concentration, and redox state, we solve the energy balance equations for the core, the convecting mantle, and the lithosphere. As shown in Fig. 1, the lithosphere comprises the uppermost part of the mantle (lithospheric mantle) and the compositionally distinct crust, which together constitute a mechanical unit that does not participate in the convection of the deeper interior due to its high viscosity but sits stably on top; because of this stability, which defines the key structural and dynamical difference from the lithosphere of our own Earth with its plate tectonics, it is also referred to as a stagnant lid. Upon parameterizing the convective heat transfer, we employ a mantle viscosity based on diffusion creep of olivine dependent on temperature, pressure, and water concentration (Hirth & Kohlstedt 2003). In addition, the model accounts for partial melting, crust production, and partitioning of incompatible elements between mantle and crust (i.e. mantle depletion and crust enrichment). By comparing the mantle temperature with a peridotitic solidus dependent on water concentration (Katz et al. 2003), we apply a model of accumulated fractional melting to extract radioactive elements and water from the mantle and partition them into the crust (Morschhauser et al. 2011). In contrast, given the poor solubility of carbon in silicate minerals and its tendency to form separate phases, we apply a model of redox melting (Hirschmann & Withers 2008, Grott et al. 2011) under the assumption that the mantle is sufficiently reducing for carbon to be present in one of its elemental forms (i.e. graphite or diamond).
The pressure at which partial melting occurs in our models is always lower than the limit of about 8 GPa, above which basaltic melts are expected to be denser than the mantle residuum (e.g. Agee 2008). The melt produced is thus positively buoyant and tends to percolate upwards from the source region through the lithosphere. Eventually, it forms new crust either by intrusion into already existing crust at depth or by extrusion at the surface, whereby the ratio of intrusive to extrusive volcanism is set to an intermediate value of 2.5 (see e.g. White et al. 2006). The melt is enriched in water and CO2. Whether or not they are ultimately outgassed into the atmosphere depends on whether the melt carrying them is erupted or intruded and on their solubility in erupted surface melts at the evolving pressure conditions of the atmosphere (Gaillard & Scaillet 2014). H2O and CO2 are therefore only released into the atmosphere if their concentration in surface melts is in excess of saturation according to the solubility curves for basaltic melts (Newman & Lowenstern 2002).
To calculate the boundaries of the HZ of a stagnant-lid Earth around M, K, G, and F dwarfs, we applied a 1D, cloud-free, radiative-convective climate model, which has been described in detail by von Paris et al. (2010) and von Paris et al. (2015), and is based on Kasting et al. (1984) and Segura et al. (2003). The radiative transfer is split into a stellar and a thermal wavelength regime. The short wavelength regime treats the absorption and scattering of stellar irradiation using a δ-two-stream method including Rayleigh scattering coefficients following the approach of Allen (1973) and four-term correlated-k exponential sums covering a wavelength regime from 273.5 nm to 4.545 μm. This wavelength coverage is optimized for solar irradiation. Especially for late M dwarfs the cut-off at 4.545 μm leads to non-negligible loss in incoming radiation of up to ≈5% (see also Wunderlich et al. 2019). Hence, HZ boundaries obtained with the models lie closer to the star than would be expected when accounting for this missing portion of irradiation. The long-wavelength regime treats the absorption by CO2 and H2O in the wavelength regime from 1 to 500 μm via correlated-ks computed based on HITEMP 1995 (Rothman et al. 1995). The ckd continuum (Clough et al. 1989), and the collision-induced absorption as described in Kasting et al. (1984) for CO2 and as described in von Paris et al. (2013) for N2 –N2 are included. Convection is treated by applying a convective adjustment when the adiabatic lapse exceeds the radiative lapse rate, including latent heat release from H2O or CO2 where applicable. The water mixing ratio profile (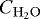 ) is calculated from the temperature profile, the saturation vapour pressure (psat), and by assuming a relative humidity (RH):
) is calculated from the temperature profile, the saturation vapour pressure (psat), and by assuming a relative humidity (RH): 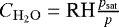 , with p the pressure of the atmosphere. By making use of our 1D climate model we estimate global diurnal mean values without accounting for effects such as slow planetary rotation or an interactive hydrological cycle. A discussion on the potential influence of 3D processes is given in Sect. 4.
, with p the pressure of the atmosphere. By making use of our 1D climate model we estimate global diurnal mean values without accounting for effects such as slow planetary rotation or an interactive hydrological cycle. A discussion on the potential influence of 3D processes is given in Sect. 4.
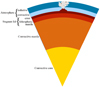 |
Fig. 1 Sketch of the combined interior and atmosphere models. |
2.2 Model set-up
We run inverse climate calculations similar to those carried out by Kasting et al. (1993) and Kopparapu et al. (2013). Instead of specifying a stellar irradiation and computing the surface and atmospheric temperatures from this (as done in Tosi et al. 2017), we specified a temperature profile, for which we then determined the planetary albedo at the top of the atmosphere and the outgoing long-wave radiation. From this we estimated the incoming stellar irradiation (Seff) required to balance the outgoing radiation via 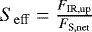 , with FIR,up the upwelling thermal (infrared) radiation and FS,net, the net stellar radiation.
, with FIR,up the upwelling thermal (infrared) radiation and FS,net, the net stellar radiation.
For the OHZ we set the surface temperatures to 273.15 K, the freezing point of water, and the stratospheric temperatures are set to 150 K for all calculations. We note that this is different from the approach of Kasting et al. (1993), who used an albedo and irradiation dependent stratospheric temperature. Using their expression would result in a range of stratospheric temperatures between ≈150 and 200 K. Varying the stratospheric temperature leads to a change in the upwelling thermal radiation, hence in Seff. When using a stratospheric temperature independent of stellar irradiation, as we did in this study, the influence of the different stellar energy distributions only enters via the variable FS,net. For the IHZ we set the surface temperature to the value at which the entire outgassed water reservoir would be in the vapour phase for the assumption of phase equilibrium. This results in surface temperatures for IHZ that depend both on time and interior composition. We assumed a stratospheric temperature of 200 K for these calculations, as in Kasting et al. (1993). Under most conditions at the inner edge of the HZ, the upper atmospheric temperatures are mainly determined via convection (see Fig. 2), and are much higher than 200 K. For these cases the assumption on the stratospheric temperatures does not influence the results. We discuss the impact of the stratospheric temperature assumption on our results in Sect. 4. With the above assumptions, habitable surface conditions can only be met if the outgassed water reservoir is larger than 6.11657 mbar, i.e. the saturation vapour pressure of water at 273.15 K. Figure 2 shows the temperature profiles at the OHZ and at the IHZ boundaries along an evolution sequence for one of the scenarios described in the following section. The increase in the surface pressure with time caused by the outgassing of volatiles is clearly visible.
2.3 Scenarios
We study the impact of secondary outgassing associated with partial melting and volcanism following accretion and a possible magma ocean phase. Raymond et al. (2007) showed that the accretion of planets around M-dwarf stars is faster than around more massive stars, which has also been calculated by Lissauer (2007) and Ida & Lin (2005). We therefore assumed that the accretion of a planet around an M dwarf is very fast (1 Myr), while for the other stellar cases we assumed an accretion time of 20 Myr. This corresponds to the lower limit in accretion times of Raymond et al. (2007) for planets around stars with masses greater than 0.8 MSun. After accretion, the planet may reside in a magma ocean stage, which we assume to last 1 Myr, following the results by Spohn & Schubert (1991) and Lebrun et al. (2013), among others. For high stellar irradiation, the planet may be trapped in a long-term magma ocean stage, which may last from several millions of years to billions of years (see e.g. Hamano et al. 2013, Nikolaou et al. 2019). For planets in a long-term magma ocean stage, Hamano et al. (2013) suggested very low water concentrations in the mantle at the end of the magma ocean stage because the planet can only exit this stage via severe atmospheric water loss because thick, water-rich atmospheres show a thermal blanketing effect suppressing the cooling of the planet via the Planck feedback. Their estimates of interior water reservoirs for such cases correspond to our lower limit of the initial mantle water concentration of 34 ppm. We nevertheless assumed in our calculations that the magma ocean has a short duration. This allows the high-luminosity pre-main sequence phase of the M dwarfs to have a larger impact on the HZ evolution. Any CO2 and H2O outgassed during the magma ocean phase is neglected in our calculations, i.e. we started our outgassing calculations with a 1 bar N2 atmosphere. Neglecting any atmospheric H2O and CO2 from the magma ocean phase results in a very narrow HZ at the beginning of our calculations, which is then only extended by secondary outgassing. This facilitates the evaluation of the potential of secondary outgassing from a stagnant-lid planet to form a HZ.
To compute the HZ boundaries depending on the thermal and outgassing evolution of our Earth-sized stagnant-lid planets, we assumed different interior compositions. For the outgassing of CO2, the mantle oxygen fugacity (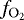 ) is important (Tosi et al. 2017); it can be thought of as an effective partial pressure of oxygen in the mantle and is a measure of how oxidizing or reducing the mantle is. A mantle with a higher oxygen fugacity will allow a larger fraction of the carbon partitioned into the melt to be in oxidized form and can therefore also release more CO2 into the atmosphere. We varied
) is important (Tosi et al. 2017); it can be thought of as an effective partial pressure of oxygen in the mantle and is a measure of how oxidizing or reducing the mantle is. A mantle with a higher oxygen fugacity will allow a larger fraction of the carbon partitioned into the melt to be in oxidized form and can therefore also release more CO2 into the atmosphere. We varied 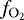 between one log10 -unit below the iron–wüstite (IW) buffer and one log10-unit above it, i.e. from IW − 1 to IW + 1. The IW buffer essentially defines the oxygen fugacity at which iron (Fe) and wüstite (FeO) are in thermodynamic equilibrium. The chosen values are two or three orders of magnitude lower than average values for common terrestrial mantle rock, and hence correspond to the absence of plate tectonics and an Earth-like water cycle.
between one log10 -unit below the iron–wüstite (IW) buffer and one log10-unit above it, i.e. from IW − 1 to IW + 1. The IW buffer essentially defines the oxygen fugacity at which iron (Fe) and wüstite (FeO) are in thermodynamic equilibrium. The chosen values are two or three orders of magnitude lower than average values for common terrestrial mantle rock, and hence correspond to the absence of plate tectonics and an Earth-like water cycle.
For the initial mantle water concentration, we considered values of 34, 62, 125, 250, and 500 ppm for planets around M-dwarf stars, while for F-, G-, and K-dwarf stars, we only discuss the impact of an initial mantle water concentration of 500 ppm (the interior modelling results for 250 and 500 ppm have already been discussed in detail by Tosi et al. 2017). We considered a range of initial mantle water concentrations especially for the planets around the M dwarfs since the long pre-main sequence phase may cause a long-term magma ocean phase, which can lead to substantial water loss and a drier planetary interior (see also Sect. 1). At the lower end, we used 34 ppm since Hamano et al. (2013) find an interior mantle water reservoir of 0.1 Earth oceans (≈34 ppm) after a planet has exited the magma ocean phase via water loss to space. Mechanisms that may lead to a larger fraction of volatiles trapped in the interior upon magma ocean crystallization have been discussed, for example by Hier-Majumder & Hirschmann (2017).
Furthermore, for the interior calculations we assumed an initial mantle temperature of 1700 K (as in the reference model of Tosi et al. 2017) and a surface temperature of 294 K. As discussed in Tosi et al. (2017), differences in the initial mantle temperature tend to be rapidly erased because of the strong temperature dependence of the viscosity. Also, considering a constant surface temperature has a minimal impact on the melt production and outgassing for the range of mantle water concentrations and oxidation states considered in this work.
For the mantle radiogenic heating, we considered bulk silicate Earth concentrations of uranium (U), thorium (Th), and potassium (K) according to McDonough & Sun (1995; i.e. 20 ppb U, 80 ppb Th, and 240 ppm K). Variations in such concentrations, which we do not consider in this study, would affect the amount and timing of melt production and, in turn, of outgassing: a higher internal heating would facilitate earlier mantle melting with subsequently earlier and more extensive outgassing. For a given oxygen fugacity and initial water concentration in the mantle, a larger amount of CO2 would be thus outgassed. However, because of the high solubility of water in surface melts (see Sect. 2.1), a rapid increase in the CO2 partial pressure would be accompanied by an early reduction of water outgassing. As a consequence, the final partial pressure of water in the atmosphere would be buffered to a nearly constant value, weakly dependent on the internal heat production.
We also assumed that no primary crust generated by magma ocean solidification (as in the case of the Moon, for example; see e.g. Warren 1985) is present at the beginning of the evolution, and set the initial stagnant lid thickness to 50 km. This choice only affects the earliest stages of the interior evolution. The lid thickness rapidly converges to a physically consistent value dictated by the internal energy budget. Simulations carried out using initial lid thickness values between 25 and 150 km lead to differences in the main diagnostic quantities (see Sect. 3.1) of only a small percentage over the evolution with respect to those presented here. In all cases, we computed the interior and outgassing evolution over a time span of 4.5 Gyr.
We modelled planetary atmospheres that are composed of CO2 and H2O evolving with outgassing from the interior, and 1 bar N2, which acts as a background gas. We further assumed a surface albedo of 0.22, and a relative humidity of 1. For the irradiation by the different host stars we accounted for the impact of different stellar spectral energy distributions as well as the luminosity evolution. We considered spectral energy distributions from the F-type dwarf star σ Bootis, the Sun as an example of a G-type star, ɛ Eridani as a K-dwarf star, and AD Leo as an M-dwarf star. These spectral energy distributions are representative of the current evolutionarystage of these stars; the Sun is the oldest, while the others have ages between 25–300 Myr and 1.7 Gyr (see e.g. Shkolnik et al. 2009, Mamajek & Hillenbrand 2008, Decin et al. 2003). Details about the spectra can be found in Kitzmann et al. (2010), among others. For the calculations of the M-star HZ boundaries in Sect. 3.3, we employed Planck curves for the stellar irradiation of M 4 and M 6-stars as in Rauer et al. (2011), with effective temperatures of 3100 K (M 4) and 2600 K (M 6), which are similar to the effective temperatures of Proxima Centauri and TRAPPIST-1.
In addition to the spectral energy distribution, we needed to assume a stellar evolution to calculate the evolution of the HZ boundaries over time. We used the stellar evolution models by Baraffe et al. (2015) to account for the change in stellar luminosity over time (see Fig. 3). The stellar parameters used are summarized in Table 1.
Figure 3 clearly shows the long pre-main sequence phase of the M stars. For the 0.4 MSun star this phase lasts about 100–200 Myr, for the 0.13 MSun star it lasts up to about 200–300 Myr, while for the very low-mass M dwarf it lasts for more than 1000 Myr. For the other dwarf stars with higher masses the pre-main sequence phase is much shorter. For them, however, a luminosity evolution during the main sequence phase exists. This luminosity increase with time has led to the famous faint young sun paradox for the Earth and Mars, which has been investigated by several groups (see e.g. Feulner 2012, von Paris et al. 2013, Wolf & Toon 2013, Kunze et al. 2014, Ramirez et al. 2014, Wordsworth et al. 2017).
While the interior evolution and outgassing is obtained from time-dependent modelling, we performed time slice calculations for the atmospheresat tint = 2, 5, 10, 50, 100, 200, 500, 700, 1000, 2000, 3000, 4000, and 4500 Myr, hence at different time steps of the interior evolution. We present the results in terms of the interior evolution time (tint), which startsat the end of the magma ocean phase (see Fig. 3).
 |
Fig. 2 Outer HZ (panel a) and inner HZ (panel b) temperature profile evolution for an initial water mantle concentration of 500 ppm andat IW + 0.5. |
 |
Fig. 3 Stellar luminosity evolutions used, following Baraffe et al. (2015). |
Stellar parameters.
3 Results
This section discusses the results of our interior evolution modelling (Sect. 3.1), and the HZ boundaries as found by the atmosphere modelling using the outgassing from the interior and the stellar evolution of the host stars (Sect. 3.2) for relatively high initial water concentrations in the mantle. We then explore the influence of the long pre-main sequence phase of M-dwarfs upon the habitability of stagnant-lid planets assuming different interior water reservoirs (Sect. 3.3).
3.1 Interior modelling results
We ran a series of interior evolution models varying the initial water concentration of the mantle and the mantle oxidation state for a range of fixed (and not evolving) oxygen fugacities. Figure 4 shows the evolution of the mantle temperature (panel a) and of the crustal and stagnant lid thickness (respectively solid and dashed lines in panel b) for different initial water concentrations in the mantle and an oxygen fugacity corresponding to the IW buffer. The time axis corresponds to the interior evolution time (tint), which starts at the end of the magma ocean phase. Additionally, the evolution of the distribution of the melt fraction for an initial water concentration of 62 ppm is shown in panel b. We show the results for 62 ppm initial mantle water concentration as an example for an evolution of a relatively dry interior. The evolution of a wetter interior with 500 ppm has been shown and discussed in Tosi et al. (2017). During the early evolution, the mantle temperature increases largely due to radiogenic heating coupled with inefficient heat loss through the stagnant lid. The maximum temperature reached and the time span over which the mantle heats up both increase with decreasing initial mantle water concentration. This is due to the increase in the mantle viscosity upon lowering the water concentration, which in turn slows down convection and hence mantle cooling.
Since the mantle solidus temperature increases with decreasing mantle water concentration, a comparatively hot mantle is needed for partial melting, crust formation, and outgassing if the initial mantle water concentration is low (34–62 ppm). For low initial water concentrations (e.g. 34 and 62 ppm), after a short adjustment phase during which 1–2 km crust are built, the bulk of the crust needs as long as ~1000 Myr to form (see partial melt zone in Fig. 4b). Consequently, for these drier cases the overall amount of crust produced tends to be relatively small compared to cases with higher initial water concentrations. This lower crust growth reduces both the reservoir from which the outgassing of volatiles can take place and the time span over which this can occur. The cases with high water concentration (250 and 500 ppm) are characterized by the rapid production of a large amount of partial melt, which causes the crust to quickly grow as thick as the stagnant lid. As soon as this condition is met (see e.g. tint ≈ 750 Myr for the case with initial water concentration of 500 ppm), crustal erosion begins and continues nearly until the end of the evolution. While in principle the crust could grow thicker according to the amount of melt that is continuously produced, it does not do this in our calculations because its base reaches the sub-lithospheric region where active convection recycles it back into the mantle. Therefore, the growth of the crust is limited by the evolution of the stagnant lid whose thickness increases upon mantle cooling (see also Tosi et al. 2017 for a detailed description of these cases).
Figure 5 shows the outgassing of H2O and CO2 for the samecases shown in Fig. 4. As expected, the amount of water outgassed from the interior increases for increasing initial water concentrations. For initial water concentrations of 250 and 500 ppm, the outgassing is continuous until it vanishes between 500 and 1000 Myr when surface melts start to be undersaturated in water (see also Tosi et al. 2017). A small amount of water can be outgassed again after 4000 Myr; for the low melt fractions occurring near the end of the evolution, surface melts, even though small in volume, tend to be highly enriched in water and hence supersaturated. For initial water concentrations below 250 ppm, the outgassing of water follows multiple steps. Some outgassing occurs during the first 10–100 Myr. After a quiet period during which no partial melting (see Fig. 4) and thus no outgassing takes place (see Fig. 5), a second period of outgassing is observed. This second period occurs later and is shorter for lower initial watermantle concentration. For initial mantle water concentrations of 62 ppm and higher, outgassing of H2O occurs again during later stages.
A similar step-wise behaviour for the outgassing is also obtained for CO2. For high initial mantle concentrations of water, more CO2 is outgassed from the interior at a given oxygen fugacity due to the decrease in the solidus temperature for increasing water concentration, which allows the production of more partial melt.
From the outgassing evolution of water in Fig. 5a it is apparent that an Earth-like stagnant-lid planet with only 34 ppm water initially cannot produce habitable surface conditions via outgassing, since the resulting water reservoir is too small, i.e. below 6.12 mbar, as indicated by the grey horizontal line. The entire outgassed water reservoir would reside within the atmosphere already at 273.15 K, assuming phase equilibrium. Additional model calculations have shown that for an oxygen fugacity at the iron–wüstite (IW) buffer and an initial mantle water concentration of 38.6 ppm, 6.12 mbar of H2O would be outgassed. The required initial mantle water concentration to reach 6.12 mbar depends on the oxygen fugacity, which can be better understood by evaluating the outgassing evolution for different values of 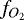 .
.
Figure 6 shows the outgassing evolution of H2O and CO2 for an initial mantle water concentration of 62 ppm for different oxygen fugacities. For the outgassing of water, the impact of the outgassed CO2 becomes visible from about 1300 Myr after the second outgassing phase. The increasing amount of CO2 in the atmosphere increases atmospheric pressure, and with this the solubility of H2O in the melt which leads to less outgassing, as discussed in Tosi et al. (2017). Hence, the scenarios with the lowest CO2 outgassing (IW − 1) have the highest amount of water outgassed from the interior. Overall the outgassing of water for this initial water concentration is very low. With a potential atmospheric and oceanic water reservoir of only about 0.05 bar, this is more than 2000 times smaller than the Earth’s ocean reservoir of 270 bar, and only about five times the amount of water within the Earth’s atmosphere, which has a volume mixing ratio of about 1% on average.
The amount of CO2 increases with oxygen fugacity. Its stepwise increase with time is due to the stepwise melt production, as explained above. For this low initial water concentration, the amount of CO2 outgassed from the interior can be as large as 6.7 bar for the highest oxygen fugacity assumed here (IW + 1). For an initial water concentration of 500 ppm, the final amount of CO2 outgassed from the interior for IW + 1 is 19.1 bar (see Tosi et al. 2017).
 |
Fig. 4 a: evolution of the mantle temperature for different water concentrations and an oxygen fugacity corresponding to the IW buffer. b: corresponding evolution of the crustal thickness (solid lines) and stagnant lid thickness (dashed lines). The coloured area denotes the distribution of the melt zone and melt fraction for the case with an initial water concentration of 62 ppm. |
 |
Fig. 5 Outgassing of H2O (a) and CO2 (b) for the same cases shown in Fig. 4. The horizontal grey line in the panel a corresponds to 6.12 mbar, i.e. the saturation vapour pressure of water at 273.15 K. |
 |
Fig. 6 Outgassing evolution of H2O (a) and CO2 (b) for an initial mantle water concentration of 62 ppm water and different oxygen fugacities. The grey horizontal line indicates the saturation vapour pressure of water at 273.15 K. The vertical axis of panel a is linear, while it is logarithmic in panel b and in Fig. 5. |
3.2 Evolution of the habitable zone boundaries of stagnant-lid planets around different dwarf stars
Figure 7 shows the evolution of the HZ boundaries of the stagnant-lid planets with an initial mantle water concentration of 500 ppm for different oxygen fugacities and host stars. The left panel shows the evolution in terms of stellar irradiation showing the impact of the build-up of the atmospheres via outgassing, while the right panel shows the evolution in terms of orbital distance, which also includes the evolution of the stellar luminosity.
3.2.1 Habitable zone boundaries in terms of stellar irradiation
In terms of stellar irradiation the HZ expands due to the build-up of H2O and CO2. For the planet around the M dwarf AD Leo (Fig. 7a) the shift of the IHZ boundaries towards the star (to higher values of Seff) mainly occurs during the first ≈100 Myr of secondary outgassing. This timescale is shorter than that of the build-up of the entire atmospheric-oceanic water reservoir, which corresponds to about 500 Myr (see dark blue line in Fig. 5a). The small amount of outgassed H2O during this initial phase of ≈100 Myr already causes the atmosphere to become opaque at similar pressure levels. Increasing the water reservoir increases the surface temperaturebut not the infrared radiation leaving the planet. This effect, called the radiation limit, has been widely discussed in the literature (e.g. Nakajima et al. 1992, Abe et al. 2011, Goldblatt & Watson 2012, Leconte et al. 2013, and references therein) and is linked to the runaway greenhouse limit. A closer look into Nakajima et al. (1992; their Fig. 5a) indicates that the radiation limit is approached at temperatures around 350 K at which the water vapour saturation pressure is about 0.4 bar. The convergence to a constant outgoing long-wave radiation when moving from temperate to warmer climates at about 350 K has also been found by Kasting et al. (1993) and Kopparapu et al. (2013).
For planets around the M dwarf AD Leo the stellar irradiation needed to reach the IHZ boundary is lower than one solar constant (S0), the amount of stellar irradiation the Earth receives from the Sun (Fig. 7a), which occurs because M stars mainly radiate at longer wavelengths. This radiation is less efficiently scattered and more effectively absorbed by H2O and CO2 in the planetary atmosphere, leading to larger heating rates. This has also been found by 3D climate models for Earth-like rotation rates (see e.g. Shields et al. 2014; Wolf et al. 2017). For slower rotations, for example due to tidal locking, 3D model calculations have found that a negative cloud feedback may allow much higher irradiations at the inner edge of the HZ (see e.g. Yang et al. 2014, Kopparapu et al. 2016, Way et al. 2018, and Sect. 4). For 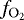 at the IW buffer or lower, results suggest that the IHZ boundaries lie at the same value of stellar irradiation, while for higher
at the IW buffer or lower, results suggest that the IHZ boundaries lie at the same value of stellar irradiation, while for higher 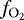 , especially at IW + 1, the IHZ moves outwards to lower values of stellar irradiation. This is due to the combined effect of increased atmospheric CO2 and decreased atmospheric-oceanic water reservoir outgassed from the interior. For a higher partial pressure of CO2, less H2O can be outgassed – about 5 bar at IW + 1 compared to 10 bar at IW − 1. This is because at higher pressures the saturation pressure of water in the melt is higher. As a consequence, H2O tends to stay in the melt, as shown in Tosi et al. (2017). Therefore, less stellar irradiation is needed to heat the planet with a dense atmosphere to temperatures at which the smaller water reservoir would reside within the atmosphere. The OHZ boundaries move to lower irradiation with time for all
, especially at IW + 1, the IHZ moves outwards to lower values of stellar irradiation. This is due to the combined effect of increased atmospheric CO2 and decreased atmospheric-oceanic water reservoir outgassed from the interior. For a higher partial pressure of CO2, less H2O can be outgassed – about 5 bar at IW + 1 compared to 10 bar at IW − 1. This is because at higher pressures the saturation pressure of water in the melt is higher. As a consequence, H2O tends to stay in the melt, as shown in Tosi et al. (2017). Therefore, less stellar irradiation is needed to heat the planet with a dense atmosphere to temperatures at which the smaller water reservoir would reside within the atmosphere. The OHZ boundaries move to lower irradiation with time for all 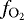 , reaching their final value at about 2000–3000 Myr. The higher the
, reaching their final value at about 2000–3000 Myr. The higher the 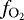 , the lower the irradiation needed to reach the OHZ surface temperature of 273.15 K, which is the temperaturewe assumed for the OHZ boundary. This is due to the larger greenhouse effect of the higher CO2 partial pressures outgassed atlarger
, the lower the irradiation needed to reach the OHZ surface temperature of 273.15 K, which is the temperaturewe assumed for the OHZ boundary. This is due to the larger greenhouse effect of the higher CO2 partial pressures outgassed atlarger 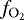 . The atmospheric partial pressure of water is the same for all OHZ scenarios as it is determined via the surface temperature, which is the same for all cases. For an
. The atmospheric partial pressure of water is the same for all OHZ scenarios as it is determined via the surface temperature, which is the same for all cases. For an 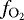 of IW + 0.5 and IW + 1, the values of the stellar irradiation at the OHZ are approximately the same, despite an increase in CO2 from about 6 to 18 bars. Increasing the amount of CO2 in the atmosphere increases the greenhouse effect, but also the scattering effect of the atmosphere. For M dwarfs these two processes balance each other for these CO2 partial pressures, while for the other stars, as discussed below, the scattering effect starts to dominate the temperature response at CO2 partial pressures above approximately 7 bar.
of IW + 0.5 and IW + 1, the values of the stellar irradiation at the OHZ are approximately the same, despite an increase in CO2 from about 6 to 18 bars. Increasing the amount of CO2 in the atmosphere increases the greenhouse effect, but also the scattering effect of the atmosphere. For M dwarfs these two processes balance each other for these CO2 partial pressures, while for the other stars, as discussed below, the scattering effect starts to dominate the temperature response at CO2 partial pressures above approximately 7 bar.
For the planet around the K star, the IHZ boundary extends towards the star up to about 700 Myr, and the irradiation to reach the IHZ is very similar for all oxygen fugacities except for IW + 1 (see Fig. 7c). The IHZ limit is found at radiations greater than one solar constant, since the amount of radiation at wavelengths where Rayleigh scattering is important is greater than for the M-dwarf star, which shows IHZ boundaries at irradiations lower than one solar constant. The OHZ boundaries extend outwards to lower values of stellar irradiation and reach their final value between 2000 and 3000 Myr. For nearly all cases, the OHZ boundary is at lower values of stellar irradiation for higher 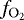 , corresponding to larger amounts of outgassed CO2. For IW + 1, however, the OHZ boundary moves inwards at later evolutionary stages due to the increased scattering effect of the accumulated CO2 molecules. The maximum greenhouse effect is obtained at about 1000 Myr, at partial pressures of CO2 around 7 bar. The maximum greenhouse effect becomes more apparent for the planets around the K-dwarf and more massive stars, since the stellar spectral energy distributions shift towards shorter wavelengths. The maximum greenhouse effect is caused by an increase in scattering of stellar light by denser atmospheres, as shown by Kasting et al. (1993), among others, for CO2-dominated atmospheres. A similar effect is also obtained for N2-dominated atmospheres, as shown by Keles et al. (2018), among others.
, corresponding to larger amounts of outgassed CO2. For IW + 1, however, the OHZ boundary moves inwards at later evolutionary stages due to the increased scattering effect of the accumulated CO2 molecules. The maximum greenhouse effect is obtained at about 1000 Myr, at partial pressures of CO2 around 7 bar. The maximum greenhouse effect becomes more apparent for the planets around the K-dwarf and more massive stars, since the stellar spectral energy distributions shift towards shorter wavelengths. The maximum greenhouse effect is caused by an increase in scattering of stellar light by denser atmospheres, as shown by Kasting et al. (1993), among others, for CO2-dominated atmospheres. A similar effect is also obtained for N2-dominated atmospheres, as shown by Keles et al. (2018), among others.
For the planet around the Sun, the HZ boundaries show a behaviour similar to that of the K-type star (Fig. 7e). However the IHZ boundaries are closer in, and move even closer to the star with time, due to the increase in scattering which is more pronounced for the Sun than for the K-type star. This also causes a stronger shift towards the star for the OHZ at high oxygen fugacity (IW + 1), although the maximum greenhouse effect is found at about 1000 Myr as for the planets around the K-type star.
This trend is continued for the planets around the F-type star (see Fig. 7g). For these scenarios the HZ has the largest extent in terms of stellar irradiation, while it shows the smallest extent for the planets around the M-type stars. This difference in extent is caused mainly by the increased scattering of stellar irradiation by the atmosphere for the hotter stars at the IHZ. Therefore, planets around F dwarfs can be habitable for higher irradiations than planets around M dwarfs. Increased scattering of stellar irradiation also occurs at the OHZ for F dwarfs compared to M dwarfs; however, the difference in total irradiation needed to reach the OHZ is much smaller than that at the IHZ boundary, which dominates the width difference of the HZ. With respect to the different oxygen fugacities of the mantle, the extent of the HZ is largest for IW + 0.5, while it is smallest for IW − 1 and IW + 1.
 |
Fig. 7 Habitable zone evolution for planets with an initial interior water content of 500 ppm. Left column: HZ boundaries in terms of stellar irradiation (S0), around an M, K, G, and F dwarf (from top to bottom). Right column: HZ boundaries in orbital distance (au), which includes the stellar luminosity evolution. For illustration we indicate the orbital distance evolution of Seff = 1S0 with a grey solid line, which is the radiation the Earth receives from the Sun today, and the orbital distances of Venus, Earth, and Mars in panel f with vertical grey dashed lines. The stellar age corresponding to the interior evolution times is indicated on the secondary y-axis where applicable. |
3.2.2 Habitable zone boundary distances
The right panels of Fig. 7 show the evolution of the HZ in terms of orbital distance, accounting for the luminosity evolution of the star.
For the planets around the M dwarf AD Leo, the pre-main sequence phase with the higher luminosity leads to a large shift in the HZ boundaries from values of around 0.43–0.5 au to smaller values of about 0.15–0.2 au during the first 200 Myr of evolution (Fig. 7b). After that large shift, the influence of outgassing, which is much stronger than that of the later evolution of the star, can be clearly identified (solid grey line). The largest extent of the HZ is again obtained for 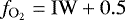 . The smallest extent is now found for the lowest value of
. The smallest extent is now found for the lowest value of  considered here (IW − 1).
considered here (IW − 1).
The other stars also show a luminosity evolution as they make the transition from the pre-main sequence to the main sequence. As stated in Sect. 2.3 we set a later start of the secondary outgassing evolution for the planets around these stars, i.e. at 21 Myr, because accretion is thought to last longer around higher mass stars (e.g. Raymond et al. 2007). This leads to a shorter time span over which these early luminosity changes have an impact on the HZ boundaries. For the planets around the K-type stars only a small shift in the HZ of around 0.05 au is caused by the stellar evolution within the first 10 Myr (Fig. 7d). For the planets around the Sun a back-and-forth shift of the HZ boundaries of up to 0.3 au is found for the first 50 Myr (Fig. 7f). For the F star the HZ moves inwards by about 0.2 au during the first 5 Myr of evolution (Fig. 7h).
At later stages, the trends in the evolution of the HZ boundaries with time and 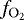 are very similar to those in stellar irradiation (shown in the left column of Fig. 7): OHZ boundaries move outwards for increased outgassing of CO2, but they move back inwards at the highest
are very similar to those in stellar irradiation (shown in the left column of Fig. 7): OHZ boundaries move outwards for increased outgassing of CO2, but they move back inwards at the highest 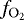 (IW + 1) considered, due to increased scattering by the atmosphere for CO2 partial pressures larger than those needed to obtain the maximum greenhouse effect. In addition, however, the inner and outer boundaries slowly move away from the star due to its brightening. This shift is largest for the planets around the F-type star and smallest for the planets around the K-type star, and seems to be absent for the planets around the M dwarf. This is caused by the faster main sequence evolution of the more massive and hotter stars (e.g. F and G dwarfs), while the cooler low-mass stars (K and M dwarfs) show only a small luminosity evolution on the main sequence over the time span we consider here. This outward shift of the OHZ due to the brightening of the stars is strongest for
(IW + 1) considered, due to increased scattering by the atmosphere for CO2 partial pressures larger than those needed to obtain the maximum greenhouse effect. In addition, however, the inner and outer boundaries slowly move away from the star due to its brightening. This shift is largest for the planets around the F-type star and smallest for the planets around the K-type star, and seems to be absent for the planets around the M dwarf. This is caused by the faster main sequence evolution of the more massive and hotter stars (e.g. F and G dwarfs), while the cooler low-mass stars (K and M dwarfs) show only a small luminosity evolution on the main sequence over the time span we consider here. This outward shift of the OHZ due to the brightening of the stars is strongest for 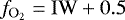 . While for the M star this shift is rather small in terms of orbital distance (from about 0.2 to 0.28 au), it becomes much larger for the other stars with a shift from about 0.6 to 0.95 au for the K dwarf, from about 1 to 1.6 au for the Sun, and more than 1 au for the F-type star from about 1.5 to 2.6 au.
. While for the M star this shift is rather small in terms of orbital distance (from about 0.2 to 0.28 au), it becomes much larger for the other stars with a shift from about 0.6 to 0.95 au for the K dwarf, from about 1 to 1.6 au for the Sun, and more than 1 au for the F-type star from about 1.5 to 2.6 au.
Our modelling results for planets around the Sun (Fig. 7f) suggest that an Earth-like planet with a stagnant lid could not be habitable at the orbital distance of Venus at any time, while a planet located at 1 au, such as the Earth, could be habitable throughout nearly the entire evolution for all oxygen fugacities assumed here. An Earth-like stagnant-lid planet at Mars’ orbit may be habitable at later evolutionary times (greater than about 1700 Myr) for oxygen fugacities at the IW buffer and higher.
3.2.3 Continuous habitable zone
For Earth there is evidence of liquid water that dates back to about 3800 Myr ago (see e.g. Kasting 1993). Our results demonstrate that the HZ boundaries shift with time not only due to the evolution of the stellar irradiation, but also because the atmosphere evolves with time. Hence, whether or not a planet is habitable depends not only on the distance to its host star, but also on its age and on its interior composition and its outgassing evolution, among other factors such as stellar metallicity, planetary rotation rate, or water delivery. Imposing the requirement that the planet has liquid water for 3800 Myr reduces the range of possible orbital distances. This range of orbital distances that allows for habitable surface conditions on an Earth-like planet over a long time span is known as the continuous habitable zone (CHZ), a concept discussed by Hart (1979) and Kasting et al. (1993), among others.
An aspect so far not considered when computing the CHZ is the impact of outgassing from the interior and the interior composition. Even when fixing the initial amount of water in the mantle, we obtain different widths of the HZ due to the different oxygen fugacities. Figure 8 shows the minimum and maximum CHZ boundaries for the different host stars assuming an initial mantle water concentration of 500 ppm. The maximum CHZ shows the range of orbital distances where an Earth-like stagnant-lid planet could be potentially habitable over 3800 Myr from tint= 700–4500 Myr. However, the CHZ depends on the oxygen fugacity of the mantle. For the boundaries of the minimum CHZ we set as a requirement that habitability is obtained for all of the oxygen fugacities assumed in this study (between IW + 1 and IW − 1) over 3800 Myrs, which reduces the orbital distances covered drastically. We compared the maximum CHZ boundaries with those of Kopparapu et al. (2013) and find a relatively good agreement, especially at the OHZ. At the inner edges differences occur that are most probably due to the treatment of H2O in the radiative transfer of the models, which is a major uncertainty in the calculation of the inner edge of the HZ as discussed by Yang et al. (2016). Interestingly, the Earth resides just at the outer edge of the minimum CHZ.
 |
Fig. 8 Continuous HZ over 3800 Myr with tint from 700 to 4500 Myr and for an initial mantle water content of 500 ppm. The minimum and maximum extent of the HZ are indicated by shadings. The oxygen fugacities responsible for the minimum and maximum extent of the CHZ are indicated bythe coloured symbols. The black circle shows the location of the Earth. |
3.3 Habitability of stagnant-lid planets around M dwarfs
For planets around M-dwarf stars the pre-main sequence phase with its much higher luminosities is thought to endanger planetary habitability even at later stages (e.g. Ramirez & Kaltenegger 2014; Tian & Ida 2015). Planets that reside within the HZ around their M-dwarf host star at later evolutionary stages (e.g. at 4500 Myr) have resided well inside the inner edge of the HZ during the pre-main sequence phase of their host star. Firstly, here we show how the edges of the HZs evolve under the combined influence of stellar luminosity and outgassing evolution accounting for different M dwarf classes and a variety of initial mantle water concentrations. Secondly, we discuss the possibility of rebuilding the water reservoir after severe water loss during the high-luminosity pre-main sequence phase. As already discussed in Sect. 3.1, for an initial water concentration of 34 ppm we do not find any habitable surface conditions in the classical sense since the outgassed amount of water lies below its saturation pressure at 273.15 K. We therefore analyse only cases where the outgassing is above 6.12 mbar.
For an initial mantle water content of 62 ppm there is a transition from outgassed water abundances below 6.12 mbar for the first 1000 Myr of evolution and above for later times (see Fig. 5a). The evolution of the HZ boundaries of a planet with this initial mantle water concentration around AD Leo is shown in Fig. 9. It is shown starting from 2000 Myr when the outgassed water reservoir is large enough to allow for liquid surface water. The boundaries of the HZ for the case of 62 ppm initial water concentration in the mantle strongly depend on the amount of outgassed CO2. The boundaries of cases with little CO2 in the atmosphere lie closer to the star, and there is no overlap in the HZs with low (IW − 1, IW − 0.5) and high (IW + 0.5, IW + 1) CO2. While the stellar irradiation no longer changes at these later times, as can be inferred from the grey line showing Seff = 1S0, the HZ boundaries still evolve due to outgassing from the interior. This effect is most pronounced for the higher oxygen fugacities.
For initial mantle water concentrations of 125 ppm and above the amount of water outgassed from the interior is almost always above 6.12 mbar. Figure 10 shows the HZ boundary evolution in terms of orbital distance for the sample M dwarf AD Leo, and the M 4 andM 6 dwarfs approximated by a Planck spectrum. The upper panels show the HZ evolution for an oxygen fugacity of IW − 1, the lower panels for an oxygen fugacity of IW + 0.5, leading to the HZs with the smallest and the largest extent in our study, respectively. From the left panels, which show the HZ boundary evolution over 4500 Myr, it can be clearly seen that the time span during which the HZ boundaries shift due to the stellar evolution is shortest for the planets around AD Leo and longest for those around the M 6 dwarf. For the low value of 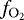 (Fig. 10a) the outward movement of the OHZ boundaries is rather small after the end of the pre-main sequence phase; instead, for IW + 0.5 (Fig. 10c) a large outward movement is apparent. For IW + 0.5 the IHZ also still shows some outward movement for the lower initial mantle water concentrations due to the build-up of CO2 in the atmosphere. The spread of the HZ boundaries for the different initial mantle water abundances is greater for higher oxygen fugacities.
(Fig. 10a) the outward movement of the OHZ boundaries is rather small after the end of the pre-main sequence phase; instead, for IW + 0.5 (Fig. 10c) a large outward movement is apparent. For IW + 0.5 the IHZ also still shows some outward movement for the lower initial mantle water concentrations due to the build-up of CO2 in the atmosphere. The spread of the HZ boundaries for the different initial mantle water abundances is greater for higher oxygen fugacities.
The long pre-main sequence phase of the M-dwarfs is believed to cause substantial atmospheric loss. This is justified not only because young M dwarfs tend to be very active, but also because the bolometric luminosity is much higher. This suggests that a planet residing within the HZ around an M dwarf at 4500 Myr would be located well inside the IHZ boundary at earlier evolutionarystages. The time span of this early atmospheric loss will strongly depend on the lifetime of the pre-main sequence phase.
We find a strong impact of the stellar luminosity evolution on the HZ position up to about 200 Myr for the planets around AD Leo (assumed to have a stellar mass of 0.4 MSun), about 1000 Myr for the planets around the M 4 dwarf, and about 2000 Myr for the planets around the M 6 dwarf with a mass of 0.08 MSun. The right panels (b, d) of Fig. 10 show the HZ boundaries of the stagnant-lid planets assuming complete water loss during the pre-main sequence phase. Results are shown starting at 200 Myr, which corresponds to a zoom into the region indicated bythe grey box in the left panels (a, c). To estimate the maximum impact of severe water loss during the pre-main sequence phase, we assume here that all water outgassed during this phase (200, 1000, and 2000 Myr for AD Leo, M 4, and M 6, respectively) has been completely lost. Habitable zone boundaries are only shown if the atmosphericand oceanic water reservoir could be rebuilt by secondary outgassing after the pre-main sequence phase.
A HZ can be rebuilt for Earth-like stagnant-lid planets around AD Leo by secondary outgassing after the pre-main sequence phase. The HZ boundaries change marginally, mainly for IW + 0.5. The amount of outgassed water during the first 200 Myr, hence the amount assumed to be lost completely, ranges from 1.25 × 10−3 to 1.59 bar. This makes up about 3–15% of the total amount of water outgassed over the 4500 Myr, which ranges from 4.02 × 10−2 to 10.31 bar.
For Earth-like stagnant-lid planets around the M 4 star with an oxygen fugacity of IW − 1 a HZ exists for all initial mantle water contents at times larger than 2000 Myr, which is the first time step after imposing complete water loss at which we computed the atmospheres again. For an oxygen fugacity of IW + 0.5 the assumption of water loss shows a large impact on the position of the IHZ, especially for the planets with higher initial mantle water concentrations of 250 and 500 ppm. For these two cases, 1.7 and 5.6 bar are outgassed until 1000 Myr, which makes up 83 and 78% of the total amount outgassed over 4500 Myr. The HZ boundaries calculated without water loss are no longer attainable via subsequent outgassing, hence water loss here leads to a decrease in HZ width.
For stagnant-lid planets around the M 6 host star, the impact of the pre-main sequence on their habitability would be most severe, as this phase lasts about 2000 Myr. For the cases with a low oxygen fugacity of IW − 1 and high initial mantle water concentrations of 250 and 500 ppm the HZ can be restored. For an initial mantle water concentration of 125 ppm it takes about 2000 Myr to re-establish habitable conditions via outgassing, and for 62 ppm only at 4500 Myr habitability can be restored. For the higher oxygen fugacity of IW + 0.5 the water loss shows, as for the other two host stars, a much stronger impact. For an initial water concentration of 500 ppm habitability is restored directly after the assumed water loss (here at the time step of 3000 Myr), yet with a strong decrease in HZ width. However, the HZ widens again with time. For an initial mantle water concentration of 250 ppm habitability is restored from 4000 Myr on, while for 125 ppm initial mantle water concentration habitability can be rebuilt only at 4500 Myr. For 62 ppm initial mantle water concentration no HZ can be rebuilt by 4500 Myr.
In Fig. 10 we also indicate the positions of Proxima Centaurib, and of three planets orbiting TRAPPIST-1. The Proxima Centauri values are similar to those we assumed for our M 4 star, while TRAPPIST-1 has stellar parameters similar to those assumed for the M 6 star. We can see that Proxima Centauri b (Anglada-Escudé et al. 2016), with an orbital distance of 0.0485 au and an estimated age of about 4800 Myr (from the age of α Centauri; see Bazot et al. 2016) lies in the range of the HZ boundaries for the planets around the M 4-dwarf star. For most assumptionson the interior composition it lies within the HZ even when assuming strong water loss. This is, however, not the case for an 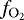 of IW + 0.5 and initial waterconcentrations of 62 ppm and 125 ppm. For 250 ppm the outgassing evolution after 4500 Myr may allow Proxima b to reside within the HZ. For 500 ppm initial water concentration secondary outgassing is large enough to rebuild a HZ after water loss during the pre-main sequence phase.
of IW + 0.5 and initial waterconcentrations of 62 ppm and 125 ppm. For 250 ppm the outgassing evolution after 4500 Myr may allow Proxima b to reside within the HZ. For 500 ppm initial water concentration secondary outgassing is large enough to rebuild a HZ after water loss during the pre-main sequence phase.
The orbital distances of the planets TRAPPIST-1 c, d, and e (Gillon et al. 2017) are indicated in green at 500 Myr because it has been found that TRAPPIST-1 is at least 500 Myr old. Burgasser & Mamajek (2017) find an age of 7.6 ± 2.2 Gyr for TRAPPIST-1. Bolmont et al. (2017) have studied the potential water loss of TRAPPIST-1b, c, and d and found that these planets could have lost water reservoirs several times larger than one Earth ocean. Estimating the habitability at this stellar age would require further model calculations. At 500 Myr an Earth-like planet at the position of TRAPPIST-1 d may be habitable for oxygen fugacities depending on the initial mantle water concentration and for water loss (see Fig. 10). Planets at the position of TRAPPIST-1 e could be habitable for IW + 0.5 and an initial mantle water concentration of 500 ppm if the water loss allowed for a water reservoir larger than 6 mbar. At later stages (e.g. at 4000 Myr) an Earth-like stagnant-lid planet at the orbital distance of TRAPPIST-1 c may become habitable for low oxygen fugacities and large initial mantle water concentrations. While a planet at the TRAPPIST-1 d position would move outside the HZ for IW − 1, a planet at the TRAPPIST-1 e location may stay habitable over longer periods for IW + 0.5 and an initial mantle water concentration of at least 250 ppm, even after severe water loss. However, the determination of the habitability of the detected planets in the TRAPPIST-1 system would require additional calculations since they are probably substantially older than Earth, and all have masses and radii different from Earth, which may lead to differences in the outgassing from the interior (see e.g. Noack et al. 2017; Dorn et al. 2018 for discussions) and in atmospheric behaviour.
 |
Fig. 9 Habitable zone evolution of Earth-like stagnant-lid planets around the M dwarf AD Leo for an initial water concentration of 62 ppm in terms of orbital distance. |
 |
Fig. 10 Habitable zone evolution for planets around the different M dwarfs with different initial water contents (see legend) and oxygen fugacities, upper panels (a, b) IW − 1, lower panels (c, d) IW + 0.5 Left panels: HZ evolution for the full outgassed amounts of H2O and CO2. Right panels: HZ boundaries assuming that all water outgassed during the pre-main sequence phase of the star has been lost for each initial water concentration. For better visibility the y-axis has been changed to linear scale in the right panels. The locations of Proxima Centauri b and TRAPPIST-1c, d, and e are also shown. The grey box in the left panels indicates the time and distance range shown in the right panels. |
4 Discussion
It has been suggested that for planets around M stars, the long, highly luminous pre-main sequence phase endangers their habitability. However, some water reservoirs may be rebuilt by secondary outgassing as shown in this paper. For low initial mantle water concentrations (34–125 ppm) that may result from atmospheric escape during a long-term magma ocean phase (see e.g. Hamano et al. 2013), we found that the outgassing from the interior starts with a time-lag that facilitates rebuilding of an oceanic-atmospheric water reservoir. In the presence of a relatively dry mantle, in fact, the solidus temperature is high (e.g. Katz et al. 2003) and the mantle then needs 1000–2000 Myr to heat up sufficiently for partial melting to occur and outgassing to be possible (see Fig. 4).
When assuming, as done here, that both the magma ocean and the accretion phases last about a million years for planets around M dwarfs the pre-main sequence phase of early and mid-M dwarfs (here AD Leo and the M 4 dwarf) ends at a time when no outgassing from the interior occurs for the low initial water concentrations. Hence, the majority of H2O and CO2 is outgassed after the transition from the pre-main sequence to the main sequence phase, allowing for rebuilding a surface water reservoir. For the planet around the M 6 star the pre-main sequence phase lasts longer, up to about 2000 Myr. Hence, outgassingfrom a water-poor interior already occurs at times when atmospheric loss should still be strong. Habitability may only be achieved for higher initial mantle water concentrations and at later evolutionary stages on these planets.
4.1 Influence of the magma ocean phase
Longer magma ocean phases would lead to a shift of the beginning of the secondary outgassing phase. For planets with low initial mantle water concentrations which show a delay in the outgassing, it may therefore be the case that the main phase of secondary outgassing begins after the end of the pre-main sequence phase. If the magma ocean phase is too long, however, atmospheric loss could deplete the interior mantle water reservoir too strongly. We have evaluated the length of the magma ocean phases for the luminosity evolutions, by using the equations given in the supplementary material of Hamano et al. (2013). They introduce two types of magma ocean phases, a long-term and a short-term magma ocean phase, the attainment of which depends on the host star’s irradiation. If the irradiation is higher than the achievable outgoing longwave radiation of a water-dominated atmosphere, also known as the radiation limit (e.g. Nakajima et al. 1992), the planet is trapped in a long-term magma ocean that can only be exited via atmospheric water loss or, in our case, by a decrease in stellar irradiation. Using Eq. (S12) in the supplementary material to Hamano et al. (2013), we find at which evolutionary time the planets could switch from such a long-term to a short-term magma ocean. For planets around AD Leo, which reside at the inner HZ boundary at 4500 Myr, a switch from the long-term magma regime into a cooling regime would occur around 70 Myr after the formation of the star. This transition would occur after about 600 Myr for the planet around the M 4 dwarf and after about 1800 Myr for the planet around the M 6 dwarf. This means that planets, especially those around later M-dwarf stars, may stay in a magma ocean phase over a very long time. Secondary outgassing may therefore set in later than assumed in our study. The influence of such a long magmaocean phase is hard to predict without detailed modelling. On the one hand, water loss during a prolonged magma ocean may lead to a mantle too dry to obtain a large enough oceanic-atmospheric water reservoir from secondary outgassing. On the other hand, if the stellar luminosity decreases quickly, the mantle may still be sufficiently wet to allow for a build-up of a water reservoir after the pre-main sequence phase via secondary outgassing.
4.2 Impact of stratospheric temperatures on the HZ
To estimate the impact of our assumptions about the stratospheric temperatures upon the width of the HZ, we ran additional calculations. We compared the results for the outer HZ at 4500 Myr with the different stratospheric temperatures, 150 and 200 K, for an oxygen fugacity of IW + 0.5 and an initial mantle water concentration of 500 ppm and found differences in orbital distance of 0.04 au for the M dwarf AD Leo (≈20%) and 0.4 au for the F dwarf σ Bootis (≈18%). At the IHZ for these cases, the stratospheric temperatures assumed influence the results only for low water abundances, hence early evolutionary stages, since for a higher partial pressure of water the temperature profile is dominated by the convective lapse rate (see Fig. 2). Decreasing the stratospheric temperature to 150 K leads to orbital distance differences of around 0.01 au. Increasing the stratospheric temperature to 250 K leads to larger orbital distance differences of up to 0.1 au for a stagnant-lid planet with an oxygen fugacity of IW + 0.5 and an initial mantle water concentration of 500 ppm around the F dwarf σ Bootis after 2 Myr of interior evolution. Comparing the effect of the stratospheric temperatures on the orbital distance of the HZ boundaries to the effect that could arise from processes not included in this study, such as clouds, or other radiative species, the impact is minor.
4.3 Extensions of the habitable zone
The amount of water outgassed from the interior can be very low for the planets considered here. Even for those with water partial pressures above 6.12 mbar, i.e. those for which liquid water may be stable on the planetary surface for temperatures above 273.15 K, the question remains as to what conditions would be present on such planets.
In our 1D calculations we assume that the atmospheres of our planets are saturated with water vapour (as done in Kasting et al. 1993; Kopparapu et al. 2013), which leads to an IHZ that is located further away from the stars compared to the 3D model results, which account for a self-consistent hydrological cycle. The drying of the atmosphere of a planet with a substantial water reservoir leads to the depression of the global mean relative humidity, and hence allows for higher irradiations, as shown by Abe et al. (2011), Leconte et al. (2013), Wolf & Toon (2014), and Popp et al. (2015). The mean relative humidity has a large impact on the HZ boundaries (Zsom et al. 2013) and surface temperatures (Godolt et al. 2016). The relative humidity of the atmospheres may additionally depend on the spectral energy distribution of the central star. Increased water concentrations have been obtained for planets around M- and K-dwarf stars, partly caused by the higher portion of stellar near-IR radiation (Godolt et al. 2015, Fujii et al. 2017).
If the water reservoir is small and water is transported towards the poles, it may be stored there. This can reduce the water vapour in the atmosphere, especially in the heated equatorial region, which then allows for a more efficient cooling of the planet since the thermal radiation of the hot planetary surface is no longer blocked by the water vapour and can radiate to space. The outgoing long-wave radiation in this case is less limited than for planets with a large, planet-wide water reservoir (see. e.g. Abe et al. 2011). Kodama et al. (2018) have investigated for what water reservoir a transition to such a land planet regime may occur. Assuming zero obliquity and eccentricity, they find that Earth-sized planets with an Earth-like topography and rotation rate become land planets if the water reservoir falls below 1% of the mass of the Earth’s oceans, i.e. about 2.7 bar. The water is then located at higher latitudes, which are not in contact with the Hadley cell. For our scenarios, the amount of outgassed water implies that planets with an initial mantle water concentration below 250 ppm would fall into the land planet regime for an Earth-like topography.
However, the rotation rate of the planet influences the meridional water transport. For rotational periods longer than that of the Earth, the Hadley cell extends over a wider range of latitudes (del Genio & Suozzo 1987). Planets around M dwarfs may be tidally locked. Depending on whether other planets exist in the system, which may excite a non-zero eccentricity (see e.g. Correia et al. 2008), it may be locked into a synchronous orbit with a permanent day side or into another resonance. For tidally locked planets in synchronous orbit at the location of the inner HZ boundary at 4500 Myr, the rotational periods would be 30.47 days for the theoretical planets around AD Leo, 7.8 days for the planets around the M 4 dwarf, and 2.32 days for planets around the M 6 dwarf. The study of del Genio & Suozzo (1987), which assumed Earth-like planets with different rotational periods (without assuming a synchronous orbit) suggests Hadley cells that spread to latitudes larger than 80° for a rotational period of 30 days. For a rotational period of 7.8 days the Hadley cell would span to a latitude of about 60° and to a latitude of about 30–40° for an orbital period of two days. Hence, this effect of storing water in the polar regions may be more effective for planets around the later M-dwarf stars, while for tidally locked planets around early M dwarfs a giant Hadley cell may extend over the entire hemisphere. Hence, especially for the planets around the later M dwarfs the storage of water at the poles may widen the HZ beyond the values we have computed here.
For cases where the water reservoir is large enough to allow water at the substellar point, the inner edge of the HZ around M-dwarfs may be extended towards the star due to the build-up of an effectively scattering cloud deck (Yang et al. 2013, 2014). The strength of this effect however depends on the rotation rate (Kopparapu et al. 2016), as well as on the oceanic heat transport (e.g. Way et al. 2018) and will certainly also depend on the water reservoir. Hence, extensions of the inner HZ boundaries computed here are possible and should be investigated further, accounting for different sizes of water reservoirs and rotation rates. Extensions beyond the outer edge of the HZ discussed here, have been proposed by studies including the effect of additional gases, such as molecular hydrogen (H2) (e.g. Pierrehumbert & Gaidos 2011) or methane (e.g. Ramirez & Kaltenegger 2018). In particular, the amount of primordial H2 retained from the accretion phase plays a decisive role in planetary habitability in general, since these large hydrogen envelopes will likely render the planets uninhabitable (see e.g. Owen & Mohanty 2016).
4.4 Potential sinks of CO2
While we estimated the effect of water for the inner HZ boundary by assuming that all water outgassed until the end of the pre-main sequence has been lost, we neglected the loss of atmospheric CO2 to space in our study. Water loss mainly occurs over photodissociation of H2O and subsequent loss of hydrogen to space. Losing molecules heavier than hydrogen is much more difficult due to the higher molar masses, but it may still be possible for strong irradiation. The outgassing of CO2 from the interior extends over longer timescales than that of water outgassing (see Sect. 3.1). For low initial mantle water concentrations the CO2 outgassing also occurs after a period of no outgassing due to the shift of the solidus to higher temperatures for low water concentrations in the mantle. Hence, CO2 outgassing can also occur after potential substantial atmospheric loss during the pre-main sequence phase.
Another important sink for CO2 is the loss of CO2 by weathering of the surface. We neglected this effect in the present study as in Tosi et al. (2017). Foley & Smye (2018) study the potential impact of weathering for stagnant-lid planets. They find that for large enough planetary carbon reservoirs and radiogenic heating, weathering and outgassing can balance each other for 1000–5000 Myr, thus enabling habitable surface conditions. On the one hand, for large carbon reservoirs they show that weathering is supply-limited, i.e. the supply of fresh surface material is likely too small such that CO2 would accumulate in the atmosphere, which leads to a Venus-like, uninhabitable hot climate. On the other hand, for low outgassing rates limited by the carbon reservoir, the planet would likely exist in a snowball state. For the snowball state limit, they use outgassing values determined by Haqq-Misra et al. (2016) and Kadoya & Tajika (2014) as lower limits, which are equal to 10 and 100% of present Earth’s outgassing, respectively; 10% of Earth’s CO2 outgassing flux, as adopted by Foley & Smye (2018), corresponds to ~2.6 ⋅ 1010 kg yr−1. In our models the rate of CO2 outgassing depends on the initial water concentration and on the assumed redox state. For 62 ppm water in the mantle and 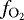 at the IW buffer, the outgassing rate during the phase of melt production peaks at about 2.5 ⋅109 kg yr−1, while for
at the IW buffer, the outgassing rate during the phase of melt production peaks at about 2.5 ⋅109 kg yr−1, while for 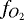 at IW+1 it is one order of magnitude higher, and hence comparable with the lower limit mentioned above. Foley & Smye (2018) discuss weathering for Earth-like water reservoirs. In our scenarios, the weathering of the surface could be limited by the smaller surface water reservoir and lower precipitation rates. Therefore, although our outgassing rates are close to the lower limits adopted by Foley & Smye (2018) that might lead to snowball states, the overall impact of weathering on our findings is not easily predictable and will require further study. Furthermore, Foley & Smye (2018) consider metamorphic outgassing as an additional source of CO2, which could increase CO2 outgassing rates. Metamorphic outgassing refers to the release of CO2 associated with the decarbonation of buried carbonated crust. On Earth, the contribution of this mechanism to the planet’s long-termcarbon cycle is thought to be potentially important, but is still poorly understood (Evans 2011). Furthermore, the release of carbon due to metamorphic processes is generally associated with partial melting in subduction zones (e.g. Dasgupta & Hirschmann 2010) and deformation in active orogenic regions (e.g. Evans et al. 2008), two settings that are intimately related to plate tectonics and hence absent in a stagnant-lid planet. Whether metamorphic outgassing on such bodies can be as relevant as on a planet with plate tectonics is therefore unclear and deserves more investigation.
at IW+1 it is one order of magnitude higher, and hence comparable with the lower limit mentioned above. Foley & Smye (2018) discuss weathering for Earth-like water reservoirs. In our scenarios, the weathering of the surface could be limited by the smaller surface water reservoir and lower precipitation rates. Therefore, although our outgassing rates are close to the lower limits adopted by Foley & Smye (2018) that might lead to snowball states, the overall impact of weathering on our findings is not easily predictable and will require further study. Furthermore, Foley & Smye (2018) consider metamorphic outgassing as an additional source of CO2, which could increase CO2 outgassing rates. Metamorphic outgassing refers to the release of CO2 associated with the decarbonation of buried carbonated crust. On Earth, the contribution of this mechanism to the planet’s long-termcarbon cycle is thought to be potentially important, but is still poorly understood (Evans 2011). Furthermore, the release of carbon due to metamorphic processes is generally associated with partial melting in subduction zones (e.g. Dasgupta & Hirschmann 2010) and deformation in active orogenic regions (e.g. Evans et al. 2008), two settings that are intimately related to plate tectonics and hence absent in a stagnant-lid planet. Whether metamorphic outgassing on such bodies can be as relevant as on a planet with plate tectonics is therefore unclear and deserves more investigation.
4.5 Impact of the stellar irradiation
In this paper, we considered the effect of an increased stellar luminosity during the pre-main sequence phase. So far, we neglected the change in the stellar spectral energy distribution and the impact of stellar activity. In particular, late-type M dwarfs may show increased stellar activity over a much longer time span than solar-like stars (e.g. Schneider & Shkolnik 2018). This may increase the duration of atmospheric water loss. To determine the potential habitability for individual planets, such as Proxima Centauri b, or the planets around TRAPPIST-1, it is therefore crucial to account for all information available for the planets and the stars in order to estimate the impact of the individual processes and their interactions (e.g. Meadows et al. 2018, Ribas et al. 2016, Turbet et al. 2016, 2018).
5 Summary and conclusion
We have studied the co-evolution of stagnant-lid Earth-like planets with their M-, K-, G-, and F-dwarf host stars, accounting for the change in atmospheric mass and composition due to the evolution of the planetary interior and secondary outgassing of H2O and CO2 together with the luminosity evolution of the host star.
We have shown that the width of the HZ for stagnant-lid planets strongly depends on the outgassing of CO2 from the interior, which is controlled by the oxygen fugacity. The classical HZ width can be obtained by secondary outgassing depending on the interior composition. The HZ may be much narrower for low oxygen fugacities or strong losses of CO2, for example via weathering or atmospheric loss processes.
The initial mantle concentration of water is crucial for the outgassing history from the interior. For low initial mantle water concentrations a period of suppressed outgassing (of H2O and CO2) can occur. This effect may allow for the build-up of a secondary water reservoir by outgassing for planets around M dwarfs after the high-luminosity pre-main sequence phase, which is thought to endanger their habitability.
Acknowledgements
The authors thank the anonymous referee for the helpful comments. M.G. gratefully acknowledges support from the DFG through the project GO 2610/1-1 and the priority programme SPP 1992 “Exploring the Diversity of Extrasolar Planets” (GO 2610/2-1). N.T. acknowledges support from the Helmholtz association (VH-NG-1017) and from the DFG through the priority programs 1922 “Exploring the diversity of extrasolar planets” (TO 704/3-1) and 1883 “Building a habitable Earth” (TO 704/2-1). T.R. was funded by DFG grant RU 1839/2.
References
- Abe, Y., Abe-Ouchi, A., Sleep, N. H., & Zahnle, K. J. 2011, Astrobiology, 11, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Agee, C. B. 2008, Philos. Trans. Royal Soc. A, 366, 4239 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, C. W. 1973, Astrophysical Quantities (London: University of London, Athlone Press) [Google Scholar]
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Baines, E. K., & Armstrong, J. T. 2012, ApJ, 744, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bazot, M., Christensen-Dalsgaard, J., Gizon, L., & Benomar, O. 2016, MNRAS, 460, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E., Selsis, F., Owen, J. E., et al. 2017, MNRAS, 464, 3728 [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., & Mamajek, E. E. 2017, ApJ, 845, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Clough, S. A., Kneizys, F. X., & Davies, R. W. 1989, Atmos Res., 23, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Levrard, B., & Laskar, J. 2008, A&A, 488, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasgupta, R., & Hirschmann, M. M. 2010, Earth Planet. Sci. Lett., 298, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, G., Dominik, C., Waters, L. B. F. M., & Waelkens, C. 2003, ApJ, 598, 636 [NASA ADS] [CrossRef] [Google Scholar]
- del Genio, A. D., & Suozzo, R. J. 1987, J. Atmos. Sci., 44, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Noack, L., & Rozel, A. B. 2018, A&A, 614, A18 [EDP Sciences] [Google Scholar]
- Evans, K. 2011, Geology, 39, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, M. J., Derry, L. A., & France-Lanord, C. 2008, Geochem. Geophys. Geosyst., 9, 4 [Google Scholar]
- Feulner, G. 2012, Rev. Geophys., 50, RG2006 [Google Scholar]
- Foley, B. J., & Smye, A. J. 2018, Astrobiology, 18, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, Y., Del Genio, A. D., & Amundsen, D. S. 2017, ApJ, 848, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Gaillard, F., & Scaillet, B. 2014, Earth Planet. Sci. Lett., 403, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Godolt, M., Grenfell, J. L., Hamann-Reinus, A., et al. 2015, Planet. Space. Sci., 111, 62 [Google Scholar]
- Godolt, M., Grenfell, J. L., Kitzmann, D., et al. 2016, A&A, 592, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldblatt, C., & Watson, A. J. 2012, Philos. Trans. R. Soc. Lond. Ser. A, 370, 4197 [Google Scholar]
- Grott, M., Morschhauser, A., Breuer, D., & Hauber, E. 2011, Earth Planet. Sci. Lett., 308, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Hamano, K., Abe, Y., & Genda, H. 2013, Nature, 497, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Haqq-Misra, J., Kopparapu, R. K., Batalha, N. E., Harman, C. E., & Kasting, J. F. 2016, ApJ, 827, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Hart, M. H. 1979, Icarus, 37, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Hier-Majumder, S., & Hirschmann, M. M. 2017, Geochem., Geophys., Geosyst., 18, 3078 [Google Scholar]
- Hirschmann, M. M., & Withers, A. C. 2008, Earth Planet. Sci. Lett., 270, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Hirth, G., & Kohlstedt, D. 2003, in Inside the Subduction Factory, Geophysical Monograph Series, ed. J. Eiler (Hoboken, NJ: Wiley), 83 [Google Scholar]
- Ida, S., & Lin,D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Kadoya, S., & Tajika, E. 2014, ApJ, 790, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. 1993, Science, 259, 920 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasting, J. F., Pollack, J. B., & Crisp, D. 1984, J. Atmos. Chem., 1, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Katz, R., Spiegelman, M., & Langmuir, C. 2003, Geochem. Geophys. Geosyst., 4, 1073 [Google Scholar]
- Keles, E., Grenfell, J. L., Godolt, M., Stracke, B., & Rauer, H. 2018, Astrobiology, 18, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kodama, T., Nitta, A., Genda, H., et al. 2018, J. Geophys. Res. Planets, 123, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Wolf, E. T., Haqq-Misra, J., et al. 2016, ApJ, 819, 84 [Google Scholar]
- Kunze, M., Godolt, M., Langematz, U., et al. 2014, Planet. Space Sci., 98, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, T., Massol, H., ChassefièRe, E., et al. 2013, J. Geophys. Res. Planets, 118, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Leconte, J., Forget, F., Charnay, B., et al. 2013, A&A, 554, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lissauer, J. J. 2007, ApJ, 660, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- McDonough, W. F., & Sun, S.-S. 1995, Chem. Geol., 120, 223 [Google Scholar]
- Meadows, V. S., Arney, G. N., Schwieterman, E. W., et al. 2018, Astrobiology, 18, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Morschhauser,A., Grott, M., & Breuer, D. 2011, Icarus, 212, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, S., Hayashi, Y.-Y., & Abe, Y. 1992, J. Atmos. Sci., 49, 2256 [Google Scholar]
- Newman, S., & Lowenstern, J. B. 2002, Comput. Geosci., 28, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolaou, A., Katyal, N., Tosi, N., et al. 2019, ApJ, 875, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Noack, L., Godolt, M., von Paris, P., et al. 2014, Planet. Space Sci., 98, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Noack, L., Rivoldini, A., & Van Hoolst, T. 2017, Phys. Earth Planet. Inter., 269, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Mohanty, S. 2016, MNRAS, 459, 4088 [NASA ADS] [CrossRef] [Google Scholar]
- Pierrehumbert, R., & Gaidos, E. 2011, ApJ, 734, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Popp, M., Schmidt, H., & Marotzke, J. 2015, J. Atmos. Sci., 72, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez, R. M., & Kaltenegger, L. 2014, ApJ, 797, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez, R. M., & Kaltenegger, L. 2018, ApJ, 858, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez, R. M., Kopparapu, R., Zugger, M. E., et al. 2014, Nat. Geosci., 7, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Gebauer, S., von Paris, P., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, S. N., Scalo, J., & Meadows, V. S. 2007, ApJ, 669, 606 [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Bolmont, E., Selsis, F., et al. 2016, A&A, 596, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Wattson, R. B., Gamache, R., Schroeder, J. W., & McCann, A. 1995, Atmospheric Propagation and Remote Sensing IV, SPIE Proc., 2471, 2471 [Google Scholar]
- Schneider, A. C., & Shkolnik, E. L. 2018, AJ, 155, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
- Shields, A. L., Bitz, C. M., Meadows, V. S., Joshi, M. M., & Robinson, T. D. 2014, ApJ, 785, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E., Liu, M. C., & Reid, I. N. 2009, ApJ, 699, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Spohn, T., & Schubert, G. 1991, Geophys. J. Int., 107, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., & Ida, S. 2015, Nat. Geosci., 8, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, N., Godolt, M., Stracke, B., et al. 2017, A&A, 605, A71 [Google Scholar]
- Turbet, M., Leconte, J., Selsis, F., et al. 2016, A&A, 596, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turbet, M., Bolmont, E., Leconte, J., et al. 2018, A&A, 612, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- Turcotte, D. L., & Schubert, G. 2002, Geodynamics (Cambridge: Cambridge University Press), 456 [Google Scholar]
- Valencia, D., Tan, V. Y. Y., & Zajac, Z. 2018, ApJ, 857, 106 [NASA ADS] [CrossRef] [Google Scholar]
- von Paris, P., Gebauer, S., Godolt, M., et al. 2010, A&A, 522, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Paris, P., Grenfell, J. L., Rauer, H., & Stock, J. W. 2013, Planet. Space Sci., 82, 149 [NASA ADS] [CrossRef] [Google Scholar]
- von Paris, P., Selsis, F., Godolt, M., et al. 2015, Icarus, 257, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, J. C. G., Hays, P. B., & Kasting, J. F. 1981, J. Geophys. Res., 86, 9776 [Google Scholar]
- Warren, P. H. 1985, Ann. Rev. Earth Planet. Sci., 13, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Way, M. J., Del Genio, A. D., Aleinov, I., et al. 2018, ApJS, 239, 24 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. M., Crisp, J. A., & Spera, F. J. 2006, Geochem. Geophys. Geosyst., 7 [Google Scholar]
- Wolf, E. T., & Toon, O. B. 2013, Astrobiology, 13, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, E. T., & Toon, O. B. 2014, Geophys. Res. Lett., 41, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, E. T., Shields, A. L., Kopparapu, R. K., Haqq-Misra, J., & Toon, O. B. 2017, ApJ, 837, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Wordsworth, R., Kalugina, Y., Lokshtanov, S., et al. 2017, Geophys. Res. Lett., 44, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wunderlich, F., Godolt, M., Grenfell, J., et al. 2019, A&A, 624, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, J., Cowan, N. B., & Abbot, D. S. 2013, ApJ, 771, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Boué, G., Fabrycky, D. C., & Abbot, D. S. 2014, ApJ, 787, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Leconte, J., Wolf, E. T., et al. 2016, ApJ, 826, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Seager, S., de Wit, J., & Stamenković, V. 2013, ApJ, 778, 109 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sketch of the combined interior and atmosphere models. |
| In the text | |
 |
Fig. 2 Outer HZ (panel a) and inner HZ (panel b) temperature profile evolution for an initial water mantle concentration of 500 ppm andat IW + 0.5. |
| In the text | |
 |
Fig. 3 Stellar luminosity evolutions used, following Baraffe et al. (2015). |
| In the text | |
 |
Fig. 4 a: evolution of the mantle temperature for different water concentrations and an oxygen fugacity corresponding to the IW buffer. b: corresponding evolution of the crustal thickness (solid lines) and stagnant lid thickness (dashed lines). The coloured area denotes the distribution of the melt zone and melt fraction for the case with an initial water concentration of 62 ppm. |
| In the text | |
 |
Fig. 5 Outgassing of H2O (a) and CO2 (b) for the same cases shown in Fig. 4. The horizontal grey line in the panel a corresponds to 6.12 mbar, i.e. the saturation vapour pressure of water at 273.15 K. |
| In the text | |
 |
Fig. 6 Outgassing evolution of H2O (a) and CO2 (b) for an initial mantle water concentration of 62 ppm water and different oxygen fugacities. The grey horizontal line indicates the saturation vapour pressure of water at 273.15 K. The vertical axis of panel a is linear, while it is logarithmic in panel b and in Fig. 5. |
| In the text | |
 |
Fig. 7 Habitable zone evolution for planets with an initial interior water content of 500 ppm. Left column: HZ boundaries in terms of stellar irradiation (S0), around an M, K, G, and F dwarf (from top to bottom). Right column: HZ boundaries in orbital distance (au), which includes the stellar luminosity evolution. For illustration we indicate the orbital distance evolution of Seff = 1S0 with a grey solid line, which is the radiation the Earth receives from the Sun today, and the orbital distances of Venus, Earth, and Mars in panel f with vertical grey dashed lines. The stellar age corresponding to the interior evolution times is indicated on the secondary y-axis where applicable. |
| In the text | |
 |
Fig. 8 Continuous HZ over 3800 Myr with tint from 700 to 4500 Myr and for an initial mantle water content of 500 ppm. The minimum and maximum extent of the HZ are indicated by shadings. The oxygen fugacities responsible for the minimum and maximum extent of the CHZ are indicated bythe coloured symbols. The black circle shows the location of the Earth. |
| In the text | |
 |
Fig. 9 Habitable zone evolution of Earth-like stagnant-lid planets around the M dwarf AD Leo for an initial water concentration of 62 ppm in terms of orbital distance. |
| In the text | |
 |
Fig. 10 Habitable zone evolution for planets around the different M dwarfs with different initial water contents (see legend) and oxygen fugacities, upper panels (a, b) IW − 1, lower panels (c, d) IW + 0.5 Left panels: HZ evolution for the full outgassed amounts of H2O and CO2. Right panels: HZ boundaries assuming that all water outgassed during the pre-main sequence phase of the star has been lost for each initial water concentration. For better visibility the y-axis has been changed to linear scale in the right panels. The locations of Proxima Centauri b and TRAPPIST-1c, d, and e are also shown. The grey box in the left panels indicates the time and distance range shown in the right panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


