| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935385 | |
| Published online | 22 April 2019 | |
Letter to the Editor
Data-driven model of the solar corona above an active region
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: warnecke@mps.mpg.de
Received:
1
March
2019
Accepted:
27
March
2019
Aims. We aim to reproduce the structure of the corona above a solar active region as seen in the extreme ultraviolet (EUV) using a three-dimensional magnetohydrodynamic (3D MHD) model.
Methods. The 3D MHD data-driven model solves the induction equation and the mass, momentum, and energy balance. To drive the system, we feed the observed evolution of the magnetic field in the photosphere of the active region AR 12139 into the bottom boundary. This creates a hot corona above the cool photosphere in a self-consistent way. We synthesize the coronal EUV emission from the densities and temperatures in the model and compare this to the actual coronal observations.
Results. We are able to reproduce the overall appearance and key features of the corona in this active region on a qualitative level. The model shows long loops, fan loops, compact loops, and diffuse emission forming at the same locations and at similar times as in the observation. Furthermore, the low-intensity contrast of the model loops in EUV matches the observations.
Conclusions. In our model the energy input into the corona is similar as in the scenarios of fieldline-braiding or flux-tube tectonics, that is, energy is transported to the corona through the driving of the vertical magnetic field by horizontal photospheric motions. The success of our model shows the central role that this process plays for the structure, dynamics, and heating of the corona.
Key words: magnetohydrodynamics (MHD) / Sun: magnetic fields / Sun: corona / methods: numerical
© J. Warnecke and H. Peter 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
When observed in the extreme ultraviolet (EUV), the corona of the Sun above an active region is dominated by plasma loops over a range of temperatures from just below one million to several million Kelvin. The magnetic field in the corona channels the plasma and guides the energy flux. A one-dimensional (1D) model can capture the distribution and variation of intensities and flows along a loop, at least if the variation in energy input is correctly prescribed. It cannot account for the spatial complexity of the real corona, however.
A 3D model can account for not only the complex interaction of the various magnetic features, but also self-consistently provides the spatial and temporal distribution of the energy input (with all its limitations; Peter 2015). The first of these 3D models (Gudiksen & Nordlund 2002, 2005a,b) created a loop-dominated corona; this confirmed the field-line braiding (Parker 1988) or flux-tube tectonics scenarios (Priest et al. 2002). One main question was then and still is now whether such a model can recreate the actually observed corona, if the model is driven by the observed changing magnetic field in the photosphere.
So far, such models have been compared to observations in a generic sense and with good success. For example, results have been compared with respect to average quantities such as emission line Doppler shifts (Peter et al. 2004, 2006; Hansteen et al. 2010). Alternatively, individual features in the models have been picked out that resemble actually observed structures. This provided interesting matches in terms of the width of coronal loops (Peter & Bingert 2012) or transient UV bursts (Hansteen et al. 2017).
The driving of the magnetic field in the photosphere in these models is prescribed by a photospheric velocity driver that mimics the solar granulation (Bingert & Peter 2011, 2013). Alternatively, magnetoconvection models are directly included in the model (Gudiksen et al. 2011; Rempel 2017) or are fed in through the boundary condition (Chen et al. 2014). Using a flux emergence model motivated by observations for the photospheric input, Cheung et al. (2018) were able to reproduce the emission signature of a C-class flare. Bourdin et al. (2013, 2014) used an observed magnetogram to drive the coronal evolution, but this was limited to an active region that was just slightly larger than an X-ray bright point.
Magneto-frictional models have been used to recreate the corona driven by the changing observed photospheric magnetic field, but by design, these models do not provide information on temperature and density (Cheung & DeRosa 2012). They can instead only derive proxies for the coronal emission that is expected. In these models, the currents are furthermore essentially almost (anti-) parallel to the magnetic field; this assumption is not fully valid above active regions (Peter et al. 2015; Warnecke et al. 2017).
Here we use a data-driven 3D magnetohydrodynamic (MHD) model in which the observed (variable) magnetic field of an active region in the photosphere is considered as a lower boundary condition. Most importantly, the model allows synthesizing the coronal emission. A direct comparison can therefore be made between the model and the observed coronal emission from the exact time of the driving magnetogram.
2. Data-driven 3D MHD model
We numerically solved the 3D resistive MHD equations, that is, the induction equation together with the mass, momentum, and energy balance, from the surface of the Sun into the corona. For this we used the PENCIL CODE1 with its special module to account for the physics of the corona (Bingert & Peter 2011, 2013). This solves for the vector potential A, the velocity u, the density ρ, and the temperature T in a fully self-consistent and time-dependent way.
One key element of a coronal model is the inclusion of (Spitzer) heat conductivity along the magnetic field that depends on temperature as T5/2. We used non-Fourier heat flux evolution and semi-relativistic Boris correction (e.g., Boris 1970; Rempel 2017), both newly implemented into the PENCIL CODE to speed up the simulation significantly (see Chatterjee 2018; Warnecke & Bingert 2018, for details). The plasma was cooled by optically thin radiative cooling calculated from a prescribed radiative loss function. The details of the model are presented in Bingert & Peter (2011, 2013) and Warnecke & Bingert (2018) and are not repeated here. We used a magnetic diffusivity of η = 5 × 109 m2 s−1, ensuring a mesh Reynolds number of around unity, and a viscosity of ν = 1010 m2 s−1, similar to the Spitzer value at coronal temperatures and densities.
Our computational domain was a Cartesian box with 1024 × 1024 × 512 grid points, representing 374 × 374 × 80 Mm3 on the Sun. This is large enough to host a typical active region. We used periodic boundary conditions in the horizontal x and y directions. At the top boundary, the box was closed for all thermodynamic quantities, and we applied a potential field condition for the magnetic field. At the bottom boundary (z = 0), which represents the solar surface, the temperature and density were fixed. Here, we prescribed the photospheric velocities using a granulation driver that mimics the distribution of flows in time and space comparable to the observed motions. We followed the original description by Gudiksen & Nordlund (2005a) for this.
The central ingredient of our model is the implementation of the bottom boundary for the magnetic field. Here, we fed a time series of observed values for the (vertical) magnetic field and thus drove the evolution of the magnetic field in the photosphere so that it matched the observed evolution. Because the time cadence of the magnetograms is much slower than the time step of the simulation, we interpolated between the magnetograms that were closest in time for every time step of the numerical model. Photospheric velocities also act on the magnetic field at the bottom boundary and alter it. To ensure that the magnetic field at the bottom boundary continued to evolve according to the observations, we employed a relaxation scheme. This smoothly forces the field at the bottom boundary to follow as prescribed by observations. We chose a timescale of 10 min for this relaxation, motivated by the general timescale of the granular magnetic fields. This approach allowed us to generate upward-directed Poynting flux and simultaneously ensured that we remained close to the observed state (see Bingert & Peter 2011, 2013; Warnecke & Bingert 2018, for details).
To feed the simulation, we used a time series of line-of-sight magnetic field measurements of active region AR 12139 from the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) that begin on 16 August 2014, start at 23:14:53 UT, and have a cadence of 45 s (Fig. 1). The region was very close to disk center, and we therefore used the line-of-sight magnetic field for the vertical component in our simulation. The grid spacing of the model (366 km) is the same as the plate scale of the HMI observation (0.5″ per pixel). We adjusted the edges of the magnetograms to ensure that ethey fulfilled the horizontally periodic boundary conditions. We first ran the simulation with the magnetic field from the first snapshot of the time series to let the temperature and density reach a quasi-stationary state. This took about four solar hours. We then began to feed the time series of the changing magnetic field into the bottom boundary; this drives the evolution in the computational domain. The simulation then evolved for another half hour. We focus our analysis below on the snapshot at 16.5 min.
 |
Fig. 1. Observed photospheric magnetic field that drives our simulation. We show the line-of-sight magnetogram from 16 August 2014 at 23:30:48 UT of active region AR 12139 observed with HMI on board of SDO. The temporal evolution of this magnetogram is used as input for the photospheric magnetic field in the simulation, see Sect. 2. The small square indicates a region of interested where a compact loop is observed, see Sects. 3 and 4. |
3. Comparison with observations
The main goal of this study comparing real observations to the coronal emission as synthesized from our 3D MHD active region model, which is driven by a time series of actually observed magnetograms. For this we derived EUV emission as it would be observed by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012). Based on the temperature and density in the model, we used the temperature response kernel (Boerner et al. 2012)2 of the 171 Å channel. This channel is dominated by emission from Fe X that originates from just below 1 MK.
Overall, the numerical model reproduces the dipole-like structure of the active region. In Fig. 2 we show the comparison of the model as viewed from straight above (left) and the observations near disk center (right) at the same time, that is, the model was evolved using the time-dependent observed magnetograms to the same time as the observations shown here (16.5 min). The peak emission from the observations and the simulation differs by a factor lower than six, which corresponds to differences in density smaller than a factor of 2.5; see Sect. 5 for a detailed discussion. Despite this quantitative difference, we find an overall qualitative agreement, in particular for the following four features (numbers as in Fig. 2).
 |
Fig. 2. Comparison of the observed emission and the emission as synthesized from model. Left panel: emission of the AIA 171 Å channel of AR 12139 on 16 August 2014 at 23:30:48 UT near disk center. Right panel: synthesized emission of the same channel from the simulation as viewed from the top of the computation box. For better visibility, we use a nonlinear scaling of the images (power of 0.7 for the observation, and power of 0.4 for the synthesized emission). The color bars reflect this. The peak count value in the observations (corresponding to 1.00) is 3500 DN pixel−1; this is a factor of six lower for the model. This difference corresponds to a factor of 2.5 in density (see Sect. 5). The inlay shows a zoom-in of the region indicated by the white square. It shows a compact small loop. The color scaling is linear here. The observations and the model cover the same physical space on the Sun with a field of view of (515.9″)2 corresponding to (374.4 Mm)2. The numbers indicate the features discussed in Sect. 3. The blue dashed rectangle indicates the zoom-in used in Fig. 3. |
(1) Long loops. We find that loops with lengths of 100 Mm to 200 Mm connect opposite polarities at the edges of the active region in the northern (top) and southern areas. These loops are associated with the large-scale potential-like magnetic field of the active region. The model loops appear to be less strongly helical than the observed loops, probably because the observed magnetograms also lack strong magnetic helicity (see Sect. 5). Like in the observations, the model shows quite a few distinct long loops in the southern part. Some even lie at roughly the same location (1a). The observations show a more complex broad bundle of loops in the northern part, where the model only shows a single long loop (1b). The long model loop in the north still shows a rather broad structure with a clear loop in the middle.
(2) Fan loops. In our model we find fan loops, in particular, on the western (right) side of the active region. They appear at the same locations as very similar features that are visible in the observations. Several thinner structures quickly diverge and form a funnel-type structure in which the thinner strands are embedded (2a). Our model even reproduces a smaller feature of this type outside of the main part of the active region (2b) in an area of enhanced magnetic field strength (cf. Fig. 1). The fan loops in this setup also appear because of the horizontal periodic domain; see the discussion in Sect. 5.
(3) Diffuse emission. Loops in the corona have a rather low contrast, they often stick out of a diffuse non-resolved background by only 10% to 30% (Del Zanna & Mason 2003; Peter et al. 2013). We see this general pattern in our model as well. Most of the thin loops are embedded in much thicker structures of diffuse emission. In our model this is due to the high magnetic resistivity, but it might well reflect the situation on the real Sun (for a discussion of the resistivity in MHD models, see Peter 2015).
(4) Compact loops. In the core of an active region, observations show an abundance of small transient features, which may be low-lying loops that are related to small-scale magnetic patches in the photosphere (Peter et al. 2013). In the model we see only a few of these, probably because of the limited spatial resolution (see Sect. 5). The example shown in the inset of Fig. 2 only exists for less than 10 min in the simulation and is indeed a low-lying loop (cf. Sect. 4) that is rooted in two small opposite-polarity patches that evolve quickly.
4. Energy deposition in the corona
The coronal structures that appear in the model do so because energy is deposited along field lines that are at their footpoints driven by horizontal motions. Here, we briefly discuss the relation of the loops that appear to the energy input per particle. In Fig. 3 we display the distribution of the energy input at the same time as the snapshot of the emission shown in Fig. 2, but integrated in time for the 120 s leading up to that time. This accounts for the Alfvén transit time through the coronal structure so that disturbances of the magnetic field have time to spread.
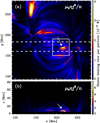 |
Fig. 3. Energy deposition in terms of Ohmic heating rate per particle μ0ηj2/n. Panel a: top view of an average over 2 min (14.5 to 16.5 min) and in the vertical direction from z =0 to 30 Mm. Panel b: average over a stripe with y = 160 to 183 Mm, as indicated in panel a (also averaged over 2 min). The white square shows the region of interest with the compact small loop (indicated by arrows in both panels); compare with Fig. 2. |
When we integrate the energy input per particle vertically, loop features become visible that are similar to those seen in emission (compare Fig. 3 to the emission in the blue dashed rectangle in Fig. 2). We see more spatial variation along the field lines in the energy input than in coronal intensity. The reason is that the energy is efficiently redistributed through (Spitzer) heat conduction parallel to the magnetic field. Heat conduction quickly evens out temperature inhomogeneities and leads to a comparably constant temperature along a field line and thus a comparably constant coronal emission along the loop. The appearance of the EUV loops is directly linked to the energy input into the corona (Peter & Bingert 2012) and is (in our model) a direct consequence of the energy injection near the loop footpoints (at the height where plasma-β is about unity; cf. Chen et al. 2014).
While the model evolves, that is, while the changing photospheric field drives the system, compact coronal loops appear in a transient fashion. One of these short loops is highlighted by the white squares in all the figures. It clearly connects opposite magnetic polarities (Fig. 1), and the photospheric motions lead to the strong heating (per particle) in what then appears as the short EUV loop (inset of Fig. 2). The greater heating is clearly visible when the computational box is viewed from the top and from the side (arrows in Fig. 3). These small features might be related to the miniature loops that were found in observations (Peter et al. 2013). Here the loop is showing up transiently because at low heights and high densities, radiative cooling apparently is efficient and thus the lifetime of the structure is short. The overall large-scale loop structure including the long loops, fan loops, and diffusive emission is even visible before we evolve the magnetic field at the bottom boundary according to the observations. However, the small compact loops only appear when we use a time-dependent photospheric field for driving. The time evolution of the magnetic field deposits more energy into the corona on smaller scales.
5. Limitations of the model
This model is generally successful in reproducing the observed corona of the active region, but several limitations need to be kept in mind. The main limitation probably is the moderate spatial resolution that does not allow us to properly resolve the small-scale magnetic features on granular scales of 1000 km and smaller. Most of the shortcomings of our model might be traced to this limitation.
A higher spatial resolution would reveal smaller features of the photospheric magnetic field that drives the model. These small magnetic patches would give rise to a higher (transient) energy input that would cause more small-scale hot structures at low heights to appear as compact transient loops. Observationally, there are clear indications that such small-scale opposite polarities cause heating of coronal structures (Chitta et al. 2017, 2019). With the current setup, we need observations of the photospheric magnetic field of the whole active region, and such data are available only at a moderate spatial resolution of about 1″, such as those provided by HMI that we use here. High-resolution observations would provide only an insufficient field of view that does not cover the whole active region.
Our model does not produce regions at high temperature of 5 MK or above at sufficiently high density to give rise to X-ray loops in the core of the active region. Again, this could be due to the lack of resolution, which prevents opposite polarities from canceling and from providing high-energy fluxes into the corona (cf. observations by Chitta et al. 2018). In a model with a smaller computational domain, Archontis & Hansteen (2014) indeed reported that plasma was heated to flare-like temperatures in compact (few Mm) structures. In general, we would therefore expect a higher energy input into the upper atmosphere if we were able to feed the model with magnetic field data at significantly higher spatial resolution.
As a consequence of the possibly too low energy flux in the model, the model density might be too low as well. According to the scaling laws of Rosner et al. (1978), the coronal density scales roughly with the heat input to the power of 4/7. The densities in our model, and consequently, the count rates, might therefore be lower than in the observed active region. The count rates in the model are too low by about a factor of six, which means that the density is too low by about a factor of 2.5. This probably also affects the density distribution along the loop and is the reason that we scaled our model emission nonlinearly with a power of 0.4 in Fig. 2 (while the observations are scaled closer to linear with a power of 0.7).
The loops in our model corona look more like those in a potential field than like the loops in the observations. In our model we only prescribed the vertical component of the magnetic field, but not the horizontal component (which is not available at 45 s cadence and for this large field of view with HMI). We would therefore miss any helical component of the magnetic field, which would lead to a more twisted appearance of the magnetic field. Moreover, this would increase the energy input into the system and thus help alleviate the problem described above, at least to some extent.
Finally, we assume periodic boundary conditions in our model (as do most other 3D MHD models of the solar atmosphere). This implies that the field lines of the fan loops on the western (right) side of the active region leave the box on that side and enter the box again on the other side. In the model, the fan loops therefore connect to an active region (different from the first). On the real Sun, such a connected active region would be far away, at a distance that is far larger than the size of an active region. We tried to account for this in the model by surrounding the active region by enough quiet Sun, so that the appearance of the fan loops is hopefully realistic.
None of the above limitations are expected to alter the main conclusion of our study: our data-driven model can account for the structures seen on the real Sun. Future models will have to address these remaining problems step by step, however.
6. Conclusions
We showed that we can reproduce many aspects of the corona above an active region using a data-driven 3D MHD model. The emission that we synthesized from the model qualitatively reproduces the observed coronal features of this active region: long loops, fan-like loops, and small transient loops in the active region core. We also showed that these model features are embedded in a diffuse background of coronal emission, as is the case on the real Sun, where a typical loop has a low contrast of only 10% to 30% to the background.
Our data-driven model shows that the structure of the observed photospheric magnetic field and its temporal evolution fully govern the appearance of the corona in an active region. Driving the magnetic field at the surface induces currents in the corona at just the correct places: here the plasma is heated and forms EUV loops in the model at exactly the same place where they also appear in the real observations. The energy input in our model is solely based on the driving of the magnetic field and is thus very similar to the scenarios of field-line braiding (Parker 1988) and flux-tube tectonics scenarios (Priest et al. 2002). The success of our model therefore supports these heating scenarios.
The main shortcoming of our work is the lack of spatial resolution of the photospheric field: to cover a full active region, observational data are available only at a moderate resolution of about 1″. However, we can expect smaller magnetic patches to play a significant role in energizing the corona. This could lead to a higher energy input, and in particular, also to a higher structuring of the corona in the core of the active region. Likewise, if we included the horizontal component of the magnetic field, the energy input would increase, and would in particular lead to a more strongly twisted appearance of the coronal loops in the model. This would bring them closer to the actual observations.
Our data-driven 3D MHD model does reproduce the overall appearance of the corona in an active region despite the limitations outlined in Sect. 5. This first look at the results shows that the driving of the corona by the observed magnetic field at the surface level indeed gives rise to coronal structures that appear in the model at (roughly) the same time and location as in the observations of the real Sun.
Implemented in SolarSoft, http://www.lmsal.com/solarsoft/
Acknowledgments
We thank Lakshmi Pradeep Chitta and Sven Bingert for discussion leading to this work. Simulations have been carried out on supercomputers at GWDG, on the Max Planck supercomputer at RZG in Garching, in the facilities hosted by the CSC–IT Center for Science in Espoo, Finland, which are financed by the Finnish ministry of education. J. W. acknowledges funding by the Max-Planck/Princeton Center for Plasma Physics and from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007-2013) under REA grant agreement No. 623609.
References
- Archontis, V., & Hansteen, V. 2014, ApJ, 788, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 530, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2013, A&A, 550, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Boris, J. P. 1970, A Physically Motivated Solution of the Alfven. Problem (NRL Memorandum Report), 2167 [Google Scholar]
- Bourdin, P.-A., Bingert, S., & Peter, H. 2013, A&A, 555, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourdin, P.-A., Bingert, S., & Peter, H. 2014, PASJ, 66, S7 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P. 2018, Geophys. Astrophys. Fluid Dyn., submitted [arXiv:1806.08166] [Google Scholar]
- Chen, F., Peter, H., Bingert, S., & Cheung, M. C. M. 2014, A&A, 564, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., & DeRosa, M. L. 2012, ApJ, 757, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Chintzoglou, G., et al. 2018, Nat. Astron., 3, 160 [Google Scholar]
- Chitta, L. P., Peter, H., Solanki, S. K., et al. 2017, ApJS, 229, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Chitta, L. P., Peter, H., & Solanki, S. K. 2018, A&A, 615, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chitta, L. P., Sukarmadji, A. R. C., Rouppe van der Voort, L., & Peter, H. 2019, A&A, 623, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., & Mason, H. E. 2003, A&A, 406, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gudiksen, B. V., & Nordlund, Å. 2002, ApJ, 572, L113 [Google Scholar]
- Gudiksen, B. V., & Nordlund, Å. 2005a, ApJ, 618, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., & Nordlund, Å. 2005b, ApJ, 618, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansteen, V. H., Hara, H., De Pontieu, B., & Carlsson, M. 2010, ApJ, 718, 1070 [Google Scholar]
- Hansteen, V. H., Archontis, V., Pereira, T. M. D., et al. 2017, ApJ, 839, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Peter, H. 2015, Trans. R. Soc. London Ser. A, 373, 20150055 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., & Bingert, S. 2012, A&A, 548, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, Å. 2004, ApJ, 617, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, Å. 2006, ApJ, 638, 1086 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peter, H., Bingert, S., Klimchuk, J. A., et al. 2013, A&A, 556, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peter, H., Warnecke, J., Chitta, L. P., & Cameron, R. H. 2015, A&A, 584, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priest, E. R., Heyvaerts, J. F., & Title, A. M. 2002, ApJ, 576, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2017, ApJ, 834, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Warnecke, J., & Bingert, S. 2018, Geophys. Astrophys. Fluid Dyn., submitted [arXiv:1811.01572] [Google Scholar]
- Warnecke, J., Chen, F., Bingert, S., & Peter, H. 2017, A&A, 607, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Observed photospheric magnetic field that drives our simulation. We show the line-of-sight magnetogram from 16 August 2014 at 23:30:48 UT of active region AR 12139 observed with HMI on board of SDO. The temporal evolution of this magnetogram is used as input for the photospheric magnetic field in the simulation, see Sect. 2. The small square indicates a region of interested where a compact loop is observed, see Sects. 3 and 4. |
| In the text | |
 |
Fig. 2. Comparison of the observed emission and the emission as synthesized from model. Left panel: emission of the AIA 171 Å channel of AR 12139 on 16 August 2014 at 23:30:48 UT near disk center. Right panel: synthesized emission of the same channel from the simulation as viewed from the top of the computation box. For better visibility, we use a nonlinear scaling of the images (power of 0.7 for the observation, and power of 0.4 for the synthesized emission). The color bars reflect this. The peak count value in the observations (corresponding to 1.00) is 3500 DN pixel−1; this is a factor of six lower for the model. This difference corresponds to a factor of 2.5 in density (see Sect. 5). The inlay shows a zoom-in of the region indicated by the white square. It shows a compact small loop. The color scaling is linear here. The observations and the model cover the same physical space on the Sun with a field of view of (515.9″)2 corresponding to (374.4 Mm)2. The numbers indicate the features discussed in Sect. 3. The blue dashed rectangle indicates the zoom-in used in Fig. 3. |
| In the text | |
 |
Fig. 3. Energy deposition in terms of Ohmic heating rate per particle μ0ηj2/n. Panel a: top view of an average over 2 min (14.5 to 16.5 min) and in the vertical direction from z =0 to 30 Mm. Panel b: average over a stripe with y = 160 to 183 Mm, as indicated in panel a (also averaged over 2 min). The white square shows the region of interest with the compact small loop (indicated by arrows in both panels); compare with Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


