| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834275 | |
| Published online | 02 April 2019 | |
Kepler-411: a four-planet system with an active host star★
1
Yunnan Observatories, Chinese Academy of Sciences,
Kunming 650216,
PR China
e-mail: sunleilei@ynao.ac.cn, wangxb@ynao.ac.cn
2
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences,
Kunming 650216,
PR China
3
University of Chinese Academy of Sciences,
Beijing 100049,
PR China
4
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112,
21029 Hamburg, Germany
e-mail: pioannidis@hs.unihamburg.de
5
Department of Mathematical Sciences, Xian Jiaotong-Liverpool University (XJTLU), 111 Renai Road, Suzhou Dushu Lake Science and Education Innovation District,
Suzhou Industrial Park,
Suzhou 215123, PR China
Received:
19
September
2018
Accepted:
13
December
2018
We present a detailed characterization of the Kepler-411 system (KOI 1781). This system was previously known to host two transiting planets: one with a period of 3 days (R = 2.4 R⊕; Kepler-411b) and one with a period of 7.8 days (R = 4.4 R⊕; Kepler-411c), as well as a transiting planetary candidate with a 58-day period (R = 3.3 R⊕; KOI 1781.03) from Kepler photometry. Here, we combine Kepler photometry data and new transit timing variation (TTV) measurements from all the Kepler quarters with previous adaptive-optics imaging results, and dynamical simulations, in order to constrain the properties of the Kepler-411 system. From our analysis, we obtain masses of 25.6 ± 2.6 M⊕ for Kepler-411b and 26.4 ± 5.9 M⊕ for Kepler-411c, and we confirm the planetary nature of KOI 1781.03 with a mass of 15.2 ± 5.1 M⊕, hence the name Kepler-411d. Furthermore, by assuming near-coplanarity of the system (mutual inclination below 30°), we discover a nontransiting planet, Kepler-411e, with a mass of 10.8 ± 1.1 M⊕ on a 31.5-day orbit, which has a strong dynamical interaction with Kepler-411d. With densities of 1.71 ± 0.39 g cm−3 and 2.32 ± 0.83 g cm−3, both Kepler-411c and Kepler-411d belong to the group of planets with a massive core and a significant fraction of volatiles. Although Kepler-411b has a sub-Neptune size, it belongs to the group of rocky planets.
Key words: planets and satellites: dynamical evolution and stability / stars: activity / planetary systems / starspots
Tables 2–4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/624/A15
© ESO 2019
1 Introduction
The data from the Kepler mission have revealed thousands of exoplanets and exoplanet candidates through the transit method (Borucki et al. 2010). After the demise of the “old”, primary Kepler mission, the extended Kepler mission K2 has been revealing many new exoplanet candidates (Howell et al. 2014). While being very powerful, the transit method cannot provide the masses of the discovered transiting bodies, and therefore mass measurements have been carried out for only a rather small fraction of the discovered planetary candidates, either with the radial velocity (RV) method or with the transit timing variation (TTV) method (Jontof-Hutter et al. 2015; Hadden & Lithwick 2017). The RV technique measures the reflex motion of a host star induced by its planet, and hence the signal shrinks with increasing orbital distance, while the latter detects the gravitational perturbations between planets in multi-planet systems by precisely measuring transit times and subsequently fitting dynamical models (or derived analytic formulae) to the observed TTVs (Miralda-Escudé 2002; Agol et al. 2005; Holman & Murray 2005; Holman et al. 2010; Nesvorný et al. 2012; Lithwick et al. 2012; Xie 2014; Jontof-Hutter et al. 2015; Deck & Agol 2015; Agol & Deck 2016). Hence, the TTV technique is very sensitive to gravitational interactions between planets that are closely spaced or near orbital resonances, in addition to the positive dependence on the orbital distance (Agol et al. 2005; Holman & Murray 2005). Characterizing planets using TTVs is therefore complementary to the RV method (Agol et al. 2005; Holman & Murray 2005; Nesvorný & Morbidelli 2008; Nesvorný et al. 2012; Jontof-Hutter et al. 2015; Agol & Fabrycky 2018).
Through an analysis of the continuous, high-precision photometric data collected by the Kepler space telescope, one can not only determine the radii and orbital paramaters of transiting exoplanets, but can also infer, or at least constrain, the masses of the exoplanets by studying their dynamical interactions. The planetary mass is a fundamental physical parameter of an exoplanet, which is required for the investigation of further planetary properties, such as the composition, structure, and also the formation and evolution of the planetary system (Seager et al. 2007; Fortney et al. 2007; Baraffe et al. 2008, 2010; Enoch et al. 2012; Lopez et al. 2012; Lopez & Fortney 2014; Kouwenhoven et al. 2016).
The vast majority of the host stars of the currently known exoplanets are of late spectral type and are therefore to some degree magnetically active. Specifically, stellar activity in late-type stars induces photometric modulations and apparent RV variations, which may hamper the detection of planets and the accurate measurement of the system parameters (Sozzetti et al. 2007; Enoch et al. 2010; Czesla et al. 2009; Oshagh et al. 2015). Star spots can deform the transit light curves, for example through spot-crossing events, and can thus possibly mimic the TTV signals induced by the gravitational perturbations of other planets (Oshagh et al. 2013; Daassou et al. 2014; Ioannidis et al. 2014, 2016; Ioannidis & Schmitt 2016; Sun et al. 2017). Therefore, appropriately accounting for the effects of stellar activity on transit light curves becomes absolutely necessary for characterizing exoplanets orbiting relatively active host stars.
In this study we present our comprehensive analysis and characterization of the multiple planetary system Kepler-411. In Sect. 2 we provide a brief description of our target system and in Sect. 3 we describe the methods used to extract the transit signals and derive the planetary properties. In Sect. 4, we give the results of our TTVs and dynamical simulation analyses and in Sect. 5, we discuss the new results and constrain the compositions of Kepler-411’s transiting planets. Finally, we summarize the study in Sect. 6.
 |
Fig. 1 Upper panel: part of the long-cadence data of Kepler-411, with apparent rotational modulations. Lower panel: light curves detrended using the Savitzky–Golay filter. The red, green, and blue vertical lines in the lower panel mark the transit events of three transiting planets of Kepler-411. |
2 The Kepler-411 planetary system
The host star, Kepler-411, is a K2V-type star located at a distance of 153.59 ± 0.48 pc (Gaia Collaboration 2018; Lindegren et al. 2018; Berger et al. 2018) exhibiting features that indicate relatively strong magnetic activity. Besides rotational modulation with a periodicity of about 10 days as seen in the Kepler light curve (Hirano et al. 2014), we find that strong emissions are detected in the cores of the Ca II H and K lines by visually inspecting the spectroscopic data in the Keck Observatory Archive1. Kepler-411 has a red companion at an angular separation of 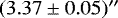 , which is fainter than Kepler-411 by ΔJ = 2.71 ± 0.1 mag (Wang et al. 2014a).
, which is fainter than Kepler-411 by ΔJ = 2.71 ± 0.1 mag (Wang et al. 2014a).
Kepler-411 was previously identified as KOI 1781. Three planetary candidates around KOI 1781 were successively discovered by the Kepler transiting planet search pipeline and the public Planet Hunters project (Tenenbaum et al. 2012; Schwamb et al. 2012; Batalha et al. 2013; Rowe et al. 2014); TTV signals of these three planetary candidates were also detected (Ford et al. 2012; Mazeh et al. 2013; Rowe et al. 2014). Subsequently, the planetary nature of KOI 1781.02 (porb = 3.0 days; Kepler-411b) and KOI 1781.01 (porb = 7.8 days; Kepler-411c) were confirmed by Wang et al. (2014a) and Morton et al. (2016), respectively, hence the designation, Kepler-411. Wang et al. (2014a) and Morton et al. (2016) derived a confidence level for the planetary nature of KOI 1781.03 (porb = 58 days; hereafter, we designate this body as Kepler-411d) of over 98.7%, but the planetary nature of this object has not yet be confirmed.
Most interestingly, the amplitude of the TTVs seen in Kepler-411d reaches up to about 50 min, while those of two confirmed planets are smaller than 5 min. Furthermore, the three orbital periods do not approach any commensurability, that is, mean-motion resonances whereby the perturbations between planets are amplified and therefore induce significant TTV signals. To further unravel the planetary architecture of the Kepler-411 system, we continue our investigation of this peculiar planetary system, and present our analysis below.
3 Data analysis
3.1 Data preparation and transit searching
The Kepler data of Kepler-411 were downloaded from the MAST archive2, which contains the data recorded in the 17 quarters; we use both long- and short-cadence data (available for quarters Q10 to Q17). We use the PDCSAP data for our analysis. We show a part of the light curve of Kepler-411 in the upper panel of Fig. 1. One easily identifies peak-to-peak variations of 2–4% in the light curve, indicating that the host star of Kepler-411 is relatively active. Through an analysis of the light curve with the generalized Lomb-Scargle periodogram (Zechmeister & Kuerster 2009), we find a clear rotation period of 10.4 ± 0.03 days.
To characterize the system and to search for and analyze TTVs, it is essential to remove the effects of stellar activity as much as possible. To that end we adopt the same methodology as in Ioannidis et al. (2014) to extract all transit signals from Kepler data and detrend each transit light curve. For “normal” transit signals, that is, single-planet transits, we select a window of twice the transit duration, approximately centered on the mid-transit time of eachglight curve, and detrend each light curve with a second-order polynomial fit to the out-of-transit data.
For “anomalous” transits, that is, two or more planet transits, we use a wider window (i.e. a window of triple the transit duration of Kepler-411d) to retrieve those transits where two or more planets transit the host star simultaneously. Furthermore, to visually validate our normalization of the transit light curves, we use a Savitzky–Golay filter set to second order with a 16-h window to remove the rotational modulations in the light curve of Kepler-411. Prior to filtering the light curves, we substitute all transits with the polynomial fit results of the out-of-transit data in order to retain the characteristics of each transit extracted with our procedure. Through inspection of the detrended light curve, we can easily identify inappropriately detrended transit signals and repeat the detrending procedure for these. Inappropriately detrended transit signals usually originate from incorrect fits due to outliers in out-of-transit data; therefore we fit the out-of-transit again without these outliers. To demonstrate our methodology, we show a part of the Kepler-411 light curve with rotational modulation signals filtered out in the bottom panel of Fig. 1.
As described above, stellar activity may hide the transit signals of Earth-like exoplanets. In order to search for possible transit signals which are obscured by stellar activity, we employ the Box-fitting Least Square algorithm (Kovács et al. 2002) to search the light curves detrended by using the Savitzky–Golay filter with the known transit signals removed. We find no evidence for any significant transit-like signal.
3.2 Model fitting
Stellar activity can not only create bumps on a transit light curve when star spots (or faculae) are occulted by the planet, but can also lead to variable depths of normalized transit light curves due to the influence of stellar activity on the total flux of the host star (Czesla et al. 2009; Ioannidis & Schmitt 2016; Sun et al. 2017).
We employ the Spot and Transit Modeling Tool (STMT), as described in Sun et al. (2017), to model the normal transit light curves of Kepler-411. The recently updated STMT has not only the capability to model the combined effect of spots and planets on the light curve simultaneously, but can also be used to efficiently simulate double transit curves of an active host star using the analytic formulae derived by Pál (2012) and Montalto et al. (2014). Even light curves that include rare mutual planet–planet eclipse events can be modeled by the updated STMT. The new version of the STMT code was successfully tested on the system KOI-94 with mutually eclipsing planets KOI-94d and KOI-94e (Hirano et al. 2012).
We adopt the standard quadratic limb-darkening law, interpolating the limb darkening coefficients from the table of Claret et al. (2013) based on the stellar parameters of Kepler-411 derived by Wang et al. (2014a). Because of the low signal-to-noise ratio (S/N) of the transits sampled with short-cadence data, we use the mean density of the host star, ρ*, derived from interpolating the empirical relation of Torres et al. (2010) as a prior to fit these data. We note that the mean density of the host star can be inferred from normalized orbital semi-major axis a∕R combined with Kepler’s third law when modeling the transit light curves. Furthermore, we adopt the calibration derived by Enoch et al. (2012) to convert the mean density ρ*, the effective temperature Teff, and the metallicity [Fe/H] of the host star into its mass, a method which is also used by the SuperWASP team and other groups (Collier Cameron et al. 2006, 2007; Brown et al. 2012; Wang et al. 2014b; Sun et al. 2015). Therefore, the ratios between the radii and masses of the exoplanet and the host star, respectively, can be converted into the actual planetary radius and mass, and hence the uncertainty of the planet’s radius and mass due to those in the host star can be appropriately estimated.
We first use the normal transit light curves extracted from the short-cadence data to construct a fiducial model of each known transiting body. We note that we only select the transit light curves near the local flux maximum to calculate the physical parameters, since these local maxima tend to be less affected by star spots. These fiducial models form the basis for modeling spot crossing events and double-transit events, because there is a strong degeneracy between transit parameters and spot properties derived from spot-distorted transit light curves (Sun et al. 2017). The short-cadence data constrain the parameters of a transiting body better than the long-cadence data. Short-cadence data, which have a sampling interval of ~ 1 min, on the one hand, keep the morphology of the transit light curve; on the other hand, when many short-cadence light curves are modeled simultaneously, short-cadence data with sufficient sampling can possibly alleviate the influence of stellar activity andthe systematic errors of the light curves of Kepler-411 on the measurement of transit parameters. In Figs. 2–4 we show our best-fit results of the respective transit light curves; we further list the best-fit system parameters of each planet in Table 1 as derived from modeling the transit light curves.
Subsequently, we calculate the transit times through fitting each transit light curve extracted from the long-cadence data with physical parameters fixed to the values derived from the short-cadence data. We adopt the resampling strategy proposed by Kipping (2010) to construct the model of transit light curves in the long-cadence sampling. Since only eight quarters of short-cadence data are available for the four-year observing baseline, we only use the long-cadence data to calculate the TTVs. For the transit light curves with apparent bumps in the ingress and/or egress parts, we adopt a similar strategy to Sun et al. (2017) to model these light curves, in order to remove the possible influences on the measured transit times induced by spot-crossing events. To briefly summarize, we employ one or two circular spot(s) to reproduce the distorted light curves by spot-crossing events with the transit model fixed. We note that we do not impose the constraint that some consecutive transits are modeled with the same spots. The derived transit times are listed in Tables 2–4. We also fit the double-transit light curves with these transit models using the updated STMT code. In Fig. 5 we show two double-transit events to demonstrate the validity of our methodology. We note that the fits of the double transits significantly improve the TTV measurements of Kepler-411d, since only seventeen transit events of this planet have been recorded during the four years of observations. Finally, we derive a more precise stellar mass (M* = 0.870 ± 0.039 M⊙) and radius (R* = 0.820 ± 0.018 R⊙) using the improved measurement of the stellar mean density obtained through our transit light-curve modeling with more data than before. These values are consistent with the previous measurements by Wang et al. (2014a), that is,  and
and 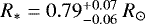 .
.
 |
Fig. 2 Fitting result of the short-cadence transit light curves of Kepler-411b. |
 |
Fig. 3 Fitting result of the short-cadence transit light curves of Kepler-411c. |
 |
Fig. 4 Fitting result of short-cadence transit light curves of Kepler-411d. |
Physical parameters of the planetary companions of Kepler-411.
Mid-transit times of the transit events of Kepler-411d.
Mid-transit times of the transit events of Kepler-411b.
4 Transit timing variation and dynamical stability analysis
4.1 Transit timing variation inversion
4.1.1 Transit timing variation inversion code
We employ the widely used TTV inversion code TTVFast (Deck et al. 2014) to generate model transit times of each of the planets at the observed epoch. The Genetic Evolution Markov Chain (GEMC) and DiffeRentialEvolution Adaptive Metropolis (DREAM) algorithms are used in the TTV inversion code to perform parameter optimization and estimation as implemented in the STMT code (see Sun et al. 2017 for further details). GEMC is an efficient optimization algorithm developed by Tregloan-Reed et al. (2013), which combines the superior global optimization power of genetic algorithms (Charbonneau 1995) with the capability of parameter estimation of widely applied Differential Evolution Markov chain Monte Carlo (DEMCMC) algorithms (ter Braak 2006) in the exoplanet research field for simulating high-dimensional, multi-modal systems. The DREAM algorithm, proposed by Vrugt et al. (2009), is another derivative ofthe DEMCMC algorithms and adopts a self-adaptive randomized subspace sampling strategy, which inherits most of the advantageous properties of the DEMCMC algorithm and performs better through increasing the diversity of the exploration of parameter space. When the code carries out the TTV inversion, it generates model TTVs and then fits them to the measured TTVs. Finally, for a preliminary evaluation of the long-term stability of the synthetic system, we implemented a Hill stability criterion in our code to remove the most unstable planetary architectures (Marchal & Bozis 1982; Gladman 1993). In addition to evaluating synthetic systems, we also tested our code on the KOI-872 system and found that the optimal solution was identical to that of Nesvorný et al. (2012).
4.1.2 Initial TTV inversion of Kepler-411d
As mentioned in the introduction, only Kepler-411d shows large TTVs, while no commensurability is found among the orbital periods of the three known transiting bodies. These observations suggest that there is (at least) one more (nonvisible) planet in orbit around Kepler-411, in addition to the three transiting planets. This additional planet may be in (or near) a mean-motion resonance with Kepler-411d. In order to test this hypothesis, we use our TTV inversion code to search for the optimal orbital architecture of this new perturber. To improve the efficiency of the dynamical modeling, we initially only include Kepler-411d in addition to the new perturber, because of the weak dynamical interactions of Kepler-411d with the two other known planets.
As the TTV patterns are most sensitive to the perturber’s mass, the orbital period (or orbital separation), the eccentricity, and the mutual inclination of the orbit (Agol et al. 2005; Holman & Murray 2005; Nesvorný & Morbidelli 2008; Nesvorný 2009; Nesvorný & Beaugé 2010; Xie 2014; Agol & Fabrycky 2018), we set appropriate constraints to these parameters during the search for the optimal solution. For the mass of the perturber, we impose a uniform prior between 0.1 M⊕ and 300 M⊕. In order to cover the possible architectures, the search interval for the orbital period of the perturber is set uniformly between 3 and 580 days (the lower limit corresponds to the orbital period of the innermost planet, while the upper limit is set to ten times the orbital period of Kepler-411d). The possibility of wider-orbit perturbers is discussed in Sects. 5.1 and 5.2. We find that the inversion code cannot always find the optimal solution for synthetic TTVs, which are similar to the TTVs of Kepler-411d, when the search interval of the orbital period of the perturber is much larger than 0.5 days and trial chains of 1000 are used in the GEMC algorithm. However, the code always finds the optimal solution when the search interval is set to 0.5 days for trial chains of 1000 in the GEMC algorithm. Therefore, we split the search interval of the orbital period of the perturber into multiples of the 0.5 day interval and search all subintervals each time when we use our code to carry out the initial inversion of the TTVs of Kepler-411d.
We impose a uniform prior to the eccentricity between e = 0 and e = 0.2 as required by the long-term stability of the system, which is demonstrated in the Kepler compact multi-planet systems (Lissauer et al. 2011a; Fabrycky et al. 2014; Xie et al. 2016). In addition, a uniform prior is imposed on the mutual inclination, which is constrained between 0° and 30° (Nesvorný 2009), mainly because larger mutual inclinations will probably trigger significant transit duration variations (TDV) for compact multiple planetary systems and tend to make this kind of system unstable for a long run (Nesvorný et al. 2012; Mills & Fabrycky 2017). On the other hand, no significant TDV signals of Kepler-411d have been detected (i.e. the root mean square of the TDVs of Kepler-411d is almost equal to the median of the uncertainties of transit duration times). The upper limit of the variation rate of the transit durations of Kepler-411d is about 4 min per 1300 days.
Besides these four parameters, three more parameters are initialized: the longitude of the ascending node Ω, the argument of periastron ω, and the mean anomaly M at a reference time (Deck et al. 2014). The tightly packed, multi-planet Kepler systems tend to be coplanar, like our solar system (Winn & Fabrycky 2015; Xie et al. 2016). We explicitly fix the Ω of Kepler-411 d to zero and vary the Ω of the new perturber among the interval between − 30° and 30°, in order to improve efficiency of TTV modeling, and the search intervals of argument of periastron and mean anomaly are set to the physical boundary, that is, ω ∈ (−180°, 180°) and M ∈ (0°, 360°). So as to accelerate the MCMC sampling, 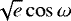 and
and 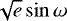 are used as free parameters to explore the parameter spaces of e and ω in our inversion code, where e and ω are the eccentricity and argument of periastron, respectively (Ford 2005; Eastman et al. 2013).
are used as free parameters to explore the parameter spaces of e and ω in our inversion code, where e and ω are the eccentricity and argument of periastron, respectively (Ford 2005; Eastman et al. 2013).
We find that the dynamical modeling uniquely generates the reduced minimum 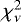 of 3.8 (i.e. the reduced minimum
of 3.8 (i.e. the reduced minimum 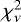 which is larger than unity is probably induced by the underestimation of transit-time uncertainties) when the orbital period of the perturber is equal to 31.5 days. Taking the possible underestimation of transit-time uncertainties into account, we use the reduced
which is larger than unity is probably induced by the underestimation of transit-time uncertainties) when the orbital period of the perturber is equal to 31.5 days. Taking the possible underestimation of transit-time uncertainties into account, we use the reduced 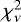 of the optimal fitting derived from GEMC simulation in the TTV inversion code to scale the errors of measured transit times (namely, all errors are multiplied by a factor of
of the optimal fitting derived from GEMC simulation in the TTV inversion code to scale the errors of measured transit times (namely, all errors are multiplied by a factor of 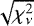 ), and then employ the MCMC algorithm to sample the parameter posterior distributions based on the scaled errors. The orbital period ratio between Kepler-411d and the newly identified perturber is 1.84, which is near the 2:1 (or 9:5) mean-motion resonance with Kepler-411d. Moreover, the orbital-period ratio between Kepler-411c and the perturber is 4.02. The impact parameter b of the perturber is 1.6 (i.e. b ≫ 1 + Rp∕R*) based on the extracted orbital architecture. This provides strong evidence for the hypothesis that the 31.5-day perturber is a nontransiting planet. Hereafter, we label this new planet as Kepler-411e.
), and then employ the MCMC algorithm to sample the parameter posterior distributions based on the scaled errors. The orbital period ratio between Kepler-411d and the newly identified perturber is 1.84, which is near the 2:1 (or 9:5) mean-motion resonance with Kepler-411d. Moreover, the orbital-period ratio between Kepler-411c and the perturber is 4.02. The impact parameter b of the perturber is 1.6 (i.e. b ≫ 1 + Rp∕R*) based on the extracted orbital architecture. This provides strong evidence for the hypothesis that the 31.5-day perturber is a nontransiting planet. Hereafter, we label this new planet as Kepler-411e.
Mid-transit times of the transit events of Kepler-411c.
 |
Fig. 5 The first light curve shows a double transit of Kepler-411b and Kepler-411d. The second light curve shows a double transit of Kepler-411c and Kepler-411d. The residuals of the second light curve have been shifted for clarity. The physical parameters of the transit models of planets Kepler-411b, c, and d are those derived using the short-cadence data. |
 |
Fig. 6 Optimal fitting result of Kepler-411b TTVs. |
4.1.3 Joint transit-timing-variation inversions
As shown in Sect. 4.1.2, an additional, nontransiting fourth planet Kepler-411e is necessary to reproduce the measured TTVs of Kepler-411 d. Moreover, Kepler-411 d is shown to be a genuine planetary companion of Kepler-411 (see Sect. 5.2). In this subsection, we jointly simulate the TTVs of the three known transit signals assuming that one additional nontransiting perturber exists in the system.
We adopt the same parameter priors and boundaries as used in Sect. 4.1.2, except for the orbital period and inclination, since these parameters are well-constrained by transit light curves. However, the values derived from modeling the transit light curves are the averages of these parameters at the observation baseline, but the input parameters of TTVFast are a set of instantaneous variables representing the dynamical state of a system at the initial reference time (Deck et al. 2014). Therefore, we sample the initial inclination corresponding to the nominal value and uncertainty derived from modeling transit light curves. The search interval of the orbital period is centered on the values derived from modeling the transit light curves, and is uniformly spread over intervals of 0.2 days. A typical uncertainty of 0.2 days is much larger than the uncertainty of orbital period derived from modeling transit light curves, but this value likely covers the possible variation of instantaneous period. The optimal physical parameters resulting from the numerous TTV inversions are illustrated in Table 1 for the four-planet orbital architecture. These optimal models are plotted in Figs. 6–8 with the measured TTV signals.
Many authors have shown the existence of degeneracies between planet mass and eccentricity, and even the differential argument of orbital periastron of two planets (i.e. Δω = |ω1 − ω2|) extracted from TTVs near by first-order (or higher-order) mean-motion resonances (Boué et al. 2012; Lithwick et al. 2012; Deck & Agol 2015; Goździewski et al. 2016; MacDonald et al. 2016; Nesvorný & Vokrouhlický 2016; Agol & Fabrycky 2018). These imply that the parameter spaces of the TTV inversion are highly correlated and hence insufficient samplings can easily misrepresent the measured TTVs. In order to validate our TTV inversion results, we carry out additional TTV modeling with two different eccentricity priors for four-planet orbital architectures: (i) an eccentricity fixed to zero, and (ii) eccentricities drawn from a uniform distribution U(0, 0.1). When the orbits ofall (or a subset of the) planets in the Kepler-411 system are circular, the measured TTVs are not well reproduced. In the second case, all TTVs are well fitted, and the results are comparable to the case when the modeling of the eccentricities is restricted to U(0, 0.2). As expected, the optimum fits for the planetary masses are mutually consistent at the 1σ significance level for the two different eccentricity priors, but the optimum fits for the orbital eccentricities are different. Similar results were also found in the TTV inversions of MacDonald et al. (2016) for the Kepler-80 system. Therefore, we are confident that the masses extracted from our TTV modeling are reliable global optimal values.
 |
Fig. 7 Optimal fitting result of Kepler-411c TTVs. |
 |
Fig. 8 Optimal fitting result of Kepler-411d TTVs. |
4.2 Dynamical stability
4.2.1 Stability analyses with analytic criterions
As described in Sect. 4.1.1, the TTV inversion code includes a Hill stability criterion for two-planet systems. Although this initial check filters out the least stable systems, it cannot guarantee the long-term stability of the derived orbital architecture of a four-planet system. On one hand, there is no analytical criterion for assessing the long-term stability of multi-planet systems (>2 planets) like that for two-planet systems (Gladman 1993; Chambers et al. 1996). Chambers et al. (1996), Smith & Lissauer (2009), Lissauer et al. (2011b), and similar numerical studies have found that long-term stability of multi-planet systems typically requires the mutual separations between planets to be at least ten mutual Hill radii, which is much larger than the cautious limit of 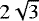 mutual Hill radii required by the Hill stability criterion that is implemented in our TTV inversion code (Gladman 1993; Chambers et al. 1996). Meanwhile, these criteria are only valid under the assumptions of low mutual inclinations and small eccentricities. These two restrictions are usually not well-defined; limiting values of 1°–2° and e = 0.1–0.2, respectively, are often adopted (Petrovich 2015; MacDonald et al. 2016). Apparently, these restrictions and stability criteria are well satisfied by the nominal orbital architecture of the Kepler-411 system inverted from the TTV data. On the other hand, the Hill criterion provides no information about the long-term behavior of the system, and repeated weak interactions between planets in Hill stable orbits may still lead to ejections and/or physical collisions; these are referred to as Lagrange unstable (Petrovich 2015). The chaotic orbits that are generated primarily by first-order (or higher-order) resonance overlap are eventually subjected to large-scale variation of the semi-major axes and hence become Lagrange unstable. Based on previous studies on the chaotic behavior induced by the first-order resonance overlap (e.g. Wisdom 1980; Duncan et al. 1989), Deck et al. 2013 supply the condition that leads to chaotic behavior in a two-planet system (see Eq. (50) in Deck et al. 2013). We apply this criterion to estimate the nominal orbital architecture extracted from the TTV data of the Kepler-411 system, and find that the orbital configuration is far away from the chaotic motion. Therefore, we conclude that the nominal orbital architecture of the Kepler-411 system extracted from measured TTVs satisfies both the Hill and Lagrange stability criteria.
mutual Hill radii required by the Hill stability criterion that is implemented in our TTV inversion code (Gladman 1993; Chambers et al. 1996). Meanwhile, these criteria are only valid under the assumptions of low mutual inclinations and small eccentricities. These two restrictions are usually not well-defined; limiting values of 1°–2° and e = 0.1–0.2, respectively, are often adopted (Petrovich 2015; MacDonald et al. 2016). Apparently, these restrictions and stability criteria are well satisfied by the nominal orbital architecture of the Kepler-411 system inverted from the TTV data. On the other hand, the Hill criterion provides no information about the long-term behavior of the system, and repeated weak interactions between planets in Hill stable orbits may still lead to ejections and/or physical collisions; these are referred to as Lagrange unstable (Petrovich 2015). The chaotic orbits that are generated primarily by first-order (or higher-order) resonance overlap are eventually subjected to large-scale variation of the semi-major axes and hence become Lagrange unstable. Based on previous studies on the chaotic behavior induced by the first-order resonance overlap (e.g. Wisdom 1980; Duncan et al. 1989), Deck et al. 2013 supply the condition that leads to chaotic behavior in a two-planet system (see Eq. (50) in Deck et al. 2013). We apply this criterion to estimate the nominal orbital architecture extracted from the TTV data of the Kepler-411 system, and find that the orbital configuration is far away from the chaotic motion. Therefore, we conclude that the nominal orbital architecture of the Kepler-411 system extracted from measured TTVs satisfies both the Hill and Lagrange stability criteria.
4.2.2 Stability analysis using numerical dynamical simulation
After completing the inversion of TTVs, we obtain the configuration of the Kepler-411 system at the reference time (i.e. BJDTDB −2454833 = 130). Using these as initial conditions, we carry out simulations to evaluate the long-term dynamics of the system. TTVFast is useful for carrying outshort-term simulations of planetary systems, such as for the baseline of the Kepler observations (i.e. several years), while general relativity and tidal effects are not included in the code (Deck et al. 2014). These effects, however, can become important on timescales beyond 1 Myr.
In order to meet our requirements, we employ another publicly available N-body package REBOUND, which uses the Wisdom-Holman symplectic integrator WHFast (Rein & Liu 2012; Rein & Tamayo 2015, 2017), to evolve the system for 1 Myr. We note that these integrations are not intended to provide a comprehensive overview of the dynamics of the planetary system, but are merely used to check whether thesystem can remain stable for at least 1 Myr. In these simulations, the stellar mass is fixed to 0.87 M⊙, and the integration step is set to 0.15 days (roughly 0.05 times the orbital period of the innermost planet). We obtain the initial semi-major axis for each planet from its period using Kepler’s third law. With the exception of orbital semi-major axis, the initial conditions for the other Jacobi orbital elements, such as the eccentricity e, the inclination i, the longitude of ascending node Ω, the argument of periastron ω, and the mean anomaly M, are fixed to the values derived from the TTV inversions so as to improve the efficiency of the simulations. This choice is made because the primary determinants are the mutual distances of the planets for the long-term stability of the system with low eccentricities (<0.2) and mutual inclinations (<2°). We draw 100 initial values for the semi-major axis from a normal distribution N(a0, σa), where a0 represents the nominal value obtained from the TTV inversion, and σa the spread in the semi-major axis, which is estimated using Monte Carlo simulations which include the uncertainties in the mass of the host star, the planetary masses, and the orbital periods.
We classify stable planetary systems as those in which the minimum distance between the planets never violates the Hill stability criterion during the simulations, since the systems that violate the criterion tend to be short-lived due to close planet-planet encounters (Gladman 1993). In addition, we also require the variations in the semi-major axes to be smaller than 10% in cases where a planet is ejected from the system or collisions occur with the star. Among all simulations, the majority (~ 60%) remain stable beyond 1 Myr.
5 Discussion
5.1 The possibility that Kepler-411 e is on a very eccentric and inclined orbit
The constraint of mutual inclination in Sect. 4.1.2 mainly comes from considerations of the long-term stability and less-significant TDV signals of the Kepler-411 system if we hypothesize that the system is similar to most Kepler compact multi-planet systems. Nesvorný (2009) finds that orbits with mutual inclinations ≥ 30° are violently unstable in the most compact planetary systems. For the Kepler-108 system, the mutual inclination of roughly 24° triggers significant TTV and TDV signals on the near 4:1 orbital architectures (Mills & Fabrycky 2017). Therefore, in order to efficiently implement the TTV inversion of Kepler-411 d, we explicitly set the upper limit of mutual inclination to 30°. However, if the perturber is on a wider orbit that is different from most Kepler compact orbital architecture, this kind of orbital architecture, even with larger eccentricity and mutual inclination, will probably be stable in the long term and will likely not trigger large TDV signals on the baseline of primary Kepler observations. In addition, this kind of orbital architecture can also probably induce large TTV signals on Kepler-411 d, due the fact that the mechanism involved is different from the MMR; for example, as the distance of the perturber changes due to its eccentricity, the orbital period of the perturbed planet changes (see Agol et al. 2005). Most importantly, the period of TTVs induced by a perturber on a very eccentric and wide orbit is approximately equal to the orbital period of the perturber (Agol et al. 2005).
We study the possibility that Kepler-411 e is on a very eccentric and inclined orbit. Firstly, we analyze the period of the TTVs of Kepler-411 d using the periodogram tool and find that the power of the periodogram exhibits an apparent peak on the period of about 918 ± 1.5 days. This period should be very close to the orbital period of the perturber if the TTVs of Kepler-411 d are induced by a massive perturber with an eccentric, wide-orbit architecture. Secondly, we set the upper limits of eccentricity and mutual inclination of the perturber to 0.9° and 30°, respectively;the upper limit of the eccentricity of Kepler-411 d is set to 0.5, however, in order to maintain the long-term stability of the inner three planets. In addition, we search for the orbital period of the perturber in the interval between 908 and 928 days, and for the masses of both Kepler-411d and the perturber between 0.1 M⊕ and 15MJup. Finally, we find that this kind of orbital architecture cannot accurately reproduce the TTVs of Kepler-411d. Therefore, we confirm that the orbital architecture of Ppert = 31.5 days is the optimal solution for the TTVs of Kepler-411d.
5.2 Possible influence of the stellar companion of Kepler-411
Although the planetary nature of Kepler-411b and Kepler-411c have been confirmed by Morton et al. (2016) and Wang et al. (2014a), the status of the third candidate, Kepler-411d, is still ambiguous. Adaptive optics and speckle imaging observations indicate a low false-positive rate for Kepler-411d, and also suggest that no other stellar companion is present, in addition to the one already known (Law et al. 2014; Wang et al. 2015; Furlan et al. 2017). In this section we consider the possibility that Kepler-411d orbits the companion, instead of Kepler-411 itself. The Kepler-band differential magnitude between Kepler-411 and its companion is roughly 3.0 mag, derived using the values and empirical relations of Wang et al. (2015) and Furlan et al. (2017). We convert this differential magnitude into a flux ratio fA ∕fB = 15.85, where fA and fB denote the fluxes of Kepler-411 and its stellar companion, respectively.
To test this hypothesis, we assume that the transit signals of Kepler-411d originate from the companion, which is eclipsed by another body. These hypthetical eclipse signals are diluted by the flux of Kepler-411. We employed STMT to fit the short-cadence transit light curves of Kepler-411d, fixing the dilution factor to 15.85 (i.e. the flux ratio). The χ2 of best fit is 20 369. Subsequently, we adopt the same procedure to fit the same data, but now fixing the dilution factor to 1/15.85. We note that the dilution of the companion to the transit light curves of Kepler-411 is negligible in this case. The χ2 is now 20 286, under the assumption that Kepler-411d orbits Kepler-411. The second hypothesis leads to a much better fit to the data than the first. Finally, we adopt the Bayesian information criterion (BIC; Schwarz 1978), proven to be very useful for model selection, to compare both hypotheses. We derive a ΔBIC of 83, which strongly supports the second hypothesis. This means that based on the Bayesian statistics theory (i.e. approximately estimated by using exp−ΔBIC∕2.0) the false-positive probability of the hypothesis that Kepler-411d orbits Kepler-411 is about 9.4 × 10−19.
We have demonstrated that the addition of planet Kepler-411e is indispensable to reproduce the measured TTVs of Kepler-411d. Furthermore, the orbital period ratio of Kepler-411c and Kepler-411e is in the vicinity of four, which implies that there is a chance of detecting the influence of Kepler-411e in the TTVs of Kepler-411c if the two planets belong to the same system. We compare the fit results of the TTVs of Kepler-411b and Kepler-411c based on a two-planet architecture and a four-planet one, respectively. For the two-planet architecture, the minimum 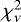 of the TTV fitting of Kepler-411b and Kepler-411c is equal to 972. For the four-planet system, the minimum
of the TTV fitting of Kepler-411b and Kepler-411c is equal to 972. For the four-planet system, the minimum 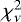 of the TTV fittings of both planets decreases to 854 by considering the gravitational perturbations of Kepler-411e to Kepler-411c. We still use the BIC to complete the model selection between these two orbital configurations. The BIC value for the two-planet model is much larger than that for the four-planet one (i.e. ΔBIC = 81); such a large ΔBIC is in favor of both planets d and e orbiting Kepler-411.
of the TTV fittings of both planets decreases to 854 by considering the gravitational perturbations of Kepler-411e to Kepler-411c. We still use the BIC to complete the model selection between these two orbital configurations. The BIC value for the two-planet model is much larger than that for the four-planet one (i.e. ΔBIC = 81); such a large ΔBIC is in favor of both planets d and e orbiting Kepler-411.
The presence of a wide-orbit stellar companion around Kepler-411 may produce TTV signals and can influence the dynamical stability of the Kepler-411 planetary system. Here, we discuss these possibilities. The possibility of the large TTVs of Kepler-411d being due to the stellar companion can easily be ruled out, based on three different TTV amplitudes of the transiting planets of Kepler-411. The TTV signals induced by the stellar companion of Kepler-411 are primarily due to the light-travel effect, that is, the time delay or advance owing to the reflex motion of the Kepler-411 system induced by the companion (Irwin 1952; Agol et al. 2005; Borkovits et al. 2016). Therefore, all the planetary companions of Kepler-411 should exhibit relatively large TTVs, and we have not considered the stellar companion as the potential perturber during our TTV inversion.
The gravitational perturbations on the Kepler-411 planetary system due to the wide-orbit companion are negligible, and do not influence their dynamical stability. Wang et al. (2015) estimated the separation of the companion to Kepler-411 to be ~ 600 AU, and the mass of the stellar companion to be ~0.13 M⊙ assuming physical association. The corresponding orbital period of the companion is then roughly 15 000 yr, if we assume that the semi-major axis is equal to the projected separation. The gravitational perturbation to the Kepler-411 system is therefore most likely negligible and should not significantly change the results of long-term dynamical simulations even if the stellar companion is actually physically related to the Kepler-411 system. Therefore, we have not included the stellar companion in long-term dynamical simulations.
 |
Fig. 9 Mass-radius diagram of the transiting planets of Kepler-411, including other exoplanets with known masses and radii, obtained from Extrasolar Planets Encyclopaedia. Theoretical models for different planetary compositions are indicated with color curves. |
5.3 Constraints on the compositions of the transiting planets of Kepler-411
Before analyzing the bulk compositions, we estimate the age of the Kepler-411 system according to the gyrochronological relation of Barnes (2007; see their Eq. (2)). We estimate an age of 212 ± 31 Myr based on the color index, the rotation period of Kepler-411, and the systematic uncertainty in the relation. We can therefore make the reasonable assumption that the gyrochronological age of the host star Kepler-411 is equal to that of the planetary system.
In addition to the age, the incident stellar flux also affects the radii of gaseous and H/He-enriched planets according to the interior structure and thermal evolution models of Fortney et al. (2007) and Lopez & Fortney (2014). In order to directly compare with these models, we derive the scaled orbital separations and incident fluxes of the transiting planets of Kepler-411 relative to those of the Earth, following the expressions in Fortney et al. (2007). The respective scaled separations for Kepler-411b−d are 0.048 ± 0.004 AU, 0.095 ± 0.008 AU, and 0.358 ± 0.029 AU, and the corresponding incident fluxes are 412 ± 71, 114 ± 18, and 7.9 ± 1.3 times what the present-day Earth receives from the Sun.
We show the mass-radius diagram in Fig. 9, which includes the transiting planets of Kepler-411 and some transiting planets with precisely measured masses and radii obtained from The Extrasolar Planets Encyclopaedia3. The model of solid planets (i.e. pure-iron, rocky, and water/ice planet) is obtained from Table 2 of Zeng et al. (2016). The cold-hydrogen model, and the 10% H/He envelope model are obtained from Seager et al. (2007) and Fortney et al. (2007), respectively. According to the expression in Zeng et al. (2016), we find that the sub-Neptune-sized planet Kepler-411b contains a 21 ± 21% mass fraction of iron core with a rocky mantle.
For Kepler-411c and Kepler-411d, however, the analysis is more complicated than that of the solid planets. This is because the radius of a H/He-enriched planet depends on many variables, such as age, incident stellar flux, the H/He envelope mass fraction andeven the composition of the heavy-element core (Fortney et al. 2007; Lopez & Fortney 2014). Nevertheless, Lopez & Fortney (2014) show that the H/He envelope fraction plays a crucial role in determining the radius of a sub-Neptune planet. On the mass–radius diagram (see Fig. 9), we find that Kepler-411c is adjacent to the region of planets with a 10% H/He envelope. Also, the two solar-system ice giants (Uranus and Neptune) are located near the position related to this model. Therefore, just like Uranus and Neptune, Kepler-411c should have a low-density H/He envelope in order to be consistent with our mass and radius measurements, but with most of the mass of the planet in the dense core.
However, the model with a 10% H/He envelope is calculated under the assumption that a planet contains a 50/50 ice-rock core and receives the incident flux identical to that of the present-day Earth, and these assumptions are not applicable to Kepler-411c. In order to derive an appropriate model for Kepler-411c and Kepler-411d, we linearly interpolate the model radii of the H/He-enriched planets with a 25 M⊕ and 10 M⊕ ice/rock core at an age of 300 Myr, respectively, in Table 2 of Fortney et al. (2007), whose irradiations are 100 times higher than that of the present-day Earth. We derive rock-ice cores with masses of 24.2± 4.8 M⊕ and 14.4± 4.4 M⊕ for Kepler-411c and Kepler-411d, respectively, which corresponds to H/He envelope fractions of 8.3 and 5.2%. Using the models of Lopez & Fortney (2014), we find that if the interior has an Earth-like composition with an iron core and a rocky mantle, the H/He envelopes around Kepler-411c and Kepler-411d should have mass fractions of 4.7 and 1.7%, respectively.
6 Summary
We investigate the orbital and physical properties of the Kepler-411 planetary system. We combine Kepler photometry data and new TTV measurements from all Kepler quarters with previous adaptive optics, speckle imaging, and dynamical simulation results. Based on the initial conditions extracted from measured TTV signals, we carry out a series of long-term dynamical simulations and find that most simulations remain stable beyond 1 Myr. Our finding can be summarized as follows.
- 1.
We obtain a mass of 25.6 ± 2.6 M⊕ for Kepler-411b and a mass of 26.4 ± 5.9 M⊕ for Kepler-411c.
- 2.
We confirm the planetary nature of the previously known exoplanet candidate KOI1781.03, now known as Kepler-411d, and find its mass to be 15.2 ± 5.1 M⊕.
- 3.
By assuming a near-coplanar system (mutual inclination restricted ≲30°), we have also discovered a nontransiting exoplanet Kepler-411e with a mass of 10.8 ± 1.1 M⊕ on a 31.5-day orbit. This planet shows evidence of dynamical interaction with Kepler-411d.
- 4.
With the newly measured masses and radii, we confirm that Kepler-411c and Kepler-411d belong to the group of planets with a massive core and a significant fraction of volatiles. Although Kepler-411b possesses a sub-Neptune size, it belongs to the group of rocky planets.
Kepler-411 is a slight bright host star (V = 12.3 mag), which makes the planetary system a promising target for follow-up spectroscopic observations. The RV semi-amplitudes of the host star reach up to 12 and 9 m s−1 respectively induced by Kepler-411b and c, and both are on short-period orbits (Porb < 10 days). The RV measurements, which are independent of the TTV technique, can provide more constraints on both masses and orbital eccentricities of the planets of Kepler-411. Although the presence of strong magnetic activity of the host star makes the characterization of the Kepler-411 system using the RV technique less feasible, the TESS mission provides an excellent opportunity to resolve this problem; the TESS mission will supply continuous, high-precision photometricdata for the Kepler-411 system covering at least 27 days. If sufficient high-precision RV measurements (σRV ≲ 1 m s−1) were obtained with TESS photometery simultaneously by employing a state-of-the-art high-precision velocimeter, such as HARPS or CARMENES, and so on, the stellar activity-induced RV variations could be appropriately modeled; there is also a chance that the RV signal of the newly discovered nontransiting planet Kepler-411e (i.e. the RV semi-amplitude Ke = 2 m s−1) could be detected (Tuomi et al. 2014; Dumusque et al. 2015; Barnes et al. 2017; Jones et al. 2017; Oshagh 2018).
Acknowledgements
We thank S. Czesla and S. Jia for helpful discussions before preparing the manuscript. We also thank the anonymous referee for valuable suggestions and comments. This research has made use of the Mikulski Archive for Space Telescopes, which is a NASA funded project to support and provide to the astronomical community a variety of astronomical data archives. This research also has made use of the Keck Observatory Archive (KOA), which is operated by the W. M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration. This work is supported by National Natural Science Foundation of China through grants No. U1531121, No. 10873031 and No.11473066. Here, we also thank the support from China Scholarship Council (CSC) and Deutscher Akademischer Austausch Dienst (DAAD) to our work. The joint research project between Yunnan Observatories and Hamburg Observatoy is funded by Sino-German Center for Research Promotion (GZ1419). M.B.N.K. was supported by the National Natural Science Foundation of China (grants 11010237, 11050110414, 11173004, and 11573004). This research was supported by the Research Development Fund (grant RDF-16-01-16) of Xi’an Jiaotong-Liverpool University (XJTLU).
References
- Agol, E., & Deck, K. 2016, ApJ, 818, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Agol, E., & Fabrycky, D. 2018, in Handbook of Exoplanets (Springer International Publishing AG), 7 [Google Scholar]
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2010, Rep. Prog. Phys., 73, 016901 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Jeffers, S. V., Anglada-Escudé, G., et al. 2017, MNRAS, 466, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. A., Huber, D., Gaidos, E., & van Saders, J. L. 2018, ApJ, 866, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boué, G., Oshagh, M., Montalto, M., & Santos, N. C. 2012, MNRAS, 422, L57 [NASA ADS] [Google Scholar]
- Brown, D. J. A., Collier Cameron, A., Díaz, R. F., et al. 2012, ApJ, 760, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Charbonneau, P. 1995, AJ, 101, 309 [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., Huber, K. F., Wolter, U., Schröter, S., & Schmitt, J. H. M. M. 2009, A&A, 505, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daassou, A., Benkhaldoun, Z., Ait Moulay Larbi, M., & Elazhari, Y. 2014, Int. J. Comput. Appl., 107, 10 [Google Scholar]
- Deck, K. M., & Agol, E. 2015, ApJ, 802, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Deck, K. M., Payne, M., & Holman, M. J. 2013, ApJ, 774, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Deck, K. M., Agol, E., Holman, M. J., & Nesvorný, D. 2014, ApJ, 787, 132 [CrossRef] [Google Scholar]
- Dumusque, X., Glenday, A., Phillips, D. F., et al. 2015, ApJ, 814, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1989, Icarus, 82, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A3 [Google Scholar]
- Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B. 2005, AJ, 129, 1706 [Google Scholar]
- Ford, E. B., Ragozzine, D., Rowe, J. F., et al. 2012, ApJ, 756, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Ciardi, D. R., Everett, M. E., et al. 2017, AJ, 153, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Goździewski, K., Migaszewski, C., Panichi, F., & Szuszkiewicz, E. 2016, MNRAS, 455, L104 [Google Scholar]
- Hadden, S., & Lithwick, Y. 2017, AJ, 154, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, T., Narita, N., Sato, B., et al. 2012, ApJ, 759, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, T., Sanchis-Ojeda, R., Takeda, Y., et al. 2014, ApJ, 783, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ioannidis, P., & Schmitt, J. H. M. M. 2016, A&A, 594, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioannidis, P., Schmitt, J. H. M. M., Avdellidou, C., von Essen, C., & Agol, E. 2014, A&A, 564, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioannidis, P., Huber, K. F., & Schmitt, J. H. M. M. 2016, A&A, 585, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. E., Stenning, D. C., Ford, E. B., et al. 2017 [arXiv:1711.01318] [Google Scholar]
- Jontof-Hutter, D., Rowe, J. F., Lissauer, J. J., Fabrycky, D. C., & Ford, E. B. 2015, Nature, 522, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., Shu, Q., Cai, M. X., & Spurzem, R. 2016, Mem. Soc. Astron. It., 87, 630 [NASA ADS] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Law, N. M., Morton, T., Baranec, C., et al. 2014, ApJ, 791, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernandez, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011a, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011b, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., Xie, J., & Wu, Y. 2012, ApJ, 761, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., Fortney, J. J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, M. G., Ragozzine, D., Fabrycky, D. C., et al. 2016, AJ, 152, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Nachmani, G., Holczer, T., et al. 2013, ApJS, 208, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Marchal, C., & Bozis, G. 1982, Celest. Mech., 26, 311 [Google Scholar]
- Mills, S. M., & Fabrycky, D. C. 2017, AJ, 153, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J. 2002, ApJ, 564, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M., Boué, G., Oshagh, M., et al. 2014, MNRAS, 444, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., Bryson, S. T., Coughlin, J. L., et al. 2016, ApJ, 822, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D. 2009, ApJ, 701, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Beaugé, C. 2010, ApJ, 709, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2008, ApJ, 688, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2016, ApJ, 823, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Kipping, D. M., Buchhave, L. A., et al. 2012, Science, 336, 1133 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oshagh, M. 2018, Asteroseismology and Exoplanets: Listening to the Stars and Searching for New Worlds (New York: Springer International Publishing), 49, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Oshagh, M., Boisse, I., Boué, G., et al. 2013, A&A, 549, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oshagh, M., Santos, N. C., Boisse, I., et al. 2015, Eur. Phys. J. Web Conf., 101, 05003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pál, A. 2012, MNRAS, 420, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovich, C. 2015, ApJ, 808, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Rowe, J. F., Bryson, S. T., Marcy, G. W., et al. 2014, ApJ, 784, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S.-F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Tamayo, D. 2017, MNRAS, 467, 2377 [NASA ADS] [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumder, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Schwamb, M. E., Lintott, C. J., Fischer, D. A., et al. 2012, ApJ, 754, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Smith, A. W., & Lissauer, J. J. 2009, Icarus, 201, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, L.-L., Gu, S.-H., Wang, X.-B., et al. 2015, Res. Astron. Astrophys., 15, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, L., Gu, S., Wang, X., et al. 2017, AJ, 153, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, P., Christiansen, J. L., Jenkins, J. M., et al. 2012, ApJS, 199, 24 [NASA ADS] [CrossRef] [Google Scholar]
- ter Braak, C. J. F. 2006, Stat. Comput., 16, 239 [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Tregloan-Reed, J., Southworth, J., Tappert, C. 2013, MNRAS, 428, 3671 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., Anglada-Escude, G., Jenkins, J. S., & Jones, H. R. A. 2014, MNRAS [arXiv:1405.2016] [Google Scholar]
- Vrugt, J. A., ter Braak, C. J. F., Diks, C. G. H., et al. 2009, Int. J. Nonlinear Sci. Numer. Simul., 10, 271 [CrossRef] [Google Scholar]
- Wang, J., Fischer, D. A., Xie, J.-W., & Ciardi, D. R. 2014a, ApJ, 791, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-b., Gu, S.-h., Collier Cameron, A., et al. 2014b, AJ, 147, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fischer, D. A., Xie, J.-W., & Ciardi, D. R. 2015, ApJ, 813, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1980, AJ, 85, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, J.-W. 2014, ApJS, 210, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, J.-W., Dong, S., Zhu, Z., et al. 2016, Proc. Natl. Acad. Sci., 113, 11431 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kuerster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: part of the long-cadence data of Kepler-411, with apparent rotational modulations. Lower panel: light curves detrended using the Savitzky–Golay filter. The red, green, and blue vertical lines in the lower panel mark the transit events of three transiting planets of Kepler-411. |
| In the text | |
 |
Fig. 2 Fitting result of the short-cadence transit light curves of Kepler-411b. |
| In the text | |
 |
Fig. 3 Fitting result of the short-cadence transit light curves of Kepler-411c. |
| In the text | |
 |
Fig. 4 Fitting result of short-cadence transit light curves of Kepler-411d. |
| In the text | |
 |
Fig. 5 The first light curve shows a double transit of Kepler-411b and Kepler-411d. The second light curve shows a double transit of Kepler-411c and Kepler-411d. The residuals of the second light curve have been shifted for clarity. The physical parameters of the transit models of planets Kepler-411b, c, and d are those derived using the short-cadence data. |
| In the text | |
 |
Fig. 6 Optimal fitting result of Kepler-411b TTVs. |
| In the text | |
 |
Fig. 7 Optimal fitting result of Kepler-411c TTVs. |
| In the text | |
 |
Fig. 8 Optimal fitting result of Kepler-411d TTVs. |
| In the text | |
 |
Fig. 9 Mass-radius diagram of the transiting planets of Kepler-411, including other exoplanets with known masses and radii, obtained from Extrasolar Planets Encyclopaedia. Theoretical models for different planetary compositions are indicated with color curves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


