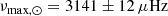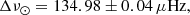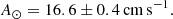| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935175 | |
| Published online | 13 March 2019 | |
Letter to the Editor
Oscillations in the Sun with SONG: Setting the scale for asteroseismic investigations⋆
1
Stellar Astrophysics Centre, Aarhus University, 8000 Aarhus C, Denmark
e-mail: madsfa@phys.au.dk
2
Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
3
Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
4
Department of Astronomy, China West Normal University, No 1 Shi Da Road, Nanchong City, Sichuan Province, PR China
5
Sydney Institute for Astronomy, School of Physics, University of Sydney, Camperdown, New South Wales 2006, Australia
6
Université Paris Diderot, AIM, Sorbonne Paris Cité, CEA, CNRS, 91191 Gif-sur-Yvette, France
7
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
8
DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 328, 2800 Kgs. Lyngby, Denmark
Received:
31
January
2019
Accepted:
25
February
2019
Context. We present the first high-cadence multiwavelength radial-velocity observations of the Sun-as-a-star, carried out during 57 consecutive days using the stellar échelle spectrograph at the Hertzsprung SONG Telescope operating at the Teide Observatory.
Aims. Our aim was to produce a high-quality data set and reference values for the global helioseismic parameters νmax, ⊙ and Δν⊙ of the solar p-modes using the SONG instrument. The obtained data set or the inferred values should then be used when the scaling relations are applied to other stars showing solar-like oscillations observed with SONG or similar instruments.
Methods. We used different approaches to analyse the power spectrum of the time series to determine νmax, ⊙: simple Gaussian fitting and heavy smoothing of the power spectrum. We determined Δν⊙ using the method of autocorrelation of the power spectrum. The amplitude per radial mode was determined using the method described in Kjeldsen et al. (2008, ApJ, 682, 1370).
Results. We found the following values for the solar oscillations using the SONG spectrograph: νmax, ⊙ = 3141 ± 12 μHz, Δν⊙ = 134.98 ± 0.04 μHz, and an average amplitude of the strongest radial modes of 16.6 ± 0.4 cm s−1. These values are consistent with previous measurements with other techniques.
Key words: Sun: oscillations / asteroseismology
© ESO 2019
1. Introduction
The Stellar Observations Network Group, SONG, aims to build a network of 1m telescopes spread in longitude, in both the northern and the southern hemispheres. Each node in the network is designed to be fully automatic; no human interactions are needed on site (Andersen et al. 2014, 2019). One of the primary goals of SONG is to target individual stars intensively for asteroseismic studies using high-precision radial-velocity measurements (e.g. Grundahl et al. 2006, 2014, 2017). Furthermore, with the complementary satellite missions such as the Transiting Exoplanet Survey Satellite, TESS (Ricker et al. 2015), simultaneous observations combining space-based photometry and radial velocities from SONG provide new and valuable insight in our understanding of stars.
Global seismic parameters obtained from observations yield fundamental global properties of stars, such as mass and radius, using well-established scaling relations (Brown et al. 1991; Kjeldsen & Bedding 1995; Stello et al. 2009; Kallinger et al. 2010). These relations are based on scaling two key properties of pressure mode (p-mode) oscillations from the Sun to other stars, namely the large frequency separation (Δν) and the frequency of maximum power (νmax). While Δν should be largely independent of the instrument used, the value of νmax is sensitive to the depth of the sounded layers, which depends on the observational technique. A number of radial-velocity observations have been carried out for the Sun using several ground-based networks (BiSON, GONG, and now SONG) and space missions (GOLF/SoHO and HMI/SDO), which are summarized in Pallé et al. (2018). Each instrument is looking at a specific part of the solar spectrum to determine the radial velocities, and so is sensitive to different depths in the solar atmosphere; the profile of the p-mode power envelope depends on the response function of every spectral line as a function of the height in the atmosphere. Hence different profiles of the envelope are observed when using different monochromatic instruments where single spectral lines are used (e.g. K-7699 Å for BiSON, Ni-6768 Å for GONG). This will translate into differences in the measured properties of the oscillations. Using the SONG spectrograph and the iodine technique where many spectral lines are used to extract the velocities will result in an average measurement insensitive to effects originating at specific heights in the solar atmosphere. Therefore, the observations of the Sun presented here are very important for applying the scaling relations when oscillations are observed in other stars using the same (or a similar) instrument in order to minimize systematic effects.
As shown in Pallé et al. (2013), simultaneous observations of the Sun using different instruments (including the SONG spectrograph) result in different profiles of the oscillation envelope, and hence in different values of νmax. In addition, the stellar background from granulation is less dominant in velocity than in intensity (e.g. Pallé et al. 1999; Kjeldsen & Bedding 2011). In this Letter we emphasize the importance of comparing stellar values determined from SONG data to our observations of the Sun using SONG. The obtained time series and power spectrum are available from the SONG Data Archive1 for future use.
2. Observations and data reduction
The Hertzsprung SONG telescope at the Teide Observatory on the island of Tenerife has been operating in scientific mode since March 2014 (Andersen et al. 2016). It has observed many asteroseismic targets using the high-resolution échelle spectrograph for radial-velocity measurements (e.g. Grundahl et al. 2017; Stello et al. 2017; Frandsen et al. 2018; Arentoft et al. 2019).
In 2017, the complementary initiative known as Solar-SONG was funded, and a solar tracker was installed next to the SONG telescope. This allows light from the Sun to be fed directly into the SONG spectrograph using an optical fibre assembly with complementary optics to scramble the sunlight (Halverson et al. 2015). The optical fibre is mounted on a dedicated Alt/Az solar tracker and pointed directly towards the Sun (see Fig. 1). The fibre is mounted on one side of the tracker, and a pyrheliometer and an active guide unit on the other. With this instrument we were able to simultaneously collect the total solar irradiance (TSI) and the solar spectra. The TSI was used to clean bad points from the data, primarily those caused by clouds. A diffuser was placed at the fibre entrance and, together with ball lenses at the interface between the octagonal and circular fibres, was intended to ensure that the solar disk was not resolved, even if the tracker does not point accurately to the same point on the Sun at all times. The active guide unit was not functioning for the observations presented in this paper and, as discussed below, some effects of the solar disk being resolved were seen in the data.
 |
Fig. 1. Solar tracker with the attached optical fibre assembly used to feed sunlight to the SONG spectrograph. The SONG dome and container are seen in the background. |
The observations were carried out from May 27 to July 22, 2018, corresponding to an extremely deep minimum of the solar activity cycle. Activity will affect the solar oscillations by lowering the p-mode amplitudes and therefore observing during an activity minimum is highly favourable. Each day more than 10 h of data were collected; each spectrum had an exposure time of 0.5 s and a readout time of 3.5 s, resulting in approximately 12 000 spectra (about 100 GB) per day and a total of more than 500 000 measurements of radial velocities after removing bad points. The extraction of the 2D spectrum into the flux-wavelength spectrum was set to work in real time. The iSONG pipeline was used to produce the radial-velocity values (Corsaro et al. 2012; Antoci et al. 2013) and was set up on a computer cluster at the Instituto de Astrofísica de Canarias on Tenerife, where the reduction tasks were handled by a HTCondor distributor.
Figure 2 (upper panel) shows the full radial-velocity time series after corrections and filtering have been applied. Only two of the 57 days in this campaign had significant interruptions resulting in a duty cycle of ∼40%. On June 2 the tracker failed after two hours of observations due to a software glitch, and on June 29 clouds were covering the observatory. The raw radial-velocity measurements for each day were first corrected for the barycentric motion of the Earth around the Sun (code from Piskunov & Valenti 2002, exported to Python). The residual time series of one full day is shown in Fig. 2 (lower left panel) where some instrumental effects are still present. The trend near noon originates from the tracker not pointing perfectly to the same point on the Sun at all times. This is also where the largest effects are expected when using an Alt/Az mount. The observations are consistent with the solar disk being partially resolved, which means that the set-up does not completely observe the Sun as a star. The downward slope in the residuals at the beginning and end of the series is a well-known effect (Belmonte et al. 1988) and is caused by differential extinction in the Earth’s atmosphere. The low-frequency trends were removed using local weighted linear regression smoothing (LOWESS; Cleveland 1978), which is seen as the red curve in Fig. 2 (lower left panel). Each data point was smoothed using a weighted linear regression on a subset of the radial-velocity measurements. The subset used around the individual points was specified as a fraction of the total number of data points, and in our case we chose a fraction value of 0.05. With roughly 12.000 data points per day, this corresponds to a high-pass filter with cut-off frequency close to 450 μHz. A number of different filters were tested in order to choose one that had no effect on our main results on the p-mode oscillations. Each filter was checked, after being applied to the barycentric velocity corrected time series, by determining νmax of the p-mode power excess, and the differences between the filters were within a few μHz. Finally, the filter that minimized the morning, noon, and evening trends was chosen. Figure 2 (lower right panel) shows a zoom-in of the corrected and filtered time series for one day where the solar oscillations are clearly visible.
 |
Fig. 2. Upper panel: full 57-day solar time series after applying corrections and filtering. Lower left panel: barycentric velocity corrected time series from one day of solar observations. Some trends in the residual RV curve are clearly visible. The red line is the local regression smoothing filter. Lower right panel: zoom-in showing the filtered and corrected time series, in which the 5 min oscillations are clearly seen. |
3. Analysis of oscillations
To determine the global helioseismic parameters, power spectra of the corrected and filtered time series were calculated using unweighted iterative least-squares sine-wave fitting. The power spectrum from the full 57 days is shown in Fig. 3 (upper panel).
 |
Fig. 3. Upper panel: power spectrum from the full 57-day filtered and corrected time series. The inset (black) shows the spectral window (∼40% duty cycle) and (grey) a zoom-in showing the individual aliases. Lower panel: power spectrum of one single day (black). The red curve is a Gaussian fit to the power excess, the cyan curve is a 8Δν smoothed version of the power spectrum, and the blue is the 4Δν smoothed curve. For this day, the 4Δν smoothing results in a double hump, giving a poorly determined νmax. To better distinguish the three coloured curves in the lower panel, the 8Δν and the 4Δν smoothed versions were multiplied by a factor of 2 and 2.5, respectively. |
3.1. Determination of νmax
To estimate uncertainties on the helioseismic parameters, the time series were split into chunks of one day each. In one day, the 5-minute oscillations still produces a significant signal in the power spectrum (S/N ∼ 40), which can be seen in Fig. 3 (lower panel). Different methods were applied to determine the frequency of maximum power (νmax) from the individual power spectra. One was to fit a simple Gaussian to the power excess. The other method was to apply the procedure of Kjeldsen et al. (2008), where the power spectrum is smoothed by a Gaussian with a FWHM of 4Δν and νmax determined as the maximum of the smoothed curve. The smoothing factor when using the second method proved to be too low, and so the value was increased to a FWHM of 8Δν. The lower value would in some cases result in multiple humps which would lead to a badly determined νmax (see lower panel of Fig. 3).
Some tests using different background models, when applying the Gaussian fit, were tried with effects well below the uncertainty and we therefore decided to omit a background term. With these two methods we obtained a series of independent measurements of νmax each day for the Sun (see Fig. 4). Calculating the standard deviation (σ) of these values gives a standard mean error of 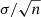 , where n = 55 is the number of independent determinations (days used). The two days with only a few data points were omitted. The determined uncertainties were ±12 μHz for the Gaussian method and ±11 μHz using the 8Δν smoothing method. We adopt the value from the Gaussian method from now on.
, where n = 55 is the number of independent determinations (days used). The two days with only a few data points were omitted. The determined uncertainties were ±12 μHz for the Gaussian method and ±11 μHz using the 8Δν smoothing method. We adopt the value from the Gaussian method from now on.
 |
Fig. 4. νmax time series showing the values determined on the single-day power spectra using a Gaussian fit. The large variations are due to the stochastic nature of the modes where excitation, damping, and interactions causes the heights of individual modes to vary with time. The red line is the mean value and the dashed cyan lines show ±1σ. |
We then measured νmax, ⊙ by fitting a Gaussian to the power excess of the full power spectrum and the value was
The mean values from the 55 independent measurements of νmax results in similar values for the two methods: νmax, ⊙ = 3139 ± 12 μHz (Gaussian; shown in Fig. 4) and νmax, ⊙ = 3140 ± 11 μHz (8Δν smoothing). We also used two widely used pipelines to extract νmax and Δν: the SYD Pipeline (Huber et al. 2009) νmax, ⊙ = 3141 ± 18 μHz, and the A2Z Pipeline (Mathur et al. 2010) νmax, ⊙ = 3151 ± 147 μHz, which agree within the uncertainties.
3.2. Determination of Δν
To determine Δν, we used the method of calculating the autocorrelation of the full power spectrum. We smoothed the power spectrum slightly before calculating the autocorrelation and determined the value by fitting a Gaussian to the peak identified as originating from Δν. The value with the standard error of the Gaussian fit was
which is in agreement with the literature (e.g. Kiefer et al. 2015; Kjeldsen et al. 2008). The results from the pipelines were Δν⊙ = 135.02 ± 0.09 μHz (SYD) and Δν⊙ = 134.81 ± 3.11 μHz (A2Z), which agree well within the uncertainties.
The determined value of Δν was evaluated further by creating an échelle diagram where the slightly smoothed power spectrum was cut into chunks with a length of Δν and placed on top of each other. With the correct value of Δν vertical ridges originating from modes with different l-values and the corresponding daily aliases will appear. The échelle diagram of the power spectrum is seen in Fig. 5.
 |
Fig. 5. Upper panel: échelle diagram of a slightly smoothed version of the power spectrum. The ridges from the p-modes with different l-value are clearly visible, as are the alias peaks from the window function. Lower panel: collapsed échelle diagram with labels centred above the peaks marking the l{0, 1, 2, 3} ridges and the ±1 and ±3 daily aliases (no secondary alias present). |
3.3. Oscillation amplitude
The amplitude of the solar oscillations was determined with the SYD pipeline, which uses the procedure described by Kjeldsen et al. (2008). This involves first converting the power spectrum of the full 57 days into power spectral density (PSD) by multiplying by the effective observing time (22.6 d), which we calculated as the reciprocal of the area under the spectral window. The PSD was then heavily smoothed by a Gaussian with a FWHM of 4Δν⊙ and multiplied by Δν⊙/c, where we took c = 4.09, which represents the effective number of modes in each order (Kjeldsen et al. 2008). We then fitted and subtracted the background using a two-component Harvey model (Harvey 1985). The combination of the components in the model were equivalent to a linear fit. Finally, we converted to amplitude by taking the square root, and found the amplitude measured in this way (i.e. amplitude per radial mode) to be
Using the same method but a different instrument (BiSON), Kjeldsen et al. (2008) found the long-term (11 years) average of the solar amplitude to be 18.7 ± 0.7 cm s−1, with significant scatter over time due to the stochastic nature of the modes and solar activity. With this in mind, our measurement appears to be consistent with the previous result. The oscillation amplitudes will generally be affected by the window function which will lower the amplitudes (Arentoft et al. 2019). Simulations were performed to check the effect on our data set and the effect was below the level of the stated uncertainty in Eq. (3).
4. Conclusion
We have presented the first multiwavelength high-cadence radial-velocity observations of the Sun-as-a-star to date, using the SONG spectrograph on Tenerife. We applied standard methods to determine the global helioseismic values νmax, ⊙ and Δν⊙. The value of νmax, ⊙ = 3141 ± 12 μHz determined here shows one way of determining νmax when analysing SONG data. Our value is an average over different depths in the solar atmosphere, which makes it (data and method) a good reference for future use in stellar scaling relations. The method of fitting a Gaussian to the p-mode envelope of the daily power spectra and to the full power spectrum to determine νmax and its associated error can be directly applied to all other asteroseismic targets observed using SONG and will lead to a homogeneous and robust way of determining νmax with a realistic uncertainty. We determined a value of Δν⊙ for the Sun using autocorrelation of 134.98 ± 0.04 μHz. The value of νmax, ⊙ and Δν⊙ determined here also confirms the instrument performance and pipeline for the radial-velocity measurements of SONG. Finally, we found the amplitude of the strongest radial modes to be 16.6 ± 0.4 cm s−1, which is consistent with previous measurements. These values, especially νmax, ⊙, will be very important when the scaling relations are applied to other stars showing solar-like oscillations observed with SONG or similar instruments. In the case that other methods are applied to extract the global asteroseismic values of SONG targets, we have made the filtered and corrected time series and corresponding power spectrum available on the SONG Data Archive (SODA).
Acknowledgments
We would like to acknowledge the contribution of the engineers at the IAC, Felix Gracia (optical), Ezequiel Ballesteros (electronic), and Antonio Dorta (HTCondor), and the support from the day operator at the SolarLab, Teide Observatory, on this Solar-SONG initiative and the campaign. We would also like to acknowledge the Villum Foundation, the Independent Research Fund Denmark, and the Carlsberg Foundation for their support in building the SONG prototype on Tenerife. The Stellar Astrophysics Centre is funded by The Danish National Research Foundation (Grant DNRF106). Funding for Solar-SONG was provided by the Excellence ‘Severo Ochoa’ programme at the IAC and the Ministry MINECO under the program AYA-2016-76378-P. R.A.G. is supported by the GOLF/SOHO grant by the CNES. S.M. acknowledges support from the Ramon y Cajal fellowship number RYC-2015-17697.
References
- Andersen, M. F., Grundahl, F., Christensen-Dalsgaard, J., et al. 2014, Rev. Mex. Astron. Astrofis. Conf. Ser., 45, 83 [NASA ADS] [Google Scholar]
- Andersen, M. F., Grundahl, F., Beck, A. H., & Pallé, P. 2016, Rev. Mex. Astron. Astrofis. Conf. Ser., 48, 54 [NASA ADS] [Google Scholar]
- Andersen, M. F., Handberg, R., Weiss, E., et al. 2019, PASP, 131, 998 [Google Scholar]
- Antoci, V., Handler, G., Grundahl, F., et al. 2013, MNRAS, 435, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Arentoft, T., Grundahl, F., White, T. R., et al. 2019, A&A, 622, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belmonte, J. A., Elsworth, Y. P., Isaak, G. R., et al. 1988, ESA SP, 286 [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Cleveland, W. S. 1978, J. Am. Stat. Assoc., 74, 829 [Google Scholar]
- Corsaro, E., Grundahl, F., Leccia, S., et al. 2012, A&A, 537, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frandsen, S., Fredslund Andersen, M., Brogaard, K., et al. 2018, A&A, 613, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundahl, F., Kjeldsen, H., Frandsen, S., et al. 2006, Mem. Soc. Astron. It., 77, 458 [NASA ADS] [Google Scholar]
- Grundahl, F., Christensen-Dalsgaard, J., Pallé, P. L., et al. 2014, IAU Symp., 301, 69 [NASA ADS] [Google Scholar]
- Grundahl, F., Fredslund Andersen, M., Christensen-Dalsgaard, J., et al. 2017, ApJ, 836, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Halverson, S., Roy, A., Mahadevan, S., et al. 2015, ApJ, 806, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. 1985, ESA SP, 235 [Google Scholar]
- Huber, D., Stello, D., Bedding, T. R., et al. 2009, Commun. Asteroseismol., 160, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Weiss, W. W., Barban, C., et al. 2010, A&A, 509, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiefer, R., Schad, A., Herzberg, W., & Roth, M. 2015, A&A, 578, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 2011, A&A, 529, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ApJ, 682, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallé, P. L., Roca Cortés, T., Jiménez, A., GOLF Team, & Virgo Team 1999, ASP Conf. Ser., 173, 297 [NASA ADS] [Google Scholar]
- Pallé, P. L., Grundahl, F., Triviño Hage, A., et al. 2013, J. Phys. Conf. Ser., 440, 012051 [NASA ADS] [CrossRef] [Google Scholar]
- Pallé, P. L., Appourchaux, T., Christensen-Dalsgaard, J., & Garcia, R. A. 2018, ArXiv e-prints [arXiv:1802.00674] [Google Scholar]
- Piskunov, N. E., & Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Chaplin, W. J., Basu, S., Elsworth, Y., & Bedding, T. R. 2009, MNRAS, 400, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Huber, D., Grundahl, F., et al. 2017, MNRAS, 472, 4110 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Solar tracker with the attached optical fibre assembly used to feed sunlight to the SONG spectrograph. The SONG dome and container are seen in the background. |
| In the text | |
 |
Fig. 2. Upper panel: full 57-day solar time series after applying corrections and filtering. Lower left panel: barycentric velocity corrected time series from one day of solar observations. Some trends in the residual RV curve are clearly visible. The red line is the local regression smoothing filter. Lower right panel: zoom-in showing the filtered and corrected time series, in which the 5 min oscillations are clearly seen. |
| In the text | |
 |
Fig. 3. Upper panel: power spectrum from the full 57-day filtered and corrected time series. The inset (black) shows the spectral window (∼40% duty cycle) and (grey) a zoom-in showing the individual aliases. Lower panel: power spectrum of one single day (black). The red curve is a Gaussian fit to the power excess, the cyan curve is a 8Δν smoothed version of the power spectrum, and the blue is the 4Δν smoothed curve. For this day, the 4Δν smoothing results in a double hump, giving a poorly determined νmax. To better distinguish the three coloured curves in the lower panel, the 8Δν and the 4Δν smoothed versions were multiplied by a factor of 2 and 2.5, respectively. |
| In the text | |
 |
Fig. 4. νmax time series showing the values determined on the single-day power spectra using a Gaussian fit. The large variations are due to the stochastic nature of the modes where excitation, damping, and interactions causes the heights of individual modes to vary with time. The red line is the mean value and the dashed cyan lines show ±1σ. |
| In the text | |
 |
Fig. 5. Upper panel: échelle diagram of a slightly smoothed version of the power spectrum. The ridges from the p-modes with different l-value are clearly visible, as are the alias peaks from the window function. Lower panel: collapsed échelle diagram with labels centred above the peaks marking the l{0, 1, 2, 3} ridges and the ±1 and ±3 daily aliases (no secondary alias present). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.