| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834515 | |
| Published online | 28 February 2019 | |
CHANG-ES
XIII. Transport processes and the magnetic fields of NGC 4666: indication of a reversing disk magnetic field⋆
1
Observatoire astronomique de Strasbourg, Université de Strasbourg, CNRS, UMR 7550, 11 rue de l’Université, 67000 Strasbourg, France
e-mail: yelena.stein@astro.unistra.fr
2
Ruhr-University Bochum, Faculty of Physics and Astronomy, Astronomisches Institut (AIRUB), Germany
3
Ruhr-University Bochum, Faculty of Physics and Astronomy, Research Department of Plasmas with Complex Interactions, Germany
4
Department of Physics, Engineering, and Astronomy, Queen’s University, Kingston, Ontario K7L 3N6, Canada
5
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6
Obserwatorium Astronomiczne Uniwersytetu Jagiellońskiego, ul. Orla 171, 30-244 Kraków, Poland
7
Universität Hamburg, Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
8
CSIRO Astronomy and Space Science, 26 Dick Perry Avenue, Kensington, WA 6151, Australia
9
Department of Astronomy, New Mexico State University, PO Box 30001, MSC 4500, Las Cruces, NM 88003, USA
10
Department of Astronomy, University of Michigan, 311 West Hall, 1085 S. University Ave, Ann Arbor, MI 48109-1107, USA
Received:
26
October
2018
Accepted:
29
November
2018
Context. The observation of total and linearly polarized synchrotron radiation of spiral galaxies in the radio continuum reveals the distribution and structure of their magnetic fields. By observing these, information about the proposed dynamo processes that preserve the large-scale magnetic fields in spiral galaxies can be gained. Additionally, by analyzing the synchrotron intensity, the transport processes of cosmic rays into the halo of edge-on spiral galaxies can be investigated.
Aims. We analyze the magnetic field geometry and the transport processes of the cosmic rays of the edge-on spiral starburst galaxy NGC 4666 from CHANG-ES radio data in two frequencies; 6 GHz (C-band) and 1.5 GHz (L-band). Supplementary X-ray data are used to investigate the hot gas in NGC 4666.
Methods. We determine the radio scale heights of total power emission at both frequencies for this galaxy. We show the magnetic field orientations derived from the polarization data. Using rotation measure (RM) synthesis we further study the behavior of the RM values along the disk in C-band to investigate the large-scale magnetic-field pattern. We use the revised equipartition formula to calculate a map of the magnetic field strength. Furthermore, we model the processes of cosmic-ray transport into the halo with the 1D SPINNAKER model.
Results. The extended radio halo of NGC 4666 is box-shaped and is probably produced by the previously observed supernova-driven superwind. This is supported by our finding of an advective cosmic-ray transport such as that expected for a galactic wind. The scale-height analysis revealed an asymmetric halo above and below the disk as well as between the two sides of the major axis. A central point source as well as a bubble structure is seen in the radio data for the first time. Our X-ray data show a box-shaped hot halo around NGC 4666 and furthermore confirm the AGN nature of the central source. NGC 4666 has a large-scale X-shaped magnetic field in the halo, as has been observed in other edge-on galaxies. The analysis furthermore revealed that the disk of NGC 4666 shows hints of field reversals along its radius, which is the first detection of this phenomenon in an external galaxy.
Key words: galaxies: spiral / galaxies: individual: NGC 4666 / surveys / polarization / radio continuum: galaxies / galaxies: magnetic fields
All reduced images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A33
© Y. Stein et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Strong star formation leads to outflow of matter over the whole disk of a galaxy (e.g., Habe et al. 1981). In addition to gas, cosmic rays (CRs) and magnetic fields play an important role in the disk-halo interaction of galaxies, which leads to the formation of radio halos in galaxies (e.g., Parker 1992). Observations of radio halos in polarization reveal that star-forming galaxies often show X-shaped magnetic-field structures if observed edge-on (Tüllmann et al. 2000; Krause 2009). Several mechanisms to generate and maintain large-scale regular magnetic fields in spiral galaxies have been proposed. One mechanism is the mean-field α − ω dynamo (see e.g., Ruzmaikin et al. 1988; Beck et al. 1996; Chamandy 2016). Shear motions due to differential rotation combined with the coriolis force acting on the vertical turbulent gas motions amplify and order large-scale regular magnetic fields from turbulent magnetic fields in spiral galaxies (e.g., Arshakian et al. 2009). The solutions of the α − ω dynamo equation in the thin-disk approximation are different dynamo modes, like the axisymmetric spiral magnetic field (ASS) or the bisymmetric spiral magnetic field (BSS). These fields in the galactic disk are generally accompanied by poloidal magnetic fields of even or odd symmetry extending into the galactic halo. However, these magnetic fields are, according to the thin-disk α − ω dynamo, a factor of about ten weaker than the disk fields and, hence, cannot explain the halo fields that are observed to be almost as strong as the disk fields. One reason for this discrepancy could be that the magneto-ionic disk of galaxies is not thin, due to outflows for example.
The complex behavior of galactic dynamos is not fully understood yet, and the influence of galactic outflows in particular is still a topic of discussion. Outflows can order a turbulent-disk magnetic field such that it evolves into a regular halo field in dwarf galaxies (Moss & Sokoloff 2017). In Milky Way-type spiral galaxies, galactic outflows lead to two countervailing effects: They are crucial to remove small-scale helicity and hence to avoid quenching of dynamo action, but also lead to field losses into the halo that are responsible for the saturation of the dynamo (e.g., Bendre et al. 2015; Chamandy et al. 2015).
In this paper, the radio halo of the edge-on spiral starburst galaxy NGC 4666 is investigated to obtain further clues about the magnetic fields and processes in spiral galaxies with high star formation rates (SFRs). With the data of NGC 4666 from the Continuum HAlos in Nearby Galaxies – an Evla Survey (CHANG-ES), observed with the Karl G. Jansky Very Large Array (VLA), it is possible to analyze the galaxy in C-band (6 GHz) and L-band (1.5 GHz) in terms of linear polarization, the magnetic field structure, and transport processes.
NGC 4666 is an actively star-forming spiral galaxy at a distance of 27.5 Mpc (Wiegert et al. 2015). The basic galaxy parameters are listed in Table 1. In the optical spectral range the star-forming disk is slightly visible. Therefore, the inclination of NGC 4666 is less than 90°. NGC 4666 is a starburst galaxy (Lehnert & Heckman 1996) and is considered a superwind galaxy with a prominent X-ray halo (Dahlem et al. 1997; Tüllmann et al. 2006). An outflow cone is associated with a galactic superwind, which can be described as a global outflow powered by the combined effect of supernova (SN) explosions and stellar winds associated with powerful starbursts (Heckman et al. 1993).
Basic galaxy parameters.
In Heesen et al. (2018), archival VLA data of NGC 4666 and other galaxies were used to model the CR transport with the 1D transport model SPINNAKER. For NGC 4666, transport by advection was concluded with a very high advection speed between 500 km s−1 and 700 km s−1 supporting the starburst phase of this galaxy.
With an SFR of 7.3 M⊙ yr−1 (Wiegert et al. 2015), NGC 4666 is very similar to the CHANG-ES galaxy NGC 5775. Like other starburst galaxies, NGC 4666 is also a member of an interacting system. It is part of a small group of galaxies containing also NGC 4632 and NGC 4668 (Garcia 1993). A small dwarf galaxy, which is also part of the group, was discovered by Walter et al. (2004). The HI data of Walter et al. (2004) show strong interaction between NGC 4666 and NGC 4668 as well as with the dwarf galaxy. The strong starburst is triggered by ongoing far-field gravitational interactions (Walter et al. 2004). The Hα image and the radio continuum maps (Dahlem et al. 1997) show a homogeneous distribution of many star-forming regions across the disk of NGC 4666. This is different from a nuclear starburst galaxy with a 1 kpc diameter of high star formation in the center. It is not clear why the star formation in NGC 4666 is widely spread along the disk and therefore looks different from many other starburst galaxies (Walter et al. 2004). Furthermore, the Hα image (Dahlem et al. 1997) shows outflow of filaments, which is represented by the diffuse ionized gas (DIG) and caused by the strong starburst. The X-ray data (Tüllmann et al. 2000) indicate a large X-ray halo. The outflow of the hot X-ray emitting gas is comparable to the size of the disk and may even extend radially beyond the Hα filaments. Additionally, a nuclear outflow (bubble structure to the southeast) is visible in the X-ray image.
NGC 4666 hosts a modestly active galactic nucleus (AGN; Dahlem et al. 1997; Persic et al. 2004), which is probably highly obscured (Dudik et al. 2005). Based on BeppoSAX and XMM-Newton data, Persic et al. (2004) found that the star burst, which extends over most of the disk, and AGN activities coexist in NGC 4666. They found a prominent emission line from Fe-Kα at ≈6.4 keV from the nuclear region. Additionally, they observed the presence of a flat continuum that is in agreement with a model in which the continuum originates from the reflection of the primary continuum by the cold inner wall of the circumnuclear torus in the nuclear region. They conclude the existence of a strongly absorbed (i.e., Compton-thick) AGN. The optical emission lines of spectroscopic measurements from the core region of Dahlem et al. (1997) also suggest a central AGN. In a further study of high-resolution X-ray imaging of nearby low-ionisation nuclear emission-line regions (LINERs) observed by Chandra, a nuclear point source of NGC 4666 was not detected (Dudik et al. 2005). They concluded either a lack of an energetically significant AGN or a highly obscured AGN with internal absorptions reaching 1.1 × 1023 cm−2–8.4 × 1024 cm−2, which would imply that the AGN shows luminosities between 2 × 1038 erg s−1 and 9.5 × 1042 erg s−1. No nuclear (point source) flux density has been determined so far in the radio wavelength regime as the resolution of the observations was insufficient.
Here, we investigate the radio properties of NGC 4666 and its central source. We present the first flux measurements of the central source from the high-resolution radio continuum data of CHANG-ES. We further analyze the data on the radio halo, scale heights, and the linear polarization. Additional archival VLA C-band data of NGC 4666 complement the polarization data. With supplementary X-ray data from XMM-Newton we are able to support the AGN classification of the central source and analyze the far-extended X-ray halo, which seems to be correlated to the radio halo. With the radio data we are able to investigate the disk magnetic field, which is axisymmetric with hints of one reversal. After the thermal/nonthermal separation, the magnetic field strength is determined. We further use the 1D SPINNAKER model for cosmic-ray transport in NGC 4666.
The paper is organized as follows. Section 2 gives an overview of the data and the adapted technique of rotation measure (RM) synthesis. In Sect. 3 the results of Stokes I, the polarization using RM synthesis, the disk field of NGC 4666, and the maps of the magnetic field strength using equipartition are presented. The 1D transport model is applied to the data. The magnetic field distribution from that model is then compared to the equipartition field. In Sect. 4 the results are summarized and conclusions are drawn.
2. Observations and data analysis
2.1. VLA data
2.1.1. CHANG-ES data
The radio continuum data are part of the CHANG-ES survey observed with the Karl G. Jansky VLA (Irwin et al. 2012a). Observations were obtained in B-, C-, and D-configurations at L-band (1.5 GHz, 500 MHz bandwidth, with a gap of 144 MHz width where strong radio frequency interference (RFI) is located), and in the C- and D-configurations at C-band (6 GHz, 2 GHz bandwidth). We used 2048 spectral channels in 32 spectral windows (spws) at 1.5 GHz and 1024 channels in 16 spws at 6 GHz. All polarization products (Stokes I, Q, U, and V) were obtained. The D-configuration data (Wiegert et al. 2015) are public1 and the C-configuration data will become public soon (Walterbos et al., in prep.).
The data reduction for Stokes I (total power) and Stokes Q and U (linear polarization) was carried out for all five data sets of NGC 4666 (see Table 2) separately, using the Common Astronomy Software Applications (CASA) package (McMullin et al. 2007) and following the calibration procedures as described in the CHANG-ES paper by Irwin et al. (2013). We used J1331+3030 (3C286) as the primary calibrator, J1246−0730 as the secondary calibrator, and J1407+2827 as the zero polarization calibrator. The calibrated data from the different configurations were then combined for C-band and L-band and these combined data were used for imaging Stokes I and the polarization.
Observation parameters of CHANG-ES.
The Stokes I maps were produced by cleaning with a robust weighting parameter of zero (Briggs 1995). The polarization and magnetic-field-orientation maps were created from the Stokes Q and U maps, which were cleaned with a robust parameter of two in order to be more sensitive to faint structures. The achieved rms from the combined C-band data for Stokes I is 4.6 μJy beam−1 with a beam of 3.0″ × 3.5″. The resulting rms of the combined L-band data for Stokes I is 30 μJy beam−1 with a beam of 11.8″ × 13.6″. Subsequently, smoothed images of Stokes I of both bands were produced to match the resolution of the polarization maps of 7″, as well as the resolution of the maps from RM synthesis of 18″.
2.1.2. Archival VLA data
Archival VLA D-configuration C-band observations exist for the galaxy NGC 4666 (Program AD326, Table 3). These observations were obtained before the upgrade of the VLA. The central frequency was 4.86 GHz with a bandwidth of 2 × 50 MHz. The calibration was done using the Astronomical Image Processing System (AIPS2) with J1331+305 (3C286) as the primary calibrator and J1246−075 as the secondary calibrator. The primary calibrator was also used for polarisation-angle correction and the secondary calibrator for polarisation leakage term determination.
Observation parameters of the archival VLA data.
The Stokes I maps were produced by cleaning with robust zero weighting. The polarization and magnetic-field-orientation maps were created from the Stokes Q and Stokes U maps, which were also cleaned with robust zero weighting. The application of RM synthesis on these data is not possible as they consist of just two channels.
2.2. XMM data
To study the nature of the possible central source, as well as of the galactic energy budget via analysis of the emission from the hot gas, XMM-Newton archive data for NGC 4666 were used (see Table 4 for the parameters of the observations). The data were processed using the SAS 15.0.0 package (Gabriel et al. 2004) with standard reduction procedures. The tasks epchain and emchain helped to obtain event lists for two EPIC-MOS cameras (Turner et al. 2001) and the EPIC-pn camera (Strüder et al. 2001). The event lists were then carefully filtered for periods of intense background radiation. From the output data an image in the soft energy range of 0.2–1 keV was produced, along with the exposure map (without vignetting correction) masked for the acceptable detector area using the images script3, modified by the authors to allow adaptive smoothing.
Parameters of the XMM-Newton X-ray observations of NGC 4666.
Furthermore, a spectral analysis was performed. The spectra of each region were created using all three EPIC cameras. The background spectra were obtained using blank sky-event lists (see Carter & Read 2007), filtered using the same procedures as for the source-event lists. For each spectrum, response matrices and effective area files were produced. Next, including these ancillary files, spectra from all three EPIC cameras and the corresponding background blank sky spectra were merged using the SAS task epicspeccombine into a final background subtracted source spectrum. Finally, the spectra were fitted using XSPEC 12 (Arnaud 1996).
2.3. RM synthesis
While propagating through a magnetized plasma, electromagnetic waves experience a frequency dependent rotation of the polarization angle. This effect is called Faraday rotation and is caused by the different propagation speeds of the left and right circular polarized waves. The rotation of the polarization angle χ is proportional to the wavelength (λ) squared and the RM:
If different regions along the line of sight emit polarized intensity and/or rotate the polarization angle, RM has to be replaced by the Faraday depth Φ (Burn 1966):
with the electron density ne and the magnetic field integrated along the line of sight B∥.
With the method of RM synthesis applied to wide-band multi-channel receiver data, multiple sources along the line of sight can be measured (Brentjens & de Bruyn 2005). The basic idea was introduced by Burn (1966) who defined a complex “Faraday dispersion function”, which connects the complex polarized surface brightness in Faraday depth space via a Fourier transform with the dependence of the complex polarized surface brightness in λ2-space. When applying this technique, several parameters are important, which are presented in Table 5.
Rotation measure synthesis parameters.
In order to find out if each channel has to be imaged for Stokes Q and U or if it is sufficient to image every spw, we calculated the rotation over both frequency bands. There are 32 spws in L-band and 16 spws in C-band. Each spw contains 64 channels before flagging. Since the rotation of the electromagnetic wave is calculated as λ2 multiplied by the RM, the rotation of the polarization angle χ can be estimated. A median value of |RM| ≈ 100 rad m−2 was found in external galaxies (e.g., Fletcher et al. 2004). With the L-band ranging in frequency from 1.2 to 1.75 GHz (wavelength range between λ = 0.25 and λ = 0.17 m), and the C-band ranging in frequency from 5 to 7 GHz (wavelength range between λ = 0.06 m and λ = 0.042 m) the rotation of the polarization angle Δχ can be calculated:
Standard imaging averages over the entire bandwidth, which in L-band leads to strong depolarization across the frequency band and no information on the RM is gained. By imaging each spw separately, the rotation of the polarization vector (in the above example 192.5°) can be lowered by a factor of 32 in L-band, which is sufficient (in the above example the rotation within the individual spw is then ∼6°). Due to the wavelength dependence, this effect is not as strong in C-band.
From the data in Xu & Han (2014), the Galactic foreground RM in the direction to NGC 4666 was determined. This value (RMforeground = −5.8 ± 1.3 rad m−2) was subtracted from the final RM cube.
To adopt RM synthesis, Stokes Q and Stokes U images for each spw were produced. These have to be convolved to the largest beam in the frequency range (the beam size being dependent on frequency). Due to RFI in L-band, spws 0, 1, and 2 were flagged before all images were merged together into an image cube with the frequency as the third axis. This was done for the Stokes Q and U images separately. Then the script “RMsynth” (B. Adebahr, priv. comm., based on Brentjens & de Bruyn 2005) was applied. A Fourier transformation was performed on the complex flux densities of the cubes in λ2-space. The result was a cube with the two image axes and Φ as the third axis. Then the RM of a single source along the line of sight was determined by fitting, for example, a parabola to the main peak of F(Φ) (Brentjens & de Bruyn 2005). The result was a cube of Stokes Q and U, as well as a polarization cube, which was then further analyzed to obtain, for example, the RM, the polarized intensity (PI), and the polarization angle (PA), as well as their corresponding error maps. The RM map represents the fitted peak position of each pixel, again assuming there is only one component along the line of sight.
3. Results and discussion
3.1. Radio continuum Stokes I
The total power map (Stokes I) of L-band is shown in Fig. 1 with total intensity contours overlayed on the optical Sloan Digital Sky Survey (SDSS)4 image made from the ugr filters using the formulas of Lupton 20055. The radio halo in the combined configuration of L-band (Fig. 1) reaches up to 9 kpc above and below the plane of the galaxy as measured to the 3-σ level corrected for the beam size. The box-like appearance of the radio halo is quite striking. It is evident that the extent of the radio continuum radiation beyond the star-forming disk only occurs in the vertical direction of the galaxy. In Appendix A, we present L-band contours from the B-, C-, and D-configurations of the VLA, which result in different resolutions. The C-band data are presented in the following section.
 |
Fig. 1. NGC 4666 Stokes I image of L-band combined (B-, C-, and D-configuration) with a robust zero weighting, overlayed onto the optical SDSS image made from the u, g, r filters. Contours start at a 3σ level with an rms noise σ of 30 μJy beam−1 and increase in powers of 2 (up to 256). The beam size is 11.8″ × 13.6″, shown in the bottom-left corner. |
Dahlem et al. (2006) investigated possible parameters influencing the existence of radio halos. They found that galaxies that show radio halos also have high energy input rates into their interstellar medium (ISM) and high average dust temperatures. These latter authors report that NGC 4666 shows the highest total nonthermal radio power at 1.49 GHz in their sample with a value of 34.1 × 1021 W Hz−1. Li & Wang (2013) calculated the total supernova (SN) mechanical energy injection rate to be 10.4 × 1038 erg s−1, which is one of the highest in their sample.
The radius of star formation in NGC 4666, which was derived in Dahlem et al. (2006) via the radial extent of Hα emission, is quite high in comparison to the optical extent of the galaxy. The radial extent of star formation was determined in this study to be 14.2 kpc (scaled to the distance used in this paper) in comparison to the radius of the major axis of 18 kpc, showing that NGC 4666 has widespread star formation across almost the entire disk. This is very different from a classical starburst galaxy with a central starburst. The SFR of 7.3 M⊙ yr−1 (Wiegert et al. 2015) is the highest among the 35 edge-on galaxies in the CHANG-ES sample. The star formation-driven winds originating from the wide-spread star forming regions may be an explanation to the box-like appearance of the halo as seen in Fig. 1.
The CHANG-ES observations of the galaxy NGC 5775 (Heald et al., in prep.) provide further evidence corroborating the explanation for the box-like radio halo from above. This galaxy is the only galaxy in the CHANG-ES sample that is comparable to NGC 4666 with regard to its size and SFR, with the second highest SFR of 5.3 M⊙ yr−1 (Wiegert et al. 2015). Furthermore, neither is strongly dominated by its central object and in both the star formation is widely spread over almost the entire disk. NGC 5775 is also defined as a starburst and superwind galaxy and shows a similarly boxy radio halo. The wind could be confined by the magnetic field lines of the disk, which mostly follow the spiral structure and reach into the halo (Henriksen & Irwin 2016), thus resulting in a box-like structure of the radio halo. NGC 4666 is a remarkable example of a clear connection between the star-formation distribution in the disk and the morphology of the radio halo.
3.2. Integrated spectral distribution
The spectral index behavior of the integrated flux densities I of NGC 4666 is shown in Fig. 2. Other integrated flux-density measurements from the literature were selected from the NASA/IPAC Extragalactic Database (NED)6 and VizieR7, complementing the two CHANG-ES flux densities from this work (Table 6); only literature values with corresponding errors were used. The fitted spectral slope is α − 0.68 ± 0.04 (where I ∝ να). This spectral index is typical for radio spectra with superposition of synchrotron and thermal radiation. The spectral index through the higher-frequency data shows hints of a steeper index. There is no indication of flattening towards the lower frequencies from the different GLEAM data.
 |
Fig. 2. NGC 4666 flux density measurements in the radio regime with a fit that gives a spectral slope of α = −0.68 ± 0.04. I: VLA Low-Frequency Sky Survey (VLSS, Cohen et al. 2007), II: GaLactic and Extragalactic All-sky MWA survey (GLEAM, Hurley-Walker et al. 2016), III: The Molonglo Reference Catalogue of Radio Sources (MRC, Large et al. 1981), IV: The NRAO VLA Sky Survey (NVSS, Condon et al. 1998), V: CHANG-ES (this work), VI: The Parkes-MIT-NRAO surveys (PMN, Griffith et al. 1995), VII: CHANG-ES (this work). |
Flux densities of NGC 4666.
3.3. Central point source
3.3.1. Radio continuum
The central point-like source is seen in both radio bands (at the J2000 position RA 12 h 45 m 08.62 s, Dec −00° 27′ 43.2″): in the high-resolution B-configuration of L-band (see Appendix, Fig. A.3, first panel) and in the combined image of C-band (Fig. 3), as well as in the C-configuration alone, which is used for the analysis performed here. These are the first detections in the radio regime. To measure the flux density of the central source, the images of both bands were smoothed to the same beam size of 4″ to allow for a better comparison of the measurements and to ensure consistency. The flux density was then measured via a Gaussian fit to the intensity profile after subtraction of the diffuse flux density from the galaxy disk. We chose a circular region of two times the size of the beam (at least twice the beam is recommended). The resulting error was very small8 and was therefore analyzed further. The chosen region was varied from twice the beam size to four times the beam size. The difference in the flux density measurements was then taken to calculate a mean error.
 |
Fig. 3. NGC 4666 C-band image (C- and D-configuration) in gray scale with an rms noise σ of 4.6 μJy beam−1 and a beam size of 3.0″ × 3.5″ (see bottom left), using robust zero weighting. The light-gray contours show the inner region with the radio point source from the same data. The corresponding flux densities are 0.22, 0.44, and 0.88 mJy beam−1. We note the bubble-like structure in the eastern direction from the point source and the filamentary structures (threads) in the northern halo. |
The resulting radio spectral index of the nuclear flux density measurements (Table 7) is α = −0.67 ± 0.12, which indicates a synchrotron source. As some AGNs show circular polarisation, Stokes V was imaged but did not show any signal in either band.
Flux densities of the central source of NGC 4666.
In Fig. 3 the combined (C- + D-configurations) C-band data are shown in gray scale with contours overlaid showing the location of the central radio source. In the eastern direction from the point source (gray contour) a bubble-like structure is seen that may indicate a jet. This further strengthens the argument that the central source is an AGN. Other interesting features of NGC 4666 seen in Fig. 3 are the filamentary structures to the western side of the galaxy. These are comparable to Hα filaments emerging from the disk. With the new high-resolution CHANG-ES data this structure is now seen in the radio regime. Since the galaxy is classified as a superwind and starburst galaxy, these structures are probably best explained by a galactic wind from the disk and up into the halo. Therefore, the magnetic fields as well as the CRs are transported with the wind. This would result in advection being the main transport process of CRs, which agrees with what is found for this galaxy by Heesen et al. (2018); this is further discussed in Sect. 3.11. Similar filamentary radio structures described as threads were found in the center of the Milky Way by LaRosa et al. (2000).
The western and eastern side of the galaxy halo look very different in terms of this filamentary structure. Beside the bubble-like structure to the east there are also thin features of radio intensity in the halo on this side of the galaxy. They are not filamentary, but shell-like structures. A possible reason for this is the ongoing interaction mainly occurring with NGC 4668 to the eastern side of the galaxy which could bend this side of the halo. Therefore, the two sides are affected differently.
3.3.2. XMM data
The analysis of the X-ray emission from the central source was performed using additional components in the model fitted to the spectrum from the disk region (Table 8). These include an absorbed power law and a simple Gaussian, with the latter accounting for a weak but clearly visible iron Fe-Kα line at around 6.4 keV. This line is considered to be a typical fingerprint of an AGN. Table 9 presents the parameters of the central source obtained from the fit, including the unabsorbed luminosity.
Model type and reduced 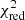 .
.
Characteristics of the central source in NGC 4666.
3.4. Further analysis of the XMM data
Figure 4 shows the large-scale emission from the hot gas in NGC 4666. While the brightest emission comes from the central parts of the disk and the nuclear point-like source, the vertical outflows reach up to 9 kpc into the halo. The hot gas around NGC 4666 is also box-shaped as seen in radio. Interestingly, the bubble-like structure from the radio map coincides with a feature in the X-rays to the southeast. The spectral analysis was performed for three regions of NGC 4666: The central disk region was chosen to supplement the analysis of the magnetic fields of NGC 4666 in radio and has a boxsize of 140″ × 28″. Two additional regions of the same size on both sides of the disk region (east and west) were selected in order to look for possible changes in the energy budget of the ISM in the disk outskirts, as well as to study the emission for the hot gas in the galactic halo. All regions are presented in Fig. 5.
 |
Fig. 4. Map of soft X-ray emission from NGC 4666 in the 0.2–1 keV band overlaid onto the DSS blue image. The contours are 3, 5, 8, 16, 32, 64, 128 × σ. The map is adaptively smoothed with the largest scale of 10″. |
 |
Fig. 5. The regions used for the spectral analysis of the disk of NGC 4666 on the DSS blue image. |
A complex model was used for the spectral analysis of the emission from the disk region. It consisted of two gaseous components represented by a mekal model, which is an emission spectrum from hot diffuse gas based on the model calculations of Mewe and Kaastra (Mewe et al. 1985; Kaastra 1992), accounting for the emission from the hot gas in the disk and the halo of NGC 4666, and a power-law model to account for the unresolved point sources in the galactic disk. As mentioned above, an additional absorbed power law and a simple Gaussian component were also used to account for the emission from the central source.
The two remaining spectra (east and west regions) were fitted with a model consisting of two mekals (hot gas from the disk and the halo), as well as a power law (unresolved disk sources). The spectra and the fitted models are presented in Fig. 6 and Table 8, and their fitted parameters in Tables 9 and 10.
Model fit parameters for the regions in NGC 4666.
The parameters from the mekal components of the model fit were used to calculate electron densities, gas masses, thermal energies, and thermal energy densities of the hot gas. In our calculations we follow the widely accepted assumption that the cooler component describes the hot gas in the halo, while the hotter corresponds to the hot gas in the disk (e.g., Tüllmann et al. 2006). Another important assumption is the emitting volume of the hot gas. In our calculations we assumed a disk thickness of 1 kpc. For the halo we needed to take into account the inclination of the galaxy. The position of the spectral regions (Fig. 5) suggests that about half of both east and west regions still include emission from the disk. While in the latter region we expect the emission from both the disk and the halo (we see the top side of the disk), the east region might show a lower contribution from the soft emission (below 1 keV) of the halo below the disk. The hardness ratio map (Fig. 7) confirms our expectations, the eastern side of the disk being significantly harder than the western part. Consequently, we assumed the path length through the halo of NGC 4666 to be 20 kpc for the west region and 10 kpc for the east region, which allows to account for different emitting volumes. All derived parameters of the hot gas both in the disk and in the halo are presented in Table 11.
 |
Fig. 7. Hardness ratio map of NGC 4666 with the spectral regions marked. |
Derived parameters of the hot gas in the studied regions of NGC 4666.
Under the assumption that hot gas and magnetic fields are responsible for the observed Faraday RMs (Fig. 19), we used the number densities of the hot gas derived from the X-ray spectra and calculated the strengths of the large-scale field parallel to the line of sight (Table 12). The resulting field strengths of 2–3 μG are several times smaller than the strengths of the total field (see Fig. 24), as expected from the action of a large-scale dynamo.
Properties of the studied regions of NGC 4666.
3.5. Scale heights
The intensity profile perpendicular to the major axis of edge-on galaxies can be best fitted by exponential or Gaussian functions. We follow the scale height determination undertaken for 13 CHANG-ES galaxies in Krause et al. (2018) to fit two-component exponentials to the radio intensity profiles. The scale height analysis was carried out on the combined C-band and L-band data. To compare the results in both bands the maps were smoothed to the same beam size of 13.3″ × 13.3″. We used the “BoxModels” tool within the NOD3 software package (Müller et al. 2017). The parameters of the analysis are presented in Table 13.
NGC 4666 parameters.
For NGC 4666 it is not easy to find good fit solutions with two-component exponentials along the whole disk if the galaxy is divided into different strips along the major axis. This is mainly due to its asymmetry between the two sides of the major axis. Therefore we used a box size of 130″ × 6″ to fit one intensity profile for the central galaxy, omitting the asymmetric outer part (see Fig. 10). Furthermore, an asymmetry was found above and below the plane between the eastern and the western halo. Therefore fits were undertaken separately for above and below the plane. The resulting fits and scale heights are presented in Figs. 8 and 9 as well as in Tables 14 and 15. We note that with the inclination of 70° from Walter et al. (2004) we were not able to fit the scale heights. Despite the fact that in optical images of this galaxy the disk is clearly seen and thus cannot be nearly 90°, we conclude from our analysis that the inclination is rather 85° ± 2°.
 |
Fig. 8. NGC 4666 scale height analysis C-band with different model fits for the northern (positive distances) and southern (negative distances) halo. |
 |
Fig. 9. NGC 4666 scale height analysis L-band with different model fits for the northern (positive distances) and southern (negative distances) halo. |
NGC 4666 scale heights of C-band.
NGC 4666 scale heights of L-band.
The resulting mean scale heights of the thin disk are 0.41 ± 0.18 kpc and 0.74 ± 0.12 kpc for C-band and L-band, respectively. The mean thick disk scale height in C-band is 1.57 ± 0.21 kpc and in L-band is 2.16 ± 0.36 kpc.
In Fig. 11 the mass surface density (MSD) is plotted against the normalized scale height for 13 CHANG-ES galaxies from Krause et al. (2018). The data point for NGC 4666 is added in red. The MSD is defined in Krause et al. (2018) as MSD = MT/π (d25/2)2 with the values for NGC 4666 of the total mass of MT = 1.3 × 1011M⊙ and d25 = 33.6 kpc from Irwin et al. (2012a). The normalized scale height is defined as z̃C = zC/dr · 100 in Krause et al. (2018). All derived values are presented in Table 16. The galaxy fits nicely within the trend of an anticorrelation between those two parameters showing that with lower mass surface densities the normalized scale heights are increasing.
 |
Fig. 10. NGC 4666 boxes with a size of 130″ × 6″ for the scale height analysis in C-band with a beam of 13.3″ × 13.3″. |
 |
Fig. 11. Mass surface density versus normalized scale height for the CHANG-ES galaxies from Krause et al. (2018) with additional data point for NGC 4666 from Table 16, which is marked in red. The data can be described by a linear fit (excluding UGC 10288). |
Mean scale heights of NGC 4666.
3.6. Synchrotron polarization
3.6.1. Magnetic field orientation
Figure 12 shows the magnetic field orientations with Stokes I contours from C-band overlayed on the optical SDSS image.
 |
Fig. 12. Color image of NGC 466 6 produced from SDSS with Stokes I contours from C-band starting at a 3σ level with a σ of 11.0 μJy beam−1 and increase in powers of 2 (up to 128) with a robust zero weighting. The corresponding beam size is 10″ × 10″ (see bottom left). The apparent magnetic field orientations are shown in white. |
The polarization data of NGC 4666 for C-band are shown in Fig. 13 (and Fig. A.1). The polarized intensity contours and magnetic field orientations generated by imaging Stokes Q and U are shown on Stokes I (Stokes I contours on polarized intensity). For C-band, when imaging Stokes Q and U with robust two weighting compared to using RM synthesis with robust two weighting, we detect a similar distribution of extended polarized emission but a little more polarized flux. Therefore, Fig. 13 shows the apparent magnetic field orientations from Q and U without RM synthesis. With the RM maps obtained from RM synthesis (as discussed in Sect. 3.6.3) the intrinsic magnetic field orientations may deviate from the apparent magnetic field vectors by less than 20° in most parts of NGC 4666.
 |
Fig. 13. Total intensity as a color image of NGC 4666 from C-band with robust zero weighting, with a beam of 7″ × 7″ in red, obtained by Gaussian smoothing to fit the resolution of the polarization map, σ is 8.1 μJy beam−1. Gray polarization contours are at 3, 6, 9, 12, 15, 18 σ levels with σ of 7.0 μJy beam−1 with a robust two weighting. The apparent magnetic field orientations are shown in white. |
In C-band, polarized intensity from nearly the entire galaxy is visible. The magnetic field orientations show an X-shaped structure and the intensity contours extend far into the halo as well as into the disk. There is no polarized intensity above 3σ from the southern side of the galaxy, which is the receding side.
In Fig. 14 (and Fig. A.2) the L-band polarization data are presented with intensity contours and magnetic field orientation on Stokes I using RM synthesis (the L-band Stokes I contours on polarized intensity).
 |
Fig. 14. Total intensity as a color image of NGC 4666 from L-band with robust zero weighting, with a beam of 18″ × 18″ in red, obtained by Gaussian smoothing to fit the resolution of the polarization map with σ of 40.1 μJy beam−1. Gray polarization contours from RM synthesis are at 3, 6, 9 σ levels with σ of 20.0 μJy beam−1 with a robust two weighting. The magnetic field orientations are shown in white. |
In L-band, the Faraday rotation effect is quite strong, meaning that some polarization is expected to be depolarized and not visible in the map. Without RM synthesis, polarized intensity in L-band is only observed in a small fraction of the disk. After applying RM synthesis, a factor of 1.4 more polarized intensity can be recovered, which is seen in Fig. 14. The polarized emission is distributed over the whole galaxy disk reaching into the halo.
Specifically, in the halo to the northwest of the galaxy, a large polarized emission region is located with vertical field components. This region is also seen in the C-band data, but the emission does not reach as far out into the halo as in L-band. This indicates a large-scale ordered magnetic field extending into the halo. In summary, an X-shaped magnetic field structure is again visible in the polarization map of L-band using RM synthesis.
3.6.2. Large-scale magnetic field in C-band – comparison between L-band and the archival VLA map
In Fig. 15 the large-scale polarization from the CHANG-ES C-band data is presented. The halo emission seen in this map is consistent with the emission in the L-band image (Fig. A.2). Especially the polarized intensity to the southeast of the galaxy is recovered (RA 12 h 45 m 10 s Dec -0° 29′ 10″). The origin of this polarization structure could be the shell-like feature marked in the total intensity image with a higher resolution (Fig. 3). Also, the extended polarized emission region in the northwestern halo of the galaxy is similar to the L-band image (Fig. 14), whereas the polarized emission region in the southeastern halo in Fig. 15 is only recovered as a small feature in the L-band image.
 |
Fig. 15. Polarized intensity as a color image of NGC 4666 from C-band with robust zero weighting and a uv-taper of 12kλ and Gaussian smoothing to obtain the beam of 18″ × 18″ in red, σ is 11 μJy beam−1. The white total intensity contour correspond to 0.04 mJy with robust zero weighting and smoothing. The apparent magnetic field orientations are shown in white. |
To compare the CHANG-ES C-band data with the archival VLA C-band data, the CHANG-ES data were imaged with robust zero weighting. Due to the fact that the archival VLA data have nearly 380 min observing in C-band D-configuration compared to only 40 min of CHANG-ES C-band data, but 3 h of C-configuration observations, a comparison is only possible by higher weighting the CHANG-ES data D-configuration using uv tapering. In general, the Stokes I background images, the polarized intensity, and the magnetic field vectors are comparable between the old VLA (Fig. 16, original published in Soida 2005) and the new CHANG-ES image (Fig. 15). Looking closer at the maps of NGC 4666 from C-band it is visible that in the CHANG-ES map there is less extended polarized flux, especially in the south (receding side) of the galaxy. In C-band this is probably not due to depolarization effects. Bandwidth depolarization can be ruled out because the polarization map produced with RM synthesis also shows only polarized emission in this region below 3σ. If we compare both maps (Figs. 16 and 15) more carefully, we have to consider the different central frequencies of 4.86 GHz and 6 GHz for the archival VLA and the CHANG-ES observations, respectively. This leads to 20% higher intensities (assuming an average spectral index of −0.8) in the archival VLA maps. For the comparison of polarized emission in the halo, especially in the south, we take the difference in central frequency into account by dividing the 4.86 GHz image by 1.2 (assuming an average spectral index of −0.8). The difference between the polarized intensities in the south is less than 5σ.
 |
Fig. 16. Polarized intensity as a color image of NGC 4666 from archival VLA C-band data with robust zero weighting, originally published in Soida (2005), with a beam of 18″ × 18″ in red, σ is 9.3 μJy beam−1. The white total intensity contour correspond to 0.04 mJy with robust zero weighting and smoothing. The apparent magnetic field orientations are shown in white. |
Significant differences between the two observations are the uv distribution and weighting as well as the integration time. The much larger bandwidth of the CHANG-ES observations does not compensate for the much shorter observation times compared to the archival data.
3.6.3. RM maps
A further outcome of the RM synthesis is the RM map, which represents the fitted peak position along the cube of each pixel. It represents the mean magnetic field component along the line of sight, where the value is positive for a field pointing towards the observer and negative for a field pointing away from the observer. The RM map of C-band is shown in Fig. 19 and the one of L-band in Fig. A.4. The RM values in C-band lie between −200 and +200 rad m−2. The L-band RM values are very different and between −14 and +26 ra m−2. In addition to the different RM values between the bands, the different beam sizes influence the scale of the local variations of these values. In the disk, the sign of RM values are comparable in both frequency bands.
3.7. Thermal/nonthermal separation
Following Vargas et al. (2018), we performed a thermal/nonthermal separation to get the nonthermal maps of C-band and L-band.
We used the Hα emission derived from the Hα map, which was provided by Dahlem et al. (1997). The Hα flux density was corrected from 38% [NII] contamination.
Then the [NII]-corrected Hα flux density (LHα, obs) was absorption corrected via infrared WISE data at 22 μm (νLν(22 μm)) with the calibration factor of 0.042 from Vargas et al. (2018):
Following Vargas et al. (2018), the thermal emission was derived using the corrected Hα flux density (LHα, corr) as:
An electron temperature of Te = 10 000 K is assumed, with ν being the central frequency of 6 GHz and 1.5 GHz for C-band and L-band, respectively. The resulting thermal map was then subtracted from the radio map to derive the nonthermal map. To apply the thermal/nonthermal separation, all maps were smoothed to the same beam of 13.3″ × 13.3″. We refer to Vargas et al. (2018) for a detailed analysis on the thermal/nonthermal separation in edge-on spiral galaxies.
3.8. Nonthermal fractions
The maps of nonthermal fraction are shown in Fig. 17 for C-band and Fig. 18 for L-band. The mean nonthermal fractions in the disk, the eastern halo, and the western halo are presented in Table 17. In the disk these are 83.0% in C-band and 93.8% in L-band. The nonthermal fractions in the halo are higher below the disk in comparison to the nonthermal fraction above the disk. In C-band, these are 88.0% in the southeastern halo and 81.0% in the northwestern halo; in L-band these are 97.7% in the southeastern halo and 96.7% in the northwestern halo. The halo below the disk is closer to the observer. The interaction with NGC 4668 could effect the distributions of CRs as well as of magnetic fields. As seen before in the C-band radio image (Fig. 3) as well as in the scale height analysis, NGC 4666 seems to be different above and below the disk.
 |
Fig. 17. NGC 4666 nonthermal fraction map at C-band. The beam of 13.3″ × 13.3″ is shown in red (left bottom). |
 |
Fig. 18. NGC 4666 nonthermal fraction map at L-band. The beam of 13.3″ × 13.3″ is shown in red (left bottom). |
Nonthermal fractions of NGC 4666.
3.9. Nonthermal spectral index
The nonthermal spectral index (αnt) map was calculated from the nonthermal maps of the two bands at the observed frequencies of 1.5 GHz and 6 GHz of the CHANG-ES data, giving the spatial distribution of the spectral index in this galaxy. The nonthermal SPI map was derived using the following equation:
where ν1 and ν2 are the central frequencies of C-band and L-band, respectively. From Eq. (8), the error Δαnt with respect to ΔI1 and ΔI2 can be determined using error propagation:
Both resulting maps are displayed in Fig. 20. The error map displays uncertainties of below 0.05 in the disk, which increase to 0.3 towards the edges. Based on the error map, the spectral index is cut off in order to only include trustable values. A mean nonthermal spectral index in the disk of αnt = −0.90 ± 0.05 is found, which is in good agreement with synchrotron radiation being the dominant radiation process. The spectral index steepens towards the edges and reaches values of αnt = −1.8 ± 0.3. The huge star formation region in the south of the galaxy is clearly visible with a flatter spectral index of αnt = −0.6 ± 0.05, which suggests synchrotron emission from young CRs.
 |
Fig. 19. RM map of NGC 4666 from C-band on Stokes I contours from Fig. 13 and a beam of 7″ × 7″ in gray. Contours start at a 3σ level with a σ of 9.3 μJy beam−1 and increase in powers of 2 (up to 64) with an additional contour at 3.5 mJy beam−1 to mark the central source. The RM map is cut below the 3σ level of 25μJy beam−1 of the polarized intensity map from RM synthesis. The mean error is 22 rad m−2. |
 |
Fig. 20. Top panel: NGC 4666 nonthermal spectral index (αnt), bottom panel: spectral index error map. The beam is 13.3″ × 13.3″. |
3.10. Magnetic field
The magnetic field structure is obtained via RM synthesis to gain the intrinsic magnetic field vectors for the field component perpendicular to the line of sights as well as for the parallel line of sight component. The magnetic field strength is determined with the assumption of energy equipartition with the CR electrons.
3.10.1. Magnetic field configuration of the disk field
The analysis of disk magnetic fields of spiral galaxies makes it possible to reveal the mode and direction of large-scale fields. In face-on spiral galaxies the analysis is done via a sector integration using an RM map, where the RM values are plotted against the azimuth angle in degrees in the plane of the galaxy (Krause 1990). Hereby, the mode of the disk field is quantified, that is, whether the field is axisymmetric (m = 0), bisymmetric (m = 1) or can be described by higher modes. However, this is not applicable to edge-on galaxies as the emission from the disk is observed in projection. Additionally, to distinguish between an even disk magnetic field parity (S, same direction above and below the mid plane) with a corresponding quadrupolar halo field and an odd disk magnetic field parity (A, opposite orientation above and below the mid plane) with a corresponding dipolar halo field, RM data at high resolution and sensitivity, and especially with a wider range in λ2-space, have to be obtained. Here, we present a modified analysis method for RM maps of edge-on galaxies for the disk magnetic field and apply it to NGC 4666.
In this new approach a rectangle along the disk is used to obtain a profile of RM values along the major axis. Figure 21 shows the expected RM behavior in projection for this analysis of an edge-on galaxy, where in the first two rows, the edge-on view of an axisymmetric disk field (left) leads to positive RM values on one side of the disk and to negative RM values on the other side. The edge-on view of a bisymmetric disk field (right) leads to negative RM values on both sides for the plotted field configuration. Both RM behaviors would be mirrored across the x-axis (major axis) if the magnetic field vectors were to point in the opposite direction. In the third and fourth rows of Fig. 21, the same is shown for a disk magnetic field with one radial reversal at half of the disk radius.
 |
Fig. 21. Expected RM variation for an edge-on view of a simplified axisymmetric disk magnetic field (left panel) and a simplified bisymmetric disk magnetic field (right panel) with trailing spiral arms, which are shaded red for the approaching side and blue for the receding side. The black arrows show the direction of the magnetic field vectors. The direction of the rotation of the disk is given by the bold black arrow below the four disks. Panel a: upper part shows the face-on view of the two different disk fields. In the case of an axisymmetric disk field (left panel) all vectors are pointing inwards or outwards; here just one configuration is shown. In case of the bisymmetric magnetic field (right panel) the vectors from one side of the galaxy are pointing inwards and on the other side of the galaxy outwards (or the other way around). In the second row, the expected RM behavior is plotted along the major axis of each galaxy model for an observer watching the system edge-on. The red curve represents the RM values from the approaching side, the blue curve from the receding side. Panel b: upper part shows again the face-on view of the two different disk fields as above (left panel: axisymmetric disk field, right panel: bisymmetric magnetic field). In a simplified approach, a radial reversal is assumed at half of the disk radius. The last row shows the expected and simplified RM value variation in case of a radial field reversal at half the radius of the disk. |
Here we assume an even disk magnetic field parity with a quadrupolar halo field, which seems to be the most readily excited dynamo mode in dynamo models (e.g., Ruzmaikin et al. 1988), especially considering a wind (e.g., Moss et al. 2010). Additionally, the even disk parity is found in the Milky Way (Sun et al. 2008) and in the external galaxies NGC 253 (Heesen et al. 2009), NGC 891 (Krause 2009), and NGC 5775 (Soida et al. 2011).
The analysis described above was carried out on the C-band RM map. Figure 22 shows the rectangle along the major axis with a box size of 7″ × 14″ (0.93 kpc × 1.87 kpc) on the RM map to the left. For this analysis RM synthesis was applied in a different way. The mean Q and U values within each box were determined from the Q and U maps of each spw. For each of these boxes there is one mean value from the Q map and one mean value from the U map. Then a cube was made and RM synthesis applied. The distance to the center against the resulting RM value of each box is plotted separately for the approaching side (left half of the galaxy, red) and the receding side (right half of the galaxy, blue). The RM error was calculated with RMSF/(2 PI/σ) (Schnitzeler & Lee 2017), where RMSF is the resolution in Faraday space, PI is the polarized flux density, and σ the noise measured when integrating over the entire frequency band. This is a good error approximation for PI/σ > 5 (Schnitzeler & Lee 2017). With the RMSF in C-band of ∼1800 rad m−2 from Table 5 and a 20σ signal, a mean RM error of 50 rad m−2 is derived.
 |
Fig. 22. Left panel: NGC 4666 C-band RM map, rotated by 50° on sky, with a beam of 7.2″ × 7.2″. The rectangle boxes of 7″ × 14″ were used for averaging. The orange cross marks the center. Right panel: RM values from boxes along the major axis for both sides of the galaxy. The sinusoidal fit was made for the different sides separately indicated by the color. The sinusoidal fit for the receding side excludes the data point at 38.5″ in Fit 1 and includes this data point in Fit 2. |
The result is displayed on the right side of Fig. 22 and on the left side of Fig. 23. The RM pattern on both sides is approximately axisymmetric with respect to the x-axis, where a maximum of the approaching curve corresponds to a minimum of the receding curve and vice versa. The resulting curve of Fig. 23 can be divided into two parts. The first part is up to ±30″ (blue shaded) and the second part is from ±30″ to the end (yellow shaded). In the first part we see that the approaching side shows mainly positive RM values and the receding side shows mainly negative RM values. This behavior is comparable to the expected RM behavior in the fourth row on the left-hand side of Fig. 21 for the axisymmetric case (m = 0) with magnetic field vectors pointing inwards in the inner part and pointing outwards in the outer part. At the radius of about 30″ (4 kpc) of Fig. 23, the behavior of the RM values of the two halves of the galaxy of the blue shaded part of the plot change to the opposite. From a radial distance of 30″ further out (in the yellow shaded part of the plot), the approaching side shows mainly negative values whereas the receding side shows mainly positive RM values. This indicates an axisymmetric field pointing outwards.
 |
Fig. 23. Left panel: NGC 4666 C-band RM values for boxes from the center outwards to the edge of the disk for both sides of the galaxy; as in the right plot of Fig. 22 but with the approaching side mirrored. The left blue-shaded part of the plot indicates the axisymmetric disk magnetic field with magnetic field vectors pointing inwards, the yellow-shaded part of the plot indicates the axisymmetric disk magnetic field with magnetic field vectors pointing outwards, and the grey dashed line marks the radius of a possible field reversal. Right panel: NGC 4666 simplified disk model. |
We further tried to fit a sinusoid (f(x) = (a0 sin(a1 x + a2)) + a3) to the data of both sides separately, which is shown with the dashed and dotted lines in Fig. 22. The receding side is fitted twice; Fit 1 excludes the data point at the radius of 38.5″, while Fit 2 includes all data points. In Table 18 we present the fit parameters. The period P of the sinus along r is given by P = 2π/a1 which results in P = 84″ ± 7″ for the approaching side and P = 71″ ± 7″ for the receding side (fit 1). These two values are slightly different.
The parameter a2 is the phase (in rad). The a2 values of the two sides are the same within the errors and show that the sinusoidal functions have similar phases. A phase of π would correspond to an ASS field with vanishing pitch angle. The average a2 value of ≃3.45 indicates a pitch angle of about 20°, which is reasonable for spiral galaxies. Hence, the RM variations due to the disk magnetic field of both sides are consistent with each other and originate from the large-scale disk magnetic field.
A simplified model is shown in Fig. 23, where one radial field reversal is assumed. The color code is equivalent to the modeled disk field of Moss et al. (2012). The inner magnetic field points inwards and then outwards. The orientation of the magnetic field vector can be determined using the simplified model of Fig. 21. In the case of trailing spiral arms, which is suggested for NGC 4666, and positive RM values on the approaching side, the magnetic field vectors point inwards. Positive RM values on the receding side correspond to magnetic field vectors that point outwards (see Krause & Beck 1998).
In conclusion, an axisymmetric magnetic field is discovered in NGC 4666. One field reversal along the radius of the orientation of the magnetic field is indicated by the C-band data at a radial distance from the center of the galaxy of about 4 kpc. This radius coincides with the optical end of the bar of NGC 4666. The L-band data (see Fig. A.4) may suggest a second reversal at about 90″ (12 kpc) radius, but these data suffer from depolarization effects and may not be reliable. The presented disk model is very simple and should be improved with better data, maybe on other galaxies. The quality of the present data is not sufficient to analyze the halo parity, higher magnetic field modes, and pitch angles. A significant deviation in phase shift between the two sides of the galaxy would indicate that the assumption of a constant pitch angle between the two sides of the galaxy and/or between the inner and outer parts may not be fulfilled.
3.10.2. Magnetic field strength via equipartition
The maps of the magnetic field strength were determined with the revised equipartition formula by Beck & Krause (2005).
The calculations were done pixel-by-pixel by taking the nonthermal intensity map and the resolved nonthermal spectral index map into account. The pixel values of the magnetic field strength Beq were calculated according to the revised equipartition formula by Beck & Krause (2005). We assumed a spheroid path length model varying between l = 19 kpc in the center and 1 = 6 kpc at the edges and K0 = 100, which is consistent with CR data from the local Milky Way.
The resulting map is presented in Fig. 24. The total magnetic field strength in the center reaches 15 μG. The field strength decreases towards the halo to 8.5 μG. The mean disk magnetic field strength is 12.3 μG, which is in agreement with the values found for 13 CHANG-ES galaxies by Krause et al. (2018). The mean halo magnetic field strength is 10.1 μG in the eastern halo and 9.6 μG in the western halo. The smallest magnetic field strength of 7 μG is seen in the south of the galaxy. It appears that the magnetic field strength is smoothly distributed over the whole galaxy.
 |
Fig. 24. NGC 4666 magnetic field strength calculated pixel-based via the equipartition formula using the resolved nonthermal spectral index map and the intensity map with a beam of 13.3″ × 13.3″ (bottom left). |
Dahlem et al. (1997) found a total field strength of 14.4 μG in the disk and 7.1 μG in the halo, using C-band data and a fixed spectral index of α ≅ −0.79 in the disk and α ≅ −0.9 in the halo. The mean value of the disk and the halo total field strength derived here are somewhat higher in comparison to those in Dahlem et al. (1997). The reason is the difference of the application of the equipartition formula. The use of a fixed spectral index leads to a faster decline of the magnetic field strength towards the halo.
3.11. One-dimensional cosmic ray transport model
The transport processes of CRs into the halo (perpendicular to the galaxy disk) are derived by using a 1D CR transport model with SPINNAKER (SPectral INdex Numerical Analysis of K(c)osmic-ray Electron Radio-emission; Heesen et al. 2016, 2018) with a fixed inner boundary condition of N(E, 0) = N0E−γ0 and a corresponding nonthermal spectral index αnt = (1 − γ0)/2. Either pure advection is modeled, with an advection speed V assumed to be constant, or pure diffusion with a diffusion coefficient of  , assumed to be along the magnetic field lines. Here, the cosmic ray electron (CRe) energy is EGeV in units of GeV and μ is between 0.3 and 0.6, as measured in the Milky Way (Strong et al. 2007). The combined synchrotron and inverse compton radiation energy loss rate for a single CRe is taken into account with one loss term.
, assumed to be along the magnetic field lines. Here, the cosmic ray electron (CRe) energy is EGeV in units of GeV and μ is between 0.3 and 0.6, as measured in the Milky Way (Strong et al. 2007). The combined synchrotron and inverse compton radiation energy loss rate for a single CRe is taken into account with one loss term.
This model is used on the total intensity profile of the pure synchrotron maps, which represent the synchrotron intensity emitted by the CRe as well as on the corresponding spectral index map of NGC 4666.
An interactive PYTHON wrapper around SPINNAKER (SPINTERACTIVE; Miskolczi 2018, priv. comm.) was used to fit the data9. We varied the input parameters manually, while checking the quality of the fit on a graphical user interface, and thus arrived at the best-fitting solution. The main input parameter is the transport process, choosing between diffusion and advection. Depending on this choice, either the diffusion coefficient or the advection speed can be changed. Further parameters to be fitted are the CRe injection spectral index, γ0, the magnetic field strengths in total and of the thin disk component (B0, B1), and magnetic field scale heights hb1 and hb2, for the thin and thick disk, respectively. SPINNAKER models the magnetic field distribution as the superposition of two exponential functions. Generally speaking, synchrotron intensity profiles can be best described by a Gaussian function for diffusion and by an exponential function for advection.
The intensity distribution of NGC 4666 is produced via BoxModels (Müller et al. 2017) using one stripe covering the width of the major axis of the galaxy (box size of 200″ × 6″). The intensity value of two boxes at the same distance to the midplane (z) of the two halo sides are averaged to get the plotted intensity distribution for NGC 4666.
We found a good solution for advection ( ), the result of which is shown in Fig. 25. The top panel shows the C-band data, the middle the L-band data and the bottom panel shows the spectral index calculated from the corresponding data points of the C-band and L-band data. All the important adjustable parameters are listed in Table 19. Figure 25 also contains the information about the final χ2 values for the L-band data, C-band data, and spectral index.
), the result of which is shown in Fig. 25. The top panel shows the C-band data, the middle the L-band data and the bottom panel shows the spectral index calculated from the corresponding data points of the C-band and L-band data. All the important adjustable parameters are listed in Table 19. Figure 25 also contains the information about the final χ2 values for the L-band data, C-band data, and spectral index.
 |
Fig. 25. CR advection transport model for NGC 4666 with SPINTERACTIVE. The data points are the observed values from 1.5 GHz (L-band), 6 GHz (C-band), and the spectral index; the red line represents the model simulation. The errors correspond to a weighted standard deviation. The basic parameters are listed in Table 19. |
SPINNAKER parameter for advection.
The advection speed of 310 km s−1 can be compared with the results from the sample of galaxies modeled with SPINNAKER by Heesen et al. (2018), which included NGC 4666. They found higher advection speeds between 500 and 700 km s−1, but this can be explained by their higher equipartition magnetic field strength of B0 = 18.2 μG as a model input; that strength was derived using a simple thin disk model with a short path length of 1 kpc, whereas we now employ a more sophisticated model (Sect. 3.10.2). If we scale their advection speeds to the magnetic field strength used here of B0 = 13.1 μG, assuming the CRe loss time-scale is  (Eq. (5) in Heesen et al. 2016), their advection speeds are now between 260 and 550 km s−1, including the uncertainties, in fair agreement with our results. Our new data, however, allow us to measure the advection speed much more precisely.
(Eq. (5) in Heesen et al. 2016), their advection speeds are now between 260 and 550 km s−1, including the uncertainties, in fair agreement with our results. Our new data, however, allow us to measure the advection speed much more precisely.
The magnetic field strength of 13.1 μG for the thin component of the magnetic field is in very good agreement with the mean disk value from equipartition of 12.3 μG. The nonthermal spectral index found with SPINTERACTIVE follows from γ0 = 2.6. This results in αnt = −0.8. This value is in good agreement with the mean value of the spectral index map (Fig. 20).
A diffusion model was tested for comparison; results of which are shown in Appendix A. Figure A.5 shows that the best-fitting diffusion model performs worse than the advection model. The total  is much higher than for advection, which mainly originates from the spectral index profile fit. Advection leads to a linearly steepening spectral index profile, whereas diffusion leads to a parabolic one. Our new results confirm that advection is the main transport process of CRs in NGC 4666. This distinction is based purely on the goodness of the fit, whereas for the old VLA data used by Heesen et al. (2018) this was not possible. In summary, advection appears to be the main transport process of CRs in NGC 4666.
is much higher than for advection, which mainly originates from the spectral index profile fit. Advection leads to a linearly steepening spectral index profile, whereas diffusion leads to a parabolic one. Our new results confirm that advection is the main transport process of CRs in NGC 4666. This distinction is based purely on the goodness of the fit, whereas for the old VLA data used by Heesen et al. (2018) this was not possible. In summary, advection appears to be the main transport process of CRs in NGC 4666.
3.12. Magnetic field strength comparison
In Fig. 26, the magnetic field strength distribution of NGC 4666 determined by using the equipartition assumption are shown and compared to the magnetic field profile from SPINNAKER. The magnetic field strength profile in the vertical direction determined with the equipartition formula using the resolved spectral index map from Fig. 24 is presented by dark blue data points with a box size of 6″ × 180″. The black line with shaded gray errors represents the magnetic field model from SPINNAKER. The magnetic field is modeled as a two-component exponential function:
with the magnetic field scale heights for the thin disk hb1 and the thick disk hb2, the magnetic field in the central midplane B0 and the magnetic field in the halo B1.
 |
Fig. 26. Intensity profile of equipartition magnetic field strength with dark blue data points from Fig. 24, magnetic field strength distribution from SPINNAKER with the black line, and gray shaded errors. |
Both distributions show similar values of the magnetic field in the midplane of the galaxy, but large discrepancies in the halo. In the halo, the SPINNAKER magnetic field strength is about 2.5 times less than the equipartition value in the halo at 5 kpc from the center. To achieve the observed synchrotron flux density, the number density of CRe (which is proportional to the CR energy density) needs to be larger by a factor of 2.51 − αnt ≈ 5 compared to the equipartition value. Together, the ratio of energy densities of cosmic rays and magnetic fields is 2.53 − αnt ≈ 35, which is a huge deviation from equipartition.
This deviation is a consequence of the cosmic ray advection equation used in SPINNAKER. For a constant advection velocity, the cosmic ray energy density is constant, neglecting radiation and adiabatic losses of the electrons. Hence, the decrease of the nonthermal radio continuum intensity is fully ascribed to a decrease of the magnetic field strength. The SPINNAKER magnetic field strength is therefore a lower bound for the actual field strength in the halo.
If we were allowing for an accelerating wind, the magnetic field strength would be closer to the equipartition value. However, our advection model with a constant speed already gives a relatively good fit to the data, and therefore seems to be sufficient. In the near future, we hope to probe radio haloes to even larger distances from the star-forming disk using low-frequency radio continuum observations that reveal the oldest CRe. For instance, the 144 MHz LOFAR study of Miskolczi et al. (2019) of the edge-on galaxy NGC 3556 detected the radio halo to heights of 15 kpc. These authors could show that an accelerated wind model fits better than one with a constant wind speed.
4. Summary and conclusions
The superwind and starburst galaxy NGC 4666 exhibits a boxy radio halo in radio total intensity. Its extent is up to 9 kpc from the midplane into the halo in L-band, which is probably produced by a supernova-driven wind across almost the entire disk. The supplemental X-ray data show large-scale hot gas surrounding the galaxy, which is also box-shaped and reaches the same height as the L-band radio data. As in other CHANG-ES galaxies, such as for example NGC 4631 (Irwin et al. 2012b), we find the magnetic field and X-ray morphologies to be similar, which indicates an important influence of the magnetic field on the hot gas dynamics.
For the first time a central point source of NGC 4666 was detected at radio wavelengths and further observed in our X-ray data with clear AGN fingerprints, which supports previous findings from X-ray observations that NGC 4666 harbors an AGN. A corresponding bubble-like structure was found below the midplane in the radio data, which was previously suggested by Dahlem et al. (1997), who found indications for a bipolar outflow with an associated galactic superwind within the central 6.5 kpc. In our X-ray data the extension of the bubble-structure is seen, which reaches far into the halo.
NGC 4666 appears different above and below the disk. First, this is visible in the total intensity image of the combined C-band observations (Fig. 3). NGC 4666 shows extraordinary filamentary structures above the disk reaching into the halo like fingers. These radio filaments are comparable to Hα filamentary structures. In contrast to this, shell-like structures are visible below the disk. Secondly, the X-ray analysis revealed higher thermal energy densities in the western part (above the disk). Thirdly, the nonthermal fraction maps in C-band and L-band show an asymmetric fraction of the two halo sides, where the western halo (above the disk) is characterized by higher thermal fractions. The most likely explanation is the interaction of the galaxy with NGC 4668, which is also discussed to be the reason for the starburst happening in NGC 4666 (Walter et al. 2004). The interacting galaxy NGC 4668 is located to the southeast of NGC 4666.
A scale-height analysis was applied to radio data smoothed to a beam of 13.3″ × 13.3″ in both bands. An asymmetry is found in the halo above and below the disk as well as between the two sides of the major axis. The mean scale height of the thick disk in C-band is 1.57 ± 0.21 kpc and the mean scale height of the thick disk in L-band is 2.16 ± 0.36 kpc.
The results of RM synthesis show that NGC 4666 is characterized by an X-shaped large-scale magnetic field structure with an observed magnetic field reaching far into the halo. In C-band, the polarized intensity and magnetic field orientation were determined by imaging Stokes Q and U with a robust two weighting. In comparison to RM synthesis with robust two weighting, the polarization map from Stokes Q and Stokes U and robust two weighting shows 1.2 times more polarized flux density. In the uv-tapered and smoothed images from archival VLA and from CHANG-ES data the large-scale X-shaped magnetic field in C-band is visible. In L-band, RM synthesis is useful and necessary to detect polarized intensity from the entire galaxy with a factor of 1.4 of enhanced polarized flux density in comparison to imaging Stokes Q and U (both with robust two weighting).
Large radio halos and large-scale magnetic fields are observed in many CHANG-ES galaxies (Wiegert et al. 2015) and in other edge-on galaxies (Krause 2009; Beck 2016). These findings suggest a general mechanism in spiral galaxies that produces and maintains the large-scale fields. A universal explanation is the mean-field dynamo theory, where a regular field is induced from seed fields. These were probably amplified beforehand by the small-scale dynamo, which amplifies turbulent magnetic fields.
Generally, the CHANG-ES galaxies tend to show less or no polarization on the receding side of the galaxy. Furthermore, the peak of polarized flux density is shifted towards the approaching side of the galaxy. In NGC 4666, polarized emission in L-band was recovered with RM synthesis also in the south side of the galaxy, which is the receding side. In C-band, RM synthesis was not able to recover the polarized emission in the south. By weighting and smoothing the C-band data, low-level polarized intensity was recovered also in the south. Differences in the C-band observations of NGC 4666 could originate from the short observing time and uv distribution leading to parts of the large scale faint polarized emission being missed. This could be the reason why less polarized intensity is detected on the receding side in C-band. Nevertheless it does not explain why the peak of polarized intensity is shifted towards the approaching side, which seems to be an intrinsic feature of the emission.
The CR transport was modeled with the 1D SPINNAKER model and found to be advection dominated with an advection speed of 310 km s−1. This velocity is slightly higher than the escape velocity of this galaxy estimated by Heesen et al. (2018) to be  vrot ≈ 280 km s−1, neglecting the contribution of a dark-matter halo. We therefore conclude that NGC 4666 has a galactic wind, as was already indicated by the box-shaped appearance of the radio halo. We assumed a constant wind speed for simplicity, but relaxing this to an accelerating wind, the escape velocity should be easily surpassed in the halo even if there is an extended dark-matter halo.
vrot ≈ 280 km s−1, neglecting the contribution of a dark-matter halo. We therefore conclude that NGC 4666 has a galactic wind, as was already indicated by the box-shaped appearance of the radio halo. We assumed a constant wind speed for simplicity, but relaxing this to an accelerating wind, the escape velocity should be easily surpassed in the halo even if there is an extended dark-matter halo.
The magnetic field strength map was then calculated using the equipartition formula from Beck & Krause (2005) with the C-band synchrotron map, the resolved spectral index map, and the spheroid path length model. The mean strength of the disk magnetic field is 12.3 μG, which is in good agreement with the field strengths of other spiral galaxies (Beck 2016). Nevertheless, there are a few drawbacks of field strength determinations via equipartition. The result of the equation leads to an overestimate if the magnetic field varies along the line of sight or within the telescope beam, whereas an underestimate of the field strength happens in regions where energy losses of the CR electrons are important, for example in starburst regions or halos (Beck 2016).
The magnetic field strength profile determined from equipartition was compared to the SPINNAKER model of the magnetic field and found to be similar in the midplane (which is a consequence of setting the B0 parameter to be similar to the equipartition field strength) and very different towards the halo with a factor of 2.5 in the magnetic field strength. In the halo, the SPINNAKER magnetic field strength is a lower limit for the actual field strength.
Analyses of the RM maps of NGC 4666 derived from RM synthesis reveals that the structure of the disk field is likely axisymmetric with indications of one magnetic field reversal at a radius of about 30″ (4 kpc). The data suggest that the field orientation points inwards and then outwards with increasing radial distance from the center. The large-scale field reversals between the central region and the disk that have been observed in M31 (Gießübel & Beck 2014) and IC342 (Beck 2015), as well as the reversal along the azimuth in NGC 4414 (Soida et al. 2002), are not comparable with the findings in this paper. This is the first time an indication of a radial field reversal within the disk of an external galaxy has been found.
In our Milky Way, there is one large-scale magnetic reversal close to the solar radius at about 7 kpc distance from the Galactic center, while the existence and location(s) of more reversals is still under debate (e.g., Haverkorn et al. 2015; Han et al. 2018).
The occurrence of radial field reversals is of fundamental importance for the theory of magnetic fields. In mean-field dynamo theory, there are different radial eigenmodes of the mean-field induction equation. Higher-order modes with many radial reversals may have a higher amplitude to begin with, but eventually the lowest order mode without reversals will win out because it grows fastest (Poezd et al. 1993). Radial field reversals may also move outward in the nonlinear dynamo stage, which is governed, at least partly, by the slow process of radial diffusion (Chamandy et al. 2013). Radial reversals may still persist in present-day galaxies hosting a dynamo in their evolutionary phase.
Moss et al. (2012) were able to predict radial field reversals in the disk of a spiral galaxy using a numerical mean-field dynamo model with continuous injection of turbulent fields to represent the effect of supernova explosions in discrete star forming regions with ongoing small-scale dynamo action. In their paper, a face-on view of a spiral galaxy is shown with multiple field reversals, which is used as an example for the construction of the simplified disk model of NGC 4666 (Fig. 23). Our finding of an indication of a reversal in NGC 4666 is in agreement with dynamo theory and supports the α − ω dynamo theory acting in spiral galaxies. Furthermore, it reveals that the Milky Way is probably not an exception in showing a radial field reversal.
CHANG-ES data release I available at www.queensu.ca/changes
From the help file of imfit (https://casa.nrao.edu/docs/taskref/imfit-task.html): “Fitting a zero level offset that is not fixed will tend to cause the reported parameter uncertainties to be slightly underestimated”.
SPINNAKER and SPINTERACTIVE are available at: www.github.com/vheesen/Spinnaker
Acknowledgments
We thank the anonymous referee for help in improving this work. We thank B. Adebahr for providing the RM synthesis scripts and A. Basu for detailed discussions and helpful suggestions. This research is kindly supported and funded by the Hans-Böckler Foundation. This research was also supported and funded by the DFG Research Unit 1254 “Magnetisation of Interstellar and Intergalactic Media: The Prospects of Low-Frequency Radio Observations”. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We made use of the NASA’s Astrophysics Data System Bibliographic Services, and the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2015, A&A, 578, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2016, A&ARv, 24, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bendre, A., Gressel, O., & Elstner, D. 2015, Astron. Nachr., 336, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briggs, D. S. 1995, BAAS, 27, 1444 [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., & Read, A. M. 2007, A&A, 464, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chamandy, L. 2016, MNRAS, 462, 4402 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Shukurov, A., & Subramanian, K. 2015, MNRAS, 446, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013, MNRAS, 428, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlem, M., Petr, M. G., Lehnert, M. D., Heckman, T. M., & Ehle, M. 1997, A&A, 320, 731 [NASA ADS] [Google Scholar]
- Dahlem, M., Lisenfeld, U., & Rossa, J. 2006, A&A, 457, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dudik, R. P., Satyapal, S., Gliozzi, M., & Sambruna, R. M. 2005, ApJ, 620, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, A., Berkhuijsen, E. M., Beck, R., & Shukurov, A. 2004, A&A, 414, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, ASP Conf. Ser., 314, 759 [Google Scholar]
- Garcia, A. M. 1993, A&AS, 100, 47 [NASA ADS] [Google Scholar]
- Gießübel, R., & Beck, R. 2014, A&A, 571, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffith, M. R., Wright, A. E., Burke, B. F., & Ekers, R. D. 1995, ApJS, 97, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Habe, A., Ikeuchi, S., & Tanaka, Y. D. 1981, PASJ, 33, 23 [NASA ADS] [Google Scholar]
- Han, J. L., Manchester, R. N., van Straten, W., & Demorest, P. 2018, ApJS, 234, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Haverkorn, M. 2015, Astrophys. Space Sci. Lib., 407, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., & Armus, L. 1993, Astrophys. Space Sci. Lib., 188, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009, A&A, 494, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heesen, V., Dettmar, R.-J., Krause, M., Beck, R., & Stein, Y. 2016, MNRAS, 458, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Krause, M., Beck, R., et al. 2018, MNRAS, 476, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, R. N., & Irwin, J. A. 2016, MNRAS, 458, 4210 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2016, VizieR Online Data Catalog: VII/100 [Google Scholar]
- Irwin, J., Beck, R., Benjamin, R. A., et al. 2012a, AJ, 144, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Beck, R., Benjamin, R. A., et al. 2012b, AJ, 144, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Krause, M., English, J., et al. 2013, AJ, 146, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S. 1992, An X-Ray Spectral Code for Optically Thin Plasmas (Internal SRON-Leiden Report, updated version 2.0) [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, F., & Beck, R. 1998, A&A, 335, 789 [NASA ADS] [Google Scholar]
- Krause, M. 1990, Geophys. Astrophys. Fluid Dyn., 50, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. 2009, RM&AC Conf. Ser., 36, 25 [Google Scholar]
- Krause, M., Irwin, J., Wiegert, T., et al. 2018, A&A, 611, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Large, M. I., Mills, B. Y., Little, A. G., Crawford, D. F., & Sutton, J. M. 1981, MNRAS, 194, 693 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Kassim, N. E., Lazio, T. J. W., & Hyman, S. D. 2000, AJ, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 472, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J.-T., & Wang, Q. D. 2013, MNRAS, 435, 3071 [NASA ADS] [CrossRef] [Google Scholar]
- Mathewson, D. S., & Ford, V. L. 1996, ApJS, 107, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mathewson, D. S., Ford, V. L., & Buchhorn, M. 1992, ApJS, 81, 413 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Miskolczi, A., Heesen, V., Horellou, C., et al. 2019, A&A, 622, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., & Sokoloff, D. 2017, A&A, 598, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2010, A&A, 512, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, P., Krause, M., Beck, R., & Schmidt, P. 2017, A&A, 606, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1992, ApJ, 401, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., Cappi, M., Rephaeli, Y., et al. 2004, A&A, 427, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poezd, A., Shukurov, A., & Sokoloff, D. 1993, MNRAS, 264, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Ruzmaikin, A. A., Sokolov, D. D., & Shukurov, A. M. 1988, Astrophys. Space Sci. Lib., 133 [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M., & Lee, K. J. 2017, MNRAS, 466, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Soida, M. 2005, in The Magnetized Plasma in Galaxy Evolution, eds. K. T. Chyzy, K. Otmianowska-Mazur, M. Soida, & R. J. Dettmar, 185 [Google Scholar]
- Soida, M., Beck, R., Urbanik, M., & Braine, J. 2002, A&A, 394, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soida, M., Krause, M., Dettmar, R.-J., & Urbanik, M. 2011, A&A, 531, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Annu. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tüllmann, R., Dettmar, R.-J., Soida, M., Urbanik, M., & Rossa, J. 2000, A&A, 364, L36 [Google Scholar]
- Tüllmann, R., Pietsch, W., Rossa, J., Breitschwerdt, D., & Dettmar, R. 2006, A&A, 448, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vargas, C. J., Mora-Partiarroyo, S. C., Schmidt, P., et al. 2018, ApJ, 853, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Dahlem, M., & Lisenfeld, U. 2004, ApJ, 606, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, T., Irwin, J., Miskolczi, A., et al. 2015, AJ, 150, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, J., & Han, J.-L. 2014, Res. A&A, 14, 942 [Google Scholar]
Appendix A: Additional figures
Radio data
In Figs. A.1 and A.2, polarized intensity is shown with Stokes I contours for both frequencies. In Fig. A.3 images of the different configurations of L-band are shown. In Fig. A.4 the RM map of L-band are presented.
 |
Fig. A.1. Polarized intensity image of NGC 4666 from C-band with robust two weighting, a beam of 7″ × 7″ in red (bottom left), and a σ of 7.0 μJy beam−1. White Stokes I contours starting at a 3σ level with a σ of 8.1 μJy beam−1 and increase in powers of 2 (up to 128) with an additional contour at 6.2 mJy to mark the central source with robust zero weighting. The magnetic field orientations are shown in white. |
 |
Fig. A.2. Polarized intensity image of NGC 4666 from L-band using RM synthesis with a robust two weighting, a beam of 18″ × 18″ in red (bottom left), and a σ of 20.0 μJy beam−1. White Stokes I contours starting at a 3σ level with a σ of 40.1 μJy beam−1 and increase in powers of 2 (up to 128) with robust two weighting. The magnetic field orientations are shown in white. |
 |
Fig. A.3. NGC 4666 Stokes I image of B-configuration L-band (BL), C-configuration L-band (CL), and D-configuration L-band (DL), contours start at a 3σ level with a σ of 18.0 μJy beam−1 (BL), 30 μJy beam−1 (CL) and 34 μJy beam−1 (DL) and increase in powers of 2 (up to 64, 128 and 512). The beam sizes of 3.9″ × 4.6″, 10.7″ × 12.3″, and 36.0″ × 37.4″ are shown in the bottom-left corner of each image. Cleaning was done with robust zero weighting. |
SPINNAKER
In Fig. A.5 we show the SPINNAKER result with diffusion, which was done for comparison and not used.
 |
Fig. A.4. RM map of NGC 4666 from L-band on Stokes I contours from Fig. 14 and a beam of 18″ × 18″ in gray. Contours start at a 3σ level with a σ of 40.1 μJy beam−1 and increase in powers of 2 (up to 256). The RM map is cut below the 3σ level of 11.1μJy beam−1 of the polarized intensity map. The mean error is 0.5 rad m−2. |
SPINNAKER parameter for diffusion.
 |
Fig. A.5. CR transport model for NGC 4666 with SPINTERACTIVE with diffusion for comparison. The data points are the observed values from 1.5 GHz (L-band), 6 GHz (C-band) and the spectral index, the red line represents the model simulation. The errors are represented by a weighted standard deviation. The adjustable parameters are listed in Table A.1. |
All Tables
All Figures
 |
Fig. 1. NGC 4666 Stokes I image of L-band combined (B-, C-, and D-configuration) with a robust zero weighting, overlayed onto the optical SDSS image made from the u, g, r filters. Contours start at a 3σ level with an rms noise σ of 30 μJy beam−1 and increase in powers of 2 (up to 256). The beam size is 11.8″ × 13.6″, shown in the bottom-left corner. |
| In the text | |
 |
Fig. 2. NGC 4666 flux density measurements in the radio regime with a fit that gives a spectral slope of α = −0.68 ± 0.04. I: VLA Low-Frequency Sky Survey (VLSS, Cohen et al. 2007), II: GaLactic and Extragalactic All-sky MWA survey (GLEAM, Hurley-Walker et al. 2016), III: The Molonglo Reference Catalogue of Radio Sources (MRC, Large et al. 1981), IV: The NRAO VLA Sky Survey (NVSS, Condon et al. 1998), V: CHANG-ES (this work), VI: The Parkes-MIT-NRAO surveys (PMN, Griffith et al. 1995), VII: CHANG-ES (this work). |
| In the text | |
 |
Fig. 3. NGC 4666 C-band image (C- and D-configuration) in gray scale with an rms noise σ of 4.6 μJy beam−1 and a beam size of 3.0″ × 3.5″ (see bottom left), using robust zero weighting. The light-gray contours show the inner region with the radio point source from the same data. The corresponding flux densities are 0.22, 0.44, and 0.88 mJy beam−1. We note the bubble-like structure in the eastern direction from the point source and the filamentary structures (threads) in the northern halo. |
| In the text | |
 |
Fig. 4. Map of soft X-ray emission from NGC 4666 in the 0.2–1 keV band overlaid onto the DSS blue image. The contours are 3, 5, 8, 16, 32, 64, 128 × σ. The map is adaptively smoothed with the largest scale of 10″. |
| In the text | |
 |
Fig. 5. The regions used for the spectral analysis of the disk of NGC 4666 on the DSS blue image. |
| In the text | |
 |
Fig. 7. Hardness ratio map of NGC 4666 with the spectral regions marked. |
| In the text | |
 |
Fig. 8. NGC 4666 scale height analysis C-band with different model fits for the northern (positive distances) and southern (negative distances) halo. |
| In the text | |
 |
Fig. 9. NGC 4666 scale height analysis L-band with different model fits for the northern (positive distances) and southern (negative distances) halo. |
| In the text | |
 |
Fig. 10. NGC 4666 boxes with a size of 130″ × 6″ for the scale height analysis in C-band with a beam of 13.3″ × 13.3″. |
| In the text | |
 |
Fig. 11. Mass surface density versus normalized scale height for the CHANG-ES galaxies from Krause et al. (2018) with additional data point for NGC 4666 from Table 16, which is marked in red. The data can be described by a linear fit (excluding UGC 10288). |
| In the text | |
 |
Fig. 12. Color image of NGC 466 6 produced from SDSS with Stokes I contours from C-band starting at a 3σ level with a σ of 11.0 μJy beam−1 and increase in powers of 2 (up to 128) with a robust zero weighting. The corresponding beam size is 10″ × 10″ (see bottom left). The apparent magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. 13. Total intensity as a color image of NGC 4666 from C-band with robust zero weighting, with a beam of 7″ × 7″ in red, obtained by Gaussian smoothing to fit the resolution of the polarization map, σ is 8.1 μJy beam−1. Gray polarization contours are at 3, 6, 9, 12, 15, 18 σ levels with σ of 7.0 μJy beam−1 with a robust two weighting. The apparent magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. 14. Total intensity as a color image of NGC 4666 from L-band with robust zero weighting, with a beam of 18″ × 18″ in red, obtained by Gaussian smoothing to fit the resolution of the polarization map with σ of 40.1 μJy beam−1. Gray polarization contours from RM synthesis are at 3, 6, 9 σ levels with σ of 20.0 μJy beam−1 with a robust two weighting. The magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. 15. Polarized intensity as a color image of NGC 4666 from C-band with robust zero weighting and a uv-taper of 12kλ and Gaussian smoothing to obtain the beam of 18″ × 18″ in red, σ is 11 μJy beam−1. The white total intensity contour correspond to 0.04 mJy with robust zero weighting and smoothing. The apparent magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. 16. Polarized intensity as a color image of NGC 4666 from archival VLA C-band data with robust zero weighting, originally published in Soida (2005), with a beam of 18″ × 18″ in red, σ is 9.3 μJy beam−1. The white total intensity contour correspond to 0.04 mJy with robust zero weighting and smoothing. The apparent magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. 17. NGC 4666 nonthermal fraction map at C-band. The beam of 13.3″ × 13.3″ is shown in red (left bottom). |
| In the text | |
 |
Fig. 18. NGC 4666 nonthermal fraction map at L-band. The beam of 13.3″ × 13.3″ is shown in red (left bottom). |
| In the text | |
 |
Fig. 19. RM map of NGC 4666 from C-band on Stokes I contours from Fig. 13 and a beam of 7″ × 7″ in gray. Contours start at a 3σ level with a σ of 9.3 μJy beam−1 and increase in powers of 2 (up to 64) with an additional contour at 3.5 mJy beam−1 to mark the central source. The RM map is cut below the 3σ level of 25μJy beam−1 of the polarized intensity map from RM synthesis. The mean error is 22 rad m−2. |
| In the text | |
 |
Fig. 20. Top panel: NGC 4666 nonthermal spectral index (αnt), bottom panel: spectral index error map. The beam is 13.3″ × 13.3″. |
| In the text | |
 |
Fig. 21. Expected RM variation for an edge-on view of a simplified axisymmetric disk magnetic field (left panel) and a simplified bisymmetric disk magnetic field (right panel) with trailing spiral arms, which are shaded red for the approaching side and blue for the receding side. The black arrows show the direction of the magnetic field vectors. The direction of the rotation of the disk is given by the bold black arrow below the four disks. Panel a: upper part shows the face-on view of the two different disk fields. In the case of an axisymmetric disk field (left panel) all vectors are pointing inwards or outwards; here just one configuration is shown. In case of the bisymmetric magnetic field (right panel) the vectors from one side of the galaxy are pointing inwards and on the other side of the galaxy outwards (or the other way around). In the second row, the expected RM behavior is plotted along the major axis of each galaxy model for an observer watching the system edge-on. The red curve represents the RM values from the approaching side, the blue curve from the receding side. Panel b: upper part shows again the face-on view of the two different disk fields as above (left panel: axisymmetric disk field, right panel: bisymmetric magnetic field). In a simplified approach, a radial reversal is assumed at half of the disk radius. The last row shows the expected and simplified RM value variation in case of a radial field reversal at half the radius of the disk. |
| In the text | |
 |
Fig. 22. Left panel: NGC 4666 C-band RM map, rotated by 50° on sky, with a beam of 7.2″ × 7.2″. The rectangle boxes of 7″ × 14″ were used for averaging. The orange cross marks the center. Right panel: RM values from boxes along the major axis for both sides of the galaxy. The sinusoidal fit was made for the different sides separately indicated by the color. The sinusoidal fit for the receding side excludes the data point at 38.5″ in Fit 1 and includes this data point in Fit 2. |
| In the text | |
 |
Fig. 23. Left panel: NGC 4666 C-band RM values for boxes from the center outwards to the edge of the disk for both sides of the galaxy; as in the right plot of Fig. 22 but with the approaching side mirrored. The left blue-shaded part of the plot indicates the axisymmetric disk magnetic field with magnetic field vectors pointing inwards, the yellow-shaded part of the plot indicates the axisymmetric disk magnetic field with magnetic field vectors pointing outwards, and the grey dashed line marks the radius of a possible field reversal. Right panel: NGC 4666 simplified disk model. |
| In the text | |
 |
Fig. 24. NGC 4666 magnetic field strength calculated pixel-based via the equipartition formula using the resolved nonthermal spectral index map and the intensity map with a beam of 13.3″ × 13.3″ (bottom left). |
| In the text | |
 |
Fig. 25. CR advection transport model for NGC 4666 with SPINTERACTIVE. The data points are the observed values from 1.5 GHz (L-band), 6 GHz (C-band), and the spectral index; the red line represents the model simulation. The errors correspond to a weighted standard deviation. The basic parameters are listed in Table 19. |
| In the text | |
 |
Fig. 26. Intensity profile of equipartition magnetic field strength with dark blue data points from Fig. 24, magnetic field strength distribution from SPINNAKER with the black line, and gray shaded errors. |
| In the text | |
 |
Fig. A.1. Polarized intensity image of NGC 4666 from C-band with robust two weighting, a beam of 7″ × 7″ in red (bottom left), and a σ of 7.0 μJy beam−1. White Stokes I contours starting at a 3σ level with a σ of 8.1 μJy beam−1 and increase in powers of 2 (up to 128) with an additional contour at 6.2 mJy to mark the central source with robust zero weighting. The magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. A.2. Polarized intensity image of NGC 4666 from L-band using RM synthesis with a robust two weighting, a beam of 18″ × 18″ in red (bottom left), and a σ of 20.0 μJy beam−1. White Stokes I contours starting at a 3σ level with a σ of 40.1 μJy beam−1 and increase in powers of 2 (up to 128) with robust two weighting. The magnetic field orientations are shown in white. |
| In the text | |
 |
Fig. A.3. NGC 4666 Stokes I image of B-configuration L-band (BL), C-configuration L-band (CL), and D-configuration L-band (DL), contours start at a 3σ level with a σ of 18.0 μJy beam−1 (BL), 30 μJy beam−1 (CL) and 34 μJy beam−1 (DL) and increase in powers of 2 (up to 64, 128 and 512). The beam sizes of 3.9″ × 4.6″, 10.7″ × 12.3″, and 36.0″ × 37.4″ are shown in the bottom-left corner of each image. Cleaning was done with robust zero weighting. |
| In the text | |
 |
Fig. A.4. RM map of NGC 4666 from L-band on Stokes I contours from Fig. 14 and a beam of 18″ × 18″ in gray. Contours start at a 3σ level with a σ of 40.1 μJy beam−1 and increase in powers of 2 (up to 256). The RM map is cut below the 3σ level of 11.1μJy beam−1 of the polarized intensity map. The mean error is 0.5 rad m−2. |
| In the text | |
 |
Fig. A.5. CR transport model for NGC 4666 with SPINTERACTIVE with diffusion for comparison. The data points are the observed values from 1.5 GHz (L-band), 6 GHz (C-band) and the spectral index, the red line represents the model simulation. The errors are represented by a weighted standard deviation. The adjustable parameters are listed in Table A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.









![$$ \begin{aligned} L_{H\alpha ,\mathrm{corr} }[\mathrm{erg\,s }^{-1}] = L_{H\alpha , \mathrm{obs} }[\mathrm{erg\,s }^{-1}] + 0.042 \cdot \nu L_{\nu }(22\mu \mathrm{m} )[\mathrm{erg\,s }^{-1}]. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34515-18/aa34515-18-eq47.gif)
![$$ \begin{aligned} F_{\mathrm{thermal} }&[\mathrm{erg\,s }^{-1}\,{\mathrm{Hz} }^{-1}\,{\mathrm{pix} }^{-1}] = \\&1.167 \times 10^{-14} \cdot \left(\frac{\mathrm{T} _e}{10^4 K}\right)^{0.45} \cdot \left(\frac{\nu }{GHz}\right)^{-0.1} \cdot L_{H\alpha , \mathrm{corr} } [{\mathrm{erg s} }^{-1}].\nonumber \end{aligned} $$](/articles/aa/full_html/2019/03/aa34515-18/aa34515-18-eq48.gif)


