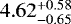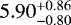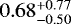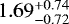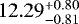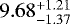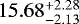EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 623 (March 2019) A&A, 623 (2019) A41 Full HTML
Free Access
Issue
A&A
Volume 623, March 2019
Article Number A41
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201834001
Published online 04 March 2019

© ESO 2019

1 Introduction

Space-based transit surveys such as CoRoT (Auvergne et al. 2009) and Kepler (Borucki et al. 2010) have revolutionized the field of exoplanetary science. Their high precision and nearly uninterrupted photometry has opened the doors to explore planet parameter spaces that are not easily accessible from the ground, most notably the Earth-radius planet domain. However, our knowledge of both super-Earths (Rp = 1–2 R⊕ and Mp = 1–10 M⊕) and Neptune planets (Rp = 2–6 R⊕ and Rp = 10–40 M⊕) is still limited, due to the small radial velocity (RV) variation induced by such planets and the relative faintness of most Kepler host stars (V > 13 mag) which make precise mass determinations difficult.

Many questions therefore remain unanswered, such as for example those referring to the composition and internal structure of small planets. Fulton et al. (2017) and Fulton & Petigura (2018) reported a radius gap at ~ 2 R⊕ in the exoplanet radius distribution using Kepler data for Sun-like stars, and Hirano et al. (2018) indicated that the gap could extend down to the M dwarf domain. This would point to a very different planetary nature for planets on each side of the gap. Is this due to planet migration? Are the larger planets surrounded by a H/He atmospheres while the smaller planet have lost these envelopes? Or, did they already form with very different bulk densities? Answering these questions requires statistically significant samples of well-characterized small planets, especially in terms of orbital parameters, mass, radius and mean density.

The extended K2 mission of Kepler is a unique opportunity to gain knowledge about small close-in planets. Every 3 months, K2 observes a different stellar field located along the ecliptic, targeting stars that are up to 15 times brighter than those targeted by the original Kepler mission. The KESPRINT collaboration1 is an international effort dedicated to the discovery, confirmation, and characterization of planet candidates from the space transit missions K2 and TESS and, in the future, PLATO. We have been focusing on determining the masses of small planets around bright stars, especially for planets in or around the radius gap.

Here, we present the discovery and characterization of four transiting planets around the star EPIC 246471491 (K2-285). While these planets are observed to have radii between 2 and 3.5 times greater than that of the Earth, our follow-up observations indicate that they have very different bulk compositions. This has significant implications for the physical nature of planets around the radius gap. In this paper we provide ground-based follow-up observations that confirm that EPIC 246471491 is a single object and establish its main stellar properties. We also jointly analyze the K2 data together with high-precision RV data from CARMENES and HARPS-N spectrographs, to retrieve orbital solutions and planetary masses. Finally, we discuss the possible bulk compositions of the planets, leading to different densities.

2 K2 photometry and candidate detection

EPIC 246471491 (RA = 23:17:32.23, Dec = 01:18:01.04, in the Aquarius constellation) was proposed as a K2 GO target for Campaign 12 in several programs (GO-12123, PI Stello; GO-12049, PI Quintana; and GO-12071, PI Charbonneau). The star was observed for78.85 days from 15 December 2016 to 4 March 2017. During this interval, the Kepler spacecraft entered safe mode from 1 to 6 February 2017, causing a gap of 5.3 days in the data.

We built the light curve of EPIC 246471491 directly from raw data (files downloaded from the Mikulski Archive for Space Telescopes2, MAST), using the long cadence (LC) version (29.4 min time stamps). Our pipeline is based on the implementation of the pixel level decorrelation (PLD) model (Deming et al. 2015), and a modified version of the Everest3 pipeline (Luger et al. 2018). The PLD model uses a Taylor expansion of the instrumental signal as regressors in a linear model. These regressors are the products of the fractional fluxes in each pixel of the target aperture. The optimal aperture is built by searching for the photo-center and selecting pixels with a threshold of 1.2σ over the previously calculated background (Fig. 1). The pipeline extracts the raw light curve from the apertures, removing time cadences with bad quality flags, and the background contribution. Next, it fits a regularized regression model to the data, iteratively up to the third order, and applies the cross-validation method to obtain the regularization matrix coefficients and Gaussian processes to compute the covariance matrix. All these steps are described in Luger et al. (2018).

Prior to planet searches, we need to flatten the K2 light curve by iteratively applying a robust locally weighted regression method (Cleveland 1979) until no outliers are detected. We remove 3σ outliers replacing these points by the median of the neighbors. We note that the first two days and the last day of data, which show anomalies probably related to thermal settling, were removed from our analysis. Applying these methods iteratively, we are able to remove any stellar flares. We then divide the original light curve by this variability model. The initial and final detrended K2 light curves are plotted in Fig. 2.

Subsequently, we present a Box-fitting Least Squares (BLS) algorithm (Kovács et al. 2002) used to detect the period of each possible planetary signal in the light curve. The BLS algorithm is very sensitive to outliers, and therefore we remove them by performing a sigma clipping. In this case, a value of 30 σ is enough. Once a planetary signal is detected in the power spectrum, the BLS provides the epoch and the period of the candidate. We then remove this signal from the light curve by masking all points in transit, that is, we mark the times of the T0 epoch and the T0 plus N times the period, and mask all points that fall in a window centered on these times with a width equal to the transit duration. In this manner, we iteratively remove every single transit until no signal is found by BLS.

Four planet detections were made in the course of the analysis of EPIC 246471491, at periods of 3.47, 7.13, 10.45, and 14.76 days (see Fig. 3). The planet periods are close to 1 : 2 : 3 : 4 commensurability, but not quite, the precise ratio numbers being 1 : 2.05 : 3.01 : 4.25. This near-commensurability may be indicative that the system is in resonance. Figure 3 shows the phase-folded light curve for each transit, and its best-fit transit model. We fit the phase-folded transit light curve of each planet with the python package batman (Kreidberg 2015). We tentatively fit the different planets with a nonlinear least-squares minimization routine, which yielded good results for the transit parameters, and took these as input for the Markov chain Monte Carlo (MCMC) algorithm implemented in emcee (Foreman-Mackey et al. 2013), which was used to sample from the joint posterior distribution, using 100 walkers and 30 000 steps. We then removed the first 22 500 steps to estimate the uncertainties in the transit parameters. Once we obtain the MCMC results for the transit parameters of a planet, we iteratively remove the points inside the transit for the next fitting. The retrieved planetary parameters derived from fitting the K2 light curve alone are given in Table A.1.

The auto-correlation analysis of the K2 photometry retrieves a stellar rotational period at around 15 days, but the auto-correlation peak is broad and insignificant. We discuss this point further in Sect. 5.

thumbnail Fig. 1

K2 image of the object EPIC 246471491. A custom-built changing aperture is fitted based on the pixel counts of the star and background. The image shows three typical apertures used at the beginning (top left panel), middle (top right panel) and end (bottom left panel) of the time series. Bottom right panel: a high-resolution image of the same field taken from Palomar Observatory.
thumbnail Fig. 2

Kepler light curves of EPIC 246471491. Top panel: original raw light curves as derived from raw flux data. Bottom panel: detrended light curve after analysis with our modified Everest-based pipeline. Stellar variability of the order of tens of days and the transits of several planets are clearly visible.
thumbnail Fig. 3

Phase-folded transit light curves of the four planets detected orbiting EPIC 246471491. Top panels: transit light curves and best-fit transit models (red) on the same flux scale. Lower panels: residuals of the transit fit.

3 Ground-based follow-up observations

3.1 Lucky imaging and AO observations

We performed Lucky Imaging (LI) of EPIC 246471491 with the FastCam camera (Oscoz et al. 2008) at the 1.52-m Telescopio Carlos Sánchez (TCS), and with the NASA Exoplanet Star and Speckle Imager (NESSI; Scott et al. 2016, 2018) on the 3.5-m WIYN telescope at the Kitt Peak National Observatory. Both results strongly constrained the possibility that the observed transit signals come from a nearby faint star. However, these upper limits (not shown here) were superseded by adaptive optics imaging at SUBARU.

We obtained high-resolution images for EPIC 246471491 using the InfraRed Camera and Spectrograph (IRCS; Kobayashi et al. 2000) and the adaptive-optics (AO) system on the Subaru 8.2-m telescope on UT 2018 June 14. To check for the absence of nearby companions, we imaged the target in the K′ band with the fine-sampling mode (1 pix = 20 mas), and implemented two types of sequences with a five-point dithering. For the first sequence we used a neutral-density (ND) filter, the transmittance of which is ~0.81% in the K′ band to obtain unsaturated frames for the absolute flux calibration. We then acquired saturated frames to look for faint nearby companions. The total integration times amounted to 450 and 45 s for the unsaturated and saturated frames, respectively. We reduced and median-combined those frames following the procedure described in Hirano et al. (2016). The combined images revealed no nearby companion around EPIC 246471491. To check for the detection limit, we drew the 5σ contrast curve following Hirano et al. (2016) based on the combined saturated image. As plotted in Fig. 4, 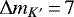ΔmK′ = 7$\Delta m_{K^{\prime}}{\,=\,}7$ was achieved at ~ 0.′′5 from the target. The inset of the figure displays the target image with field-of-view of 4′′ × 4′′.

3.2 CARMENES radial velocity observations

Radial-velocity measurements of EPIC 246471491 were taken with the CARMENES spectrograph, mounted at the 3.5-m telescope at the Calar Alto Observatory in Spain. The CARMENES instrument has two arms (Quirrenbach et al. 2014), the visible (VIS) arm covering the spectral range 0.52–0.96 μm and a near-infrared (NIR) arm covering the 0.96–1.71 μm range. Here we use only the VIS channel observations to derive RV measurements. The overall instrumental performance of CARMENES has been described by Reiners et al. (2018).

A total of 29 measurements were taken over the period 2017 September 20–2017 December 17, covering a time span of 98 days. In all cases exposure times were set at 1800 s. Radial-velocity values, chromatic index (CRX), differential linewidth (dLW), and Hα index were obtained using the SERVAL program (Zechmeister et al. 2018). For each spectrum, we also computed the cross-correlation function (CCF) and its full width half maximum (FWHM), contrast (CTR), and bisector velocity span (BVS) following Reiners et al. (2018). The RV measurements are given in Table 1, corrected for barycentric motion, secular acceleration and nightly zero-points. For more details, see Trifonov et al. (2018) and Luque et al. (2018).

thumbnail Fig. 4

Subaru AO image (inset) and 5σ contrast light curve of EPIC 246471491. The inset image has a FOV of 4′′ × 4′′.

3.3 HARPS-N RV observations

Radial-velocity measurements were also taken with the HARPS-North spectrograph, mounted at the 3.5-m TNG telescope at the Roque de los Muchachos Observatory in Spain. The HARPS-N instrument (Cosentino et al. 2012) covers the spectral range 0.383–0.693 μm. In total, nine HARPS-N measurements were taken over the period 16 September 2017 to 10 January 2018, covering a time span of 112 days. Exposure times were set at 3600 s. To derive radial velocities, SERVAL was also applied to the data. The performance of SERVAL RV extraction compared to the standard HARPS and HIRES pipelines is described in Trifonov et al. (2018). Both CARMENES and HARPS-N RV measurements are given in Table 1.

4 Host star properties

To retrieve the physical properties of EPIC 246471491, we analyzed the co-added, RV-corrected CARMENES spectra using the Spectroscopy Made Easy (SME) code (Piskunov & Valenti 2017) which is designed to derive the fundamental parameters of stars. It iteratively calculates the synthesized spectrum based on a large grid of model spectra. The synthesized spectrum is fitted to the observed spectra using a χ2 minimization process. In this case, we used one-dimensional MARCS models (Gustafsson et al. 2008). Providing the code with fixed turbulent velocities vmac = 2.5 ± 0.7 km s−1 (Doyle et al. 2014) and vmic = 0.82 ± 0.4 km s−1 (Bruntt et al. 2010), we solved for Teff by analyzing the Balmer profile of Hα, log g⋆ by fitting the Ca I triplet at 6102, 6122 and 6162 Å, and [Fe/H] and v sin i by fitting approximately 50 Fe lines. We find Teff = 4975 ± 95 K, log g⋆ = 4.4 ± 0.1 dex, [Fe∕H] = 0.00 ± 0.05 dex, and v sin i = 3.9 ± 0.8 km s−1, respectively.See Table 2 for a summary of EPIC 246471491 stellar parameters.

We confirmed the effective temperature and the value for log g⋆ by also modeling the Na I doublet (5889.95/5895.9Å) using SME and deriving the abundance for Na I from fainter lines in our CARMENES spectrum. Also, by analyzing the equivalent width of the interstellar sodium components (Poznanski et al. 2012), we find an extinction of E(B − V) = 0.02 ± 0.003 that corresponds to AV = 0.07 ± 0.01 mag.

We alsoused the HARPS-N co-added spectrum to derive stellar parameters. In particular, we fitted the spectral energy distribution using low-resolution model spectra with the same spectroscopic parameters as those found using the CARMENES co-added spectrum. Our results return an interstellar reddening value of AV = 0.1 ± 0.05 mag.

We thenused the Teff and [Fe/H] values retrieved by SME, along with the new Gaia parallax value of π = 6.43 ± 0.11 mas (Lindegren et al. 2018). We quadratically added 0.1 mas to the nominal uncertainty of Gaia to account for systematics (see Luri et al. 2018).

The stellar magnitude in V band is taken from the AAVSO Photometric All Sky Survey (APASS) and corrected for extinction. The PARAM4 models (da Silva et al. 2006) return a stellar mass of M⋆ = 0.830 ± 0.023 M⊙, a radius of R⋆ = 0.787 ± 0.016 R⊙ and a log g⋆ = 4.539 ± 0.024 cgs. The latter value of surface gravity is consistent with the SME value within less than 2σ. As a sanity check, we used the bolometric correction from Torres et al. (2010) and got a radius of R⋆ = 0.880 ± 0.080 R⊙, which is roughly consistent with the previous value.

Table 1

Radial-velocity measurements derived from HARPS-N and CARMENES observations used in this paper.

Table 2

Stellar parameters of EPIC 246471491 (K2-285).

5 Frequency analysis of relative velocity and photometric data

We performed a frequency analysis of the available RV observations. In Fig. 5, we plot the generalized Lomb–Scargle periodogram (GLS; Zechmeister & Kürster 2009) of the CARMENES RV data. For each periodogram, we compute the theoretical false-alarm probability (FAP) following Zechmeister & Kürster (2009), and mark the 10, 1, and 0.1% significance levels. The vertical red lines mark the orbital frequencies of planets b, c, d and e, and the thick blue lines mark the stellar rotational frequencies associated with stellar variability.

It is easily seen that the dominant signals in the CARMENES periodogram are those at 12.1 days and ~22 days. These periodicities are suggested in the CARMENES chromatic index (CRX), but with FAP > 10%, an indicator developed for CARMENES data to recognize wavelength-dependent variability attributable to stellar activity (Zechmeister et al. 2018), the dLW, the CCF BVS, and the CCF FWHM indices. Based solely on the data available to us, it is not clear which one of the two periods is the true rotational period of the star, and which one is indeed an alias or a harmonic of the other.

There is evidence that sin i should be in fact close to unity for these types of systems (Winn et al. 2017). A simple calculation (Prot sin i = 2πR v sin i), using the stellar v sin i value and assuming sin i = 1 gives an expected stellar rotational period upper limit of 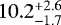10.2−1.7+2.6$10.2^{+2.6}_{-1.7}$ days. Therefore, we adopt 12.1 days as the true rotational period of the star, Prot, seen in the CARMENES GLS periodogram. The ~22 days peak is then an alias originated from the window function peak at ~ 27.5 days, caused by our scheduling of optimal observations along the lunar cycle.

In light of these results, it is clear that the dominant signal in the RV data is that of stellar activity, and that this needs to be taken into account in order to retrieve the planetary masses. In Fig. 6 we show the GLS periodograms of the CARMENES data with the stellar and planetary periodicities marked, the spectral power being dominated by the former. In the middle panel, we filter the data by removing the Prot periodicity. We do this by fitting the amplitude and phase of a sinusoidal signal, and computing the GLS periodogram of the residuals of this fit, in the same way as is done for planetary signals.

This procedure eliminates both the 12.1-day and 22-day signals, confirming that the latter is in fact an alias. Now the major peaksin the power spectra correspond to the planetary orbital periods, although they are not above the FAP = 10% level. In the bottom panel, the HARPS-N data are added accounting for the RV offset between both instruments using the measurements taken in consecutive days with HARPS-N (JD ~ 2458046.5) and CARMENES (JD ~ 2458047.5). Removing Prot signal from HARPS-N data does not have a strong effect on the final result. Regardless, for the sake of consistency, we removed it in our analysis. A possible explanation may lie in the fact that there is only a handful of measurements (9), or that the HARPS-N and CARMENES spectrographs cover different spectral ranges and therefore their sensitivity to stellar activity is different. The GLS periodogram of the combined data shows significance peaks (FAP ≈ 0.1%) at the orbital periods of planets c and d, and above FAP = 10% for planets b and e.

thumbnail Fig. 5

Generalized Lomb–Scargle periodograms (GLS) of the EPIC 246471491 RVs from CARMENES data (panel a), the K2 photometry (panel b), and the CRX (panel c), dLW (panel d), FWHM (panel e), CTR (panel f), and BVS (panel g) indices. Panel h: window function of the data. Vertical red lines indicate the frequencies associated with each of the four transiting planets, and the blue vertical lines mark the frequencies associated with the activity of the host star. The highest peaks in the CARMENES GLS are located at f = 0.045 d−1 (P ~ 22 d) and f = 0.081 d−1 (P = 12.1 d) and are linked to the rotation of the star. These periodicities are also significant in the K2 photometry and the CRX index. Horizontal lines show the FAP levels of 10% (short-dashed line), 1% (long-dashed line) and 0.1% (dot-dashed line).
thumbnail Fig. 6

Generalized Lomb–Scargle periodograms (GLS) of the EPIC 246471491 RVs from CARMENES and HARPS-N. Panel a: same data and analysis is shown as panel a of Fig. 5. Panel b: GLS of the CARMENES data after removing the prominent peak at f = 0.081 d−1, corresponding to Prot = 12.1 days. In this case the frequency associated with the alias peak at ~22 days also loses all the power, and the higher peaks are located at the periodicities of the four planets. Panel c: HARPS-N data (also Prot corrected) are added to the CARMENES data. The joint GLS shows significant periodicities for two of the four planets in this system. As in Fig. 5, horizontal lines show the FAP levels of 10 (short-dashed line), 1 (long-dashed line), and 0.1% (dot-dashed line).
thumbnail Fig. 7

Time series of the RV measurements of K2-285 derived from CARMENES (blue dots) and HARPS-N (red diamonds). The black line corresponds to the best-fit model to the data, which includes the RV signal of each of the four planets and the stellar activity.

6 Joint analysis and mass determinations

In order to retrieve the masses of the planets in the EPIC 246471491 system, we performed a joint analysis of the photometric K2 data and the RV measurements from CARMENES and HARPS-N. We make use of the Pyaneti5 code (Barragán et al. 2016), which uses MCMC techniques to infer posterior distributions for the fitted parameters. The RV data are fitted with Keplerian orbits, The transit model follows the quadratic limb-darkened law of Mandel & Agol (2002). 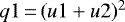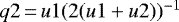For the linear u1 and quadratic u2 limb-darkening coefficients, we use the q1 = (u1+u2)2$q1{\,=\,}(u1 + u2)^2$ and q2 = u1(2(u1+u2))−1$q2{\,=\,}u1(2(u1+u2))^{-1}$ parameterization described in Kipping (2013). For q1 and q2 we set uninformative uniform priors in the range [0, 1] to sample a physical solution for the limb-darkening coefficients. These methods have already been successfully applied to several planets; see for example Niraula et al. (2017) or Prieto-Arranz et al. (2018) for details.

Although no coherent rotational modulation is found in the K2 data alone, as in Prieto-Arranz et al. (2018), the light curve of EPIC 246471491 suggests that the evolution timescale of active regions is longer than the K2 observations (80 days). Since our combined observations cover 112 days, we decided to model the stellar activity signal with a sinusoid (Pepe et al. 2013; Barragán et al. 2018). Therefore, on top of the planetary signals, we include in the fit a fifth RV signal corresponding to the stellar variability at Prot, which we identified as the dominant RV signal in the previous section. Van Eylen & Albrecht (2015) reported that the eccentricity of small planets in Kepler multi-planet systems is low. Given that K2-285 is a compact short-period multi-planetary system, we also assumed tidal circularization of the orbits and fixed the eccentricity to zero for all four planets.

Figure 7 shows the combined CARMENES and HARPS-N RV measurements plotted against time, with a superimposed best-fit model containing the RV variations due to the four planets and a stellar activity signal. In our analysis, we did not discard RV observations that were obtained during transits, but the expected Rossiter-McLaughlin amplitude is negligible.

The individual phased RV signals for each of the four planets, once the stellar variability signal and the signals from the other planets havebeen removed, are shown in Fig. 8. Also shown is the phased stellar activity signal once the signals of the four planets have been removed. The residuals around the best-fit model are shown below each panel. The RV signal of the stellar activity is readily detectable and has the largest RV semi-amplitude. We can also identify at larger than 3σ significance level the semi-amplitudes of planets b and c, while we can only place upper limits on the masses of planets d and e. In Table A.1 the planet properties of the K2-285 system are summarized.

As a further test, we used the code SOAP2 (Dumusque et al. 2014) to estimate the expected induced RV signal coming from stellar activity. We assume that spots generate a flux decrement of 1.5% from the largest depth in the light curve (Fig. 2). We used the stellar parameters from Table 2 and a stellar rotation period of 12.3 days. We assume that the star has two spots separated by 180° located at the stellar equator. The output of SOAP2 gives an expected induced RV signal of ~ 13 m s−1. This result is consistent with the fitted amplitude in our model.

thumbnail Fig. 8

Top left panel: phase-folded RV measurements of K2-285 over the period of planet b, after eliminating the signal from planets c, d, and e, and the stellar activity signal. Top right panel: as in the top-left panel but for planet c. Middle left panel: as in the top-left panel but for planet d. Middle right panel: as in the top-left panel but for planet e. Bottom panel: as in the top-left panel but for the stellar activity signal. The derived semi-amplitudes for these planets are 4.62−0.65+0.58$4.62 _{ - 0.65 } ^ { + 0.58 }$ m s−1, 5.90−0.80+0.86$5.90 _{ - 0.80 } ^ { + 0.86 } $ m s−1, 0.68−0.50+0.77$0.68 _{ - 0.50 } ^ { + 0.77 } $ m s−1 and 1.69−0.72+0.74$1.69 _{ - 0.72 } ^ { + 0.74 } $ m s−1, while the stellar activity signal has an amplitude of 12.29−0.81+0.80$12.29 _{ - 0.81 } ^ { + 0.80} $ m s−1. This translates into a mass determination of 9.68−1.37+1.21$9.68 _{ - 1.37 } ^ { + 1.21 } $ M⊕ and 15.68−2.13+2.28$15.68 _{ - 2.13 } ^ { + 2.28 } $ M⊕ for planets b and c, respectively, and upper-limit mass determinations of 6.5 M⊕ and 10.7 M⊕ (at 99% confidence level) for planets d and e, respectively.

7 Discussion and conclusions

We determined masses, radii, and densities for two of the four planets known to transit K2-285. We find that K2-285b has a mass of Mb = 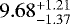9.68−1.37+1.21$9.68 _{ - 1.37 } ^ { + 1.21 }$ M⊕ and a radius of Rb = 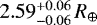2.59−0.06+0.06 R⊕$2.59 _{ - 0.06 } ^ { + 0.06 }\,R_{\oplus}$, yielding a mean density of ρb = 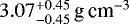3.07−0.45+0.45 g cm−3$3.07 _{ - 0.45 } ^ { + 0.45 }\,\textrm{g\,cm}^{-3}$, while K2-285c has a mass of Mc = 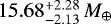15.68−2.13+2.28 M⊕$15.68 _{ - 2.13 } ^ { + 2.28 }\,M_{\oplus}$, radius of Rc = 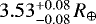3.53−0.08+0.08 R⊕$3.53 _{ - 0.08 } ^ { + 0.08 }\,R_{\oplus}$, and a mean density of ρc = 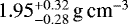1.95−0.28+0.32 g cm−3$1.95 _{ - 0.28 } ^ { + 0.32 }\,\textrm{g\,cm}^{-3} $. For K2-285d and K2-285e, we are able to calculate upper limits for the masses at 6.5 M⊕ and 10.7 M⊕, respectively.The upper limits are determined by multiplying the semi-amplitude upper limit of the error bar by three (3-sigma error) and adding this value to that of the value of the semi-amplitude. The resulting semi-amplitude value is then transformed into an upper mass limit.

Fulton et al. (2017) and Van Eylen et al. (2018) reported a bi-modal distribution in the radii of small planets at the boundary between super-Earths and sub-Neptunes. A clear distinction between two different families of planets is reported: on the one hand, super-Earths have a radius distribution that peaks at Rp ~ 1.5 R⊕, and on the other sub-Neptune planets have a radius distribution that peaks at Rp ~ 2.5 R⊕. These two populations are separated by a gap in the radius distribution.

Figure 9 illustrates the mass-radius diagram of all known planets with precise mass determination, extending the full parameter space encompassing Earth-like, super-Earth, and Neptune planets (1–4 R⊕, 0.5–20 M⊕). The four planets of the K2-285 system are also plotted. Two of the planets, b and d, fall in the sub-Neptune category, with radius very close to one of the peaks of the bi-modal distribution at 2.5 R⊕, while planet e belongs to the scarce population of planets located within the radius gap. Planet c is a larger object with only a slightly smaller radius and larger density than Neptune (3.9 vs. 3.5 R⊕ and 1.64 vs. 1.95 g cm−3; for Neptune and K2-285c, respectively).

Using the values in Table A.1, the estimated transmission signals corresponding to H/He atmospheres (which would be the optimistic case for super-Earth size planets) of the four planets would be of 20, 32, 21, and 8 ppm for planets b, c, d, and e, respectively. For planets d and e, the upper mass limit has been used for the calculations, so presumably the true signals would be larger. Still, with such relatively small atmospheric signatures, the planets are not optimal for transmission spectroscopy studies using current instrumentation due to the faintness of the parent star.

However, as in the case of the triple transiting system K2-135 (Niraula et al. 2017; Prieto-Arranz et al. 2018), the four planets around K2-285 could provide a great test case to study comparative atmospheric escape and evolution within the same planetary system. From Fig. 9 it is readily seen that the two planets with well-determined mass have very different densities. Planet b has a bulk density close to pure water, while planet c is a much more inflated, lower-density planet. Assuming that all planets in the system were formed with similar composition, the different bulk densities could be explained by the factor-five larger insolation flux received by planet b compared to c, driving atmospheric escape and mass loss. While the masses of the other two planets are only upper limits, planet d (the third in distance from the star) clearly falls in the low-density regime, which would be consistent with this hypothesis. For planet e, a larger range in densities is possible, from pure MgSiO3 to extremely low densities. Therefore, to further research this possibility, precise measurements of the ultraviolet flux of K2-285 and comparative atmospheric studies using high-resolution transmission spectroscopy focused on exosphere and atmospheric escape processes through the detection of Hα, Lyα, or He lines should be conducted in the near future with the next generation of Extremely Large Telescopes (ELTs).

thumbnail Fig. 9

Mass-radius diagram for all known planets with masses in the range 0.5–20 M⊕ and radius 1–4 R⊕, comprising Earth-like to super-Earth to sub-Neptune regimes. Data are taken from the TEPCat database (Southworth 2011). Planets belonging to multiple systems are marked as open gray dots while single planets are marked as solid gray dots. The four planets of the K2-285 system are marked in different colors. Theoretical models for the internal composition of the planets are taken from Zeng et al. (2016).

Acknowledgements

CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Economy, the German Science Foundation through the Major Research Instrumentation Programme and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. This article is based on observations made in the Observatorios de Canarias del IAC with the TNG telescope operated on the island of La Palma by the Galileo Galilei Fundation, in the Observatorio del Roque de los Muchachos (ORM). HARPS-N data were taken under observing programs CAT17A-91, A36TAC-12 and OPT17B-59. This work is partly financed by the Spanish MINECO through grants ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R and AYA2016-79425-C3-3-P. This work was also supported by JSPS KAKENHI Grants Numbers JP16K17660 and JP18H01265.

Appendix A Additional table

Table A.1

Summary of the system parameters of K2-285 determined in Sect. 2 using only the fit to the photometric data from the K2 mission, and in Sect. 5 with the Pyaneti code fitting the photometric and RV data simultaneously.

References

  1. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Barragán, O., Grziwa, S., Gandolfi, D., et al. 2016, AJ, 152, 193 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barragán, O., Gandolfi, D., Dai, F., et al. 2018, A&A, 612, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  5. Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
  6. Cleveland, W. S. 1979, ASA, 74, 829 [Google Scholar]
  7. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84461V [Google Scholar]
  8. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Deming, D., Knutson, H., Kammer, J., et al. 2015, ApJ, 805, 132 [NASA ADS] [CrossRef] [Google Scholar]
  10. Doyle, A. P., Davies, G. R., Smalley, B., Chaplin, W. J., & Elsworth, Y. 2014, MNRAS, 444, 3592 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
  12. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  13. Fulton, B. J., & Petigura, E. A. 2018, AJ, 156, 264 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Hirano, T., Fukui, A., Mann, A. W., et al. 2016, ApJ, 820, 41 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hirano, T., Dai, F., Gandolfi, D., et al. 2018, AJ, 155, 127 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
  19. Kobayashi, N., Tokunaga, A. T., Terada, H., et al. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye & A. F. Moorwood, Proc. SPIE, 4008, 1056 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Luger, R., Kruse, E., Foreman-Mackey, D., Agol, E., & Saunders, N. 2018, AJ, 156, 99 [NASA ADS] [CrossRef] [Google Scholar]
  24. Luque, R., Nowak, G., Pallé, E., et al. 2018, A&A, 620, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  27. Niraula, P., Redfield, S., Dai, F., et al. 2017, AJ, 154, 266 [NASA ADS] [CrossRef] [Google Scholar]
  28. Oscoz, A., Rebolo, R., López, R., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701447 [CrossRef] [Google Scholar]
  29. Pepe, F., Cameron, A. C., Latham, D. W., et al. 2013, Nature, 503, 377 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Poznanski, D., Prochaska, J. X., & Bloom, J. S. 2012, MNRAS, 426, 1465 [NASA ADS] [CrossRef] [Google Scholar]
  32. Prieto-Arranz, J., Palle, E., Gandolfi, D., et al. 2018, A&A, 618, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471F [Google Scholar]
  34. Reiners, A., Ribas, I., Zechmeister, M., et al. 2018, A&A, 609, L5 [Google Scholar]
  35. Scott, N. J., Howell, S. B., & Horch, E. P. 2016, in Optical and Infrared Interferometry and Imaging V, Proc. SPIE, 9907, 99072R [CrossRef] [Google Scholar]
  36. Scott, N. J., Howell, S. B., Horch, E. P., & Everett, M. E. 2018, PASP, 130, 054502 [Google Scholar]
  37. Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
  38. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  39. Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Van Eylen, V., & Albrecht, S. 2015, ApJ, 808, 126 [NASA ADS] [CrossRef] [Google Scholar]
  41. Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [NASA ADS] [CrossRef] [Google Scholar]
  42. van Leeuwen F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Winn, J. N. 2010, Exoplanet Transits and Occultations (Tucson, AZ: University of Arizona Press) [Google Scholar]
  44. Winn, J. N., Petigura, E. A., Morton, T. D., et al. 2017, AJ, 154, 270 [Google Scholar]
  45. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
  47. Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Radial-velocity measurements derived from HARPS-N and CARMENES observations used in this paper.

In the text
Table 2

Stellar parameters of EPIC 246471491 (K2-285).

In the text
Table A.1

Summary of the system parameters of K2-285 determined in Sect. 2 using only the fit to the photometric data from the K2 mission, and in Sect. 5 with the Pyaneti code fitting the photometric and RV data simultaneously.

In the text

All Figures

thumbnail Fig. 1

K2 image of the object EPIC 246471491. A custom-built changing aperture is fitted based on the pixel counts of the star and background. The image shows three typical apertures used at the beginning (top left panel), middle (top right panel) and end (bottom left panel) of the time series. Bottom right panel: a high-resolution image of the same field taken from Palomar Observatory.
In the text
thumbnail Fig. 2

Kepler light curves of EPIC 246471491. Top panel: original raw light curves as derived from raw flux data. Bottom panel: detrended light curve after analysis with our modified Everest-based pipeline. Stellar variability of the order of tens of days and the transits of several planets are clearly visible.
In the text
thumbnail Fig. 3

Phase-folded transit light curves of the four planets detected orbiting EPIC 246471491. Top panels: transit light curves and best-fit transit models (red) on the same flux scale. Lower panels: residuals of the transit fit.
In the text
thumbnail Fig. 4

Subaru AO image (inset) and 5σ contrast light curve of EPIC 246471491. The inset image has a FOV of 4′′ × 4′′.
In the text
thumbnail Fig. 5

Generalized Lomb–Scargle periodograms (GLS) of the EPIC 246471491 RVs from CARMENES data (panel a), the K2 photometry (panel b), and the CRX (panel c), dLW (panel d), FWHM (panel e), CTR (panel f), and BVS (panel g) indices. Panel h: window function of the data. Vertical red lines indicate the frequencies associated with each of the four transiting planets, and the blue vertical lines mark the frequencies associated with the activity of the host star. The highest peaks in the CARMENES GLS are located at f = 0.045 d−1 (P ~ 22 d) and f = 0.081 d−1 (P = 12.1 d) and are linked to the rotation of the star. These periodicities are also significant in the K2 photometry and the CRX index. Horizontal lines show the FAP levels of 10% (short-dashed line), 1% (long-dashed line) and 0.1% (dot-dashed line).
In the text
thumbnail Fig. 6

Generalized Lomb–Scargle periodograms (GLS) of the EPIC 246471491 RVs from CARMENES and HARPS-N. Panel a: same data and analysis is shown as panel a of Fig. 5. Panel b: GLS of the CARMENES data after removing the prominent peak at f = 0.081 d−1, corresponding to Prot = 12.1 days. In this case the frequency associated with the alias peak at ~22 days also loses all the power, and the higher peaks are located at the periodicities of the four planets. Panel c: HARPS-N data (also Prot corrected) are added to the CARMENES data. The joint GLS shows significant periodicities for two of the four planets in this system. As in Fig. 5, horizontal lines show the FAP levels of 10 (short-dashed line), 1 (long-dashed line), and 0.1% (dot-dashed line).
In the text
thumbnail Fig. 7

Time series of the RV measurements of K2-285 derived from CARMENES (blue dots) and HARPS-N (red diamonds). The black line corresponds to the best-fit model to the data, which includes the RV signal of each of the four planets and the stellar activity.
In the text
thumbnail Fig. 8

Top left panel: phase-folded RV measurements of K2-285 over the period of planet b, after eliminating the signal from planets c, d, and e, and the stellar activity signal. Top right panel: as in the top-left panel but for planet c. Middle left panel: as in the top-left panel but for planet d. Middle right panel: as in the top-left panel but for planet e. Bottom panel: as in the top-left panel but for the stellar activity signal. The derived semi-amplitudes for these planets are 4.62−0.65+0.58$4.62 _{ - 0.65 } ^ { + 0.58 }$ m s−1, 5.90−0.80+0.86$5.90 _{ - 0.80 } ^ { + 0.86 } $ m s−1, 0.68−0.50+0.77$0.68 _{ - 0.50 } ^ { + 0.77 } $ m s−1 and 1.69−0.72+0.74$1.69 _{ - 0.72 } ^ { + 0.74 } $ m s−1, while the stellar activity signal has an amplitude of 12.29−0.81+0.80$12.29 _{ - 0.81 } ^ { + 0.80} $ m s−1. This translates into a mass determination of 9.68−1.37+1.21$9.68 _{ - 1.37 } ^ { + 1.21 } $ M⊕ and 15.68−2.13+2.28$15.68 _{ - 2.13 } ^ { + 2.28 } $ M⊕ for planets b and c, respectively, and upper-limit mass determinations of 6.5 M⊕ and 10.7 M⊕ (at 99% confidence level) for planets d and e, respectively.
In the text
thumbnail Fig. 9

Mass-radius diagram for all known planets with masses in the range 0.5–20 M⊕ and radius 1–4 R⊕, comprising Earth-like to super-Earth to sub-Neptune regimes. Data are taken from the TEPCat database (Southworth 2011). Planets belonging to multiple systems are marked as open gray dots while single planets are marked as solid gray dots. The four planets of the K2-285 system are marked in different colors. Theoretical models for the internal composition of the planets are taken from Zeng et al. (2016).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.