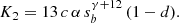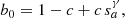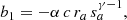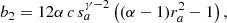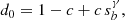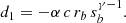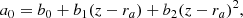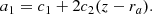| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 7 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201834563 | |
| Published online | 24 January 2019 | |
qpower2: A fast and accurate algorithm for the computation of exoplanet transit light curves with the power-2 limb-darkening law
Astrophysics Group, Keele University, Keele, Staffordshire ST5 5BG, UK
e-mail: p.maxted@keele.ac.uk
Received:
2
November
2018
Accepted:
30
November
2018
Context. The power-2 law, Iλ( μ) = 1 − c(1−μα), accurately represents the limb-darkening profile for cool stars. It has been implemented in a few transit models to-date using numerical integration but there is as-yet no implementation of the power-2 law in analytic form that is generally available.
Aims. Our aim is to derive an analytic approximation that can be used to quickly and accurately calculate light curves of transiting exoplanets using the power-2 limb-darkening law.
Methods. An algorithm to implement the power-2 law is derived using a combination of an approximation to the required integral and a Taylor expansion of the power-2 law. The accuracy of stellar and planetary radii derived by fitting transit light curves with this approximation is tested using light curves computed by numerical integration of limb-darkening profiles from 3D stellar model atmospheres.
Results. Our algorithm (qpower2) is accurate to about 100 ppm for broad-band optical light curves of systems with a star-planet radius ratio p = 0.1. The implementation requires less than 40 lines of python code so can run extremely fast on graphical processing units (GPUs; ∼1 million models per second for the analysis of 1000 data points). Least-squares fits to simulated light curves show that the star and planet radius are recovered to better than 1% for p < 0.2.
Conclusions. The qpower2 algorithm can be used to efficiently and accurately analyse large numbers of high-precision transit light curves using Monte Carlo methods.
Key words: methods: data analysis / binaries: eclipsing / planets and satellites: fundamental parameters / techniques: photometric
© ESO 2019
1. Introduction
Limb darkening is the variation of specific intensity emitted from a stellar photosphere as a function of the viewing angle. The advent of very high precision photometry for transiting exoplanet systems has led to extensive discussion in the literature of the best way to parameterise limb darkening in transit models, e.g., Espinoza & Jordán (2016), Müller et al. (2013), Howarth (2011), Sing et al. (2008), Morello et al. (2017), Neilson et al. (2017), Kipping (2013), etc. One well-established result from such studies is that using a linear limb-darkening law can lead to significant bias in the parameters derived from the analysis of high quality photometry. For example, Espinoza & Jordán (2016) found systematic errors in the radius estimates for small planets as large as 3% as a result of using linear limb-darkening coefficients. There are several alternative ways to parametrise limb darkening. Among the alternative two-parameter laws used to model the limb darkening profile Iλ( μ) for a given bandpass λ is the quadratic limb-darkening law (Kopal 1950) –
where μ is the cosine of the angle between the surface normal and the line of sight. This limb darkening law has the advantage of being relatively simple and well-understood in terms of the correlations between the coefficients (Pál 2008; Kipping & Bakos 2011; Howarth 2011) and how to sample the parameter space to achieve a non-informative prior (Kipping 2013). It is frequently used for studies of transiting exoplanets because several implementations of the algorithm by Mandel & Agol (2002) to rapidly and precisely calculate transit light curves with quadratic limb darkening are widely available.
Among the limb darkening laws with 2 coefficients, the power-2 limb darkening law (Hestroffer 1997) has been recommended by Morello et al. (2017) as they find that it outperforms other two-coefficient laws adopted in the exoplanet literature in most cases, particularly for cool stars. The form of this limb darkening law is
Using an exponent of μ rather than a coefficient of some power of μ enables this two-parameter law to match accurately the shape of the limb darkening profile towards the limb of the star using only one extra parameter cf. a linear limb-darkening law. The power-2 law has been implemented in the ellc binary star model (Maxted 2016) and the batman transit model (Kreidberg 2015). For both models, the transit light curve is calculated using numerical integration. The time required to perform the numerical integration is not generally a concern if one is analysing individual targets, but can be a limiting factor if the aim is to detect and analyse transits in large numbers of high precision light curves from surveys such as Kepler (Twicken et al. 2016), K2 (Howell et al. 2014) or TESS (Ricker et al. 2015). Maxted (2018) provides a tabulation of the parameters c and α for cool stars based on limb darkening profiles calculated using 3-dimensional radiative hydrodynmical models. These limb darkening profiles were tested against the limb darkening properties of stars measured from Kepler light curves of transiting exoplanets. The agreement between the computed and observed limb-darkening parameters was very good for inactive solar-type stars.
Here we present the qpower2 algorithm for calculating light curves of transiting exoplanets and related systems for which the star and planet can be approximated by spheres and the intensity profile on the star is described by the power-2 limb darkening law. The algorithm is extremely fast and accurate enough to model light curves from space-based instruments for systems with a radius ratio up to p ≈ 0.2. The algorithm can be applied equally to brown dwarf or low-mass stellar companions to normal stars in eclipsing binary systems. The deriviation of the algorithm is outlined in Sect. 2. In Sect. 3 we investigate the accuracy of the parameters recovered by least-squares fitting of transit light curves using the qpower2 algorithm and compare its performance to the quadratic limb-darkening law. In Sect. 4 we make some comments regarding the use of the algorithm and execution speed in various implementations. Our conclusions are given in Sect. 5.
2. Derivation of the qpower2 algorithm
The problem to be solved is to calculate the flux measured by a distant observer from a spherical star of radius r⋆ eclipsed by an opaque spherical body (“planet”) of radius rp ≪ r⋆. We set r⋆ = 1 for the following derivation. The star-planet radius ratio is p = rp/r⋆. For this derivation we assume that the smaller companion emits no flux.
The specific intensity on the stellar disk in some passband λ is described by the power-2 law,
where 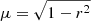 is the cosine of the angle between the line of sight and the normal to the stellar surface, and r is the distance on the sky from the centre of the star, so the limb of the star is at r = 1. The normalizing constant I0 is introduced so that the total flux from the unocculted star is 1, i.e.
is the cosine of the angle between the line of sight and the normal to the stellar surface, and r is the distance on the sky from the centre of the star, so the limb of the star is at r = 1. The normalizing constant I0 is introduced so that the total flux from the unocculted star is 1, i.e.
where Iλ(r)=I0[1−c+c(1−r2)γ] and we have defined γ = α/2 for convenience. From this definition we obtain
To calculate the light curve we need to evaluate the integral
where the area to be integrated over, S, is the part of the star obscured by the planet. In general, evaluating this integral requires use of hypergeometric functions, which is computational expensive. Instead, we derive an approximation to this integral by replacing Iλ(r) by a truncated Taylor series –
where primed symbols denote derivatives with respect to r.
The coordinate system used for the following derivation is defined such that the centre of the planet is at the position (x, y)=(z, 0). For the case with z < 1 − p the disk of the planet lies competely within the disc of the star, as illustrated in Fig. 1. For these phases we use r0 = z as the reference point for the Taylor series expansion. We also use a Taylor series expansion for (1 − r2)=(1 − x2 − y2) around the value y = 0 to obtain the following approximation –
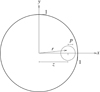 |
Fig. 1. Coordinate system used for our derivation illustrated for the case |z − 1|< p. |
where ℓ = p2 − (z − x)2. Approximating (1 − x2) by (1 − z2) in the second integral and expanding the term in square brackets in the first integral with a Taylor series around z, we obtain
where
and s = 1 − z2. Using c0 only from the term in square brackets in Eq. (7) is equivalent to using the “small planet approximation” described by Mandel & Agol (2002).
A similar approach can be taken for ingress and egress phases of the light curve where 1 − p < z < 1 + p. In these cases the integral is evaluated in two regions separated by the chord defined by the intersections between the two limbs. This chord is at a distance d = (z2−p2+1)/2z from the origin. Care must be taken in choosing the reference point r0 in the Taylor expansion because 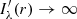 for r → 1. To avoid this problem and to ensure continuity with the light curve at other phases we choose r0 = ra = (z − p + d)/2 to evaulate the integral over the region between the chord and the limb of the planet, and r0 = rb = (1 + d)/2 for the region between the chord and the limb of the star. These are the midpoints on the perpendicular bisector of the chord between the chord and the limb of the star/planet, as illustrated in Fig. 2. The region between the chord and the limb of the star is always small for cases where p ≪ 1 so we only use the first two terms in the Taylor expansion in this region.
for r → 1. To avoid this problem and to ensure continuity with the light curve at other phases we choose r0 = ra = (z − p + d)/2 to evaulate the integral over the region between the chord and the limb of the planet, and r0 = rb = (1 + d)/2 for the region between the chord and the limb of the star. These are the midpoints on the perpendicular bisector of the chord between the chord and the limb of the star/planet, as illustrated in Fig. 2. The region between the chord and the limb of the star is always small for cases where p ≪ 1 so we only use the first two terms in the Taylor expansion in this region.
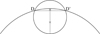 |
Fig. 2. Geometry of the star and planet at a phase where 1 − p < z < 1 + p. The chord DD′ is defined by the intersections between the limb of the star and the limb of the planet. Crosses mark the mid-points of the perpendicular bisector of DD′ between DD′ and the two limbs. These points are at distances ra and rb from the origin, respectively. |
For convenience we define 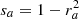 ,
, 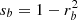 , and also q = (z − d)/p and
, and also q = (z − d)/p and 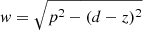 before proceeding as before. We then find that the light curve at these phases can be approximated by
before proceeding as before. We then find that the light curve at these phases can be approximated by
where
The coefficients in these expressions arising from the Taylor expansion of Iλ(z) are
and
These are then grouped according to their common factors to form the factors
and
An implementation of this algorithm in python is given in the appendix. The calculations in this paper were done using an equivalent implementation of the qpower2 algorithm that is included in the python module pycheops1 that is currently under development to facilitate analysis of data from the CHEOPS mission (Cessa et al. 2017).
3. Performance tests
In this section we report results of our tests to assess the accuracy of the qpower2 algorithm. All these tests have been done with light curves calculated for the CHEOPS passband. The results for the Kepler and TESS passbands are very similar. The light curves were simulated using the ellc binary star model assuming that both the star and planet are spherical and using the “very_fine” numerical integration option so that numerical noise is no more than a few ppm. The stellar radius has very little effect on the shape of the transit light curve so we fix this parameter at a value r⋆/a = 0.1 for all these simulations. The light curve is simulated for a planet on a circular orbit at 1001 points evenly distributed over a phase range covering the transit plus 5% of the transit width before and after the first and last contact points, respectively.
The limb darkening profile for the star is taken from the tabulated values provided at 10 values of μ calculated by Magic et al. (2015) using the STAGGER-grid 3D stellar atmosphere models. The limb darkening profile is interpolated to the desired values of Teff, log g and [Fe/H], and then interpolated onto a regular grid of 101 μ values using a monotonic piecewise cubic Hermite interpolating polynomial2. We used the values log g = 4.5 and [Fe/H]=0 for all the tests presented here.
For the optimisation of the least-squares fits we used the Nelder-Mead simplex algorithm as implemented in the minimize function of the python package scipy.optimize. We found that this algorithm converged on the correct solution more reliably than the other algorithms available in this function.
An example of a simulated light curve is shown in Fig. 3 for an impact parameter b = acos(i)/r⋆ = 0 and radius ratio p = rp/r⋆ = 0.1. This value of p is typical for gas giant planets in short-period orbits around solar-type stars (“hot Jupiters”). Also shown in this figure is the light curve calculated using the power-2 limb-darkening law calculated with ellc using values of c and α from Maxted (2018). From this figure it can be seen that the qpower2 algorithm reproduces light curves for the power-2 limb-darkening law accurate to better than 0.008% for these parameters.
 |
Fig. 3. Upper panel: light curve computed using the ellc light curve model with a limb darkening profile from the STAGGER-grid for Teff = 6000 K, log g = 4.5, [Fe/H] = 0. The parameters for this light curve are r⋆ = 0.05, p = 0.1 and b = 0. Lower panel: difference between light curves computed with the “sparse” numerical grid option in ellc and the power-2 limb darkening law (dashed green line) or with the qpower2 algorithm (dotted cyan line) and the light curve shown in the upper panel. The power-2 and qpower2 light curves were calculated using the same parameters as in the upper panel. |
3.1. Accuracy compared to other algorithms
We compared the performance of the qpower2 algorithm to numerical integration of the power-2 limb-darkening law with ellc and the algorithm for quadratic limb darkening by Mandel & Agol (2002). The results are shown as a function of p in Fig. 4 for a star with Teff = 6000 K. The results from the power-2 light curve fits are extremely accurate across the whole range of p for all three values of the impact parameter used here (b = 0.3, 0.6, 0.9). Note that we used the “sparse” numerical integration grid option in ellc to calculate these results. Better accuracy, if needed, can be achieved using a finer numerical integration grid but at the expense of increased computation time.
 |
Fig. 4. Errors in selected light curve parameters from least-squares fits to light curves generated from limb darkening profiles from the STAGGER-grid, as a function of radius ratio, p, for three different algorithms. From left to right panels: ellc light curve model with the power-2 limb-darkening law; Mandel & Agol algorithm for the quadratic limb-darkening law; qpower2 algorithm. Results are shown for three values of the impact parameter, as follows: b = 0.3 – solid green line, b = 0.6 – dotted blue line, b = 0.9 – dashed cyan line. |
The sharp decrease in the accuracy of the recovered values of rp and r⋆ at p = 0.2 for b = 0.9 is a result of the eclipse being grazing for this configuration. The light curve for a grazing eclipse contains very little information about the geometry of the system so there are large degeneracies in the least-squares fits and the results are very sensitive to numerical noise. The eclipse is also very shallow and lacks the characteristic shape of an eclipse due to a planetary transit that is typically used to identify these systems in photometric surveys so we ignore grazing eclipses for the remainder of this discussion.
The radii and radius ratio determined with the quadratic limb-darkening law are accurate to approximately 0.5% over the same range of p and b. The performance of this algorithm in terms of the recovered values of rp and r⋆ is worst for small values of p, while the recovered value of p is accurate to better than 0.5% for all values of p for impact parameters b = 0.3 and b = 0.6. We have not investigated these trends in detail but strongly suspect that they are due to the poor match between the quadratic limb-darkening law and the realistic limb darkening profiles for solar-type stars from the STAGGER-grid at small values of μ, i.e. towards the limb of the star.
The performance of the qpower2 algorithm overall is very similar to the quadratic limb-darkening algorithm, i.e., the results are accurate to better than approximately 0.5% for transits with p < 0.2. One clear difference is that the qpower2 algorithm performs better than quadratic limb-darkening law for p ≲ 0.06. For b = 0.3 and b = 0.6 there is a small bias in the recovered values that varies slowly with p. This suggests that it should be possible to correct for this bias in the analysis of high-quality light curves using simulations similar to those presented here. The best fit from the least-squares fit using the qpower2 algorithm can also be used as an accurate starting point for further least-squares fits using numerical integration of the power-2 limb darkening law with ellc or batman.
3.2. Accuracy as a function of effective temperature
The results as a function of stellar effective temperature, Teff, for the qpower2 algorithm with p = 0.1 are shown in Fig. 5. The range Teff = 4500 K–7000 K is set by the range of stellar effective temperature available from the STAGGER-grid for log g = 4.5. The accuracy of the recovered parameter values is quite consistent across the full range of Teff and is, in general, better than 0.5%.
 |
Fig. 5. Errors in selected light curve parameters from least-squares fits to light curves generated from limb darkening profiles from the STAGGER-grid, as a function of radius ratio, p, for qpower2 algorithm for three different values of Teff, as noted in the titles to the upper panels. Results are shown for three values of the impact parameter, as follows: b = 0.3 – solid green line, b = 0.6 – dotted blue line, b = 0.9 – dashed cyan line. |
4. Implementation notes and timing tests
In this section we make some comments regarding the implementation of the algorithm and present the results of some tests we have conducted to assess the speed of the qpower2 algorithm.
4.1. Python implementation
The python implementation of the qpower2 algorithm shown in Fig. A.1 uses the function select to assign the output of either function q1 or q2 to the output array depending on whether z ≤ p or |z − 1|< p. This requires that these functions are valid for any input value of z. We have used the clip function to restrict the value of z and so avoid invalid calculations inside these functions. Similarly, the function finfo(0.0).eps is used to generate a small floating-point number (typically 2−52) to avoid errors due to an attempt to raise 0 to a negative power. Alternative methods for applying the conditions z ≤ p and |z − 1|< p can avoid some of these complications and may be faster in some cases since fewer calls to q1 and q2 will be required. For clarity, we have not included good programming practices such as error and warning message generation, checks for invalid input parameters, in-line documentation or comments in this code fragment.
The implementation of qpower2 in the current development version of pycheops (0.1.0) uses a loop to pass once through the input values of z with an if ...then ...else if ... logical structure to apply the conditions z ≤ p and |z − 1|< p. This structure is well suited to “just-in-time” compilation and optimisation using the package numba3. We found this to be an effective and easy way to dramatically improve the speed of the calculation, as described below.
4.2. Comparison with other algorithms
We tested the speed of various algorithms to calculate the transit light curve of a system with p = 0.1, r⋆ = 0.1 and b = 0. For all the algorithms tested we simulated a light curve with 1000 observations uniformly sampled over one transit plus 5% in phase before and after the start and end of the transit.
The algorithms tested were: the qpower2 implementation from pycheops with and without optimisation using numba; the qpower2 implementation from Fig. A.1; batman using quadratic limb darkening; batman using power-2 limb-darkening. Quadratic limb darkening in batman uses a variant of the algorithm by Mandel & Agol (2002). The power-2 algorithm in batman uses a numerical integration scheme with the option to set the maximum numerical error in ppm. We ran simulations with the default option maxerr = 1 and also simulations with maxerr = 70 for direct comparison with the qpower2 algorithm. These tests were all performed on an Apple MacBook Pro with a 2 GHz Intel® Core i7 CPU. Timings were calculated using the %timeit function in IPython.
From the results shown in Table 1 for these simulations (Data set A) we see that the optimised qpower2 implementation from pycheops is the fastest of the algorithms tested and is just over twice as fast as the batman algorithm for power-2 limb-darkening with maxerr = 70, and 50% faster than batman with quadratic limb darkening.
Execution time per light curve for simulations containing either 1000 data points (Data set A) or 3840 data points (Data set B) for the transit of a star by a planet with p ≈ 0.1.
4.3. CPU versus GPU timing tests
The qpower2 algorithm is a small piece of code than can be executed in parallel on a data set of moderate size. This makes it well-suited to acceleration by executing it on a graphical processing unit (GPU). We have experimented with this option using the CUDA® toolkit by NVIDIA®4. This option works particularly well if the code can be refactored to send a single array with multiple sets of parameter values to the GPU, i.e. it is much faster to loop over the calls to the qpower2 function on the GPU rather than the CPU. Another effective optimisation for Markov chain Monte Carlo routines such as EMCEE (Foreman-Mackey et al. 2013) is to calculate the log-likelihood (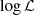 ) for each model on the GPU and to return only these values, rather than incurring the overhead of returning the simulated light curve from the GPU to the CPU.
) for each model on the GPU and to return only these values, rather than incurring the overhead of returning the simulated light curve from the GPU to the CPU.
We used a PC running linux (Ubuntu 17.10) with eight 4.2 GHz Intel® Core i7-7700K CPUs (overclocked to 4.8 GHz) and a GeForce GTX 1080 GPU to compare the execution speed of the qpower2 algorithm running on CPUs and GPUs. The parameters used for these simulations were the similar to those for the comparison between algorithms in the previous section except that we used 3840 points per eclipse. We used an implementation of the qpower2 algorithm written in C using OpenMP5 for parallelization. The results are shown in Table 1 (Data set B).
From Table 1 we see that the speed-up using this option does not scale with the number of CPUs used. This is a consequence of the overheads in the parallelization. Nevertheless, with 8 CPUs it is possible to increase the speed of an MCMC analysis by more than a factor of 3. However, gains in speed of an order of magnitude are possible by using a GPU to calculate the light curves, and an additional speed-up by more than a factor of ×5 is possible if the MCMC code can refactored so that the log-likelihood (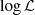 ) calculation is performed on the GPU, rather than returning the computed light curve to the CPU. With these optimisations it is possible to calculate up to 1 million
) calculation is performed on the GPU, rather than returning the computed light curve to the CPU. With these optimisations it is possible to calculate up to 1 million 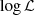 values per second on a GPU for a transit light curve with 1000 data points.
values per second on a GPU for a transit light curve with 1000 data points.
5. Conclusion
The qpower2 algorithm is straightforward to implement, very fast and sufficiently accurate to model the light curves of transiting exoplanet systems and related objects from instruments such as Kepler, TESS, CHEOPS, and PLATO (Rauer et al. 2014). For a typical hot Jupiter system, the log-likelihood for a transit light curve of 1000 observations can be computed for a model light curve accurate to 100 ppm in approximately 1 μs on a GPU. This makes this algorithm an attractive choice for en masse analysis of light curves from these massive photometric surveys.
Acknowledgments
SG acknowledges support from Doctoral Training Partnership grant number ST/N504348/1 from the Science and Technology Facilities Council (STFC). PM acknowledges support from STFC research grant number ST/M001040/1.
References
- Cessa, V., Beck, T., Benz, W., et al. 2017, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 10563, 105631L [Google Scholar]
- Espinoza, N., & Jordán, A. 2016, MNRAS, 457, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Hestroffer, D. 1997, A&A, 327, 199 [NASA ADS] [Google Scholar]
- Howarth, I. D. 2011, MNRAS, 418, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kipping, D., & Bakos, G. 2011, ApJ, 730, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Kopal, Z. 1950, Harvard College Observatory Circular, 454, 1 [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L. 2016, A&A, 591, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxted, P. F. L. 2018, A&A, 616, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morello, G., Tsiaras, A., Howarth, I. D., & Homeier, D. 2017, AJ, 154, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., McNeil, J. T., Ignace, R., & Lester, J. B. 2017, ApJ, 845, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A. 2008, MNRAS, 390, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, Instrum. Syst., 1, 014003 [Google Scholar]
- Sing, D. K., Vidal-Madjar, A., Désert, J.M., Lecavelier des Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Twicken, J. D., Jenkins, J. M., Seader, S. E., et al. 2016, AJ, 152, 158 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Python implementation
An implementation of the qpower2 algorithm written for python version 3.6 is shown in Fig. A.1. Note that this implementation is written for clarity rather than optimised for speed.
 |
Fig. 6. A python implementation of the qpower2 algorithm. |
All Tables
Execution time per light curve for simulations containing either 1000 data points (Data set A) or 3840 data points (Data set B) for the transit of a star by a planet with p ≈ 0.1.
All Figures
 |
Fig. 1. Coordinate system used for our derivation illustrated for the case |z − 1|< p. |
| In the text | |
 |
Fig. 2. Geometry of the star and planet at a phase where 1 − p < z < 1 + p. The chord DD′ is defined by the intersections between the limb of the star and the limb of the planet. Crosses mark the mid-points of the perpendicular bisector of DD′ between DD′ and the two limbs. These points are at distances ra and rb from the origin, respectively. |
| In the text | |
 |
Fig. 3. Upper panel: light curve computed using the ellc light curve model with a limb darkening profile from the STAGGER-grid for Teff = 6000 K, log g = 4.5, [Fe/H] = 0. The parameters for this light curve are r⋆ = 0.05, p = 0.1 and b = 0. Lower panel: difference between light curves computed with the “sparse” numerical grid option in ellc and the power-2 limb darkening law (dashed green line) or with the qpower2 algorithm (dotted cyan line) and the light curve shown in the upper panel. The power-2 and qpower2 light curves were calculated using the same parameters as in the upper panel. |
| In the text | |
 |
Fig. 4. Errors in selected light curve parameters from least-squares fits to light curves generated from limb darkening profiles from the STAGGER-grid, as a function of radius ratio, p, for three different algorithms. From left to right panels: ellc light curve model with the power-2 limb-darkening law; Mandel & Agol algorithm for the quadratic limb-darkening law; qpower2 algorithm. Results are shown for three values of the impact parameter, as follows: b = 0.3 – solid green line, b = 0.6 – dotted blue line, b = 0.9 – dashed cyan line. |
| In the text | |
 |
Fig. 5. Errors in selected light curve parameters from least-squares fits to light curves generated from limb darkening profiles from the STAGGER-grid, as a function of radius ratio, p, for qpower2 algorithm for three different values of Teff, as noted in the titles to the upper panels. Results are shown for three values of the impact parameter, as follows: b = 0.3 – solid green line, b = 0.6 – dotted blue line, b = 0.9 – dashed cyan line. |
| In the text | |
 |
Fig. 6. A python implementation of the qpower2 algorithm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



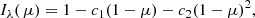
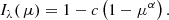
![$$ \begin{aligned} I_{\lambda }(\,\mu ) = I_0\left[1 - c\left( 1 - \mu ^\alpha \right) \right], \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq3.gif)
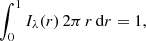
![$$ \begin{aligned} I_0 = \frac{\alpha +2}{\pi \left[(1-c)\alpha +2\right]}\cdot \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq6.gif)
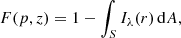
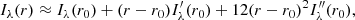
![$$ \begin{aligned} F(p,z)&\approx 1 - 2I_0\int _{z-p}^{z+p} \left[1-c+c\left(1-x^2\right)^{\gamma } \right] \sqrt{\ell } \,\mathrm{d}x \nonumber \\&\quad +{1}{3}I_0\,\alpha \,c\int _{z-p}^{z+p} \left(1-x^2\right)^{\gamma -1} \ell ^{{3}{2}}\,\mathrm{d}x, \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq9.gif)
![$$ \begin{aligned} F(p,z) \approx 1 - I_0\,\pi \,p^2\left[c_0 + {1}{4} p^2 c_2 - {1}{8} \alpha \,c\, p^2 s^{\gamma -1} \right], \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq10.gif)
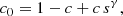
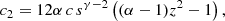
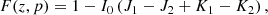
![$$ \begin{aligned} J_1 =&\left[a_0(d-z)-{2}{3}a_1\,w^2 +{1}{4}b_2\,(d-z)\left(2(d-z)^2-p^2\right)\right]\,w \nonumber \\&+ \left(a_0\,p^2 + {1}{4}b_2\,p^4\right)\,\cos ^{-1}(q), \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq18.gif)
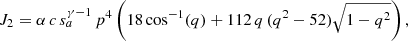
![$$ \begin{aligned} K_1 =&\left(d_0-r_b\,d_1\right)\cos ^{-1}(d) \nonumber \\&+ \left([r_b\,d+{2}{3}\,(1-d^2)]\,d_1 - d\,d_0\right) \sqrt{1-d^2}, \end{aligned} $$](/articles/aa/full_html/2019/02/aa34563-18/aa34563-18-eq20.gif)