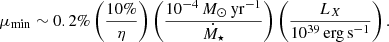| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834543 | |
| Published online | 25 January 2019 | |
Letter to the Editor
Wind Roche lobe overflow in high-mass X-ray binaries
A possible mass-transfer mechanism for ultraluminous X-ray sources
1
Centre for Mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: ileyk.elmellah@kuleuven.be
2
KU Leuven, Instituut voor Sterrenkunde, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received:
30
October
2018
Accepted:
30
December
2018
Ultraluminous X-ray sources (ULXs) have such high X-ray luminosities that they were long thought to be accreting intermediate-mass black holes. Yet, some ULXs have been shown to display periodic modulations and coherent pulsations suggestive of a neutron star in orbit around a stellar companion and accreting at super-Eddington rates. In this Letter, we propose that the mass transfer in ULXs could be qualitatively the same as in supergiant X-ray binaries (SgXBs), with a wind from the donor star highly beamed towards the compact object. Since the star does not fill its Roche lobe, this mass transfer mechanism known as “wind Roche lobe overflow” can remain stable even for large donor-star-to-accretor mass ratios. Based on realistic acceleration profiles derived from spectral observations and modeling of the stellar wind, we compute the bulk motion of the wind to evaluate the fraction of the stellar mass outflow entering the region of gravitational predominance of the compact object. The density enhancement towards the accretor leads to mass-transfer rates systematically much larger than the mass-accretion rates derived by the Bondi-Hoyle-Lyttleton formula. We identify orbital and stellar conditions for a SgXBs to transfer mass at rates necessary to reach the ULX luminosity level. These results indicate that Roche-lobe overflow is not the only way to funnel large quantities of material into the Roche lobe of the accretor. With the stellar mass-loss rates and parameters of M101 ULX-1 and NGC 7793 P13, wind Roche-lobe overflow can reproduce mass-transfer rates that qualify an object as an ULX.
Key words: X-rays: binaries / accretion / accretion disks / stars: black holes / supergiants / stars: winds / outflows / stars: neutron
© ESO 2019
1. Introduction
Ultraluminous X-ray sources are spatially unresolved persistent sources with luminosities in excess of 1039 erg s−1 (for a recent review see Kaaret et al. 2017). This X-ray luminosity threshold corresponds approximately to the Eddington luminosity LEdd of a 10 M⊙ black hole (BH), the limit above which isotropic accretion onto a body of this mass is thought to be self-regulated by the radiative field it produces (Rappaport et al. 2005). They are found off-centered in galaxies within approximately 20 Mpc, ruling against a supermassive BH origin. If the emission is not beamed, sub-Eddington accretion can only be sustained for accretors of at least several tens of to several hundred solar masses, suggestive of the long- awaited population of intermediate-mass BHs (Colbert & Mushotzky 1999). Hints in favor of the existence of intermediate-mass BHs recently emerged: the observation of gravitational waves emitted by merging compact objects unearthed BHs of several tens of solar masses which could be the low-mass tail of this population (Abbott et al. 2016).
However, the detections of coherent pulsations and cyclotron resonance scattering features from several ULXs demonstrate that other ULXs host super-Eddington-accreting neutron stars (NSs; Bachetti et al. 2014; Fürst et al. 2016; Israel et al. 2017a,b; Carpano et al. 2018; Brightman et al. 2018). In one of them, NGC 7793 P13 (hereafter P13), Motch et al. (2014) identified a stellar spectrum consistent with a 20 M⊙ B9 Ia star, in a ∼64-day orbit with an X-ray source they assumed to be a BH but which later turned out to be an accreting NS (Fürst et al. 2016; Israel et al. 2017a). It was further argued that the star has to fill its Roche lobe because the stellar mass-loss rate would be too low and wind accretion would not be able to lead to a significant fraction of the stellar wind being captured by the accretor. On the other hand, Liu et al. (2013) showed that in M101 ULX-1 (hereafter M101), the Helium emission lines are best explained by a Wolf-Rayet donor star twice smaller than its Roche lobe. This suggests that mass-transfer rates suitable for ULX X-ray luminosity levels are possible without Roche-lobe overflow (RLOF). Finally, in three ULXs, near-infrared counterparts consistent with red-supergiant donors have been identified (Heida et al. 2015, 2016).
Most ULXs hosting a stellar mass accretor are now thought to be the high-mass-accretion-rate end of the supergiant X-ray binaries (SgXBs), where the wind from a supergiant donor star acts as a reservoir of matter tapped by the orbiting compact object. The X-ray luminosity functions of SgXBs and ULXs follow the same power law, without an apparent break (Gilfanov et al. 2004; Swartz et al. 2011). Super-orbital periods are observed in SgXBs (Corbet & Krimm 2013; Coley et al. 2018) and in ULXs (Walton et al. 2016; Fürst et al. 2018), although their origins might differ from one system to another and several models have been suggested (Wijers & Pringle 1998; Moreno & Koenigsberger 1999; Bozzo et al. 2017). All these elements support the idea that both types of objects belong to the same population and that the mass-transfer mechanism at the orbital scale might be qualitatively the same.
The final absolute X-ray luminosity LX released by accretion onto a compact object fed by a stellar companion depends on (i) the stellar mass-loss rate Ṁ⋆, (ii) the rate μṀ⋆ at which mass is transferred from the star into the domain of gravitational influence of the accretor, (iii) the mass which actually ends up being accreted onto the compact object, and (iv) the efficiency ζ of the conversion of accreted mass to radiation, set here to 10% (Kaaret et al. 2017). The relevance of the classical LEdd limit in ULXs is a matter of debate. For instance, it is derived assuming a smooth stellar wind outflow but since radiation line-driving leads naturally to clumpy and porous winds (Sundqvist et al. 2018; Owocki & Sundqvist 2018), this may also allow for super-Eddington accretion (Dotan & Shaviv 2011).
We further note that the mass-transfer rate (also called mass-capture rate hereafter) sets an upper limit on the stationary mass-accretion rate the system can reach but that we do not compute. The actual fraction of the wind captured which ends up being accreted depends on mechanisms out of the scope of the present Letter; here, we set aside the question of how super-Eddington accretion itself proceeds in the vicinity of the accretor, that is, how the compact object can accrete at a rate leading to LX > LEdd. Rather, we ask whether stellar material can be transferred to the compact object at a rate Ṁ high enough to reach the ULX luminosity level, without necessarily assuming RLOF. In the context of symbiotic binaries, Mohamed & Podsiadlowski (2007) showed that a low-enough wind speed when compared to the orbital speed could lead to a significant enhancement of the mass-transfer rate. This mechanism, known as wind Roche-lobe overflow (wind-RLOF), is characterized by a strongly beamed wind in the orbital plane and towards the accretor. This mass transfer does not experience runaway RLOF expected for high mass ratios since the process is not conservative and the star does not fill its Roche lobe.
2. Stellar winds in SgXBs
We solve the ballistic equation of motion in the three-dimensional co-rotating frame of a binary system for test-masses starting at the stellar surface and subjected to the two gravitational forces, the noninertial forces and the wind acceleration. We use the numerical integrator described in El Mellah & Casse (2016). Figure 1 illustrates the geometry of the problem in two configurations representative of Vela X-1 (upper panel) and M101 (lower panel). In SgXBs hosting an O/B supergiant, the wind-launching mechanism relies on the resonant absorption of UV photons by partially ionized metal ions (Lucy & Solomon 1970; Castor et al. 1975). In an isotropic situation, this leads to radial-velocity profiles which can be well approximated by a β-law (Puls et al. 2008):
 |
Fig. 1. Slices in the orbital plane with the stellar center as the origin and the orbital separation as the length scale. The solid black line shows the contour of the Roche potential at the first Lagrangian point L1. The color map shows ρ/ρiso, the local relative density enhancement with respect to a mass density ρiso evolving with the reverse of the distance to the stellar center and scaled such that it has the same median value as the density ρ we measure. The upper panel is representative of the shape of the flow in Vela X-1 (and possibly P13) while the lower panel is adapted to parameters compatible with M101. The white area stands for the capture region, where material can be accreted, given by the accretion radius in the top panel and the Roche lobe in the bottom panel. The gray area is the wake of the accretor that our simulations do not cover. We note the much larger density enhancement in the bottom panel where the flow is also much more structured compared to that in the top one. |
where R⋆ is the stellar radius, v∞ the terminal wind speed, and β is a positive exponent which represents the efficiency of the acceleration, that is, how fast the wind reaches its terminal speed: the lower β, the earlier v∞ is matched. We note that, although the wind launching mechanism of cool stars is still largely unknown, the wind velocity profiles observed around red supergiants and asymptotic giant branch stars turn out to be in reasonable agreement with this law beyond the condensation radius (Decin et al. 2006, 2010). The terminal wind speeds are much lower than for winds from hot stars but they display similar β exponents, and mass-loss rates above 10−5 M⊙ yr−1 are common (De Beck et al. 2010). Many uncertainties subsist on the velocity profile of line-driven winds in SgXBs, as illustrated by the case of the hot supergiant HD 77581, the donor star in the classic SgXBs Vela X-1. From observations of UV spectral lines, Gimenez-Garcia et al. (2016) derived a best β-law with v∞ ∼ 700 km s−1 and β = 1 while Sander et al. (2017) computed the hydrodynamic atmosphere solution for the wind stratification, best-fitted by a β-law with v∞ ∼ 500 km s−1 and β ∼ 2.3. Given these uncertainties, we evaluate the wind acceleration in an empirical manner by relying on representative velocity profiles from which we can derive steady radial line-driven accelerations. We also need to assume that the departure from the isotropic case due to the presence of an orbiting accretor does not significantly alter the radial component of the wind acceleration, still given by vβdrvβ.
To evaluate the fraction of wind captured, μ = Ṁ/Ṁ⋆, we need to define the region of gravitational influence of the accretor, that is, the region where the flow is significantly deflected from its trajectory by the gravitational field of the accretor (white region in Fig. 1). When the wind speed at the orbital separation is large compared to the orbital speed, the effective cross section of the accretor is described by the accretion radius Racc defined by
where a is the orbital separation, G the constant of gravity, and M• the mass of the accretor (El Mellah & Casse 2015). It is the fast wind regime which is doomed to yield low mass-transfer rates due to the fast drop of the cross section with the wind speed. However, in SgXBs and ULXs, the accreting compact object lies deep in the wind, in a region where the wind is still accelerating and where the fast wind assumption might break up. In this case, the domain of gravitational influence of the accretor is better defined by its Roche lobe: material entering the Roche lobe is expected to participate in the accretion process (e.g., via the formation of a wind-captured disk El Mellah et al. 2019), although only a fraction of it will end up being accreted and producing the X-rays we observe. Consequently, we define the region of gravitational influence of the accretor as its Roche lobe if the accretion radius Racc is larger than the Roche lobe radius, and the sphere of radius Racc centered on the accretor otherwise. Given the uncertainties which remain on the velocity profile and the important dependency of the accretion radius on the wind speed, we need to consider several β exponents: for instance, in Vela X-1, the uncertainty on the wind-velocity profile leads to a discrepancy of a factor of ∼10 on the accretion radius of the NS.
In dimensionless form, the solutions of the equation of motion depend only on the mass ratio q, the filling factor f (the ratio of the stellar radius to the Roche lobe radius, Eggleton 1983), the β exponent, and the ratio of the terminal wind speed to the orbital speed η = v∞/vorb, with vorb = 2πa/Porb, with Porb being the orbital period. In particular, these four parameters entirely determine the ratio μ of stellar wind significantly beamed towards the accretor. We quantify μ by monitoring the fraction of stellar wind entering the domain of gravitational influence of the accretor. For instance, in Fig. 1, the upper (resp. lower) panel corresponds to η = 4, β = 1, f = 90% and q = 15 (resp. η = 3, β = 2, f = 50% and q = 2). Previous estimates of the mass-accretion rate do not account for the density enhancement. Instead, an isotropic dilution of the flow around the donor star is assumed. We do account for the beaming of the wind towards the accretor and show in the following section its significant impact, along with the impact of an accurate representation of the capture radius of the accretor.
3. Mass transfer via wind-RLOF
3.1. Fraction of stellar wind available for accretion
We probe a range of parameters realistic for ULXs, whether the donor star is a Wolf-Rayet or a supergiant. The few orbital periods and mass measures available indicate that the orbital speed might vary by a factor of a few from one ULX to another, while the terminal wind speeds of cool supergiants are generally more than an order of magnitude lower than those of hot supergiants and Wolf-Rayet stars: here, we span values of η from 1.1 to 20. We work with a β exponent of 1 and 2, with 2 giving a more progressive velocity increase to the terminal speed. Observed filling factors lie between 50 and 100% (RLOF). Two extreme mass ratios have been considered, q = 2 and q = 15, which correspond respectively to a stellar mass BH and a NS accreting from a ∼20 M⊙ supergiant.
Figure 2 illustrates the evolution of the fraction of wind captured with the four dimensionless parameters of the problem. Its aim is to provide the reader with a feeling for the evolution of the mass-transfer rate with the parameters, which is not easy to appreciate without performing the actual computation we carried out. A first significant effect is the drop of μ with increasing η: when the terminal wind speed becomes a few times greater than the orbital speed, the effective cross-section set by the accretion radius decreases quickly and much below the radius of the Roche lobe of the accretor. This effect is tempered for slowly accelerating winds (i.e., for high β) which, provided the distance from the photosphere to the accretor is small (i.e., for large f), are still far from their terminal wind speeds when they enter the Roche lobe of the accretor. On the contrary, the dependency of μ on the filling factor vanishes when the wind accelerates quickly because then, by the time it reaches the accretor, the wind has almost reached its terminal speed. Slow wind launching leads to a significant contribution of the high-latitude stellar regions: the flow is strongly beamed in the orbital plane and the value of μ surges.
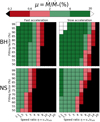 |
Fig. 2. Logarithmic color maps of the fraction μ of stellar wind captured by the accretor as a function of the stellar filling factor and of the ratio of the terminal wind speed by the orbital speed. Left panel: (resp. right) column is for β = 1 (resp. β=2). Upper panel: (resp. lower) row stands for a mass ratio of 2 (resp. 15) typical of a BH (resp. a NS) accreting from a supergiant companion. From white to black, the fraction of stellar material captured varies by more than two orders of magnitude, with the configurations in green (and white) being more susceptible to giving large X-ray luminosities than the regions in red (and black). |
We now compare our results to the commonly used Bondi-Hoyle-Lyttleton (BHL) mass-accretion-rate formula (Bondi & Hoyle 1944; Edgar 2004):
where ṀBHL is the BHL mass accretion rate, 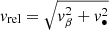 is the relative speed between the wind and the compact object whose orbital speed is given by v• = vorb[q/(1+q)], and
is the relative speed between the wind and the compact object whose orbital speed is given by v• = vorb[q/(1+q)], and 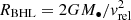 is the modified accretion radius. In the literature, the density of the wind at orbital separation ρ• is evaluated assuming an isotropic dilution of the wind around the star. We can now write the fraction of wind captured according to the BHL formula (3), μBHL = ṀBHL/Ṁ⋆, as a function of the four dimensionless parameters:
is the modified accretion radius. In the literature, the density of the wind at orbital separation ρ• is evaluated assuming an isotropic dilution of the wind around the star. We can now write the fraction of wind captured according to the BHL formula (3), μBHL = ṀBHL/Ṁ⋆, as a function of the four dimensionless parameters:
where ℰ is the ratio of the stellar Roche lobe radius by the orbital separation given by Eggleton (1983) which depends only on q. In Fig. 3, we use dashed lines to plot the evolution of μBHL with the speed ratio η for different mass ratios and β exponents and compare it with our results. Since our setup does account for the geometrical beaming of matter non-negligible for slow winds (see bottom panel in Fig. 1), and does not assume isotropic dilution of the stellar wind, we find values of μ systematically higher, except when the wind speed at the orbital separation is so low compared to the orbital speed that the effective cross section given by the BHL formula is larger than the orbital separation and looses any meaning: relying on the Roche lobe instead makes much more sense in this regime.
 |
Fig. 3. Comparison of the mass-transfer rates we measure as a function of η (solid lines) to the BHL mass-accretion-rate formula (dashed lines) for a filling factor of 90% and mass ratios of 2 (upper panel) and 15 (lower panel). The BHL prescription leads to mass-accretion rates much lower than the mass-transfer rates we derive, sometimes by more than an order of magnitude. |
3.2. Accretion luminosity
Another insight revealed by this analysis is the identification of the configurations where ULXs cannot be the product of mass transfer via wind-RLOF and can be explained only if the star fills its Roche lobe. In Fig. 2, we represented in black the regions where μ is inferior to 0.2%, the minimum fraction of stellar wind captured under which mass transfer without RLOF is not able to produce a stationary X-ray luminosity of 1039 erg s−1, even for a stellar mass-loss rate as high as 10−4 M⊙ yr−1:
Given the maximal μ we found at ∼20%, this analysis suggests that mass transfer via wind-RLOF in a ULX is only possible for stellar mass-loss rates above ∼10−6 M⊙ yr−1. We note here that matching a mass-transfer rate Ṁ high enough to reach ULX levels is a necessary but not sufficient condition: the final X-ray luminosity is determined by the physics at stake within the Roche lobe of the accretor, where the flow geometry can be disk-like (El Mellah et al. 2019) or spherical (Shakura et al. 2012) and where, for an accreting NS, the magnetosphere eventually dominates the dynamics (Bozzo et al. 2008). For accreting BHs, powerful disk outflows come into play in the vicinity of the compact object, lowering the final mass-accretion rate (Pinto et al. 2016).
Rather than covering the large scope of regimes possible, let us focus on three donor stars in one SgXBs and two ULXs. In the SgXBs Vela X-1, Gimenez-Garcia et al. (2016) reported a stellar mass-loss rate Ṁ⋆ ∼ 6.3 × 10−7 M⊙ yr−1 for the B0.5 Ib supergiant donor star. In M101, Liu et al. (2013) inferred a mass-loss rate of 2 × 10−5 M⊙ yr−1 for the Wolf-Rayet donor. In P13, we think the stellar mass-loss rate of the B9 Ia supergiant donor star could have been underestimated: in Motch et al. (2014), it is assumed that the donor star fills its Roche lobe on the basis that the wind mass-loss rate derived by Kudritzki et al. (1999) would be inferior to 10−6 M⊙ yr−1. However, Kudritzki et al. (1999) did not include late-type B supergiants in their study because of the difficulty to measure their terminal wind speed (Howarth et al. 1997). Vink et al. (2000, 2001) provided fits for the mass-loss rate and the terminal wind speed which extend below the second bi-stability jump (i.e., for effective temperatures Teff ≲ 12kK, Lamers et al. 2000). With the values reported by Motch et al. (2014) (Teff ∼ 11kK, stellar luminosity L⋆ ∼ 105.1 L⊙ and stellar mass ∼20 M⊙), we compute a mass-loss rate of ∼10−5 M⊙ yr−1 for solar metallicity, comparable to the one found in M101.
Let us now estimate the four dimensionless parameters for each system. For P13, Fürst et al. (2018) determined orbital elements which indicate, in combination with the stellar parameters above, f ≳ 90%, q ∼ 15 and vorb = 100–200 km s−1 (for an inclination angle of respectively the maximum one set by the absence of eclipse, ∼55°, and 20°). At the bi-stability jump, the terminal wind speed should be between 0.7 and 1.3 times the escape velocity at the stellar surface, that is, v∞ = 150–300 km s−1, hence η = 1–3. According to Fig. 2, μmin = 6% for the observed LX ∼ 3 × 1039 erg s−1 is reached only if β ≳ 2 and for minimal speed ratios η ≲ 1.5. Stellar material at a sufficiently high rate could then be supplied via wind-RLOF, although marginally.
In M101, the mass function indicates that the accretor must be a BH, with q ∼ 2 for an intermediate orbital inclination (Liu et al. 2013). Their best fit to explain the Helium emission lines leads to a filling factor of at most f = 50% and a terminal wind speed of 1300 km s−1, three to four times larger than the orbital speed. This leads to μ ≳ 6%, in agreement with the mass-accretion rate required to reproduce the ULX luminosity with the stellar mass-loss rate observed. Since the star does not fill its Roche lobe at all, this ULX can only be explained with the wind-RLOF mass-transfer mechanism.
Vela X-1 has dimensionless parameters which lie in the same ranges as P13, but has a comparatively low stellar mass-loss rate and might suffer several effects which prevents a significant fraction of the mass captured from eventually being accreted. For instance, hydrodynamics simulations within the Roche lobe of the compact object suggest that, when the flow cannot radiate away the energy it gains as it is adiabatically compressed and/or shocked, the effective mass accretion rate can be lowered by a factor of approximately ten compared to the mass capture rate μṀ⋆ computed here (El Mellah et al. 2019). Since the wind speeds are comparable in ULXs and SgXBs, the flow density in Vela X-1 must be much lower than in P13 or M101, leading to a less efficient radiative cooling. Also, the very high X-ray luminosities in ULXs are expected to considerably ionize the wind, even for orbital separations as large as in P13 (Blondin et al. 1991; Manousakis & Walter 2015). At high ionization, the wind acceleration is inhibited which participates in the efficient accretion of the material entering the sphere of gravitational influence of the accretor. Interestingly, one study has already shown that a high-luminosity solution could exist when the wind was highly ionized (Ho & Arons 1987). For Vela X-1, the low-luminosity solution matches the observed luminosity of a few times 1036 erg s−1 but once the wind is in the high ionization stage, the X-ray luminosity is 2000 times larger, matching a ULX level, although such a flare has never been observed in Vela X-1 (but see Krticka et al. 2018, for the consequences for supergiant fast X-ray transients). To a lesser extent, the fraction of captured mass that ends up being accreted can also be altered by the clumpiness of the wind (Sundqvist et al. 2018; El Mellah et al. 2018). These combined effects might explain why many SgXBs such as Vela X-1 have luminosities much lower than the Eddington luminosity of a NS or a stellar-mass BH, in spite of similar dimensionless parameters.
4. Discussion and conclusions
We showed that efficient mass transfer without RLOF could occur in a binary system from a supergiant donor star to its compact accretor in SgXBs. When the wind is slow enough compared to the orbital speed to see its dynamics significantly altered by the Roche potential, it is beamed towards the accretor. Under these conditions, the wind density in the orbital plane is enhanced, which considerably increases the fraction of the stellar wind captured up to several tens of percent. If the mass-loss rate of the star is large enough, it can result in a mass available for accretion being supplied at a rate suitable to produce X-ray accretion luminosity of the order of the ones observed in ULXs. The final mass accretion rate, however, depends also on the compressibility of the flow, on the X-ray ionizing feedback and on the clumpiness of the wind being captured: the X-ray luminosity is determined by the innermost regions of the flow whose geometry and properties are influenced but not entirely set by the dynamics at the orbital scale.
Some ULXs are also expected to undergo RLOF mass transfer which is bound to be unstable when the mass ratio is as high as in P13 (King 2002; Rappaport et al. 2005). This mechanism is most reliable scenario when the stellar mass-loss rate is found to be smaller than 10−6 M⊙ yr−1 or for hyperluminous X-ray sources (Webb et al. 2017). Alternatively, in ULXs where the donor star has a sufficient mass-loss rate and is found to not fill its Roche lobe, such as M101 ULX-1, wind-RLOF provides a good description of the geometry of the flow at the orbital scale. Regardless of the nature of the wind-launching mechanism, the same arguments apply to the red supergiant donors identified in a few ULXs (Heida et al. 2015, 2016). Due to their low terminal speeds and high mass-loss rates, they are good candidates to transfer large amounts of mass via wind-RLOF (Mohamed & Podsiadlowski 2007; de Val-Borro et al. 2017) and to be well described by the formalism developed here, even for long orbital periods.
With this Letter, we emphasize the compelling need to improve our knowledge of the nature of the donor star and in particular of its mass loss to understand not only SgXBs but also the high-mass-accretion tail of the distribution, ULXs. In this attempt, observational campaigns have been carried out (Ptak et al. 2006; Tao et al. 2011; Grisé et al. 2012; Gladstone et al. 2013; Heida et al. 2014; López et al. 2017). Theoretical arguments have been made to constrain the donor star but they often presuppose a RLOF mass transfer and thus might not hold for ULXs in general (Karino 2017). If the stellar mass-loss rate is too low or the source too bright (typically, hyperluminous X-ray sources), wind-RLOF cannot channel enough matter, but otherwise, when the wind is slow enough, it is a fully viable scenario to enhance the mass-transfer rate.
In several ULXs, the presence of a disk has been inferred from super-orbital modulations or systematic spinning-up of the NS (e.g., in P13, Fürst et al. 2018). A disk can form only if the wind is slow enough (Illarionov & Sunyaev 1975) but in a pure wind-accretion situation, the mass-accretion rate increases quickly when the wind speed decreases. Tutukov & Fedorova (2016) noticed that in IC 10 X-1 and NGC 300 X-1, two systems where a stellar mass BH accretes from a Wolf-Rayet companion, no wind speed could explain both the accretion disk and the limited X-ray luminosity of 1038 erg s−1. The wind-RLOF mechanism, fully compatible with the formation of a wind-captured disk while not necessarily leading to large mass-accretion rates, solves this issue (El Mellah et al. 2019).
Last, since this mechanism leads to enhanced mass-transfer rates while still being stable, it could have important consequences on population synthesis of binary systems. The results presented here provide the community with estimates for the mass-transfer rate as a function of a limited number of dimensionless parameters.
Acknowledgments
IEM is grateful to Marianne Heida and Natalie Webb for insightful exchanges on the observational features of ultraluminous X-ray sources and for their comments and suggestions on this Letter. IEM wishes to thank Andreas Sander and Jorick Vink for their estimates on the stellar mass-loss rates of hot stars. IEM has received funding from the Research Foundation Flanders (FWO) and the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 665501. IEM and JOS thank the Instituto de Física de Cantabria for its hospitality and for sponsoring a meeting which brought together the massive-star and X-ray binary communities. This research was supported by FWO and by KU Leuven Project No. GOA/2015-014 and by the Interuniversity Attraction Poles Programme by the Belgian Science Policy Office (IAP P7/08 CHARM).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., & Al, E. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Stevens, I. R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Falanga, M., & Stella, L. 2008, ApJ, 683, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Oskinova, L., Lobel, A., & Hamann, W. R. 2017, A&A, 606, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brightman, M., Harrison, F. A., Fürst, F., et al. 2018, Nat. Astron., 2, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Carpano, S., Haberl, F., Maitra, C., & Vasilopoulos, G. 2018, MNRAS, 476, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Colbert, E. J. M., & Mushotzky, R. F. 1999, ApJ, 519, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Coley, J., Pottschmidt, K., Corbet, R., et al. 2018, in 42nd COSPAR Scientific Assembly, COSPAR Meeting, 42, E1.10 [Google Scholar]
- Corbet, R. H. D., & Krimm, H. A. 2013, ApJ, 778, A45 [NASA ADS] [CrossRef] [Google Scholar]
- De Beck, E., Decin, L., de Koter, A., et al. 2010, A&A, 523, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Karovska, M., Sasselov, D. D., & Stone, J. M. 2017, MNRAS, 468, 3408 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, L., Hony, S., De Koter, A., et al. 2006, A&A, 456, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., De Beck, E., Brünken, S., et al. 2010, A&A, 516, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotan, C., & Shaviv, N. J. 2011, MNRAS, 413, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Edgar, R. G. 2004, New Astron. Rev., 48, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., & Casse, F. 2015, MNRAS, 454, 2657 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., & Casse, F. 2016, MNRAS, 467, 2585 [Google Scholar]
- El Mellah, I., Sundqvist, J. O., & Keppens, R. 2018, MNRAS, 475, 3240 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Sander, A. A. C., Sundqvist, J. O., & Keppens, R. 2019, A&A, in press, DOI:10.1051/0004-6361/201834498 [EDP Sciences] [Google Scholar]
- Fürst, F., Walton, D. J., Harrison, F. A., et al. 2016, ApJ, 831, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Fürst, F., Walton, D. J., Heida, M., et al. 2018, A&A, 616, A186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilfanov, M., Grimm, H.-J., & Sunyaev, R. 2004, Nucl. Phys. B Proc. Suppl., 132, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Gimenez-Garcia, A., Shenar, T., Torrejon, J. M., et al. 2016, A&A, 591, 25 [Google Scholar]
- Gladstone, J. C., Copperwheat, C., Heinke, C. O., et al. 2013, ApJS, 206, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Grisé, F., Kaaret, P., Corbel, S., et al. 2012, ApJ, 745, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Heida, M., Jonker, P. G., Torres, M. A., et al. 2014, MNRAS, 442, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Heida, M., Torres, M. A., Jonker, P. G., et al. 2015, MNRAS, 453, 3510 [NASA ADS] [CrossRef] [Google Scholar]
- Heida, M., Jonker, P. G., Torres, M. A., et al. 2016, MNRAS, 459, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, C., & Arons, J. 1987, ApJ, 316, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Israel, G. L., Papitto, A., Esposito, P., et al. 2017a, MNRAS, 466, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017b, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Karino, S. 2017, MNRAS, 4570, 4564 [Google Scholar]
- King, A. R. 2002, MNRAS, 335, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Krticka, J., Kubat, J., & Krtickova, I. 2018, A&A, 620, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Nugis, T., Vink, J. S., & de Koter, A. 2000, in Therm. Ioniz. Asp. Flows from Hot Stars, eds. H. Lamers, & A. Sapar, ASP Conf. Ser., 204, 395 [NASA ADS] [Google Scholar]
- Liu, J. F., Bregman, J. N., Bai, Y., Justham, S., & Crowther, P. 2013, Nature, 503, 500 [NASA ADS] [CrossRef] [Google Scholar]
- López, K. M., Heida, M., Jonker, P. G., et al. 2017, MNRAS, 469, 671 [NASA ADS] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., & Walter, R. 2015, A&A, 58, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2007, ASP Conf. Ser., 372, 397 [Google Scholar]
- Moreno, E., & Koenigsberger, G. 1999, Rev. Mex. Astron. Astrofis., 35, 157 [NASA ADS] [Google Scholar]
- Motch, C., Pakull, M. W., Soria, R., Grisé, F., & Pietrzyński, G. 2014, Nature, 514, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Sundqvist, J. O. 2018, MNRAS, 475, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, C., Middleton, M. J., & Fabian, A. C. 2016, Nature, 533, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ptak, A., Colbert, E., van der Marel, R., et al. 2006, ApJS, 166, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S. A., Podsiadlowski, P., & Pfahl, E. 2005, MNRAS, 356, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A. A. C., Fürst, F., Kretschmar, P., et al. 2017, A&A, 610, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N., Postnov, K., Kochetkova, A., & Hjalmarsdotter, L. 2012, MNRAS, 420, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Owocki, S. P., & Puls, J. 2018, A&A, 611, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swartz, D. A., Soria, R., Tennant, A. F., & Yukita, M. 2011, ApJ, 741, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Tao, L., Feng, H., Grisé, F., & Kaaret, P. 2011, ApJ, 737, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V., & Fedorova, A. V. 2016, Astron. Rep., 60, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 61 [Google Scholar]
- Walton, D. J., Fürst, F., Bachetti, M., et al. 2016, ApJ, 827, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, N. A., Guérou, A., Ciambur, B., et al. 2017, A&A, 602, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijers, R. A. M. J., & Pringle, J. E. 1998, MNRAS, 308, 207 [Google Scholar]
All Figures
 |
Fig. 1. Slices in the orbital plane with the stellar center as the origin and the orbital separation as the length scale. The solid black line shows the contour of the Roche potential at the first Lagrangian point L1. The color map shows ρ/ρiso, the local relative density enhancement with respect to a mass density ρiso evolving with the reverse of the distance to the stellar center and scaled such that it has the same median value as the density ρ we measure. The upper panel is representative of the shape of the flow in Vela X-1 (and possibly P13) while the lower panel is adapted to parameters compatible with M101. The white area stands for the capture region, where material can be accreted, given by the accretion radius in the top panel and the Roche lobe in the bottom panel. The gray area is the wake of the accretor that our simulations do not cover. We note the much larger density enhancement in the bottom panel where the flow is also much more structured compared to that in the top one. |
| In the text | |
 |
Fig. 2. Logarithmic color maps of the fraction μ of stellar wind captured by the accretor as a function of the stellar filling factor and of the ratio of the terminal wind speed by the orbital speed. Left panel: (resp. right) column is for β = 1 (resp. β=2). Upper panel: (resp. lower) row stands for a mass ratio of 2 (resp. 15) typical of a BH (resp. a NS) accreting from a supergiant companion. From white to black, the fraction of stellar material captured varies by more than two orders of magnitude, with the configurations in green (and white) being more susceptible to giving large X-ray luminosities than the regions in red (and black). |
| In the text | |
 |
Fig. 3. Comparison of the mass-transfer rates we measure as a function of η (solid lines) to the BHL mass-accretion-rate formula (dashed lines) for a filling factor of 90% and mass ratios of 2 (upper panel) and 15 (lower panel). The BHL prescription leads to mass-accretion rates much lower than the mass-transfer rates we derive, sometimes by more than an order of magnitude. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



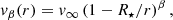
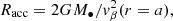
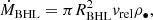
![$$ \begin{aligned} \mu _{\rm BHL}=\frac{\left(1+q\right)/q^3}{\eta \left(1-f\mathcal{E} \right)^{\beta }\left[1+\left(\eta \left(1+q\right)\left(1-f\mathcal{E} \right)^{\beta }/q\right)\right]^{3/2}}, \end{aligned} $$](/articles/aa/full_html/2019/02/aa34543-18/aa34543-18-eq6.gif)