| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834056 | |
| Published online | 24 January 2019 | |
Asteroid cratering families: recognition and collisional interpretation
1
Department of Mathematics, University of Pisa,
Largo Pontecorvo 5,
56127
Pisa,
Italy
2
Serbian Academy Sci. Arts,
Kneza Mihaila 35,
11000
Belgrade,
Serbia
e-mail: zoran.knezevic@sanu.ac.sr
3
IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06,
Univ. Lille, 77 av. Denfert-Rochereau,
75014
Paris,
France
e-mail: fspoto@oca.eu
4
Department of Physics, University of Pisa,
Largo Pontecorvo 3,
56127
Pisa,
Italy
e-mail: paolo.paolicchi@unipi.it
Received:
9
August
2018
Accepted:
17
November
2018
Aims. We continue our investigation of the bulk properties of asteroid dynamical families identified using only asteroid proper elements to provide plausible collisional interpretations. We focus on cratering families consisting of a substantial parent body and many small fragments.
Methods. We propose a quantitative definition of cratering families based on the fraction in volume of the fragments with respect to the parent body; fragmentation families are above this empirical boundary. We assess the compositional homogeneity of the families and their shape in proper element space by computing the differences of the proper elements of the fragments with respect to the ones of the major body, looking for anomalous asymmetries produced either by post-formation dynamical evolution, or by multiple collisional/cratering events, or by a failure of the hierarchical clustering method (HCM) for family identification.
Results. We identified a total of 25 dynamical families with more than 100 members ranging from moderate to heavy cratering. For three families (4, 15 and 283) we confirm the occurrence of two separate cratering events, while family (569) Misa is a mixed case, with one cratering event and one fragmentation event. The case of family 3 remains dubious, in that there could be either one or two collisions. For family 20, we propose a double collision origin, not previously identified. In four cases (31, 480, 163 and 179) we performed a dedicated search for dynamical resonant transport mechanisms that could have substantially changed the shape of the family. By using a new synthetic method for computation of secular frequencies, we found possible solutions for families 31, 480, and 163, but not for family 179, for which we propose a new interpretation, based on a secular resonance contaminating this family: the family of 179 should be split into two separate clusters, one containing (179) itself and the other, family (9506) Telramund, of fragmentation type, for which we have computed an age.
Key words: minor planets, asteroids: general / celestial mechanics / chaos / methods: numerical
© ESO 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The method that we proposed to study asteroid families (Milani et al. 2014) and applied in our research over the last few years (Knežević et al. 2014; Spoto et al. 2015; Milani et al. 2016, 2017) is as follows. We first compute (and periodically update) very large catalogs of asteroid proper elements, using the synthetic method (Knežević & Milani 2000). We then use a modified form of the hierarchical clustering method (HCM; Zappalà et al. 1990) to identify clusters, representing density contrast in the three-dimensional (3D) space of proper elements a, e, sinI. After confirming some of the clusters with a statistical significance test, we proclaim these as dynamical families. The classification is updated when the catalogs of proper elements are increased.
In the second stage we add physical observation data (absolute magnitude and albedo) to estimate ages of these families by exploiting nongravitational perturbations, which are size dependent. This sometimes forces the splitting of dynamical families into multiple collisional families of different ages. In the third stage, specific to this paper, we use available physical data to remove interlopers, that is background asteroids randomly present in the volume occupied by the families.
This complex procedure is used because the amount of information contained in the proper elements is greater (by a factor of at least 5; see Table 1 in Milani et al. 2014) than the information contained in consistent catalogs of physical observations: the proper element sets are both more accurate and more numerous. Because families are statistical entities, the number of data records matters more than anything else. In particular, the proper element catalogs contain much smaller asteroids than the ones for which good physical observations are available, for obvious observational selection effects: this is especially important in the context of the present paper, which is about cratering families, that typically have smaller members.
As a result of this procedure, we believe we can claim that our work is mathematically sound in all steps, including the computation of proper elements, the application of HCM, and the computation of ages. However, the use of rigorous mathematics is a necessary condition for the successful application of a mathematical model in science, not a sufficient one. We need to test whether the use of our sophisticated model actually leads to a better understanding of the collisional history of the asteroid belts. The question to be addressed is whether our methods produce superior results to the ones obtained with simpler models: lower-accuracy proper elements (e.g., analytical rather than synthetic), and simpler clustering methods (e.g., the ones not including a test of the statistical significance of the families).
The main goal of this paper is to display a large set of data, summarized in tables, describing detailed properties of the collisional events giving rise to the cratering families (in full or, in some cases, in part). If these data are meaningful, then not just the classification, which is the existence of the most important families (e.g., the ones with > 100 members) and the decomposition of some of them in multiple collisional families, but even details of the shape of the families in the space ofproper elements contains information constraining the collisional event itself. Although we cannot claim that all our families have “good shapes”, because some problematic cases still need more data and more work, the fact is that the large majority of them are compatible with simple and physically possible collisional models, for example, with ejection velocities of the same order of magnitude as the escape velocity from the parent body.
Although the arguments above can apply to the outcomes of all collisional events, those pertaining to cratering type, on which we are focusing in this paper, are especially interesting for three reasons: first, by forming families with smaller members, we have found many more cratering families than previously known. Second, by definition (see Sect. 2), a cratering event leaves a parent body with essentially the same collisional cross section as before, and therefore it is normal that another crater can be formed, leading to overlapping families. Third, a cratering event must generate a distribution of relative velocities strongly anisotropic with respect to the parent body, and this should be detectable from the family shape. In some cases we have not found the expected anisotropy, but either an overly small one, which can suggest a multiple collisional origin, or an overly large one, corresponding to unrealistic escape velocities, indicating a post-collision dynamical evolution.
Obtaining such a well behaved original escape velocity distribution is by no means guaranteed. There are necessarily cases in which the distribution is strange, even bizarre, and these cases are analyzed to find an explanation. Two possible causes for such strange distributions are already clear, namely the possibility of detecting a multiple collisional origin that was not previously recognized, and the presence of a dynamical mechanism, such as resonances and chaos, leading to an important change in the shape of thefamily after its formation. A third possibility, which has been largely overlooked so far, is that statistical methods, HCM not excluded, cannot provide absolute certainty on the membership of families; in some critical cases not even on their statistical significance. The presence of interlopers in any family is a well known phenomenon that needs to be accounted for as well as possible (Radović et al. 2017), but in few cases substantial corrections to the family membership may be needed, including merging and splitting of previously identified families. In this paper we deal with examples of both merge and split corrections.
The paper is organized as follows: in Sect. 2 we discuss the quantitative definition of cratering and present our proposed list of cratering families. The data include the fraction (by volume) of fragments with respect to the total reconstructed volume of the parent body, and the data on interlopers which could be recognized. In Sect. 3 we measure the asymmetry of the shape of the family in proper element space, and discuss its interpretation. In Sect. 4 we discuss possible dynamical, statistical and/or collisional interpretation of family shapes which do not have a simple interpretation in terms of original escape velocities. In Sect. 5 we draw our conclusions and outline possible future work. In Appendix A we present an empirical model showing that the initial change in the proper semimajor axis (with respect to the parent body) can be either correlated or anticorrelated with the Yarkovsky secular effect. In Appendix B we present a compilation of the data on the age of the collisional events in the cratering families, which are mostly not new results but collected for the convenience of the reader from our previous papers (Spoto et al. 2015; Milani et al. 2016, 2017); two new ages have been computed for the families of (87) Sylvia and (9506) Telramund.
2 Recognition of cratering families
An asteroid family is of cratering type if it is formed by a collision leaving a parent body with the same impact cross section and a new, large crater on its surface. It is of fragmentation type if the largest fragment is significantly smaller than the parent body.
In practice, it is comparatively easy to label some families as cratering type, especially when concerning the largest asteroids (like (4) Vesta, (10) Hygiea, and (2) Pallas) because of a huge gap in size between the namesake asteroid and the other family members.
It is also easy to label some families as fragmentation type, like the one of (24) Themis, because it can be estimated that the parent body was approximately of diameter D = 284 km against D = 202 km of (24) Themis itself; that is, the parent body was significantly larger. An example of total fragmentation is the family of (158) Koronis, named after an asteroid which is not even the largest remnant but just the one with the lowest number. (158) Koronis itself has D = 48 km and the parent body can be estimated to have had D = 96 km.
There are, of course, intermediate cases in which the recognition of cratering vs. fragmentation families is not obvious.
Historically, at the beginning of the research on asteroid families, no cratering families were known, because the first identified families consisted only of comparatively large members (Hirayama 1918; Brouwer 1951). Later, cratering families began to appear because of the discovery of smaller and smaller asteroids. The most striking example is the family of (4) Vesta which appeared as a “tiny” family (7 members) in Zappalà et al. (1990), then as a “small” family (64 members) in Zappalà et al. (1995). Later Knežević & Milani (2003) argued that the Vesta family should have thousands of members, almost all smaller than D = 7 km, with a very large spread in proper a, more than 0.1 au, although the numbers were so large that the methods of classification available at the time were not adequate. Indeed, with the multistep HCM classification method of Milani et al. (2014), the Vesta family was found to have 7865 members, and in the latest classification update is seen to have 10 612 members, with a spread in proper a of 0.246 au. Both properties are now fully understood: the small size of fragments, because of the limit of the size of fragments from a cratering event (controlled by the depth, not the diameter of the crater), and the spread in proper a because of the Yarkovsky effect (changing proper a in a way proportional to the time elapsed from the collision and inversely proportional to the fragment diameter).
Now, with our most recent classification including 130 933 members in 118 families, we can find many cratering families not previously recognized as such. In light of these new findings however a clear criterion for cratering families needs to be defined.
We propose a method to identify cratering families by using the fraction (in volume) of fragments with respect to the total (including the parent body). This fraction needs to be computed after removing from the membership list both interlopers (identified by means of physical observations showing incompatible composition) and outliers (excluded from the V-shape fit used to estimate the age; see Spoto et al. 2015). These removals may significantly affect the fraction of fragments, because the family has a steeper size distribution with respect to the background.
2.1 List of cratering families
The results of the analysis of the 66 families with more than 100 members in our current updated classification1 are summarized in Table 1. The horizontal lines split into cratering with age, young (<100 Myr of age) cratering, heavy cratering fv > 0.125, and cratering without age.
Included in the table are all the cases where the fraction in volume of the fragments (with respect to the estimated volume of the parent body) is fv < 0.22; this could be a critical value for the definition of cratering. The adopted boundary may appear somewhat arbitrary, but the fact is that we have found a gap in the values, that is, there are no families with 0.22 < fv < 0.26. Hence, we can define families of cratering type those with fv < 1∕4 and families of fragmentation type as those with fv > 1∕4. Above this value we have a region with few fv values, extending up to 0.50. Due to the lack of an explicit model justifying the choice of a very specific value for this boundary, we propose also to define heavy cratering families as those with 1∕8 < fv < 1∕4 and marginal fragmentation families as those with 1∕4 < fv < 1∕2. A family with 1∕8 < fv < 1∕4 still has most of the mass, and therefore most of the internal structure, in the parent body and the impact cross section is not significantly changed; however we should expect that most of the original surface has not been preserved.
In summary, we propose a list of 15 cratering families for which we have computed (in one of our previous papers) an age, 4 heavy cratering families (also with age), and 6 cratering families for which we have no age estimate. Moreover there is the already mentioned family of (2) Pallas which can be recognized as cratering even though it has only 62 members (even after merging 45 members of the family of (2) with the 17 members of the family of (14916) 1993 VV7, because they are separated by the three body resonance 3J-1S-1A).
The family of (87) Sylvia is strongly depleted by mean motion resonances, especially 9∕5 and 11∕6 with Jupiter, and the low a side appears to be missing entirely. Nevertheless it must belong to the cratering type, although the current fv < 0.01 might have originally been larger by a factor of several. The age of this family has been computed in this paper at 1120 ± 282 Myr; see Appendix B.
The cratering families for which we have not computed an age include those of (179) Klytaemnestra (Sect. 4) and of (778) Theobalda; an age of 6.9 ± 2.3 Myr was computed for the latter using two methods specific to very young families (Novaković 2010). The other four families have ≤140 members and are not yet suitable for a reliable application of our V-shape method.
The four families we rate as marginal fragmentations are (808) Merxia (fv = 0.2669), (845) Naema (0.3045), (1118) Hanskya (0.3709) and (1128) Astrid (0.4020). All the other cases tested (37 families with > 100 members) have fv > 0.5, and are therefore to be considered of (nonmarginal) fragmentation type.
Table 1 is sorted by Col. 2, that is, by collisional family number. This is due to the possibility of Name Change (note: NC) when the namesake of the dynamical family is shown to be an interloper, as for families 194 and 110. In this case the new name is given by the lowest numbered member which is not an interloper: then the diameter, the fraction of fragments, the albedo, and the taxonomy refer to the new namesake.
Other notes in Tables 1 and 2 have the following meaning:2 ag = 2 distinct ages; NA = no age computed; HI = high proper inclination > 17°; OS = one sided V-shape; sat = included satellite family; sub = with subfamily; merg = two families merged because they form a single V-shape; Y = young families (age < 100 Myr); R = too recent (<10 Myr) for V-shape computation of age.
In Table 1 the family albedo is the albedo of the parent body, if available, otherwise the mean albedo of the members with albedo measurements. The taxonomy is given by large groups C, S, and V; I corresponds to intermediate albedo.
The most problematic result of Table 1 concerns the family of (569) Misa, because it contains a subfamily with namesake (15124) 2000 EZ39, and a much younger age (see Table B.2), but the identity of its parent body is unclear. If it were (569), then it would be a second cratering, and it should have analogous shape properties to the other craterings; see Sect. 3.1.
Cratering families.
2.2 Compositional homogeneity
Columns 3, 4 and 9 of Table 1 contain data that can be used to assess the homogeneity of the composition of the family. In most cases the families with a parent body belonging to the C complex of dark asteroids have an overwhelming majority of members with WISE data (Masiero et al. 2011) showing a low albedo, see for examples families 10, 31, 163, 283, 569, and 363. Families with a parent body belonging to the S complex of brighter asteroids, such as families 3, 15, 20, and 480, have a majority of bright members (the same for the V-type family 4), although the ratio bright/dark is not particularly large2.
There are some cases where the composition appears more mixed, for example families 5 and 686. For the dynamical family of prevalent type S with parent body (5) Astraea, physical observations suggest the presence of another family of type C asteroids locked in the same secular resonance g + g5 − 2 g6 as family 5, with parent body (91) Aegina (Milani et al. 2017). Parent body (91) is large, with WISE D = 105 km, and could not be a fragment of (5) due to both its size and its composition. Even if all the other 185 C-type interlopers in the dynamical family 5 were members of family 91 (which is not necessarily the case), family 5 would have fv = 0.0239, and would thereforse be of cratering type nonetheless. Another interesting example of cratering family which can be derived from physical observations inside a dynamical family is the one of (423) Diotima, which has been proposed in Masiero et al. (2013) and Milani et al. (2016), and appears as a subfamily of the family of (221) Eos formed by C-type interlopers3.
The family of (686) Gersuind is characterized by an intermediate albedo which does not allow a reliable subdivision into bright and dark. Apart from these two exceptions, for which an explanation is available, all the cratering families of Table 1 appear to be homogeneous, in the sense that they contain an acceptable fraction of interlopers.
Indeed, families are statistical entities defined by a contrast of density, formed by spreading fragments in a large volume of proper element space which could not have been empty before: these preexisting asteroids remain as interlopers, and can be detected by physical observations when the background is of a different taxonomic type from the prevalent family one. Taking into account that the membership of our “dynamical” families has been determined using only their proper elements, the a posteriori verification that the families are compositionally homogeneous, as much as can be expected, is a validation of our procedure; it confirms not only the existence of the families we have proposed, but also that our methods to terminate the aggregation of families are effective for our declared purpose of providing a reliable membership. We note that it would be relatively straightforward to use some method of classification giving many more members to the families, but then this property of compositional homogeneity could get lost.
3 Properties of cratering families
As discussed in Sect. 1, one of our goals is to show that not only is the composition homogeneous, but also the shape (in the proper element space) of the families is consistent with a possible original (immediately after the collision) distribution of the escape velocities of the fragments.
Please note that we cannot use the information from the distribution for the proper a of the family members because these are affected by nongravitational Yarkovsky (Spoto et al. 2015) and YORP (Paolicchi & Knežević 2016) effects acting over the age of the family. Therefore the distribution of proper a does not at all represent the original distribution of relative velocities in the direction along track (apart for the case of recent families, with age < 10 Myr), but mostly contains information which can be used to compute the ages.
On the contrary, the proper elements e and sinI computed today may preserve information on the original distribution of escape velocities, mostly in directions orthogonal to the velocity of the parent body. This should occur in most cases, although not for all families, because there are dynamical mechanisms allowing a secular change also of proper e and/or sinI. Moreover, it is necessary to remember at this point the distinction between dynamical and collisional families: for example, if a dynamical family contains two collisional families, there have been two collisions, therefore two escape velocity distributions contributingto the present shape of the family.
3.1 Asymmetry of velocity distribution
Table 2 contains information, for each cratering family we have identified, on the distribution of the differences δe and δ sin I in the proper elements e, sinI between the fragments and the current position of the major body. More precisely, the columns list family number, mean differences in e, sin I, corresponding STandard Deviations, Converted Escape Velocity, and notes (explained in Sect. 2.1). Giventhat the families are all of cratering type, that is, the fraction of fragments is <1/4 in volume (even less in mass, since the fragments should be more fractured, and therefore less dense) the difference between the current position (in proper e, sinI) of the family namesake and the original position of the parent body should be significantly smaller.
For each family we have computed the two lowest-order moments of the δe and δ sin I distribution, namely mean and variance, and we show in the table the mean and the standard deviation for each of the two proper element distributions, centered at the parent body. Higher moments of these distributions could be computed easily, but let us first understand the information contained in the first two.
The factthat these distributions of δe and δsinI are representative of the original ejection velocities of the fragments is not an assumption but something to be tested case by case. In particular, a necessary condition for this interpretation to be legitimate is that both the mean and the standard deviation are of the same order of the escape velocity from the parent body. Therefore, in the table we also list the estimated escape velocity, converted into 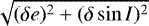 by the Zappalà et al. (1990) metric (converted escape velocity, CEV). Please note that this conversion is valid only “on average”, because the actual value of the difference in orbital elements due to a given escape velocity (outside of the gravitational sphere of influence of the parent body) actually depends on short-periodic quantities such as the true anomaly f and the argument of latitude ω + f at the time of the impact. For this reason, and also because the masses of the parent bodies are only approximately known, a difference between the mean δe, δ sin I and the CEV, by a factor of approximately 2, is not a problem, while differences of an order of magnitude require an explanation.
by the Zappalà et al. (1990) metric (converted escape velocity, CEV). Please note that this conversion is valid only “on average”, because the actual value of the difference in orbital elements due to a given escape velocity (outside of the gravitational sphere of influence of the parent body) actually depends on short-periodic quantities such as the true anomaly f and the argument of latitude ω + f at the time of the impact. For this reason, and also because the masses of the parent bodies are only approximately known, a difference between the mean δe, δ sin I and the CEV, by a factor of approximately 2, is not a problem, while differences of an order of magnitude require an explanation.
In principle, values of the mean and/or of the STD of δe and/or δ sin I which are larger (by a significant factor) than the conversion of the escape velocity, imply some dynamical evolution occurring after the family formation. The dynamical evolution mechanisms, acting on proper e and/or sin I of a large fraction of family members, would then need to be identified; otherwise, the family definition should be reconsidered.
On the other hand, values that are too small, such as those one order of magnitude smaller than the conversion of the escape velocity, are unlikely to occur by chance in a single collisional process. The reason for this is simply the formula 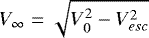 , where V0 is the launch velocity of the fragment from the crater, Vesc is the escape velocity from the surface of the parent body, and V∞ is the velocity of the fragment after leaving the gravitational well of the parent body. This means that values of V∞ much lower than Vesc are unlikely, although they are not strictly impossible4. Therefore these cases should be investigated for possible interpretation as families generated by two (or more) cratering events.
, where V0 is the launch velocity of the fragment from the crater, Vesc is the escape velocity from the surface of the parent body, and V∞ is the velocity of the fragment after leaving the gravitational well of the parent body. This means that values of V∞ much lower than Vesc are unlikely, although they are not strictly impossible4. Therefore these cases should be investigated for possible interpretation as families generated by two (or more) cratering events.
Indeed, from the computation of the ages of the families (see Appendix B), we do know some cases of families with two different ages, computed from the IN (smaller proper a) and OUT (larger a) side of the V-shape in the (a, 1∕D) plane. This includes three cratering families: 4, 15, and 283; moreover, we know two dubious cases for the cratering families 3 and 1222. In these cases we have therefore computed separate values of mean and STD for the proper a > a0 and for the a < a0 portions of the family, where a0 is the proper a of the parent body.
We have not included the family of (2) Pallas in this table, because it is too depleted by mean motion resonances (of the three-body type), which at such a high inclination (sinI ~ 0.54) open large gaps.
We now briefly commenting on some cases with asymmetry that is either too large or too small.
Asymmetry of cratering families.
3.2 Families with two ages
For the three cratering families (4, 15, 283) already known to have two ages (from the different slopes of the V-shape in a) the separation of the IN and OUT sides of the family (see the symbols such as 4+ and 4− in the first column of Table 2) nicely confirms, with clearly distinct mean values, the existence of two separate jets with very different directions in proper element space: see for example, Fig. 1, which visually confirms the interpretation of the dynamical family of (283) Emma as two well separated jets. The same applies to the family of (4) Vesta; see Fig. 12 of Milani et al. (2014).
For the family of (3) Juno, which was a dubious case of two ages from the V-shape (Spoto et al. 2015), the data on the asymmetry do not confirm the interpretation as two separate collisional families. The values for the momenta of the distribution of proper elements are somewhat low, although by less than a factor 3 for sin I, and there isno improvement if the family is split into IN and OUT side (see rows marked 3+ and 3−). Given that the significance of the separation into two ages is marginal (about 1.2 STD; see Table B.1), this case remains dubious.
For the family of (569) Misa, as shown in Table 2, the asymmetry is indeed too low in e, sin I for it to be the outcomeof a single cratering event. On the other hand, we do know that this family was formed by two separate collisions; see the figure in the (a, 1∕D) plane showing a W shape rather than a V (Milani et al. 2016; Fig. 1). There is therefore another collisional family, much younger than the other one (see Table B.2). We have separated the family 15124 from 569 using this W-shape; see the top panel of Fig. 2. Admittedly, a few members from 569 could be attributed to 15124, but this does not affect the results because our 15124 family has many more members.
If family 15124 were the outcome of a second cratering on (569), then it should have shown an appropriate asymmetry of δe and δ sin I with respect to (569). As a matter of fact, as shown in the bottom panel of Fig. 2, (569) is right in the center of the distribution of 15124 in the proper (sinI, e) plane. For the family 15124 the mean differences with respect to (569) are mean(δe) = −0.00004, mean(δsinI) = −0.003, by far too small with respect to the escape velocity from (569), with CEV = 0.0015. From this we conclude that family 15124 is not a second cratering but a fragmentation. The total volume of the known members of 15124 corresponds to a sphere of diameter D ≃ 25 km, too large to be an ejecta from a crater on (569), which is a body with D ≃ 73 km.
Neither the second cratering on (569) nor the fragmentation of a first generation fragment from (569) are therefore possible. The only other explanation which we could find is that family 15124 is a complete fragmentation of a background object, which by unlikely coincidence has a center in proper element space very close to the location of (569). Following a well known argument5 we are obliged to accept the latter explanation.
The 15124 family therefore appears to have nothing to do with (569), not even as a second-generation parent. The albedo of (569) is 0.0297 ± 0.001 (Tedesco et al. 2002), and that of (15124) is 0.077 ± 0.007 (Masiero et al. 2011), both well within the C-type range, but different enough to support the model we are proposing of a fully independent fragmentation family which is by chance overlapping a cratering family.
In the dubious case of the family of (1222) Tina, discussed in Milani et al. (2017), the hypothesis of a double collision origin is confirmed, as shown in the rows marked 1222+ and 1222−, by the presence of two very distinct jets. The value of mean(δe) is very high, but this can be interpreted as being due to the g − g6 secular resonance, which affects the family (Carruba & Morbidelli 2011), in particular in the form of anti-aligned libration states. This family still only has 107 members, and therefore no statistically robust conclusions can be made at this stage.
After handling these double-collision cases, the most prominent cases of anomalous values, both larger and smaller than the CEV by factors more that four, are shown in bold in Table 2.
 |
Fig. 1 Family of (283) Emma projected on the proper (a, sinI) plane. Red points represent family members, black points are background objects and blue crosses are objects in mean motion resonances. Position of (283) is marked by a large cyan cross. The two separate jets indicate a double collision origin. |
 |
Fig. 2 Top panel: family of (569) Misa is separated into a family 569 with 70 members (crosses encircled in red) and a family 15124 with 577 members (blue crosses; stars are also in mean motion resonances). Bottom panel: distribution of the family 15124 in the proper (sinI, e) plane, showing the central position of (569) (cyan cross) and the peripheral location of (15124), not necessarily representative of the position of the parent body. |
3.3 Overly large asymmetries
The most striking case of overly large value is the mean of δe for the family of (31) Euphrosyne. Since the asymmetry of the proper element distribution in the IN and OUT portions is obvious, in particular in the proper e, as shown by Fig. 3, we have computed the separate values for the two sides; see the rows 31+ and 31−. However, this separation has made the situation worse, in that the mean(δe) limited to the members with a < a0 has grown to the value of − 0.03, which is more than five times the value corresponding to the estimated escape velocity. In Fig. 3 we have plotted a running mean of the proper e: it shows that the distribution of e for a < a0 is completely different from the one for a > a0. This is even more interesting considering that the V-shape in (a, 1∕D) does not indicate two different ages for this family; see Table B.1 and the top panel of Fig. 7. This case needs to be investigated to find a suitable explanation, acting mostly on proper e, the asymmetry in sinI being less than the CEV (see Sect. 4).
The second largest asymmetry is in the δe of the family (480) Hansa: we had thought this depended upon lower accuracy of the proper e computed in this region, with large proper sinI and low proper e. This lower accuracy resulted from a failure to correctly identify the proper mode because other forced oscillations are larger (Carruba & Michtchenko 2009). After improving proper e using a form of frequency analysis, that is using as proper e the amplitude of the highest peak in the spectrum of esin(ϖ) in the range of periods between 50 000 and 70 000 y, the asymmetry was slightly increased. Therefore, the quality of the proper elements has been improved, especially for very low proper e, but this was not the problem. Neither mean nor RMS of e can be explained by ejection velocity, being larger by more than an order of magnitude, or by mean motion resonances in the model (there is 11∕4J at a= 2.649 au, but its effect is limited to a small portion of the family; see Fig. 8 (top)). We tried the separation IN/OUT, and found that the asymmetry is much more pronounced in the portion with a < a0, with mean(δe) as large as ~ 30 times the CEV. The value of mean(δe) is also too large also a > a0. There is less asymmetry in δ sin I, but also in this the two sides are different. This case therefore also needs an explanation for the peculiar δe distribution (see Sect. 4).
In the family of (179) Klytaemnestra, to explain the large asymmetry in proper e, we tried the separation IN/OUT, but the situation did not improve, actually the mean(δe) value in the row 179+ is even larger than the one for the entire family, and is approximately five times the CEV. Moreover, as already mentioned in Milani et al. (2017; Sect. 5.3), the V-shape in (a, 1∕D) appears impossible to model collisions. The interaction with the Eos family has to be considered to provide an explanation, see Sect. 4.
There are two cases in which the asymmetry is marginally high, for example between 3 and 4 times the CEV, namely families 410 and 163.
One unusual feature of the family of (410) Chloris is that the proper sin I of the parent body (410) is the top value in the family, which contributes to the comparatively large negative mean(δsinI). We note that there is another family, (32418) 2000 RD33, separated from 410 in proper a by the three-body resonance 3J-1S-1A. The range of values of both proper e and sinI for 32418 is included in the corresponding ranges for 410. Therefore we have considered the possibility that these two families arise from a single cratering event on (410): the merged family would still be of cratering type, and would have a somewhat smaller asymmetry in δ sin I. However, we do not think there is convincing evidence for this merger; for example, the average WISE albedos of the two families are both uncertain and only marginally consistent6. We can only wait for more data to make a decision, either as more and more accurate physical observations or as new family members. The family (410) without this merge has only 120 members, and therefore we do not think it is useful to investigate this case in depth.
In Spoto et al. (2015) the two families of (163) Erigone and (5026) Martes have been considered together for the purpose of computing an age, since they form a single V-shape with the same age; see Table B.2. We have therefore merged them for computing the entry in Table 2: together they give a somewhat large asymmetry, with mean(sinI) equal to 3.07 times the CEV. If the family of (163) were considered separate from the one of (5026), the largest asymmetry parameter, which is mean(δsinI), would increase from 3.07 to 3.33 times the CEV. Therefore the analysis of the family shape in proper (e, sinI) supports the merger. This case should be analyzed to provide an explanation for the peculiar δe distribution (see Sect. 4).
 |
Fig. 3 Family of (31) Euphrosyne projected on the proper (a, e) plane; the big blue dot shows the position of the parent body (31) Euphrosyne. The red line is the running mean of the values of proper e vs. proper a, for the members of the family, showing the substantial jump to lower values in the IN side of the family. |
3.4 Overly small asymmetries
One possible solution for the cases in which the asymmetry parameters are too low is to find indications for a possible double collision. There is onecase in which this is possible: for the family of (20) Massalia. Indeed, the asymmetry is somewhat low, equal about one third of the CEV forδsinI. However, a close look at the distribution of the proper elements of the family members, especially in the proper (sin I, e) plane (Fig. 4), shows a halo at lower e, higher sin I. This indicates a second collisional family, with positive mean(δsinI) and negative mean(δe), compensated for the larger collisional family with opposite asymmetry. Unfortunately, the second family appears to be heavily superimposed, to the point that we currently can neither separate it nor compute a second age.
For theonly other case with overly low asymmetry (by a factor 9 in both coordinates), the family of (96) Aegle, we currently have no explanation. On the other hand, this family has too few members (only 120) to understand details of its structure. A solution of this case may be found when the number of members has grown to ~200 or more.
 |
Fig. 4 Family of (20) Massalia projected on the proper (e, sinI) plane, showing a halo in the lower right quadrant (with respect to the position of the parent body, marked by the cyan cross). Points are marked as in Fig. 1. |
4 Family shapes in need of dynamical explanation
After solving, or at least proposing a solution for most of the cases of anomalous asymmetry, we are left with only three cases with overly large asymmetry, namely families 31, 480, 179, and one case with marginally large asymmetry, family 163. In this section, we discuss possible collisional and/or dynamical interpretation of these four cases.
4.1 Family of (31) Euphrosyne
The main dynamical feature of family 31 is the presence of the strongest linear secular resonance g − g6 which cuts the family; see Carruba et al. (2018a; Fig. 4). According to our new computations of the location of the secular resonances, family 31 is cut by the g − g6 into two parts, very nearly corresponding to the IN and OUT sides with respect to the parent body. Figure 5 shows the resonance strip, which has been computed by means of a new synthetic theory for the secular frequencies g and s; the fixed value of the third coordinate is sinI = 0.45 for the top plot and e = 0.19 for the bottom one.
The method to compute these frequencies as a smooth function of proper (a, e, sinI) is a generalization of the one used in Milani (1993), and is fully described in Knežević & Milani (in prep.). The modeling of g, s as smooth functions (in fact polynomials) is possible only after removing the asteroids in the region that are strongly affected by mean motion resonances, as detected by the estimated Lyapounov Characteristic Exponent and/or instability of proper a. The lines drawn in the figure are level lines of the best fit polynomial representation of g − g6.
The parent body (31) Euphrosyne is very close to the secular resonance, therefore fragments ejected from it with δa = a − a0 < 0 in most cases end up in the g − g6. Even if the ejection velocity is large enough to put the fragment on the other side of the resonance, the fragment is likely to have a secular da/dt > 0 due to the Yarkovsky effect. This is because the presence of a negative V-base (see Fig. 7, top) in the V-shape plot may indicate that δa < 0 corresponds mostly to prograde spin (see Appendix A). Therefore, even the fragments which are not originally inserted in the secular resonance end up falling into it as a result of the Yarkovsky effect, and in both cases most of them may have been pushed by g − g6 to high eccentricities (such as 0.5), leading to close approaches to Jupiter and subsequently to ejection from our solar system, and the formation of interstellar asteroids. The occurrence of instability for ejecta from (31) has been studied with extensive numerical simulations by other authors, such as Masiero et al. (2015), with the result that 80% of the test particles entering the g − g6 resonance are evacuated from the family region into either near-Earth of Jupiter-crossing orbits. Given our analysis below, this estimate of survival rate may even be optimistic7.
The fragments ejected with δa > 0 are mostly with retrograde spin and secular da/dt < 0 due to Yarkovsky. Even in this case, there are two possible outcomes: if they are ejected initially to a proper a > 3.174 au, where the strong three-body resonance 5J-2S-2A is located, they come back to lower a until they meet this resonance, becoming very strongly chaotic and also, in most cases, being ejected from our solar system. The fragments ejected with smaller δa also migrate to lower values of a and therefore end up in the g − g6 resonance.
Figure 6 shows the output of a numerical experiment which refers to this case: the initial osculating a = 3.165 au is larger than that of the parent body (a0 = 3.1561 au) and the Yarkovsky secular drift is da/dt = −2 × 10−4 au/Myr, a value corresponding to a C-type asteroid with diameter D ≃ 3 km and retrograde spin; see Table B.2.
When the body enters the g − g6 secular resonance (at ≃ +50 Myr of the orbit propagation) the smoothed eccentricity at first oscillates between values very close to 0 and 0.3, and later between 0.1 and 0.4. At + 76 Myr it also enters in the three-body resonance inside the secular one, and e grows even more, oscillating between 0.2 and 0.5. Starting at + 84 Myr there are close approaches to Jupiter, until the last at + 91.35 Myr results in ejection to a hyperbolic orbit; this example ends up in an interstellar asteroid, after a time span an order of magnitude smaller than the age of family 31.
As shown by this and other examples, entering into the g − g6 secular resonance, both from the lower a edge and from the higher a one, is like Swiss roulette8, in which most of the objects are lost in interstellar space. The dynamics due to this interaction of resonances and Yarkovsky effect is too complex to be quantitatively modeled, but from the qualitative point of view it is clear that the original family 31 must have been much larger than it is today, with the majority of the original members now being interstellar.
As for the asymmetry in proper e, when the g − g6 resonance is crossed from higher to lower proper a as in Fig. 6, there is no “transport” along the resonance but rather there could be a selection effect, by which the objects exiting g − g6 at high eccentricity are no longer there, while the ones lucky enough to exit at low to moderate eccentricity form the IN side of the family. This IN side of 31 has a proper element span 0.149 < e < 0.206 and a mean of 0.177; we do not have a quantitative theory explaining these values, not even approximately, but qualitatively it is possible that the passage across the resonance g − g6 with da/dt < 0 leads to lower proper e for a selected minority of survivors. It is not possible to test this by a Monte Carlo approach, because it is not appropriate to select the initial conditions randomly, but it is necessary to take into account the asymmetry of the ejection velocities and the correlation between change in orbital elements and the orientation of the spin axis; this is difficult to model in a quantitative and reliable way.
The problem which is not solved by the model above is that the number density as a function of proper a is highly variable, with two peaks around a = 3.12 and 3.16 au. The gap around a = 3.145 is due to the g − g6 resonance, not to the YORP eye, which would be located in a nearly empty region of comparatively large bodies (Paolicchi & Knežević 2016).
A possible way to explain this structure is to assume that the age computed by the V-shape of Fig. 7 (top) only refers to the largest remnants of an ancient family, with an age estimated at ≃ 1.2 Gyr, consistent with a YORP age which is determined by a gap around D ≃ 14 km (see Paolicchi et al. 2018); to the contrary, the gap occurring also at much smaller diameters around a = 3.145 au has nothing to do with the YORP effect, but with the dynamical removal by the g − g6 resonance.
The alternative explanation is that the concentrations of smaller bodies belong to more recent collisional families, which in Fig. 7 (top) are somewhat detached from the larger members forming the V-shape. Figure 7 (bottom) shows one possible, but by no means unique, decomposition in which smaller members form a V-shape with higher slopes, and therefore lower ages, different between the IN and the OUT side. For the OUT side the inverse slope 1∕S= 0.478 ± 0.035, corresponding to an estimated age of 778 ± 165 Myr, on the IN side 1∕S = −0.259 ± 0.007, corresponding to an age of 422 ± 85 Myr. Since the discordance of the ages implies that these two possible families, one on the IN side, that is g − g6 < −2 of the secular resonance, the other on the OUT side, that is g − g6 > +2 “/y, could have had different parent bodies, with different proper e. Moreover, the members of the two possible families currently found would not have crossed the g − g6 resonance: the ones that had entered the resonance might have been eliminated by the Swiss roulette.
We acknowledge that we have found two possible interpretations of the collisional and dynamical history of the dynamical family 31, without sufficient evidence to select one of the two.
 |
Fig. 5 Family of (31) Euphrosyne projected on the proper (a, e) plane (top panel) and the proper (a, sinI) plane (bottom panel). The g − g6 resonance isdescribed in two ways, with green points for individual asteroids with their synthetic proper frequencies g such that |g − g6| < 2 arcsec y−1, and with contour lines of the synthetic theory of proper frequencies with values (−2, 0, +2) arcsec y−1. Red points are family members, black are background objects found in the family box, and blue crosses indicate chaotic orbits. The parent body (31) is marked by the cyan crosses. |
 |
Fig. 6 Digitally filtered time series from the output of a numerical experiment for 100 Myr, with initial conditions equal to those of (31) but for osculating a = 3.165 au, and a Yarkovsky model such that the secular drift should be da/dt = −2 × 10−4 au/Myr.Top panel: filtered semimajor axis (au). Bottom panel: filtered eccentricity, showing much larger oscillations after the entry into the secular resonance g − g6 at about + 50 Myr. |
 |
Fig. 7 Top panel: V-shape for the family of (31) Euphrosyne, considered as a single family, showing the negative V-base. Bottom panel: one possible decomposition of the family 31, showing an additional V-shape with two different slopes: this implies a model with three separate collisions. |
4.2 Family of (480) Hansa and of (163) Erigone
Family 480 is affected by the secular resonance 2g − g5 − g6 + s − s6, with very different effects on the IN and OUT sides.
The increased dispersion of proper e for the portion of the family with a < a0, where a0 is the proper a of the parent body, shown in Fig. 8 (bottom) and in the line 480− of Table 2 can be explained by Fig. 8 (top) because most of the intersection between the secular resonance and the family is for a < a0. Moreover, the members in the IN side are moving towards lower values of a due to the Yarkovsky effect, and therefore many members currently outside of the secular resonance zone must have passed through it in the past: in Fig. 8 (top) these are the points marked in red but on the left of the strip of blue crosses. We note that the family members moving towards lower proper a are the ones originally ejected to an orbit with a < a0, as suggestedby the positive V-base of the V-shape; see Fig. 9.
Also in Fig. 8 we show the level curves 2g − g6 − g5 + s − s6 = (−0.5, 0, +0.5) in arcsec y−1, computed by means of our new synthetic theory for the secular frequencies g, s. In the (a, sinI) plane of Fig. 8 (top) the resonance strip is well defined: although we have computed it only for the mean value of proper e in the family, which is 0.342, the asteroids strongly affected by this resonance are all either within or very near the strip. On the contrary, in the plane (a, e) of Fig. 8 (bottom) the resonance strip moves very much as the third coordinate, proper sin I, changes in the family range, which is 0.364 < sinI < 0.385: we are showing the two resonant strips for the minimum and maximum of sin I, demonstrating that the resonance sweeps the entire range in proper a and e. This can explain the spread of green points in Fig. 8 (bottom) indicating the members affected by the resonance, both in the IN and OUT portions of the family.
The scattering takes place during the time span in which the family members are crossing the resonant strip, pushed by Yarkovsky: the width of the libration strip is narrower than the resonance strip shown in the figure, but we have checked that there are indeed members of the family currently in libration. It does not matter how wide the actual libration strip is, the fact is that it is a barrier which must be crossed by the members drifting towards lower values of proper a. This affects the proper e much more than the proper sinI because of the D’Alembert rule, by which the perturbation term associated with the 2g − g5 − g6 + s − s6 contains a factor e2 sinIe5e6 sinI6. Of the quantities included in this factor, sinI is large and the others are small. Therefore, in the Hansa region the derivative with respect to sin I is much smaller than the derivative with respect to e. It follows from the analytical theory of secular perturbations that the changes in e due to this resonance, in this region, are much larger than the ones in sinI. This explains why in Table 2 the mean and standard deviation of δ sin I are much smaller than those of δe.
In addition to this, it is also necessary to take into account that some unusual asymmetry in the proper δe is caused by the fact that proper e cannot be negative, by definition. Indeed, a negative δe, starting from the value 0.0043 of (480), can lead to a negative e, which of course only means a positive proper e with a shift by π of the proper longitude of perihelion ϖ.
The family of (163) Erigone, which we have merged with the family (5026) of Martes, is affected by several mean motion three-body resonances, resulting in 394 out of 1023 members of the merged family, or 38.5%, with Lyapounov time Tlyap < 20 000 yr. Therefore, it is to be expected that the asymmetry is growing with time because of chaotic diffusion; this applies mostly to the OUT side of the family and can increase the spread of both δe and δ sin I; see Fig. 10. However, the asymmetry is larger in the IN side; and is larger in δ sin I, due to the fact that the parent body (163) has one of the lowest values of this proper element.
A larger dynamical effect can be due to the z2 = 2(g − g6) + s − s6 secular resonance, which is very relevant for this family as shown in Carruba et al. (2016). In Fig. 10 the members of the family with a small divisor |z1| = |2(g − g6) + s − s6| < 0.5 arcsec y−1 are marked in green. The analogy, but also the differences, with Fig. 8, are clear: a secular resonance crosses the family 163 as it is now, but only on the IN side. During the dynamical evolution of the family, the members with negative Yarkovsky drift in proper a have been pushed into the secular resonance, and even beyond it, with the result being an increase of the spread in both δe and δ sin I; the dominant asymmetry is in δsinI because of the position of (163).
 |
Fig. 8 Projection of the family of (480) Hansa on the proper (a, sinI) plane (top panel). Blue crosses indicate chaotic members: they are in the 11∕4 resonance with Jupiter. The green points indicate that the divisor 2g − g5 − g6 + s − s6 is smaller in absolute value than 0.5 arcsec y−1. The same family in the proper (a, e) plane (bottom panel). The level curves of the divisor are explained in the text. |
 |
Fig. 9 Family of (480) Hansa projected on the plane proper a vs. 1∕D, where the diameter D has been estimated from the absolute magnitude H and the mean family albedo. Note that the V-base is positive. |
 |
Fig. 10 Projection of the family of (163) Erigone on the proper (a, sinI) plane (top panel). Blue crosses indicate chaotic members. The green points indicate that the divisor z2 = 2(g − g6) + s − s6 is smaller in absolute value than 0.5 arcsec y−1. The same family in the proper (a, e) plane (bottom panel). |
4.3 Family of (179) Klytaemnestra
The family of (179) Klytaemnestra has for a long time been a problem in our family classification. Indeed we have not been able to identify a meaningful V-shape from which to compute its age; family 179 currently has 513 members, while we have computed ages for all other families in our classification with > 300 members9.
In addition, from Table 2 we find a strong asymmetry, especially in δe, which in the OUT side is almost five times the CEV from (179), too much to be accepted as a realistic initial velocity distribution. We therefore have a dynamical family, statistically very significant as density contrast in proper element space, for which we do not have a plausible collisional model. We have always emphasized that asteroid families are statistical entities, that is, their membership can never be completely and exactly identified. However, to explain the bizarre shape of family 179 it is not enough to remove a few interlopers; we need to consider decomposing the family into components for which it is possible to provide collisional and dynamical interpretations.
The first indication that this might be advisable comes from Fig. 11, showing that in the proper (sin I, e) plane this family appears as bimodal, with a larger (in number of members) component far from another, smaller component including the dominant body (179) Klytaemnestra. Although in Table 1 the family 179 appears with a fraction of fragments fv = 0.047, the global shapeof the family is incompatible with a cratering event on (179): how can fragments from a crater form a compact swarm of fragments at a distance in velocity space so much larger than the escape velocity? The best possible explanation is that this could be a typical failure of the HCM method, probably in the form of chaining at the stage of formation of the core family (indicated by red stars in Fig. 11), obtained using only proper elements of asteroids with absolute magnitude H < 14. Indeed, the fainter members (green points, H ≥ 14) attached to the core follow the elongated shape of the core family; we note that (5922) is a C-type interloper in an S-type family (marked with a black star; other attached C interlopers are marked with a black dot). This suggests that the dynamical family 179 should be decomposed in at least two collisional families, a smaller one containing (179) and the larger one with (9506) Telramund as the least populated.
Another element of the explanation we propose is the presence of the secular resonance z1 = g − g6 + s − s6 which crosses family 179 but also heavily affects the much larger family 221 (Vokrouhlický et al. 2006). By marking in Fig. 11 the family members with |z1| < 0.5 arcsec y−1, it is clear that they form a bridge connecting the cluster containing (179), with z1 < − 0.5 arcsec y−1, and the cluster containing (9506), with z1 > 0.5 arcsec y−1. If these resonant members belong neither to the collisional family including (9506), nor to the one including (179), then they are responsible for the chaining.
Using our new synthetic theory for the secular frequencies g, s, and also the values of the same frequencies, computed together with the proper elements, for the members of both families 221 and 179, we have produced Fig. 12 showing, in the (a, sinI) plane, a portion of the family of (221) Eos and the nearby family 179. We have also overlaid the level lines of z1 computed for two fixed values of proper e, corresponding to the minimum and the maximum of the values found in family 179 (namely 0.0514 and 0.0808, respectively).
The family of (221) Eos is, in our recently updated classification, the largest, with more than 16 000 members. It is clear that such a family needs to be surrounded by a halo, in which a good fraction of the asteroids belong to the family, although with a lower number density than in the recognized family; see Brož & Morbidelli (2013); Tsirvoulis et al. (2018). The asteroids in the halo have “escaped” from the family through different dynamical routes, mostly driven by the Yarkovsky effect. In particular, if a secular resonance is effective in a layer in proper element space which has a large width in proper a, a Yarkovsky driven transport is possible10. Indeed, Carruba et al. (2014a) show the results of a large-scale numerical experiment on transport due to the Yarkovsky effect inside and near secular resonances, and in particular the z1 resonance; see their Fig. 9, in the top-left corner, which refers to a portion of the Eos family more or less corresponding to the one shown in Fig. 12. The size of the transport in proper e and sin I shown by these experiments is sufficient to explain the contamination of the dynamical family 179 with resonant escapers from Eos.
If we assume that resonant members of 221 can be transported along the resonance, as driven by the negative da∕dt due to the Yarkovsky effect (as shown by the cyan cross (221) Eos itself is at a larger value of proper a), then the transport is towards lower values of proper sinI. In this way escapers from 221 may enter the region of the dynamical 179 family, and contribute to the chaining effect joining the two separate clusters. An alternative route is possible (see Fig. 12) by moving to lower proper a until crossing the three-body resonance at proper a ≃ 2.985, then along the mean motion resonance to lower values of proper sinI, before exiting from it inside the secular resonance and ending up in the region of family 179.
As suggested by the arguments above, we propose that family 179 should be split into three parts: a small cluster around (179) with z1 < −0.5, the resonant interlopers (|z1| < 0.5 arcsec y−1), and a family currently with 321 members, (9506) Telramund, with z1 > +0.5 arcsec y−111. The smaller cluster around (179) is too small (65 members) to be interpreted, but could be a cratering family distinct from both 221 and 9506.
The reality of family 9506 can be confirmed by computing a V-shape in the plane with coordinates proper a and 1∕D, where the diameter D has been computed from absolute magnitude H assuming an average albedo (which is 0.25 after removing the interlopers with albedos of < 0.1): this is shown in Fig. 13. The fit gives an inverse slope for the IN side of − 0.073 ± 0.020, and + 0.082 ± 0.018 for the OUT side, that is, they are compatible and the family has just one age, which is around 220 Myr (see Table B.2). Also this age is compatible with the YORP age (Paolicchi et al. 2018). Figure 13 also shows that this family is a complete fragmentation; the two largest members, (9506) and (18993), are of about the same size, and near the center of the proper a distribution, as determined by the V-shape. As shown in Fig. 11, the position of these two largest members is peripheral in the proper sinI and e distribution, but this asymmetry cannot be interpreted by the same methods used for cratering families.
 |
Fig. 11 Dynamical family 179 projected on the proper (sinI, e) plane. The cyan cross indicates the position of the largest member, (179) Klytaemnestra. Most of the family members, more than 300, appear to belong to a clump centered too far from (179) for a physically possible distribution of ejection velocities. Red stars are core family members (with absolute magnitude H < 14, green points are fainter members attached to the core. The members with |z1 | < 0.5 arcsec y−1 are marked by blue circles for core members and blue crosses for attached ones. |
 |
Fig. 12 Projection of the dynamical family of (179) Klytaemnestra, and of part of the family of (221) Eos, on the proper (a, sin I) plane. The members of Eos are in green, in blue if they are within 0.5 arcsec y−1 from the z1 = g − g6 + s − s6 = 0 secular resonance. The ones of Klytaemnestra are red points if not in the resonance, red crosses overlaid by blue points if they have |z1 | < 0.5 arcsec y−1. The dynamical family 179 is split in two parts by the resonance, which also affects 221. |
 |
Fig. 13 Proposed family of (9506) Telramund, in the (a, 1∕D) plane; the C-type interlopers are marked with a red circle, the outliers rejected from the fit are marked with a blue circle. The two sides of the V-shape have compatible slopes. |
5 Conclusions
5.1 Definition and identification of cratering families
We have proposed to use the fraction fv of the total volume of an asteroid family consisting of fragments (excluding the largest member) as a metric to discriminate the cratering from the fragmentation families. We have tested the 66 families in our classification which currently have more than 100 members and found a bimodal distribution: 21 families with fv < 1∕8 and 37 with fv > 1∕2. In the middle there are only 8 families, 4 with 1∕8 < fv < 0.22 and 4 with 0.27 < fv < 0.40. Therefore, we selected the value fv = 1∕4 as a boundary: if fv > 1∕4 we say that the family is the results of a fragmentation event (41 found) and if fv < 1∕4 we define a family as the result of a cratering event (25 found). We additionally use, for the few marginal cases, the terms heavy cratering for 1∕8 < fv < 1∕4 and marginal fragmentation for 1∕4 < fv < 1∕2. We do not claim that the specific boundary values we have chosen have a deep geophysical meaning, but simply that they are appropriate to describe the distribution empirically found for the quantity fv.
Although the boundary value of more than 100 members has been chosen arbitrarily, just as a round number, it appears that indeed 100 members are enough to discriminate cratering. We have even identified some smaller families as being of cratering type. For example, the family of (2) Pallas with only 62 members, and even some cratering families for which we do not have a complete list of members, such as (91) Aegina, (429) Diotima, and (179) Klytaemnestra, because of overlap with other families.
An important result is that all these families appear compositionally homogeneous, in that the number of interlopers (identified by physical observations, mostly WISE albedos) is small, with an exception being family 5, for which the presence of another family of asteroids with incompatible composition had already been proposed in Milani et al. (2017). Nevertheless, we have discarded two namesake asteroids as interlopers: (110) Lydia and (194) Prokne, and correspondingly adopted the new namesakes (363) Padua and (686) Gersuind. This is not a surprise, because the size distribution of the background needs to be more shallow than that of the family. Indeed, the position inside the resonance of families with Padua and Gersuind as namesake have already been proposed in Carruba (2009) and in Gil-Hutton (2006); Carruba (2010); Novaković et al. (2011), respectively; moreover, that (110) Lydia undergoes high amplitude libration inside the z1 resonance has already been shown by Milani & Knežević (1992).
5.2 No problem with asymmetry for most cratering families
We then analyzed the scatter of the proper elements in the (e, sinI) plane with respect to the parent body to check whether it is compatible with a realistic model of the relative velocities of the fragments, immediately after ejection from the gravitational sphere of influence of the parent body.
In a way, the most important result shown by the summary Table 2 is that, in most cases, there is nothing remarkable in the four values of the mean and standard deviation for both δe and δ sin I. Indeed, in 15 out of 25 cratering families (with more than 100 members) there appears to be no problem, that is, the first two moments of the distributions of both proper e and sin I are of the order of the CEV. This certainly occurs for families 3, 5, 10, 686, 302, 396, 606, 363, 1303, 1547, 87, 148, 778.
The following five families have asymmetries explained by the presence (either known or at least proposed) of two collisional families: 4, 15, 283, 20, 569. For three families we believe the number of members is currently too low to draw reliable conclusions: 1222, 96, 410.
5.3 Difficult cases, only partially explained
This left us with only 4 families out of 25 for which we had to look for an explanation for an anomalous asymmetry: 31, 179, 480, and 163. In these 4 cases the asymmetry is too large to be attributed to the initial escape velocity of the fragments from a cratering event. For all these we have found at least a plausible cause for the anomalous asymmetries.
For the family (31) Euphrosyne we have a dynamical explanation, based on the negative V-shape and the consequent Yarkovsky evolution which leads to a past crossing of the g − g6 secular resonance with either increasing or decreasing proper a. This model, together with the suggestions from some numerical-propagation experiments, proposes that a large fraction of the original fragments has been ejected from the family, mostly on hyperbolic orbits. An alternative model assumes that the original collisional family, which has an age of >1 Gyr old, has been deeply eroded (see Milani et al. 2017) by the same dynamical mechanism as in the other, above model, but the central part of the family has been replenished by a number of more recent collisions; probably two of them, one for each side with respect to the g − g6 resonance. We do not have enough information to decide which of these two models represents the true history of family 31, and therefore it is not even clear if the main cause is collisional rather than dynamical.
For thefamily of (480) Hansa we have identified the secular resonance 2g − g5 − g6 + s − s6, combined with the effects of the Yarkovsky secular perturbation, as the main cause of the scattering of the proper e to values significantly higher than those of (31) itself. Some contribution to the asymmetry parameters for δe could also be due to the fact that proper e is greater than 0 by definition. In this case the explanation is fully dynamical. For the family of (163) Erigone we also find a dynamical explanation for the current family shape, that is, due to the consequences of both a secular resonance and several mean-motion resonances.
For the family of (179) Klytaemnestra, which had been rated as a problem for its unexplained shape in our previous papers (Spoto et al. 2015; Milani et al. 2016, 2017), we have found an explanation by decomposing the dynamical family, as assembled by our multistage HCM procedure, into three pieces, each of a different origin. We propose that one component is composed by escapers from the extra large family of (221) Eos, transported also by means of the z1 = g − g6 + s − s6 = 0; the second is a small cratering family from (179), and the third (with most members) a fragmentation family with namesake (9506) Telramund. This model has been confirmed by finding a good age estimate, using our V-shape method, for family 9506. In this case the explanation requires both dynamics and a different collisional model, with two collisions.
All these three solutions of the problem of a realistic collisional model need to be confirmed by additional work, both by dynamical studies and using new and improved data. We confirm that the existence of a realistic collisional model for every single dynamical family cannot be taken for granted. Indeed, in one case we now think it does not exist, and the dynamical family 179 needs to be reinterpreted with a completely different collisional model, and with a largely different membership with respect to the one suggested by the HCM method.
The fact that this was found necessary in only 1 out of 25 cratering families, with 2 more dubious cases of families with ≤120 members, indicates that the HCM method is not bad at all, but nonetheless must not be taken as a ground truth. In Milani et al. (2017; Sect. 5) we already indicated a few fragmentation families for which to obtain a consistent collisional and dynamical explanation we need to split dynamical families into three, four, or even more components. In another case, family 163, we had already proposed to merge two dynamical families into one collisional family, and this choice has been supported by the asymmetry data.
We believe that this paper has shown that the dynamical families, obtained by an automated HCM procedure in the space of proper elements, can provide information not only on the existence of either one or more “true” collisional families in them, but also first-order information on the original distribution of ejection velocities of the fragments, in the case of cratering events. If there are some cases in which there are problems, we can identify them, and find reasonable dynamical explanations in most cases. In a few cases, the outcome of the HCM procedure needs to be modified, and this can also be done in a rational way.
5.4 Possible future work
The best way to improve on the understanding of cratering families is to obtain more data, in particular more members for the families currently in the range between 100 and 200 members, and more physical data to perform a much better identification of interlopers. Dynamical studies need to be conducted, in particular on the problem of Yarkovsky transport along secular resonances, which obviously depends upon the orientation in the proper element space of the resonance surface.
For fragmentation families, asymmetry parameters might have to be defined and used in a different way.
Acknowledgments
We thank the referee (V. Carruba) for useful suggestions, in particular in solving the problems with the two difficult cases of families 163 and 179. ZK acknowledges support from the Serbian Academy of Sciences and Arts via project F187, and from the Ministry of Education, Science and Technological Development of Serbia through the project 176011. PP acknowledges funding by the University of Pisa and INFN/TASP.
Appendix A Effects of spin-velocity correlation
The overall properties of ejecta from cratering impacts have been widely analyzed in the literature. Most relevant results have been summarized and discussed in Housen & Holsapple (2011). The general features of a cratering process can be represented in Fig. A.1. In this latter quoted publication it is also shown that several results from the experiments can be framed within the general scaling equations. For the present task, the most relevant equation correlates the velocity of the ejecta (v) with the distance (x) from the impact point:
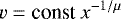 (A.1)
(A.1)
where μ depends on the properties of the colliding bodies, but is often μ ≃ 0.4, therefore v ≃const x−2.5.
 |
Fig. A.1 General features of ejecta from a cratering impact. |
Unfortunately, in the literature there is no explicit analysis of the rotational properties of the ejecta from a cratering event. The rotational properties of ejecta created in a catastrophic impact have been widely discussed in the literature (Fujiwara et al. 1989; Giblin et al. 1994; Holsapple et al. 2002). In Fujiwara & Tsukamoto (1981) also the properties of the spin vector have been discussed, showing that the direction of rotation is correlated with the place of ejection, as shown in the figure.
This experimental evidence, confirmed also by Giblin et al. (1994) was included in the so-called semi-empirical model (Paolicchi et al. 1989, 1996). In this model the fragmentation and ejection of fragments are driven by a velocity field v(x). The rotation of fragments due to the fragmentation process, apart from a term connected to the shape, is proportional to the rotor ∇ ×v. The dependence of both translational and rotational properties of ejecta on the residual stress in targets has been discussed by Kadono et al. (2009).
Although the generalization of these ideas to cratering processes is not based on any experimental evidence, there are several similarities concerning the ejecta properties, and it is reasonable to assume that they hold also for cratering. According to this assumption, the v(x) relation given above implies also that the fragments from a crater should rotate in such a way that the side of the body nearest to the impact point rotates away from it, that is clockwise on the right of the figure and counterclockwise on the left Milani et al. (2014; Sect. 5.2). In Fig. A.1 this property is indicated by the labels “expected to rotate clockwise/counterclockwise".
If so, also when a family is formed as the outcome of a cratering event, the Yarkovsky drift may be, depending on the impact geometry, either parallel or antiparallel to the original Δa, due to the ejection velocity, as proposed in Milani et al. (2014) where Fig. 8 actually refers to a fragmentation family.
A consequence of this effect is the possibility of explaining at least some negative V-bases. If the fragments ejected at larger a have a retrograde rotation, their a, initially larger, decreases with time due to Yarkovsky effect. Therefore, original δa and Yarkovsky da/dt have a different sign, and the wings appear to cross at 1∕D > 0 (negative V-base). The family of (31) Euphrosyne discussed in Sect. 4 exhibits this feature; see Fig. 7 (top). Moreover, (31) is located near the outer edge of the most populated portion of the main belt, implying that a projectile coming from inside (sunward direction) is more likely; this would result in a negative correlation of the original δa due to the relative velocity of the fragments and the da/dt from Yarkovsky.
Appendix B Age estimation for cratering families
This section contains all the ages we have been able to compute for cratering-type families identified in this paper. Most of these ages have originally been published in the papers by Spoto et al. (2015); Milani et al. (2016, 2017); however, in these papers some of these families were considered as fragmentations, but now we have found them to be of cratering type, according to our definition. Moreover, some families had a different namesake (because we have recognized the previous namesake as an interloper).
Two new ages have been computed in this paper, namely for the family of (87) Sylvia and (9506) Telramund; however, 9506 is not a cratering family, as a result of the decomposition of the family 179. Therefore in Tables B.1 and B.2 we list the age data of 9506 below a line at the bottom, together with the age for family 15124 which has been shown to be a fragmentation, although it was discovered as a subfamily of a cratering-type family. The V-shape for family 87 is shown in Fig. B.1: we note that the IN side of the V-shape is missing, probably because of the effect of the strong 11∕6 mean motion resonance with Jupiterat 3.472 au. The gap in the middle of the remaining OUT side is due to the resonance 9∕5 with Jupiter at 3.515 au, therefore it is not due to the YORP effect. An age of 1220 ± 40 Myr has been estimated in Carruba et al. (2015); the nominal value is well consistent with our estimate, while we are rather skeptical about their claim for such a low uncertainty, because they might not include the calibration uncertainty. On the contrary, wegive a separate estimate for this error term, which is the dominant one. In a Monte Carlo simulation of the family formation, the calibration uncertainty is hidden in the choices made to include the Yarkovsky effect in the numerical integrations.
Slopes of the V-shape for the cratering families.
Age estimation for the cratering families.
The V-shape for the new family of (9506) Telramund was already shown in Fig. 13.
One of the age estimates merits additional comments to what has already been written in the previous papers. In Spoto et al. (2015) we mentioned that the very young age estimated for the family of (1547) Nele, as obtained from the V-shape, could be overestimated because of the contribution of the initial velocity field to the inverse slope. Recently, Carruba et al. (2018b) provided an estimate of the age for the same family at about 7 Myr, calculated using a method based on the past clustering of the secular arguments ϖ and Ω, which is not significantly affected by the initial velocity spread. This implies that of the 14 Myr age estimated from the V-shape about half is due to the contribution from the original velocity spread. This result is remarkable, because it allows, by scaling (linearly with the diameter of the parent body), to estimate the order of magnitude of this contribution for other families. As an example, for the family of (31) Euphrosyne the age estimated from the main V-shape (Fig. 7), about 1400 ± 300 Myr, is affected by a contribution from the initial velocity spread of ~100 Myr, which is lessthan the uncertainty of the age estimate, implying that it is not strictly necessary to include this contribution. We note that it can be both positive and negative (see Sect. 4), and this may contribute to explain why the method used in Carruba et al. (2014b) estimates a lower age than for family 31 than our method does here: their family evolution simulation assumes an isotropic velocity field, implying that the contribution to the inverse slope (and to the age) from the initial velocity spread is positive.
Table B.1 contains the data on the fits of V-shapes in the (a, 1∕D) plane: family number/name, number of members, side, slope (S), inverse slope (1∕S), STD of 1∕S, ratio OUT/IN of 1∕S, and STD of the ratio.
Table B.2 gives the age estimation for the cratering families: family number and name, da∕dt, age estimation, uncertainty of the age due to the fit, uncertainty of the age due to the calibration, and total uncertainty of the age estimation.
Tables 3 and 4 do not contain the data on the new supposed subfamilies of family 31, because the necessary family split has not been identified unambiguously. However, in the graphic summary of all the ages of cratering families, Fig. B.2, we have also indicated the two additional ages which could be found in family 31, to show that there would be nothing strange in assuming that a parent body as large as (31) Euphrosyne could have been affected by multiple craterings, spaced several hundreds of millions of years apart.
 |
Fig. B.2 Ages of cratering families; colored bars are for families with two ages (red: OUT side, blue: IN. Note that family 31 could have three ages. |
 |
Fig. B.1 Family of (87) Sylvia on the proper a, 1∕D plane, showing a one-sided V-shape, with the gaps due to resonances: (5914) is an outlier. |
References
- Brouwer, D. 1951, AJ, 56, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Brož, M., & Morbidelli, A. 2013, Icarus, 223, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V. 2009, MNRAS, 395, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V. 2010, MNRAS, 408, 580 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carruba, V., & Michtchenko, T. A. 2009, A&A, 493, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carruba, V., & Morbidelli, A. 2011, MNRAS, 412, 2040 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Domingos, R. C., Huaman, M. E., Santos, C. R. d., & Souami, D. 2014a, MNRAS, 437, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Aljbaae, S., & Souami, D. 2014b, ApJ, 792, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Nesvorný, D., Aljbaae, S., & Huaman, M. E. 2015, MNRAS, 451, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Aljbaae, S., & Winter, O. C. 2016, MNRAS, 455, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Vokrouhlický, D., & Novaković, B. 2018a, Planet. Space Sci., 157, 72 [CrossRef] [Google Scholar]
- Carruba, V., Vokrouhlický, D., Nesvorný, D., & Aljbaae, S. 2018b, MNRAS, 477, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, A., & Tsukamoto, A. 1981, Icarus, 48, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, A., Cerroni, P., Davis, D. R., et al. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews, 240 [Google Scholar]
- Giblin, I., Martelli, G., Smith, P. N., et al. 1994, Icarus, 110, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Hutton, R. 2006, Icarus, 183, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, K. 1918, AJ, 31, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Holsapple, K., Giblin, I., Housen, K., Nakamura, A., & Ryan, E. 2002, in Asteroid Impacts: Laboratory Experiments and Scaling Laws, eds. W. F. Bottke, Jr., Cellino, A. Cellino, P. Paolicchi, & R. P. Binzel (Arizona: Arizona University Press), 443 [Google Scholar]
- Housen, K. R., & Holsapple, K. A. 2011, Icarus, 211, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Kadono, T., Arakawa, M., Ito, T., & Ohtsuki, K. 2009, Icarus, 200, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Knežević, Z., & Milani, A. 2000, Celest. Mech. Dyn. Astron., 78, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Knežević, Z., & Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knežević, Z., Milani, A., Cellino, A., et al. 2014, in Complex Planetary Systems, Proceedings of the International Astronomical Union, IAU Symp., 310, 130 [NASA ADS] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Bauer, J. M., et al. 2013, ApJ, 770, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Carruba, V., Mainzer, A., Bauer, J. M., & Nugent, C. 2015, ApJ, 809, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A. 1993, Celest. Mech. Dyn. Astron., 57, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., & Knežević Z. 1992, Icarus, 98, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Cellino, A., Knežević, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Spoto, F., Knežević, Z., Novaković, B., & Tsirvoulis, G. 2016, in Asteroids: New Observations, New Models, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, IAU Symp., 318, 28 [NASA ADS] [Google Scholar]
- Milani, A., Knežević, Z., Spoto, F., et al. 2017, Icarus, 288, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Brož, M., & Carruba, V. 2015, in Identification and Dynamical Properties of Asteroid Families, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Arizona: Arizona University Press), 297 [Google Scholar]
- Novaković, B. 2010, MNRAS, 407, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Novaković, B., Cellino, A., & Knežević Z. 2011, Icarus, 216, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Paolicchi, P., & Knežević Z. 2016, Icarus, 274, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Paolicchi, P., Cellino, A., Farinella, P., & Zappala, V. 1989, Icarus, 77, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Paolicchi, P., Verlicchi, A., & Cellino, A. 1996, Icarus, 121, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Paolicchi, P., Spoto, F., Knežević, Z., & Milani, A. 2018, MNRAS, submitted [Google Scholar]
- Radović, V., Novaković, B., Carruba, V., & Marčeta D. 2017, MNRAS, 470, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Spoto, F., Milani, A., & Knežević Z. 2015, Icarus, 257, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F., Noah, P. V., Noah, M., & Price, S. D. 2002, AJ, 123, 1056 [Google Scholar]
- Tsirvoulis, G., Morbidelli, A., Delbo, M., & Tsiganis, K. 2018, Icarus, 304, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Brož Morbidelli, A., et al. 2006, Icarus, 182, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalà, V., Cellino, A., Farinella, P., & Knežević, Z. 1990, AJ, 100, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalà, V., Bendjoya, P., Cellino, A., Farinella, P., & Froeschlé, C. 1995, Icarus, 116, 291 [NASA ADS] [CrossRef] [Google Scholar]
Available from AstDyS at http://hamilton.dm.unipi.it/astdys/index.php?pc=5
This is due to the observational selection typical of infrared instruments: there are many more low-albedo (<0.1) asteroids with WISE data than high albedo (>0.2) ones; the ones with albedo >0.1 are as many as those with <0.1, but this is due to a significant contribution from intermediate albedo between 0.1 and 0.2.
The g − g6 resonance contains an island of relative stability, due to anti-aligned libration, similarly to what was reported for the Tina family (Carruba & Morbidelli 2011). However, this island has a small volume in proper element space, and therefore such a relative stability affects only a few members, and does not change the overall picture of a dominant strong instability.
In the Russian roulette, as defined in 1840 by the Russian writer M. Lermontov, one of the chambers is loaded, the other five are empty: the game of pulling the trigger with the gun pointed to one’s head is very dangerous. In the Swiss version, introduced in 1937 by the Swiss writer G. Surdez, five of the six chambers are loaded, and the game is very likely to be fatal.
Nesvorný et al. (2015) propose a Telramund family in their Table 2, but leave the doubt that (179) might belong to it. We believe we have solved this problem.
All Tables
All Figures
 |
Fig. 1 Family of (283) Emma projected on the proper (a, sinI) plane. Red points represent family members, black points are background objects and blue crosses are objects in mean motion resonances. Position of (283) is marked by a large cyan cross. The two separate jets indicate a double collision origin. |
| In the text | |
 |
Fig. 2 Top panel: family of (569) Misa is separated into a family 569 with 70 members (crosses encircled in red) and a family 15124 with 577 members (blue crosses; stars are also in mean motion resonances). Bottom panel: distribution of the family 15124 in the proper (sinI, e) plane, showing the central position of (569) (cyan cross) and the peripheral location of (15124), not necessarily representative of the position of the parent body. |
| In the text | |
 |
Fig. 3 Family of (31) Euphrosyne projected on the proper (a, e) plane; the big blue dot shows the position of the parent body (31) Euphrosyne. The red line is the running mean of the values of proper e vs. proper a, for the members of the family, showing the substantial jump to lower values in the IN side of the family. |
| In the text | |
 |
Fig. 4 Family of (20) Massalia projected on the proper (e, sinI) plane, showing a halo in the lower right quadrant (with respect to the position of the parent body, marked by the cyan cross). Points are marked as in Fig. 1. |
| In the text | |
 |
Fig. 5 Family of (31) Euphrosyne projected on the proper (a, e) plane (top panel) and the proper (a, sinI) plane (bottom panel). The g − g6 resonance isdescribed in two ways, with green points for individual asteroids with their synthetic proper frequencies g such that |g − g6| < 2 arcsec y−1, and with contour lines of the synthetic theory of proper frequencies with values (−2, 0, +2) arcsec y−1. Red points are family members, black are background objects found in the family box, and blue crosses indicate chaotic orbits. The parent body (31) is marked by the cyan crosses. |
| In the text | |
 |
Fig. 6 Digitally filtered time series from the output of a numerical experiment for 100 Myr, with initial conditions equal to those of (31) but for osculating a = 3.165 au, and a Yarkovsky model such that the secular drift should be da/dt = −2 × 10−4 au/Myr.Top panel: filtered semimajor axis (au). Bottom panel: filtered eccentricity, showing much larger oscillations after the entry into the secular resonance g − g6 at about + 50 Myr. |
| In the text | |
 |
Fig. 7 Top panel: V-shape for the family of (31) Euphrosyne, considered as a single family, showing the negative V-base. Bottom panel: one possible decomposition of the family 31, showing an additional V-shape with two different slopes: this implies a model with three separate collisions. |
| In the text | |
 |
Fig. 8 Projection of the family of (480) Hansa on the proper (a, sinI) plane (top panel). Blue crosses indicate chaotic members: they are in the 11∕4 resonance with Jupiter. The green points indicate that the divisor 2g − g5 − g6 + s − s6 is smaller in absolute value than 0.5 arcsec y−1. The same family in the proper (a, e) plane (bottom panel). The level curves of the divisor are explained in the text. |
| In the text | |
 |
Fig. 9 Family of (480) Hansa projected on the plane proper a vs. 1∕D, where the diameter D has been estimated from the absolute magnitude H and the mean family albedo. Note that the V-base is positive. |
| In the text | |
 |
Fig. 10 Projection of the family of (163) Erigone on the proper (a, sinI) plane (top panel). Blue crosses indicate chaotic members. The green points indicate that the divisor z2 = 2(g − g6) + s − s6 is smaller in absolute value than 0.5 arcsec y−1. The same family in the proper (a, e) plane (bottom panel). |
| In the text | |
 |
Fig. 11 Dynamical family 179 projected on the proper (sinI, e) plane. The cyan cross indicates the position of the largest member, (179) Klytaemnestra. Most of the family members, more than 300, appear to belong to a clump centered too far from (179) for a physically possible distribution of ejection velocities. Red stars are core family members (with absolute magnitude H < 14, green points are fainter members attached to the core. The members with |z1 | < 0.5 arcsec y−1 are marked by blue circles for core members and blue crosses for attached ones. |
| In the text | |
 |
Fig. 12 Projection of the dynamical family of (179) Klytaemnestra, and of part of the family of (221) Eos, on the proper (a, sin I) plane. The members of Eos are in green, in blue if they are within 0.5 arcsec y−1 from the z1 = g − g6 + s − s6 = 0 secular resonance. The ones of Klytaemnestra are red points if not in the resonance, red crosses overlaid by blue points if they have |z1 | < 0.5 arcsec y−1. The dynamical family 179 is split in two parts by the resonance, which also affects 221. |
| In the text | |
 |
Fig. 13 Proposed family of (9506) Telramund, in the (a, 1∕D) plane; the C-type interlopers are marked with a red circle, the outliers rejected from the fit are marked with a blue circle. The two sides of the V-shape have compatible slopes. |
| In the text | |
 |
Fig. A.1 General features of ejecta from a cratering impact. |
| In the text | |
 |
Fig. B.2 Ages of cratering families; colored bars are for families with two ages (red: OUT side, blue: IN. Note that family 31 could have three ages. |
| In the text | |
 |
Fig. B.1 Family of (87) Sylvia on the proper a, 1∕D plane, showing a one-sided V-shape, with the gaps due to resonances: (5914) is an outlier. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


